Electromechanical Coupling Dynamic and Vibration Control of Robotic Grinding System for Thin-Walled Workpiece
Abstract
:1. Introduction
2. Dynamic Model of the Coupling System
3. Dynamic Characteristics of the Coupling System
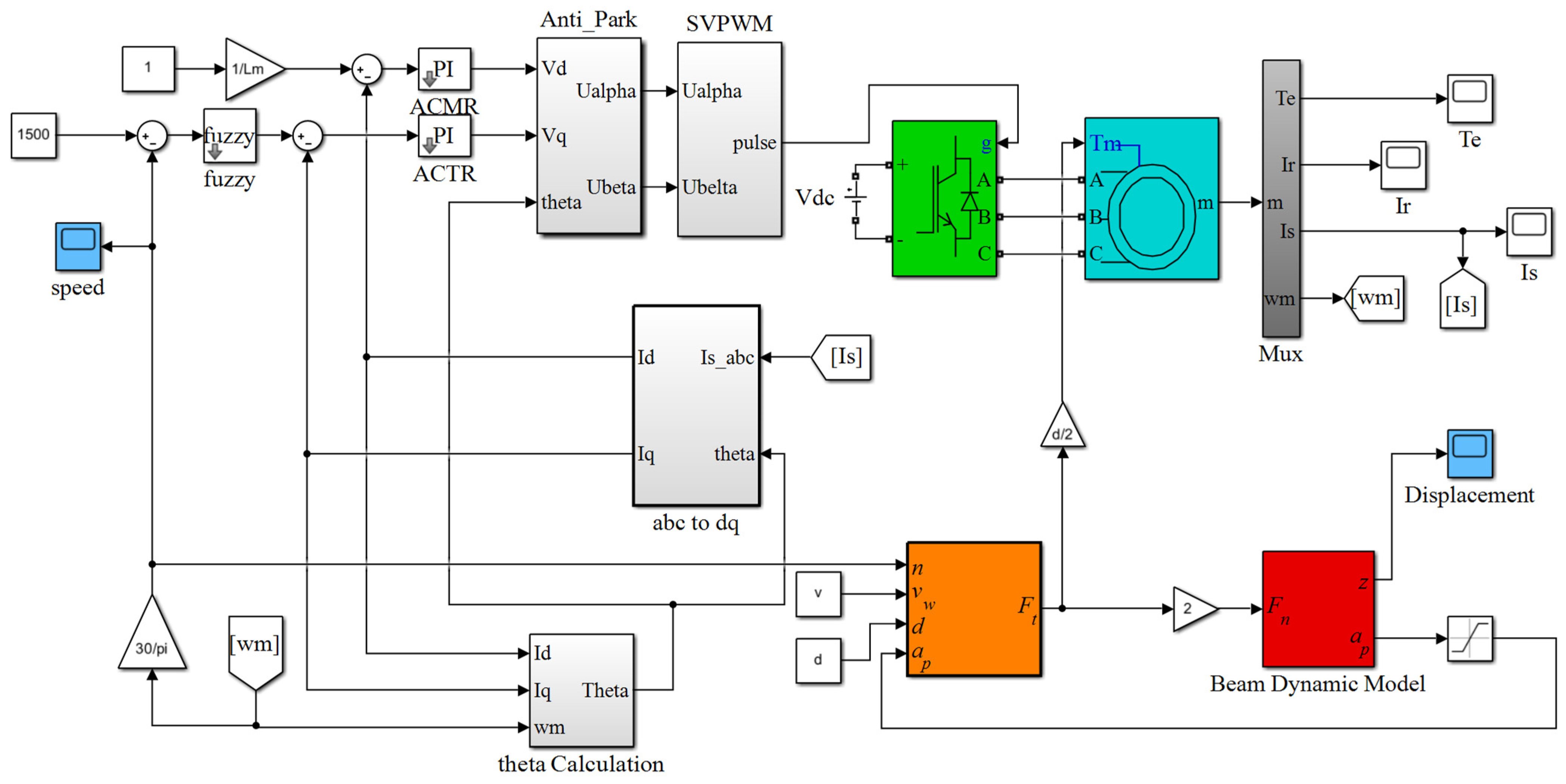
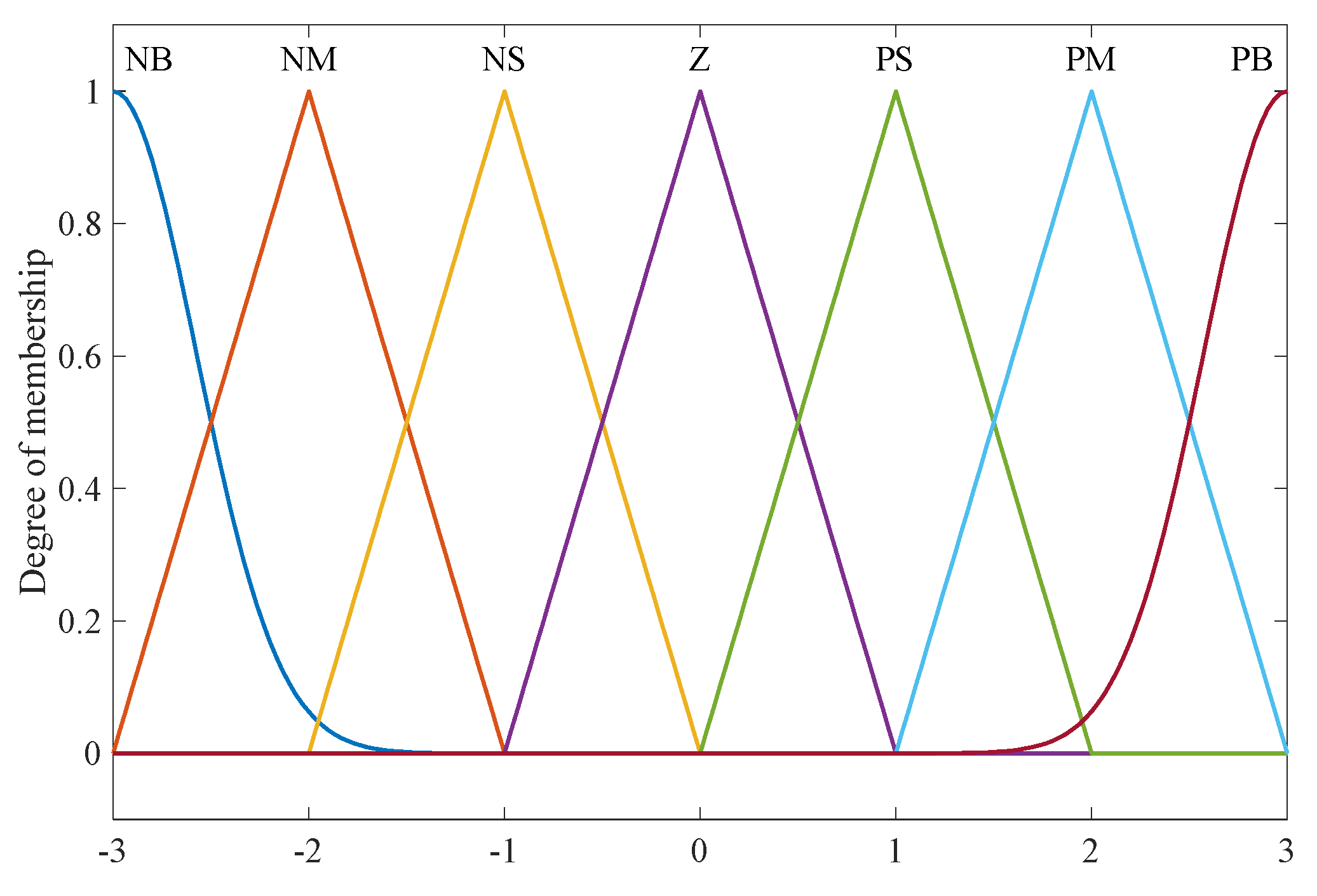
4. Speed Adaptive Control of Grinding Spindle
5. Conclusions
- (1)
- the thin-walled workpiece has obvious vibration in the grinding process and exhibits dynamic time-varying characteristics for moving grinding loads that vary with the grinding point, which directly cause fluctuations of the grinding depth and grinding force and affect the dynamic response characteristics of the grinding spindle;
- (2)
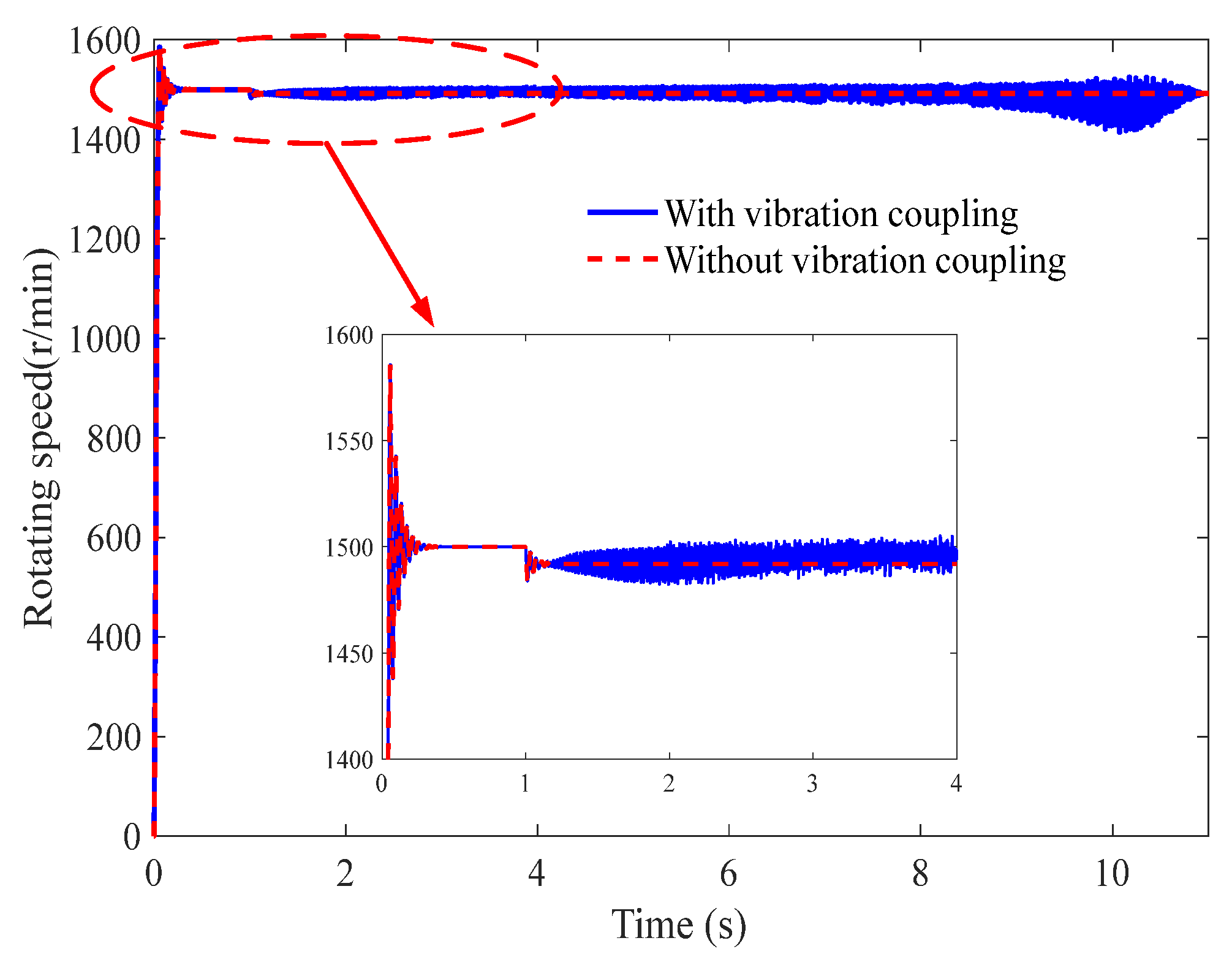
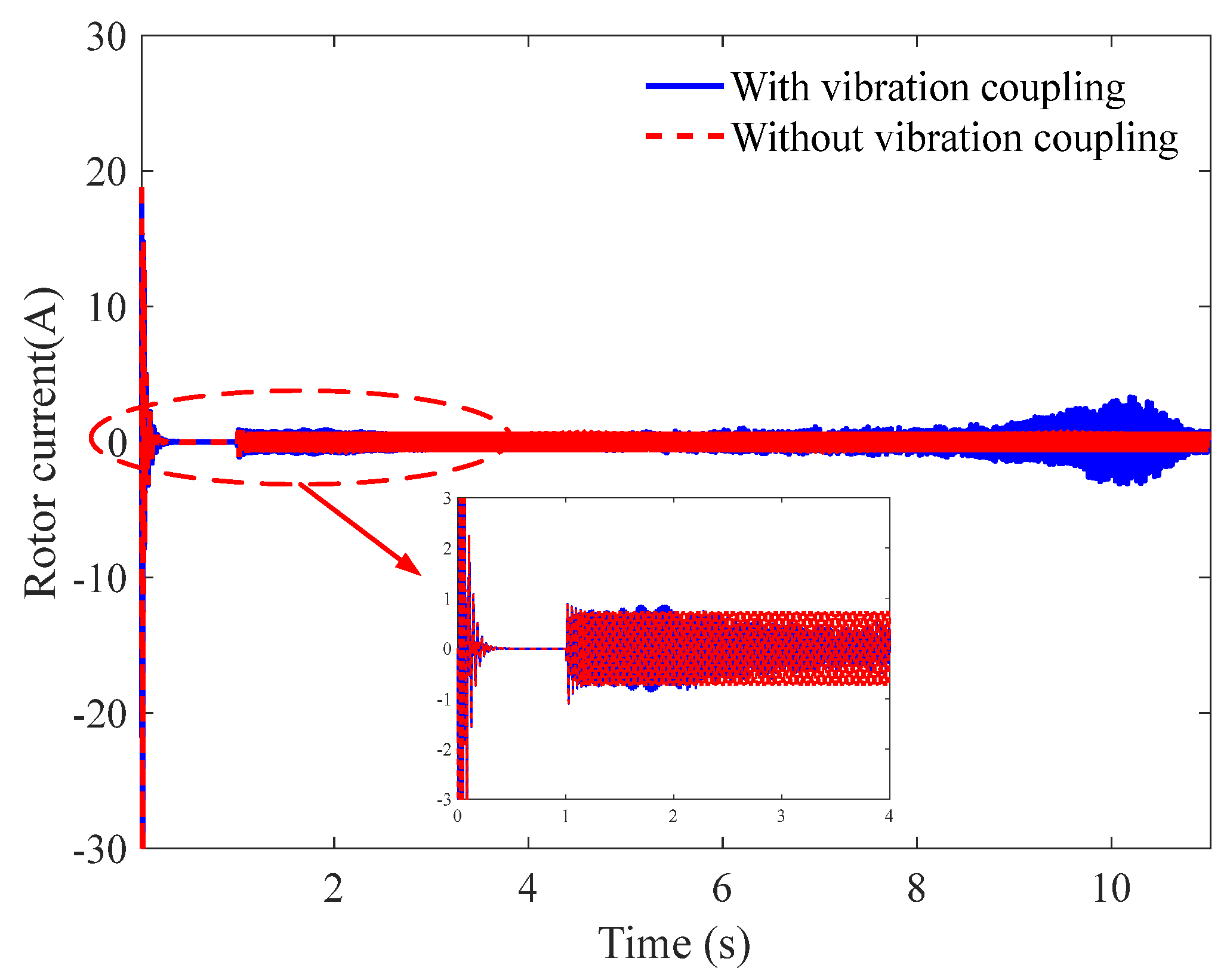
- the electromechanical coupling dynamic response characteristics of the grinding spindle with the vibration coupling of thin-walled workpiece are obviously different from the ideal constant load condition, ignoring the vibration coupling of thin-walled workpiece, specifically the vibration coupling that obviously enhances the response fluctuations of the output speed, electromagnetic torque and rotor current; thus, ignoring the vibration coupling effect of the thin-walled workpiece causes certain errors for the dynamic analysis and subsequent control;
- (3)
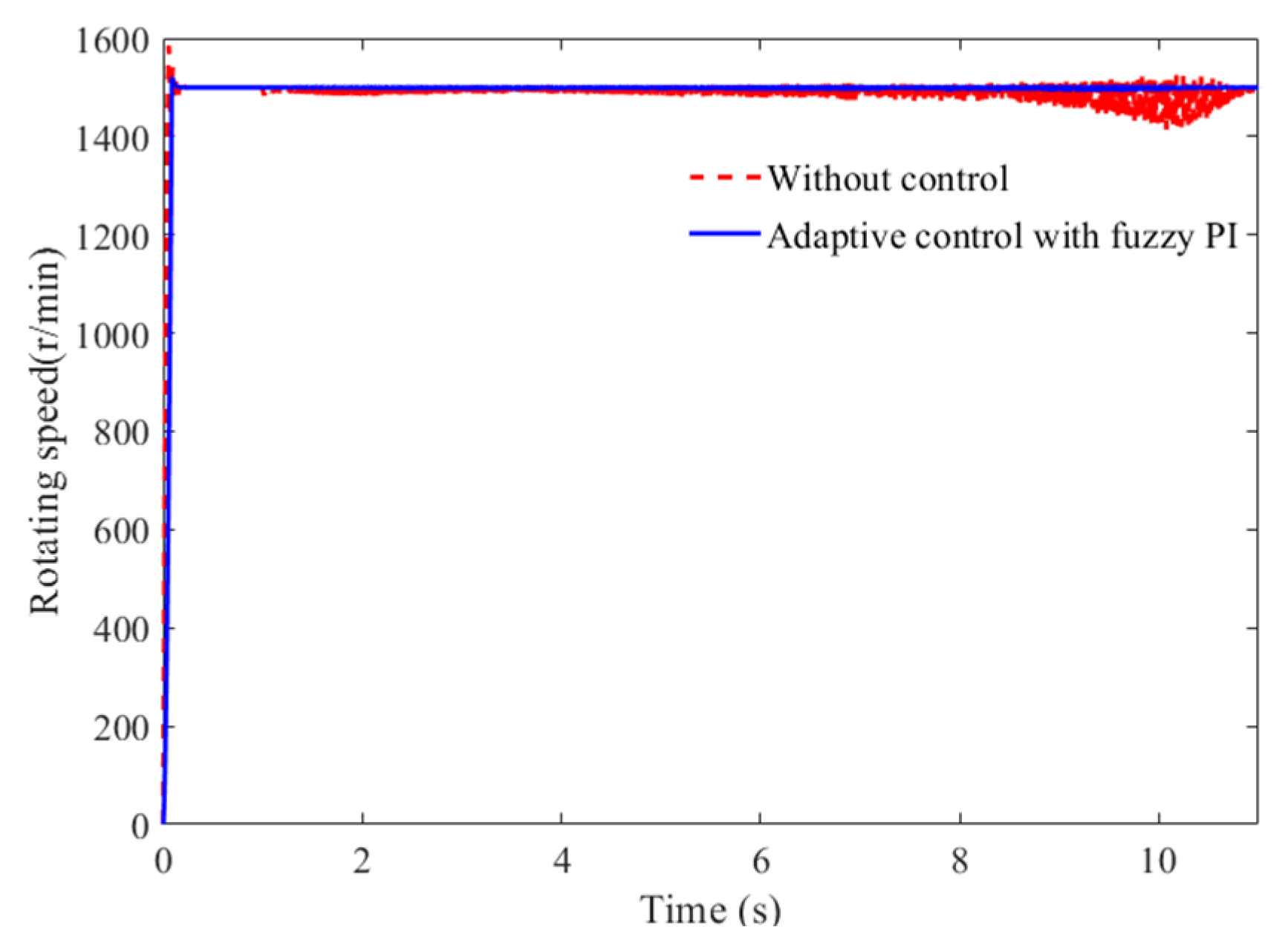
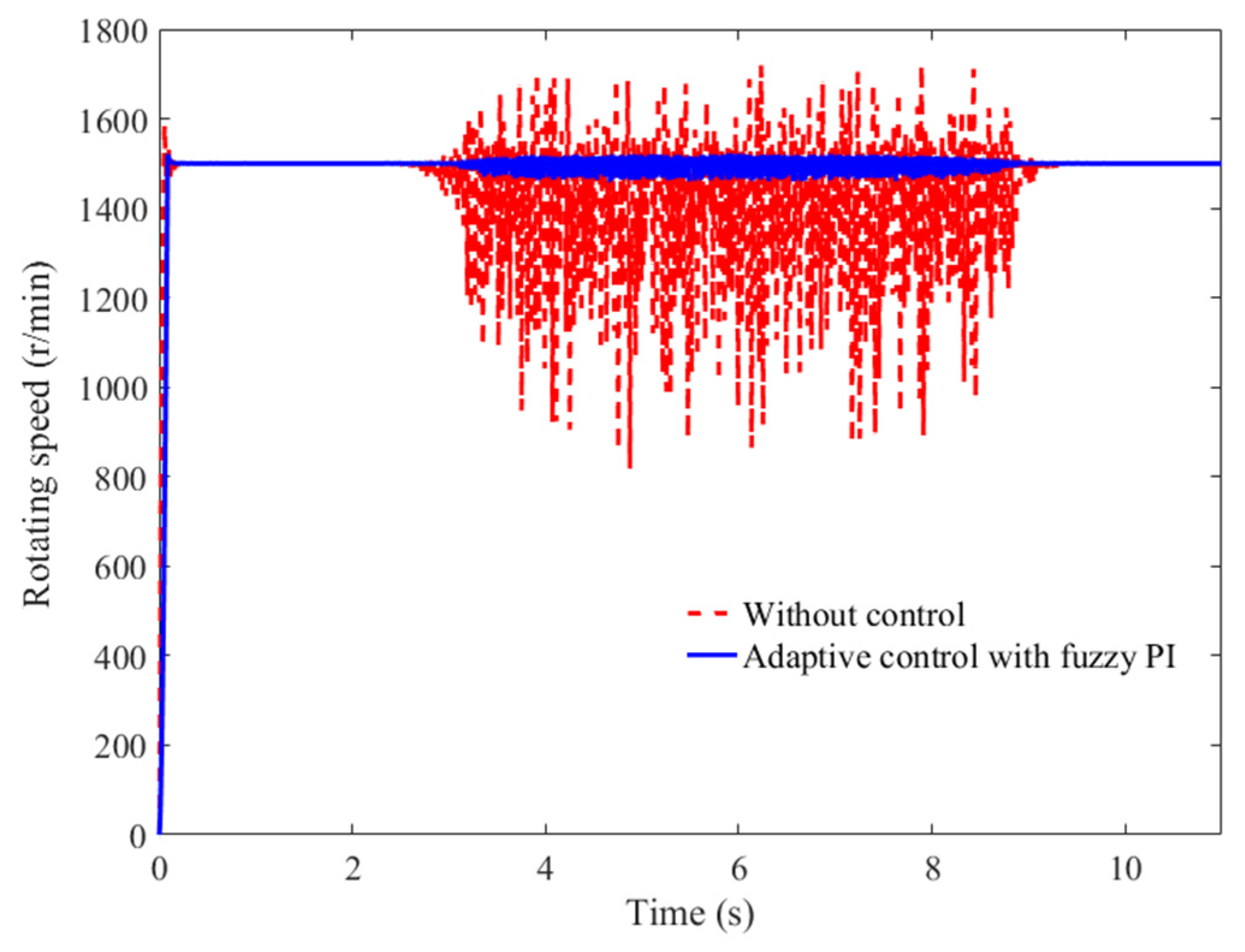
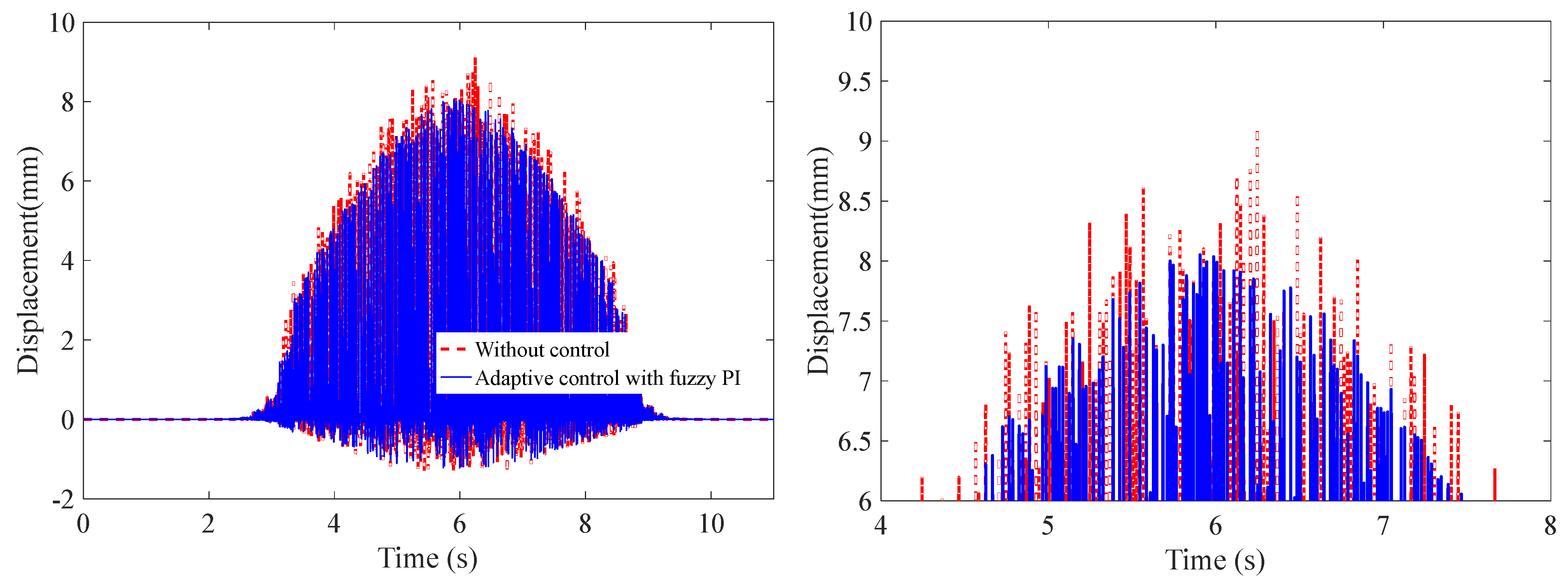
- the proposed speed adaptive control of the grinding spindle based on the fuzzy PI controller can realize the stability of the grinding spindle speed under vibration coupling and has a certain suppression effect on the elastic vibration of the thin-walled workpiece, with a reduction in vibration amplitude of about 38.5%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rodriguez, A.; López De Lacalle, L.N.; Pereira, O.; Fernandez, A.; Ayesta, I. Isotropic finishing of austempered iron casting cylindrical parts by roller burnishing. Int. J. Adv. Manuf. Technol. 2020, 110, 753–761. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Ruiz, J.D.; Marin, F.; Martínez, S.; Lamikiz, A.; Urbikain, G.; Lacalle, L. Stiffening near-net-shape functional parts of Inconel 718 LPBF considering material anisotropy and subsequent machining issues. Mech. Syst. Signal Process. 2022, 168, 108675. [Google Scholar] [CrossRef]
- Jimenez, A.; Bidare, P.; Hassanin, H.; Tarlochan, F.; Dimov, S.; Essa, K. Powder-based laser hybrid additive manufacturing of metals: A review. Int. J. Adv. Manuf. Technol. 2021, 114, 63–96. [Google Scholar] [CrossRef]
- Duan, Q.Q.; Wang, B.; Zhang, P.; Yang, K.; Zhang, Z.F. Improvement of notch fatigue properties of ultra-high CM400 maraging steel through shot peening. J. Mater. Res. 2017, 32, 1–9. [Google Scholar]
- Rodriguez, A.; Calleja, A.; Lacalle, L.; Pereira, O.; Laye, J. Burnishing of fsw aluminum Al–Cu–Li components. Metals 2019, 9, 260. [Google Scholar] [CrossRef] [Green Version]
- Ukar, E.; Lamikiz, A.; Lacalle, L.; Pozo, D.D.; Arana, J.L. Laser polishing of tool steel with co2 laser and high-power diode laser. Int. J. Mach. Tools Manuf. 2010, 50, 115–125. [Google Scholar] [CrossRef]
- González, H.; Pereira, O.; Fernández-Valdivielso, A.; López de Lacalle, L.N.; Calleja, A. Comparison of flank super abrasive machining vs. flank milling on inconel® 718 surfaces. Materials 2018, 11, 1638. [Google Scholar] [CrossRef] [Green Version]
- Klocke, F.; Schmitt, R.; Zeis, M.; Heidemanns, L.; Kerkhoff, J.; Heinen, D.; Klink, A. Technological and economical assessment of alternative process chains for blisk manufacture. Procedia CIRP 2015, 35, 67–72. [Google Scholar] [CrossRef]
- González, H.; Calleja, A.; Pereira, O.; Ortega, N.; López de Lacalle, L.N.; Barton, M. Super abrasive machining of integral rotary components using grinding flank tools. Metals 2018, 8, 24. [Google Scholar] [CrossRef]
- Lu, Y.; Xu, X.; Wang, L. Smart manufacturing process and system automation: A critical review of the standards and envisioned scenarios. J. Manuf. Syst. 2020, 56, 312–325. [Google Scholar] [CrossRef]
- Rodriguez, A.; González, M.; Pereira, O.; de Lacalle, L.N.L.; Esparta, M. Edge finishing of large turbine casings using defined multi-edge and abrasive tools in automated cells. Int. J. Adv. Manuf. Technol. 2021, 1–11. [Google Scholar] [CrossRef]
- Mohammadi, Y.; Ahmadi, K. Chatter in grinding with robots with structural nonlinearity. Mech. Syst. Signal Process. 2022, 167, 108523. [Google Scholar] [CrossRef]
- Kim, S.H.; Nam, E.; Ha, T.I.; Hwang, S.H.; Lee, J.H.; Park, S.H.; Min, B.K. Robotic Machining: A Review of Recent Progress. Int. J. Precis. Eng. Manuf. 2019, 2, 1629–1642. [Google Scholar] [CrossRef]
- Corral, J.; Pinto, C.; Campa, F.J.; Altuzarra, O. Surface location error of a parallel robot for routing processes. Int. J. Adv. Manuf. Technol. 2013, 67, 1977–1986. [Google Scholar] [CrossRef]
- Aviles, R.; Albizuri, J.; Ukar, E.; Lamikiz, A.; Aviles, A. Influence of laser polishing in an inert atmosphere on the high cycle fatigue strength of aisi 1045 steel. Int. J. Fatigue 2014, 68, 67–79. [Google Scholar] [CrossRef]
- Rodríguez, A.; López De Lacalle, L.N.; Fernández, A.; Braun, S. Elimination of surface spiral pattern on brake discs. J. Zhejiang Univ. Sci. A 2014, 15, 53–60. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.J.; Dong, H.Y.; Ke, Y.L. Stiffness-oriented posture optimization in robotic machining applications. Robot. Comput.-Integr. Manuf. 2015, 35, 69–76. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, S.H.; Min, B.K. Posture optimization in robotic drilling using a deformation energy model. Robot. Comput.-Integr. Manuf. 2022, 78, 102395. [Google Scholar] [CrossRef]
- Chen, C.; Peng, F.; Yan, R.; Li, Y.; Wei, D.; Fan, Z.; Tang, X.; Zhu, Z. Stiffness performance index based posture and feed orientation optimization in robotic milling process. Robot. Comput.-Integr. Manuf. 2019, 55, 29–40. [Google Scholar] [CrossRef]
- Zargarbashi, S.; Khan, W.; Angeles, J. Posture optimization in robot-assisted machining operations. Mech. Mach. Theory 2012, 51, 74–86. [Google Scholar] [CrossRef]
- Hintze, W.; Wenserski, R.V.; Junghans, S.; Junghans, S.; Mller, C. Finish machining of Ti6Al4V SLM components under consideration of thin walls and support structure removal. Procedia Manuf. 2020, 48, 485–491. [Google Scholar] [CrossRef]
- Wan, M.; Dang, X.B.; Zhang, W.H.; Yang, Y. Chatter suppression in the grinding process of the weakly-rigid workpiece through a moving fixture. J. Mater. Process. Technol. 2022, 299, 117293. [Google Scholar] [CrossRef]
- Guo, Y.; Dong, H.; Wang, G.; Ke, Y. Vibration analysis and suppression in robotic boring process. Int. J. Mach. Tools Manuf. 2016, 101, 102–110. [Google Scholar] [CrossRef]
- Wang, G.; Dong, H.; Guo, Y.; Ke, Y. Chatter mechanism and stability analysis of robotic boring. Int. J. Adv. Manuf. Technol. 2017, 91, 411–421. [Google Scholar] [CrossRef]
- Corral, J.; Pinto, C.; Campa, F.J.; Altuzarra, O. Dynamic behavior verification of a lightweight machine for routing. Int. J. Adv. Manuf. Technol. 2016, 86, 1151–1163. [Google Scholar] [CrossRef]
- Cao, H.; Bing, L.; He, Z. Chatter stability of milling with speed-varying dynamics of spindles. Int. J. Mach. Tools Manuf. 2012, 52, 50–58. [Google Scholar] [CrossRef]
- Shi, J.; Jin, X.; Cao, H. Chatter stability analysis in micro-milling with aerostatic spindle considering speed effect. Mech. Syst. Signal Process. 2022, 169, 108620. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, X.; Liu, Y.; Cao, H.; Chen, X. Stiffness variation method for milling chatter suppression via piezoelectric stack actuators. Int. J. Mach. Tools Manuf. 2018, 124, 53–66. [Google Scholar] [CrossRef]
- Cen, L.; Melkote, S.N. CCT-based mode coupling chatter avoidance in robotic grinding. J. Manuf. Process. 2017, 29, 50–61. [Google Scholar] [CrossRef]
- Chen, C.; Peng, F.; Yan, R.; Fan, Z.; Li, Y.; Wei, D. Posture-dependent stability prediction of a grinding industrial robot based on inverse distance weighted method. Procedia Manuf. 2018, 17, 993–1000. [Google Scholar] [CrossRef]
- Nguyen, V.; Johnson, J.; Melkote, S. Active vibration suppression in robotic grinding using optimal control. Int. J. Mach. Tools Manuf. 2020, 152, 103541. [Google Scholar] [CrossRef]
- Yuan, L.; Sun, S.; Pan, Z.; Ding, D.; Gienke, O.; Li, W. Mode coupling chatter suppression for robotic machining using semi-active magnetorheological elastomers absorber. Mech. Syst. Signal Process. 2019, 117, 221–237. [Google Scholar] [CrossRef]
- Liu, D.; Luo, M.; Zhang, Z.; Hu, Y.; Zhang, D. Operational modal analysis based dynamic parameters identification in grinding of thin-walled workpiece. Mech. Syst. Signal Process. 2022, 167, 108469. [Google Scholar] [CrossRef]
- Wang, X.; Song, Q.; Liu, Z. Dynamic model and stability prediction of thin-walled component milling with multi-modes coupling effect. J. Mater. Process. Technol. 2020, 288, 116869. [Google Scholar] [CrossRef]
- Ma, J.; Li, Y.; Zhang, D.; Zhao, B.; Wang, G.; Pang, X. Dynamic response prediction model of thin-wall workpiece-fixture system with magnetorheological damping in milling. J. Manuf. Process. 2022, 74, 500–510. [Google Scholar] [CrossRef]
- Tian, W.; Ren, J.; Zhou, J.; Wang, D. Dynamic modal prediction and experimental study of thin-walled workpiece removal based on perturbation method. Int. J. Adv. Manuf. Technol. 2018, 94, 2099–2113. [Google Scholar] [CrossRef]
- Meng, J.; Chen, X.; He, Y. Electromechanical coupling Dynamic modeling of High speed motorized spindle’s motor-spindle subsystem. J. Mech. Eng. 2007, 43, 160–165. [Google Scholar] [CrossRef]
- Cao, H.; Holkup, T.; Altintas, Y. A comparative study on the dynamics of high speed spindles with respect to different preload mechanisms. Int. J. Adv. Manuf. Technol. 2011, 57, 871–883. [Google Scholar] [CrossRef]
- Zhang, S.J.; Yu, J.J.; To, S.; Xiong, Z.W. A theoretical and experimental study of spindle imbalance induced forced vibration and its effect on surface generation in diamond turning. Int. J. Mach. Tools Manuf. 2018, 133, 61–71. [Google Scholar] [CrossRef]
- Hou, Y.L.; Li, C.H.; Zhang, Q. Investigation of structural parameters of high speed grinder spindle system on dynamic performance. Int. J. Mater. Prod. Technol. 2012, 44, 92–114. [Google Scholar] [CrossRef]
- Xi, S.; Cao, H.; Chen, X. Dynamic modeling of spindle bearing system and vibration response investigation. Mech. Syst. Signal Process. 2019, 114, 486–511. [Google Scholar] [CrossRef]
- Jia, W.; Gao, F.; Li, Y.; Wu, W.W.; Li, Z.W. Nonlinear dynamic analysis and chaos prediction of grinding motorized spindle system. Shock. Vib. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Guo, M.; Jiang, X.; Ding, Z.; Wu, Z.P. A frequency domain dynamic response approach to optimize the dynamic performance of grinding machine spindles. Int. J. Adv. Manuf. Technol. 2018, 98, 2737–2745. [Google Scholar] [CrossRef]
- Karagiannis, D.; Clayton, G.; Nataraj, C. Boundary control of harmonic disturbances on flexible cantilever beams using piezoelectric patch actuators. J. Vib. Control 2016, 22, 3916–3929. [Google Scholar] [CrossRef]
- Qiu, Z.; Wang, T.; Zhang, X. Sliding mode predictive vibration control of a piezoelectric flexible plate. J. Intell. Mater. Syst. Struct. 2020, 32, 65–81. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Inman, D. Active vibration control of flexible cantilever plates using piezoelectric materials and artificial neural networks. J. Sound Vib. 2016, 363, 33–53. [Google Scholar] [CrossRef]
- Jiang, X.; Zhao, G.; Lu, W. Vibration suppression of complex thin-walled workpiece based on magnetorheological fixture. Int. J. Adv. Manuf. Technol. 2020, 106, 1043–1055. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, D.; Wu, B.; Luo, M.; Chen, B. Vibration suppression of thin-walled workpiece machining considering external damping properties based on magnetorheological fluids flexible fixture. Chin. J. Aeronaut. 2016, 29, 1074–1083. [Google Scholar] [CrossRef] [Green Version]
- Xiong, G.; Ding, Y.; Zhu, L. Stiffness-based pose optimization of an industrial robot for five-axis milling. Robot. Comput.-Integr. Manuf. 2019, 55, 19–28. [Google Scholar] [CrossRef]
- Janez, G.; Timi, K.; Karl, G.; Miran, B. Accuracy improvement of robotic machining based on robot’s structural properties. Int. J. Adv. Manuf. Technol. 2020, 108, 1309–1329. [Google Scholar] [CrossRef]
- Shen, N.; Guo, Z.; Li, J.; Tong, L.; Zhu, K. A practical method of improving hole position accuracy in the robotic drilling process. Int. J. Adv. Manuf. Technol. 2018, 96, 2973–2987. [Google Scholar] [CrossRef]
- Yin, C.; Zhou, Z. Concise and Quick Reference Manual of Machining Process; Chemical Industry Press: Beijing, China, 2017. [Google Scholar]
- Li, B.M.; Zhao, B.; Li, Q. Abrasives, Abrasive Tools and Grinding Techniques; Chemical Industry Press: Beijing, China, 2015. [Google Scholar]
- Wang, D.; Fan, H.; Xu, D.; Zhang, Y. Research on grinding force of ultrasonic vibration-assisted grinding of C/SiC composite materials. Appl. Sci. 2022, 12, 10352. [Google Scholar] [CrossRef]
- Zhang, D.K.; Li, C.; Jia, D.; Zhang, Y. Investigation into engineering ceramics grinding mechanism and the influential factors of the grinding force. Int. J. Control Autom. 2014, 7, 19–34. [Google Scholar] [CrossRef]
- Singiresu, S.R. Mechanical Vibration, 5th ed.; Pearson Education Inc.: New York, NY, USA, 2011. [Google Scholar]
- Wen, X.; Qiu, J.; Tao, J. Analytical Dynamics of Electromechanical Systems and Applications; Science Press: Beijing, China, 2007. [Google Scholar]





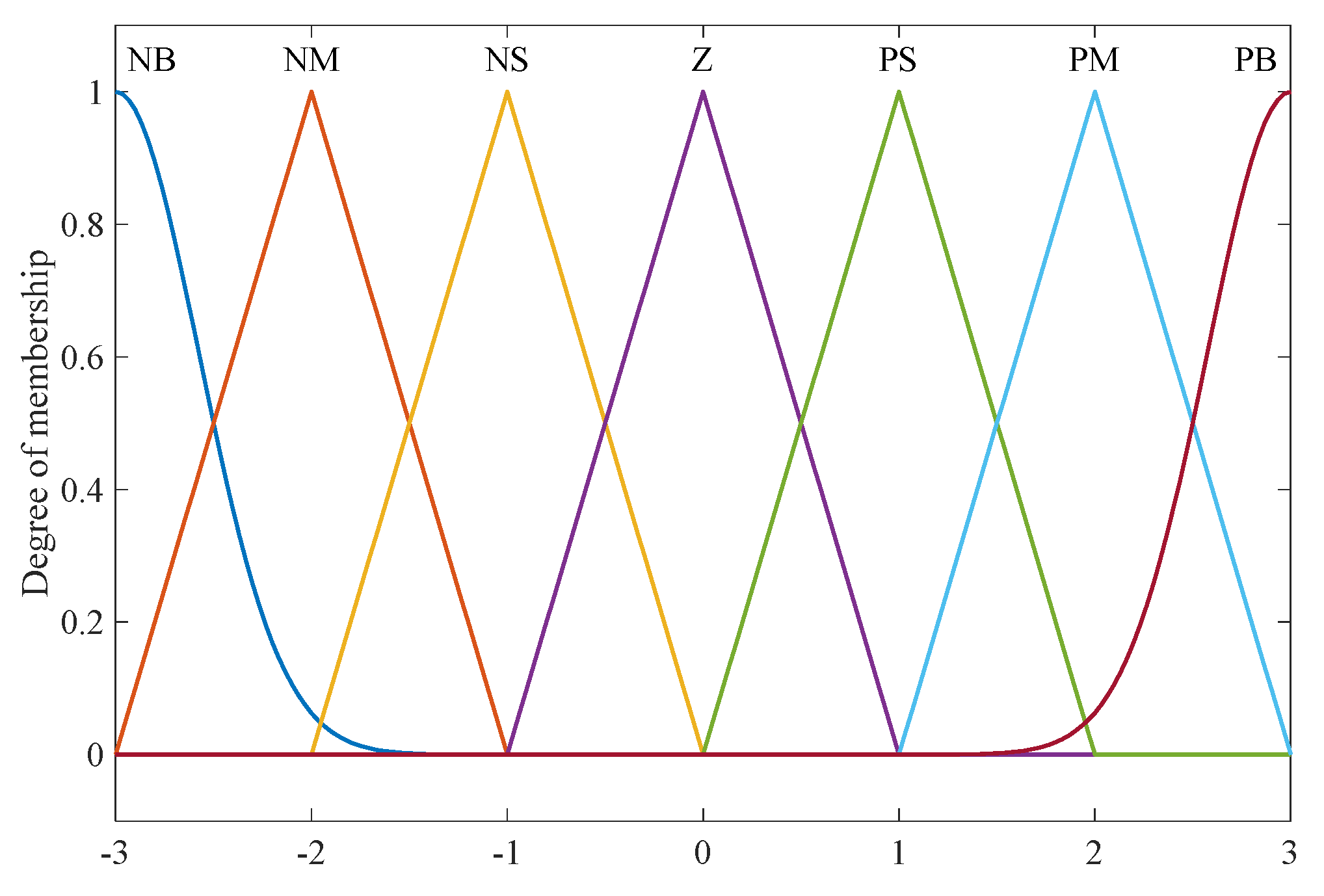
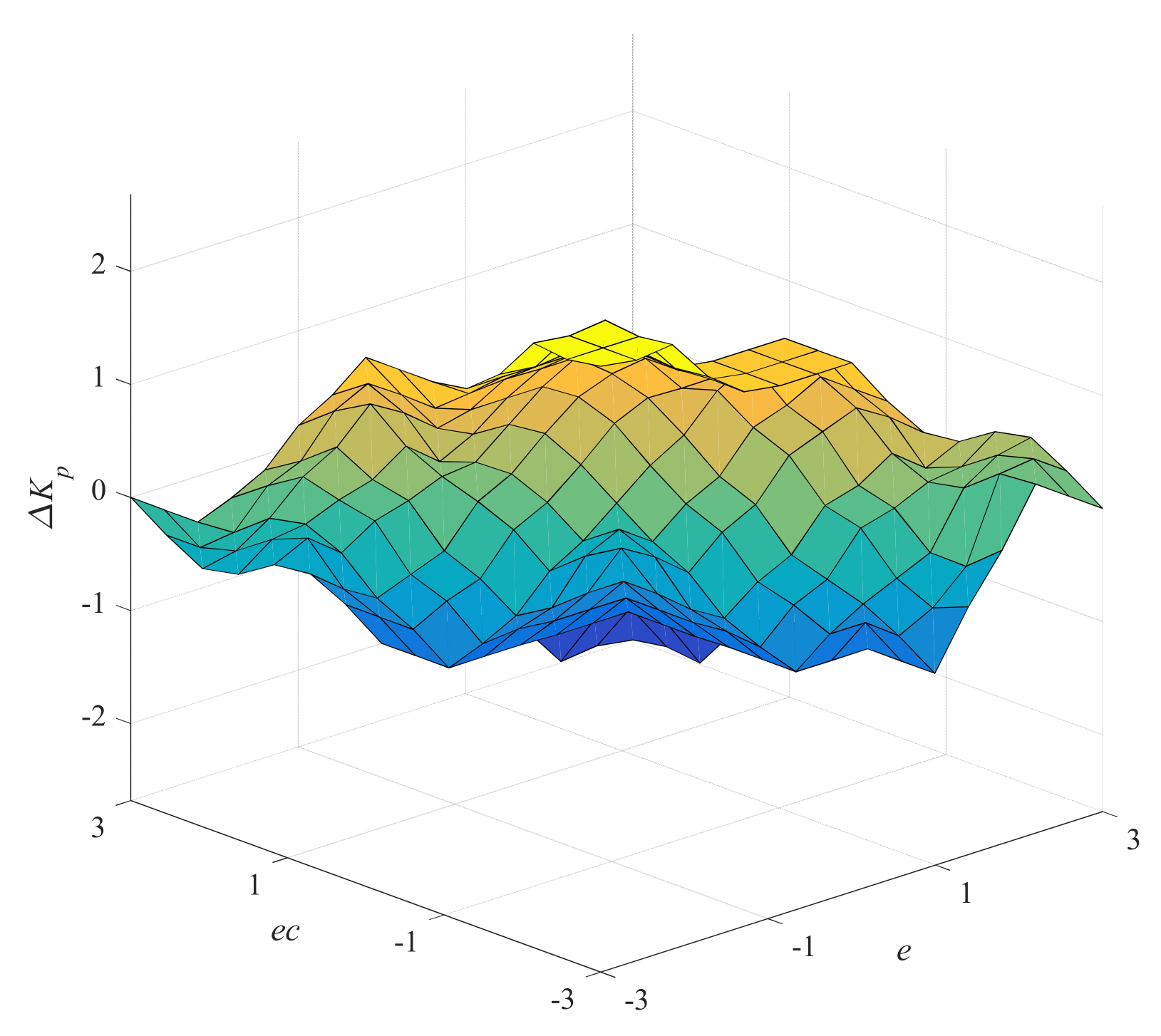
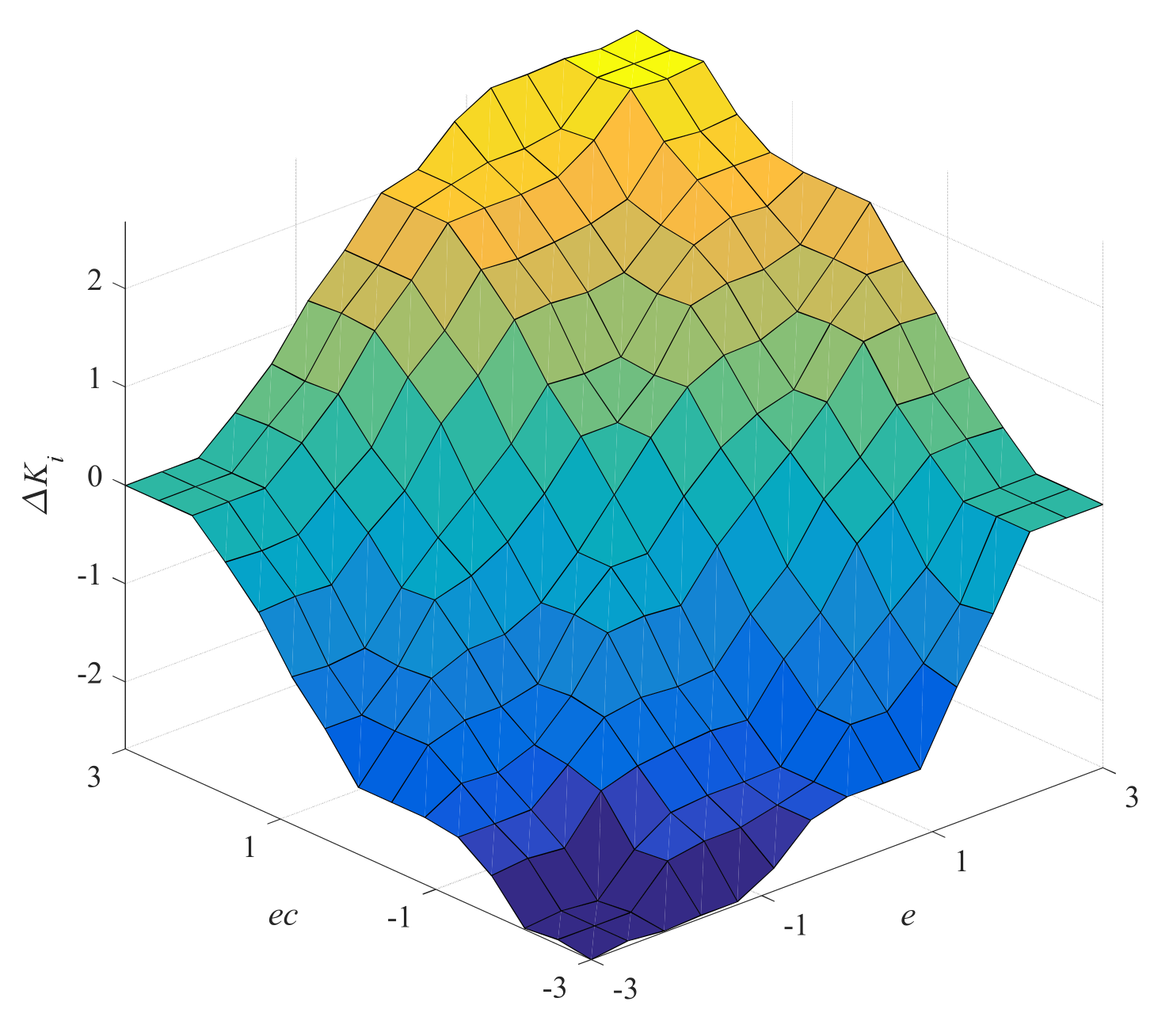


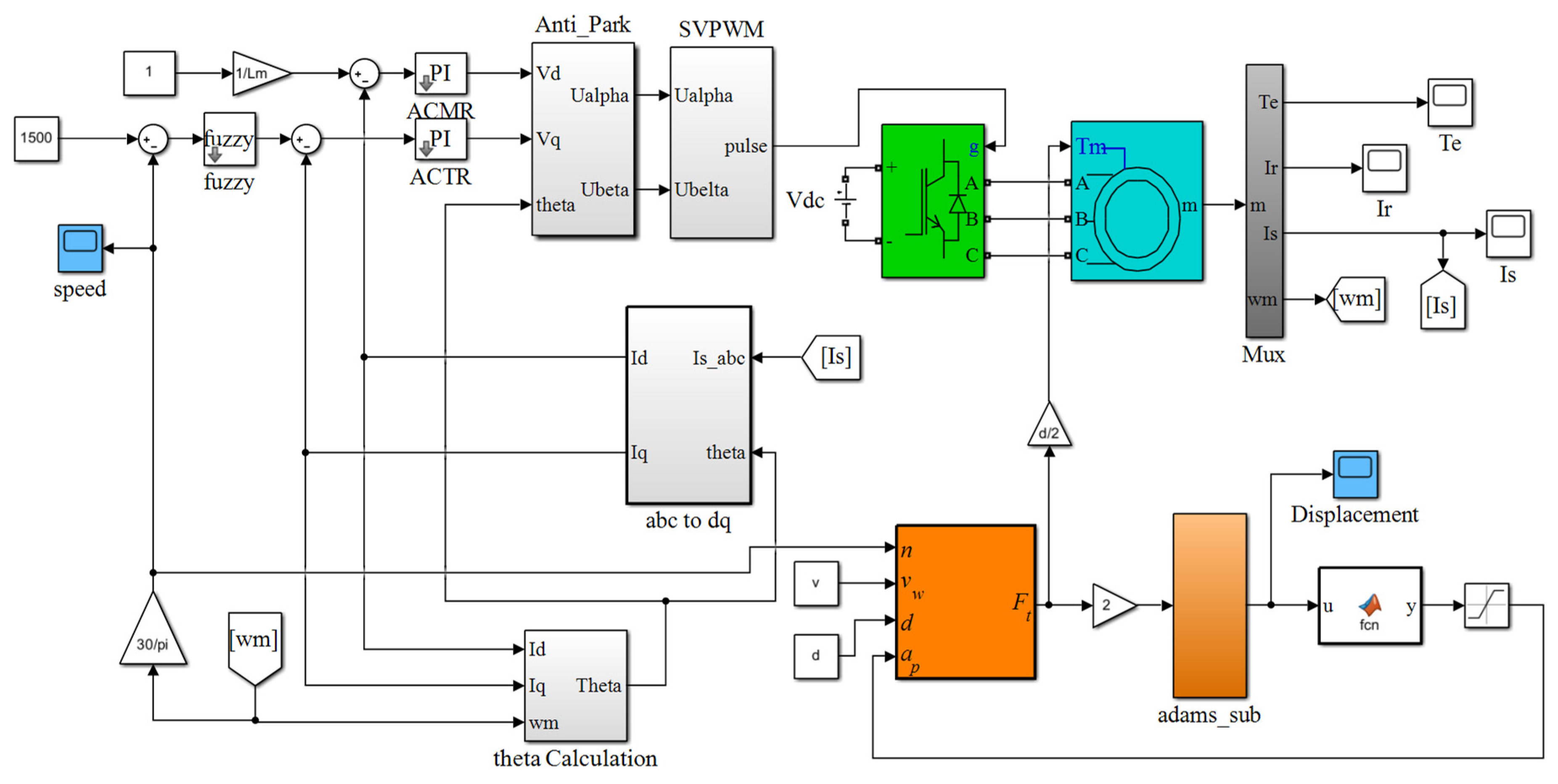
| Generalized Coordinates | Electromagnetic Subsystem | Mechanical Subsystem | |||||
|---|---|---|---|---|---|---|---|
| Stator | Rotor | ||||||
| j = 1 | j = 2 | j = 3 | j = 4 | j = 5 | j = 6 | j = 7 | |
| ξj | - | - | - | - | - | - | θ |
| iA | iB | iC | ia | ib | ic | ωs | |
| Qj | uA | uB | uC | ua | ub | uc | TL |
| Parameter | Value |
|---|---|
| Diameter of grinding wheel d | 0.35 m |
| Speed of grinding wheel n | 1500 r/min |
| Grinding depth ap0 | 0.05 mm |
| Feed speed vw | 0.05 m/s |
| Length of beam l | 0.5 m |
| Width of beam b | 0.02 m |
| Height of beam h | 0.002 m |
| Density of beam ρ | 7850 kg/m2 |
| Elastic modulus of beam E | 2.1 × 1011 Pa |
| Rated power PN | 3000 W |
| Rated voltage U | 380 V |
| Power Frequency f | 50 Hz |
| Resistance of stator winding Rs | 1.7980 Ω |
| Resistance of rotor winding Rr | 1.5880 Ω |
| Mutual inductance of the stator winding Lms | 0.2580 H |
| Moment of inertia J | 0.0067 Nm2 |
| Number of magnetic poles np | 2 |
| e | ec | ||||||
|---|---|---|---|---|---|---|---|
| NB | NM | NS | Z | PS | PM | PB | |
| NB | PB | PB | PM | PM | PS | Z | Z |
| NM | PB | PB | PM | PS | PS | Z | NS |
| NS | PM | PM | PM | PS | Z | NS | NS |
| Z | PM | PM | PS | Z | NS | NM | NM |
| PS | PS | PS | Z | NS | NS | NM | NM |
| PM | PS | Z | NS | NM | NM | NM | NB |
| PB | Z | Z | NM | NM | NM | NB | NB |
| e | ec | ||||||
|---|---|---|---|---|---|---|---|
| NB | NM | NS | Z | PS | PM | PB | |
| NB | NB | NB | NM | NM | NS | Z | Z |
| NM | NB | NB | NM | NS | NS | Z | Z |
| NS | NB | NM | NS | NS | Z | PS | PS |
| Z | NM | NM | NS | Z | PS | PM | PM |
| PS | NM | NS | Z | PS | PS | PM | PB |
| PM | Z | Z | PS | PS | PM | PB | PB |
| PB | Z | Z | PS | PM | PM | PB | PB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Tang, D.; Ju, J. Electromechanical Coupling Dynamic and Vibration Control of Robotic Grinding System for Thin-Walled Workpiece. Actuators 2023, 12, 37. https://doi.org/10.3390/act12010037
Liu Y, Tang D, Ju J. Electromechanical Coupling Dynamic and Vibration Control of Robotic Grinding System for Thin-Walled Workpiece. Actuators. 2023; 12(1):37. https://doi.org/10.3390/act12010037
Chicago/Turabian StyleLiu, Yufei, Dong Tang, and Jinyong Ju. 2023. "Electromechanical Coupling Dynamic and Vibration Control of Robotic Grinding System for Thin-Walled Workpiece" Actuators 12, no. 1: 37. https://doi.org/10.3390/act12010037
APA StyleLiu, Y., Tang, D., & Ju, J. (2023). Electromechanical Coupling Dynamic and Vibration Control of Robotic Grinding System for Thin-Walled Workpiece. Actuators, 12(1), 37. https://doi.org/10.3390/act12010037






