Extended State Observer-Based Sliding Mode Control Design of Two-DOF Lower Limb Exoskeleton
Abstract
:1. Introduction
- (I)
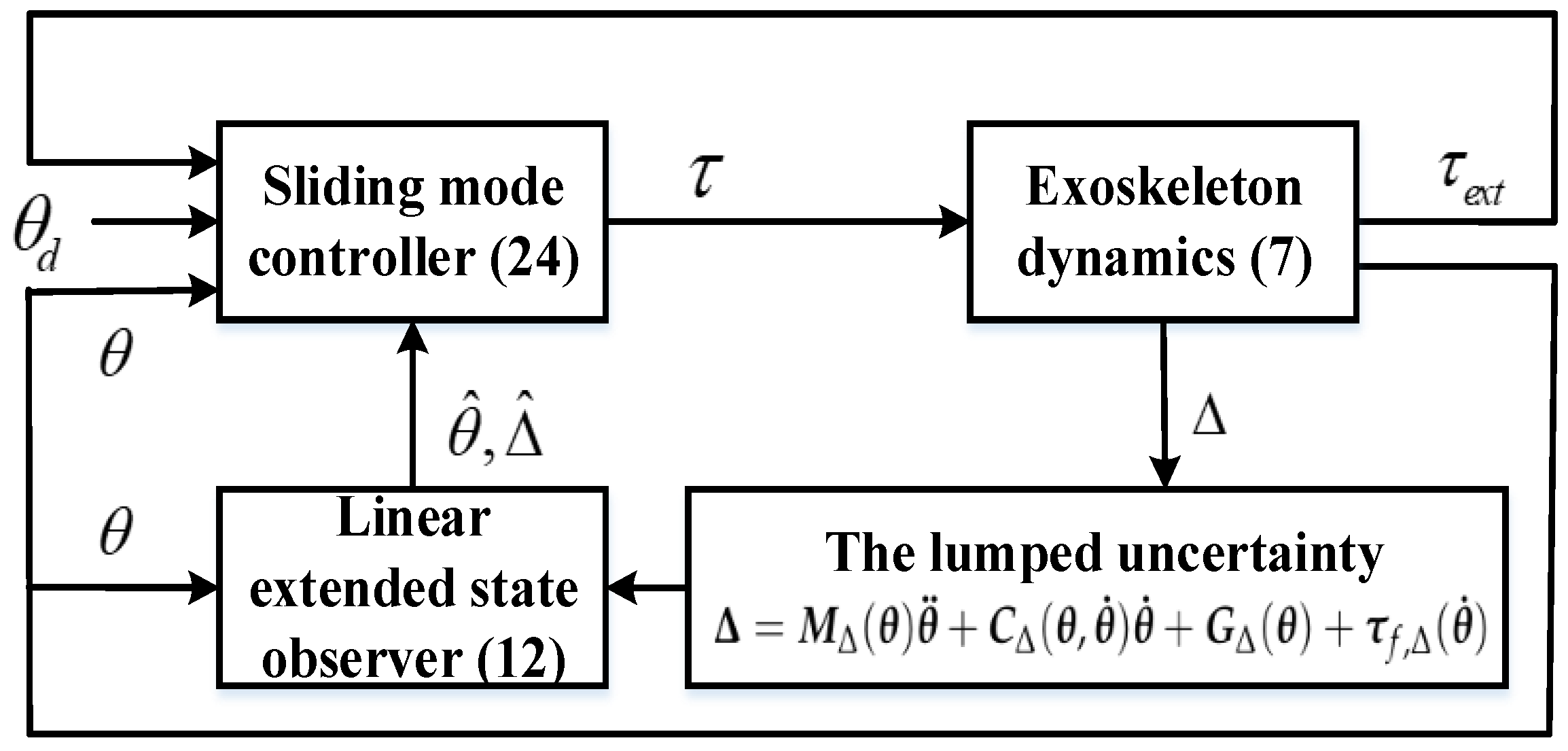
- A linear extended state observer (LESO) is used to estimate the unmeasurable angular velocity of two joints and the model uncertainties in the exoskeleton Lagrangian model, which can avoid the numerical differentiation of the encoder data for the angular velocity estimation. In fact, the LESO is a high-gain observer that guarantees a satisfactory estimation error in the exoskeleton inner-loop by regulating the observer bandwidth.
- (II)
- A sliding mode controller is designed to improve the tracking performance of the passive control mode of human–exoskeleton cooperative motion under model uncertainties and the unknown angular velocity of the exoskeleton. Meanwhile, the sliding mode controller guarantees that the joint tracking error converges to a small-enough zero neighborhood by regulating the control gains, which is easily realized in the experimental bench.
2. Exoskeleton Dynamic Model
3. Linear ESO Design
4. Sliding Mode Control
5. Simulation
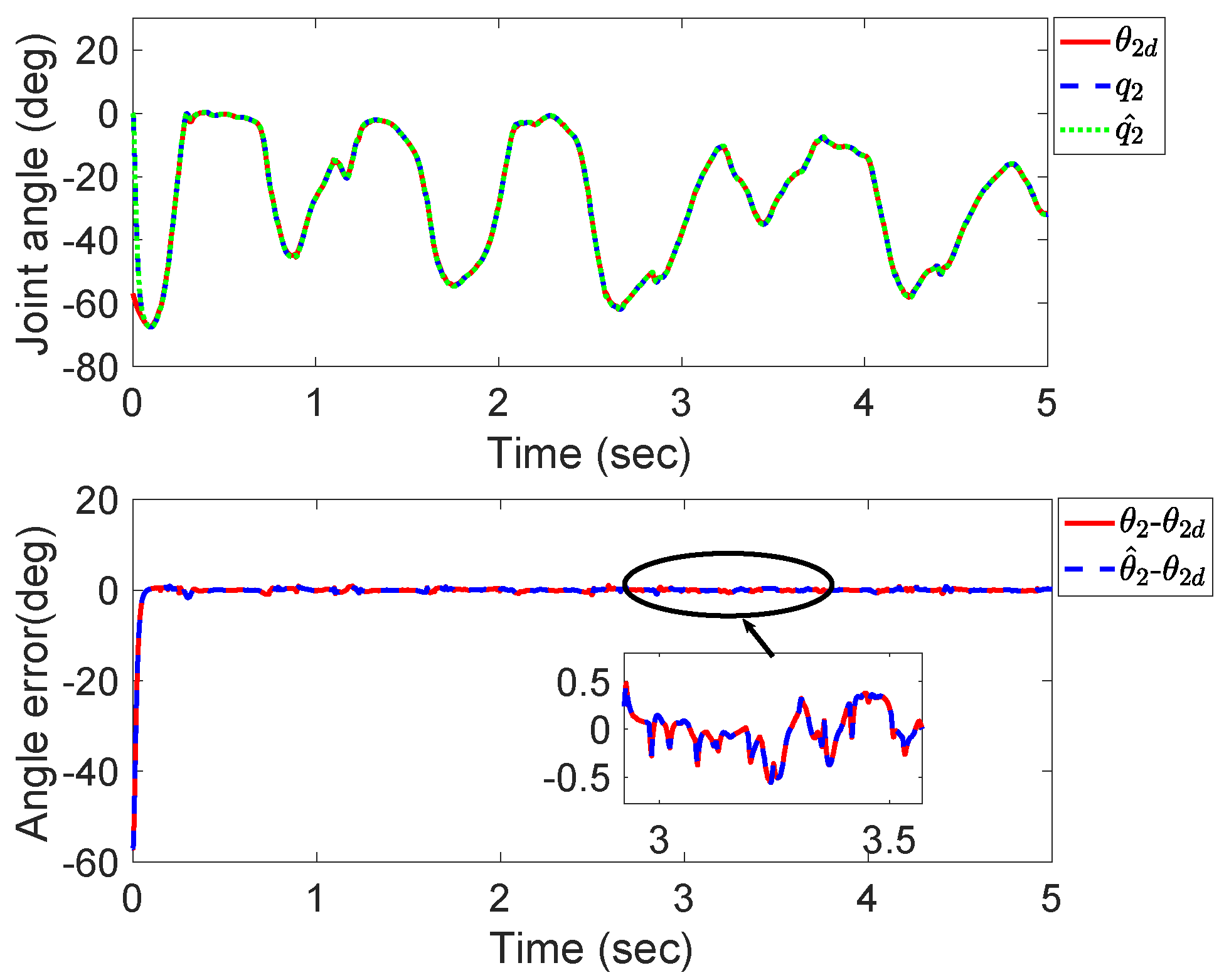
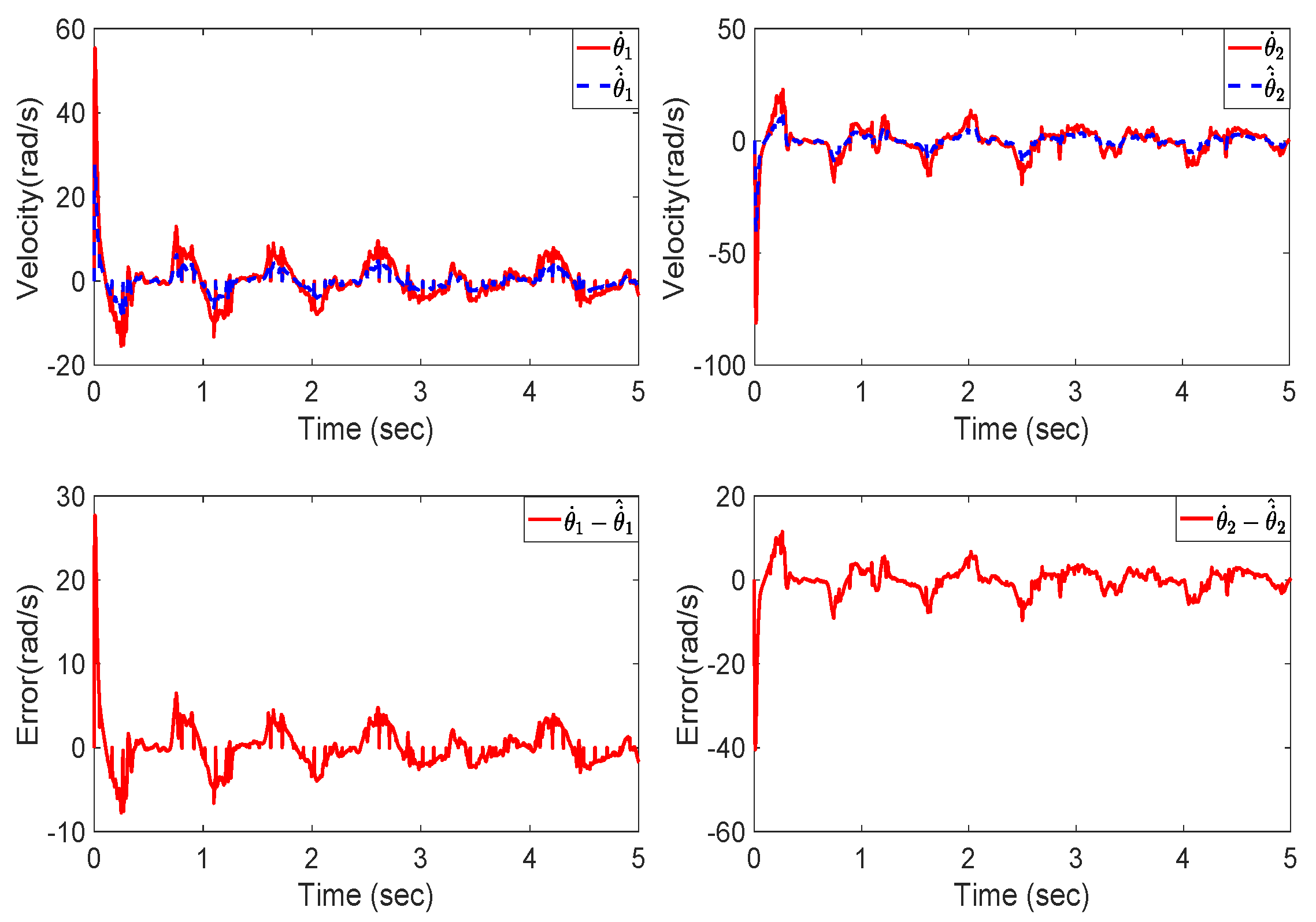
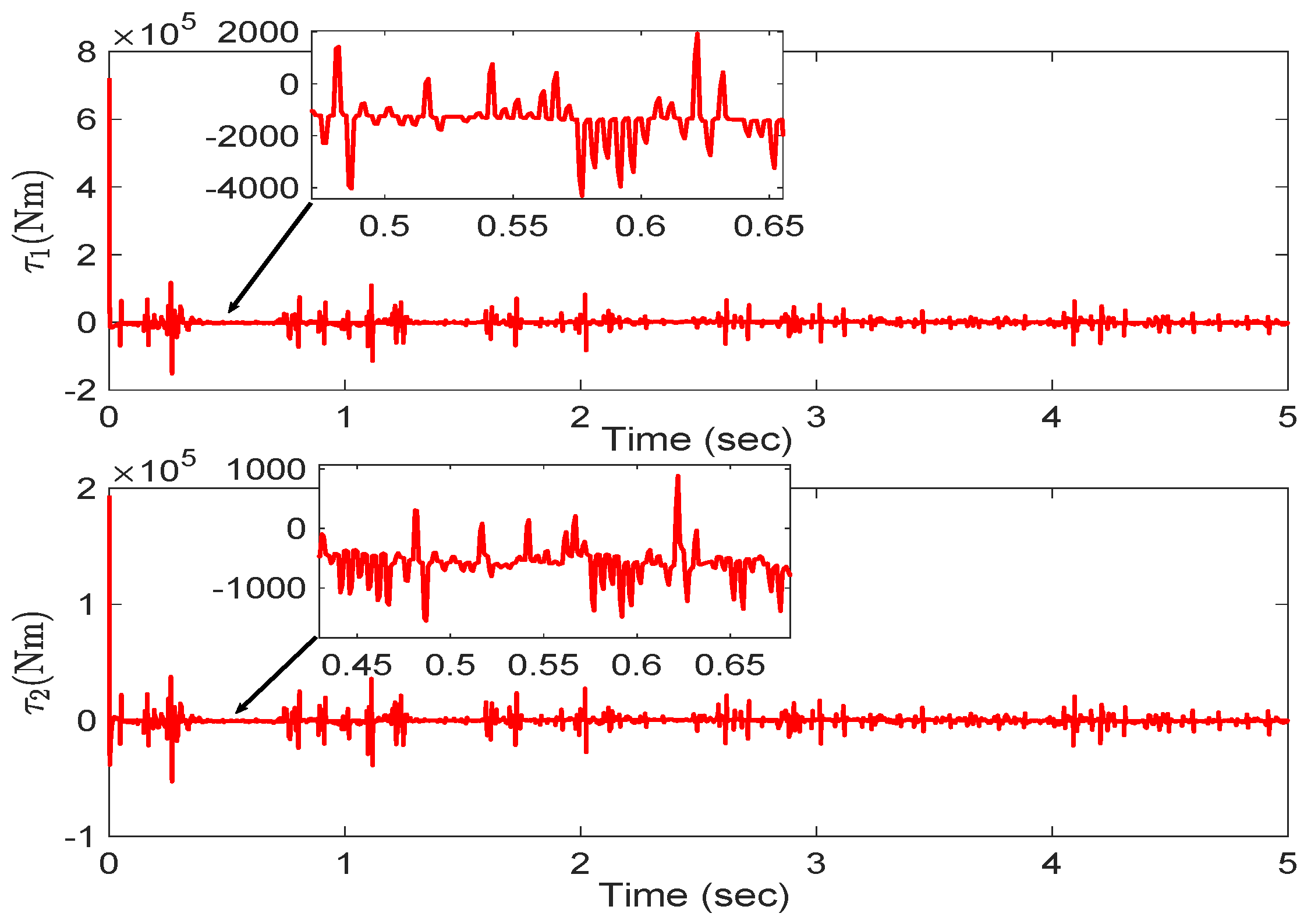
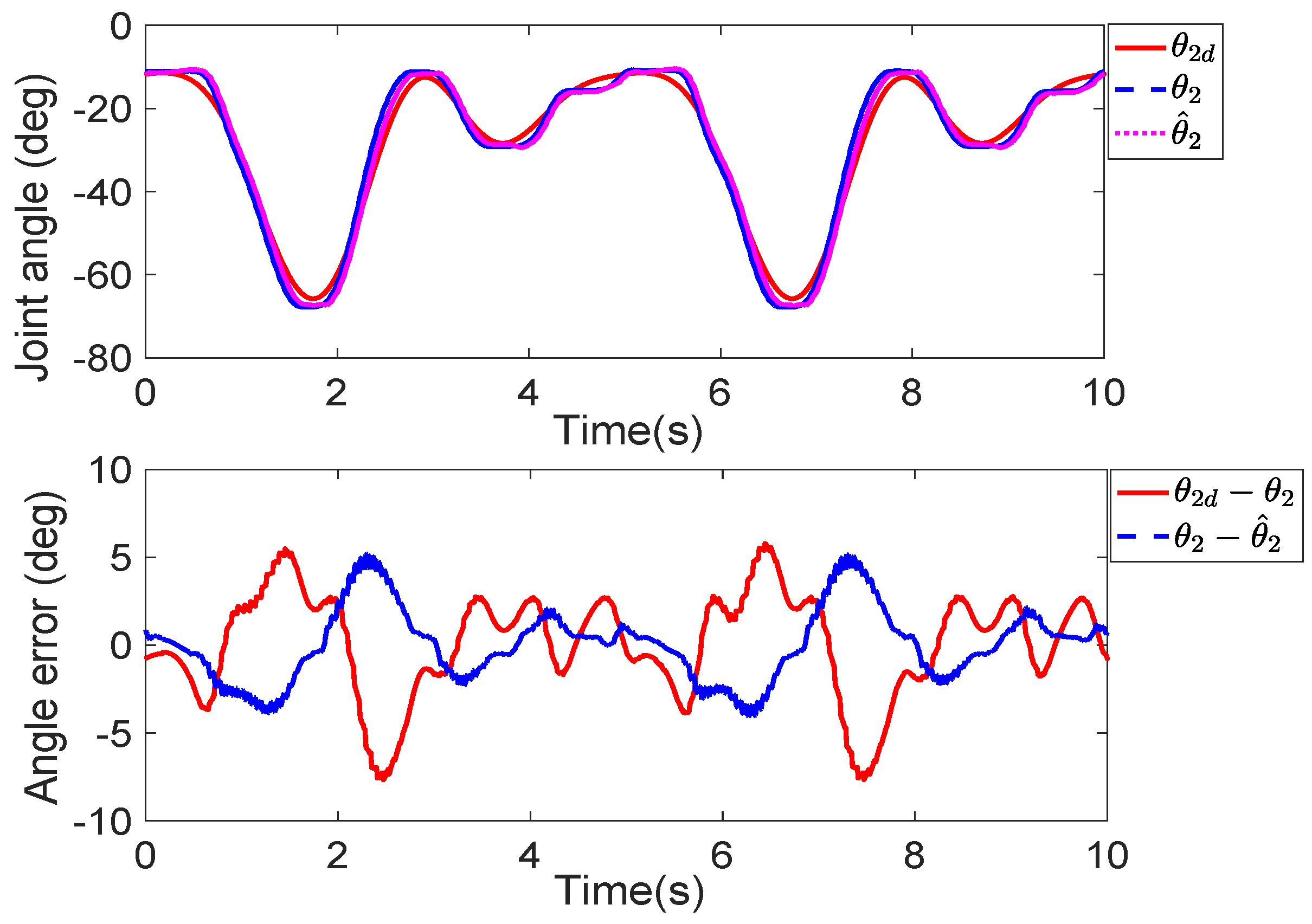
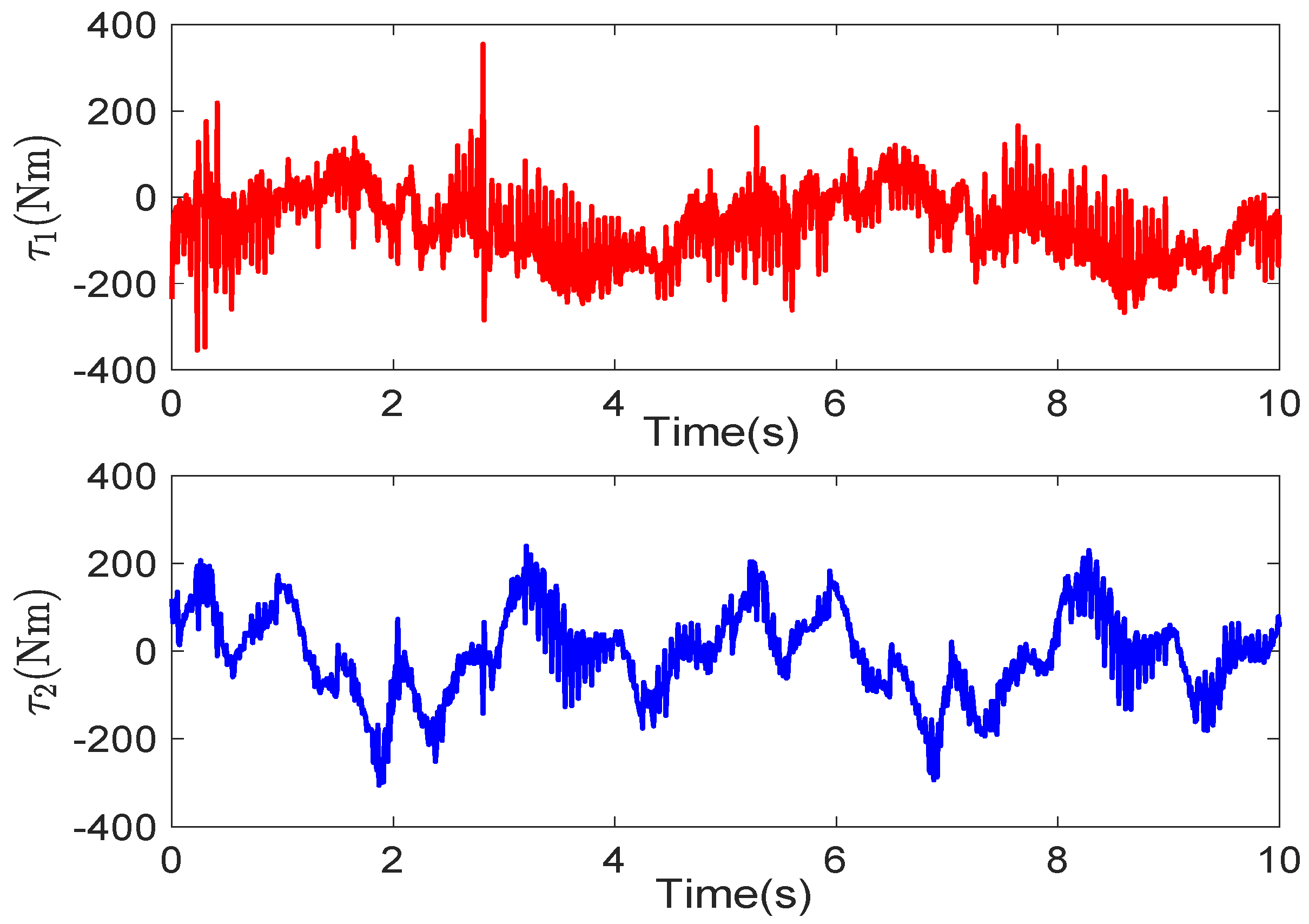
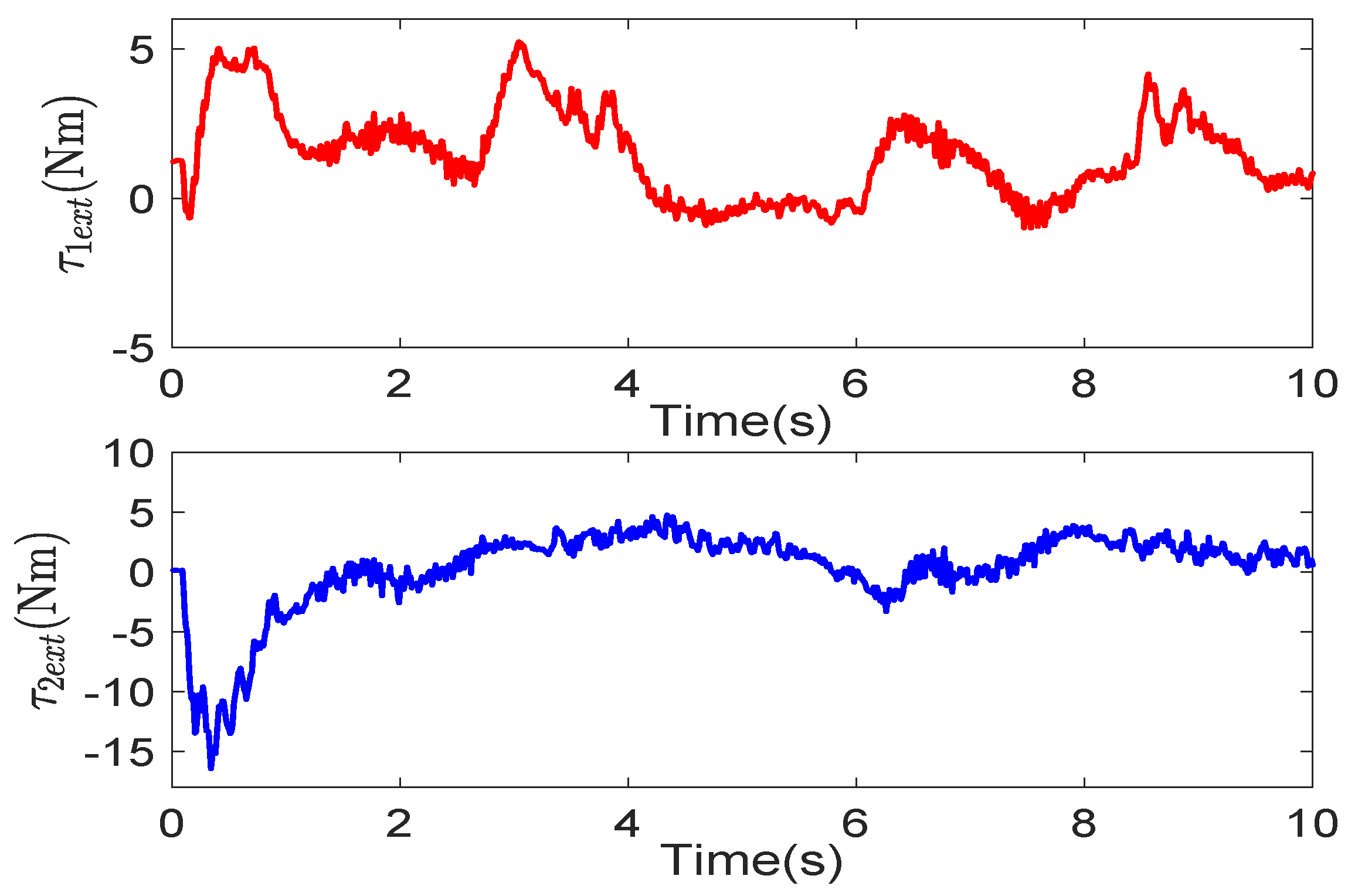
6. Experiment Verification
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Collins, S.H.; Wiggin, M.B.; Sawicki, G.S. Reducing the energy cost of human walking using an unpowered exoskeleton. Nature 2015, 522, 212–215. [Google Scholar] [CrossRef]
- Gregorczyk, K.N.; Hasselquist, L.; Schiffman, J.M.; Bensel, C.K.; Obusek, J.P.; Gutekunst, D.J. Effects of a lower-body exoskeleton device on metabolic cost and gait biomechanics during load carriage. Ergonomics 2010, 53, 1263–1275. [Google Scholar] [CrossRef]
- Kawamoto, H.; Sankai, Y. Power assist method based on Phase Sequence and muscle force condition for HAL. Adv. Robot. 2005, 19, 717–734. [Google Scholar] [CrossRef]
- Lee, J.W.; Kim, H.; Jang, J.; Park, S. Virtual model control of lower extremity exoskeleton for load carriage inspired by human behavior. Autonom. Robot. 2015, 38, 211–223. [Google Scholar] [CrossRef]
- Zoss, A.; Kazerooni, H. Design of an electrically actuated lower extremity exoskeleton. Adv. Robot. 2006, 20, 967–988. [Google Scholar] [CrossRef]
- Shields, B.; Goldfarb, M. Design and Energetic Characterization of a Solenoid Injected Liquid Monopropellant Powered Actuator for Self-Powered Robots. In Proceedings of the 2005 IEEE-ICRA, Barcelona, Spain, 18–22 April 2005. [Google Scholar]
- Lu, R.; Li, Z.; Su, C.Y.; Xue, A. Development and Learning Control of a Human Limb With a Rehabilitation Exoskeleton. IEEE Trans. Ind. Electron. 2014, 61, 3776–3785. [Google Scholar] [CrossRef]
- Chen, Z.; Guo, Q.; Li, T.; Yan, Y.; Jiang, D. Gait prediction and variable admittance control for lower limb exoskeleton with measurement delay and extended-state-observer. IEEE Trans. Neural Netw. Learn. Syst. 2022. [Google Scholar] [CrossRef]
- Chen, Z.; Guo, Q.; Li, T.; Yan, Y. Output constrained control of lower limb exoskeleton based on knee motion probabilistic model with finite-time extended state observer. IEEE/ASME Trans. Mechatron. 2023, 28, 2305–2316. [Google Scholar] [CrossRef]
- Yang, Y.; Ma, L.; Huang, D. Development and repetitive learning control of lower limb exoskeleton driven by electro-hydraulic actuators. IEEE Trans. Ind. Electron. 2017, 64, 4169–4178. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, Y.; Jiang, D. A control approach for human-mechatronic-hydraulic-coupled exoskeleton in overload-carrying condition. Int. J. Robot. Autom. 2016, 31, 272–280. [Google Scholar]
- Li, Z.; Su, C.; Li, G.; Hang, S. Fuzzy approximation-based adaptive backstepping control of an exoskeleton for human upper limbs. IEEE Trans. Fuzzy Syst. 2014, 23, 555–566. [Google Scholar] [CrossRef]
- Li, Z.; Su, C.Y.; Wang, L.; Chen, Z.; Chai, T. Nonlinear disturbance observer-based control design for a robotic exoskeleton incorporating fuzzy approximation. IEEE Trans. Ind. Electron. 2015, 62, 5763–5775. [Google Scholar] [CrossRef]
- He, W.; Li, Z.; Dong, Y.; Zhao, T. Design and adaptive control for an upper limb robotic exoskeleton in presence of input saturation. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 97–108. [Google Scholar] [CrossRef]
- Han, S.; Wang, H.; Tian, Y. A linear discrete-time extended state observer-based intelligent PD controller for a 12 DOFs lower limb exoskeleton LLE-RePA. Mech. Syst. Signal Proc. 2020, 138, 106547. [Google Scholar] [CrossRef]
- Meng, W.; Liu, Q.; Zhou, Z.; Ai, Q.; Sheng, B.; Xie, S.S. Recent development of mechanisms and control strategies for robot-assisted lower limb rehabilitation. Mechatronics 2015, 31, 132–145. [Google Scholar] [CrossRef]
- Hussain, S.; Xie, S.Q.; Jamwal, P.K. Robust nonlinear control of an intrinsically compliant robotic gait training orthosis. IEEE Trans. Syst. Man Cybern. Syst. 2012, 43, 655–665. [Google Scholar] [CrossRef]
- Saglia, J.A.; Tsagarakis, N.G.; Dai, J.S.; Caldwell, D.G. Control strategies for patient-assisted training using the ankle rehabilitation robot (ARBOT). IEEE/ASME Trans. Mechatron. 2012, 18, 1799–1808. [Google Scholar] [CrossRef]
- Chen, Z.; Guo, Q.; Yan, Y.; Shi, Y. Model identification and adaptive control of lower limb exoskeleton based on neighborhood field optimization. Mechatronics 2022, 81, 102699. [Google Scholar] [CrossRef]
- Chen, Z.; Guo, Q.; Li, T.; Shi, Y. Distributed adaptive impedance control of networked Lagrangian systems with neighborhood interaction feedback. Int. J. Robust Nonlin. 2022, 32, 2251–2272. [Google Scholar] [CrossRef]
- Keemink, A.Q.; van der Kooij, H.; Stienen, A.H. Admittance control for physical human-robot interaction. Int. J. Robot. Res. 2018, 37, 1421–1444. [Google Scholar] [CrossRef]
- Li, Z.; Huang, B.; Ye, Z.; Deng, M.; Yang, C. Physical human-robot interaction of a robotic exoskeleton by admittance control. IEEE Trans. Ind. Electron. 2018, 65, 9614–9624. [Google Scholar] [CrossRef]
- Yu, X.; He, W.; Li, Y.; Xue, C.; Li, J.; Zou, J.; Yang, C. Bayesian estimation of human impedance and motion intention for human-robot collaboration. IEEE Trans. Cybern. 2019, 51, 1822–1834. [Google Scholar] [CrossRef]
- Guo, Q.; Chen, Z. Neural adaptive control of single-rod electrohydraulic system with lumped uncertainty. Mech. Syst. Signal Proc. 2021, 146, 106869. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, Y.; Celler, B.G.; Su, S.W. Neural adaptive backstepping control of a robotic manipulator with prescribed performance constraint. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 3572–3583. [Google Scholar] [CrossRef]
- Binh, N.T.; Tung, N.A.; Nam, D.P.; Quang, N.H. An adaptive backstepping trajectory tracking control of a tractor trailer wheeled mobile robot. Int. J. Control Autom. Syst. 2019, 17, 465–473. [Google Scholar] [CrossRef]
- Liu, J.; Gai, W.; Zhang, J.; Li, Y. Nonlinear adaptive backstepping with ESO for the quadrotor trajectory tracking control in the multiple disturbances. Int. J. Control Autom. Syst. 2019, 17, 2754–2768. [Google Scholar] [CrossRef]
- He, W.; Meng, T.; Huang, D.; Li, X. Adaptive boundary iterative learning control for an Euler-Bernoulli beam system with input constraint. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1539–1549. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, K.; Zhang, L.; Wu, X.; Zhang, T.; Li, Q.; Li, X.; Su, C.Y. Human-in-the-loop control of a wearable lower limb exoskeleton for stable dynamic walking. IEEE/ASME Trans. Mechatron. 2021, 26, 2700–2711. [Google Scholar] [CrossRef]
- Sun, W.; Lin, J.W.; Su, S.F.; Wang, N.; Er, M.J. Reduced adaptive fuzzy decoupling control for lower limb exoskeleton. IEEE Trans. Cybern. 2020, 51, 1099–1109. [Google Scholar] [CrossRef]
- Han, J.; Yang, S.; Xia, L.; Chen, Y.H. Deterministic adaptive robust control with a novel optimal gain design approach for a fuzzy 2-DOF lower limb exoskeleton robot system. IEEE Trans. Fuzzy Syst. 2020, 29, 2373–2387. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.; Liu, X.; Huang, D. Adaptive neural network control for a hydraulic knee exoskeleton with valve deadband and output constraint based on nonlinear disturbance observer. Neurocomputing 2022, 473, 14–23. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, J.; Yang, P.; Guo, S. Iterative learning sliding mode control for output-constrained upper-limb exoskeleton with non-repetitive tasks. Appl. Math. Model. 2021, 97, 366–380. [Google Scholar] [CrossRef]
- Liu, Y.; Fu, Y.; He, W.; Hui, Q. Modeling and observer-based vibration control of a flexible spacecraft with external disturbances. IEEE Trans. Ind. Electron. 2018, 66, 8648–8658. [Google Scholar] [CrossRef]
- Nie, J.; Wang, H.; Lu, X.; Lin, X.; Sheng, C.; Zhang, Z.; Song, S. Finite-time output feedback path following control of underactuated MSV based on FTESO. Ocean Eng. 2021, 224, 108660. [Google Scholar] [CrossRef]
- Ali, N.; Tawiah, I.; Zhang, W. Finite-time extended state observer based nonsingular fast terminal sliding mode control of autonomous underwater vehicles. Ocean Eng. 2020, 218, 108179. [Google Scholar] [CrossRef]
- Tuo, Y.; Wang, S.; Guo, C. Finite-time extended state observer-based area keeping and heading control for turret-moored vessels with uncertainties and unavailable velocities. Int. J. Nav. Archit. Ocean Eng. 2022, 14, 100422. [Google Scholar] [CrossRef]
- Wu, Q.; Chen, Y. Adaptive cooperative control of a soft elbow rehabilitation exoskeleton based on improved joint torque estimation. Mech. Syst. Signal Proc. 2023, 184, 109748. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, X.; Chen, B.; Wu, H. Development of a minimal-intervention-based admittance control strategy for upper extremity rehabilitation exoskeleton. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1005–1016. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, Y.; Celler, B.G.; Su, S.W. Backstepping control of electro-hydraulic system based on extended-state-observer with plant dynamics largely unknown. IEEE Trans. Ind. Electron. 2016, 63, 6909–6920. [Google Scholar] [CrossRef]
- Cui, R.; Chen, L.; Yang, C.; Chen, M. Extended state observer-based integral sliding mode control for an underwater robot with unknown disturbances and uncertain nonlinearities. IEEE Trans. Ind. Electron. 2017, 64, 6785–6795. [Google Scholar] [CrossRef]
- Chen, Z.; Guo, Q.; Xiong, H.; Jiang, D.; Yan, Y. Control and implementation of 2-DOF lower limb exoskeleton experiment platform. Chin. J. Mech. Eng. 2021, 34, 22. [Google Scholar] [CrossRef]
- Chen, Z.; Guo, Q.; Jiang, D.; Yan, Y. Robust sliding mode control for a 2-DOF lower limb exoskeleton base on linear extended state observer. Mech. Eng. Sci. 2020, 2, 1–6. [Google Scholar] [CrossRef]
- Nadhynee, M.F.; Luis, A.C.; Agustin, U.; Alberto, L.J.; Isaac, C. Robust disturbance rejection control of a biped robotic system using high-order extended state observer. ISA Trans. 2016, 62, 276–286. [Google Scholar]
- Fareh, R.; Khadraoui, S.; Abdallah, M.Y.; Baziyad, M.; Bettayeb, M. Active disturbance rejection control for robotic systems: A review. Mechatronics 2021, 80, 102671. [Google Scholar] [CrossRef]
- Siciliano, B.; Sciavicco, L.; Villani, L.; Oriolo, G. Robotics: Modelling, Planning and Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Zheng, Q.; Gao, L.Q.; Gao, Z. On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics. In Proceedings of the 46th IEEE Conference on Decision and Control, DEC 2007, New Orleans, LA, USA, 12–14 December 2007; pp. 4090–4095. [Google Scholar]
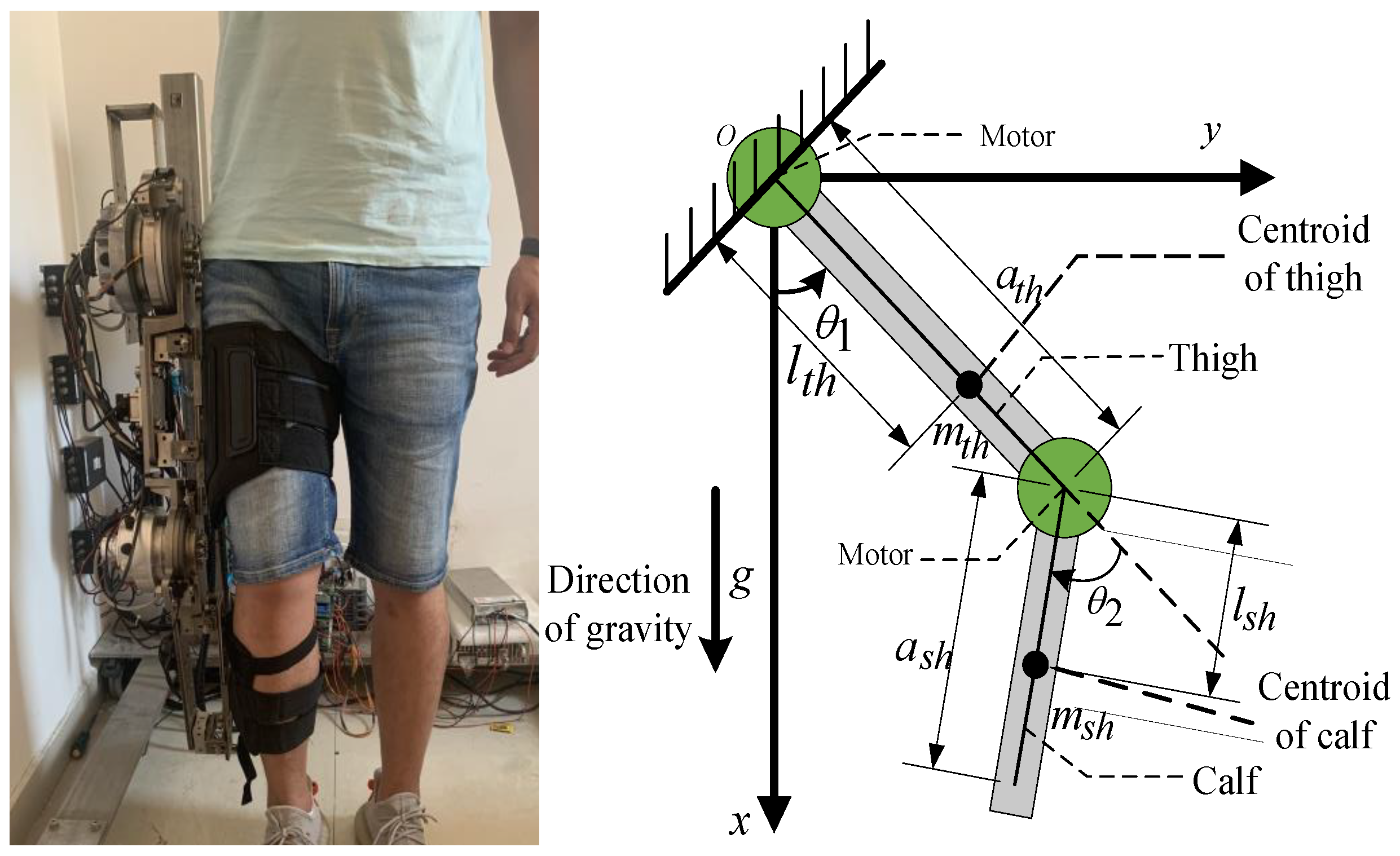





| Parameter | Symbol | Parameter | Symbol |
|---|---|---|---|
| Thigh weight | Shank weight | ||
| Thigh length | Shank length | ||
| Thigh centroid length | Shank centroid length | ||
| Thigh moment of inertia | Shank moment of inertia |
| Component | Brand | Number |
|---|---|---|
| Servo motor | GDM1-100N2/120N2 | 2 |
| Motor driver | Elmo-G-SOLHOR15/100EE | 2 |
| Absolute encoders | INC-4-150/3-125 | 2 |
| 3-D force sensors | JNSH-2-10kg-BSQ-12 | 4 |
| Controller | NI cRIO-9035 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Gao, W.; Guo, Q. Extended State Observer-Based Sliding Mode Control Design of Two-DOF Lower Limb Exoskeleton. Actuators 2023, 12, 402. https://doi.org/10.3390/act12110402
Zhang J, Gao W, Guo Q. Extended State Observer-Based Sliding Mode Control Design of Two-DOF Lower Limb Exoskeleton. Actuators. 2023; 12(11):402. https://doi.org/10.3390/act12110402
Chicago/Turabian StyleZhang, Jiyu, Wei Gao, and Qing Guo. 2023. "Extended State Observer-Based Sliding Mode Control Design of Two-DOF Lower Limb Exoskeleton" Actuators 12, no. 11: 402. https://doi.org/10.3390/act12110402
APA StyleZhang, J., Gao, W., & Guo, Q. (2023). Extended State Observer-Based Sliding Mode Control Design of Two-DOF Lower Limb Exoskeleton. Actuators, 12(11), 402. https://doi.org/10.3390/act12110402






