Plasma Actuators for Cycloidal Rotor Thrust Vectoring Enhancement in Airships
Abstract
:1. Introduction
2. Numerical Modeling
2.1. Cycloidal Rotor Test Case
2.2. Fluid Flow Equations
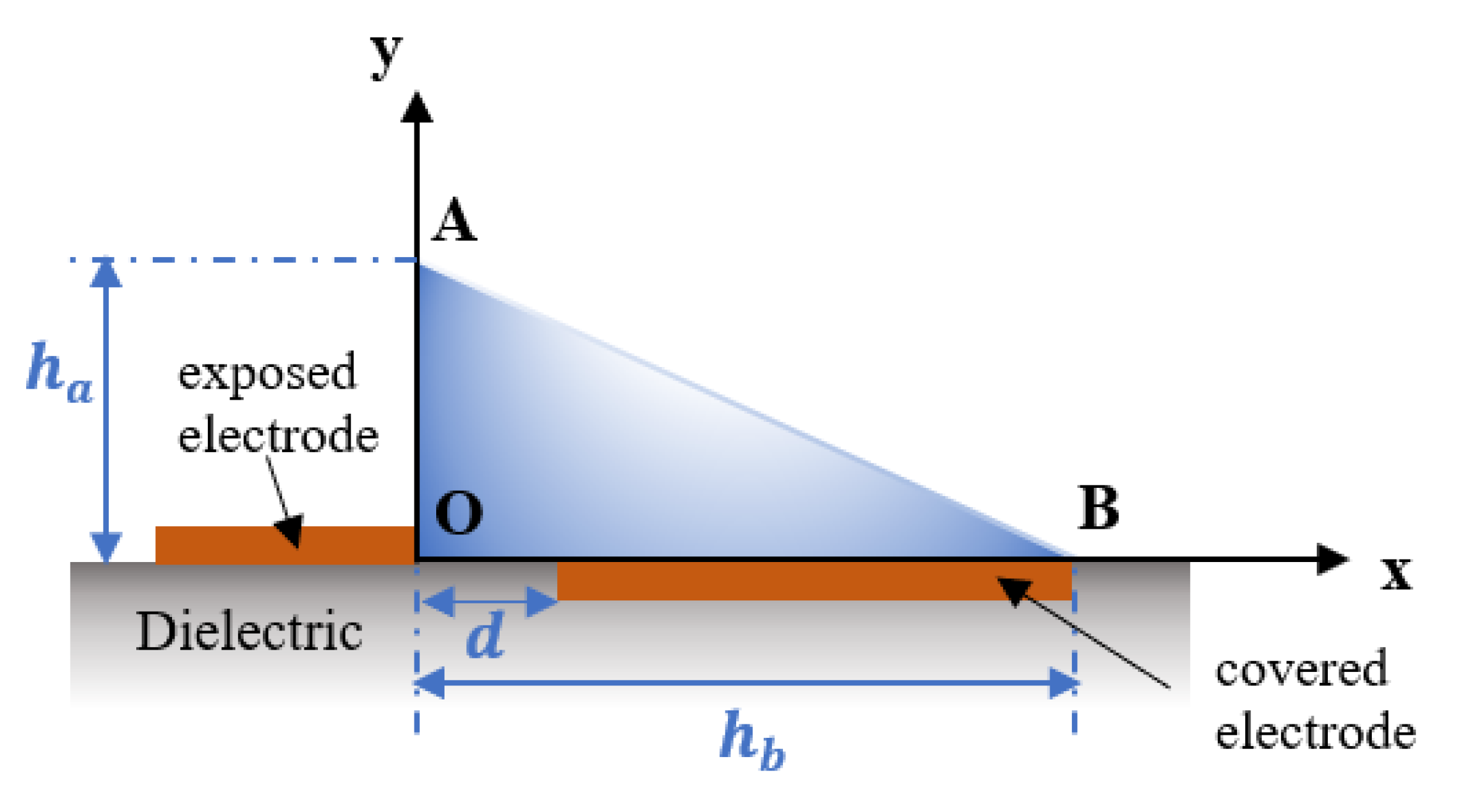
2.3. Plasma Model
2.4. Solver Setting
3. Results and Interpretations
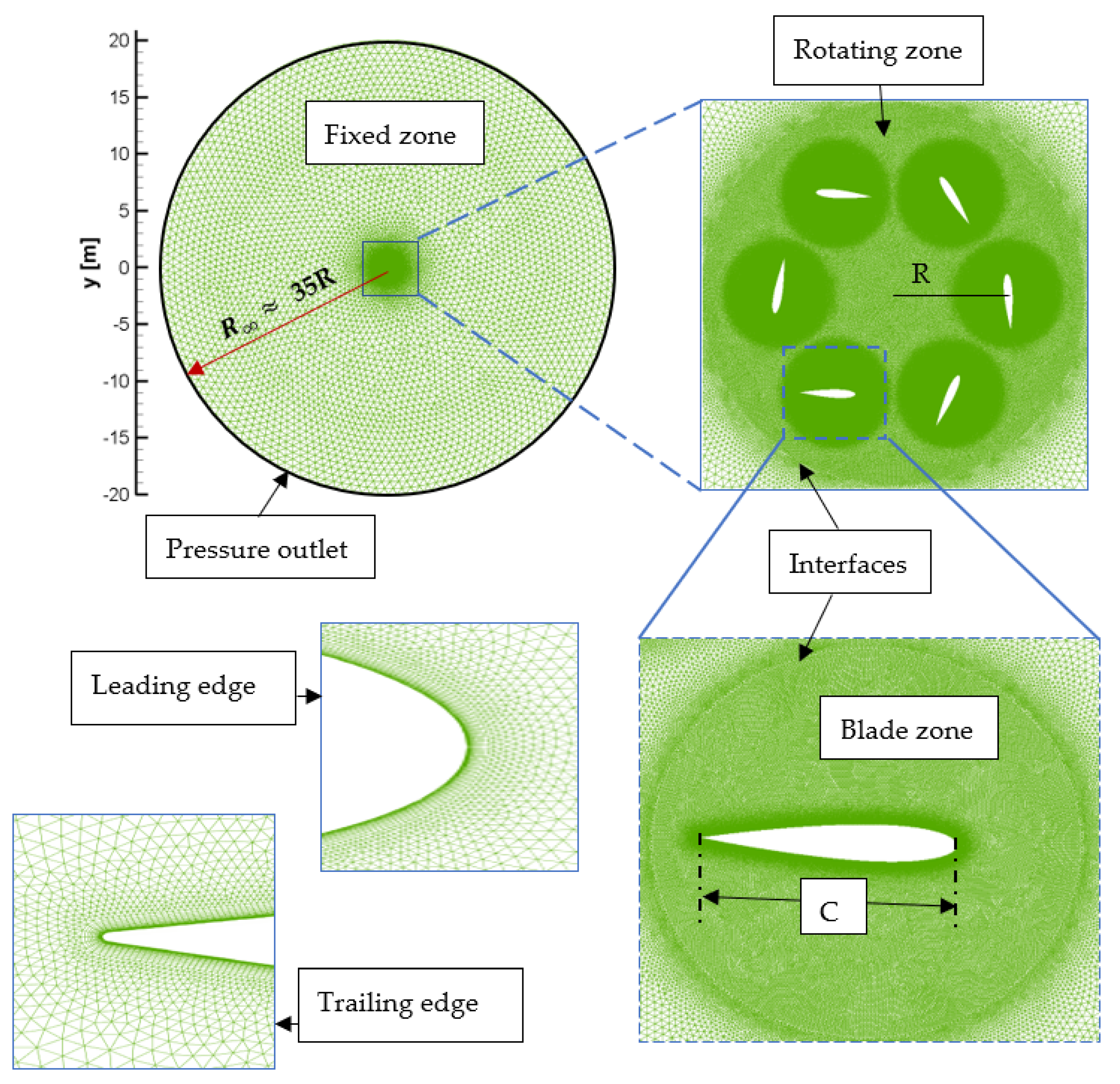
3.1. Mesh Independence Test
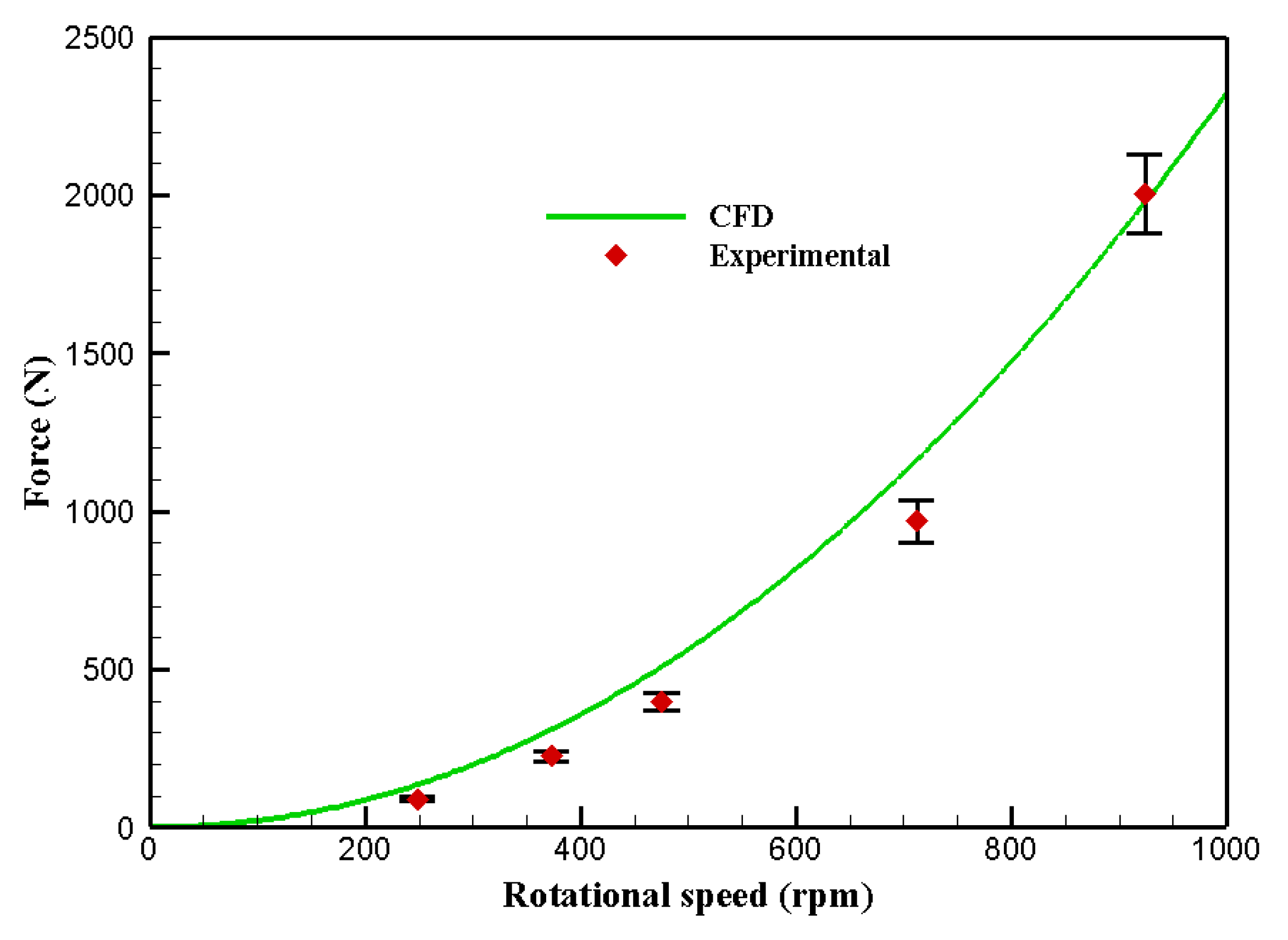
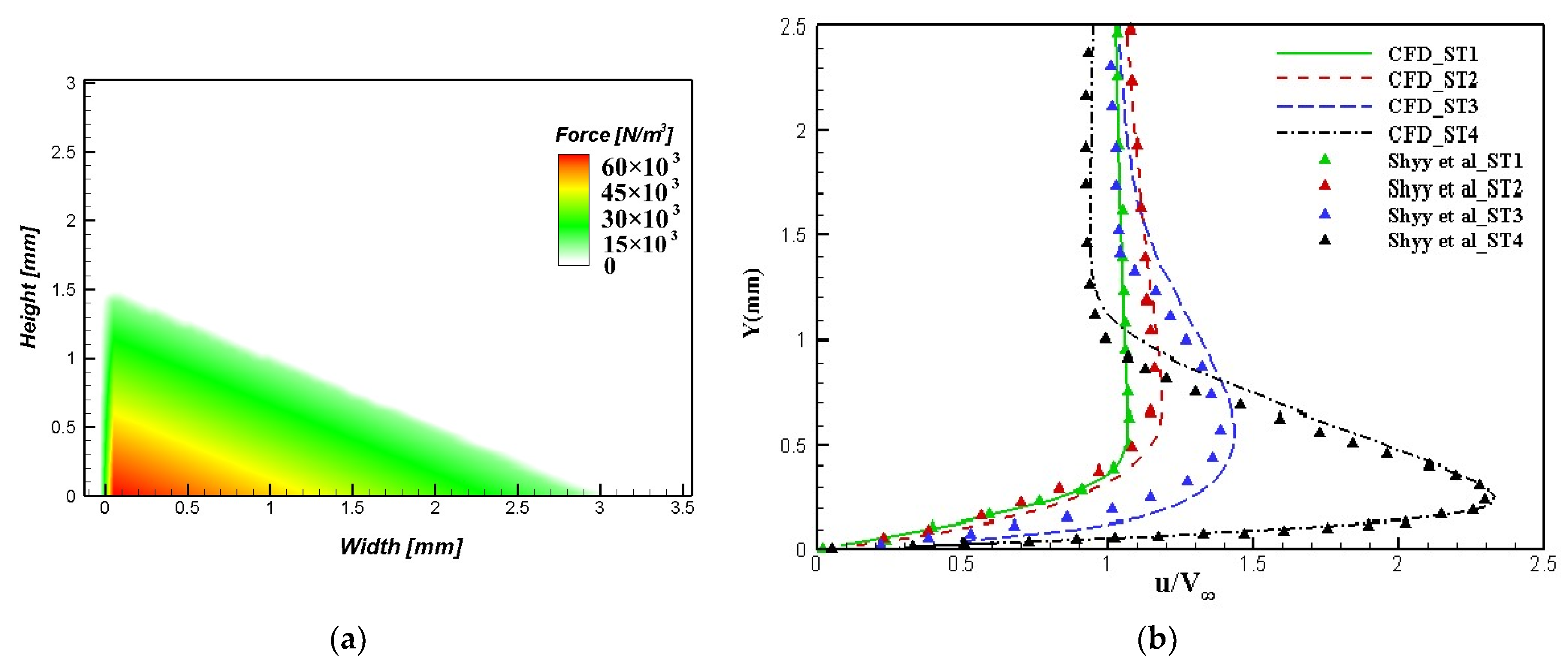
3.2. Model Validation
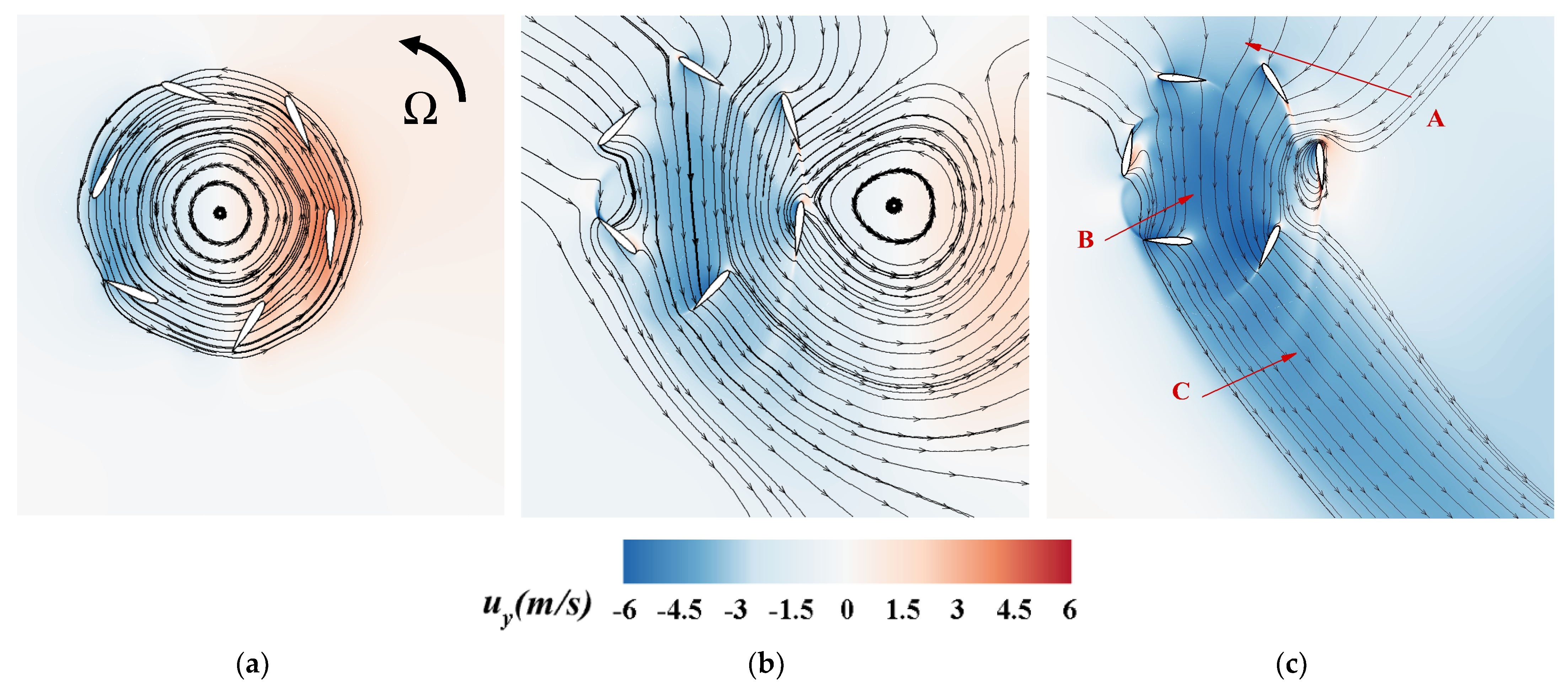
3.3. Cyclorotor Base Case
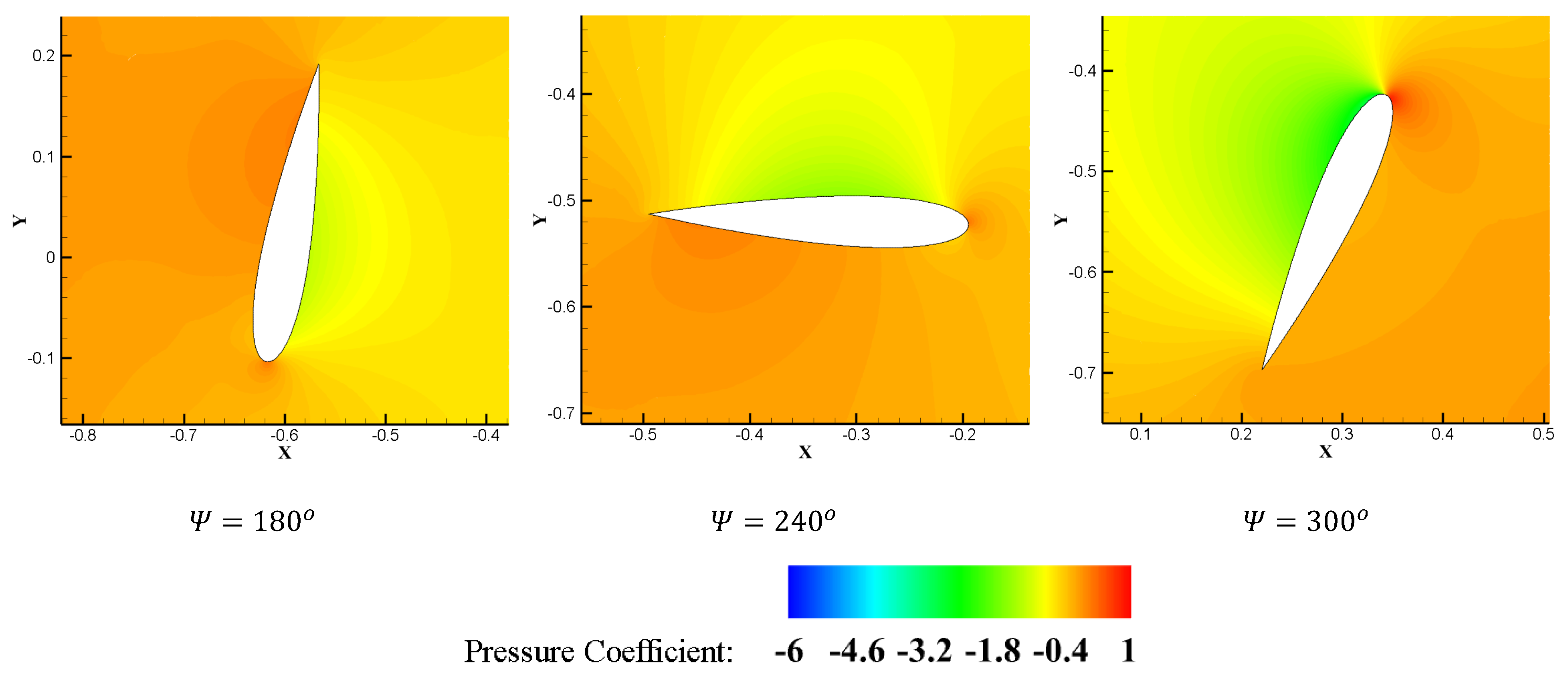
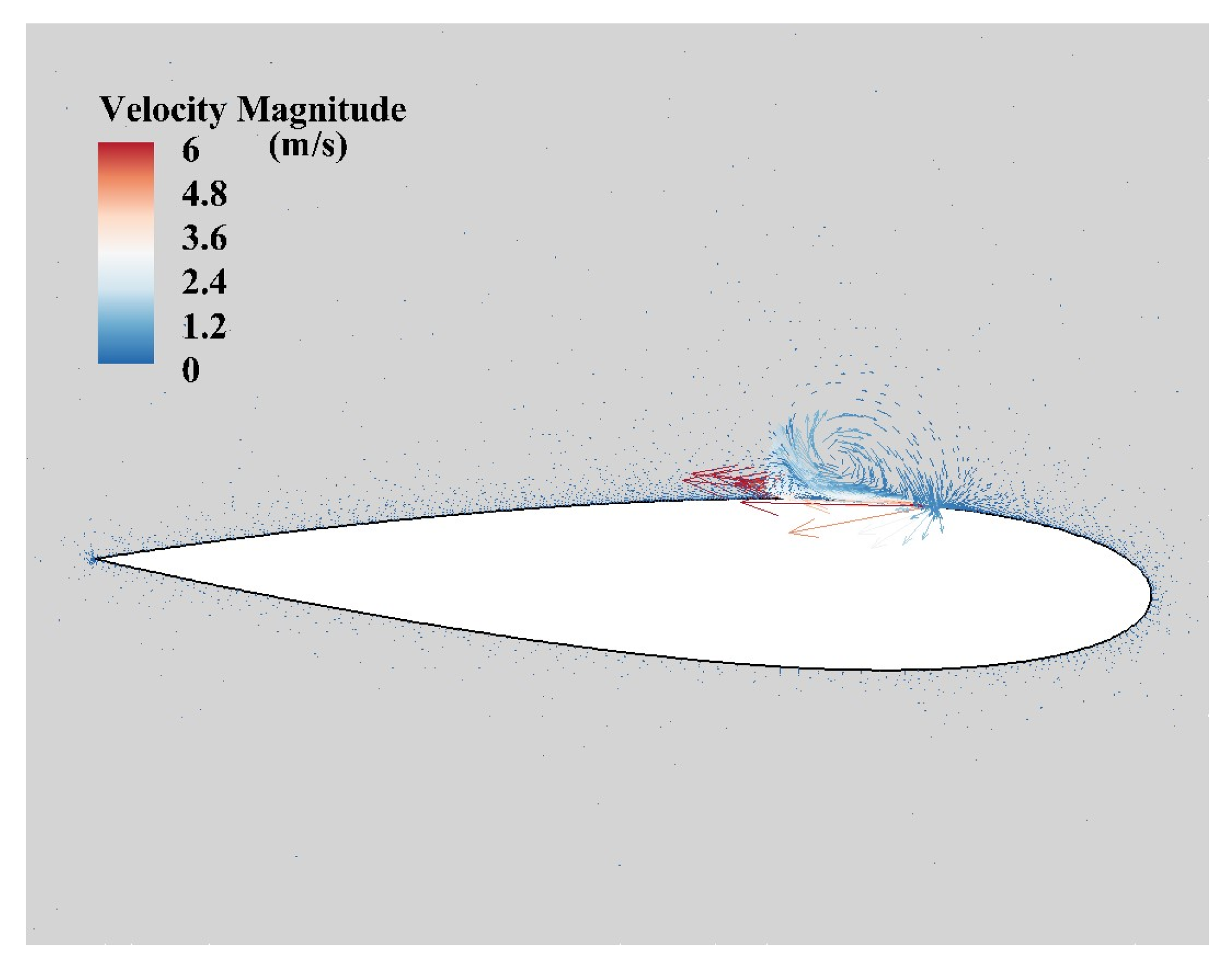
3.4. Effect of DBD Plasma Actuator
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Manikandan, M.; Pant, R.S. Research and Advancements in Hybrid Airships—A Review. Prog. Aerosp. Sci. 2021, 127, 100741. [Google Scholar] [CrossRef]
- Chen, L.; Zhou, G.; Yan, X.J.; Duan, D.P. Composite Control of Stratospheric Airships with Moving Masses. J. Aerosp. Eng. 2012, 49, 794–801. [Google Scholar] [CrossRef]
- Manikandan, M.; Vaidya, E.; Pant, R.S. Design and analysis of hybrid electric multi-lobed airship for cargo transportation. Sustain. Energy Technol. Assess. 2022, 51, 101892. [Google Scholar] [CrossRef]
- Bonnici, M.; Tacchini, A.; Vucinic, D. Long Permanence High Altitude Airships: The Opportunity of Hydrogen. Eur. Transp. Res. Rev. 2014, 6, 253–266. [Google Scholar] [CrossRef]
- Cimarelli, A.; Madonia, M.; Angeli, D.; Dumas, A. Aerodynamic Study of Advanced Airship Shapes. J. Aerosp. Eng. 2017, 30, 04016087. [Google Scholar] [CrossRef]
- Smith, T.; Bingham, C.; Stewart, P.; Allarton, R.; Stewart, J. Energy harvesting and power network architectures for the multibody advanced airship for transport high altitude cruiser–feeder airship concept. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2013, 227, 586–598. [Google Scholar] [CrossRef]
- Boschma, J.H. Modern Aviation Applications for Cycloidal Propulsion. In Proceedings of the 1st AIAA Aircraft, Technology Integration, and Operations Forum, Los Angeles, CA, USA, 16–18 October 2001. [Google Scholar] [CrossRef]
- Onda, M.; Matsuuchi, K.; Ohtsuka, N.; Kimura, Y. Cycloidal Propeller and Its Application to Advanced LTA Vehicles. In Proceedings of the AIAA’s 3rd Annual Aviation Technology, Integration, and Operations (ATIO) Forum, Denver, CO, USA, 17–19 November 2003. [Google Scholar] [CrossRef]
- Onda, M.; Matsuuchi, K.; Kimura, Y.; Hashimoto, S. Aerobatic Airship Robot with Advanced Propulsors. In Proceedings of the IEEE Conference on Robotics and Automation, Minato, Japan, 18–19 November 2004; Available online: https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=1425014 (accessed on 23 August 2023).
- Onda, M.; Sano, M.; Iwata, K.; Tomita, K.; Watanabe, M.; Koyama, N.; Akinaga, W.; Maruyama, M. Airship-Type Crane Robot with Cycloidal Propellers. In Proceedings of the 6th AIAA Aviation Technology, Integration, and Operations Conference, Wichita, KS, USA, 25–27 September 2006. [Google Scholar] [CrossRef]
- Benmoussa, A.; Gamboa, P.V. Effect of Control Parameters on Hybrid Electric Propulsion UAV Performance for Various Flight Conditions: Parametric Study. Appl. Mech. 2023, 4, 493–513. [Google Scholar] [CrossRef]
- Hwang, I.S.; Min, S.Y.; Lee, C.H.; Kim, S.J. Development of a Four-Rotor Cyclocopter. J. Aircr. 2008, 45, 1251–1257. [Google Scholar] [CrossRef]
- Xisto, C.M.; Leger, J.A.; Páscoa, J.C.; Gagnon, L.; Masarati, P.; Angeli, D.; Dumas, A. Parametric Analysis of a Large-Scale Cycloidal Rotor in Hovering Conditions. J. Aerosp. Eng. 2016, 30, 04016066. [Google Scholar] [CrossRef]
- Benedict, M.; Jarugumilli, T.; Chopra, I. Effect of Rotor Geometry and Blade Kinematics on Cycloidal Rotor Hover Performance. J. Aircr. 2013, 50, 1340–1352. [Google Scholar] [CrossRef]
- Jarugumilli, T.; Benedict, M.; Chopra, I. Wind tunnel studies on a micro air vehicle-scale cycloidal rotor. J. Am. Helicopter Soc. 2014, 59, 1–10. [Google Scholar] [CrossRef]
- Sachse, H. Kirsten-Boeing Propeller; National Advisory Committee for Aeronautics: Washington, DC, USA, 1926.
- Garrick, I.E. Propulsion of a Flapping and Oscillating Airfoil; National Advisory Committee for Aeronautics: Washington, DC, USA, 1937.
- Wheatley, J.B.; Windler, R. Wind-Tunnel Tests of a Cyclogiro Rotor; National Advisory Committee for Aeronautics: Washington, DC, USA, 1935.
- Wheatley, J.B. Simplified Aerodynamic Analysis of the Cyclogiro Rotating Wing System; National Advisory Committee for Aeronautics: Washington, DC, USA, 1930.
- Boirum, C.G.; Post, S.L. Review of historic and modern cyclogyro design. In Proceedings of the 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Denver, CO, USA, 2–5 August 2009. [Google Scholar] [CrossRef]
- Xisto, C.M.; Páscoa, J.C.; Abdollahzadeh, M.; Leger, J.A.; Masarati, P.; Gagnon, L.; Schwaiger, M.; Wills, D. PECyT—Plasma Enhanced Cycloidal Thruster. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014. [Google Scholar] [CrossRef]
- Gibbens, R.P.; Boschma, J.H. Construction and Testing of a New Aircraft Cycloidal Propeller. In Proceedings of the 13th Lighter-Than-Air Systems Technology Conference, Norfolk, VA, USA, 28 June–1 July 1999; pp. 131–140. [Google Scholar] [CrossRef]
- Hwang, I.S.; Min, S.Y.; Kim, M.K.; Kim, S.J. Multidisciplinary Optimal Design of Cyclocopter Blade System. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Austin, TX, USA, 18–21 April 2005; pp. 6005–6011. [Google Scholar] [CrossRef]
- Hwang, I.S.; Hwang, C.S.; Kim, S.J. Structural Design of Cyclocopter Blade System. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Austin, TX, USA, 18–21 April 2005; pp. 2743–2749. [Google Scholar] [CrossRef]
- Benedict, M.; Ramasamy, M.; Chopra, I.; Leishman, J.G. Performance of a Cycloidal Rotor Concept for Micro Air Vehicle Applications. J. Am. Helicopter Soc. 2010, 55, 22002. [Google Scholar] [CrossRef]
- Benedict, M.; Mattaboni, M.; Chopra, I.; Masarati, P. Aeroelastic Analysis of a Micro-Air-Vehicle-Scale Cycloidal Rotor in Hover. AIAA J. 2012, 49, 2430–2443. [Google Scholar] [CrossRef]
- Leger, J.A.; Páscoa, J.C.; Xisto, C.M. Analytical Modeling of a Cyclorotor in Hovering State. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 2163–2177. [Google Scholar] [CrossRef]
- Monteiro, J.A.L.; Páscoa, J.C.; Xisto, C.M. Aerodynamic Optimization of Cyclorotors. Aircr. Eng. Aerosp. Tech. 2016, 88, 232–245. [Google Scholar] [CrossRef]
- Gagnon, L.; Morandini, M.; Quaranta, G.; Muscarello, V.; Masarati, P. Aerodynamic models for cycloidal rotor analysis. Aircr. Eng. Aerosp. Technol. 2016, 88, 215–231. [Google Scholar] [CrossRef]
- Singh, K.; Páscoa, J.C. Numerical Modeling of Stall and Poststall Events of a Single Pitching Blade of a Cycloidal Rotor. J. Fluids Eng. 2019, 141, 011103. [Google Scholar] [CrossRef]
- Schwaiger, M.; Wills, D. D-Dalus VTOL—Efficiency Increase in Forward Flight. Aircr. Eng. Aerosp. Tech. 2016, 88, 594–604. [Google Scholar] [CrossRef]
- Cycloidal Rotor Optimized for Propulsion | CROP | Project | Fact Sheet | FP7 | CORDIS | European Commission, (n.d.). Available online: https://cordis.europa.eu/project/id/323047 (accessed on 7 August 2023).
- Habibnia, R.M.; Pascoa, J.C. Performance Optimization of Forward-Flight and Lift-Up Phases in a Cycloidal Rotor Using an Active Control Mechanism. J. Aerosp. Eng. 2021, 34, 04021039. [Google Scholar] [CrossRef]
- Habibnia, R.M.; Pascoa, J. Active Control Assessments Towards Optimizing the Performance of a Cycloidal Rotor at Hover. Aerosp. Sci. Technol. 2021, 119, 107141. [Google Scholar] [CrossRef]
- Habibnia, M.; Pascoa, J. ANN Assisted Flow Modeling and Analysis for a Cyclorotor in Ground Effect. Aerosp. Sci. Technol. 2019, 95, 105495. [Google Scholar] [CrossRef]
- Benmoussa, A.; Páscoa, J.C. Performance Improvement and Start-Up Characteristics of a Cyclorotor Using Multiple Plasma Actuators. Meccanica 2021, 56, 2707–2730. [Google Scholar] [CrossRef]
- Benmoussa, A.; Páscoa, J.C. Cycloidal Rotor Coupled with DBD Plasma Actuators for Performance Improvement. Aerosp. Sci. Technol. 2021, 110, 106468. [Google Scholar] [CrossRef]
- Liu, C.; Roth, J.R. An Atmospheric Glow Discharge Plasma For Aerodynamic Boundary Layer Control. In Proceedings of the 1994 IEEE 21st International Conference on Plasma Sciences (ICOPS), Santa Fe, NM, USA, 6–8 June 1994. [Google Scholar]
- Roth, J.R.; Sherman, D.M.; Wilkinson, S.P. Boundary Layer Flow Control with a One Atmosphere Uniform Glow Discharge Surface Plasma. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998. [Google Scholar] [CrossRef]
- Rodrigues, F.; Abdollahzadehsangroudi, M.; Nunes-Pereira, J.; Páscoa, J. Recent Developments on Dielectric Barrier Discharge (DBD) Plasma Actuators for Icing Mitigation. Actuators 2022, 12, 5. [Google Scholar] [CrossRef]
- Benard, N.; Moreau, E. Electrical and mechanical characteristics of surface AC dielectric barrier discharge plasma actuators applied to airflow control. Exp. Fluids 2014, 55, 1–43. [Google Scholar] [CrossRef]
- Hink, R.; Pipa, A.V.; Schafer, J.; Caspari, R.; Weichwald, R.; Foest, R.; Brandenburg, R. Influence of dielectric thickness and electrode structure on the ion wind generation by micro fabricated plasma actuators. J. Phys. D Appl. Phys. 2020, 53, 405201. [Google Scholar] [CrossRef]
- Pescini, E.; Suma, A.; De Giorgi, M.G.; Francioso, L.; Ficarella, A. Optimization of Plasma Actuator Excitation Waveform and Materials for Separation Control in Turbomachinery. Energy Procedia 2017, 126, 786–793. [Google Scholar] [CrossRef]
- Wang, J.J.; Choi, K.S.; Feng, L.H.; Jukes, T.N.; Whalley, R.D. Recent developments in DBD plasma flow control. Prog. Aerosp. Sci. 2013, 62, 52–78. [Google Scholar] [CrossRef]
- Singh, K.P.; Roy, S. Force approximation for a plasma actuator operating in atmospheric air. J Appl Phys. 2008, 103, 13305. [Google Scholar] [CrossRef]
- Moreau, E.; Sosa, R.; Artana, G. Electric wind produced by surface plasma actuators: A new dielectric barrier discharge based on a three-electrode geometry. J. Phys. D Appl. Phys. 2008, 41, 115204. [Google Scholar] [CrossRef]
- Erfani, R.; Erfani, T.; Utyuzhnikov, S.V.; Kontis, K. Optimisation of multiple encapsulated electrode plasma actuator. Aerosp. Sci. Technol. 2013, 26, 120–127. [Google Scholar] [CrossRef]
- Nunes-Pereira, J.; Rodrigues, F.F.; Abdollahzadehsangroudi, M.; Páscoa, J.C.; Lanceros-Mendez, S. Improved Performance of Polyimide Cirlex-Based Dielectric Barrier Discharge Plasma Actuators for Flow Control. Polym. Adv. Technol. 2022, 33, 1278–1290. [Google Scholar] [CrossRef]
- Portugal, S.; Roy, S.; Lin, J. Functional relationship between material property, applied frequency and ozone generation for surface dielectric barrier discharges in atmospheric air. Sci. Rep. 2017, 7, 6388. [Google Scholar] [CrossRef] [PubMed]
- Shvydyuk, K.O.; Rodrigues, F.F.; Nunes-Pereira, J.; Páscoa, J.C.; Lanceros-Mendez, S. Long-Lasting Ceramic Composites for Surface Dielectric Barrier Discharge Plasma Actuators. J. Eur. Ceram. Soc. 2023, 43, 6112–6121. [Google Scholar] [CrossRef]
- Huang, J.; Corke, T.C.; Thomas, F.O. Plasma actuators for separation control of low-pressure turbine blades. AIAA J. 2016, 44, 51–57. [Google Scholar] [CrossRef]
- Das Gupta, A.; Roy, S. Effect of plasma actuator control parameters on a transitional flow. J. Phys. D Appl. Phys. 2018, 51, 135204. [Google Scholar] [CrossRef]
- Mclaughlin, T.E.; Munska, M.D.; Vaeth, J.P.; Dauwalter, T.E.; Goode, J.R.; Siegeli, S.G. Plasma-Based Actuators for Cylinder Wake Vortex Control. In Proceedings of the 2nd AIAA Flow Control Conference, Portland, OR, USA, 28 June–1 July 2004. [Google Scholar] [CrossRef]
- Anzalotta, C.; Joshi, K.; Fernandez, E.; Bhattacharya, S. Effect of forcing the tip-gap of a NACA0065 airfoil us-ing plasma actuators: A proof-of-concept study. Aerosp. Sci. Technol. 2020, 107, 106268. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Gregory, J.W. The optimum wavelength of spanwise segmented plasma actuator forcing of a circular cylinder wake. In Proceedings of the 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar] [CrossRef]
- Joshi, K.; Latrobe, B.; Bhattacharya, S. Altering the wake dynamics of a circular cylinder with harmonic forcing. Phys. Fluids 2023, 35, 65139. [Google Scholar] [CrossRef]
- Joshi, K.; Bhattacharya, S. Large-eddy simulation of the effect of distributed plasma forcing on the wake of a circular cylinder. Comput. Fluids 2019, 193, 104295. [Google Scholar] [CrossRef]
- Kopiev, V.F.; Kazansky, P.N.; Kopiev, V.A.; Moralev, I.A.; Zaytsev, M.Y. HF DBD Plasma Actuators for Reduction of Cylinder Noise in Flow. J. Phys. D Appl. Phys. 2017, 50, 475204. [Google Scholar] [CrossRef]
- Neretti, G.; Cristofolini, A.; Borghi, C.A. Experimental investigation on a vectorized aerodynamic dielectric barrier discharge plasma actuator array. J. Appl. Phys. 2014, 115, 163304. [Google Scholar] [CrossRef]
- Benmoussa, A.; Páscoa, J.C. Enhancement of a Cycloidal Self-Pitch Vertical Axis Wind Turbine Performance Through DBD Plasma Actuators at Low Tip Speed Ratio. Int. J. Thermofluids 2023, 17, 100258. [Google Scholar] [CrossRef]
- Kaneko, Y.; Nishida, H.; Tagawa, Y. Visualization of the Electrohydrodynamic and Thermal Effects of AC-DBD Plasma Actuators of Plate- and Wire-Exposed Electrodes. Actuators 2022, 11, 38. [Google Scholar] [CrossRef]
- Meng, X.; Hu, H.; Li, C.; Abbasi, A.A.; Cai, J.; Hu, H. Mechanism study of coupled aerodynamic and thermal effects using plasma actuation for anti-icing. Phys. Fluids 2019, 31, 37103. [Google Scholar] [CrossRef]
- Xie, L.; Liang, H.; Zong, H.; Liu, X.; Li, Y. Multipurpose distributed dielectric-barrier-discharge plasma actuation: Icing sensing, anti-icing, and flow control in one. Phys. Fluids 2022, 34, 71701. [Google Scholar] [CrossRef]
- Zhong, Y.; Jin, Z.; Chen, M.; Yang, Z. An experimental investigation of the thermal effects in AC-DBD plasma actuator on the melting process of an ice bead. Exp. Therm. Fluid Sci. 2023, 147, 110950. [Google Scholar] [CrossRef]
- Yun, C.Y.; Park, I.K.; Hwang, I.N.S.; Kim, S.J. Thrust Control Mechanism of VTOL UAV Cyclocopter with Cycloidal Blades System. J. Intell. Mater. Syst. Struct. 2005, 16, 937–943. [Google Scholar] [CrossRef]
- Shyy, W.; Jayaraman, B.; Andersson, A. Modeling of Glow Discharge-Induced Fluid Dynamics. J. Appl. Phys. 2002, 92, 6434–6443. [Google Scholar] [CrossRef]
- Abdelraouf, H.; Elmekawy, A.M.N.; Kassab, S.Z. Simulations of flow separation control numerically using different plasma actuator models. Alex. Eng. J. 2020, 59, 3881–3896. [Google Scholar] [CrossRef]
- Suzen, Y.B.; Huang, P.G. Simulations of flow separation control using plasma actuators. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; Volume 14, pp. 10456–10464. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Motta, V.; Suma, A. Influence of actuation parameters of multi-DBD plasma actuators on the static and dynamic behaviour of an airfoil in unsteady flow. Aerosp. Sci. Technol. 2020, 96, 105587. [Google Scholar] [CrossRef]
- Yu, H.; Zheng, J. Numerical investigation of control of dynamic stall over a NACA0015 airfoil using dielectric barrier discharge plasma actuators. Phys. Fluids 2020, 32, 35103. [Google Scholar] [CrossRef]
- Ma, L.; Wang, X.; Zhu, J.; Kang, S. Dynamic Stall of a Vertical-Axis Wind Turbine and Its Control Using Plasma Actuation. Energies 2019, 12, 3738. [Google Scholar] [CrossRef]
- Daraee, M.A.; Abbasi, S. A novel approach to performance improvement of a VAWT using plasma actuators. J. Clean. Prod. 2023, 424, 138876. [Google Scholar] [CrossRef]
- Yoon, J.-S.; Han, J.-H. Semiempirical Thrust Model of Dielectric Barrier Plasma Actuator for Flow Control. J. Aerosp. Eng. 2013, 28, 04014041. [Google Scholar] [CrossRef]
- Abdollahzadeh, M.; Páscoa, J.C.; Oliveira, P.J. Modified Split-Potential Model for Modeling the Effect of DBD Plasma Actuators in High Altitude Flow Control. Curr. Appl. Phys. 2014, 14, 1160–1170. [Google Scholar] [CrossRef]
- Roth, J.R.; Sherman, D.M.; Wilkinson, S.P. Electrohydrodynamic Flow Control with a Glow-Discharge Surface Plasma. AIAA J. 2000, 38970, 1166–1177. [Google Scholar] [CrossRef]
- Tang, J.; Hu, Y.; Song, B. Investigation on the Unsteady Aerodynamics of Cycloidal Propeller in Hovering Flight. J. Intell. Robot. Syst. 2015, 229, 2519–2536. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Montazeri, H.; Blocken, B. On the Accuracy of Turbulence Models for CFD Simulations of Vertical Axis Wind Turbines. Energy 2019, 180, 838–857. [Google Scholar] [CrossRef]
- Shi, L.; Wang, Y.; Bayeul-Lainé, A.C.; Coutier-Delgosha, O. Effect of Time-Varying Freestream on Performance and Vortex Dynamics of Forward and Reversed Pitching Airfoils. J. Fluids Struct. 2022, 110, 103508. [Google Scholar] [CrossRef]
- Zare Chavoshi, M.; Ebrahimi, A. Plasma Actuator Effects on the Flow Physics of Dynamic Stall for a Vertical Axis Wind Turbine. Phys. Fluids 2022, 34, 075131. [Google Scholar] [CrossRef]
- Zhou, D.; Zhou, D.; Xu, Y.; Sun, X. Performance enhancement of straight-bladed vertical axis wind turbines via active flow control strategies: A review. Meccanica. 2022, 57, 255–282. [Google Scholar] [CrossRef]
- Wills, D.; Schwaiger, M. D-Dalus. In Proceedings of the US EUCOM Science & Technology Conference, Stuttgart, Germany, 24 April 2012. [Google Scholar]
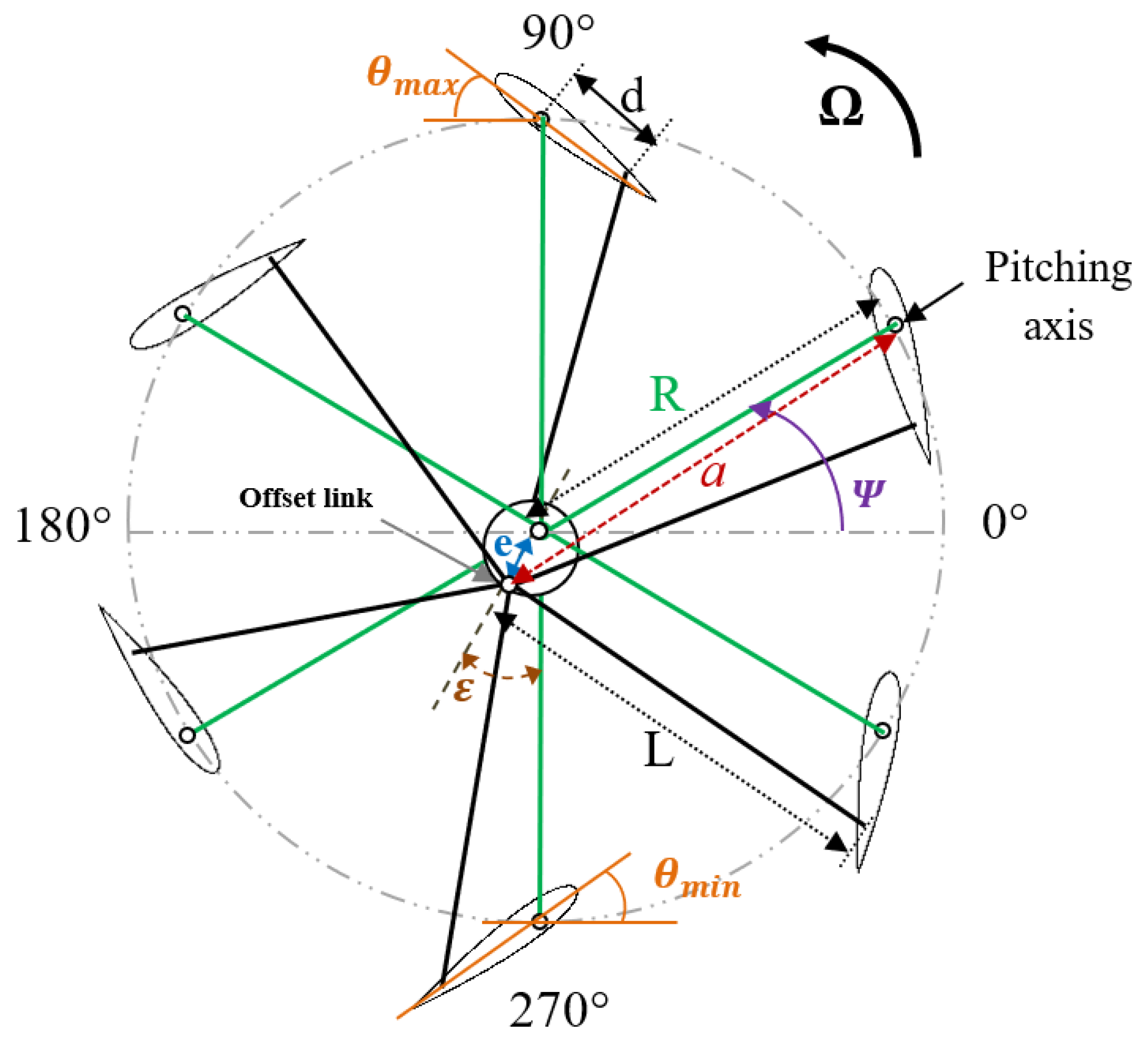






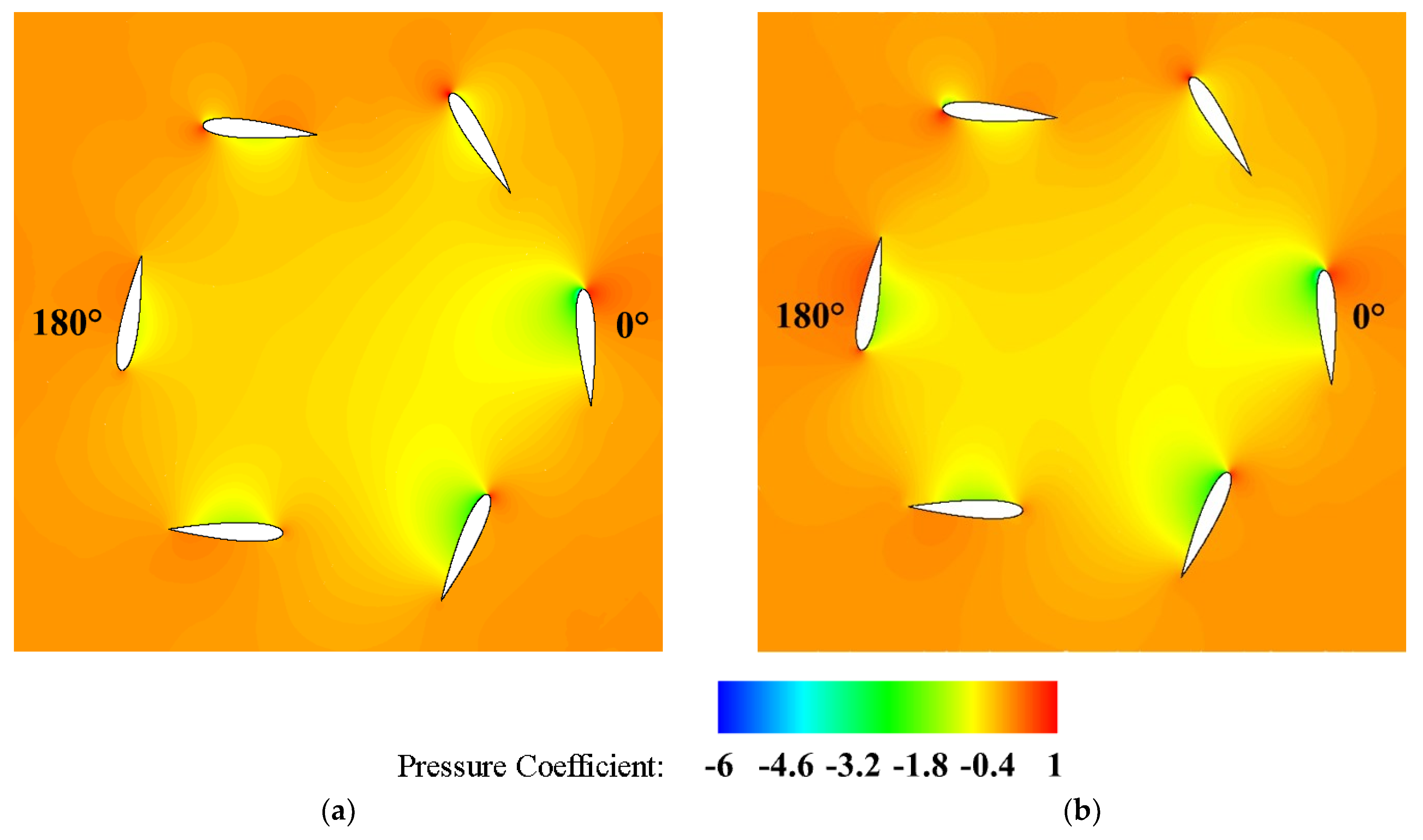

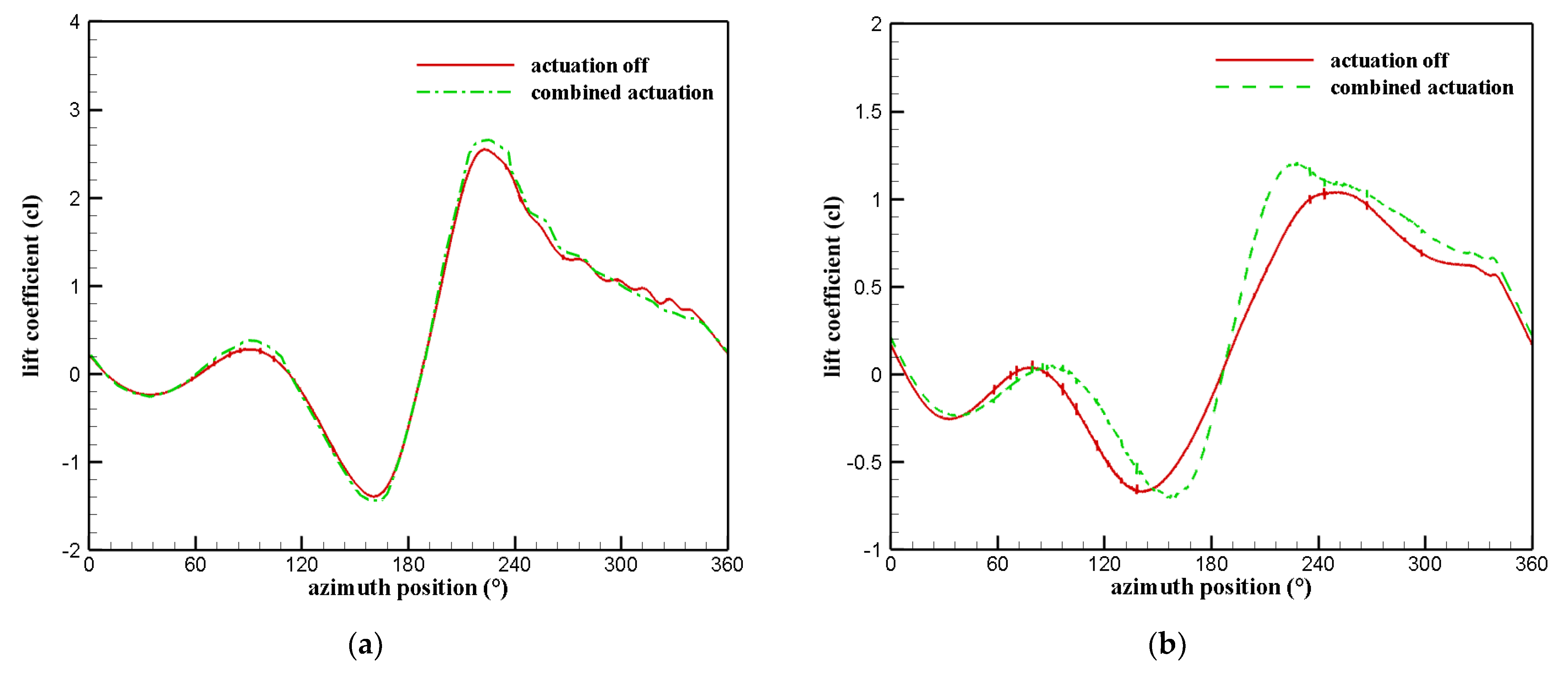
| Variable | Value |
|---|---|
| Profile | NACA 0016 |
| Number of blades | 6 |
| Rotor radius (R) | 0.6 m |
| Chord (c) | 0.3 m |
| Pitching axis | 0.105 m |
| Control rod length (L) | 0.61 m |
| Magnitude of eccentricity (e) | 0.072 m |
| Eccentricity phase angle (ε) | 0° |
| Control rod distance (d) | 0.12 m |
| Pitching angle extremities () | 36°; −39° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benmoussa, A.; Rodrigues, F.F.; Páscoa, J.C. Plasma Actuators for Cycloidal Rotor Thrust Vectoring Enhancement in Airships. Actuators 2023, 12, 436. https://doi.org/10.3390/act12120436
Benmoussa A, Rodrigues FF, Páscoa JC. Plasma Actuators for Cycloidal Rotor Thrust Vectoring Enhancement in Airships. Actuators. 2023; 12(12):436. https://doi.org/10.3390/act12120436
Chicago/Turabian StyleBenmoussa, Amine, Frederico F. Rodrigues, and José C. Páscoa. 2023. "Plasma Actuators for Cycloidal Rotor Thrust Vectoring Enhancement in Airships" Actuators 12, no. 12: 436. https://doi.org/10.3390/act12120436
APA StyleBenmoussa, A., Rodrigues, F. F., & Páscoa, J. C. (2023). Plasma Actuators for Cycloidal Rotor Thrust Vectoring Enhancement in Airships. Actuators, 12(12), 436. https://doi.org/10.3390/act12120436








