Effect of the Magnetorheological Damper Dynamic Behaviour on the Rail Vehicle Comfort: Hardware-in-the-Loop Simulation
Abstract
:1. Introduction
Problem Formulation
2. Materials and Methods
2.1. Vehicle Model
2.2. Hardware-in-the-Loop Simulation
2.3. Magnetorheological Damper
2.3.1. F-v-I Map
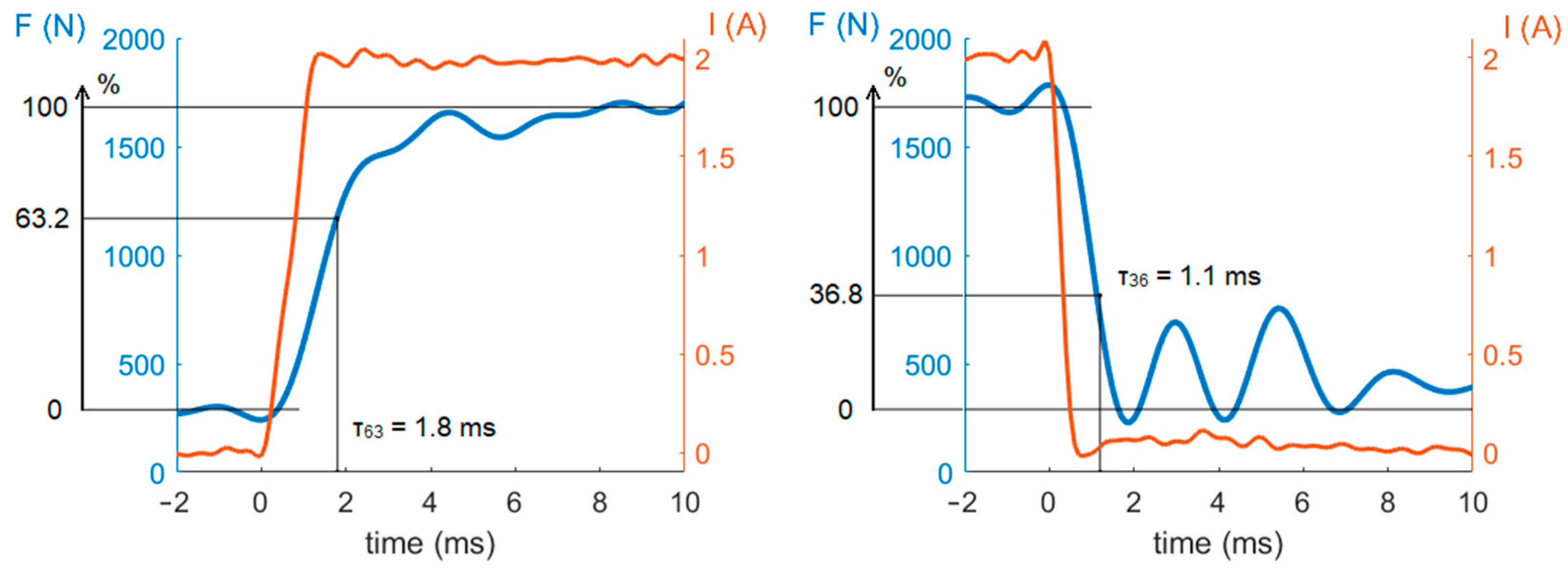
2.3.2. Response Time
2.4. Semi-Active Control
2.4.1. Skyhook
2.4.2. Skyhook Linear
2.4.3. Acceleration Driven Damper
2.4.4. Acceleration Driven Damper Linear
2.5. Plan of Experiments and Evaluation Method
3. Results and Discussion
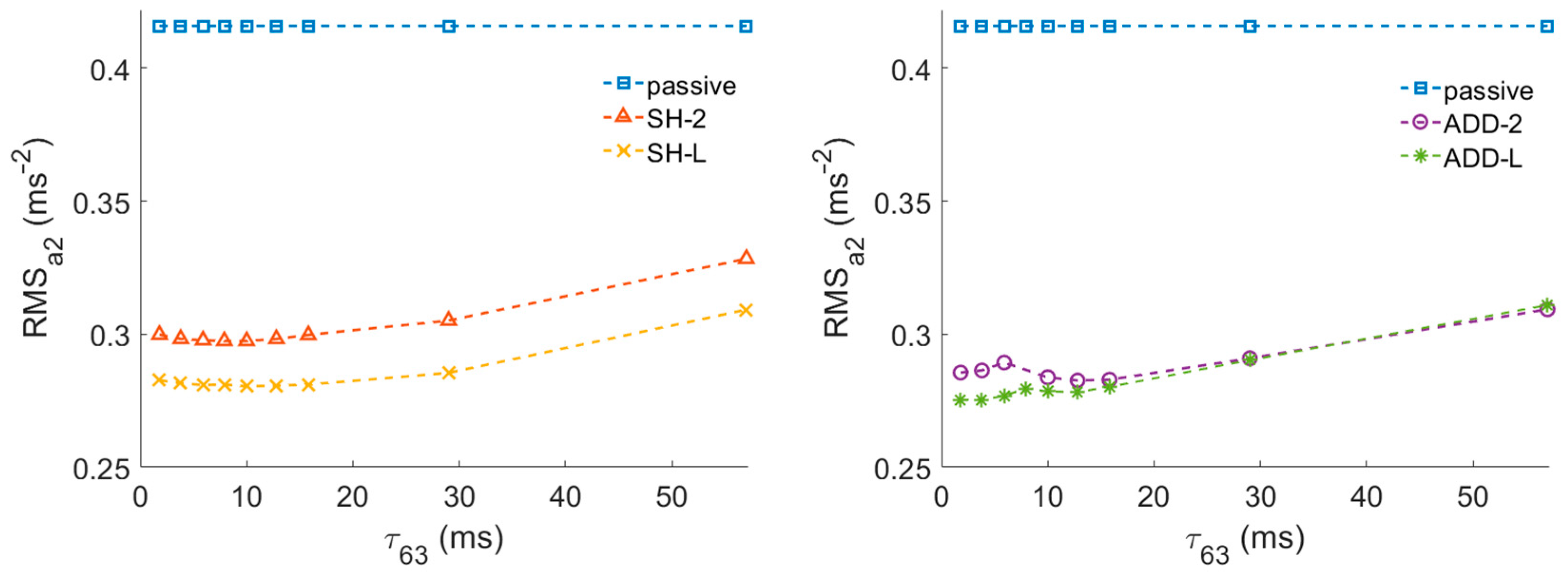
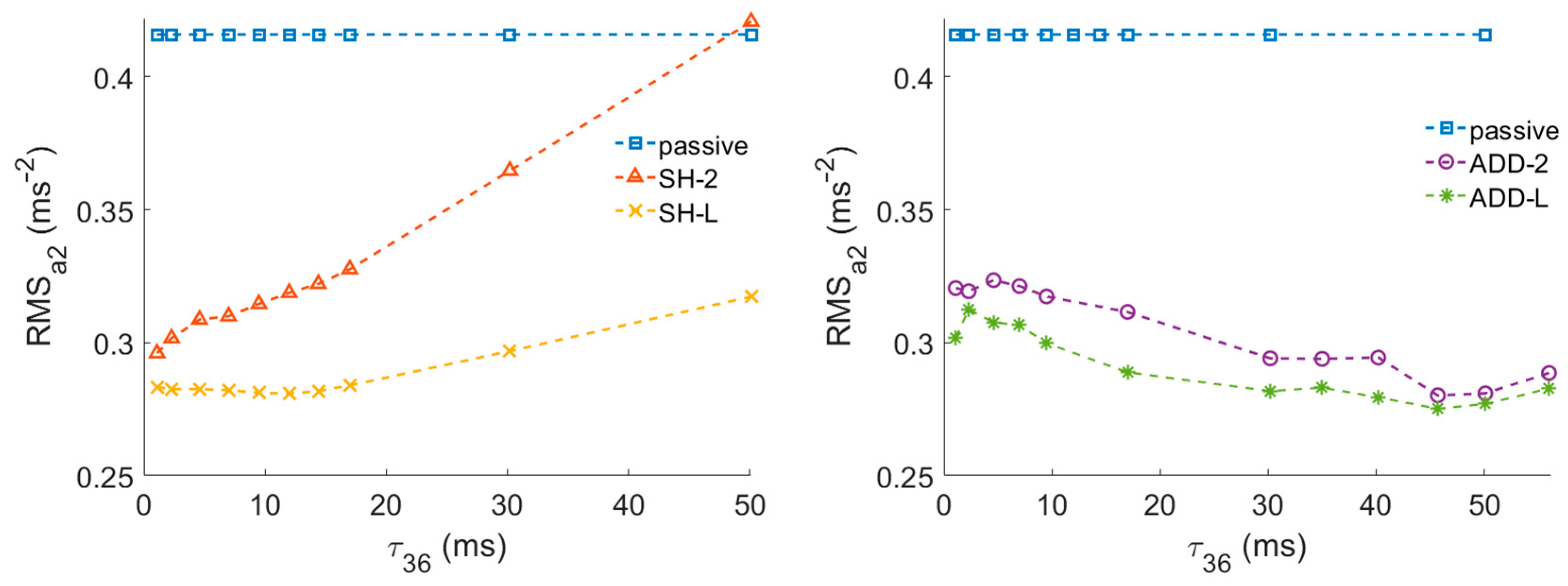
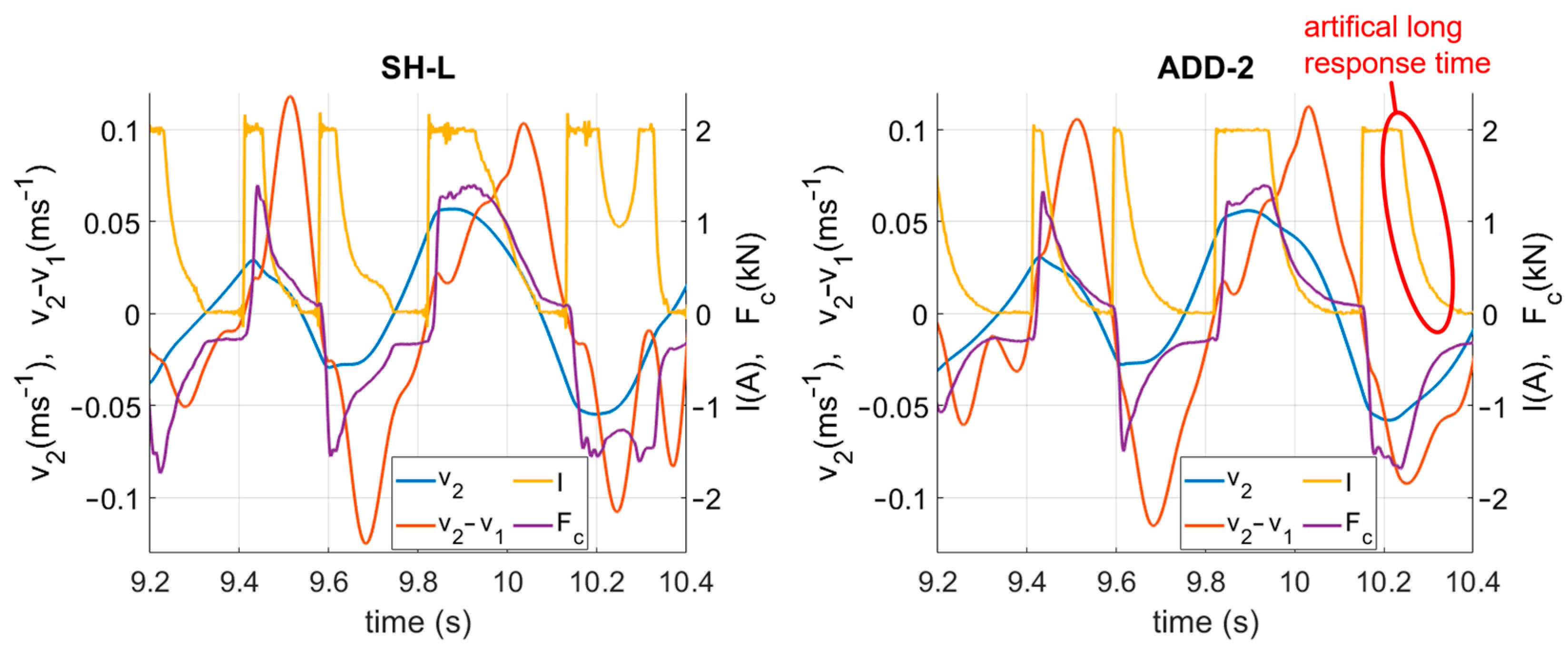
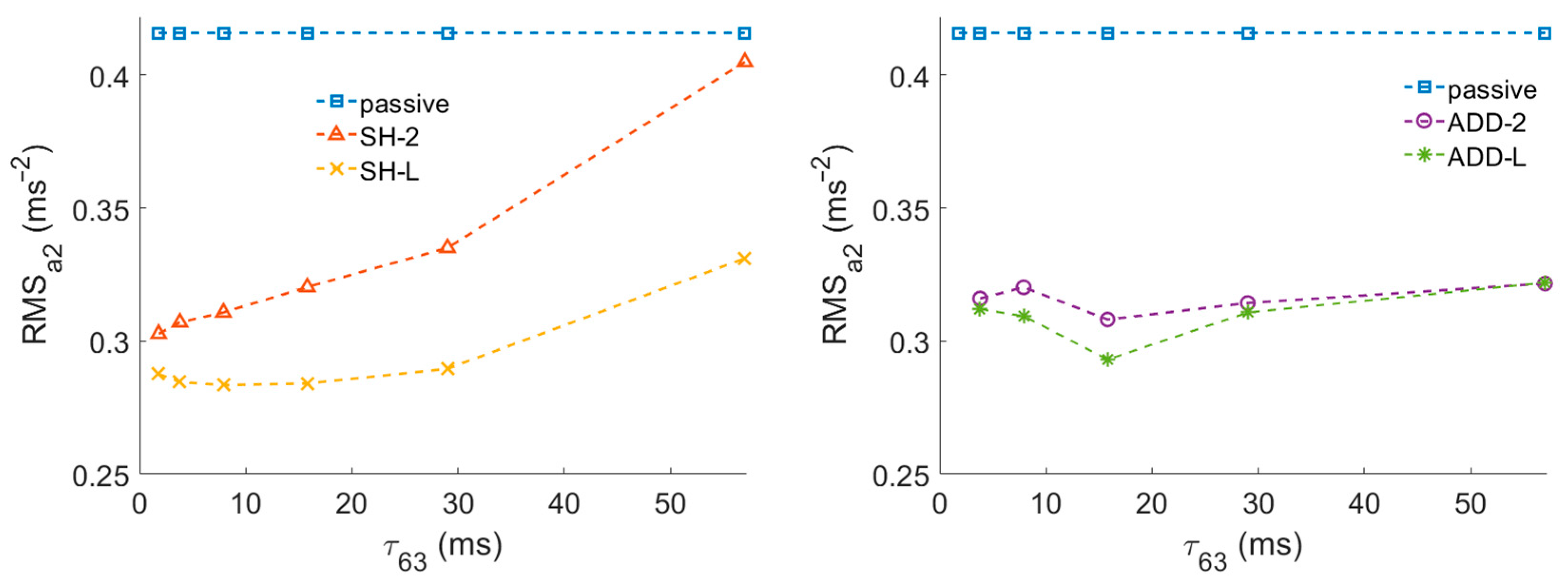
3.1. Response Time Effect
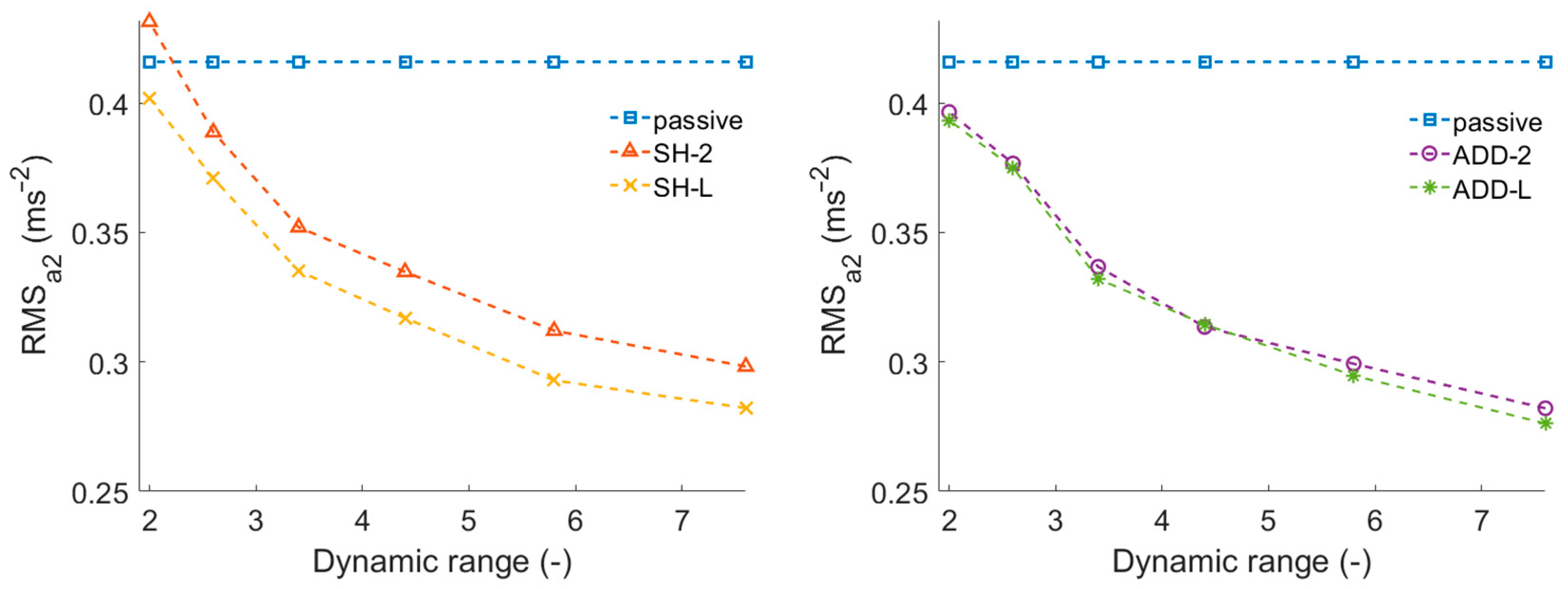
3.2. Dynamic Force Range Effect
3.3. Benefits of Each Algorithm
4. Conclusions
- Force drop response time is more important than force rise response time for S/A control performance.
- In this dynamic system, there is no point in shortening the response time to less than τ63 = 8 ms.
- The newly designed Acceleration Driven Damper Linear algorithm is best suited for damping the railway vehicle’s carbody lateral movement.
- Under ideal conditions, vibrations were reduced by 34%.
- Acceleration Driven Damper (two states) achieves the same effectiveness as Skyhook Linear, but Acceleration Driven Damper is easier to implement in real vehicles.
- For better results, it would be appropriate to increase the dynamic range by at least 10.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goodall, R.M. Control Engineering Challengs for Railway Trains of the Future. Meas. Control 2011, 44, 16–24. [Google Scholar] [CrossRef]
- Pérez, J.; Busturia, J.M.; Goodall, R.M. Control Strategies for Active Steering of Bogie-Based Railway Vehicles. Control Eng. Pract. 2002, 10, 1005–1012. [Google Scholar] [CrossRef]
- Shin, Y.J.; You, W.H.; Hur, H.M.; Park, J.H. Semi-Active Control to Reduce Carbody Vibration of Railway Vehicle by Using Scaled Roller Rig. J. Mech. Sci. Technol. 2012, 26, 3423–3431. [Google Scholar] [CrossRef]
- Codecà, F.; Savaresi, S.M.; Spelta, C.; Montiglio, M.; Ieluzzi, M. Semiactive Control of a Secondary Train Suspension. In Proceedings of the 2007 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Zurich, Switzerland, 4–7 September 2007. [Google Scholar] [CrossRef]
- Strecker, Z.; Jeniš, F.; Kubík, M.; Macháček, O.; Choi, S.B. Novel Approaches to the Design of an Ultra-Fast Magnetorheological Valve for Semi-Active Control. Materials 2021, 14, 2500. [Google Scholar] [CrossRef] [PubMed]
- Jeniš, F.; Kubík, M.; Macháček, O.; Šebesta, K.; Strecker, Z. Insight into the Response Time of Fail-Safe Magnetorheological Damper. Smart Mater. Struct. 2021, 30, 017004. [Google Scholar] [CrossRef]
- Spelta, C.; Savaresi, S.M.; Codecà, F.; Montiglio, M.; Ieluzzi, M. Smart-Bogie: Semi-Active Lateral Control of Railway Vehicles. Asian J. Control 2012, 14, 875–890. [Google Scholar] [CrossRef]
- Lau, Y.K.; Liao, W.H. Design and Analysis of Magnetorheological Dampers for Train Suspension. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2005, 219, 261–276. [Google Scholar] [CrossRef]
- Shin, Y.-J.; You, W.-H.; Hur, H.-M.; Park, J.-H.; Lee, G.-S. Improvement of Ride Quality of Railway Vehicle by Semiactive Secondary Suspension System on Roller Rig Using Magnetorheological Damper. Adv. Mech. Eng. 2014, 6, 298382. [Google Scholar] [CrossRef] [Green Version]
- Hudha, K.; Harun, M.H.; Harun, M.H.; Jamaluddin, H. Lateral Suspension Control of Railway Vehicle Using Semi-Active Magnetorheological Damper. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 728–733. [Google Scholar] [CrossRef]
- Žáček, J.; Šebesta, K.; Mohammad, H.; Jeniš, F.; Strecker, Z.; Kubík, M. Experimental Evaluation of Modified Groundhook Car Suspension with Fast Magnetorheological Damper. Actuators 2022, 11, 354. [Google Scholar] [CrossRef]
- Jeyasenthil, R.; Yoon, D.S.; Choi, S.B. Response Time Effect of Magnetorheological Dampers in a Semi-Active Vehicle Suspension System: Performance Assessment with Quantitative Feedback Theory. Smart Mater. Struct. 2019, 28, 054001. [Google Scholar] [CrossRef]
- Koo, J.H.; Goncalves, F.D.; Ahmadian, M. A Comprehensive Analysis of the Response Time of MR Dampers. Smart Mater. Struct. 2006, 15, 351–358. [Google Scholar] [CrossRef]
- Yoon, D.S.; Park, Y.J.; Choi, S.B. An Eddy Current Effect on the Response Time of a Magnetorheological Damper: Analysis and Experimental Validation. Mech. Syst. Signal Process. 2019, 127, 136–158. [Google Scholar] [CrossRef]
- Macháček, O.; Kubík, M.; Strecker, Z.; Roupec, J.; Mazůrek, I. Design of a Frictionless Magnetorheological Damper with a High Dynamic Force Range. Adv. Mech. Eng. 2019, 11, 1687814019827440. [Google Scholar] [CrossRef] [Green Version]
- Choi, S.B.; Nam, M.H.; Lee, B.K. Vibration Control of a MR Seat Damper for Commercial Vehicles. J. Intell. Mater. Syst. Struct. 2001, 11, 936–944. [Google Scholar] [CrossRef]
- Lee, H.S.; Choi, S.B. Control and Response Characteristics of a Magneto-Rheological Fluid Damper for Passenger Vehicles. J. Intell. Mater. Syst. Struct. 2000, 11, 80–87. [Google Scholar] [CrossRef]
- Misselhorn, W.E.; Theron, N.J.; Els, P.S. Investigation of Hardware-in-the-Loop for Use in Suspension Development. Veh. Syst. Dyn. 2006, 44, 65–81. [Google Scholar] [CrossRef]
- Kwak, M.K.; Lee, J.H.; Yang, D.H.; You, W.H. Hardware-in-the-Loop Simulation Experiment for Semi-Active Vibration Control of Lateral Vibrations of Railway Vehicle by Magneto-Rheological Fluid Damper. Veh. Syst. Dyn. 2014, 52, 891–908. [Google Scholar] [CrossRef]
- Oh, Y.J.; Lee, J.K.; Liu, H.C.; Cho, S.; Lee, J.; Lee, H.J. Hardware-in-the-Loop Simulation for Active Control of Tramcars with Independently Rotating Wheels. IEEE Access 2019, 7, 71252–71261. [Google Scholar] [CrossRef]
- Zelenka, J.; Michalek, T.; Kohout, M. Comparative Simulations of Guiding Behaviour of an Electric Locomotive. In Proceedings of the 20th International Conference Engineering Mechanics 2014, Svratka, Czech Republic, 12–15 May 2014; pp. 740–743. [Google Scholar]
- Goncalves, F.D.; Koo, J.H.; Ahmadian, M. Experimental Approach for Finding the Response Time of Mr Dampers for Vehicle Applications. In Proceedings of the ASME Design Engineering Technical Conference; ASME: New York, NY, USA, 2003; Volume 5 A, pp. 425–430. [Google Scholar]
- Guan, X.; Guo, P.; Ou, J. Study of the Response Time of MR Dampers. In Proceedings of the Second International Conference on Smart Materials and Nanotechnology in Engineering, Weihai, China, 8–11 July 2009; Volume 7493, p. 74930U. [Google Scholar] [CrossRef]
- Koo, J.-H.; Goncalves, F.D.; Ahmadian, M. Investigation of the Response Time of Magnetorheological Fluid Dampers. In Smart Structures and Materials 2004: Damping and Isolation; SPIE: Bellingham, WA, USA, 2004; Volume 5386, p. 63. [Google Scholar] [CrossRef]
- Strecker, Z.; Roupec, J.; Mazurek, I.; Machacek, O.; Kubik, M.; Klapka, M. Design of Magnetorheological Damper with Short Time Response. J. Intell. Mater. Syst. Struct. 2015, 26, 1951–1958. [Google Scholar] [CrossRef]
- Karnopp, D.; Crosby, M.J.; Harwood, R.A. Vibration Control Using Semi-Active Force Generators. J. Eng. Ind. 1974, 96, 619. [Google Scholar] [CrossRef] [Green Version]
- Sammier, D.; Sename, O.; Dugard, L. Skyhook and H∞ Control of Semi-Active Suspensions: Some Practical Aspects. Veh. Syst. Dyn. 2003, 39, 279–308. [Google Scholar] [CrossRef]
- Savaresi, S.M.; Silani, E.; Bittanti, S. Acceleration-Driven-Damper (ADD): An Optimal Control Algorithm for Comfort-Oriented Semiactive Suspensions. J. Dyn. Syst. Meas. Control. Trans. ASME 2005, 127, 218–229. [Google Scholar] [CrossRef]
- Savaresi, S.M.; Spelta, C. Mixed Sky-Hook and ADD: Approaching the Filtering Limits of a Semi-Active Suspension. J. Dyn. Syst. Meas. Control. Trans. ASME 2007, 129, 382–392. [Google Scholar] [CrossRef]
- EN 14363:2016+A1; Railway Applications—Testing and Simulation for the Acceptance of Running Characteristics of Railway Vehicles—Running Behaviour and Stationary Tests. CEN (European Committee for Standardization): Brusel, Belgium, 2020.
- Strecker, Z.; Mazůrek, I.; Roupec, J.; Klapka, M. Influence of MR Damper Response Time on Semiactive Suspension Control Efficiency. Meccanica 2015, 50, 1949–1959. [Google Scholar] [CrossRef]
- Kubík, M.; Strecker, Z.; Jeniš, F.; Macháček, O.; Přikryl, M.; Špalek, P. Magnetorheological Yaw Damper with Short Response Time for Rail- Way Vehicle Bogie. In Proceedings of the International Conference and Exhibition on New Actuator Systems and Applications 2021, Online, 17–19 February 2021; Volume 36, pp. 373–376. [Google Scholar]
- Yang, G.; Spencer, B.F.; Carlson, J.D.; Sain, M.K. Large-Scale MR Fluid Dampers: Modeling and Dynamic Performance Considerations. Eng. Struct. 2002, 24, 309–323. [Google Scholar] [CrossRef]
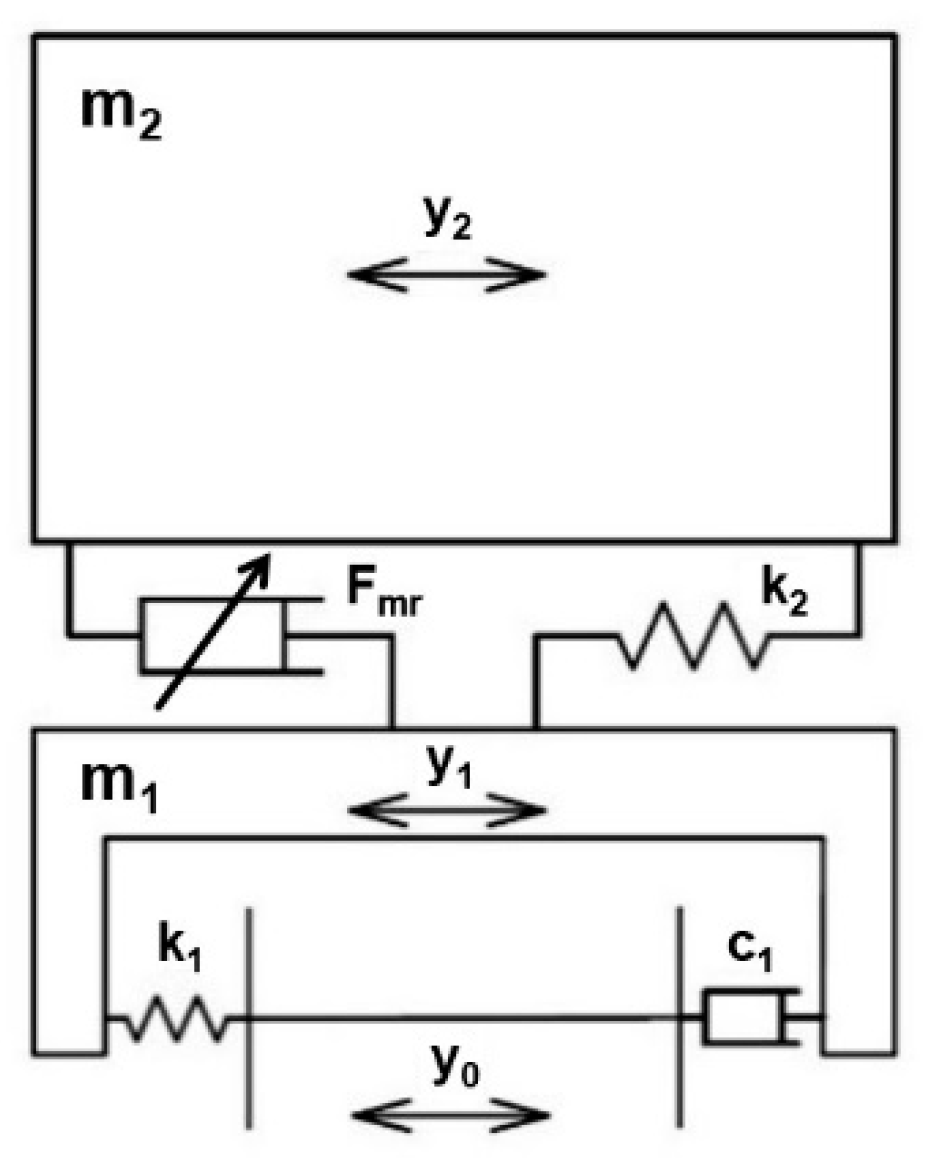
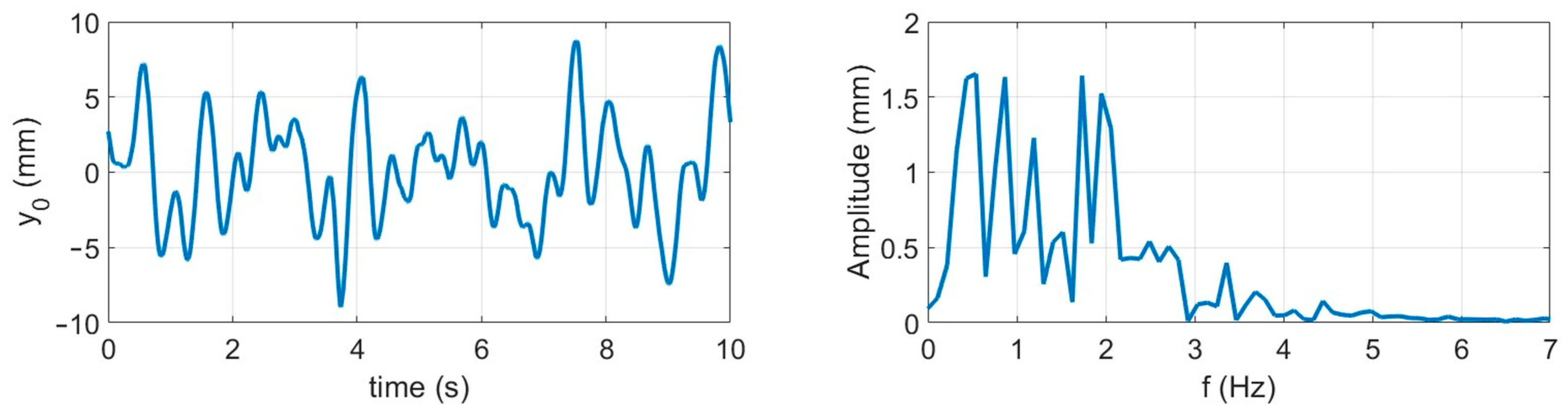
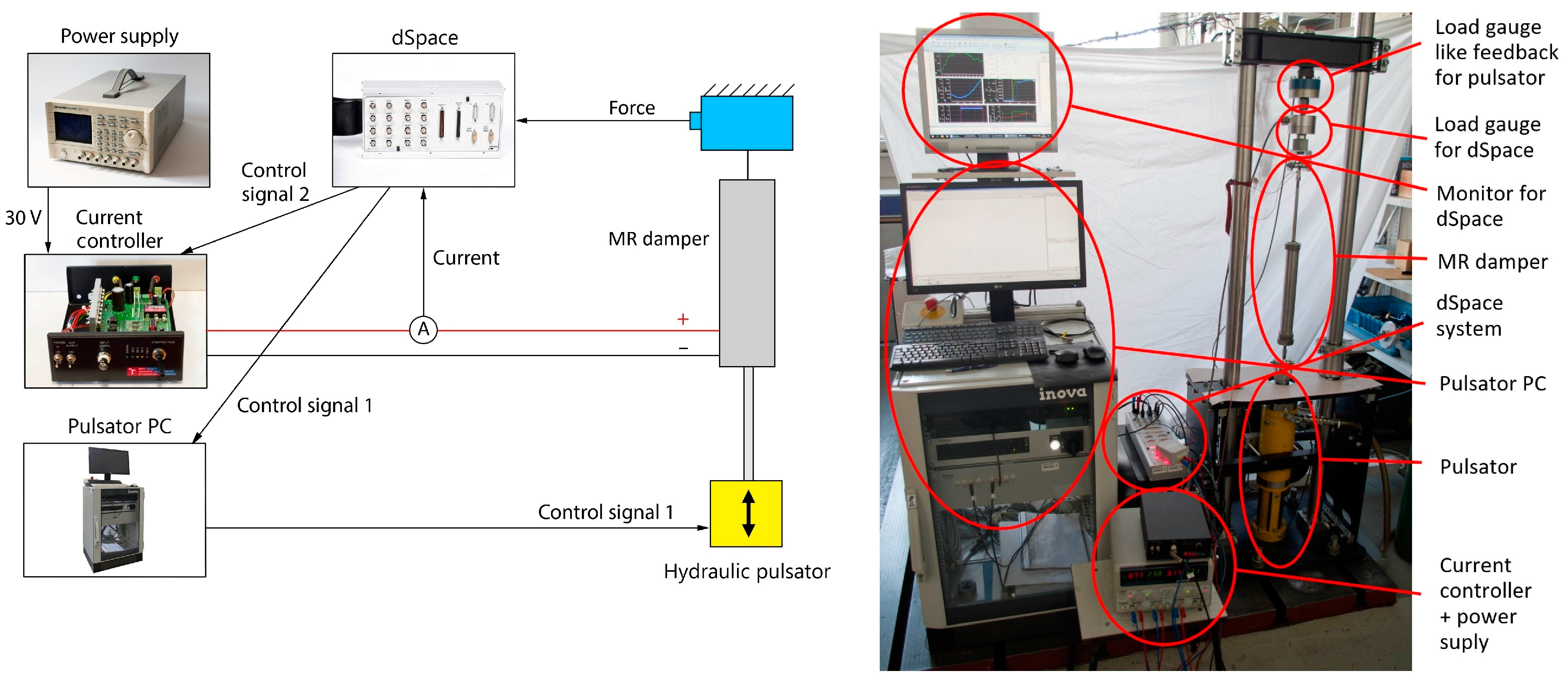
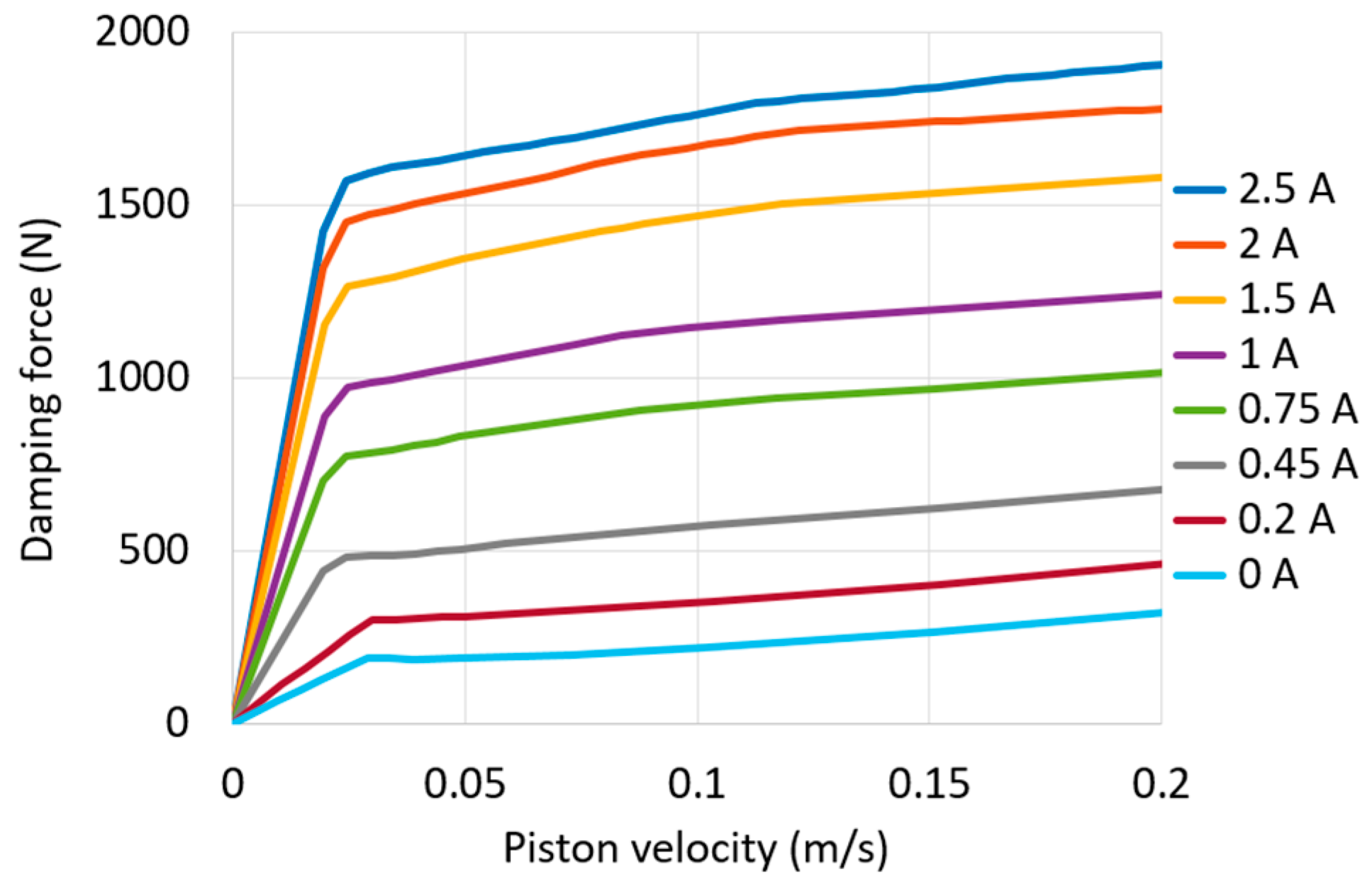

| Parameter | Symbol | Original | 1:5 Scale |
|---|---|---|---|
| half bogie frame weight | m1 | 5000 kg | 1000 kg |
| quarter carbody weight | m2 | 13,750 kg | 2750 kg |
| wheelset-bogie frame bond stiffness | k1 | 10 kN/mm | 2 kN/mm |
| bogie frame-carbody bond stiffness | k2 | 1 kN/mm | 0.2 kN/mm |
| wheelset-bogie frame bond damping | c1 | 10 kNs/m | 2 kNs/m |
| Case | DR at 0.1 m/s (-) | ||
|---|---|---|---|
| 1 | 1.8–56 | * | 7.6 |
| 2 | * | 1.1–56 | 7.6 |
| 3 | 1.8–56 | /1.7 | 7.6 |
| 4 | * | * | 2–7.6 |
| Algorithm | ||
|---|---|---|
| SH-2 | 7.9 | 1.1 |
| SH-L | 10 | 9.5 |
| ADD-2 | 12.8 | 46 |
| ADD-L | 3.8 | 46 |
| Mode | RMS (ms−2) | Improvement (%) |
|---|---|---|
| passive | 0.416 | 0 |
| SH-2 | 0.298 | 28.3 |
| SH-L | 0.282 | 32.2 |
| ADD-2 | 0.282 | 32.2 |
| ADD-L | 0.276 | 33.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeniš, F.; Kubík, M.; Michálek, T.; Strecker, Z.; Žáček, J.; Mazůrek, I. Effect of the Magnetorheological Damper Dynamic Behaviour on the Rail Vehicle Comfort: Hardware-in-the-Loop Simulation. Actuators 2023, 12, 47. https://doi.org/10.3390/act12020047
Jeniš F, Kubík M, Michálek T, Strecker Z, Žáček J, Mazůrek I. Effect of the Magnetorheological Damper Dynamic Behaviour on the Rail Vehicle Comfort: Hardware-in-the-Loop Simulation. Actuators. 2023; 12(2):47. https://doi.org/10.3390/act12020047
Chicago/Turabian StyleJeniš, Filip, Michal Kubík, Tomáš Michálek, Zbyněk Strecker, Jiří Žáček, and Ivan Mazůrek. 2023. "Effect of the Magnetorheological Damper Dynamic Behaviour on the Rail Vehicle Comfort: Hardware-in-the-Loop Simulation" Actuators 12, no. 2: 47. https://doi.org/10.3390/act12020047
APA StyleJeniš, F., Kubík, M., Michálek, T., Strecker, Z., Žáček, J., & Mazůrek, I. (2023). Effect of the Magnetorheological Damper Dynamic Behaviour on the Rail Vehicle Comfort: Hardware-in-the-Loop Simulation. Actuators, 12(2), 47. https://doi.org/10.3390/act12020047







