Position Control of a Cost-Effective Bellow Pneumatic Actuator Using an LQR Approach
Abstract
:1. Introduction
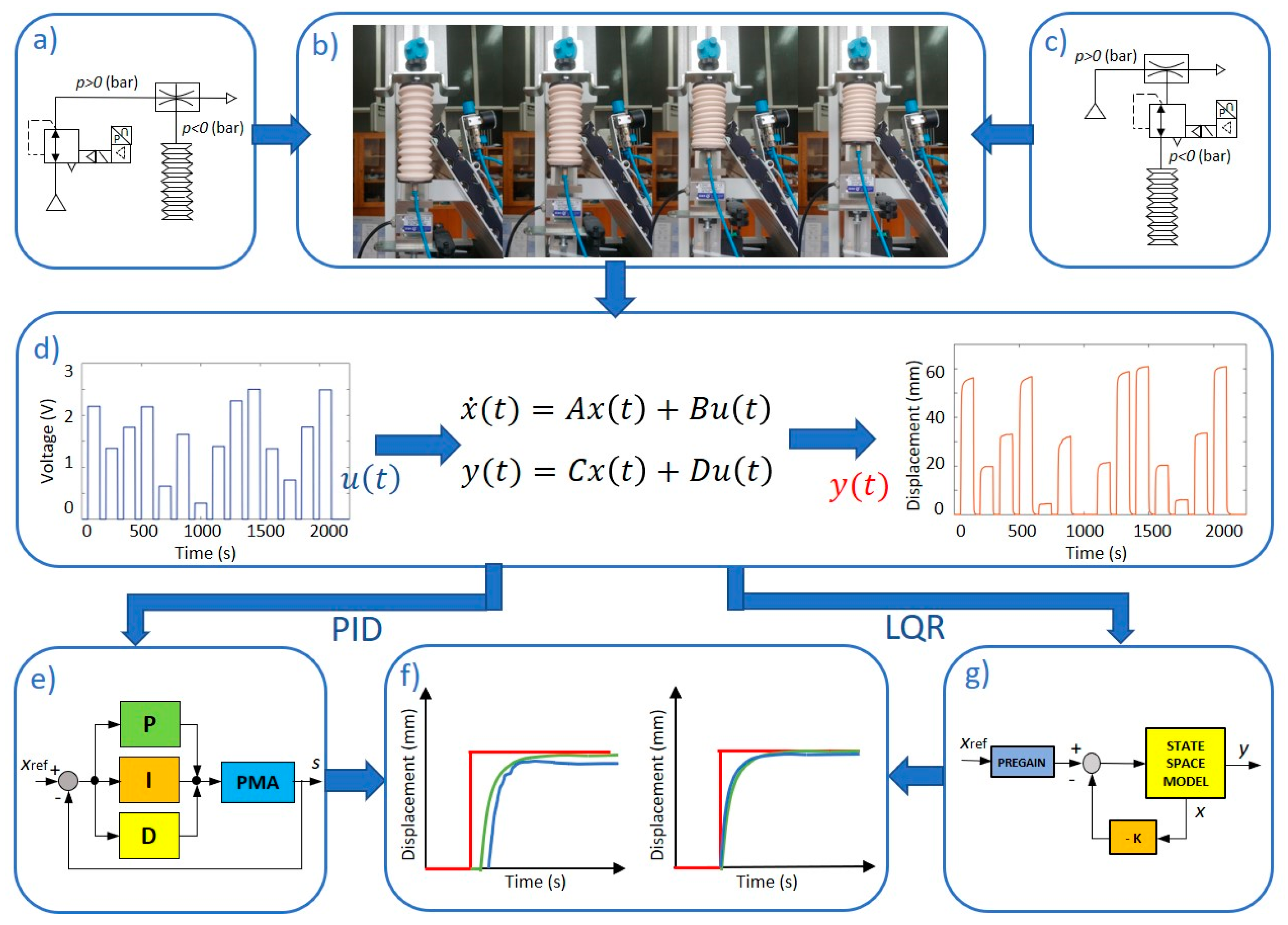
2. Materials and Methods
2.1. Experimental Apparatus
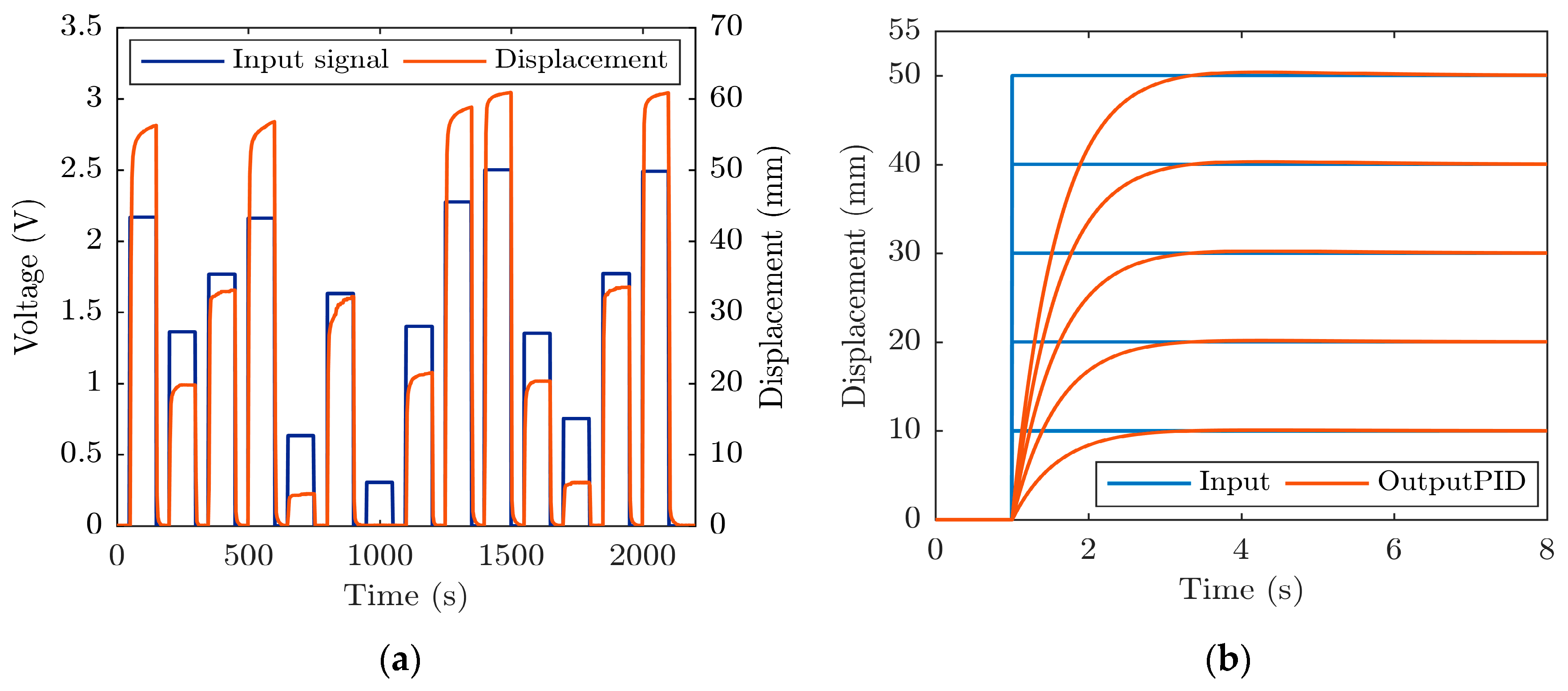
2.2. Numerical Modeling, PID Controller Development and Initial Experiments
2.3. Numerical Modeling, LQR Controller Development and Initial Experiments
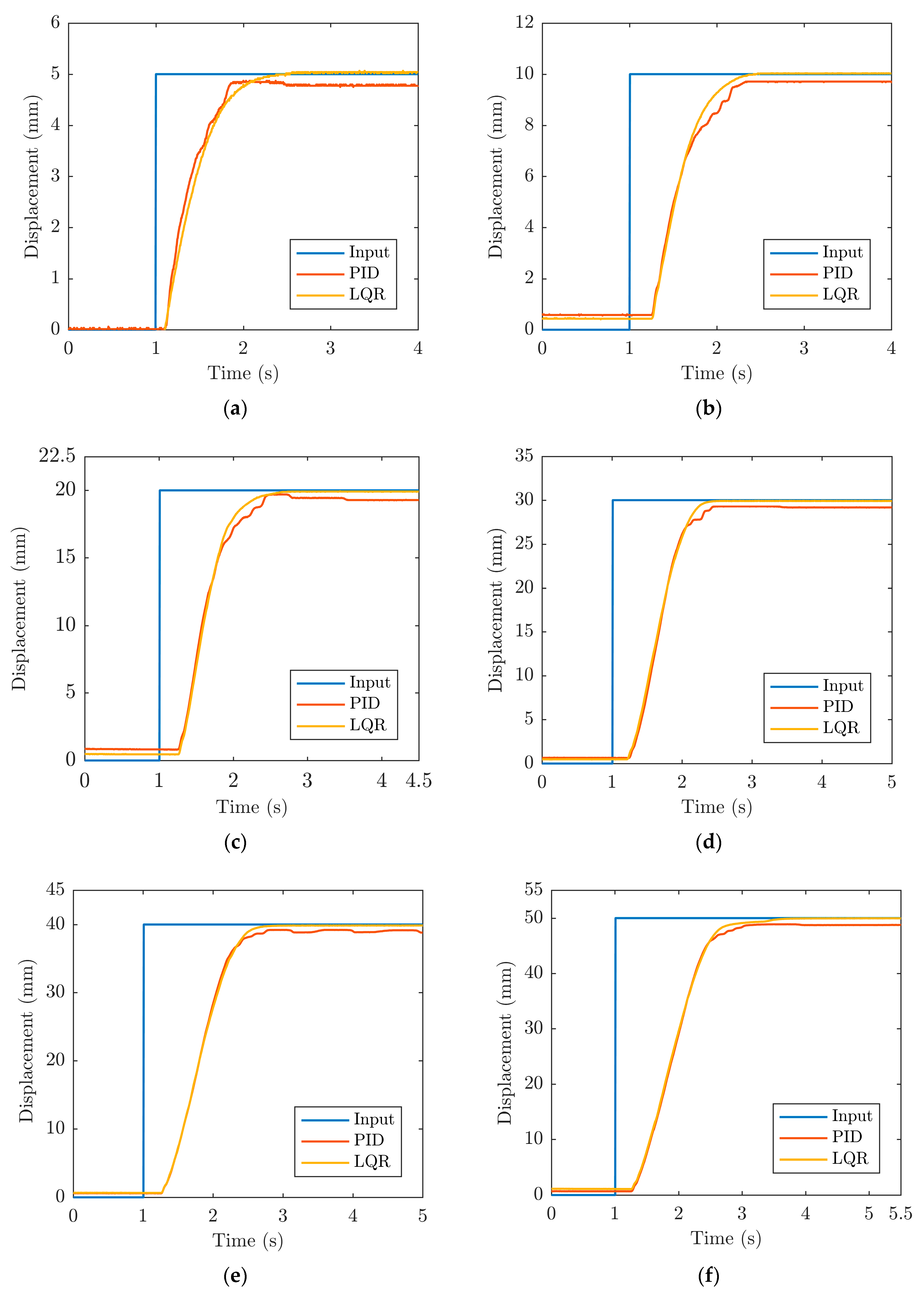
3. Results
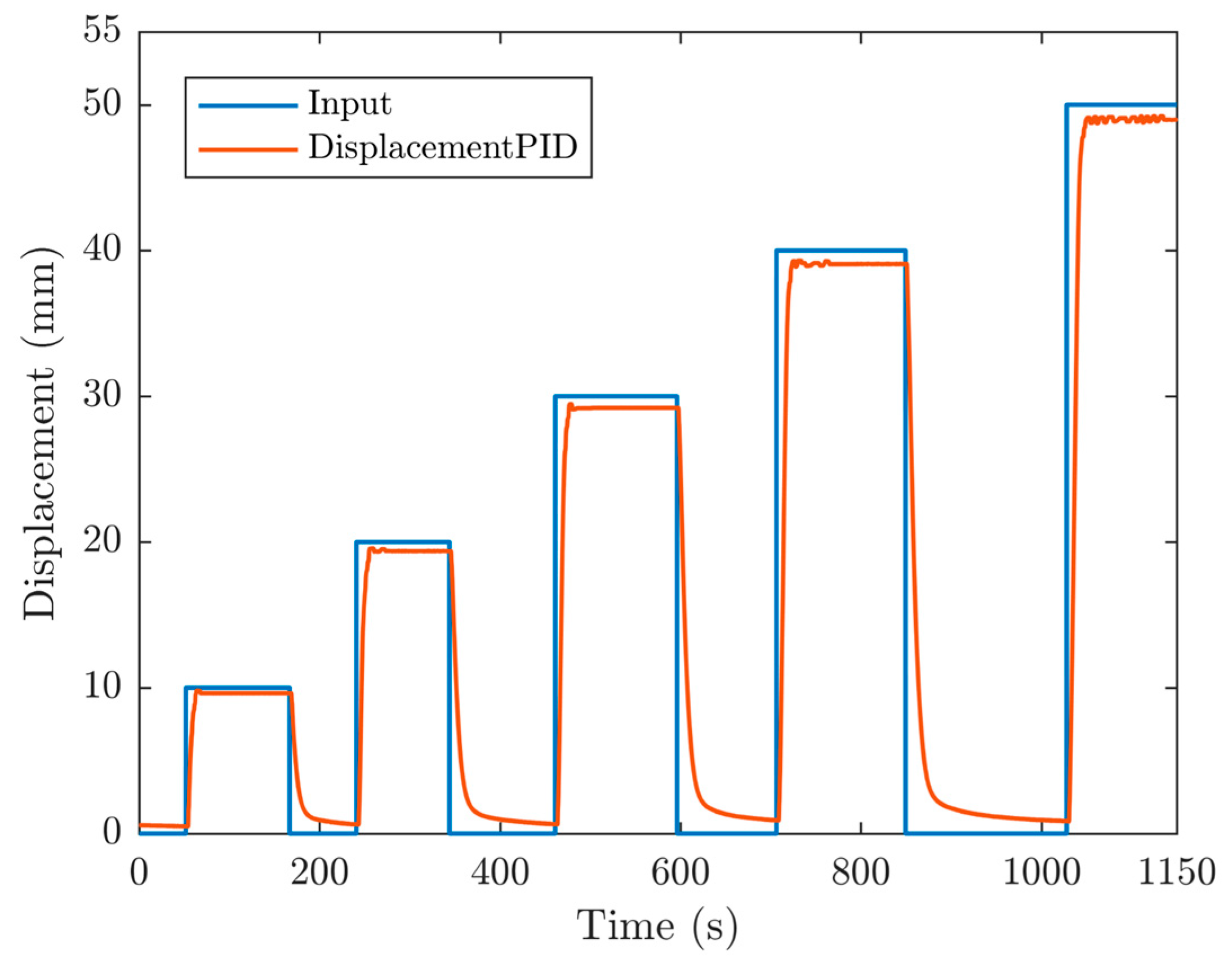
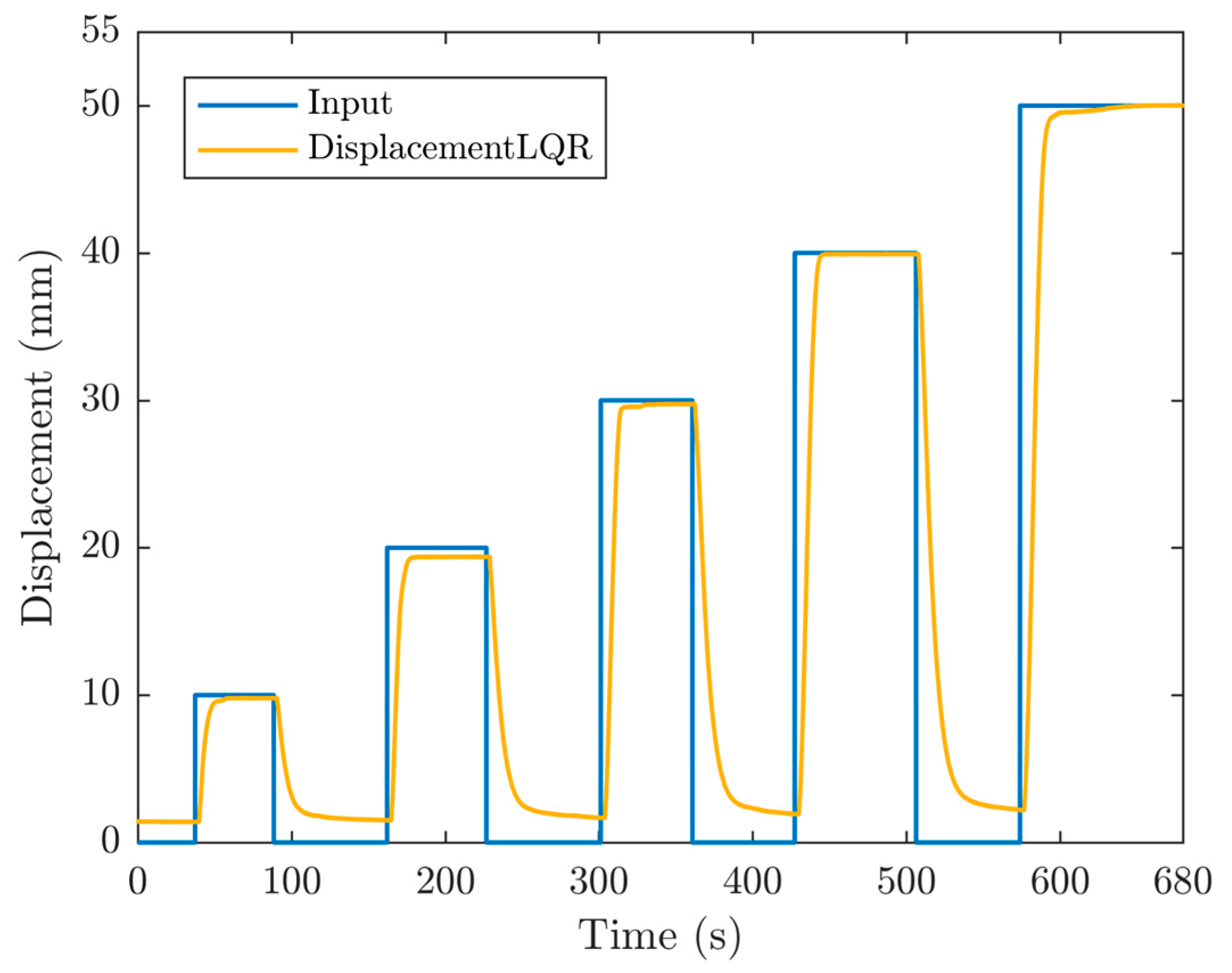
3.1. Position Performances of the Bellow PMA by Utilizing Indirect Vacuum Control
3.2. Position Performances of the Bellow PMA by Utilizing Direct Vacuum Control
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Su, H.; Hou, X.; Zhang, X.; Qi, W.; Cai, S.; Xiong, X.; Guo, J. Pneumatic soft robots: Challenge and benefits. Actuators 2022, 11, 92. [Google Scholar] [CrossRef]
- Walker, J.; Zidek, T.; Harbel, C.; Yoon, S.; Strickland, F.S.; Kumar, S.; Shin, M. Soft robotics: A review of recent developments of pneumatic soft actuators. Actuators 2020, 9, 3. [Google Scholar] [CrossRef]
- Majidi, C. Soft Robotics: A Perspective—Current Trends and Prospects for the Future. Soft Robot. 2014, 1, 5–11. [Google Scholar] [CrossRef]
- Dong, W.; Wang, Y.; Zhou, Y.; Bai, Y.; Ju, Z.; Guo, J.; Gu, G.; Bai, K.; Ouyang, G.; Chen, S.; et al. Soft human-machine interfaces: Design, sensing and simulation. Int. J. Intell. Robot. Appl. 2018, 2, 313–338. [Google Scholar] [CrossRef]
- Yu, M.; Cheng, X.; Peng, S.; Cao, Y.; Lu, Y.; Li, B.; Feng, X.; Znang, Y.; Wang, H.; Jiao, Z.; et al. A self-sensing soft pneumatic actuator with closed-loop control for haptic feedback wearable devices. Mater. Des. 2022, 223, 111149. [Google Scholar] [CrossRef]
- Pan, M.; Yuan, C.; Liang, X.; Dong, T.; Liu, T.; Zhang, J.; Zou, J.; Yang, H.; Bowen, C. Soft Actuators and Robotic Devices for Rehabilitation and Assistance. Adv. Intell. Syst. 2022, 4, 2100140. [Google Scholar] [CrossRef]
- Belforte, G.; Eula, G.; Ivanov, A.; Sirolli, S. Soft Pneumatic Actuators for Rehabilitation. Actuators 2014, 3, 84–106. [Google Scholar] [CrossRef]
- Kamenar, E.; Črnjarić-Žic, N.; Haggerty, D.; Zelenika, S.; Hawkes, E.; Mezić, I. Prediction of the behavior of a pneumatic soft robot based on Koopman operator theory. In Proceedings of the 2020 43rd International Convention on Information, Communication and Electronic Technology, Opatija, Croatia, 28 September–2 October 2020. [Google Scholar]
- Tanaka, J.; Ogawa, A.; Nakamoto, H.; Sonoura, T.; Eto, H. Suction pad unit using a bellows pneumatic actuator as a support mechanism for an end effector of depalletizing robots. Robomech J. 2020, 7, 2. [Google Scholar] [CrossRef]
- Gregov, G.; Ploh, T.; Kamenar, E. Design, Development and Experimental Assessment of a Cost-Effective Bellow Pneumatic Actuator. Actuators 2022, 11, 170. [Google Scholar] [CrossRef]
- Petre, I.M. Studies regarding the Use of Pneumatic Muscles in Precise Positioning Systems. Appl. Sci. 2021, 11, 9855. [Google Scholar] [CrossRef]
- Xavier, M.S.; Fleming, A.J.; Yong, Y.K. Design and Control of Pneumatic Systems for Soft Robotics: A Simulation Aproach. IEEE Robot. Autom. Lett. 2021, 6, 5800–5807. [Google Scholar] [CrossRef]
- Tang, T.F.; Chong, S.H.; Chan, C.Y.; Sakthivelu, V. Point-to-Point Positioning Control of a Pneumatic Muscle Actuated System Using Improved-PID Control. In Proceedings of the 2016 IEEE International Conference on Automatic Control and Intelligent Systems (I2CACIS), Selangor, Malaysia, 22 October 2016. [Google Scholar]
- Al-Ibadi, A.; Nefti-Meziani, S.; Davis, S. Controlling of Pneumatic Muscle Actuators Systems by Parallel Structure of Neural Network and Proportional Controllers (PNNP). Front. Robot. AI 2020, 7, 115. [Google Scholar] [CrossRef]
- Zhao, J.; Zhong, J.; Fan, J. Position Control of a Pneumatic Muscle Actuators Using RBF Neural Network Tuned PID Controller. Math. Probl. Eng. 2015, 2015, 810231. [Google Scholar] [CrossRef]
- Scaff, W.; Horikawa, O.; Tsuzuki, M.S. Pneumatic Artificial Muscle Optimal Control with Simulated Annealing. IFAC 2018, 51, 333–338. [Google Scholar] [CrossRef]
- Nuchkrua, T.; Leephakpreeda, T. Fuzzy Self-Tuning PID Control of Hydrogen-Driven Pneumatic Artificial Muscle Actuator. J. Bionic Eng. 2013, 10, 329–340. [Google Scholar] [CrossRef]
- Šitum, Ž.; Herceg, S.; Bolf, N.; Željka, U.A. Design, Construction and Control of a Manipulator Driven by Pneumatic Artificial Muscles. Sensors 2023, 23, 776. [Google Scholar] [CrossRef] [PubMed]
- Kazemi, S.; Hashem, R.; Stommel, M.; Cheng, L.K.; Xu, W. Experimental Study on the Closed-Loop Control of a Soft Ring-Shaped Actuator for In-Vitro Gastric Simulator. IEEE/ASME Trans. Mechatron. 2022, 27, 3548–3558. [Google Scholar] [CrossRef]
- Conte, G.Y.C.; Marques, F.G.; Garcia, C. LQR and PID Control Design for a Pneumatic Diaphragm Valve. In Proceedings of the IEEE International Conference on Automation/XXIV Congers of the Chilean Association of Automatic Control (ICA-ACCA), Valparaiso, Chile, 22–26 March 2021. [Google Scholar]
- Baćac, N.; Slukić, V.; Puškarić, M.; Štih, B.; Kamenar, E.; Zelenika, S. Comparison of different DC motor positioning control algorithms. In Proceedings of the 2014 37th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 26–30 May 2014; pp. 1654–1659. [Google Scholar]
- Control_Algorithms. Available online: https://github.com/ekamenar/control_algorithms (accessed on 6 February 2023).
- Signal_Generator. Available online: https://github.com/ekamenar/signal_generator (accessed on 6 February 2023).
- Kamenar, E.; Zelenika, S. Micropositioning mechatronics system based on FPGA architecture. In Proceedings of the 2013 36th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 20–24 May 2013; pp. 125–130. [Google Scholar]
- Levine, W.S. The Control Handbook; Three Volume Set; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]


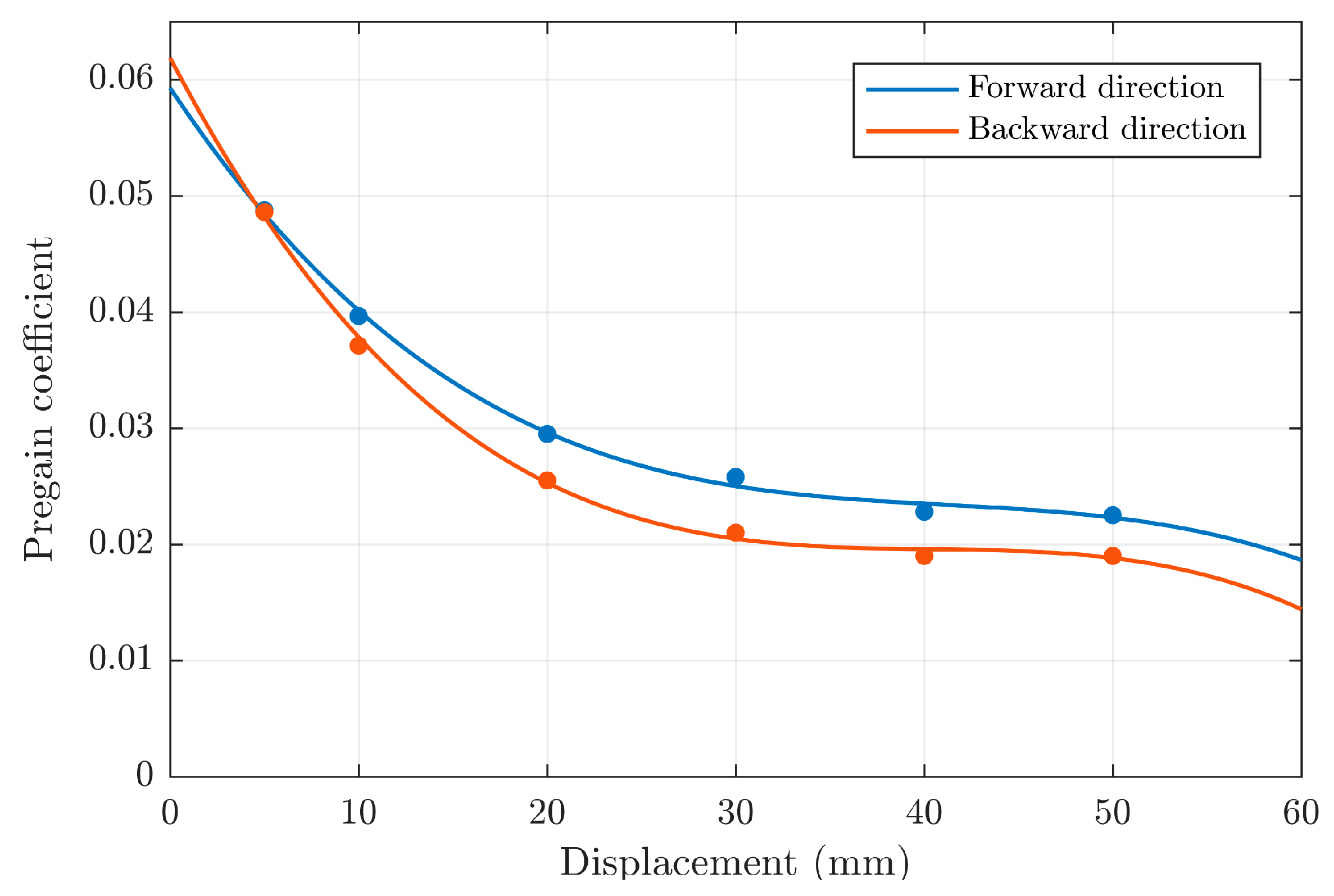



| Motion Direction | a | b | c |
|---|---|---|---|
| Forward | 3.03 × 10−5 | −3.07 × 10−3 | 1.161 × 10−1 |
| Backward | 1.1 × 10−5 | −1.4 × 10−3 | 8.057 × 10−2 |
| τs (s) | Steady-State Error (µm) | |||
|---|---|---|---|---|
| Displacement (mm) | PID | LQR | PID | LQR |
| 5 | 0.64 | 0.675 | 227 | 17 |
| 10 | 0.85 | 0.644 | 291 | 30 |
| 20 | 0.865 | 0.665 | 620 | 90 |
| 30 | 0.705 | 0.725 | 830 | 100 |
| 40 | 0.86 | 0.89 | 1000 | 140 |
| 50 | 1.01 | 1.03 | 1230 | 30 |
| Motion Direction | a | b | c | d |
|---|---|---|---|---|
| Forward | −4.6 × 10−7 | 5.724 × 10−5 | −2.442 × 10−1 | 5.929 × 10−2 |
| Backward | −6 × 10−7 | 7.65 × 10−5 | −3.11 × 10−3 | 6.188 × 10−2 |
| τs (s) | Steady-State Error (µm) | |||
|---|---|---|---|---|
| Displacement (mm) | PID | LQR | PID | LQR |
| 5 | 0.095 | 0.1 | 642 | 17 |
| 10 | 0.185 | 0.205 | 144 | 80 |
| 20 | 0.42 | 0.44 | 380 | 10 |
| 30 | 0.65 | 0.625 | 520 | 50 |
| 40 | 0.86 | 0.84 | 730 | 20 |
| 50 | 1.05 | 1.005 | 960 | 50 |
| τs | Steady-State Error | |||
|---|---|---|---|---|
| Displacement (mm) | PIDB vs. PIDA | PIDB vs. PIDA | PIDB vs. PIDA | PIDB vs. PIDA |
| 5 | 85% less | 85% less | 65% more | same |
| 10 | 69% less | 69% less | 50% less | 62% more |
| 20 | 48% less | 34% less | 39% less | 90% less |
| 30 | 8% less | 14% less | 38% less | 50% less |
| 40 | same | 6% less | 28% less | 85% less |
| 50 | 4% more | 2% less | 22% less | 40% more |
| τs (s) | Steady-State Error (µm) | |||
|---|---|---|---|---|
| Displacement (mm) | PID | LQR | PID | LQR |
| 5 | 0.205 | 0.12 | 911 | 32 |
| 10 | 0.23 | 0.225 | 608 | 27 |
| 20 | 0.435 | 0.44 | 890 | 30 |
| 30 | 0.63 | 0.635 | 1150 | 40 |
| 40 | 0.83 | 0.83 | 1410 | 30 |
| 50 | 1.015 | 1.085 | 1790 | 70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gregov, G.; Pincin, S.; Šoljić, A.; Kamenar, E. Position Control of a Cost-Effective Bellow Pneumatic Actuator Using an LQR Approach. Actuators 2023, 12, 73. https://doi.org/10.3390/act12020073
Gregov G, Pincin S, Šoljić A, Kamenar E. Position Control of a Cost-Effective Bellow Pneumatic Actuator Using an LQR Approach. Actuators. 2023; 12(2):73. https://doi.org/10.3390/act12020073
Chicago/Turabian StyleGregov, Goran, Samuel Pincin, Antonio Šoljić, and Ervin Kamenar. 2023. "Position Control of a Cost-Effective Bellow Pneumatic Actuator Using an LQR Approach" Actuators 12, no. 2: 73. https://doi.org/10.3390/act12020073
APA StyleGregov, G., Pincin, S., Šoljić, A., & Kamenar, E. (2023). Position Control of a Cost-Effective Bellow Pneumatic Actuator Using an LQR Approach. Actuators, 12(2), 73. https://doi.org/10.3390/act12020073








