Path Tracking Control of Intelligent Vehicles Considering Multi-Nonlinear Characteristics for Dual-Motor Autonomous Steering System
Abstract
:1. Introduction
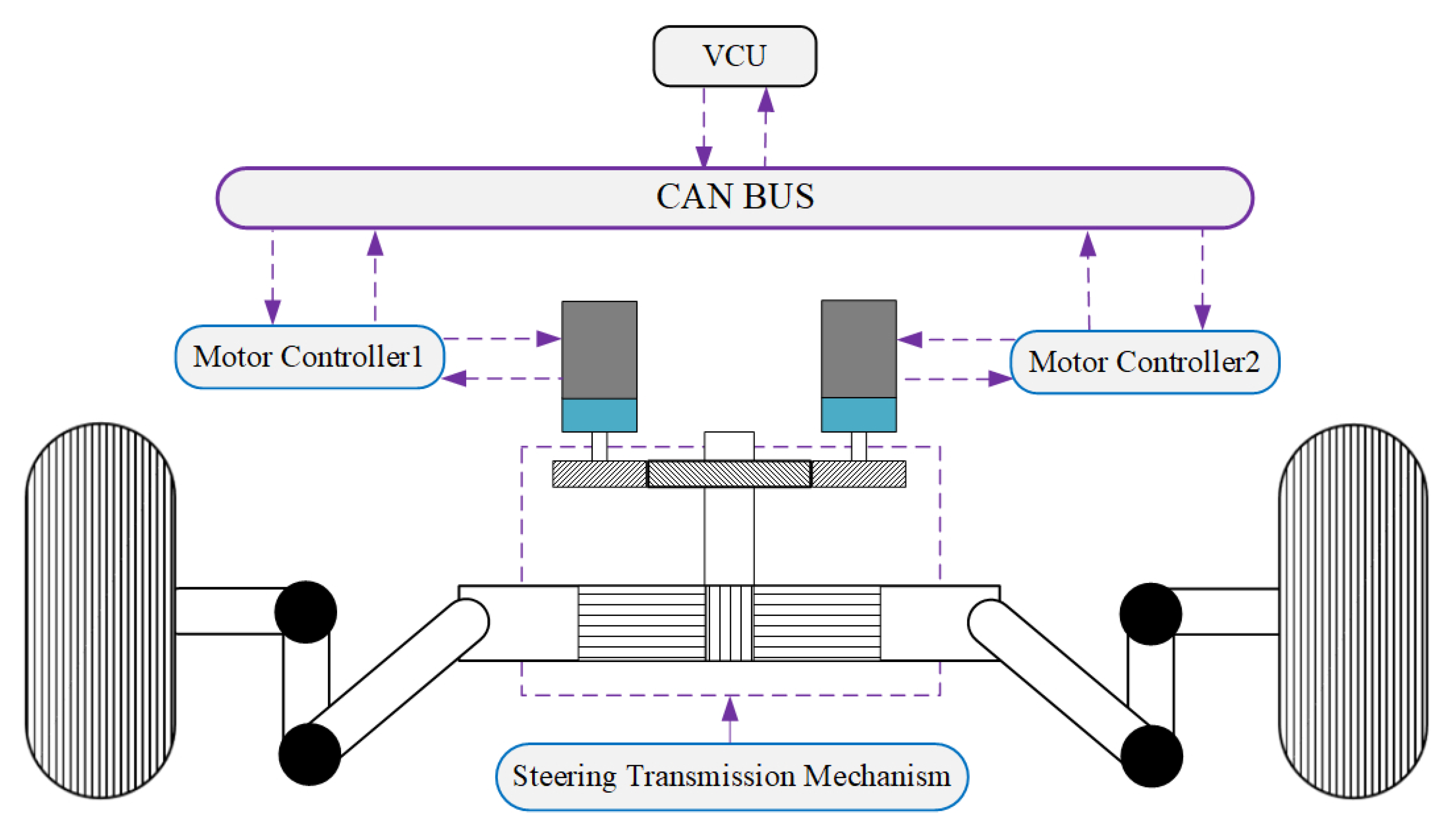
2. Autonomous Steering System
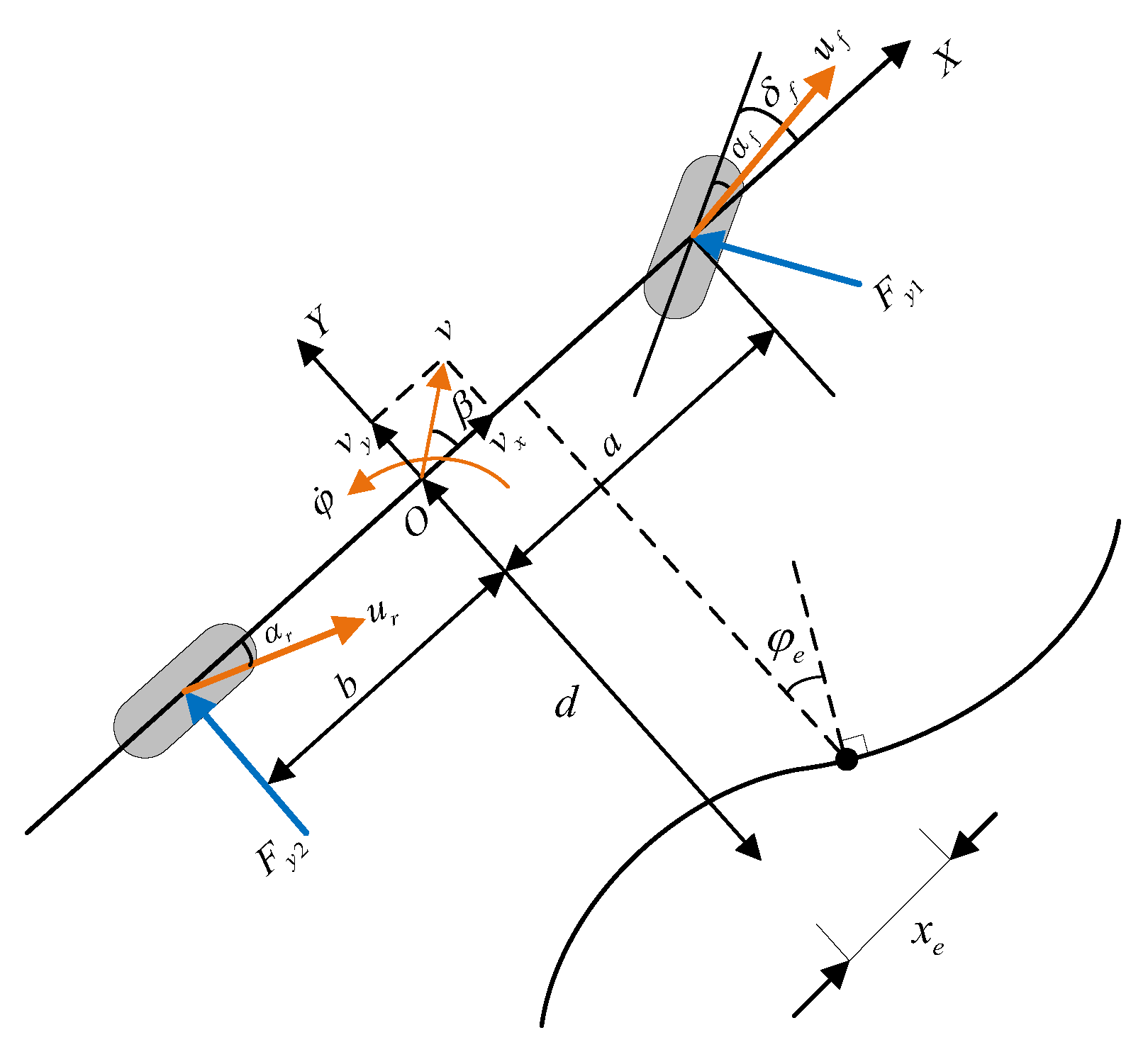
2.1. Model for Autonomous Steering System
2.2. Model for Self-Aligning Torque
3. Estimation of the Tire Cornering Stiffness
3.1. Data Establishment
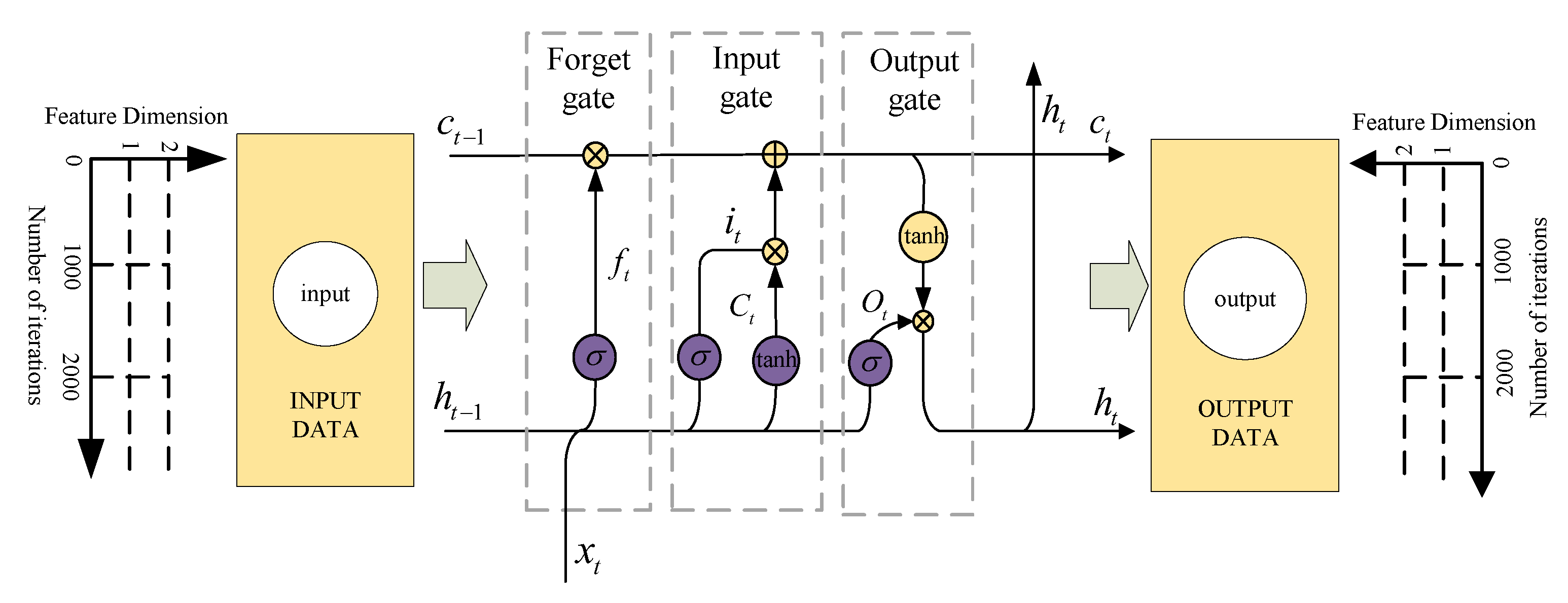
3.2. LSTM Model
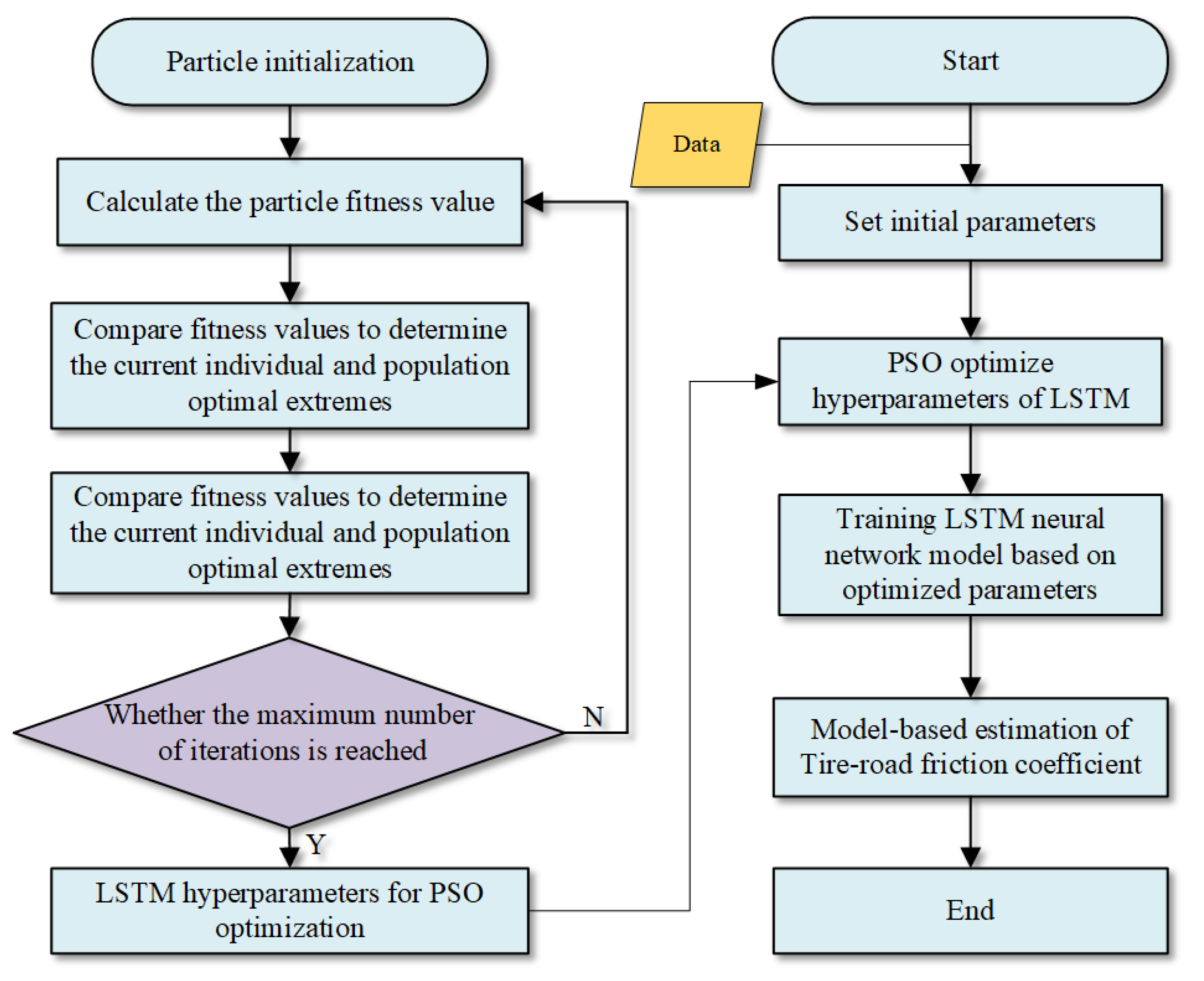
3.3. Establishment of the PSO-LSTM Model
3.4. Method for Estimating the Tire Cornering Stiffness Based on PSO-LSTM
4. Control Strategy of the Dual-Motor Autonomous Steering System
4.1. Front Wheel Control Strategy Based on Adaptive Sliding Mode Control
4.2. Design of the LQR Controller
5. The Simulation Results
5.1. Validation of Tire Cornering Stiffness Estimation
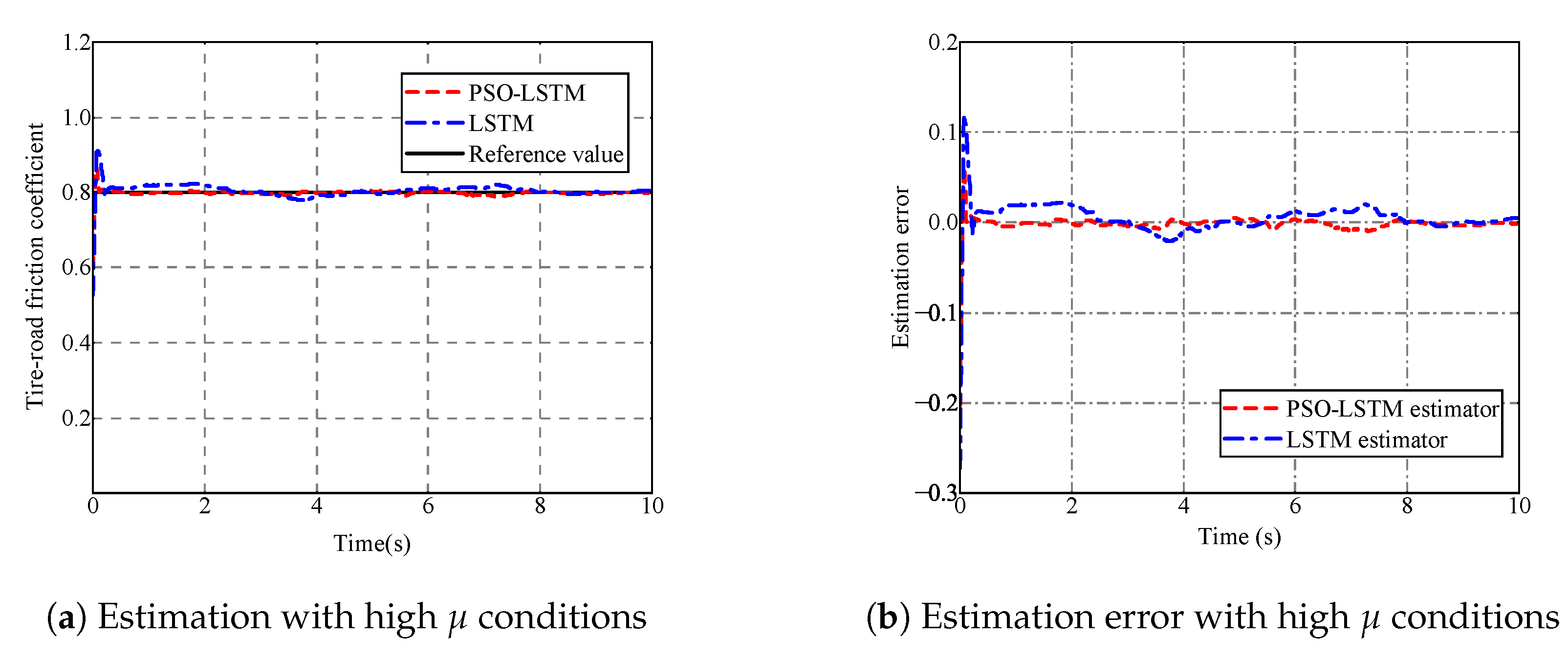
5.1.1. Analysis of Tire–Road Friction Coefficient Estimator
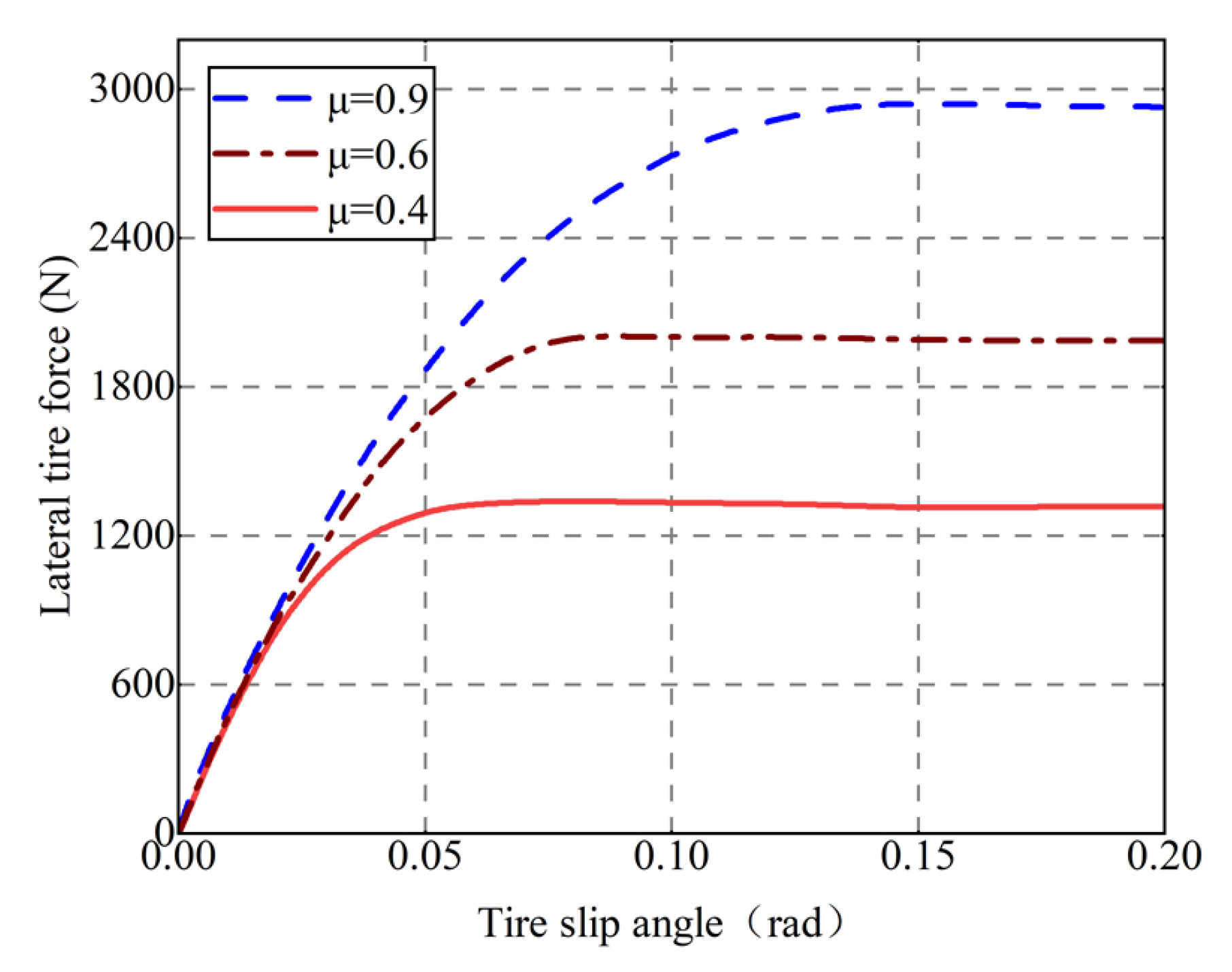
5.1.2. Analysis of Tire Cornering Stiffness for Different Tire–Road Friction Coefficients
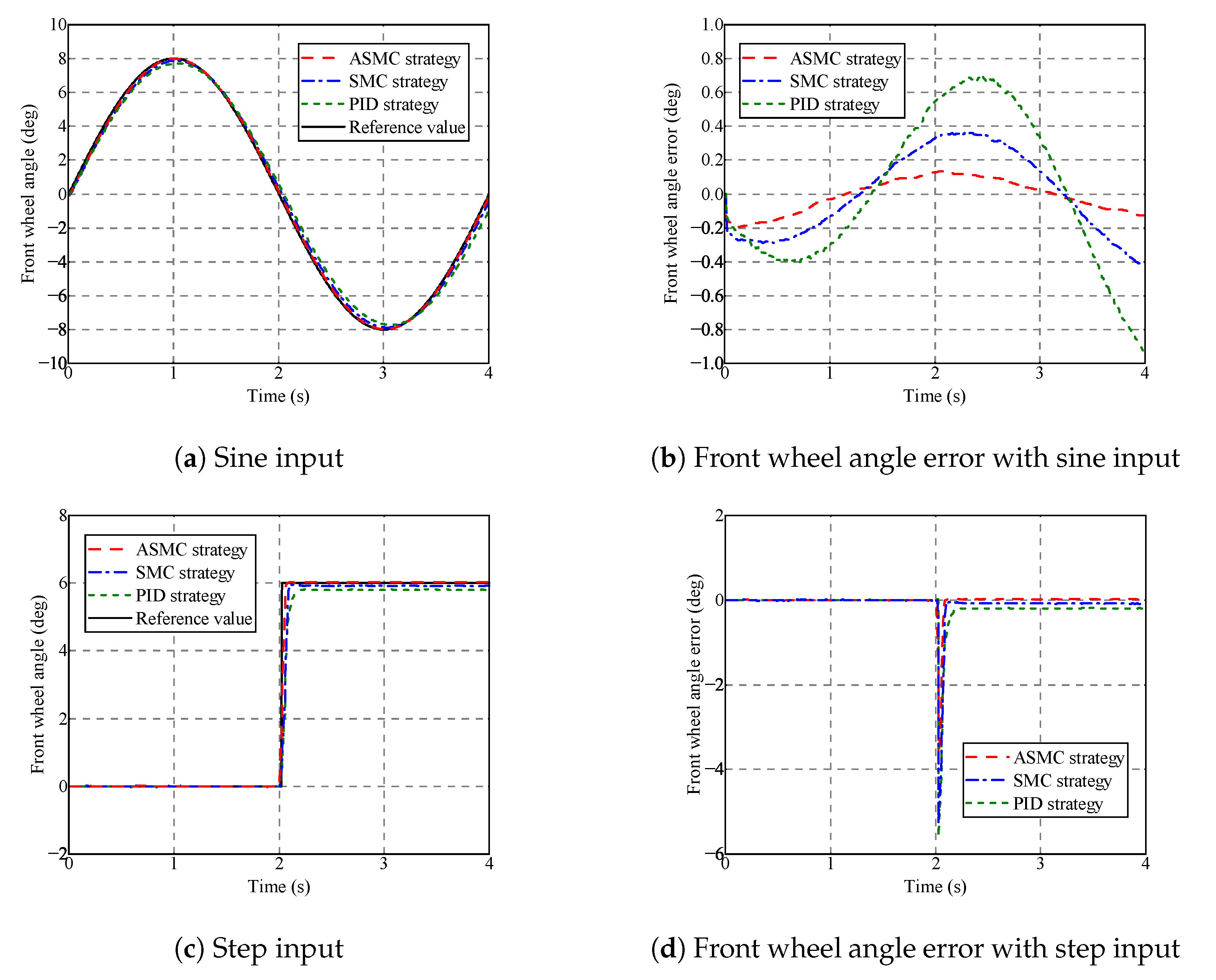
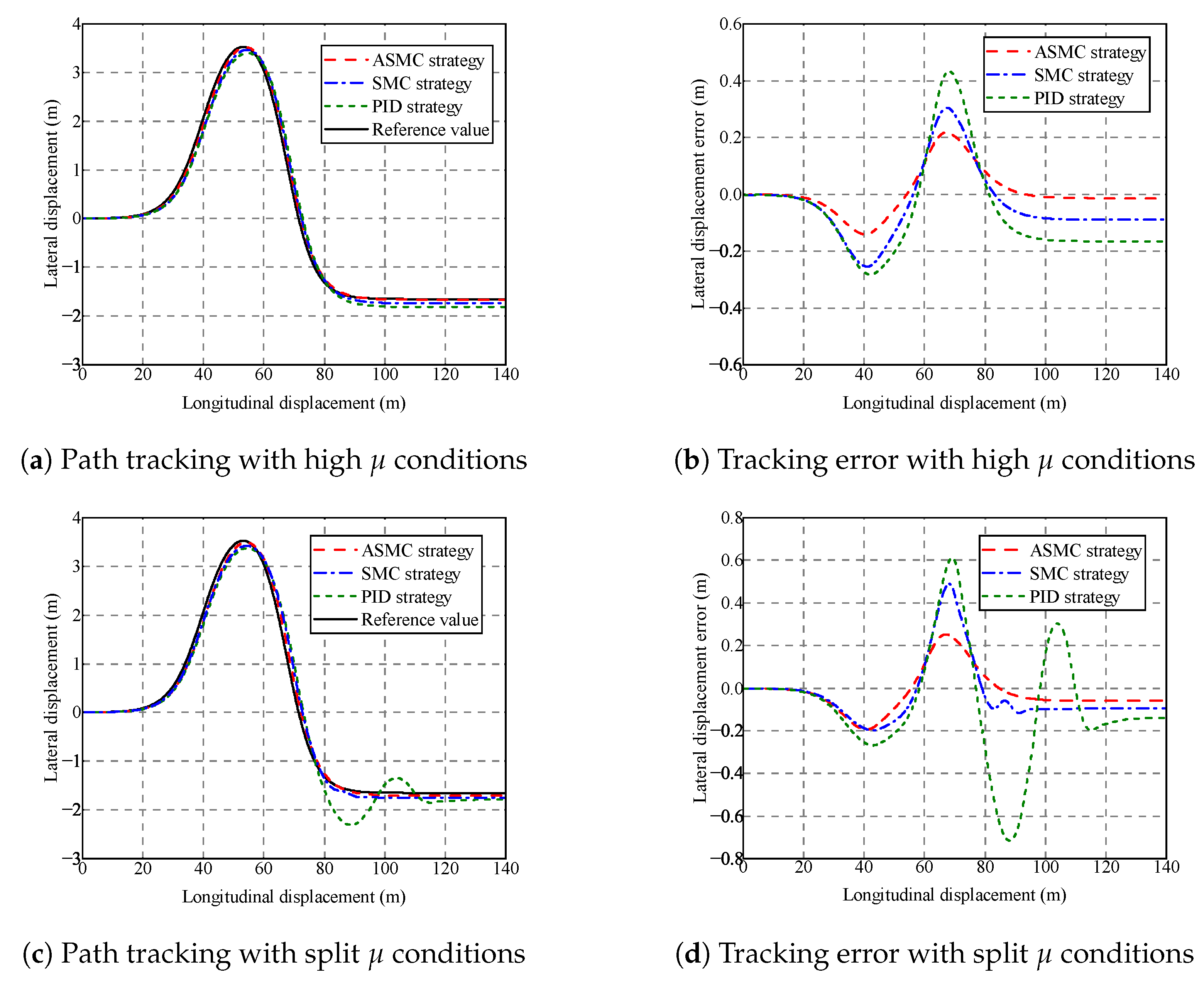
5.2. Validation of the Adaptive Sliding Mode Control Strategy
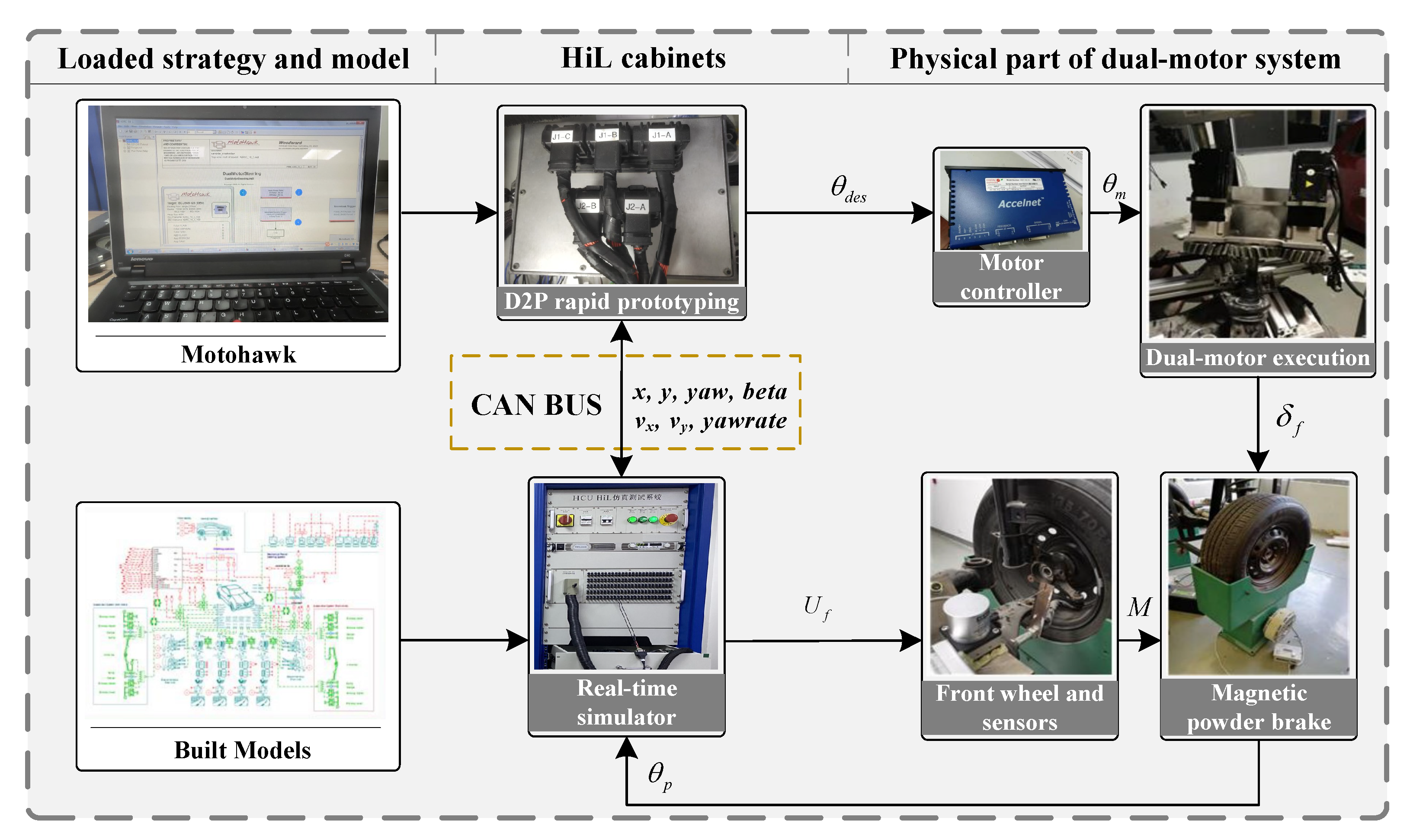
6. Hardware-in-Loop Test Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, T.; Chen, L.; Xu, X.; Cai, Y.; Jiang, H.; Sun, X. Passive fault-tolerant path following control of autonomous distributed drive electric vehicle considering steering system fault. Mech. Syst. Signal Process. 2019, 123, 298–315. [Google Scholar] [CrossRef]
- Xie, J.; Xu, X.; Wang, F.; Liu, Z.; Chen, L. Coordination Control Strategy for Human-Machine Cooperative Steering of Intelligent Vehicles: A Reinforcement Learning Approach. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21163–21177. [Google Scholar] [CrossRef]
- Yan, M.; Chen, W.; Wang, Q.; Zhao, Q.; Liang, X.; Cai, B. Human–Machine Cooperative Control of Intelligent Vehicles for Lane Keeping—Considering Safety of the Intended Functionality. Actuators 2021, 10, 210. [Google Scholar] [CrossRef]
- Lin, F.; Sun, M.; Wu, J.; Qian, C. Path Tracking Control of Autonomous Vehicle Based on Nonlinear Tire Model. Actuators 2021, 10, 242. [Google Scholar] [CrossRef]
- Yang, T.; Bai, Z.; Li, Z.; Feng, N.; Chen, L. Intelligent Vehicle Lateral Control Method Based on Feedforward + Predictive LQR Algorithm. Actuators 2021, 10, 228. [Google Scholar] [CrossRef]
- Zou, S.; Zhao, W. Synchronization and stability control of dual-motor intelligent steer-by-wire vehicle. Mech. Syst. Signal Process. 2020, 145, 106925. [Google Scholar] [CrossRef]
- Xu, X.; Su, P.; Wang, F.; Chen, L.; Xie, J. Coordinated control of dual-motor using the interval type-2 fuzzy logic in autonomous steering system of AGV. Int. J. Fuzzy Syst. 2021, 23, 1070–1086. [Google Scholar] [CrossRef]
- He, L.; Chen, G.; Zheng, H. Fault tolerant control method of dual steering actuator motors for steer-by-wire system. Int. J. Automot. Technol. 2015, 16, 977–987. [Google Scholar] [CrossRef]
- Mi, J.; Wang, T.; Lian, X. A system-level dual-redundancy steer-by-wire system. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 3002–3025. [Google Scholar] [CrossRef]
- Anwar, S.; Niu, W. A Nonlinear Observer Based Analytical Redundancy for Predictive Fault Tolerant Control of a Steer-by-Wire System. Asian J. Control 2014, 16, 321–334. [Google Scholar] [CrossRef]
- Xie, J.; Xu, X.; Wang, F.; Tang, Z.; Chen, L. Adaptive coordination control strategy for path-following of DDAEV with neural network based moving weight coefficients. Trans. Inst. Meas. Control 2022, in press. [CrossRef]
- Huang, C.; Huang, H.; Naghdy, F. Actuator fault tolerant control for steer-by-wire systems. Int. J. Control 2021, 94, 3123–3134. [Google Scholar] [CrossRef]
- Li, S.; Wang, G.; Chen, G.; Chen, H.; Zhang, B. Tire state stiffness prediction for improving path tracking control during emergency collision avoidance. IEEE Access 2019, 7, 179658–179669. [Google Scholar] [CrossRef]
- Peng, H.; Wang, W.; An, Q.; Xiang, C.; Li, L. Path tracking and direct yaw moment coordinated control based on robust MPC with the finite time horizon for autonomous independent-drive vehicles. IEEE Trans. Veh. Technol. 2020, 69, 6053–6066. [Google Scholar] [CrossRef]
- Hao, J.; Liang, C.; Yang, R.; Lin, Z. A recognition method of road adhesion coefficient based on Recurrent Neural Network. In Proceedings of the 2021 International Conference on Computer Information Science and Artificial Intelligence (CISAI), Kunming, China, 17–19 September 2021; pp. 79–82. [Google Scholar]
- Yu, M.; Xu, X.; Wu, C.; Li, S.; Li, M.; Chen, H. Research on the prediction model of the friction coefficient of asphalt pavement based on tire-pavement coupling. Adv. Mater. Sci. Eng. 2021, 2021, 6650525. [Google Scholar] [CrossRef]
- Ribeiro, A.M.; Moutinho, A.; Fioravanti, A.R.; Paiva, E.C. Estimation of tire–road friction for road vehicles: A time delay neural network approach. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Zheng, J.; Wang, H.; Man, Z. Adaptive fast non-singular terminal sliding mode control for a vehicle steer-by-wire system. IET Control Theory Appl. 2017, 11, 1245–1254. [Google Scholar] [CrossRef]
- Kazemi, R.; Janbakhsh, A.A. Nonlinear adaptive sliding mode control for vehicle handling improvement via steer-by-wire. Int. J. Automot. Technol. 2010, 11, 345–354. [Google Scholar] [CrossRef]
- Li, H.; Zhang, T.; Tie, M.; Wang, Y. Fuzzy-Based Adaptive Higher-Order Sliding Mode Control for Uncertain Steer-by-Wire System. J. Dyn. Syst. Meas. Control 2022, 144, 041005. [Google Scholar] [CrossRef]
- Wang, Z. Adaptive fuzzy system compensation based Model-free control for steer-by-wire systems with uncertainty. Int. J. Innov. Comput. Inf. Control 2021, 17, 141–152. [Google Scholar]
- Pikunov, D.; Stefanski, A. Numerical analysis of the friction-induced oscillator of Duffing’s type with modified LuGre friction model. J. Sound Vib. 2019, 440, 23–33. [Google Scholar] [CrossRef]
- Shi, Q.; Zhang, H. Fault diagnosis of an autonomous vehicle with an improved SVM algorithm subject to unbalanced data sets. IEEE Trans. Ind. Electron. 2020, 68, 6248–6256. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Smagulova, K.; James, A.P. A survey on LSTM memristive neural network architectures and applications. Eur. Phys. J. Spec. Top. 2019, 228, 2313–2324. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H.; Chen, S. LSTM fully convolutional networks for time series classification. IEEE Access 2017, 6, 1662–1669. [Google Scholar] [CrossRef]
- Yang, J.; He, L.; Fu, S. An improved PSO-based charging strategy of electric vehicles in electrical distribution grid. Appl. Energy 2014, 128, 82–92. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, W.; Yu, L.; Lu, K. The accuracy and efficiency of GA and PSO optimization schemes on estimating reaction kinetic parameters of biomass pyrolysis. Energy 2019, 176, 582–588. [Google Scholar] [CrossRef]
- Chu, Z.; Chen, N.; Zhang, N.; Li, G. Path-tracking for autonomous vehicles with on-line estimation of axle cornering stiffnesses. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 6651–6657. [Google Scholar]
- Jiang, C.; Wang, Q.; Li, Z.; Zhang, N.; Ding, H. Nonsingular terminal sliding mode control of PMSM based on improved exponential reaching law. Electronics 2021, 10, 1776. [Google Scholar] [CrossRef]






| Driving Condition | Range of Velocity (km/h) | Range of Tire–Road Friction Coefficient |
|---|---|---|
| Single lane change of left turn | 20∼100 | 0.3∼0.9 |
| Single lane change of right turn | 20∼100 | 0.3∼0.9 |
| Double lane change of left turn | 30∼80 | 0.3∼0.9 |
| Double lane change of right turn | 30∼80 | 0.3∼0.9 |
| Straight ahead | 20∼120 | 0.2∼1.0 |
| Sine input | 20∼60 | 0.4∼1.0 |
| Constant circle steering | 20∼60 | 0.4∼1.0 |
| Step input | 20∼80 | 0.3∼1.0 |
| Parameter | Definition | Value |
|---|---|---|
| m | Total vehicle mass | 1110 kg |
| Vehicle yaw inertia | 1343 | |
| Distance from the front axle to CG | 1.04 m | |
| Distance from the back axle to CG | 1.56 m | |
| Front wheel cornering stiffness | 47,461 N/rad | |
| Rear wheel cornering stiffness | 35,572 N/rad |
| RMSE | PSO-LSTM | LSTM |
|---|---|---|
| Estimation with a high coefficient | 0.0187 | 0.0245 |
| Estimation with a low coefficient | 0.0234 | 0.0297 |
| Estimation with a split coefficient | 0.0212 | 0.0269 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, H.; Geng, G.; Xu, X.; Xie, J.; He, S. Path Tracking Control of Intelligent Vehicles Considering Multi-Nonlinear Characteristics for Dual-Motor Autonomous Steering System. Actuators 2023, 12, 97. https://doi.org/10.3390/act12030097
Shi H, Geng G, Xu X, Xie J, He S. Path Tracking Control of Intelligent Vehicles Considering Multi-Nonlinear Characteristics for Dual-Motor Autonomous Steering System. Actuators. 2023; 12(3):97. https://doi.org/10.3390/act12030097
Chicago/Turabian StyleShi, Haozhe, Guoqing Geng, Xing Xu, Ju Xie, and Shenguang He. 2023. "Path Tracking Control of Intelligent Vehicles Considering Multi-Nonlinear Characteristics for Dual-Motor Autonomous Steering System" Actuators 12, no. 3: 97. https://doi.org/10.3390/act12030097
APA StyleShi, H., Geng, G., Xu, X., Xie, J., & He, S. (2023). Path Tracking Control of Intelligent Vehicles Considering Multi-Nonlinear Characteristics for Dual-Motor Autonomous Steering System. Actuators, 12(3), 97. https://doi.org/10.3390/act12030097






