Design and Simulation of a Single Piezoelectric-Driven Rotary Actuator with Double-Layer Flexible Mechanism
Abstract
:1. Introduction
2. Mechanical Design of the RA-DFM
3. Theoretical Modeling and Analysis of the RA-DFM
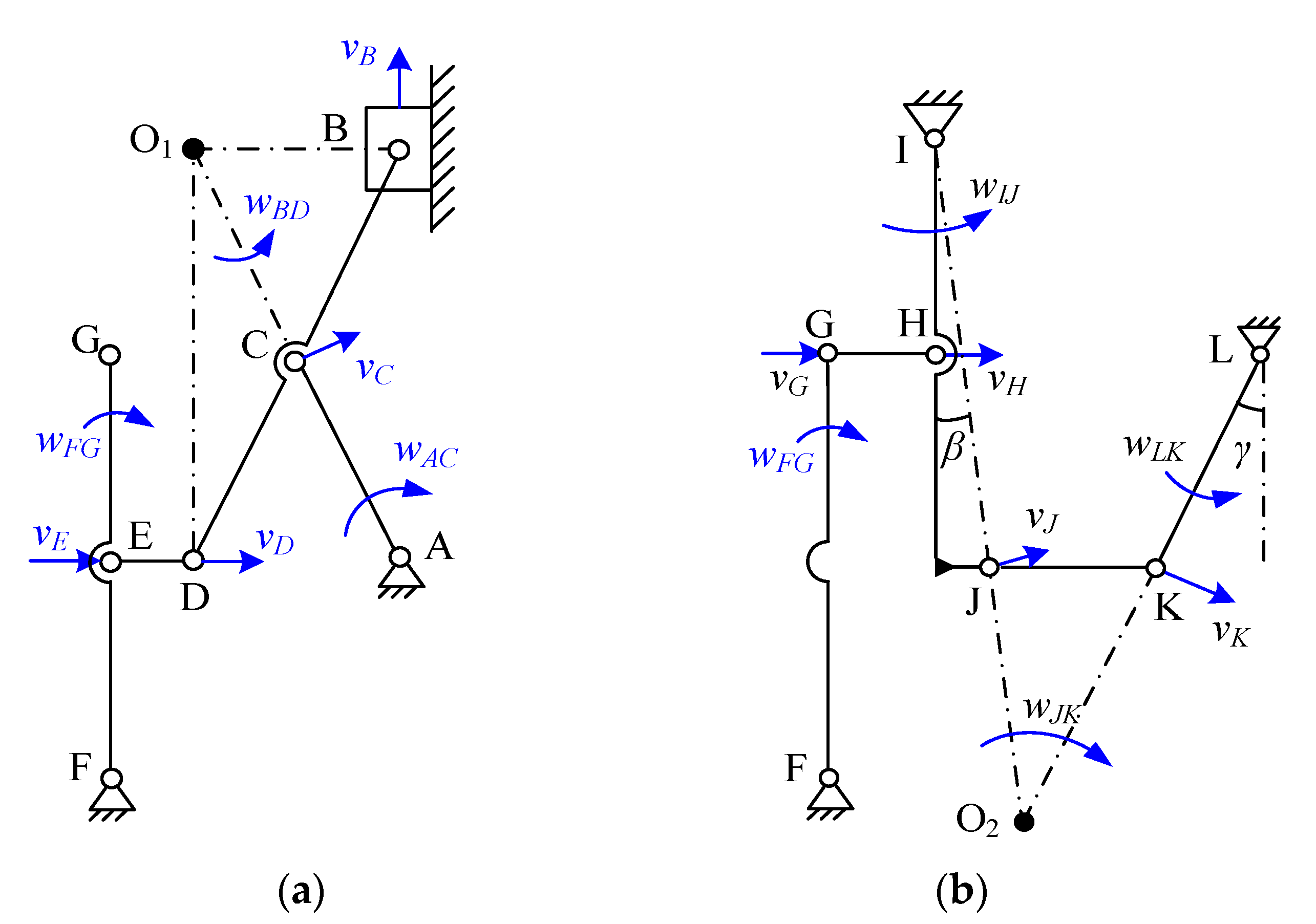
3.1. The Kinematic Modeling
3.2. The Output of Piezoelectric Ceramic
3.3. The Stress Analysis
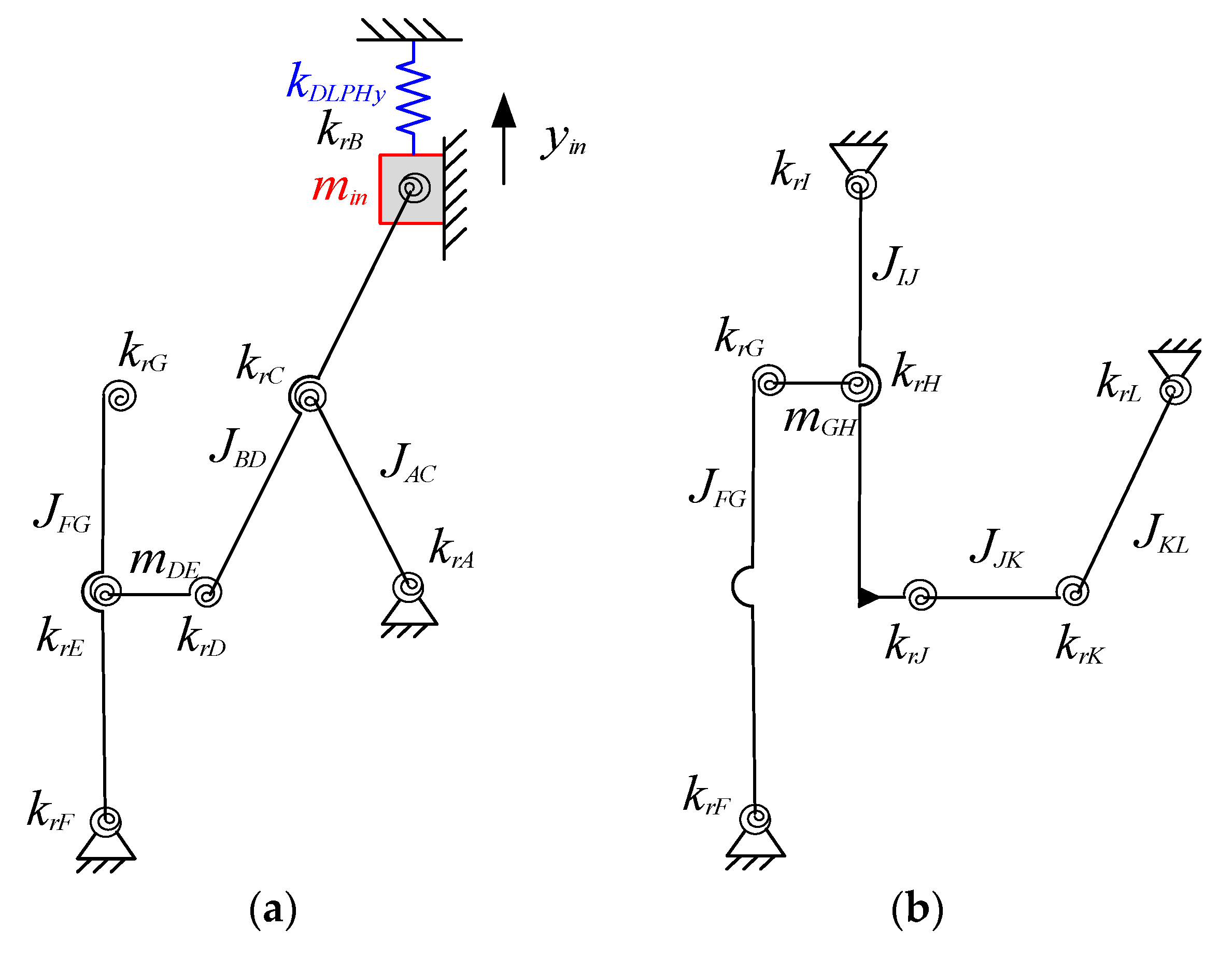
3.4. The Dynamic Modeling
4. The Optimization
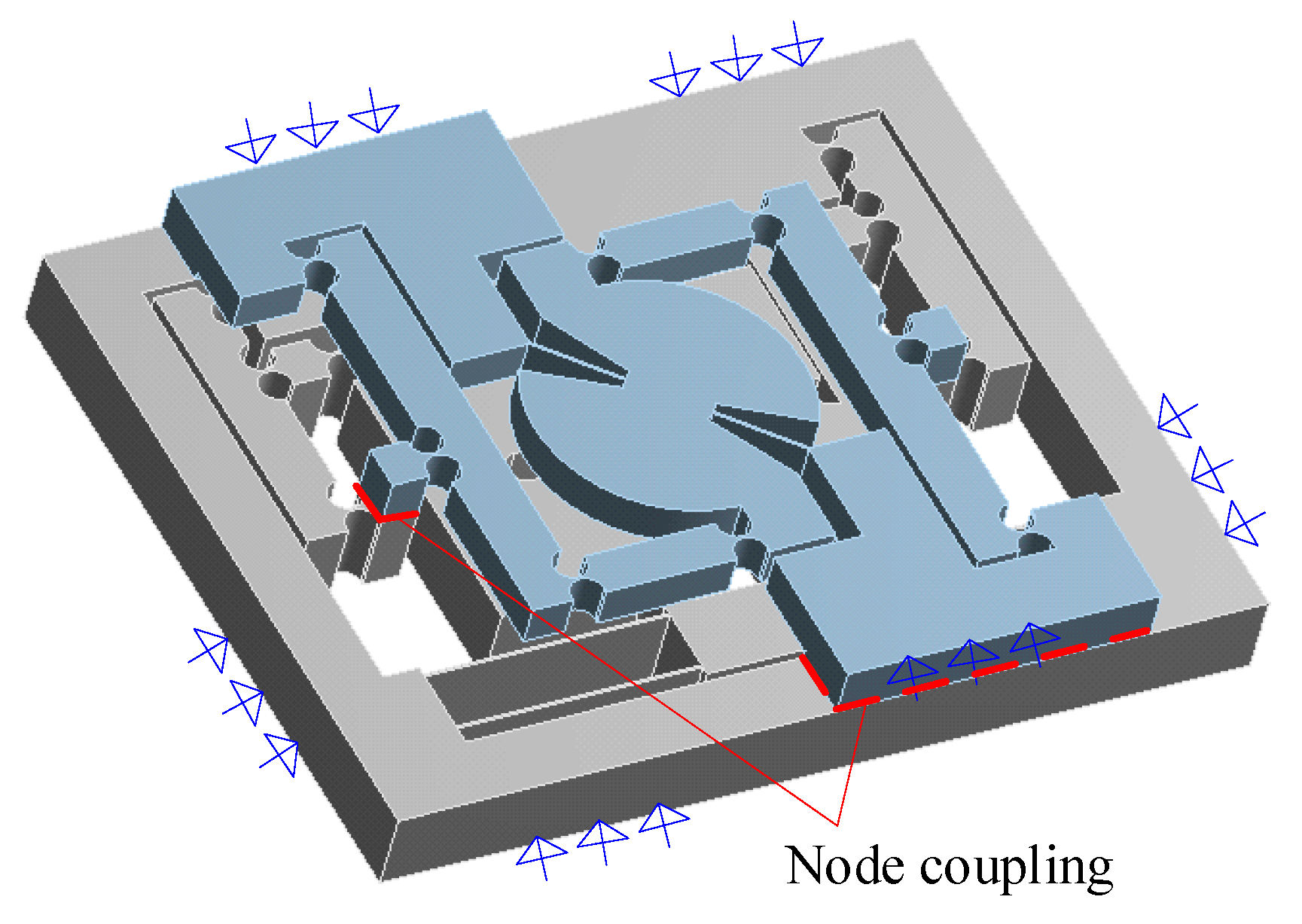
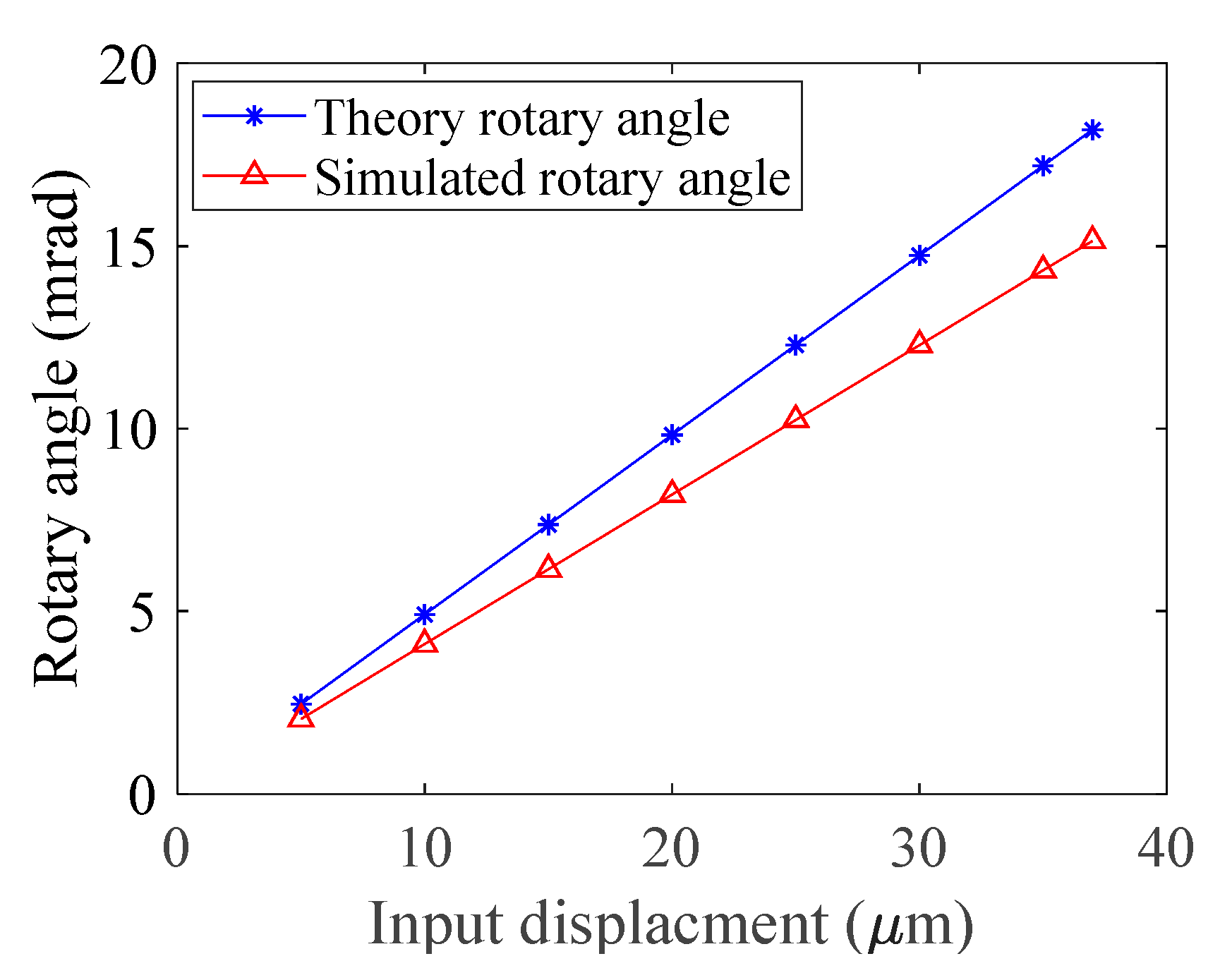
5. The Finite Element Analysis of RA-DFM
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Habibullah, H. 30 Years of atomic force microscopy: Creep, hysteresis, cross-coupling, and vibration problems of piezoelectric tube scanners. Measurement 2020, 159, 107776. [Google Scholar] [CrossRef]
- Wei, Y.; Xu, Q. Design and Testing of a New Force-Sensing Cell Microinjector Based on Soft Flexure Mechanism. IEEE Sens. J. 2019, 19, 6012–6019. [Google Scholar] [CrossRef]
- Qin, Y.; Soundararajan, R.; Jia, R.; Huang, S. Direct inverse linearization of piezoelectric ceramic’s initial loading curve and its applications in full-field optical coherence tomography (FF-OCT). Mech. Syst. Signal Process. 2021, 148, 107147. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, X.; Yan, P. Large dynamic range tracking of an XY compliant nanomanipulator with cross-axis coupling reduction. Mech. Syst. Signal Process. 2019, 117, 757–770. [Google Scholar] [CrossRef]
- Wang, T.; Li, Y.; Zhang, Y.; Lin, R.; Qain, J.; Dou, Z. Design of a flexure-based parallel XY micropositioning stage with millimeter workspace and high bandwidth. Sens. Actuators A Phys. 2021, 331, 112899. [Google Scholar] [CrossRef]
- Bazaei, A.; Ettefagh, M.; Chen, Z. Displacement amplification and differential actuation in piezo driven nanopositioners. Mech. Syst. Signal Process. 2021, 151, 107356. [Google Scholar] [CrossRef]
- Lyu, Z.; Wu, Z.; Xu, Q. Design and development of a novel piezoelectrically actuated asymmetrical flexible microgripper. Mech. Mach. Theory 2022, 171, 104736. [Google Scholar] [CrossRef]
- Baek, S.; Cho, N.; Lee, D. Fabrication of a piezoelectrically driven micropositioning 3-DOF stage with elastic body using a multi-material 3D printer. Rapid Prototyp. J. 2020, 26, 1579–1591. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, X. Optimal design of a planar parallel 3-DOF nanopositioner with multi-objective. Mech. Mach. Theory 2017, 112, 61–83. [Google Scholar] [CrossRef]
- Zhan, W.; He, X.; Yang, J.; Lai, J.; Zhu, D. Optimal design method for 3-DOF planar compliant mechanisms based on mapping matrix constraints. Structures 2020, 26, 1–5. [Google Scholar] [CrossRef]
- Al-Jodah, A.; Shirinzadeh, B.; Ghafarian, M.; Das, T.; Pinskier, J. Design, modeling, and control of a large range 3-DOF micropositioning stage. Mech. Mach. Theory 2021, 156, 104159. [Google Scholar] [CrossRef]
- Kim, H.; Gweon, D. Development of a compact and long range XYθz nano-positioning stage. Rev. Sci. Instrum. 2012, 83, 085102. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.; Lee, M.; Choi, Y. Six Degrees-of-Freedom Direct-Driven Nanopositioning Stage Using Crab-Leg Flexures. IEEE/ASME Trans. Mechatron. 2020, 25, 513–525. [Google Scholar] [CrossRef]
- Lee, M.; Park, E.; Yeom, J.; Hong, D.; Lee, D. Pure Nano-Rotation Scanner. Adv. Mech. Eng. 2012, 4, 962439. [Google Scholar] [CrossRef]
- Zhu, X.; Wen, Z.; Chen, G.; Liang, J.; Liu, P. A decoupled flexure-based rotary micropositioning stage with compact size. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 4167–4179. [Google Scholar] [CrossRef]
- Clark, L.; Shirinzadeh, B.; Zhong, Y.; Tian, Y.; Zhang, D. Design and analysis of a compact flexure-based precision pure rotation stage without actuator redundancy. Mech. Mach. Theory 2016, 105, 129–144. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, X.; Huang, H.; Dong, J.; Fan, Z.; Zhao, H. On the Suppression of the Backward Motion of a Piezo-Driven Precision Positioning Platform Designed by the Parasitic Motion Principle. IEEE Trans. Ind. Electron. 2020, 67, 3870–3878. [Google Scholar] [CrossRef]
- Chang, Q.; Liu, Y.; Deng, J.; Zhang, S.; Chen, W. Design of a precise linear-rotary positioning stage for optical focusing based on the stick-slip mechanism. Mech. Syst. Signal Process. 2022, 165, 108398. [Google Scholar] [CrossRef]
- Sun, X.; Chen, W.; Zhang, J.; Zhou, R.; Chen, W. A novel piezo-driven linear-rotary inchworm actuator. Sens. Actuators A Phys. 2015, 224, 78–86. [Google Scholar] [CrossRef]
- Song, S.; Shao, S.; Xu, M.; Shao, Y.; Tian, Z.; Feng, B. Piezoelectric inchworm rotary actuator with high driving torque and self-locking ability. Sens. Actuators A Phys. 2018, 282, 174–182. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, W.; Tian, Y.; Zhang, Z.; Cao, Y.; Lu, X.; Zhang, T. Design, modeling, and testing of a one degree of freedom manipulator with three stage amplification mechanism. Rev. Sci. Instrum. 2022, 93, 123705. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, Z. A large range compliant XY nano-manipulator with active parasitic rotation rejection. Precis. Eng. 2021, 72, 640–652. [Google Scholar] [CrossRef]
- Yuan, L.; Wang, L.; Qi, R.; Zhao, Z.; Jin, J.; Zhao, C. A novel hollow-type XY piezoelectric positioning platform. Int. J. Mech. Sci. 2023, 255, 108496. [Google Scholar] [CrossRef]
- Duan, Y.; Ou, K.; Sun, Y.; Tian, Y. Stress Analysis of the Circular Arc Flexure Hinge. J. Mech. Transm. 2016, 40, 148–170. [Google Scholar]






| Variables | Original Values (mm) | Ranges (mm) | Optimization Results (mm) |
|---|---|---|---|
| blow | 12.00 | [10, 15] | 10.00 |
| bup | 8.00 | [5, 10] | 5.00 |
| tDLPH | 0.5 | [0.3, 1] | 0.30 |
| lDLPH | 15 | [10, 30] | 30.00 |
| lAB | 40 | [30, 50] | 41.11 |
| lAD | 20 | [15, 30] | 20.00 |
| lFG | 40 | [30, 50] | 31.45 |
| lIJ | 40 | [30, 50] | 49.54 |
| tFSM | 0.5 | [0.3, 1] | 0.30 |
| lFSM | 15 | [10, 30] | 10.98 |
| lJK | 15 | [10, 20] | 20.00 |
| rR | 1 | [0.5, 2] | 2.00 |
| tR | 0.5 | [0.3, 1] | 0.30 |
| Kin-Y | f1 | ||||
|---|---|---|---|---|---|
| Theoretical calculation | 2.05 | 2.88 | 1.71 | 1.75 N/μm | 189.35 Hz |
| Simulation results | 1.78 | 2.82 | 1.68 | 1.71 N/μm | 192.45 Hz |
| Modeling error | 15.16% | 2.13% | 1.79% | 2.34% | 1.61% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Zhao, P.; Zhang, W.; Tian, Y.; Hu, G. Design and Simulation of a Single Piezoelectric-Driven Rotary Actuator with Double-Layer Flexible Mechanism. Actuators 2023, 12, 231. https://doi.org/10.3390/act12060231
Guo Z, Zhao P, Zhang W, Tian Y, Hu G. Design and Simulation of a Single Piezoelectric-Driven Rotary Actuator with Double-Layer Flexible Mechanism. Actuators. 2023; 12(6):231. https://doi.org/10.3390/act12060231
Chicago/Turabian StyleGuo, Zhiyong, Pengchao Zhao, Wenchao Zhang, Yanling Tian, and Gaofeng Hu. 2023. "Design and Simulation of a Single Piezoelectric-Driven Rotary Actuator with Double-Layer Flexible Mechanism" Actuators 12, no. 6: 231. https://doi.org/10.3390/act12060231
APA StyleGuo, Z., Zhao, P., Zhang, W., Tian, Y., & Hu, G. (2023). Design and Simulation of a Single Piezoelectric-Driven Rotary Actuator with Double-Layer Flexible Mechanism. Actuators, 12(6), 231. https://doi.org/10.3390/act12060231






