Model Order Reduction of Microactuators: Theory and Application
Abstract
:1. Introduction
1.1. State of the Art: Projection-Based Linear Model Order Reduction for Microactuators
1.2. State of the Art: Projection-Based Nonlinear Model Order Reduction for Microactuators
1.3. Alternatives to Projection-Based Model Order Reduction
1.4. Outline of the Article
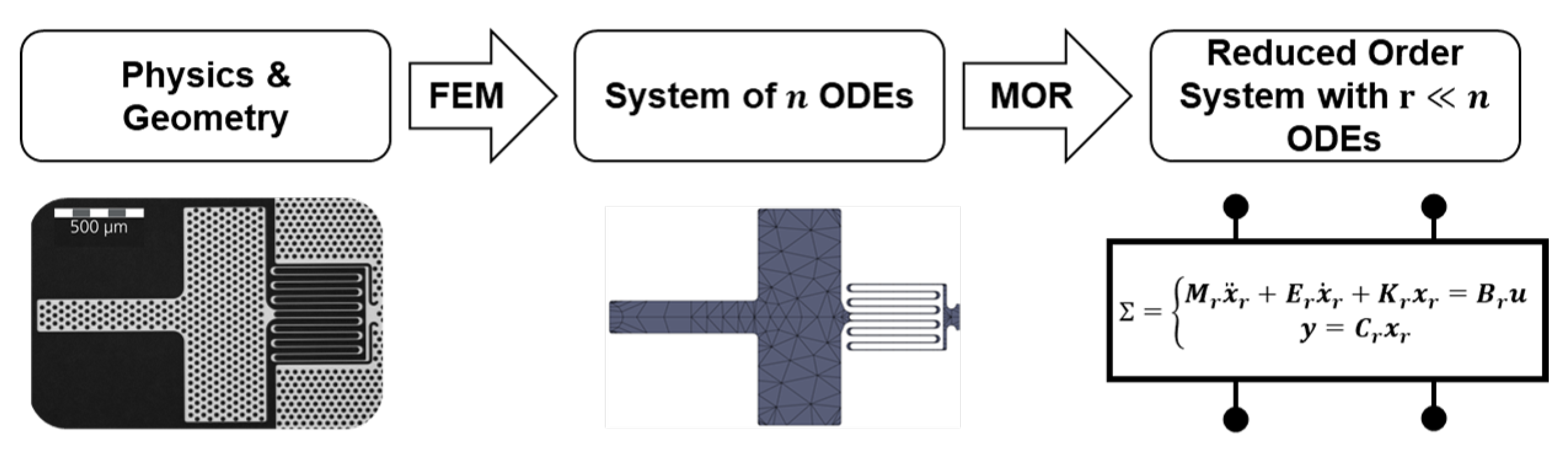
2. Compact Modeling by Means of Mathematical Model Order Reduction
2.1. Mathematical Modeling of Microactuators
2.2. Projection-Based Linear Model Order Reduction
2.3. Projection-Based Nonlinear Model Order Reduction
| Algorithm 1 Weighting scheme for TPWL. |
|
3. Exemplary Applications of MOR to Microactuators
3.1. Piezoelectric Chip Actuator
3.2. Electromechanical Beam Actuator
3.3. Geometrically Nonlinear Beam Actuator
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | artificial neural network |
| DAE | differential algebraic equation |
| DEIM | discrete empirical interpolation method |
| DOF | degree of freedom |
| ECSW | energy conserving mesh sampling and weighting |
| FEM | finite element method |
| GKN | generalized Kirchoffian network |
| MEMS | microelectromechanical system |
| MOR | model order reduction |
| ODE | ordinary differential equation |
| PDE | partial differential equation |
| POD | proper orthogonal decomposition |
| ROM | reduced order model |
| TPWL | trajectory piecewise-linear |
References
- Bechtold, T.; Schrag, G.; Feng, L. (Eds.) System-Level Modeling of MEMS; Wiley-VCH-Verl.: Weinheim, Germany, 2013; Advanced Micro and Nanosystems Volume 10. [Google Scholar]
- Benner, P.; Ohlberger, M.; Cohen, A.; Willcox, K. Model Reduction and Approximation; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2017. [Google Scholar]
- Baur, U.; Benner, P.; Feng, L. Model Order Reduction for Linear and Nonlinear Systems: A System-Theoretic Perspective. Arch. Comput. Methods Eng. 2014, 21, 331–358. [Google Scholar] [CrossRef]
- Rutzmoser, J. Model Order Reduction for Nonlinear Structural Dynamics: Simulation-Free Approaches. Ph.D. Thesis, Technischen Universität München, Garching, Germany, 2018. [Google Scholar]
- Benner, P.; Grivet-Talocia, S.; Quarteroni, A.; Rozza, G.; Schilders, W.; Silveira, L.M. (Eds.) Model Order Reduction: Volume 1: System- and Data-Driven Methods and Algorithms, 1st ed.; De Gruyter: Berlin, Germany, 2021; Volume 1. [Google Scholar]
- Benner, P.; Grivet-Talocia, S.; Quarteroni, A.; Rozza, G.; Schilders, W.; Silveira, L.M. (Eds.) Model Order Reduction: Volume 2: Snapshot-Based Methods and Algorithms; De Gruyter: Berlin, Germany, 2021; Volume 2. [Google Scholar]
- Benner, P.; Grivet-Talocia, S.; Quarteroni, A.; Rozza, G.; Schilders, W.; Silveira, L.M. (Eds.) Model Order Reduction: Volume 3: Applications, 1st ed.; De Gruyter: Berlin, Germany, 2021; Volume 3. [Google Scholar]
- Lord Rayleigh, J. The Theory of Sound; Macmillan: New York, NY, USA, 1894. [Google Scholar]
- Weeger, O.; Wever, U.; Simeon, B. On the use of modal derivatives for nonlinear model order reduction. Int. J. Numer. Methods Eng. 2016, 108, 1579–1602. [Google Scholar] [CrossRef]
- Vizzaccaro, A.; Salles, L.; Touzé, C. Comparison of nonlinear mappings for reduced-order modelling of vibrating structures: Normal form theory and quadratic manifold method with modal derivatives. Nonlinear Dyn. 2021, 103, 3335–3370. [Google Scholar] [CrossRef]
- Mehner, J.; Gabbay, L.D.; Senturia, S.D. Computer-aided generation of nonlinear reduced-order dynamic macromodels. II. Stress-stiffened case. J. Microelectromech. Syst. 2000, 9, 270–278. [Google Scholar] [CrossRef]
- Mehner, J.; Doetzel, W.; Schauwecker, B.; Ostergaard, D. Reduced order modeling of fluid structural interactions in MEMS based on model projection techniques. In Proceedings of the Transducers ’03, Boston, MA, USA, 8–12 June 2003; pp. 1840–1843. [Google Scholar]
- Bennini, F.; Mehner, J.; Dötzel, W. Computational Methods for Reduced Order Modeling of Coupled Domain Simulations. In Transducers ’01 Eurosensors XV; Obermeier, E., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 260–263. [Google Scholar]
- Putnik, M.; Sniegucki, M.; Cardanobile, S.; Kehrberg, S.; Kuehnel, M.; Nagel, C.; Degenfeld-Schonburg, P.; Mehner, J. Incorporating geometrical nonlinearities in reduced order models for MEMS gyroscopes. In Proceedings of the IEEE Inertial Sensors 2017, Kauai, HI, USA, 28–30 March 2017; pp. 43–46. [Google Scholar]
- Putnik, M.; Sniegucki, M.; Cardanobile, S.; Kuhnel, M.; Kehrberg, S.; Mehner, J. Predicting the Resonance Frequencies in Geometric Nonlinear Actuated MEMS. J. Microelectromech. Syst. 2018, 27, 954–962. [Google Scholar] [CrossRef]
- Putnik, M.; Cardanobile, S.; Sniegucki, M.; Kehrberg, S.; Kuehnel, M.; Degenfeld-Schonburg, P.; Nagel, C.; Mehner, J. Simulation methods for generating reduced order models of MEMS sensors with geometric nonlinear drive motion. In Proceedings of the the 5th IEEE International Symposium on Inertial Sensors & Systems, Lake Como, Italy, 26–29 March 2018; pp. 1–4. [Google Scholar]
- Putnik, M. Simulation Methods for the Mechanical Nonlinearity in MEMS Gyroscopes. Ph.D. Thesis, Fakultät für Elektrotechnik und Informationstechnik, Chemnitz, Germany, 2019. [Google Scholar]
- Guyan, R.J. Reduction of Stiffness and Mass Matrices. AIAA J. 1964, 3, 380. [Google Scholar] [CrossRef]
- de Klerk, D.; Rixen, D.J.; Voormeeren, S.N. General Framework for Dynamic Substructuring: History, Review and Classification of Techniques. AIAA J. 2008, 46, 1169–1181. [Google Scholar] [CrossRef]
- Craig, R.R.; Bampton, M.C.C. Coupling of substructures for dynamic analyses. AIAA J. 1968, 6, 1313–1319. [Google Scholar] [CrossRef] [Green Version]
- MacNeal, R.H. A hybrid method of component mode synthesis. Comput. Struct. 1971, 1, 581–601. [Google Scholar] [CrossRef] [Green Version]
- Rubin, S. Improved Component-Mode Representation for Structural Dynamic Analysis. AIAA J. 1975, 13, 995–1006. [Google Scholar] [CrossRef]
- Craig, R.R.; Ni, Z. Component mode synthesis for model order reduction of nonclassicallydamped systems. J. Guid. Control. Dyn. 1989, 12, 577–584. [Google Scholar] [CrossRef]
- Lienemann, J. Complexity Reduction Techniques for Advanced MEMS Actuators Simulation. Ph.D. Thesis, Albert-Ludwigs-Universität Freiburg, Freiburg, Germany, 2006. [Google Scholar]
- Sadek, K.; Moussa, W. Application of adaptive multilevel substructuring technique to model CMOS micromachined thermistor gas sensor, part (I): A feasibility study. In Proceedings of the International Conference on MEMS, NANO and Smart Systems, Banff, AB, Canada, 20–23 July 2003; pp. 279–284. [Google Scholar]
- Sadek, K.; Lueke, J.; Moussa, W. A Coupled Field Multiphysics Modeling Approach to Investigate RF MEMS Switch Failure Modes under Various Operational Conditions. Sensors 2009, 9, 7988–8006. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Binion, D.; Chen, X. Coupled electrothermal–mechanical analysis for MEMS via model order reduction. Finite Elem. Anal. Des. 2010, 46, 1068–1076. [Google Scholar] [CrossRef]
- Giannini, D.; Bonaccorsi, G.; Braghin, F. Size optimization of MEMS gyroscopes using substructuring. Eur. J. Mech. A/Solids 2020, 84, 104045. [Google Scholar] [CrossRef]
- Mullis, C.; Roberts, R. Synthesis of minimum roundoff noise fixed point digital filters. IEEE Trans. Circuits Syst. 1976, 23, 551–562. [Google Scholar] [CrossRef]
- Moore, B. Principal component analysis in linear systems: Controllability, observability, and model reduction. IEEE Trans. Autom. Control 1981, 26, 17–32. [Google Scholar] [CrossRef]
- Chahlaoui, Y.; Lemonnier, D.; Vandendorpe, A.; van Dooren, P. Second-order balanced truncation. Linear Algebra Its Appl. 2006, 415, 373–384. [Google Scholar] [CrossRef]
- Reis, T.; Stykel, T. Balanced truncation model reduction of second-order systems. Math. Comput. Model. Dyn. Syst. 2008, 14, 391–406. [Google Scholar] [CrossRef]
- Wolf, T.; Castagnotto, A.; Eid, R. Moderne Methoden der Regelungstechnik 3-Teil B-Einführung in die Modellreduktion; Technische Universität München: München, Germany, 2016. [Google Scholar]
- M’Closkey, R.T.; Gibson, S.; Hui, J. System Identification of a MEMS Gyroscope. J. Dyn. Syst. Meas. Control 2001, 123, 201–210. [Google Scholar] [CrossRef]
- Kamon, M.; Wang, F.; White, J. Generating nearly optimally compact models from Krylov-subspace based reduced-order models. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 2000, 47, 239–248. [Google Scholar] [CrossRef] [Green Version]
- Rudnyi, E.B.; Korvink, J.G. Review: Automatic Model Reduction for Transient Simulation of MEMS-based Devices. Sens. Update 2002, 11, 3–33. [Google Scholar] [CrossRef]
- Grimme, E.J. Krylov Projection Methods for Model Reduction. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 1997. [Google Scholar]
- Freund, R.W. Krylov-subspace methods for reduced-order modeling in circuit simulation. J. Comput. Appl. Math. 2000, 123, 395–421. [Google Scholar] [CrossRef] [Green Version]
- Freund, R.W. Model reduction methods based on Krylov subspaces. Acta Numer. 2003, 12, 267–319. [Google Scholar] [CrossRef] [Green Version]
- Rudnyi, E.B.; Korvink, J.G. Model Order Reduction for Large Scale Engineering Models Developed in ANSYS. In Applied Parallel Computing. State of the Art in Scientific Computing; Hutchison, D., Kanade, T., Kittler, J., Kleinberg, J.M., Mattern, F., Mitchell, J.C., Naor, M., Nierstrasz, O., Pandu Rangan, C., Steffen, B., et al., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3732, pp. 349–356. [Google Scholar]
- Bai, Z.; Su, Y. SOAR: A Second-order Arnoldi Method for the Solution of the Quadratic Eigenvalue Problem. SIAM J. Matrix Anal. Appl. 2005, 26, 640–659. [Google Scholar] [CrossRef] [Green Version]
- Gugercin, S.; Antoulas, A.C.; Beattie, C. H2 Model Reduction for Large-Scale Linear Dynamical Systems. SIAM J. Matrix Anal. Appl. 2008, 30, 609–638. [Google Scholar] [CrossRef]
- Hung, E.S.; Yang, Y.J.; Senturia, S.D. Low-order models for fast dynamical simulation of MEMS microstructures. In Proceedings of the International Solid State Sensors and Actuators Conference (Transducers ’97), Chicago, IL, USA, 19 June 1997; pp. 1101–1104. [Google Scholar]
- Bechtold, T.; Rudnyi, E.B.; Korvink, J.G. Automatic order reduction of thermo-electric model for micro-ignition unit. In Proceedings of the International Conference on Simulation of Semiconductor Processes and Devices, Granada, Spain, 4–6 September 2002; pp. 131–134. [Google Scholar]
- Bechtold, T. Model Order Reduction of Electro-Thermal MEMS. Ph.D. Thesis, Albert-Ludwigs-Universität Freiburg, Freiburg, Germany, 2005. [Google Scholar]
- Bechtold, T.; Rudnyi, E.B.; Korvink, J.G. Fast Simulation of Electro-Thermal MEMS; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Liu, Y.; Yuan, W.; Chang, H.; Ma, B. Compact thermoelectric coupled models of micromachined thermal sensors using trajectory piecewise-linear model order reduction. Microsyst. Technol. 2014, 20, 73–82. [Google Scholar] [CrossRef]
- Yuan, C.; Kreß, S.; Sadashivaiah, G.; Rudnyi, E.B.; Hohlfeld, D.; Bechtold, T. Towards efficient design optimization of a miniaturized thermoelectric generator for electrically active implants via model order reduction and submodeling technique. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3311. [Google Scholar] [CrossRef]
- Yuan, C.; Hu, S.; Bechtold, T. Stable Compact Modeling of Piezoelectric Energy Harvester Devices. COMPEL 2020, 39, 868. [Google Scholar] [CrossRef]
- Yuan, C.; Hu, S.; Castagnotto, A.; Lohmann, B.; Bechtold, T. Implicit Schur Complement for Model Order Reduction of Second Order Piezoelectric Energy Harvester Model. In MATHMOD 2018 Extended Abstract Volume; Volume ARGESIM Report 55; ARGESIM: Vienna, Austria, 2018; pp. 77–78. ISBN 978-3-901608-91-9. [Google Scholar]
- Schütz, A.; Maeter, S.; Bechtold, T. System-Level Modelling and Simulation of a Multiphysical Kick and Catch Actuator System. Actuators 2021, 10, 279. [Google Scholar] [CrossRef]
- Schütz, A.; Farny, M.; Olbrich, M.; Hoffmann, M.; Ament, C.; Bechtold, T. Model Order Reduction of a Nonlinear Electromechanical Beam Actuator by Clustering Nonlinearities. In ACTUATOR 2022; GMM-Fachbericht, VDE VERLAG: Berlin, Germany; Offenbach, Germany, 2022; pp. 354–357. [Google Scholar]
- Pierquin, A.; Henneron, T.; Clenet, S.; Brisset, S. Model-Order Reduction of Magnetoquasi-Static Problems Based on POD and Arnoldi-Based Krylov Methods. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Bonotto, M.; Cenedese, A.; Bettini, P. Krylov Subspace Methods for Model Order Reduction in Computational Electromagnetics. IFAC-PapersOnLine 2017, 50, 6355–6360. [Google Scholar] [CrossRef]
- Chang, H.; Zhang, Y.; Xie, J.; Zhou, Z.; Yuan, W. Integrated Behavior Simulation and Verification for a MEMS Vibratory Gyroscope Using Parametric Model Order Reduction. J. Microelectromech. Syst. 2010, 19, 282–293. [Google Scholar] [CrossRef]
- Han, J.S.; Rudnyi, E.B.; Korvink, J.G. Efficient optimization of transient dynamic problems in MEMS devices using model order reduction. J. Micromech. Microeng. 2005, 15, 822–832. [Google Scholar] [CrossRef]
- Liang, Y.C.; Lin, W.Z.; Lee, H.P.; Lim, S.P.; Lee, K.H.; Sun, H. Proper Orthogonal Decomposition and Its Applications—Part II: Model Reduction for Mems Dynamical Analysis. J. Sound Vib. 2002, 256, 515–532. [Google Scholar] [CrossRef]
- Binion, D.; Chen, X. A Krylov enhanced proper orthogonal decomposition method for frequency domain model reduction. Eng. Comput. 2017, 34, 285–306. [Google Scholar] [CrossRef]
- Corigliano, A.; Dossi, M.; Mariani, S. Domain decomposition and model order reduction methods applied to the simulation of multi-physics problems in MEMS. Comput. Struct. 2013, 122, 113–127. [Google Scholar] [CrossRef]
- Gobat, G.; Opreni, A.; Fresca, S.; Manzoni, A.; Frangi, A. Reduced order modeling of nonlinear microstructures through Proper Orthogonal Decomposition. Mech. Syst. Signal Process. 2022, 171, 108864. [Google Scholar] [CrossRef]
- Benner, P.; Gugercin, S.; Willcox, K. A Survey of Projection-Based Model Reduction Methods for Parametric Dynamical Systems. SIAM Rev. 2015, 57, 483–531. [Google Scholar] [CrossRef]
- Benner, P.; Ohlberger, M.; Patera, A.; Rozza, G.; Urban, K. (Eds.) Model Reduction of Parametrized Systems; MS&A; Springer International Publishing: Cham, Switerland, 2017. [Google Scholar]
- Rudnyi, E.B.; Moosmann, C.; Greiner, A.; Bechtold, T.; Korvink, J.G. Parameter Preserving Model Reduction for MEMS System-level Simulation and Design. In MATHMOD; Vienna University of Technology: Vienna, Austria, 2006. [Google Scholar]
- Moosmann, C. ParaMOR–Model Order Reductionfor Parameterized MEMS Applications. Ph.D. Thesis, Albert-Ludwigs-Universität Freiburg, Freiburg, Germany, 2007. [Google Scholar]
- Panzer, H.; Mohring, J.; Eid, R.; Lohmann, B. Parametric Model Order Reduction by Matrix Interpolation. Automatisierungstechnik 2010, 58, 958. [Google Scholar] [CrossRef]
- Bond, B.; Daniel, L. Parameterized model order reduction of nonlinear dynamical systems. In Proceedings of the ICCAD-2005, IEEE/ACM International Conference on Computer-Aided Design, San Jose, CA, USA, 6–10 November 2005; pp. 487–494. [Google Scholar]
- Baur, U.; Benner, P.; Greiner, A.; Korvink, J.G.; Lienemann, J.; Moosmann, C. Parameter preserving model order reduction for MEMS applications. Math. Comput. Model. Dyn. Syst. 2011, 17, 297–317. [Google Scholar] [CrossRef]
- Feng, L.; Benner, P.; Korvink, J.G. Subspace recycling accelerates the parametric macro-modeling of MEMS. Int. J. Numer. Methods Eng. 2013, 94, 84–110. [Google Scholar] [CrossRef]
- del Tin, L. Reduced-Order Modelling, Circuit-Level Design and SOI Fabrication of Microelectromechanical Resonators. Ph.D. Thesis, Università di Bologna, Bologna, Italy, 2007. [Google Scholar]
- Rewieński, M.; White, J. A trajectory piecewise-linear approach to model order reduction and fast simulation of nonlinear circuits and micromachined devices. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2003, 22, 155–170. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.J.; Shen, K.Y. Nonlinear heat-transfer macromodeling for MEMS thermal devices. J. Micromech. Microeng. 2005, 15, 408–418. [Google Scholar] [CrossRef]
- Liu, Y.; Chang, H.; Yuan, W. A Global Maximum Error Controller-Based Method for Linearization Point Selection in Trajectory Piecewise-Linear Model Order Reduction. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2014, 33, 1100–1104. [Google Scholar]
- Liu, Y.; Wang, X. A Two-Step Global Maximum Error Controller-Based TPWL MOR with POD Basis Vectors and Its Applications to MEMS. Math. Probl. Eng. 2017, 2017, 5014235. [Google Scholar] [CrossRef] [Green Version]
- Albunni, M.N. Model Order Reduction of Moving Nonlinear Electromagnetic Devices. Ph.D. Thesis, Technischen Universität München, Munich, Germany, 2010. [Google Scholar]
- Chen, J.; Kang, S.M.; Zou, J.; Liu, C.; Schutt-Aine, J.E. Reduced-Order Modeling of Weakly Nonlinear MEMS Devices with Taylor-Series Expansion and Arnoldi Approach. J. Microelectrmech. Syst. 2004, 13, 441–451. [Google Scholar] [CrossRef]
- Mignolet, M.P.; Przekop, A.; Rizzi, S.A.; Spottswood, S.M. A review of indirect/non-intrusive reduced order modeling of nonlinear geometric structures. J. Sound Vib. 2013, 332, 2437–2460. [Google Scholar] [CrossRef]
- Chaturantabut, S.; Sorensen, D.C. Nonlinear Model Reduction via Discrete Empirical Interpolation. SIAM J. Sci. Comput. 2010, 32, 2737–2764. [Google Scholar] [CrossRef]
- Roy, A.; Nabi, M. Modeling of MEMS Electrothermal Microgripper employing POD-DEIM and POD method. Microelectron. Reliab. 2021, 125, 114338. [Google Scholar] [CrossRef]
- Hochman, A.; Bond, B.N.; White, J. A stabilized discrete empirical interpolation method for model reduction of electrical, thermal, and microelectromechanical systems. In Proceedings of the 48th Design Automation Conference, San Diego, CA, USA, 5–10 June 2011; Stok, L., Dutt, N., Hassoun, S., Eds.; ACM: New York, NY, USA, 2011; pp. 540–545. [Google Scholar]
- Farhat, C.; Avery, P.; Chapman, T.; Cortial, J. Dimensional reduction of nonlinear finite element dynamic models with finite rotations and energy-based mesh sampling and weighting for computational efficiency. Int. J. Numer. Methods Eng. 2014, 98, 625–662. [Google Scholar] [CrossRef]
- Farhat, C.; Chapman, T.; Avery, P. Structure-preserving, stability, and accuracy properties of the energy-conserving sampling and weighting method for the hyper reduction of nonlinear finite element dynamic models. Int. J. Numer. Methods Eng. 2015, 102, 1077–1110. [Google Scholar] [CrossRef]
- Chapman, T. Nonlinear Model Order Reduction for Structural Systems with Contact. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2019. [Google Scholar]
- Gao, H.; Wang, J.X.; Zahr, M.J. Non-intrusive model reduction of large-scale, nonlinear dynamical systems using deep learning. Phys. D Nonlinear Phenom. 2020, 412, 132614. [Google Scholar] [CrossRef]
- Cicci, L.; Fresca, S.; Manzoni, A. Deep-HyROMnet: A deep learning-based operator approximation for hyper-reduction of nonlinear parametrized PDEs. J. Sci. Comput. 2022, 93, 57. [Google Scholar] [CrossRef]
- Simpson, T.W.; Poplinski, J.D.; Koch, P.N.; Allen, J.K. Metamodels for Computer-based Engineering Design: Survey and recommendations. Eng. Comput. 2001, 17, 129–150. [Google Scholar] [CrossRef] [Green Version]
- Schrag, G.; Wachutka, G. System-Level Modeling of MEMS Using Generalized Kirchhoffian Networks-Basic Principles. In System-Level Modeling of MEMS; Bechtold, T., Schrag, G., Feng, L., Eds.; Advanced Micro and Nanosystems; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013; pp. 19–51. [Google Scholar]
- Lenk, A.; Ballas, R.G.; Werthschützky, R.; Pfeifer, G. Electromechanical Systems in Microtechnology and Mechatronics: Electrical, Mechanical and Acoustic Networks, Their Interactions and Applications; Microtechnology and MEMS; Springer: Berlin, Germany, 2010. [Google Scholar]
- Bosetti, G.; Manz, J.; Dehé, A.; Krumbein, U.; Schrag, G. Modeling and physical analysis of an out-of-plane capacitive MEMS transducer with dynamically coupled electrodes. Microsyst. Technol. 2019, 3, 81. [Google Scholar] [CrossRef]
- Bosetti, G.; Schrag, G. Efficient Modeling of Acoustic Channels – Towards Tailored Frequency Response of Airborne Ultrasonic MEMS Transducers. In Proceedings of the 2022 23rd International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Graz, Austria, 25–27 April 2022; pp. 1–5. [Google Scholar]
- Gruber, A.; Gunzburger, M.; Ju, L.; Wang, Z. A comparison of neural network architectures for data-driven reduced-order modeling. Comput. Methods Appl. Mech. Eng. 2022, 393, 114764. [Google Scholar] [CrossRef]
- Peherstorfer, B.; Willcox, K. Data-driven operator inference for nonintrusive projection-based model reduction. Comput. Methods Appl. Mech. Eng. 2016, 306, 196–215. [Google Scholar] [CrossRef] [Green Version]
- Benner, P.; Goyal, P.; Kramer, B.; Peherstorfer, B.; Willcox, K. Operator inference for non-intrusive model reduction of systems with non-polynomial nonlinear terms. Comput. Methods Appl. Mech. Eng. 2020, 372, 113433. [Google Scholar] [CrossRef]
- Qian, E.; Kramer, B.; Peherstorfer, B.; Willcox, K. Lift & Learn: Physics-informed machine learning for large-scale nonlinear dynamical systems. Phys. D Nonlinear Phenom. 2020, 406, 132401. [Google Scholar]
- Antoulas, A.C. Approximation of Large-Scale Dynamical Systems; Advances in Design and Control; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2005. [Google Scholar]
- Ryckelynck, D. A priori hyperreduction method: An adaptive approach. J. Comput. Phys. 2005, 202, 346–366. [Google Scholar] [CrossRef] [Green Version]
- Rewieński, M. A Trajectory Piecewise-Linear Approach to Model Order Reduction of Nonlinear Dynamical Systems. Ph.D. Thesis, Technical University of Gdansk, Gdansk, Poland, 2003. [Google Scholar]
- Schütz, A.; Bechtold, T. Performance Comparison for Stable Compact Modelling of Piezoelectric Microactuator. In Proceedings of the 2022 23rd International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Graz, Austria, 25–27 April 2022; pp. 1–8. [Google Scholar]
- Rudnyi, E.B.; Lienemann, J.; Greiner, A.; Korvink, J.G. mor4ansys: Generating Compact Models Directly from ANSYS Models; Routledge: Oxfordshire, UK, 2004. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kudryavtsev, M.; Rudnyi, E.B.; Korvink, J.G.; Hohlfeld, D.; Bechtold, T. Computationally efficient and stable order reduction methods for a large-scale model of MEMS piezoelectric energy harvester. Microelectron. Reliab. 2015, 55, 747–757. [Google Scholar] [CrossRef]
- Hu, S.; Yuan, C.; Castagnotto, A.; Lohmann, B.; Bouhedma, S.; Hohlfeld, D.; Bechtold, T. Stable reduced order modeling of piezoelectric energy harvesting modules using implicit Schur complement. Microelectron. Reliab. 2018, 85, 148–155. [Google Scholar] [CrossRef]
- Farny, M.; Hoffmann, M. Kick & Catch: Elektrostatisches Rotieren einer Kugel. In MikroSystemTechnik Kongress; VDE Verlag GmbH: Stuttgart-Ludwigsburg, Germany, 2021; pp. 274–277. [Google Scholar]











Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schütz, A.; Bechtold, T. Model Order Reduction of Microactuators: Theory and Application. Actuators 2023, 12, 235. https://doi.org/10.3390/act12060235
Schütz A, Bechtold T. Model Order Reduction of Microactuators: Theory and Application. Actuators. 2023; 12(6):235. https://doi.org/10.3390/act12060235
Chicago/Turabian StyleSchütz, Arwed, and Tamara Bechtold. 2023. "Model Order Reduction of Microactuators: Theory and Application" Actuators 12, no. 6: 235. https://doi.org/10.3390/act12060235




