Robust Adaptive Composite Learning Integrated Guidance and Control for Skid-to-Turn Interceptors Subjected to Multiple Uncertainties and Constraints
Abstract
:1. Introduction
- As elaborated in the paper, this study proposes a novel adaptive dynamic surface control framework based on online composite learning and the BLF principle for the IGC by considering multiple uncertainties and the overload constraint;
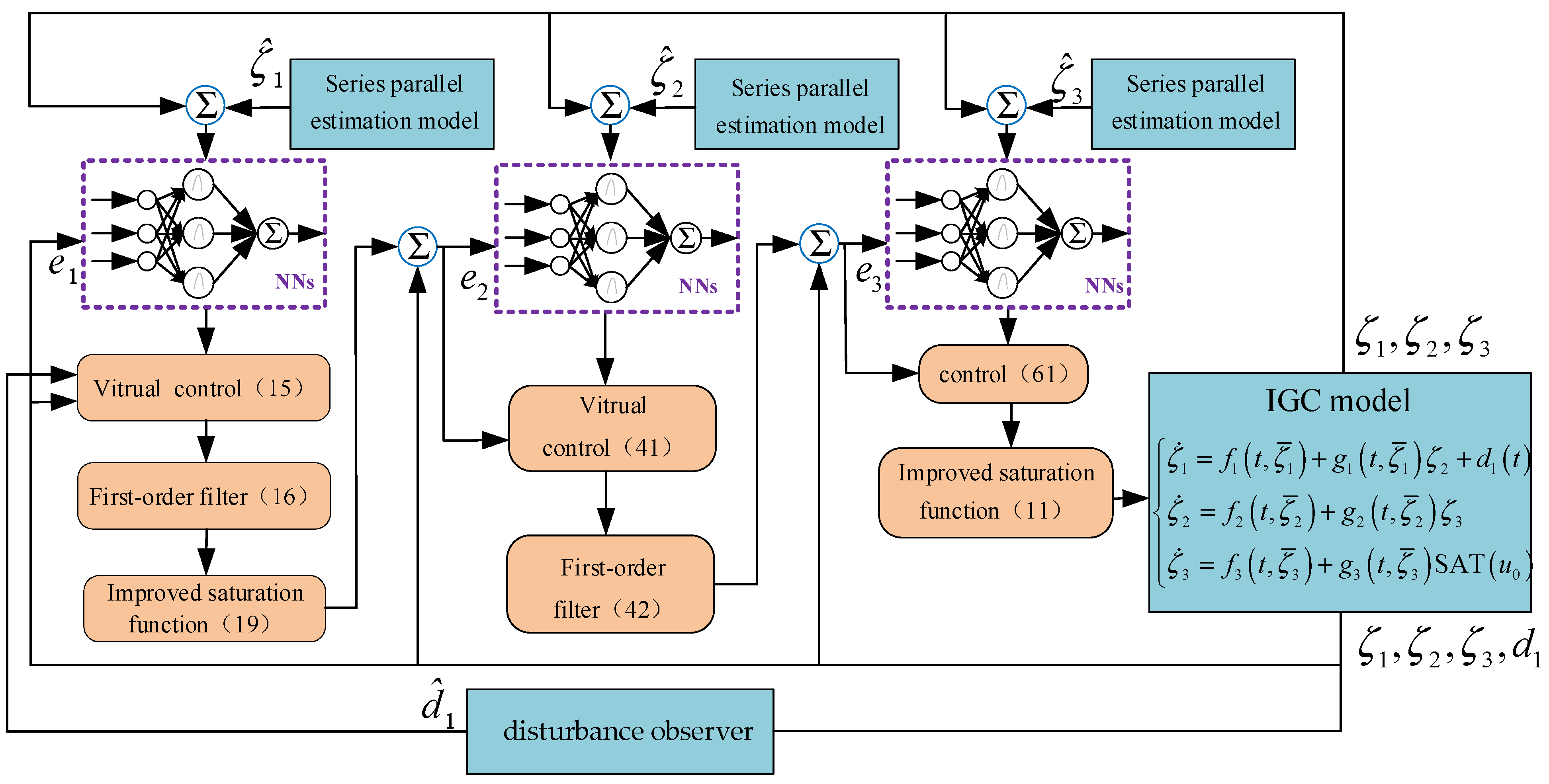
- Different from previous studies in which the learning law is designed only by tracking errors, the serial-parallel estimation model established in this study estimates the system state and provides “critic” information for the neural network (NN) and disturbance observer that approximates the system uncertainties. Then, these three are combined to realize online composite learning of the multiple uncertainties of the system and improve interception accuracy;
- Aiming at the state constraint of the interceptor, the application of the improved saturation function and BLF can restrict the specific state to a certain range, while the design of the auxiliary system guarantees the system stability.
2. Preliminaries
2.1. IGC Model
2.2. Intelligent Approximation Scheme
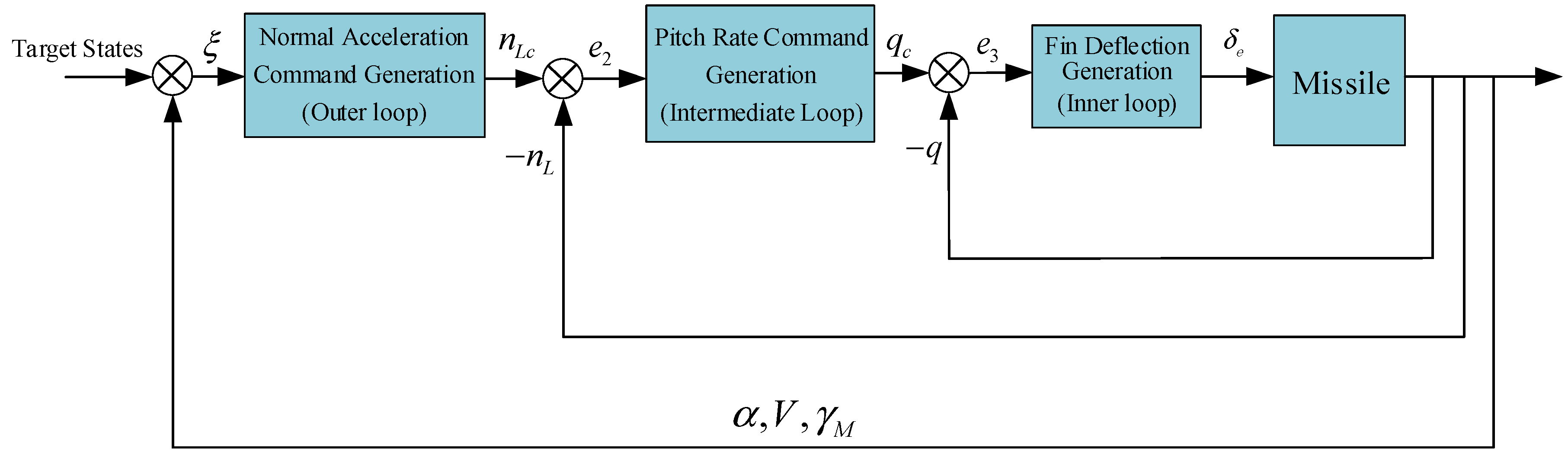
3. The Design of Adaptive Composite Learning IGC Scheme
- Outer Loop
- B.
- Intermediate Loop
- C.
- Inner Loop
4. Stability Analysis
- The output of the system can converge to a neighborhood of zero;
- All signals such as , , , , , , , , , , and are uniformly ultimately bounded;
- The constraint of the state variable will not be violated.
5. Simulation Study
5.1. Simulation Parameters
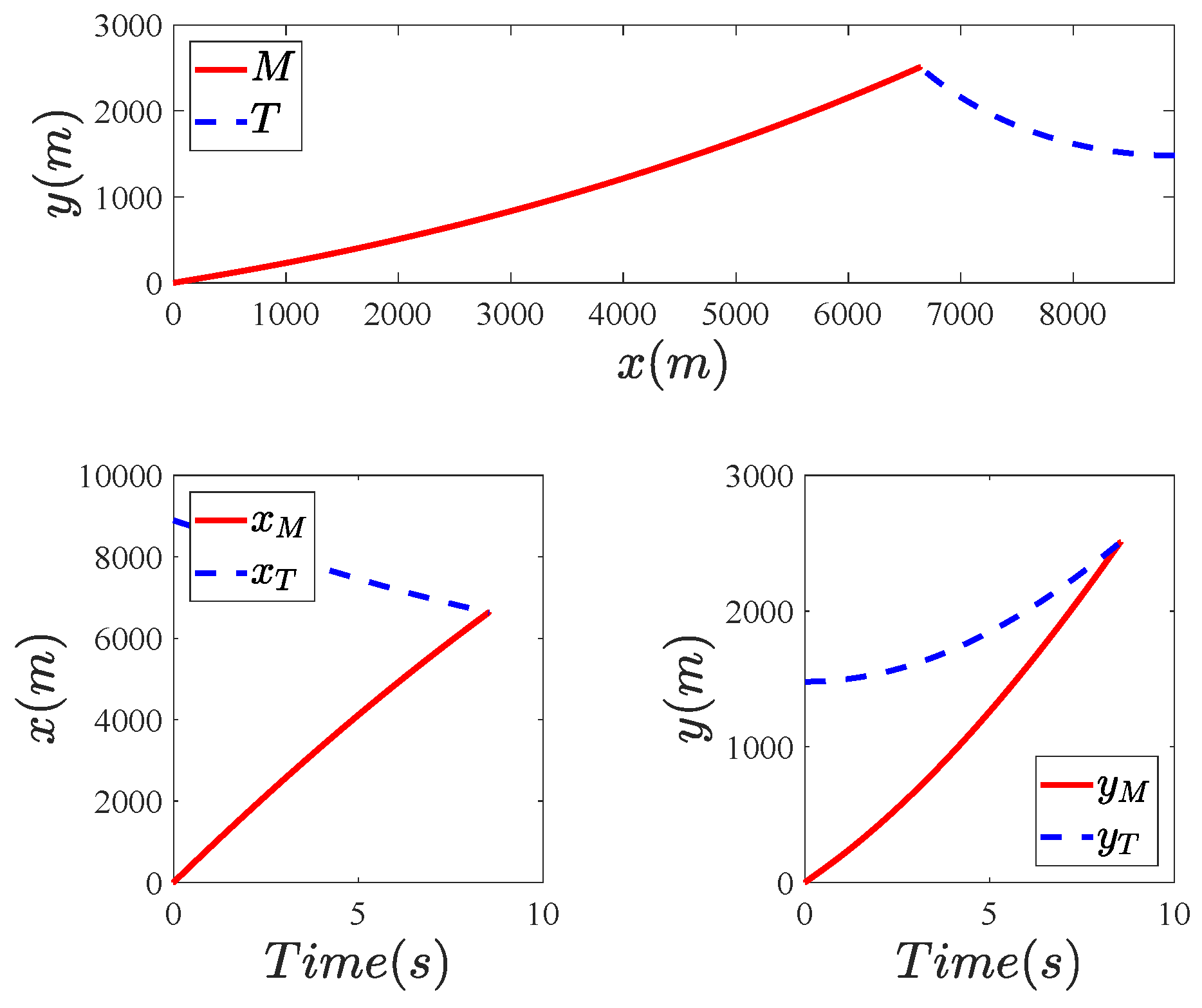
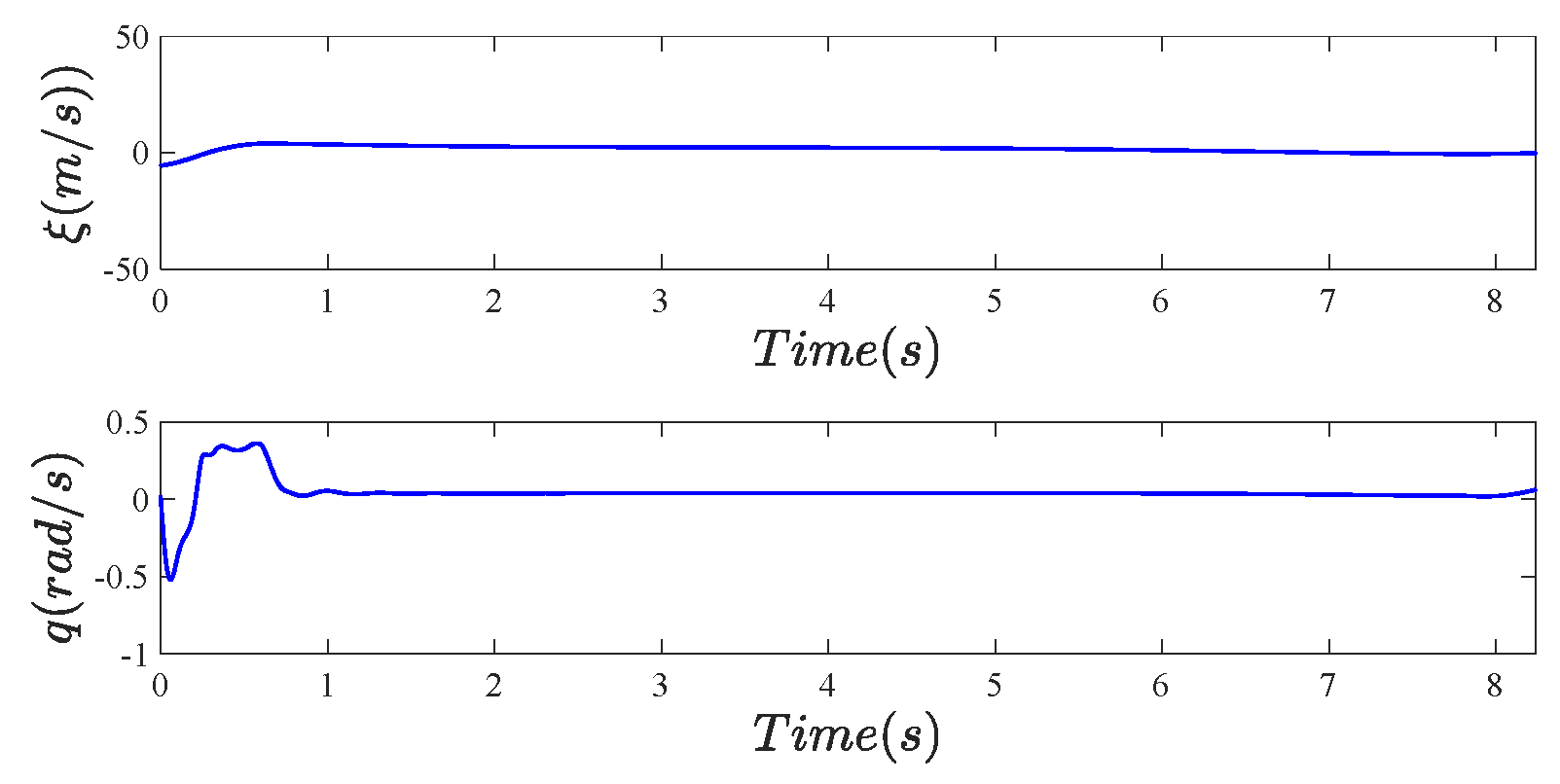
5.2. Simulation Results
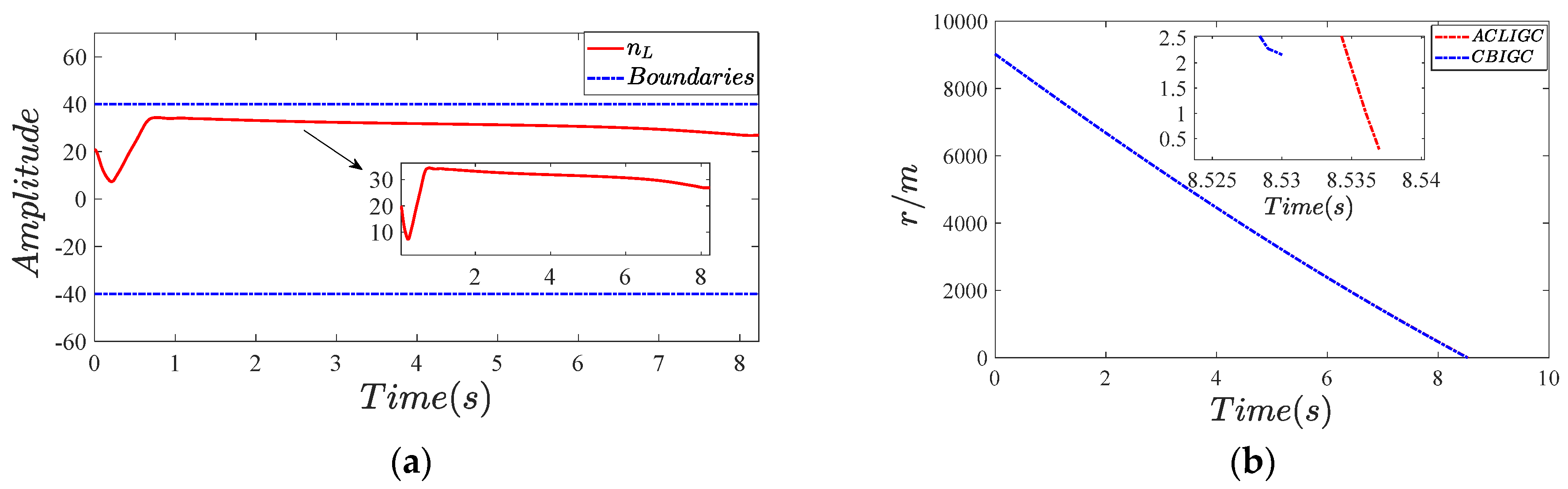
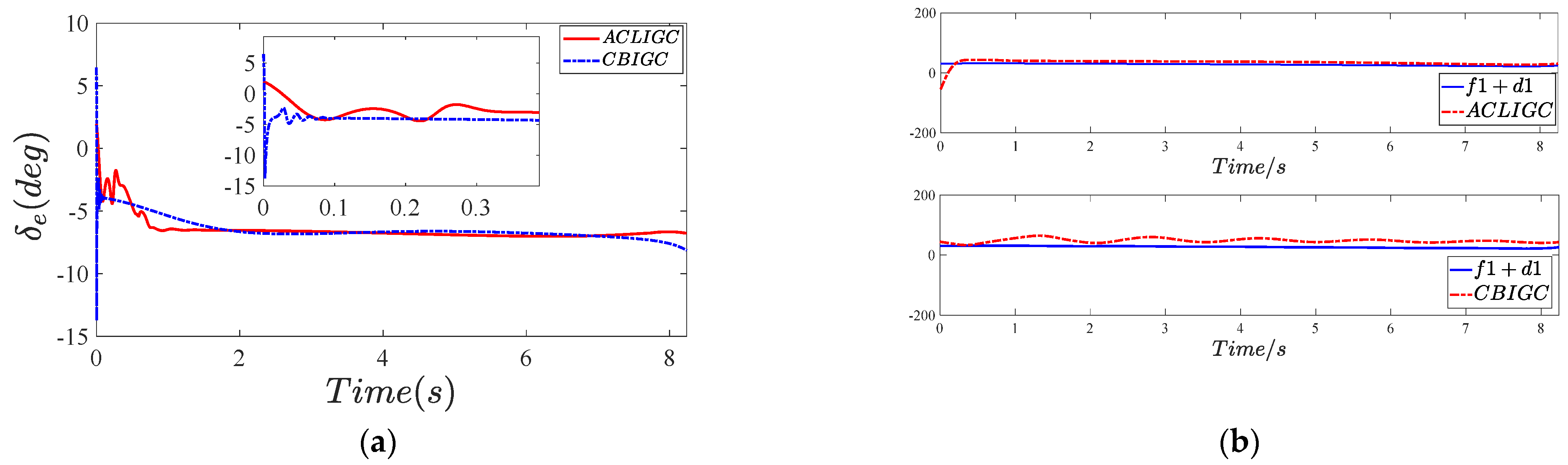
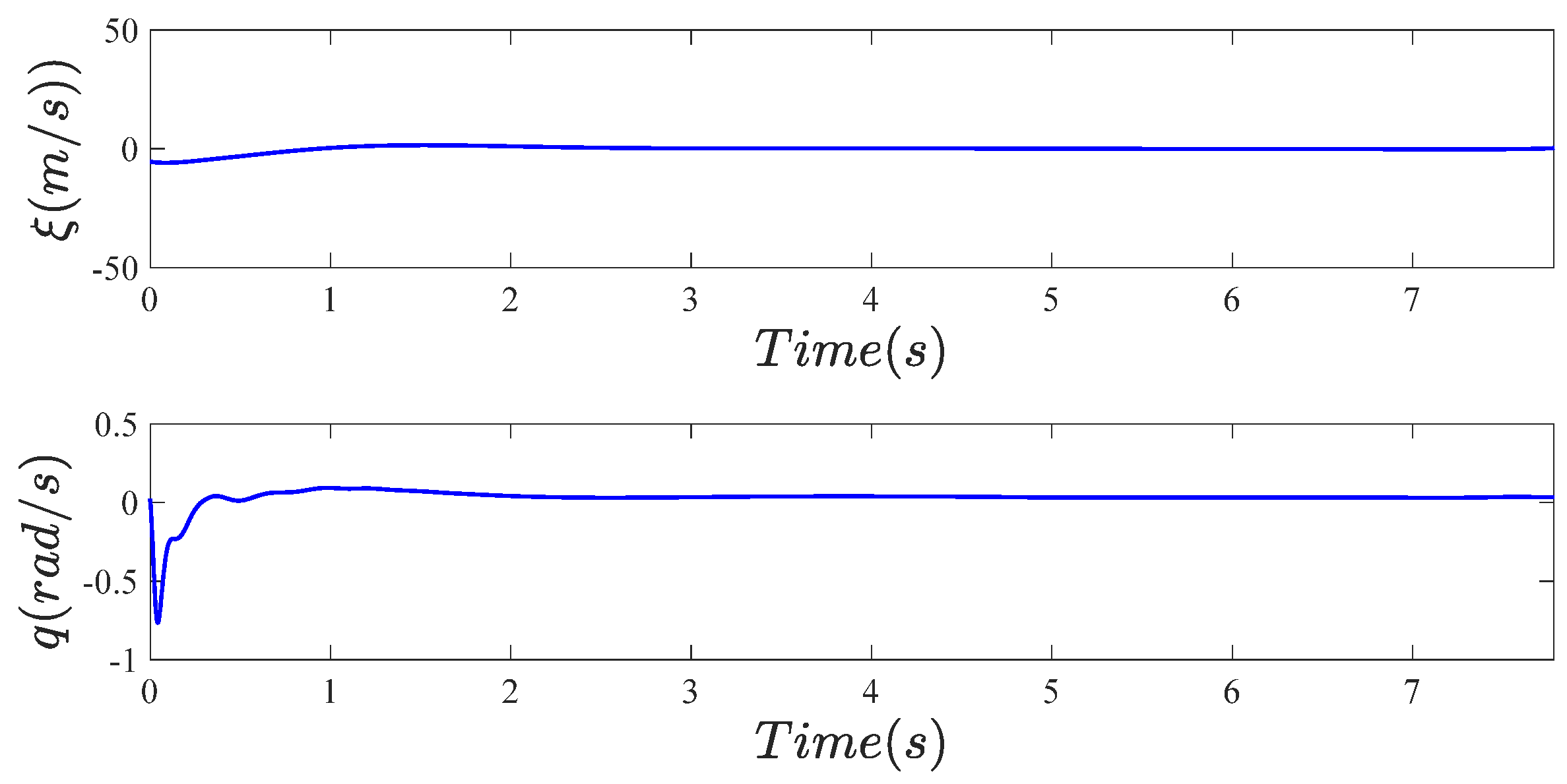
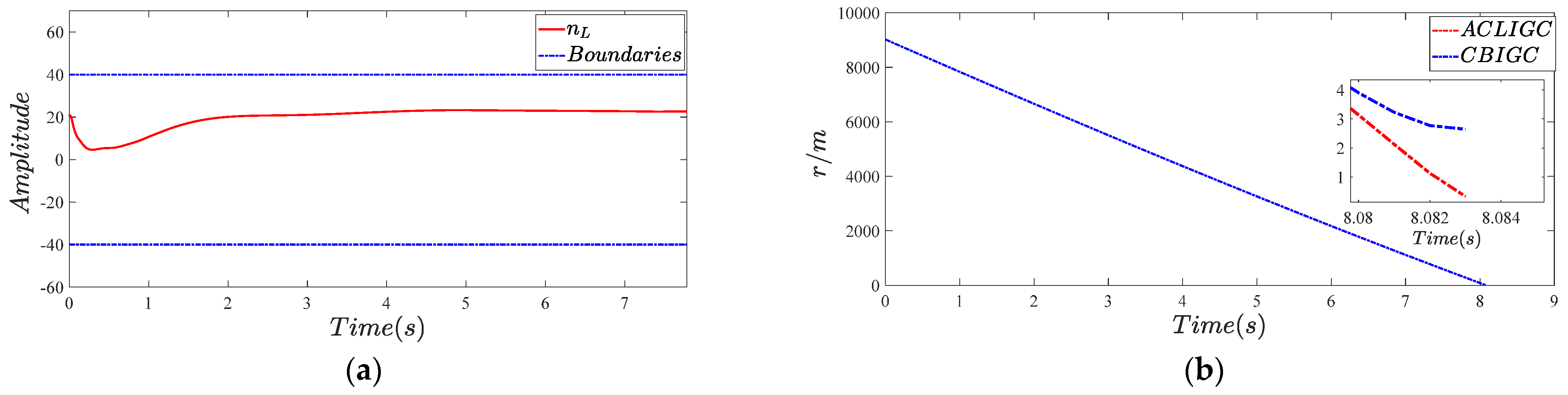
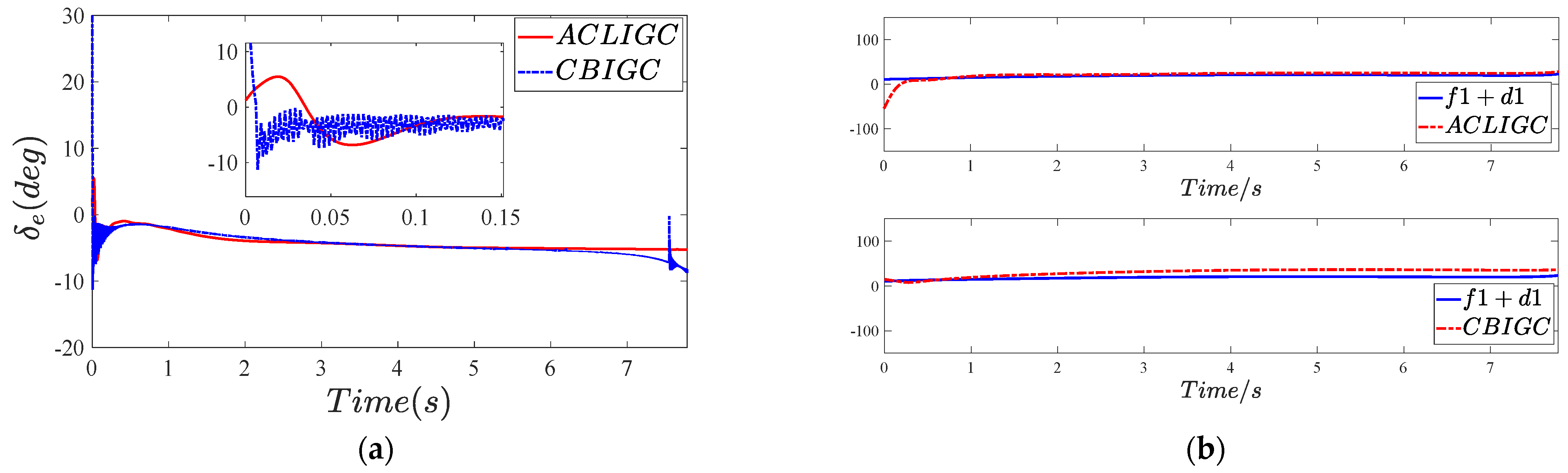
5.2.1. Effectiveness Verification
5.2.2. Robustness Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Z.; Shima, T. Nonlinear optimal guidance for intercepting a stationary target. J. Guid. Control Dyn. 2019, 42, 2418–2431. [Google Scholar] [CrossRef]
- Wang, Z.; Yuan, J.P. Fuzzy adaptive fault tolerant IGC method for STT missiles with time-varying actuator faults and multisource uncertainties. J. Franklin. Inst. 2020, 357, 59–81. [Google Scholar] [CrossRef]
- Liu, W.K.; Wei, Y.Y.; Duan, G.R. Barrier Lyapunov function-based integrated guidance and control with input saturation and state constraints. Aerosp. Sci. Technol. 2019, 84, 845–855. [Google Scholar] [CrossRef]
- Liang, X.L.; Hou, M.Z.; Duan, G.R. Adaptive dynamic surface control for integrated missile guidance and autopilot in the presence of input saturation. J. Aerosp. Eng. 2015, 28, 04014121. [Google Scholar] [CrossRef]
- Park, J.; Kim, Y.; Kim, J.H. Integrated guidance and control using model predictive contrSol with flight path angle prediction against pull-up maneuvering target. Sensors 2020, 20, 3143. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.G.; Xiong, Y.; Zhou, J. A new sliding mode control design for integrated missile guidance and control system. Aerosp. Sci. Technol. 2018, 78, 54–61. [Google Scholar] [CrossRef]
- Zhou, X.H.; Wang, W.H.; Liu, Z.H.; Liang, C.; Lai, C. Impact angle constrained three-dimensional integrated guidance and control based on fractional integral terminal sliding mode control. IEEE Access 2019, 7, 126857–126870. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, H.; Huang, H.Q.; Zhao, X. Integrated guidance and control design of the suicide UCAV for terminal attack. J. Syst. Eng. Electron. 2017, 28, 546–555. [Google Scholar]
- Shao, X.L.; Wang, H.L. Back-stepping active disturbance rejection control design for integrated missile guidance and control system via reduced-order ESO. ISA Trans. 2015, 57, 10–22. [Google Scholar]
- Liu, W.K.; Wei, Y.Y.; Duan, G.R.; Hou, M.Z. Integrated guidance and control with input saturation and disturbance observer. J. Control Decis. 2018, 5, 277–299. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, Y.J. Non-singular terminal dynamic surface control based integrated guidance and control design and simulation. ISA Trans. 2016, 63, 112–120. [Google Scholar]
- Jiang, S.; Tian, F.Q.; Sun, S.Y.; Liang, W.G. Integrated guidance and control of guided projectile with multiple constraints based on fuzzy adaptive and dynamic surface. Def. Technol. 2020, 16, 1130–1141. [Google Scholar] [CrossRef]
- Yan, X.H.; Shao, G.W.; Yang, Q.Y.; Yu, L.; Yao, Y.W.; Tu, S.X. Adaptive Robust Tracking Control for Near Space Vehicles with Multi-Source Disturbances and Input–Output Constraints. Actuators 2022, 11, 273. [Google Scholar] [CrossRef]
- Wu, B.; Wu, J.L.; Zhang, J.; Tang, G.J.; Zhao, Z.J. Adaptive Neural Control of a 2DOF Helicopter with Input Saturation and Time-Varying Output Constraint. Actuators 2022, 11, 336. [Google Scholar] [CrossRef]
- Panchal, B.; Mate, N.; Talole, S.E. Continuous-time predictive control-based integrated guidance and control. J. Guid. Control Dyn. 2017, 40, 1579–1595. [Google Scholar] [CrossRef]
- He, S.M.; Song, T.; Lin, D.F. Impact angle constrained integrated guidance and control for maneuvering target interception. J. Guid. Control Dyn. 2017, 40, 2653–2661. [Google Scholar] [CrossRef]
- Zhou, D.; Xu, B. Adaptive dynamic surface guidance law with input saturation constraint and autopilot dynamics. J. Guid. Control Dyn. 2016, 39, 1155–1162. [Google Scholar] [CrossRef]
- Guo, J.; Zhou, J.; Zhao, B. Three-dimensional integrated guidance and control for strap-down missiles considering seeker’s field-of-view angle constraint. Trans. Inst. Meas. Control 2020, 42, 1097–1109. [Google Scholar] [CrossRef]
- Liu, X.D.; Huang, W.W.; Du, L.F. An integrated guidance and control approach in three-dimensional space for hypersonic missile constrained by impact angles. ISA Trans. 2017, 66, 164–175. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, W.H.; Wang, D.H.; Peng, K.; Yang, H.B. Command filtered back-stepping missile integrated guidance and autopilot based on extended state observer. Adv. Mech. Eng. 2017, 9, 1687814017733251. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.B.; Dong, Q.L.; Zhang, X.Y.; Gao, Y.F. Impact angle-constrained integrated guidance and control for supersonic skid-to-turn missiles using backstepping with global fast terminal sliding mode control. Aerosp. Sci. Technol. 2022, 122, 107386. [Google Scholar] [CrossRef]
- Chao, M.; Wang, X.M.; Sun, R.S. A novel non-singular terminal sliding mode control-based integrated missile guidance and control with impact angle constraint. Aerosp. Sci. Technol. 2019, 94, 105368. [Google Scholar]
- Tian, J.Y.; Chen, H.F.; Liu, X.C.; Yang, H.B.; Zhang, S.F. Integrated strapdown missile guidance and control with field-of-view constraint and actuator saturation. IEEE Access 2020, 8, 123623–123638. [Google Scholar] [CrossRef]
- Peng, Q.; Guo, J.G.; Zhou, J. Integrated guidance and control system design for laser beam riding missiles with relative position constraints. Aerosp. Sci. Technol. 2020, 98, 105693. [Google Scholar] [CrossRef]
- Ai, X.L.; Shen, Y.C.; Wang, L.L. Adaptive integrated guidance and control for impact angle constrained interception with actuator saturation. Aeronaut. J. 2019, 123, 1437–1453. [Google Scholar] [CrossRef]
- Wang, W.H.; Xiong, S.F.; Wang, S.; Song, S.Y.; Lai, C. Three dimensional impact angle constrained integrated guidance and control for missiles with input saturation and actuator failure. Aerosp. Sci. Technol. 2016, 53, 169–187. [Google Scholar] [CrossRef]
- Wang, S.; Wang, W.H.; Xiong, S.F. Impact angle constrained three-dimensional integrated guidance and control for STT missile in the presence of input saturation. ISA Trans. 2016, 64, 151–160. [Google Scholar] [CrossRef]
- Khankalantary, S.; Sheikholeslam, F. Robust extended state observer-based three dimensional integrated guidance and control design for interceptors with impact angle and input saturation constraints. ISA Trans. 2020, 104, 299–309. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.H.; Ma, P.; Wang, S.Y.; Chao, T. Multi-constraints adaptive finite-time integrated guidance and control design. Aerosp. Sci. Technol. 2020, 107, 106334. [Google Scholar] [CrossRef]
- Huang, J.; Lin, C.F. Application of sliding mode control to bank-to-turn missile systems. In Proceedings of the First IEEE Regional Conference on Aerospace Control Systems, Westlake Village, CA, USA, 25–27 May 1993. [Google Scholar]
- Zhou, J.L.; Yang, J.Y. Smooth sliding mode control for missile interception with finite-time convergence. J. Guid. Control Dyn. 2015, 38, 1311–1318. [Google Scholar] [CrossRef]
- Shtessel, Y.B.; Shkolnikov, I.A.; Levant, A. Guidance and control of missile interceptor using second-order sliding modes. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 110–124. [Google Scholar] [CrossRef]
- Liu, W.K.; Wei, Y.Y.; Hou, M.Z.; Duan, G.R. Integrated guidance and control with partial state constraints and actuator faults. J. Frankl. Inst.-Eng. Appl. Math. 2019, 356, 4785–4810. [Google Scholar] [CrossRef]
- Chen, M.; Ge, S.S. Adaptive neural output feedback control of uncertain nonlinear systems with unknown hysteresis using disturbance observer. IEEE Trans. Ind. Electron. 2015, 62, 7706–7716. [Google Scholar] [CrossRef]
- Liu, W.K.; Wei, Y.Y.; Duan, G.R. Integrated guidance and control with input saturation. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017. [Google Scholar]



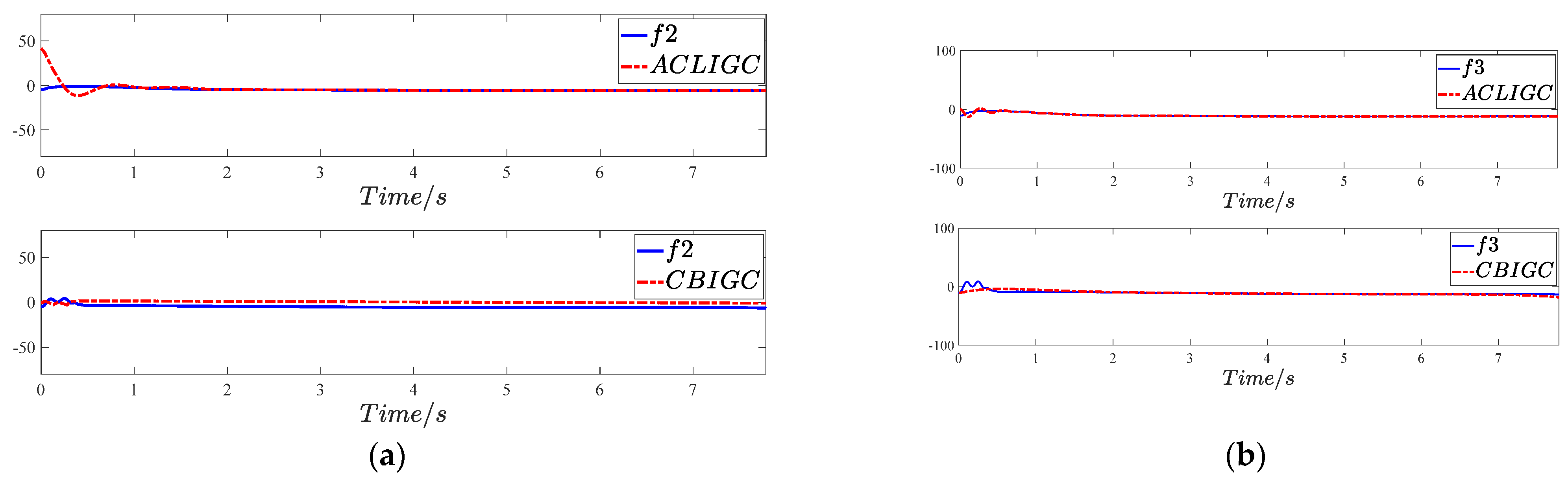
| Variable | Implication |
|---|---|
| The relative distance along the line of sight (LOS) | |
| The projections of relative velocity along the LOS | |
| The projections of relative velocity perpendicular to the LOS | |
| The projections of target acceleration along the LOS | |
| The projections of target acceleration perpendicular to the LOS | |
| LOS angle | |
| Atmosphere density | |
| Reference area | |
| Reference length |
| Variable | Variable |
|---|---|
| Pitch angle | |
| Angle of attack | |
| Variable | Maximum Value | Minimum Value |
|---|---|---|
| 40 | −40 | |
| 30 | −30 |
| Scheme | Miss Distance, m | |
|---|---|---|
| Scenario 1 | Scenario 2 | |
| ACLIGC | 0.267 | 0.332 |
| CBIGC | 2.161 | 2.648 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Yan, T.; Fu, W.; Li, T.; Huang, J. Robust Adaptive Composite Learning Integrated Guidance and Control for Skid-to-Turn Interceptors Subjected to Multiple Uncertainties and Constraints. Actuators 2023, 12, 243. https://doi.org/10.3390/act12060243
Bai Y, Yan T, Fu W, Li T, Huang J. Robust Adaptive Composite Learning Integrated Guidance and Control for Skid-to-Turn Interceptors Subjected to Multiple Uncertainties and Constraints. Actuators. 2023; 12(6):243. https://doi.org/10.3390/act12060243
Chicago/Turabian StyleBai, Yu, Tian Yan, Wenxing Fu, Tong Li, and Junhua Huang. 2023. "Robust Adaptive Composite Learning Integrated Guidance and Control for Skid-to-Turn Interceptors Subjected to Multiple Uncertainties and Constraints" Actuators 12, no. 6: 243. https://doi.org/10.3390/act12060243
APA StyleBai, Y., Yan, T., Fu, W., Li, T., & Huang, J. (2023). Robust Adaptive Composite Learning Integrated Guidance and Control for Skid-to-Turn Interceptors Subjected to Multiple Uncertainties and Constraints. Actuators, 12(6), 243. https://doi.org/10.3390/act12060243







