Multi-Physics Simulation and Experimental Verification of Magnetorheological Damper with Additional Stiffness
Abstract
:1. Introduction
2. Introduction the Gas-Compensated Single-Rod MRD
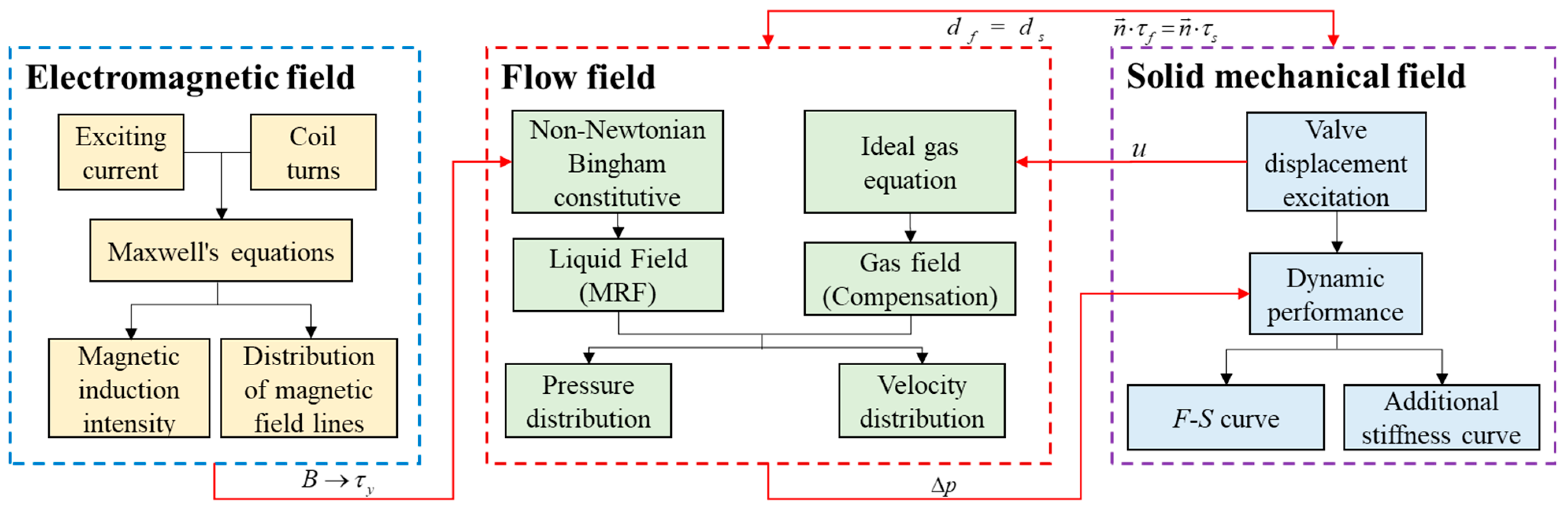
3. Multi-Physics FIELD Analysis
3.1. Electromagnetic Field Analysis
- (1)
- Field control equation
- (2)
- Boundary conditions
3.2. Flow Field Analysis
3.2.1. MRF Flow Field
- (1)
- Field control equation
- (2)
- Boundary conditions
3.2.2. Gas Flow Field
- (1)
- Field control equation
- (2)
- Boundary conditions
3.3. Solid Mechanics Field
- (1)
- Field control equation
- (2)
- Boundary conditions
4. Multi-Physics Field Coupling Simulation
4.1. Simulation Model Building
- The displacement of the solid and fluid on the coupling boundary is equal .
- The stress at the boundary between solid and fluid is equal .
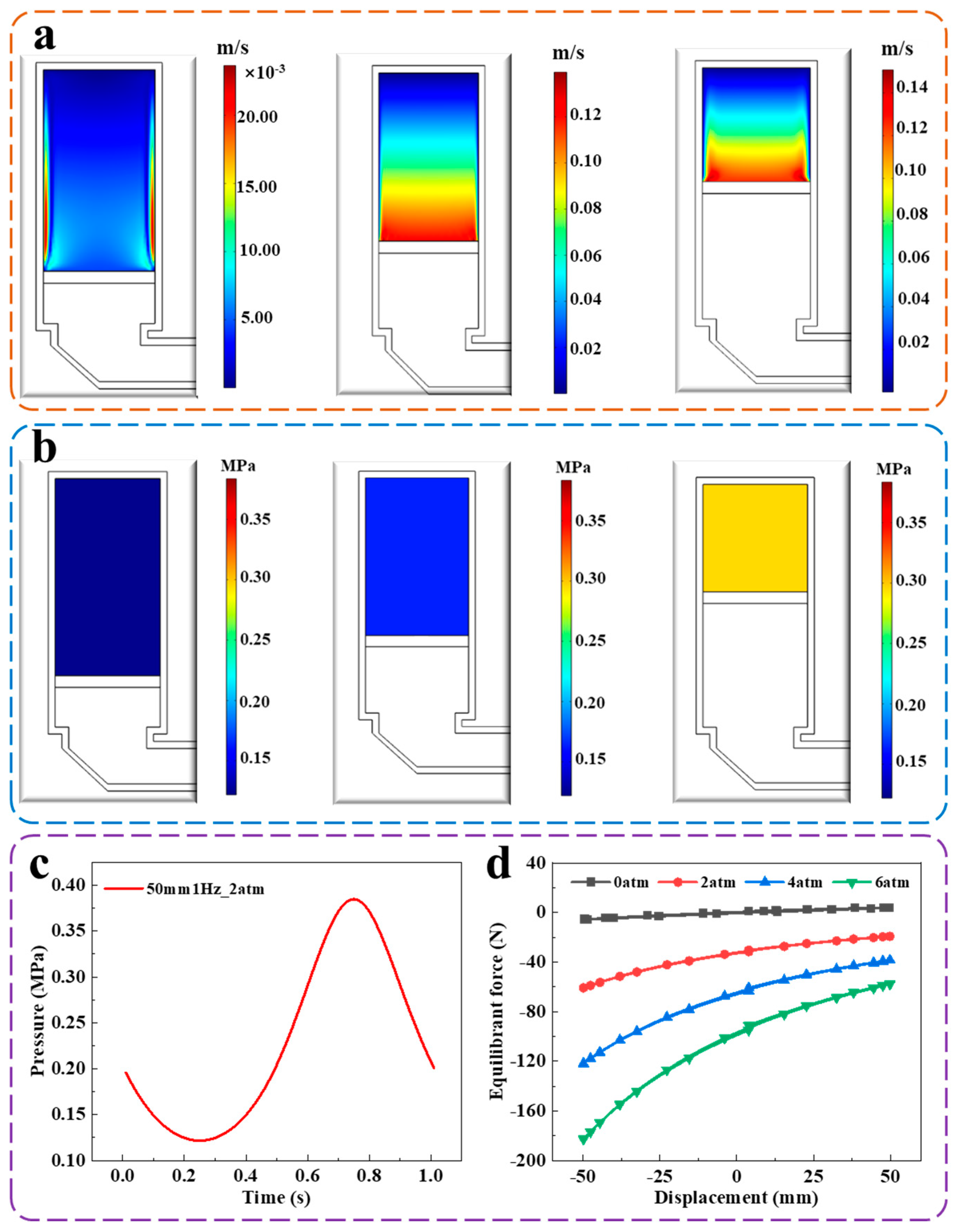
4.1.1. Magnetic Field Simulation
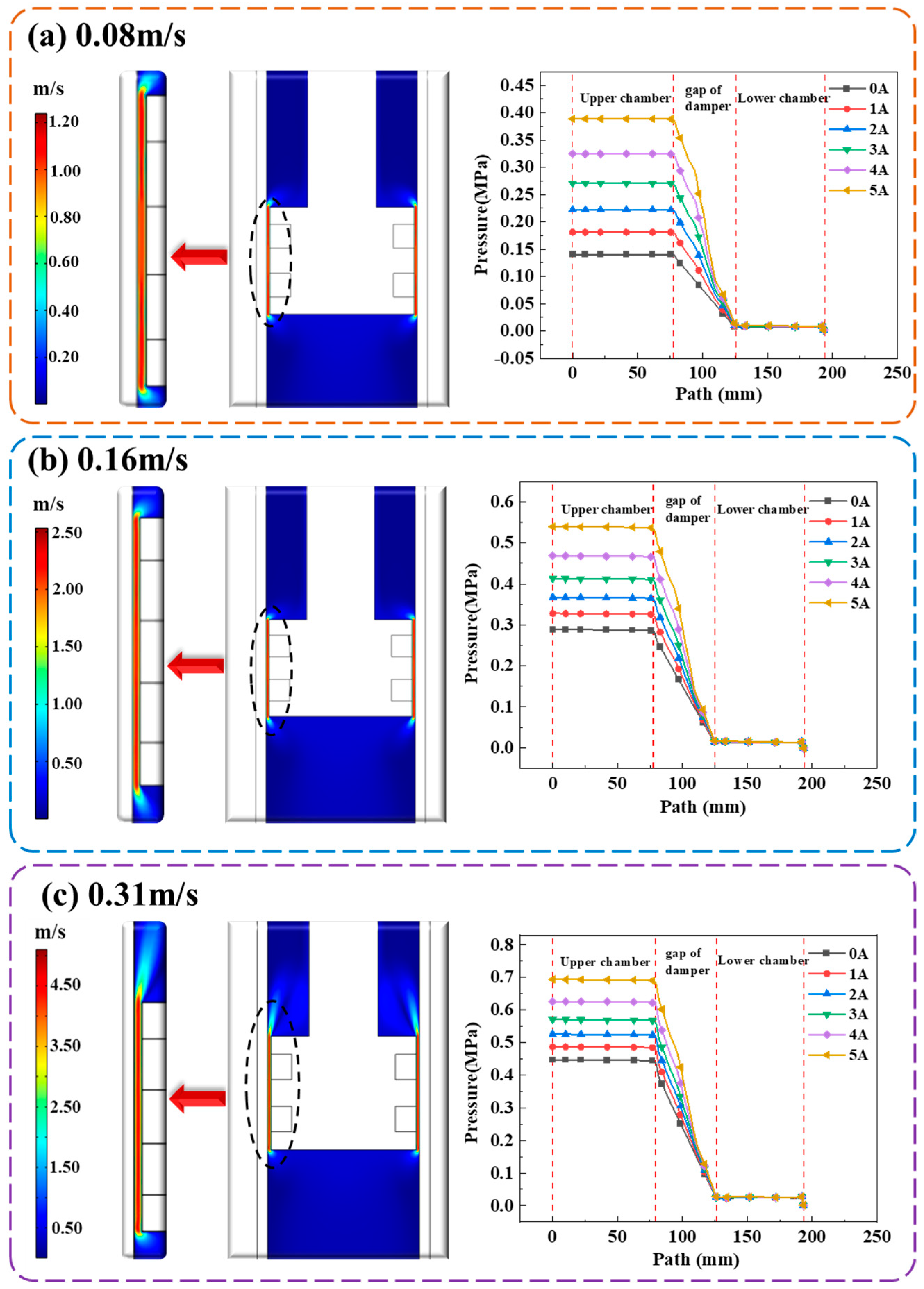
4.1.2. Flow Field Simulation
- (1)
- MRF flow field
- (2)
- Gas flow field
4.1.3. Solid Force Field Simulation
5. Experimental Testing and Verification
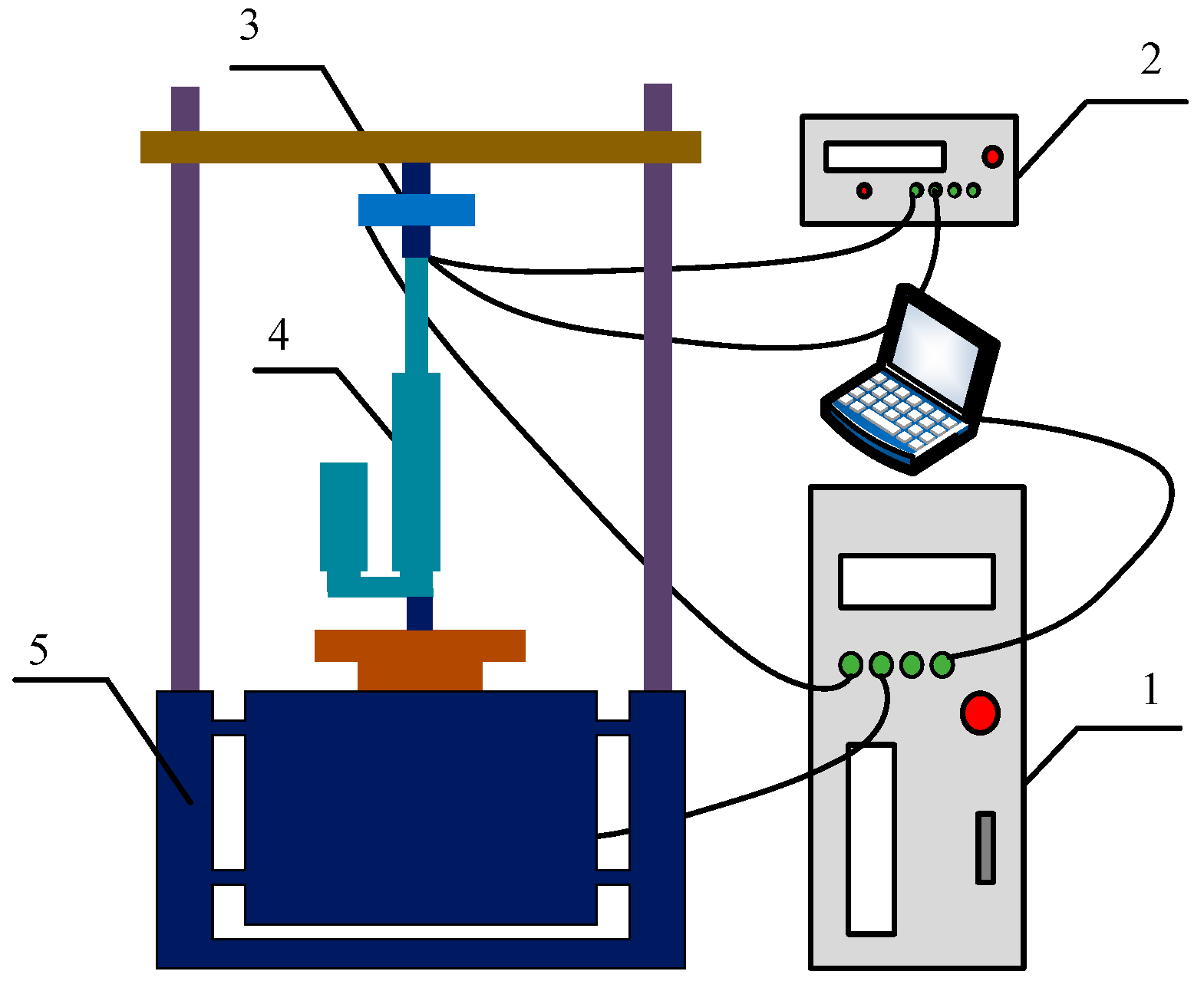
5.1. Experimental Tests
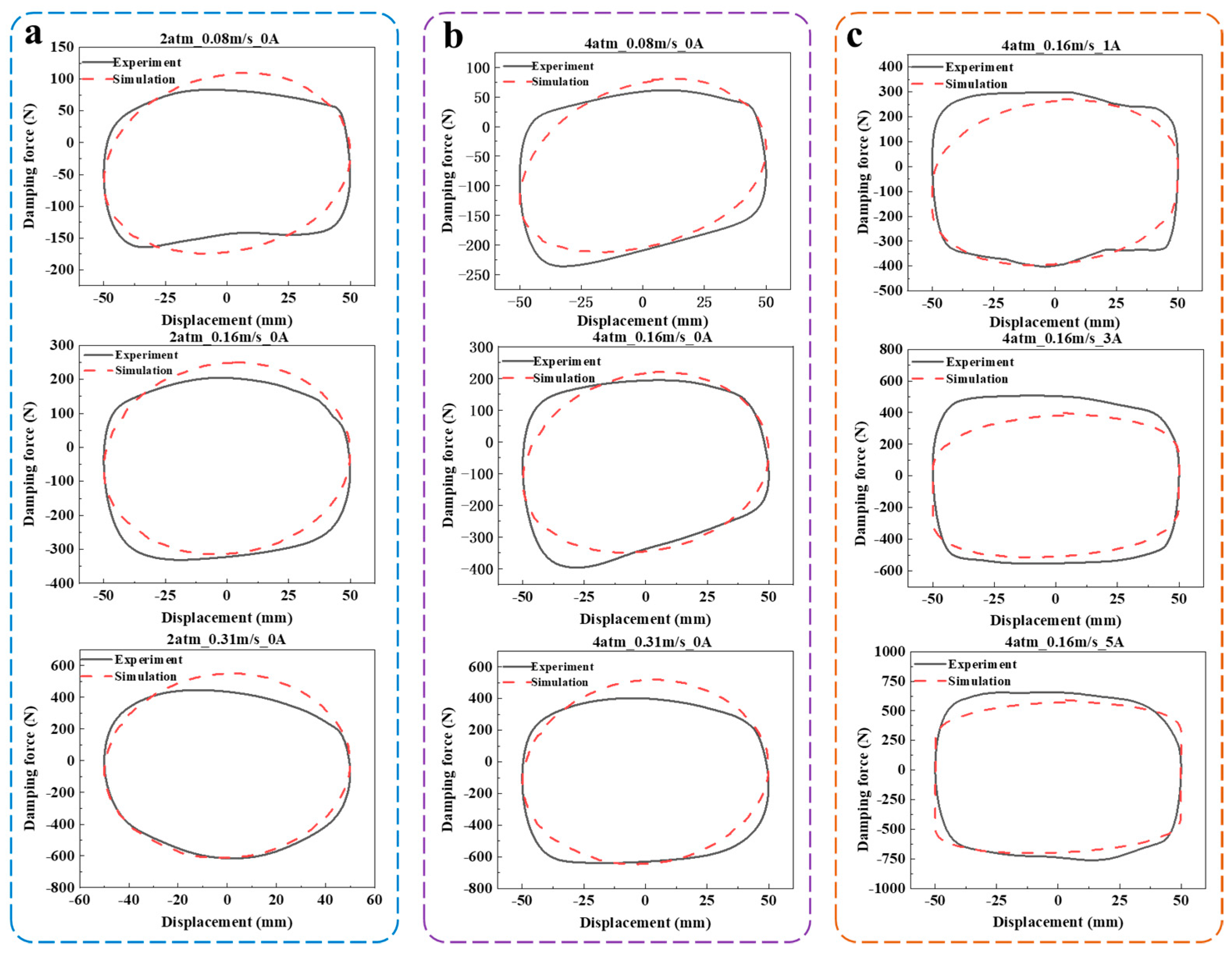
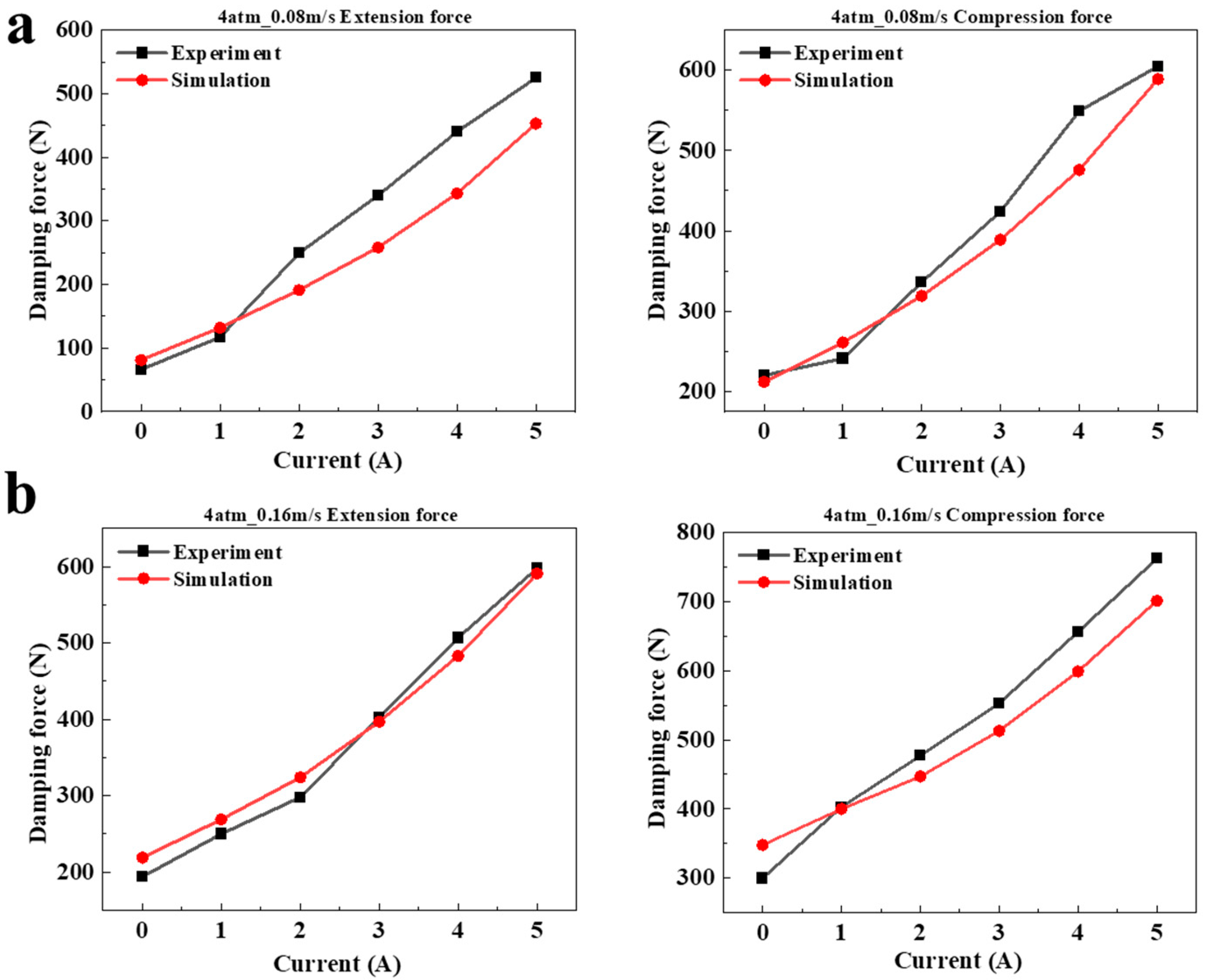
5.2. Experimental Verification
6. Conclusions
- (1)
- The simulation model was built based on the non-Newtonian constitutive relationship of the MRF, and the coupling analysis of the three fields utilized COMSOL. The simulation results showed the feasibility of the damper simulation system, including the magnetic field characteristics, MRF liquid flow characteristics, compensating mechanism of gas flow characteristics, and the damper dynamic mechanical diagram under the coupling action of multiple physical fields.
- (2)
- The damping force was experimentally tested, and the F-S curves were compared under different excitation conditions, with error analysis conducted. The experimental and simulation results had a high degree of coincidence, with a maximum error of 24.1% and a minimum error of only 0.7% for the damping force under different currents. The accuracy of the Multiphysics coupling simulation was further verified. The average error between experimental value and simulation value is 7%.
- (3)
- As the maximum error between the experiment and simulation was 24.1%, further analysis was necessary to determine the cause and improve the accuracy of the experiment and simulation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deng, X.; Pan, Z.W.; Xing, J.W.; Zhang, Z.Y.; Li, Y.X.; Yan, M.S.; Dong, X.M. Controllability analysis and intelligent control of magnetorheological whole-satellite under small amplitude and medium-high frequency vibration. J. Intell. Mater. Syst. Struct. 2023, 34, 229–248. [Google Scholar] [CrossRef]
- Dong, L.; Chen, Z.Q.; Sun, M.W.; Sun, Q.L. Phase compensation active disturbance rejection control for shimmy vibration with magnetorheological damper of aircraft. Expert Syst. Appl. 2023, 213, 119126. [Google Scholar] [CrossRef]
- Deng, Z.X.; Wei, X.X.; Li, X.Q.; Zhao, S.E.; Zhu, S.K. Design and multi-objective optimization of magnetorheological damper considering vehicle riding comfort and operation stability. J. Intell. Mater. Syst. Struct. 2021, 33, 1215–1228. [Google Scholar] [CrossRef]
- Marathe, A.P.; Khot, S.M.; Nagler, J. Development of low-cost optimal magneto-rheological damper for automotive application. J. Vib. Eng. Technol. 2022, 10, 1831–1850. [Google Scholar] [CrossRef]
- Du, X.M.; Han, G.W.; Yu, M.; Peng, Y.X.; Xu, X.Y.; Fu, J. Fault detection and fault tolerant control of vehicle semi-active suspension system with magneto-rheological damper. Smart Mater. Struct. 2021, 30, 014004. [Google Scholar] [CrossRef]
- Hou, S.; Liu, G. Research on Theoretical Modeling and Parameter Sensitivity of a Single-Rod Double-Cylinder and Double-Coil Magnetorheological Damper. Math. Probl. Eng. 2020, 2020, 5489896. [Google Scholar] [CrossRef] [Green Version]
- Xiao, W.; Fei, C.; Aimin, L.; Nana, S. Research on the Performance of a Novel Magnetorheological Damper for Mining. J. Vib. Eng. Technol. 2023. [Google Scholar] [CrossRef]
- Abdeddaim, M.; Djerouni, S.; Ounis, A.; Athamnia, B.; Noroozinejad Farsangi, E. Optimal design of magnetorheological damper for seismic response reduction of Base-Isolated structures considering Soil-Structure interaction. Structures 2022, 38, 733–752. [Google Scholar] [CrossRef]
- Şahin, Ö.; Gökhan Adar, N.; Kemerli, M.; Çaglar, N.; Şahin, İ.; Parlak, Z.; Kükrek, S.; Engin, T. A comparative evaluation of semi-active control algorithms for real-time seismic protection of buildings via magnetorheological fluid dampers. J. Build. Eng. 2021, 42, 102795. [Google Scholar] [CrossRef]
- Tell, S.; Andersson, A.; Najafi, A.; Spencer, B.F.; Karoumi, R. Real-time hybrid testing for efficiency assessment of magnetorheological dampers to mitigate train-induced vibrations in bridges. Int. J. Rail Transp. 2021, 10, 436–455. [Google Scholar] [CrossRef]
- Xu, Z.D.; Xu, Y.W.; Wang, C.; Zhao, Y.L.; Ji, B.H.; Du, Y.L. Force tracking model and experimental verification on a novel magnetorheological damper with combined compensator for stay cables of bridge. Structures 2021, 32, 1971–1985. [Google Scholar] [CrossRef]
- Kanarachos, S.; Savitski, D.; Lagaros, N.; Fitzpatrick, M.E. Automotive magnetorheological dampers: Modelling and parameter identification using contrast-based fruit fly optimisation. Soft Comput. 2017, 22, 8131–8149. [Google Scholar] [CrossRef]
- Kim, B.-G.; Yoon, D.-S.; Kim, G.-W.; Choi, S.-B.; Tan, A.S.; Sattel, T. Design of a Novel Magnetorheological Damper Adaptable to Low and High Stroke Velocity of Vehicle Suspension System. Appl. Sci. 2020, 10, 5586. [Google Scholar] [CrossRef]
- Song, X.Y.; Dong, X.M.; Yan, M.S.; Li, X. Investigation of an Automobile magnetorheological damper with asymmetric mechanical characteristics. J. Phys. Conf. Ser. 2020, 1678, 012012. [Google Scholar] [CrossRef]
- Guo, D.L.; Hu, H.Y. Nonlinear stiffness of a magneto-rheological damper. Nonlinear Dyn. 2005, 40, 241–249. [Google Scholar] [CrossRef]
- Graczykowski, C.; Pawłowski, P. Exact physical model of magnetorheological damper. Appl. Math. Model. 2017, 47, 400–424. [Google Scholar] [CrossRef]
- Sun, M.; Li, X.; Zhou, Z.; Zhu, Q.; Liu, B.; Chen, X.; Wang, J.; Zhang, G.; Cai, S. Analysis of Damping Characteristics of Magnetorheological Damper under Impact Load. Materials 2022, 15, 4161. [Google Scholar] [CrossRef] [PubMed]
- Tu, J.; Li, Z.; Zhang, J.; Gao, K.; Liao, J.; Gao, J. Development, Test, and Mechanical Model of the Leak-Proof Magnetorheological Damper. Front. Mater. 2019, 6, 118. [Google Scholar] [CrossRef] [Green Version]
- Elsaady, W.; Oyadiji, S.O.; Nasser, A. Magnetic Circuit Analysis and Fluid Flow Modelling of an MR Damper with Enhanced Magnetic Characteristics. IEEE Trans. Magn. 2020, 56, 4600420. [Google Scholar] [CrossRef]
- Jian, Y.; Longlei, D. Design and modeling of a magnetorheological damper with double annular damping gap. J. Intell. Mater. Syst. Struct. 2022, 34, 976–989. [Google Scholar] [CrossRef]
- Palomares, E.; Morales, A.L.; Nieto, A.J.; Chicharro, J.M.; Pintado, P. Modelling Magnetorheological Dampers in Preyield and Postyield Regions. Shock Vib. 2019, 2019, 5636053. [Google Scholar] [CrossRef] [Green Version]
- Pei, P.; Peng, Y.; Qiu, C. Magnetorheological damper modeling based on a refined constitutive model for MR fluids. J. Intell. Mater. Syst. Struct. 2021, 33, 1271–1291. [Google Scholar] [CrossRef]
- Xu, F.H.; Dong, D.W.; Huang, Y.; Song, S.; Yan, B. Physical modeling and experimental verification of magneto-rheological damper under medium and high frequency excitation. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2020, 235, 353–365. [Google Scholar] [CrossRef]
- Sternberg, A.; Zemp, R.; de la Llera, J.C. Multiphysics behavior of a magneto-rheological damper and experimental validation. Eng. Struct. 2014, 69, 194–205. [Google Scholar] [CrossRef]
- Gurubasavaraju, T.M.; Kumar, H.; Mahalingam, A. An approach for characterizing twin-tube shear-mode magnetorheological damper through coupled FE and CFD analysis. J. Braz. Soc. Mech. Sci. Eng. Struct. 2018, 40, 139. [Google Scholar] [CrossRef]
- Hu, G.L.; Wu, L.F.; Deng, Y.J.; Yu, L.F.; Luo, B. Damping Performance Analysis of Magnetorheological Damper Based on Multiphysics Coupling. Actuators 2021, 10, 176. [Google Scholar] [CrossRef]
- Hu, G.L.; Wu, L.F.; Deng, Y.J.; Yu, L.F.; Li, G. Optimal design and performance analysis of magnetorheological damper based on multiphysics coupling model. J. Magn. Magn. Mater. 2022, 558, 169527. [Google Scholar] [CrossRef]
- Nie, S.L.; Xin, D.K.; Ji, H.; Yin, F.L. Optimization and performance analysis of magnetorheological fluid damper considering different piston configurations. J. Intell. Mater. Syst. Struct. 2019, 30, 764–777. [Google Scholar] [CrossRef]
- Liu, G.; Gao, F.; Liao, W.-H. Magnetorheological damper with multi-grooves on piston for damping force enhancement. Smart Mater. Struct. 2020, 30, 025007. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, H.X.; Qing, O.Y.; Wang, J. Numerical analysis of multiphysical field for independent three-stage magnetorheological damper of double rod during recoil process of artillery. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4960–4979. [Google Scholar] [CrossRef]
- Zheng, J.J.; Li, Y.C.; Wang, J. Design and multi-physics optimization of a novel magnetorheological damper with a variable resistance gap. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2017, 231, 3152–3168. [Google Scholar] [CrossRef]
- Zheng, J.J.; Li, Z.C.; Koo, J.; Wang, J. Magnetic Circuit Design and Multiphysics Analysis of a Novel MR Damper for Applications under High Velocity. Adv. Mech. Eng. 2014, 6, 402501. [Google Scholar] [CrossRef] [Green Version]
- Yuan, X.J.; Qiu, T.Y.; Tian, T.Y. Design and modelling methodology for a new magnetorheological damper featuring a multi-stage circumferential flow mode. Int. J. Mech. Mater. Des. 2022, 18, 785–806. [Google Scholar] [CrossRef]
- Hu, G.; Long, M.; Huang, M.; Li, W. Design, Analysis, Prototyping, and Experimental Evaluation of an Efficient Double Coil Magnetorheological Valve. Adv. Mech. Eng. 2014, 6, 403410. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.; Wereley, N.M. Hybrid magnetorheological fluid–elastomeric lag dampers for helicopter stability augmentation. Smart Mater. Struct. 2008, 17, 045021. [Google Scholar] [CrossRef]
- Susan-Resiga, D. A Rheological Model for Magneto-rheological Fluids. J. Intell. Mater. Syst. Struct. 2009, 20, 1001–1010. [Google Scholar] [CrossRef]
- Min, J.; Xiaoting, R.; Fufeng, Y.; Wei, Z.; Hongtao, Z.; Wenjiao, H. Design and dynamic performance research of MR hydro-pneumatic spring based on multi-physics coupling model. Nonlinear Dyn. 2023, 111, 8191–8215. [Google Scholar] [CrossRef]
- Li, S.; Yu, M.; Liu, J.; Fu, J.; Gan, R.; Li, Y.; Yao, H.; Qi, S. Attenuation of magneto-induced yield stress by magnetic carrier liquid in magnetorheological fluids. Appl. Phys. Lett. 2022, 121, 162901. [Google Scholar] [CrossRef]
- Takaddus, A.T.; Chandy, A.J. A three-dimensional (3D) two-way coupled fluid-structure interaction (FSI) study of peristaltic flow in obstructed ureters. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e3122. [Google Scholar] [CrossRef]

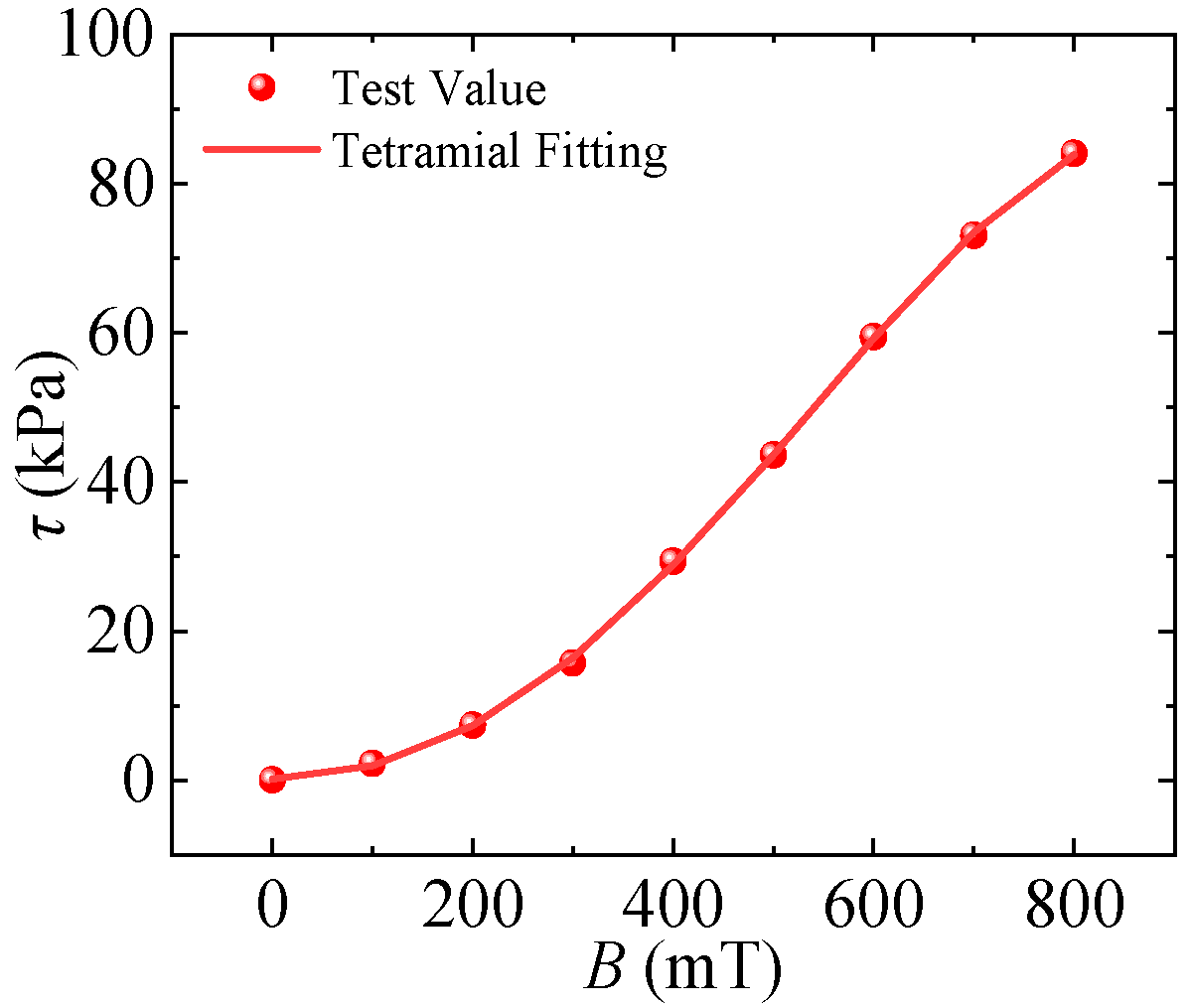
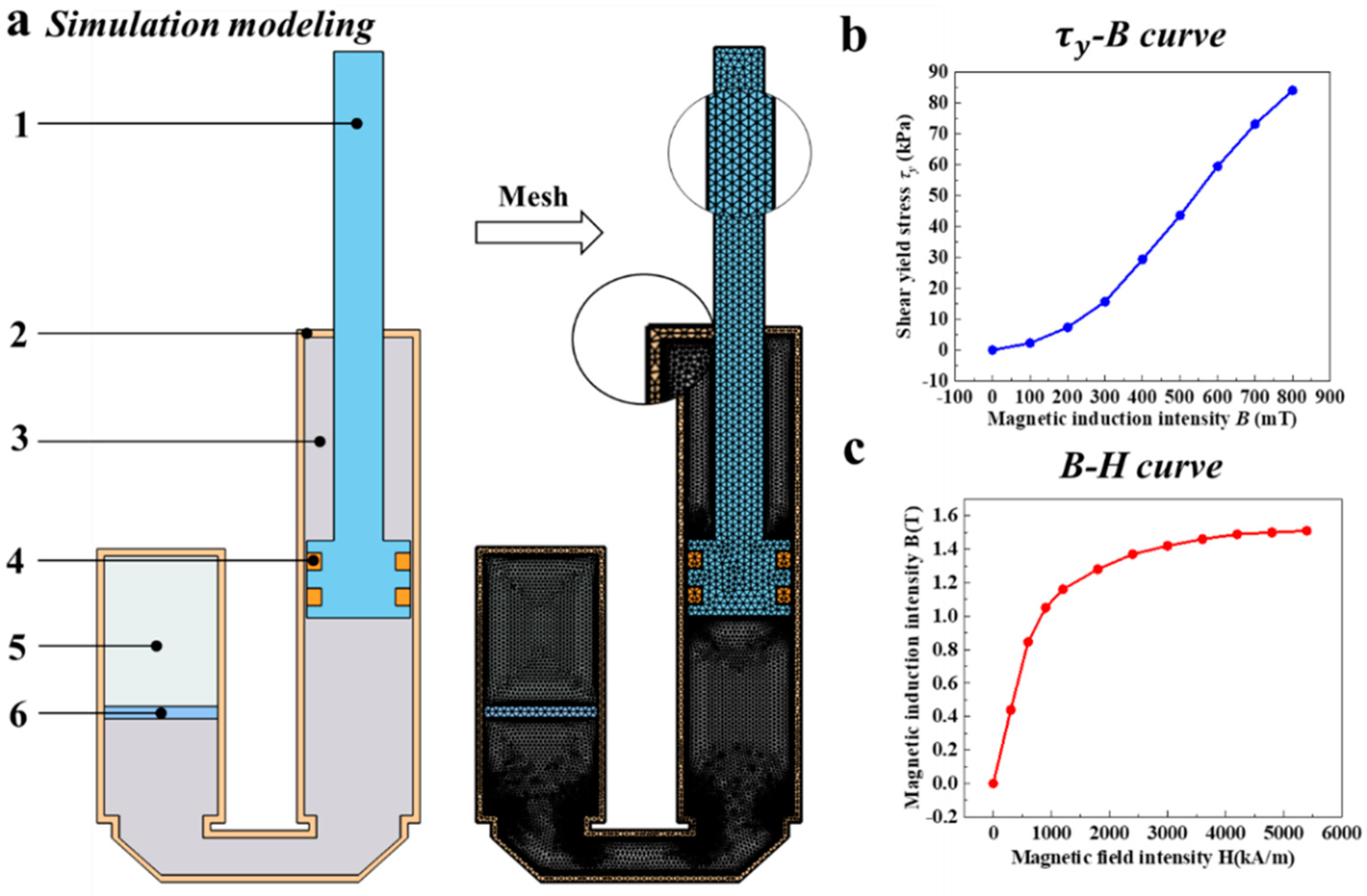


| Parameters | Value (mm) | Parameters | Value (mm) |
|---|---|---|---|
| Valve rod length | 233 | Compensating cylinder length | 103 |
| Valve diameter/D1 | 44 | Valve rod diameter/d | 15 |
| Valve radius/r2 | 20 | Floating valve diameter | 46 |
| Valve length/L | 38.4 | Channel gap/h | 1 |
| Iron core radius/r0 | 13 | Outer cylinder thickness/h1 | 1.75 |
| Velocity (m/s) | 0 A | 1 A | 2 A | 3 A | 4 A | 5 A |
|---|---|---|---|---|---|---|
| Extension/0.08 | −22.7% | −12.8% | 23.3% | 24.1% | 22.1% | 13.7% |
| Compression/0.08 | 3.6% | −8.3% | 5.1% | 8.3% | 13.3% | 1.2% |
| Extension/0.16 | −12.9% | −7.6% | −8.7% | 1.5% | 4.7% | 1.2% |
| Compression/0.16 | −16.0% | 0.7% | 6.3% | 7.2% | 8.7% | 8.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, H.; Li, J.; Wang, Y.; Liu, M.; Fu, J.; Luo, L.; Yu, M. Multi-Physics Simulation and Experimental Verification of Magnetorheological Damper with Additional Stiffness. Actuators 2023, 12, 251. https://doi.org/10.3390/act12060251
Liang H, Li J, Wang Y, Liu M, Fu J, Luo L, Yu M. Multi-Physics Simulation and Experimental Verification of Magnetorheological Damper with Additional Stiffness. Actuators. 2023; 12(6):251. https://doi.org/10.3390/act12060251
Chicago/Turabian StyleLiang, Huijun, Jie Li, Yongsheng Wang, Mingkun Liu, Jie Fu, Lei Luo, and Miao Yu. 2023. "Multi-Physics Simulation and Experimental Verification of Magnetorheological Damper with Additional Stiffness" Actuators 12, no. 6: 251. https://doi.org/10.3390/act12060251
APA StyleLiang, H., Li, J., Wang, Y., Liu, M., Fu, J., Luo, L., & Yu, M. (2023). Multi-Physics Simulation and Experimental Verification of Magnetorheological Damper with Additional Stiffness. Actuators, 12(6), 251. https://doi.org/10.3390/act12060251







