Dynamic Response Analysis of the Bi-Tandem Axial Piston Pump with Dual-Loop Positive Flow Control under Pressure Disturbance
Abstract
:1. Introduction
2. Models and Methods
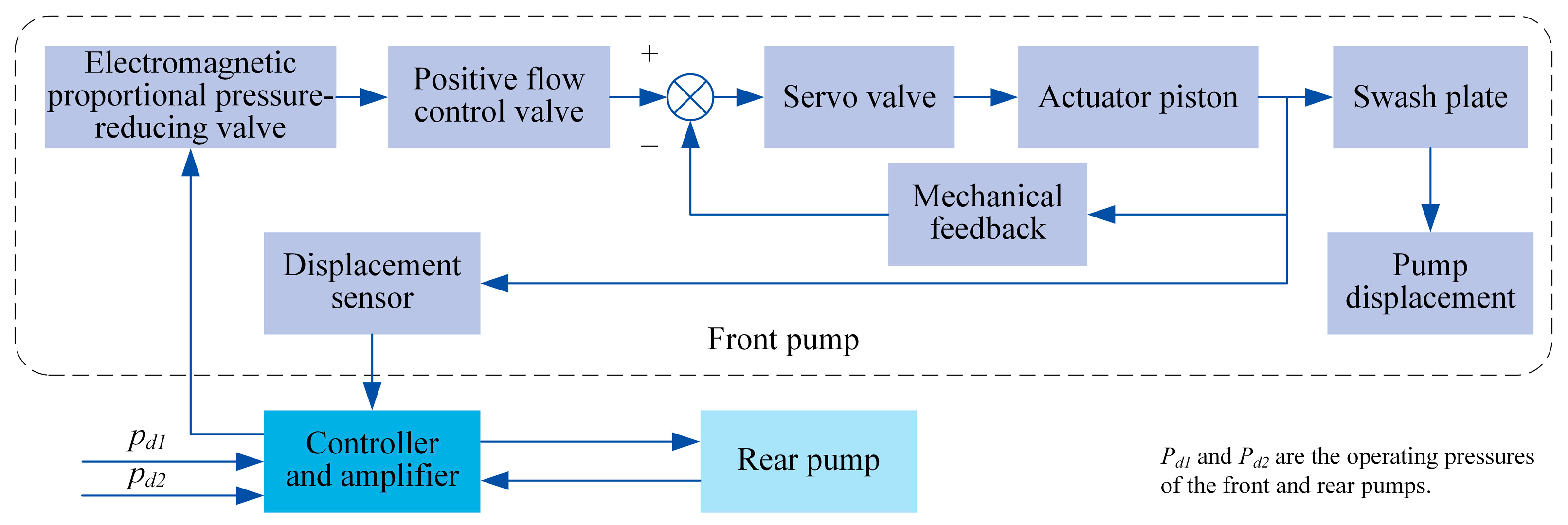
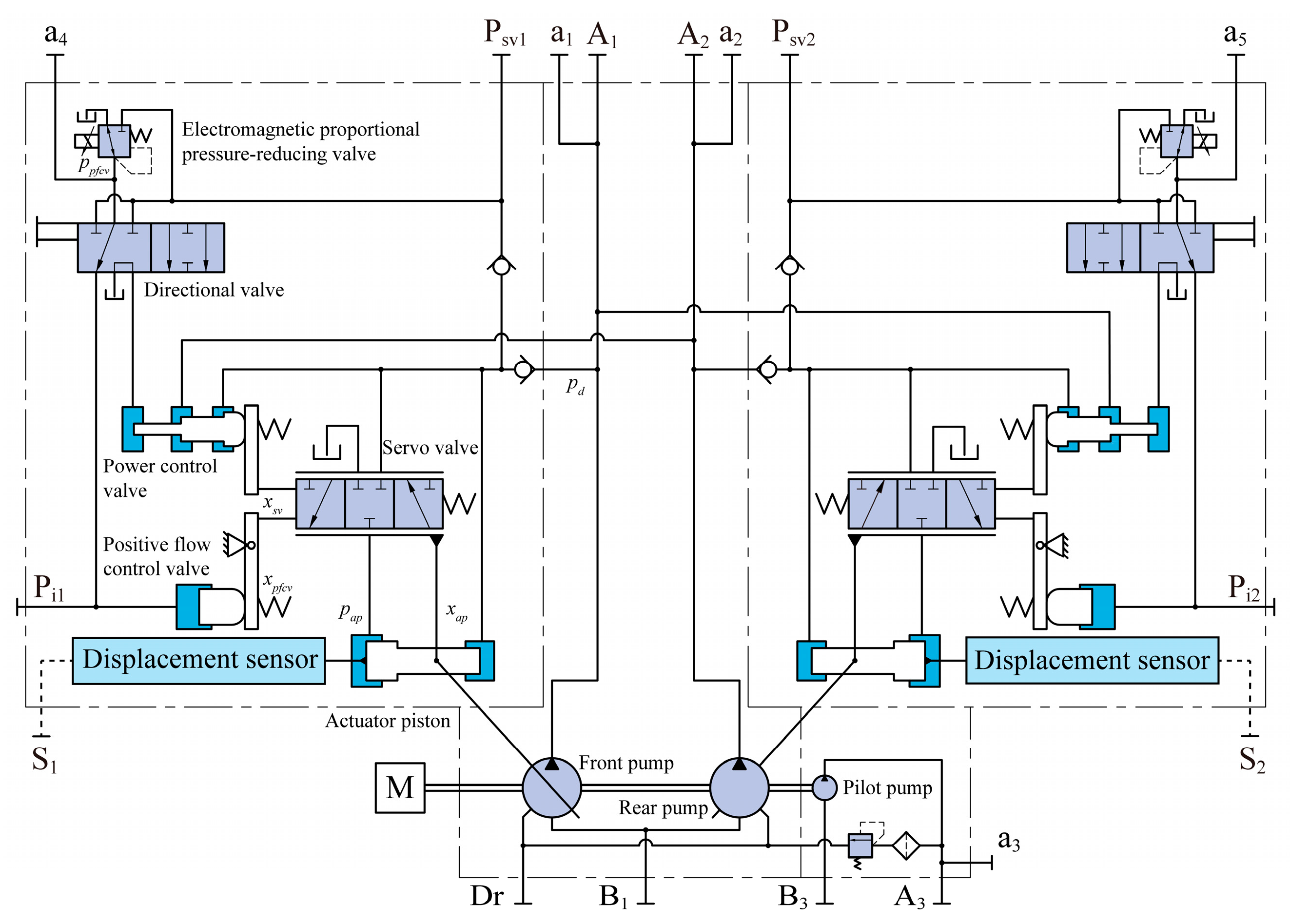
2.1. Dual-Loop Positive Flow Control Method
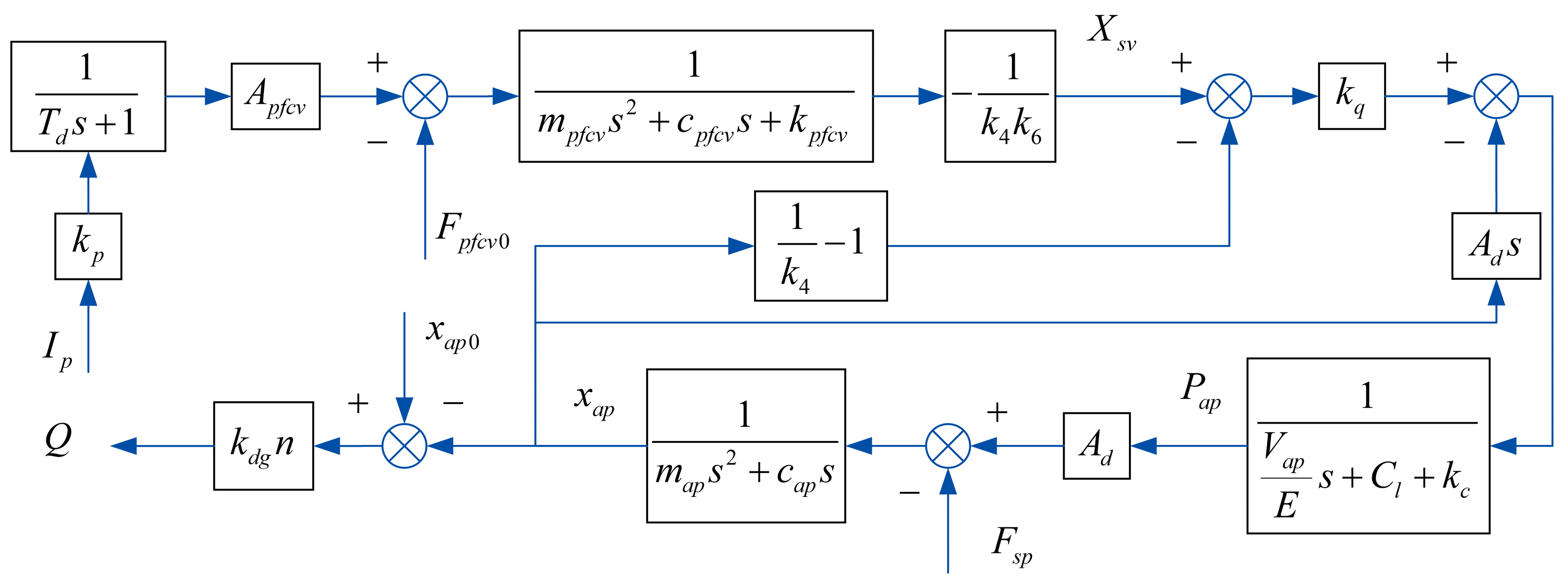
2.2. Inner-Loop Control Model
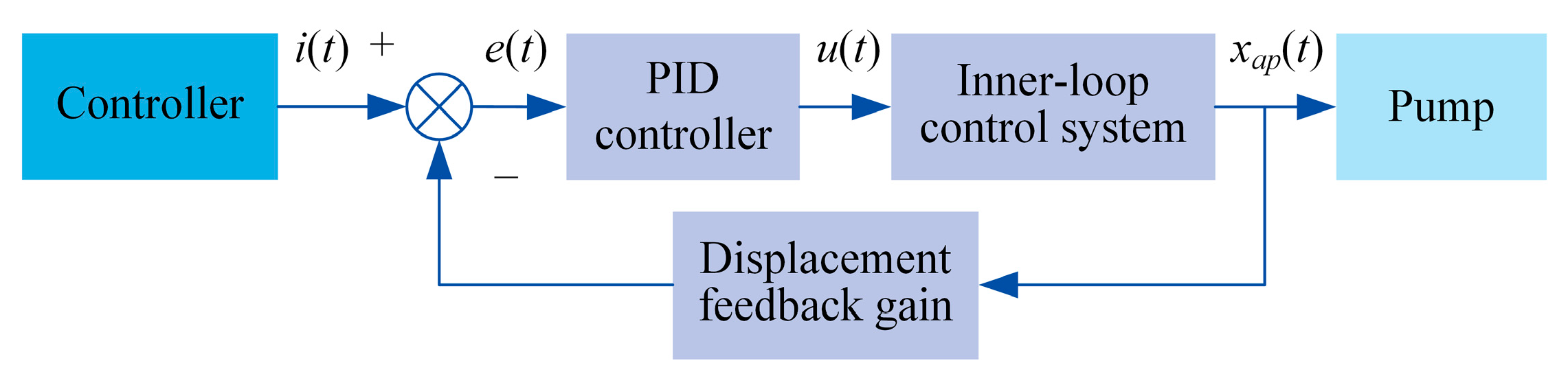
2.3. Outer-Loop Control Model
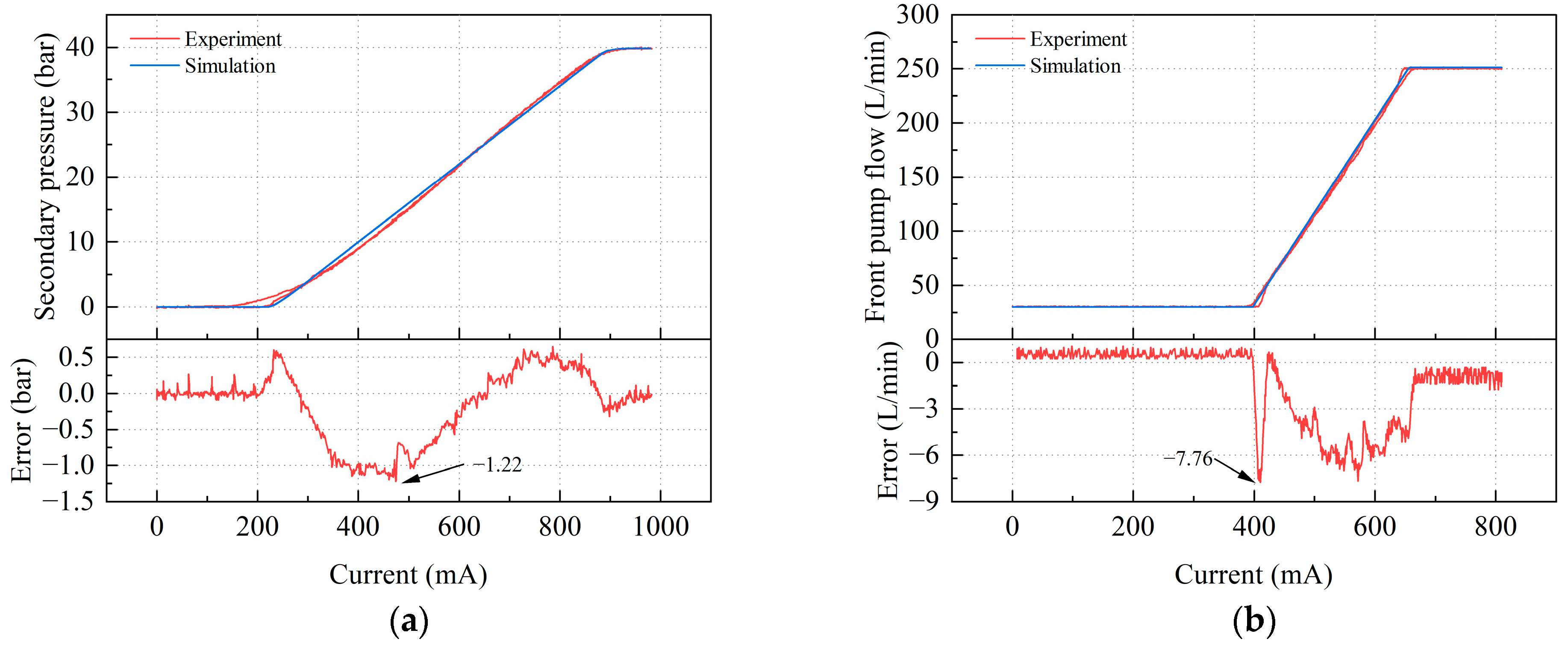
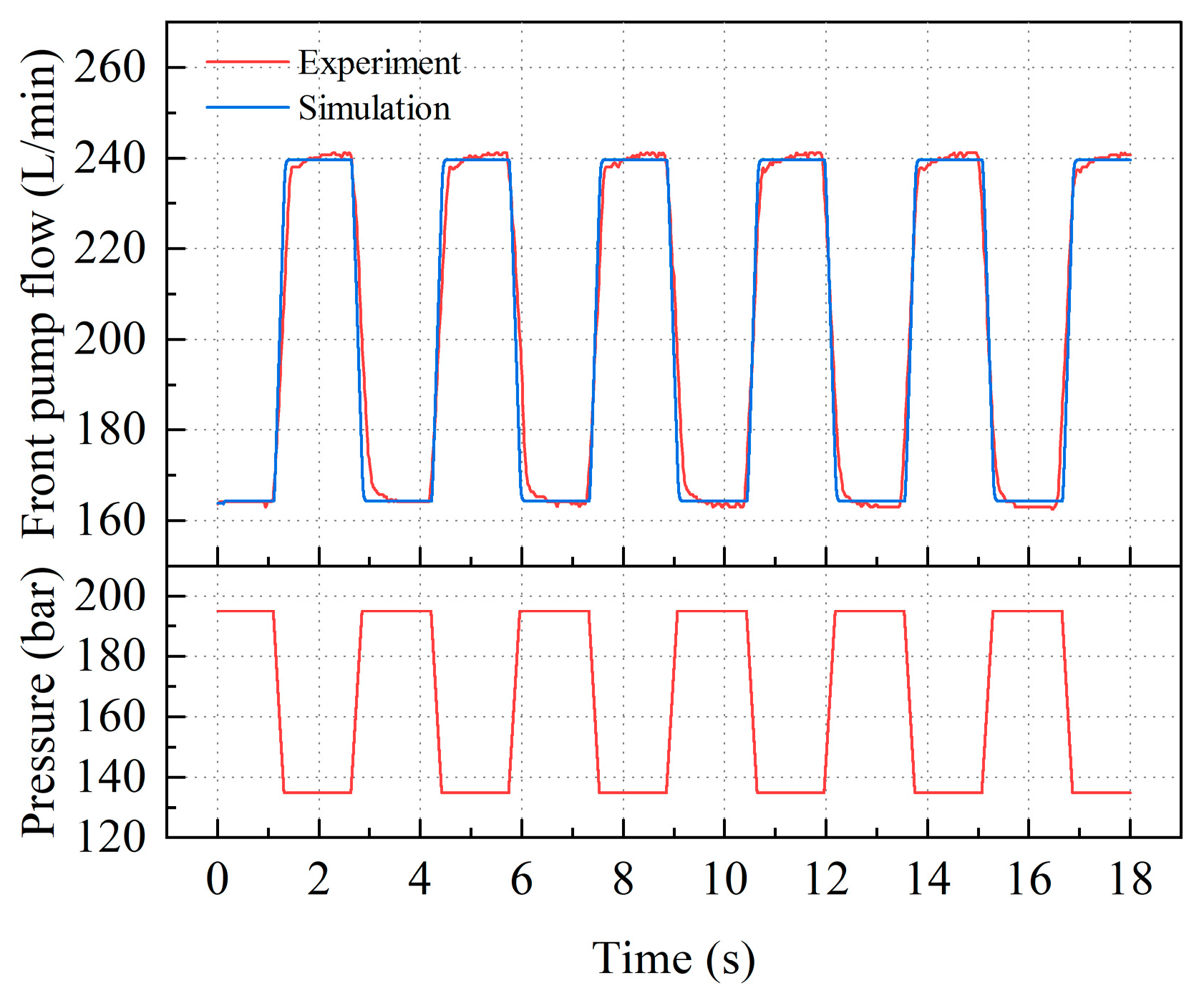
2.4. Simulation Model and Experimental Verification
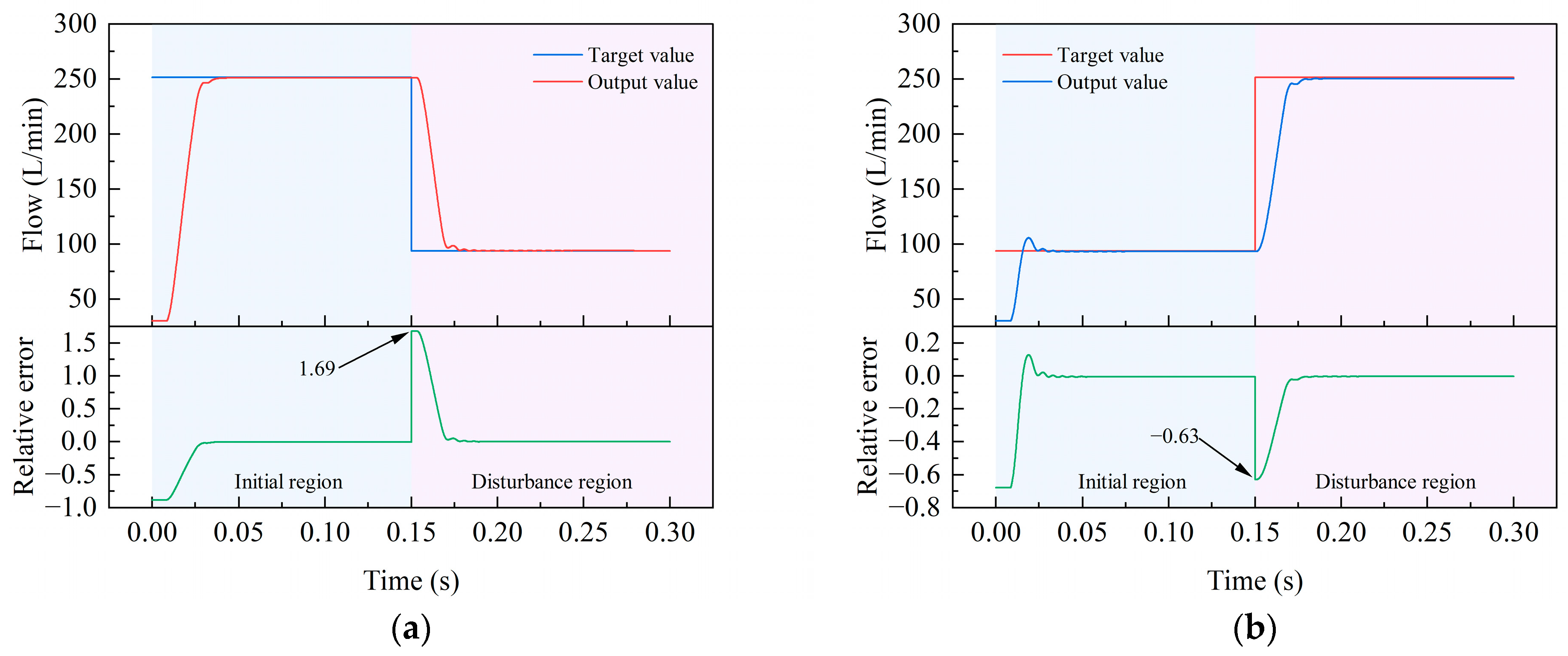
3. Comparative Analysis of the Dynamic Response of the Piston Pump with Single-Loop and Dual-Loop Positive Flow Control Results
4. Dynamic Response Analysis of the Bi-Tandem Axial Piston Pump under Pressure Disturbance
4.1. Effect of Symmetric Pressure Disturbance on Dynamic Response
4.1.1. Degree of Symmetric Pressure Disturbance
4.1.2. Direction of Symmetric Pressure Disturbance
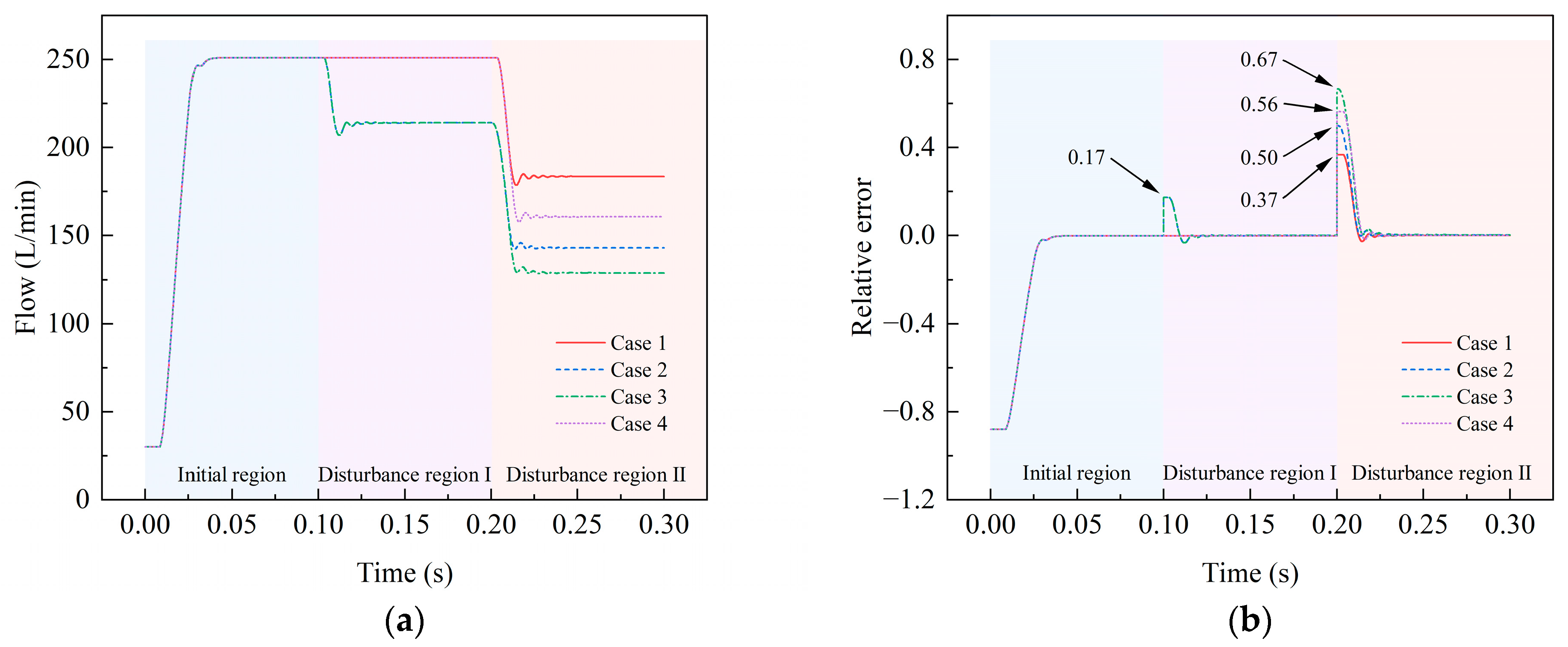
4.2. Effect of Asymmetric Pressure Disturbance oTan Dynamic Response
4.2.1. Degree of Asymmetric Pressure Disturbance
4.2.2. Direction of Asymmetric Pressure Disturbance
5. Conclusions
- (1)
- In response to the problem that the stability of the original single-loop mechanical–hydraulic servo control system is susceptible to uncertain interferences, a dual-loop positive flow control method is developed for the bi-tandem axial piston pump. Based on Simulink, the simulation model of the bi-tandem axial piston pump with dual-loop positive flow control is established. The model is verified to be accurate and reliable through experiments.
- (2)
- Compared with the single-loop positive flow control, the axial piston pump with dual-loop positive flow control has faster response speed and smaller steady-state error under no pressure disturbance and pressure disturbance.
- (3)
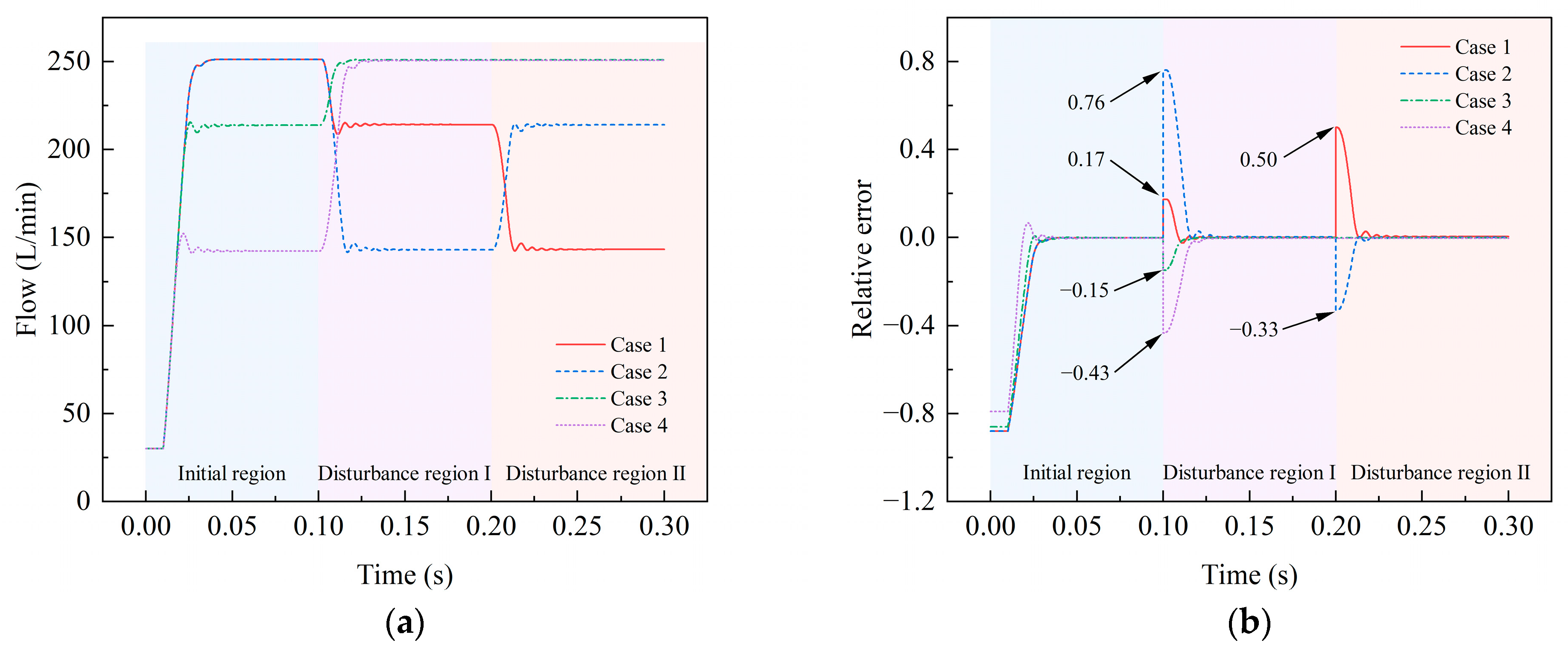
- Under symmetric pressure disturbance, the output characteristics of double pumps are identical. When the pressure disturbance exceeds the starting pressure, the output flow of the piston pump declines sharply, with stability eventually reached after a brief period of oscillation. Notably, the corresponding adjustment time increases with the increase in the degree of symmetrical pressure disturbance. Furthermore, the maximum relative error in output flow at the action point of the symmetric pressure disturbance increases with the increase in symmetrical pressure disturbance. It is worth noting that unloading pressure disturbances elicit less pronounced effects on the system compared to loading pressure disturbances.
- (4)
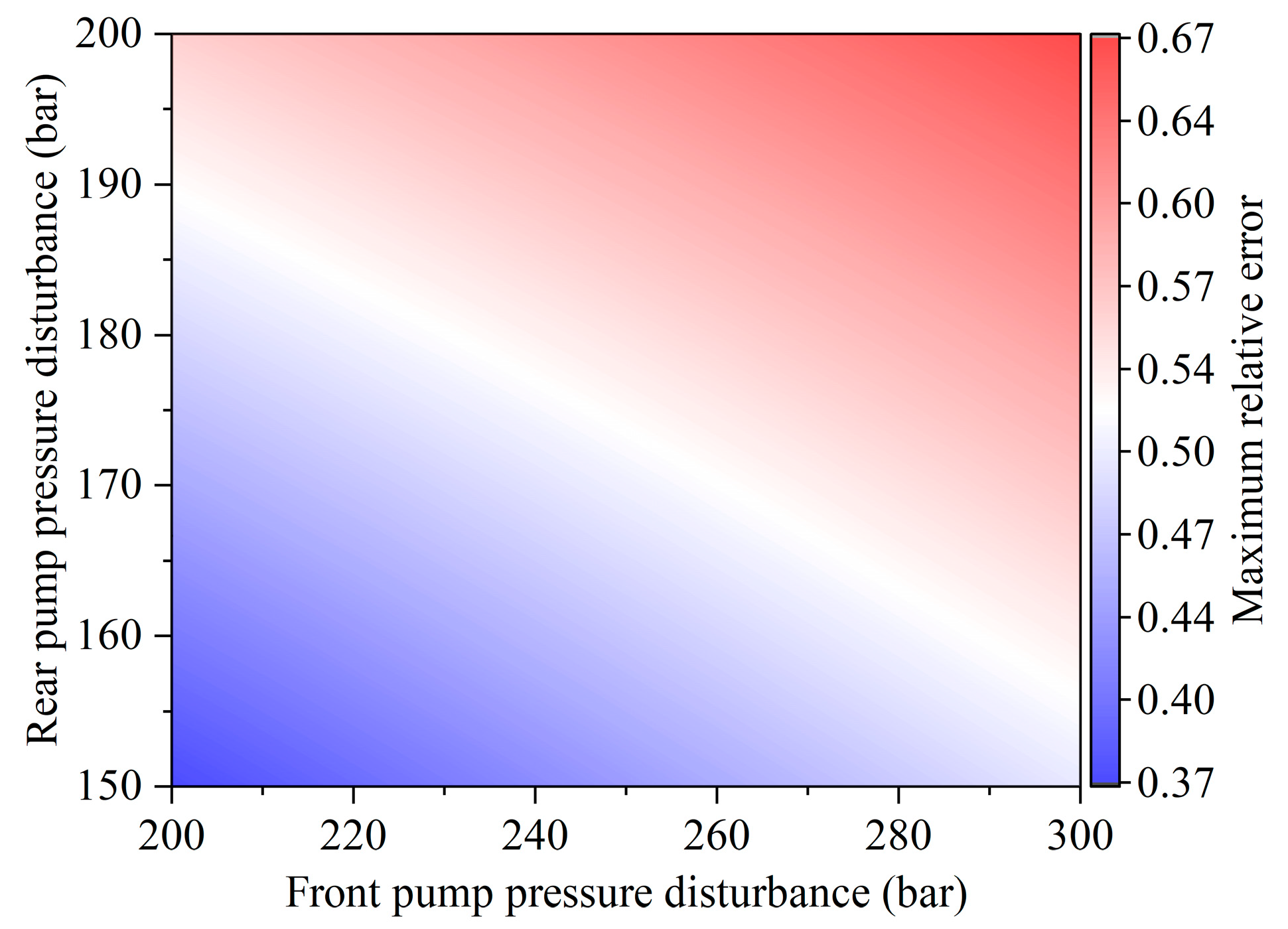
- In the presence of asymmetric pressure disturbance, the maximum relative error at the second disturbance point increases with the increase in pressure disturbance of the rear pump for the same pressure disturbance of the front pump. Similarly, the maximum relative error at the second disturbance point increases with the increase in the pressure disturbance of the front pump for the same pressure disturbance of the rear pump, and this pattern remains consistent, regardless of whether the piston pump adjusts its output under the pressure disturbance of the rear pump. The effect of asymmetric pressure disturbance of double pumps on output flow is of a superimposable nature, with the steady-state value of the output flow strongly influenced by the superimposed pressure disturbance while displaying lesser sensitivity to the action time points of asymmetric pressure disturbance. Furthermore, across all disturbance regions, the maximum relative error caused by unloading pressure disturbance is smaller than that caused by loading pressure disturbance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, L.K.; Book, W.J.; Huggins, J.D. Application of Singular Perturbation Theory to Hydraulic Pump Controlled Systems. IEEE-ASME Trans. Mechatron. 2012, 17, 251–259. [Google Scholar] [CrossRef]
- Lu, L.; Chen, Y.; Tong, C.; Ruan, J.; Li, S. Design strategy and performance evaluation of novel miniature two-dimensional (2D) piston pump with a dual stacking mechanism. Alex. Eng. J. 2023, 62, 541–554. [Google Scholar] [CrossRef]
- Zhao, J.A.; Fu, Y.L.; Ma, J.M.; Fu, J.; Chao, Q.; Wang, Y. Review of cylinder block/valve plate interface in axial piston pumps: Theoretical models, experimental investigations, and optimal design. Chin. J. Aeronaut. 2021, 34, 111–134. [Google Scholar] [CrossRef]
- Manring, N.; Williamson, C.; Asme. Calculating the Mechanical and Volumetric Efficiencies for Check-Valve Type, Digital Displacement Pumps. In Proceedings of the BATH/ASME Symposium on Fluid Power and Motion Control, University of Bath, Bath, UK, 12–14 September 2018; pp. 1–10. [Google Scholar]
- De Negri, V.J.; Wang, P.; Plummer, A.; Johnston, D.N. Behavioural prediction of hydraulic step-up switching converters. Int. J. Fluid Power 2014, 15, 1–9. [Google Scholar] [CrossRef]
- Kogler, H. High dynamic digital control for a hydraulic cylinder drive. Proc. Inst. Mech. Eng. Part I-J. Syst. Control Eng. 2022, 236, 382–394. [Google Scholar] [CrossRef]
- Tang, H.B.; Yang, W.X.; Wang, Z.C. A Model-Based Method for Leakage Detection of Piston Pump Under Variable Load Condition. IEEE Access 2019, 7, 99771–99781. [Google Scholar] [CrossRef]
- Ying, P.; Tang, H.; Chen, L.; Ren, Y.; Kumar, A. Dynamic modeling and vibration characteristics of multibody system in axial piston pump. Alex. Eng. J. 2023, 62, 523–540. [Google Scholar] [CrossRef]
- Ivantysynova, M.; Grabbel, J.; Ossyra, J.-C. Prediction of swash plate moment using the simulation tool CASPAR. In Proceedings of the ASME 2002 International Mechanical Engineering Congress and Exposition, IMECE 2002, New Orleans, LA, USA, 17–22 November 2002; pp. 1–9. [Google Scholar]
- Grabbel, J.; Ivantysynova, M. An investigation of swash plate control concepts for displacement controlled actuators. Int. J. Fluid Power 2005, 6, 19–36. [Google Scholar] [CrossRef]
- Bergada, J.M.; Watton, J.; Kumar, S. Pressure, flow, force, and torque between the barrel and port plate in an axial piston pump. J. Dyn. Sys. Meas. Control. 2008, 130, 16. [Google Scholar] [CrossRef]
- Cui, H.-X.; Feng, K.; Li, H.-L.; Han, J.-H. Response Characteristics Analysis and Optimization Design of Load Sensing Variable Pump. Math. Probl. Eng. 2016, 2016, 6379121. [Google Scholar] [CrossRef] [Green Version]
- Du, C.; Plummer, A.R.; Johnston, D.N. Performance analysis of a new energy-efficient variable supply pressure electro-hydraulic motion control method. Control Eng. Pract. 2017, 60, 87–98. [Google Scholar] [CrossRef]
- Gao, Y.S.; Cheng, J.; Huang, J.H.; Quan, L. Simulation Analysis and Experiment of Variable-Displacement Asymmetric Axial Piston Pump. Appl. Sci. 2017, 7, 328. [Google Scholar] [CrossRef] [Green Version]
- Hasan, M.E.; Ghoshal, S.K.; Dasgupta, K.; Kumar, N. Dynamic analysis and estimator design of a hydraulic drive system. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 1097–1108. [Google Scholar] [CrossRef]
- Li, J.; Li, H.L.; Cui, H.X.; Zhu, Y.W. Nonlinear dynamics characteristics and influence factors analysis of servo hydraulic cylinder. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 2018, 232, 3629–3638. [Google Scholar] [CrossRef]
- Huang, J.H.; Zhao, H.; Quan, L.; Zhang, X.G. Development of an asymmetric axial piston pump for displacement-controlled system. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 2014, 228, 1418–1430. [Google Scholar] [CrossRef]
- Huang, J.; He, W.; Hao, H.; Quan, L. Analysis of Control Characteristics of Variable-displacement Asymmetric Axial Piston Pump. Trans. Chin. Soc. Agric. Mach. 2019, 50, 368–376. [Google Scholar] [CrossRef]
- He, W.; Huang, J.H.; Hao, H.M.; Quan, L.; Ji, S.X.; Zhao, B. Design and Analysis of a Swashplate Control System for an Asymmetric Axial Piston Pump. J. Dyn. Syst. Meas. Control-Trans. ASME 2020, 142, 11. [Google Scholar] [CrossRef]
- Mitov, A.; Kralev, J.; Slavov, T.; Angelov, I. Design of Embedded Control System for Open Circuit Axial Piston Pump. In Proceedings of the 22nd International Symposium on Electrical Apparatus and Technologies, SIELA 2022, Bourgas, Bulgaria, 1–4 June 2022; pp. 1–4. [Google Scholar]
- Mitov, A.; Slavov, T.; Kralev, J. Rapid Prototyping of H∞ Algorithm for Real-Time Displacement Volume Control of Axial Piston Pumps. Algorithms 2023, 16, 120. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Zeng, Q.L.; Wan, L.R.; Dai, H.Z. Control and Dynamic Characteristics Analysis for the Double-Compound Axial Piston Pump Based on Working Conditions. Machines 2022, 10, 411. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Luo, H.; Zhang, J. An Empirical Model for the Churning Losses Prediction of Fluid Flow Analysis in Axial Piston Pumps. Micromachines 2021, 12, 398. [Google Scholar] [CrossRef]
- Zhao, K.P.; He, T.; Wang, C.L.; Chen, Q.M.; Li, Z.P. Lubrication characteristics analysis of slipper pair of digital valve distribution axial piston pump. Adv. Mech. Eng. 2022, 14, 1–15. [Google Scholar] [CrossRef]
- Chao, Q.; Xu, Z.; Tao, J.; Liu, C. Capped piston: A promising design to reduce compressibility effects, pressure ripple and cavitation for high-speed and high-pressure axial piston pumps. Alex. Eng. J. 2023, 62, 509–521. [Google Scholar] [CrossRef]
- Kim, H.; Cheon, D.; Lim, J.; Nam, K. Robust Flow Control of a Syringe Pump Based on Dual-Loop Disturbance Observers. IEEE Access 2019, 7, 135427–135438. [Google Scholar] [CrossRef]
- Wang, H.; Wang, X.H.; Huang, J.H.; Quan, L. Flow Control for a Two-Stage Proportional Valve with Hydraulic Position Feedback. Chin. J. Mech. Eng. 2020, 33, 13. [Google Scholar] [CrossRef]
- Li, Y.; Ang, K.H.; Chong, G.C.Y. Patents, software, and hardware for PID control: An overview and analysis of the current art. IEEE Control Syst. Mag. 2006, 26, 42–54. [Google Scholar] [CrossRef] [Green Version]
- Ang, K.H.; Chong, G.; Li, Y. PID control system analysis, design, and technology. IEEE Trans. Control Syst. Technol. 2005, 13, 559–576. [Google Scholar] [CrossRef] [Green Version]




| Pump | Parameter | Value | |
|---|---|---|---|
| Main pump | Displacement (cm3/rev) | 2 × (125 ± 2) | |
| Speed (rpm) | Rated | 2000 | |
| Max. | 2700 | ||
| Pressure (bar) | Rated | 343 | |
| Peak | 400 | ||
| Flow (L/min) | Max. | 2 × (251 ± 3) | |
| Min. | 2 × (30 ± 3) | ||
| Pilot pump | Displacement (cm3/rev) | 10 | |
| Rated pressure (bar) | 40 ± 1 | ||
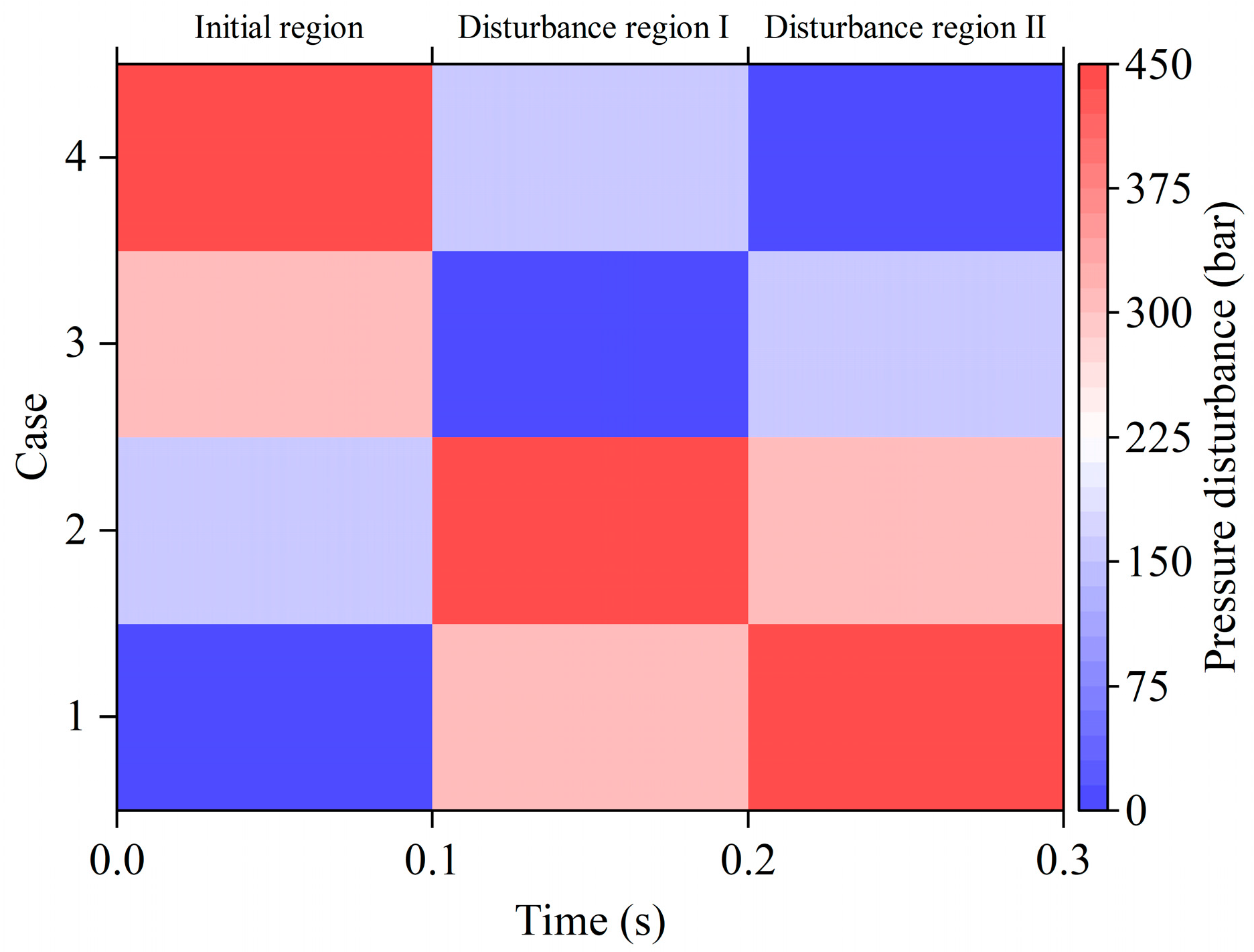
| Case No. | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Front pump pressure disturbance (bar) | 200 | 300 | 300 | 200 |
| Rear pump pressure disturbance (bar) | 150 | 150 | 200 | 200 |
| Case No. | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Front pump | Loading | Loading | Unloading | Unloading |
| Rear pump | Loading | Unloading | Loading | Unloading |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Zeng, Q.; Wan, L.; Xiao, Y. Dynamic Response Analysis of the Bi-Tandem Axial Piston Pump with Dual-Loop Positive Flow Control under Pressure Disturbance. Actuators 2023, 12, 260. https://doi.org/10.3390/act12070260
Sun Z, Zeng Q, Wan L, Xiao Y. Dynamic Response Analysis of the Bi-Tandem Axial Piston Pump with Dual-Loop Positive Flow Control under Pressure Disturbance. Actuators. 2023; 12(7):260. https://doi.org/10.3390/act12070260
Chicago/Turabian StyleSun, Zhiyuan, Qingliang Zeng, Lirong Wan, and Yuanjiang Xiao. 2023. "Dynamic Response Analysis of the Bi-Tandem Axial Piston Pump with Dual-Loop Positive Flow Control under Pressure Disturbance" Actuators 12, no. 7: 260. https://doi.org/10.3390/act12070260
APA StyleSun, Z., Zeng, Q., Wan, L., & Xiao, Y. (2023). Dynamic Response Analysis of the Bi-Tandem Axial Piston Pump with Dual-Loop Positive Flow Control under Pressure Disturbance. Actuators, 12(7), 260. https://doi.org/10.3390/act12070260





