1. Introduction
With the advent of the high-capacity grid era, an increasing number of nonlinear loads are installed in the grid, and sine wave voltages on nonlinear loads become distorted into harmonics. Reactors and transformers are also installed in populated areas, hence, transformers and reactors in the course of work will produce vibration noise; the presence of harmonic vibration noise is particularly noticeable, which has led to increasing concern about environmental noise pollution. Noise can not only affect people’s hearing, but also cause great psychological damage unconsciously. The improvement and optimization of electrical equipment is one of the important means to solve the noise pollution of industrial equipment at the source.
In order to solve the noise problem, there are plenty of noise reduction methods for reactor vibration, such as: timing and regular adjustment of the tank base of the correction oil immersion reactor. These noise cancellation methods generally do not address the root causes of vibration problems in terms of isolation and noise reduction. Therefore, this paper will study the vibration problem of iron cores, the main source of vibration from the reactor.
The ferromagnetic material of the core of the reactor is mainly electrical steel sheet; the magnetic domain of the electrical steel turns in the same direction under the action of the external magnetic field. The outward manifestation of the electrical steel sheet shape and size is the phenomenon of the shortening or elongation of the nanoscale; this phenomenon is called magnetostrictive. Since the upper and lower iron yoke of the reactor and the discus are stacked from electrical steel sheets, the magnetostrictive effect causes vibration of the reactor, whose vibration period is closely related to the frequency at which the excitation is applied. Because the reactor core air gap is larger, the electromagnetic force is larger, so the electromagnetic force in the reactor caused by the core vibration must not be ignored.
As an important parameter for reactor noise simulation, magnetostriction has attracted much attention. In 2011, scholars such as Piotr K. Klimczyk used the Epstein Frame to study the magnetostriction phenomenon, and the research showed that the peak value of rotational magnetostriction in the vertical rolling direction of the electrical steel sheet was smaller. A measuring device of rotating magnetostrictive can be used to predict the data measured by the Epstein Frame under stress [
1]. In 2012, Piotr K. Klimczyk et al. used different processing methods to explore the sensitivity of magnetostrictive stress, and the results showed that laser cutting would produce greater sensitivity curve deviation [
2]. Since 2013, Yuichiro Kai and other scholars have designed vector magnetic properties and magnetostriction measurement devices under stress and tested electrical steel sheets under uniaxial stress. The results show that uniaxial stress increases the amplitude of magnetostriction. In 2014, two mutually perpendicular biaxial stresses were applied, and the research showed that the biaxial tension could improve the magnetic characteristics of the electrical steel sheet and reduce magnetostriction at the same time. In 2015, the shear stress under alternating and rotating magnetic fields was studied, and the results showed that the amplitude and phase of magnetostriction changed [
3,
4,
5]. In 2013, Hirotoshi Tada et al. studied magnetostriction and hysteresis loss under different stresses and crystal structures, so they added different proportions of silicon and aluminum to electrical steel sheets and measured their hysteresis loss [
6]. In 2014, Yoshihiko Oda found that when the proportion of silicon elements exceeded 3.5%, the strain decreased significantly [
7]. In 2015, Daisuke Wakabayashi et al. discussed the vector characteristics of magnetostriction under alternating magnetization and adopted a new measurement method to deal with the angular relationship between magnetostriction and magnetic flux density [
8]. In 2016, Sakda Somkun studied local deformation caused by magnetostriction [
9]. In the same year, Setareh Gorji Ghalamestani and other scholars measured electrical steel sheets under higher harmonics and explained this phenomenon with magnetic domains [
10]. In 2018, Otmane Lahyaoni et al. performed finite element calculations using a laminated model and performed vibration measurements, demonstrating that magnetostrictive strain can induce mechanical resonance at a very low amplitude [
11]. Since 2020, a large number of scholars have studied the giant magnetostrictive brake. A giant magnetostrictive actuator has the characteristics of small volume, large stress, large strain, and fast response, and has been widely used in ultra-precision machining, micro-machining, micro-vibration control, precision positioning, and other fields. Xiaojun Ju et al. established the displacement model of giant magnetostrictive actuators based on the Jiles–Atherton theory and the quadratic law. Zhaoqi Zhou et al. analyzed the internal magnetic field characteristics of giant magnetostrictive brakes based on electromagnetic theory and the finite element method [
12,
13,
14,
15].
In terms of vibration research on a reactor, Liu Ji analyzed the vibration of the reactor core through a multi-physics coupling simulation and showed that the vibration was caused by both magnetostrictive force and electromagnetic force, in which the magnetostrictive force was dominant [
16]. Zhu Lihua and other scholars carried out multi-physical field simulation on a 4.4 kVar/220 V reactor. The time-domain and frequency-domain signals of the core vibration are analyzed, and it is pointed out that changing the excitation magnitude will change the vibration of adjacent periods of the reactor [
17]. Zhang Pengning et al. studied the vibration characteristics of magnetron reactors under different working conditions. The rated voltage of a 10.5 kV reactor is modeled, and a finite element analysis shows that the air gap of different Young’s moduli has a great influence on the vibration performance of the reactor. Later, the vibration of the transformer core and shunt reactor model was simulated by the magnetostrictive quadrature calculation method. The results show that the air gap has a great influence on the vibration of the shunt reactor core [
18,
19,
20]. Yan Rongge et al. established a reactor simulation model. After harmonic injection, the vibration decreases and the stress is concentrated in the air gap, corner, and core surface [
21]. Wu Shuyu et al. conducted a coupling calculation of the multi-physical field on the vibration noise of the reactor by electromagnetic structure-noise and obtained the conclusions that the force direction of the winding makes the reactor tend to diverge, the axial force is small in the middle and the two sides are large, the radial force is large in the middle and the two sides are small, and the maximum noise point is located in the upper yoke of the core [
22]. Wu Yongye proposed a method of operating the state recognition of converter transformers based on vibration detection technology and a deep belief network optimization algorithm [
23]. Scholars such as Guo Jiayi have provided a vibration reduction scheme based on an air gap length differential arrangement for the iron core design of existing UHV shunt reactors [
24]. Ben Tong et al. combined the vector magnetostriction model with the finite element method to simulate the vector vibration characteristics of a DC biased magnetron reactor [
25,
26]. Yang Kai et al. conducted an in-depth study on the wideband active vibration isolation of nonlinear bistable electromagnetic actuators with elastic boundaries [
27].
In order to reduce the vibration noise of the reactor and ensure the safety and reliability of the reactor and power system operation, the vibration performance of the reactor core is studied from the angle of combining experiment and theory, and the vibration and noise reduction scheme is put forward. By modifying the anisotropy characteristics of the Young’s modulus of the reactor core disc, a reactor core model is simulated based on the modified data and the vibration reduction effect of changing the core disc parameters is tested according to the modified reactor core model.
3. Vibration Performance Analysis of Reactor Core
3.1. Establishment of Magnetic Mechanical Coupling Model of Iron Core Reactor
Under the action of magnetostrictive force and electromagnetic force, electrical equipment such as reactors will produce vibration. In order to study the electromagnetic vibration of reactors, it is necessary to couple the electromagnetic field with solid mechanics, and then solve the vibration of reactors under working conditions.
Stress and strain can describe the mechanical state of any continuum. When studying the stress state at a point in the object, the stress is usually decomposed into normal stress and shear stress, which are perpendicular to the action surface and parallel to the action surface. The stress tensor is generally used to represent the multiple directionality of the stress state at a point in the object. A tiny parallelepiped is taken around the point along the x, y, and z directions, as shown in
Figure 4.
In
Figure 4, the normal vectors of each side of the parallelepiped coincide with the three-dimensional coordinate axis, respectively. There are nine stress components in the six faces, namely the normal stress
σx,
σy,
σz, and the shear stress
τxy,
τyx,
τxz,
τzx,
τyz,
τzy. According to the law of reciprocal shear force,
τxy = −
τyx,
τxz = −
τzx,
τyz = −
τzy, and the nine stress components can be reduced to six independent components. That is, the stress state at a certain point of the object is described by the normal stresses
σx,
σy,
σz, and the shear stresses
τxy,
τyz, and
τzx.
A non-contact force like electromagnetic force, gravity, and so on is a volumetric force acting on all particles inside an object. If the object is in equilibrium under the action of volume force, then the object is divided into arbitrary shape units, and the units are also in equilibrium. In elasticity, the equation describing the relationship between volume force and stress is called an equilibrium differential equation and is expressed in Equation (1).
In the formula, the unit forces in the x, y, and z directions are represented by Fx, Fy, and Fz.
The length and thickness of the object will change after the force is exerted. Generally, the length is lengthened or shortened, and the thickness will become thinner or thicker. This deformation is described by strain. Similar to the method of studying stress, the strain at a point of an object can take three line segments along the x, y, z directions near the point. The elongation of the line segment is positive and the direction is the elongation direction, denoted by εx, εy, and εz. The right angle between line segments decreases to positive, and the direction is the direction in which the angle decreases, expressed by γxy, γyz, and γzx.
In elasticity, geometric equations are used to express the relationship between the strain and displacement of a stressed object. The displacement generated by the force object in space is decomposed into three directions
x,
y, and
z along the coordinate axis, then the geometric equation is as shown in Equation (2).
where
u,
v, and
w represent the displacement in the
x,
y, and
z directions, respectively.
In order to describe the relationship between stress and strain in space objects, the constitutive equation of elastic materials is also needed, that is, the physical equation. In elasticity, the physical equation is expressed as Formula (3).
where
E is the Young’s modulus of the material;
α is Poisson’s ratio.
The potential energy of the current of the core reactor, the potential energy of the magnetic field and its boundary, the magnetostrictive energy, the strain energy, and the work force balance achieved by external forces are as follows (4):
where, Ω
1, Ω
2, Γ
1, and Γ
2 are the analytical domains and boundaries of the electromagnetic field and the mechanical field;
ƒΓ,
ƒΩ are the outer surface force and outer volume force densities of the mechanical field.
σT is the magnetostrictive stress under the external magnetic field; d is the magnetostrictive coefficient.
The reactor is stationary when it works; it is balanced by gravity and supporting forces, and the reactor can be regarded as not subject to external forces, namely:
Formula (6) is expanded according to Formula (3) to get Formula (7):
The relationship between vector magnetic potential and magnetic flux density is as follows (8):
Node vector magnetic potential and vibration displacement are as follows (9):
where,
m and
n are the nodes of the electromagnetic field and the mechanical field.
The finite element matrix equation can be obtained, which can be expressed as:
where,
K is the stiffness matrix;
X is the column matrix of vector magnetic potential
A and vibration displacement
u;
F is the column matrix of impressed current density and external force density. The vector magnetic potential
A and vibration displacement
u of the reactor core can be obtained by solving the finite element matrix equation.
3.2. Comparative Analysis of Simulation Results of Core Reactors under Different Prestrains
The vibration of the reactor core is the primary contributing factor to the overall reactor vibration, and the electromagnetic force between the core discs induces mutual attraction, leading to deformation. Next, the magnetic mechanical coupling model of core reactors considering the elastic modulus in the direction of core disc lamination and different pre strains will be established, and the core reactor with a rated current of 28 A will be simulated and analyzed. The core simulation model of the reactor is shown in
Figure 5.
The specific size and material of the iron core are as follows: the length of the upper and lower iron yoke is 180 mm, the height is 30 mm, and the thickness is 40 mm. The core disc is 40 mm long, 30 mm high, and 40 mm thick, and the upper and lower iron yoke and core disc are oriented electrical steel sheet 30Q120. There are 12 square air gaps between the core disc and the upper and lower yoke as well as between the core disc. Each air gap has a side length of 40 mm and a thickness of 1 mm. The material of the air gap is epoxying laminated glass cloth plate.
In order to describe the magnetostrictive effect accurately and effectively in the simulation software, it is necessary to set the prestrain on the material properties of the electrical steel sheet of the reactor core and core disc. The magnetostrictive measuring instrument was used to measure the materials of oriented electrical steel 30Q120 and non-oriented electrical steel 50AW40 several times. After taking the average of the multiple measurement results, the cubic spline interpolation method was used to fit. The results of curve fitting are shown in
Figure 6.
In order to enhance the accuracy and effectiveness of modeling and simulating vibrations in a core reactor, the Young’s modulus of the core disc stacking direction was adjusted using the modal experimental verification method. The final modified orthogonal anisotropic structural mechanical parameters of the core disc are presented in
Table 4.
When current excitation is applied to the reactor, the coil is set to uniform multiple turns and a 50 Hz 28A sinusoidal current is applied to the winding.
Figure 7a–d shows the distribution of the magnetic flux density modulus of the reactor core when t is 0.004 s, 0.008 s, 0.01 s, and 0.02 s, respectively.
It can be seen that the current sizes of the four moments are different, and the magnetic flux density modulus are also different. When t = 0.004 s, the maximum flux density modulus is 0.34 T, and when t = 0.01, the maximum flux is 1.08 T, and the maximum flux is at the upper and lower yoke corners of the core. Due to the significant air gap at the core disc, the magnetic flux density modulus value is not large, which is half of the maximum magnetic flux density modulus value at the corresponding time.
In order to explore the contribution of electromagnetic force and magnetostriction to the reactor vibration, the force distribution diagram of the iron core under the combined action of them is shown in
Figure 8, when t = 0.004 s and t = 0.01 s. It can be seen from
Figure 8 that the reactor is subjected to different stresses at different times. At t = 0.004 s, the force is measured to be 6.46 × 10
4 N/m
2, while at t = 0.01 s, it increases to 6.58 × 10
4 N/m
2, indicating a larger force magnitude. Compared with
Figure 7, it is found that when t = 0.004 s, the magnetic flux density is small, and the force is small. When t = 0.01 s, the magnetic flux density is larger, and the force on the reactor is also larger; so, the force on the reactor is closely related to the magnetic field distribution.
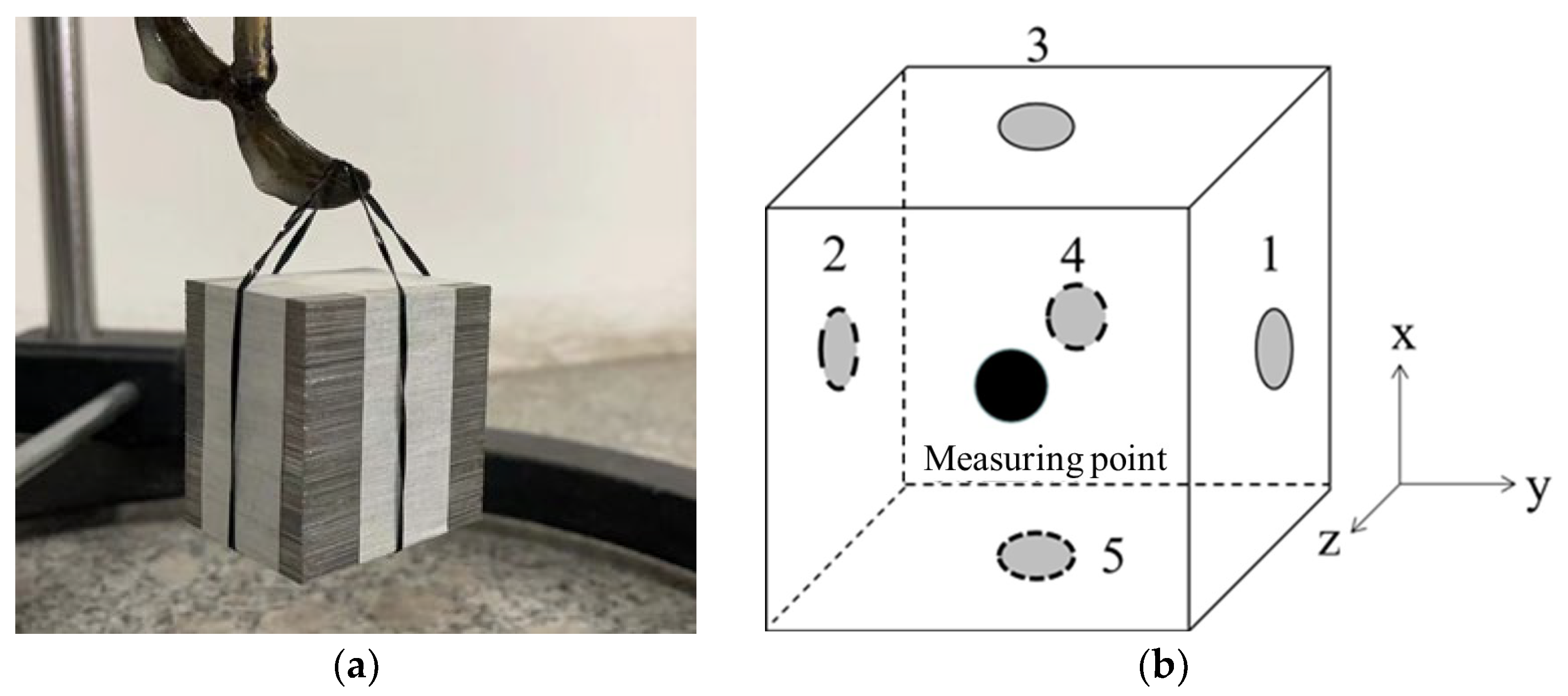
In order to investigate the vibration acceleration resulting from the separate influence of the electromagnetic force and the magnetostriction effect on the reactor core in different directions, the positive center of the upper yoke A was selected as the test point to simulate the vibration acceleration of the test point A, as shown in
Figure 9.
In the figure, the red line represents the vibration acceleration at point A when only electromagnetic force is applied, and the blue line represents the vibration acceleration at point A when only magnetostriction is applied.
It is not difficult to find that the contribution of electromagnetic force to vibration at the test point A in different directions is greater than that of the magnetostriction effect. The vibration frequency of the reactor core is 100 Hz, that is, the period is 0.01 s. When the magnetostrictive effect is not considered, the amplitude of vibration acceleration in the z direction is the largest, with a maximum value of 0.95 m/s2; when the electromagnetic force is not considered, the amplitude of vibration acceleration in the z direction is the largest, with a maximum value of 0.16 m/s2.
5. Conclusions
Based on the experimental measurements, the elastic modulus in the lamination direction of the core sheet is modified, and the structural anisotropic of the mechanical parameters of the electrical steel sheet are considered. On this basis, the simulation and experimental verification of the core reactor are carried out and the vibration reduction scheme of the reactor core vibration performance is proposed. The results are as follows:
(1) Through a modal experimental proofreading method, the Young’s modulus in the lamination direction is adjusted. The experimental data show that the adjusted simulation results are closer to the experimental values, which lays a foundation for the subsequent vibration performance research of the reactor to be closer to the actual situation.
(2) The results show that the magnetostrictive force and the electromagnetic force of the reactor have different effects on its vibration in different directions. When the two act together, the vibration acceleration amplitude of the reactor core in the z direction is the largest.
(3) A self-made detachable single-phase series core reactor is experimentally analyzed. The effects of the air gap length between different core discs and the arrangement of the core disc electrical steel sheet on the vibration acceleration of the reactor are measured; the results show that the vibration reduction in the reactor is about 11.6% after comprehensive improvement. It provides a theoretical basis for further research on vibration and noise reduction in reactors.