Optimal Design of a Surface Permanent Magnet Machine for Electric Power Steering Systems in Electric Vehicle Applications Using a Gaussian Process-Based Approach
Abstract
:1. Introduction
- Development of a design optimization process utilizing adaptive sampling that blends exploitation and exploration to simultaneously improve model accuracy and convergence speed.
- Validation of the developed optimization process through its application to a 72-slot/8-pole IPMSM for traction applications.
- Comprehensive design and analysis of surface permanent magnet (SPM) machines to address design challenges for EPS applications.
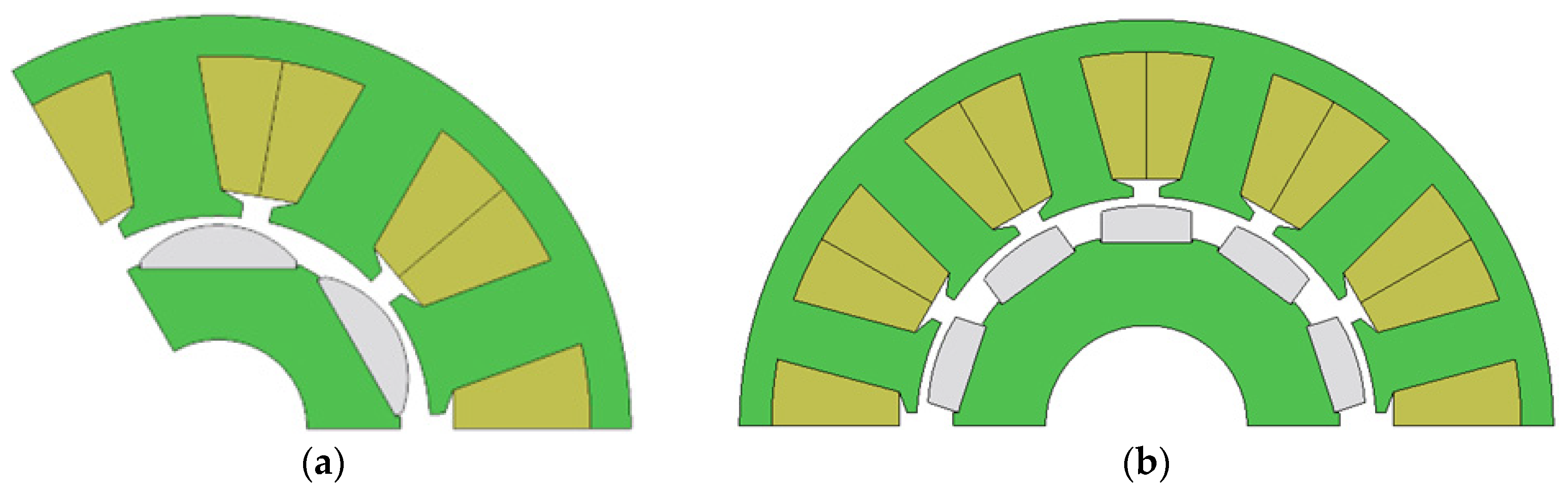
- Comparative analysis and design optimization of two promising PM machine topologies: SPM machines equipped with fractional-slot concentrated windings (FSCW) with 9-slot/6-pole and 12-slot/10-pole.
- Experimental verification of the optimal design through the construction and testing of a prototype machine.
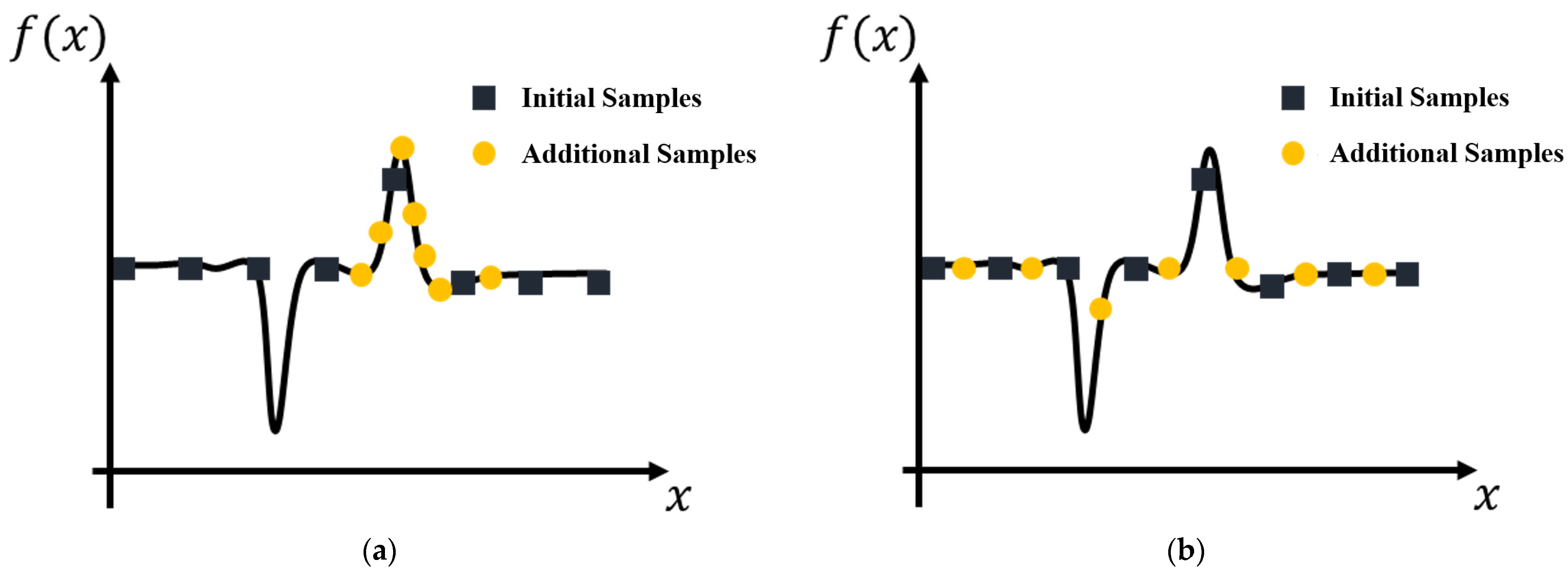
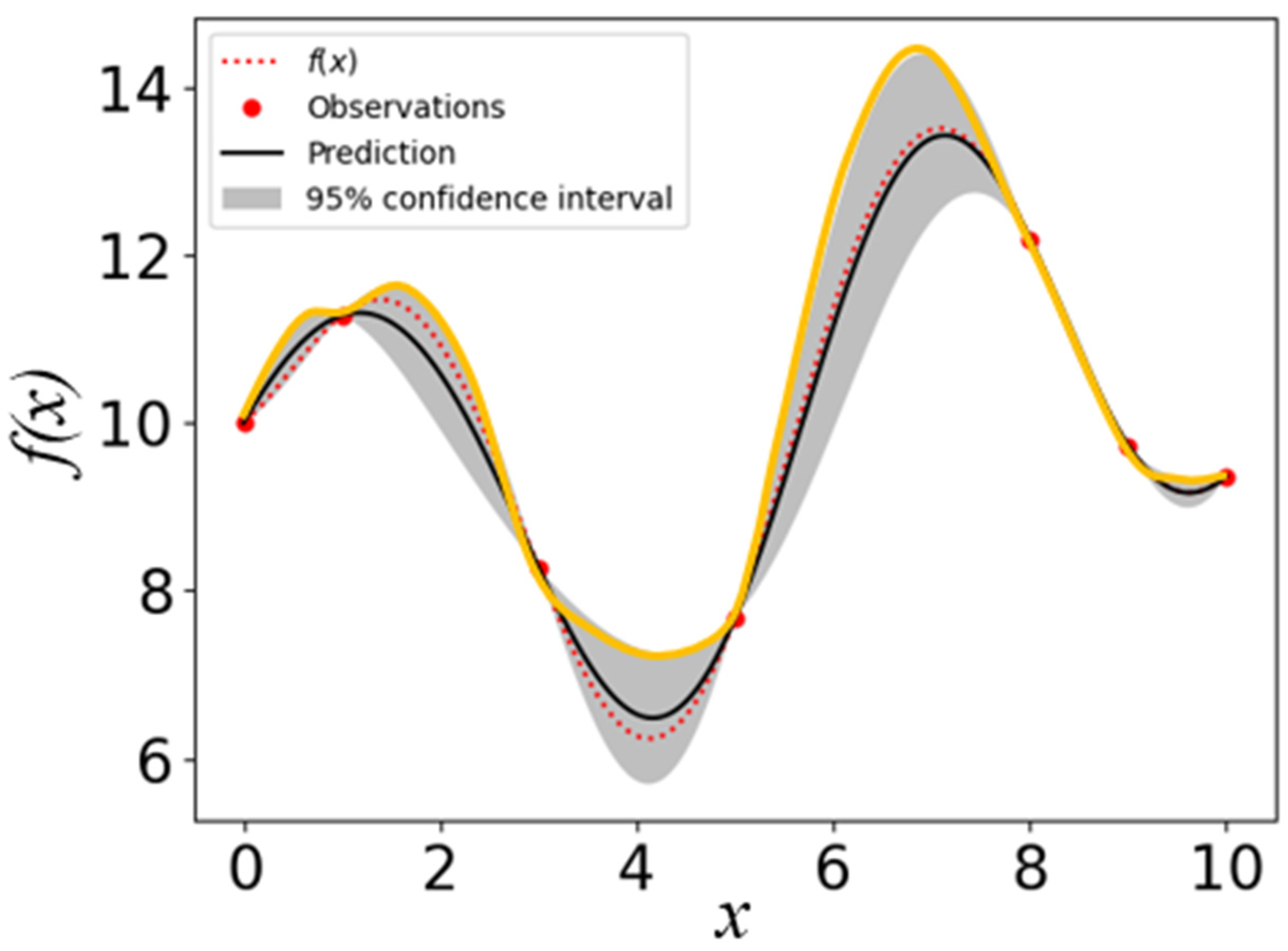
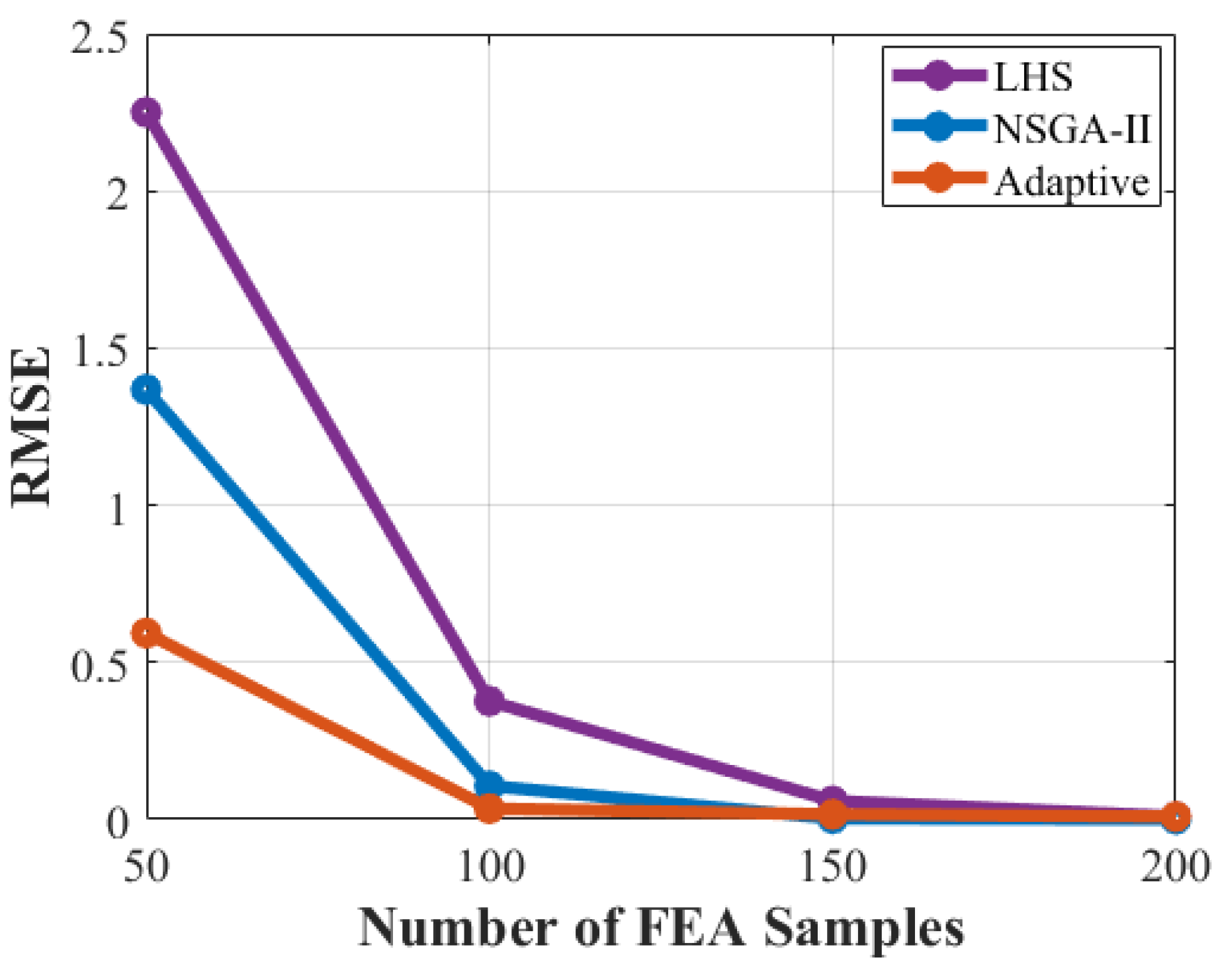
2. Gaussian Process-Based Adaptive Sampling Algorithm
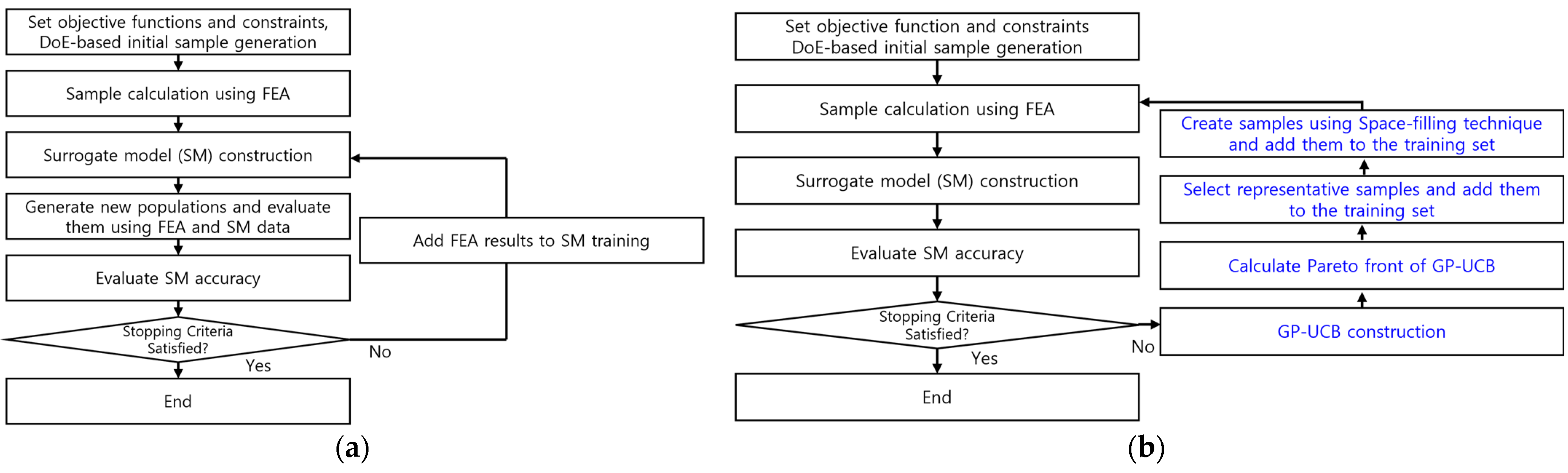
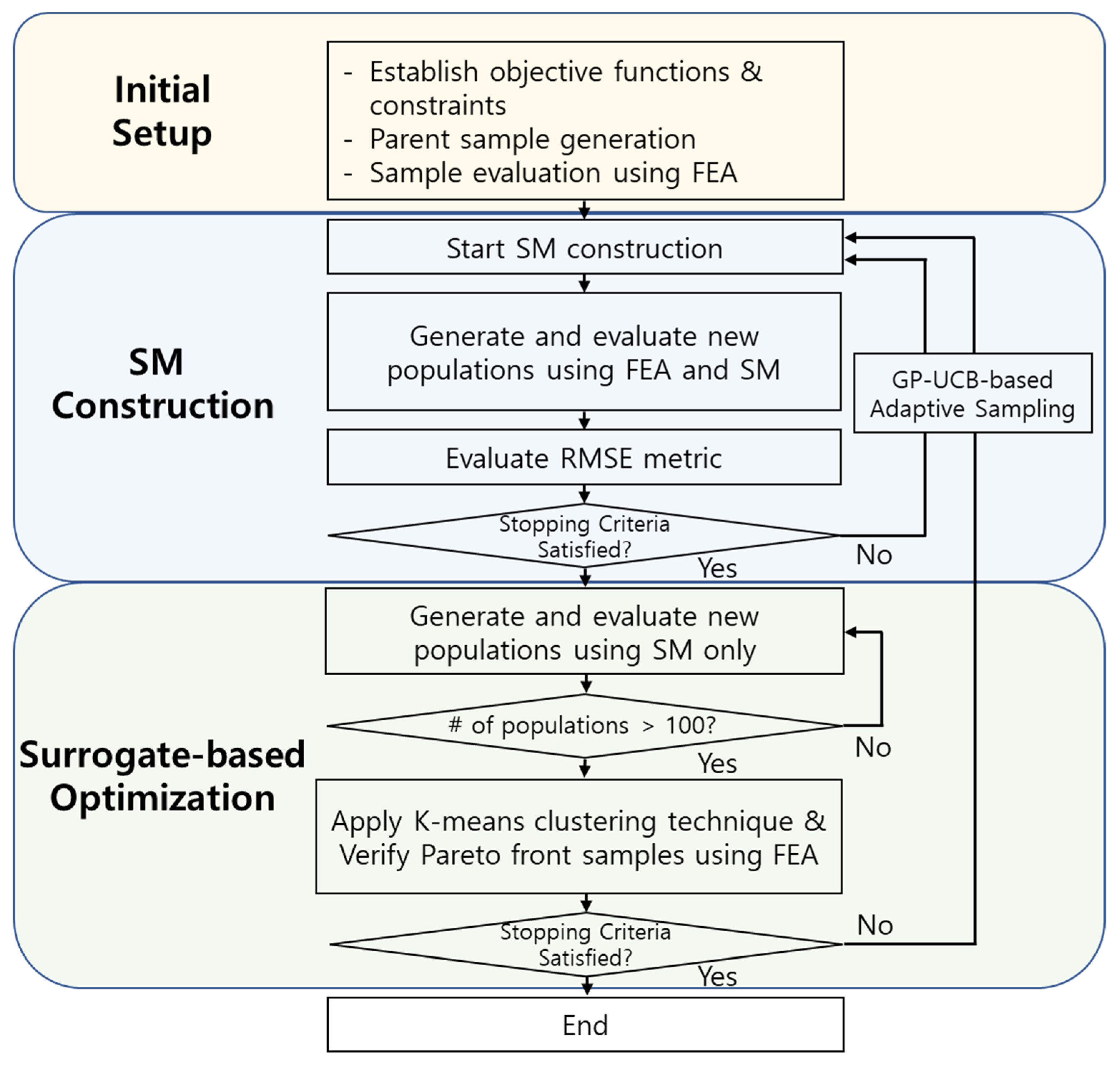
2.1. Proposed Optimization Process
2.2. Case Study: 72-Slot/8-Pole IPM Traction Machine
| minimize: | 1. −(Tpk/mtotal) [Nm/kg] |
| 2. Active material cost [$] |
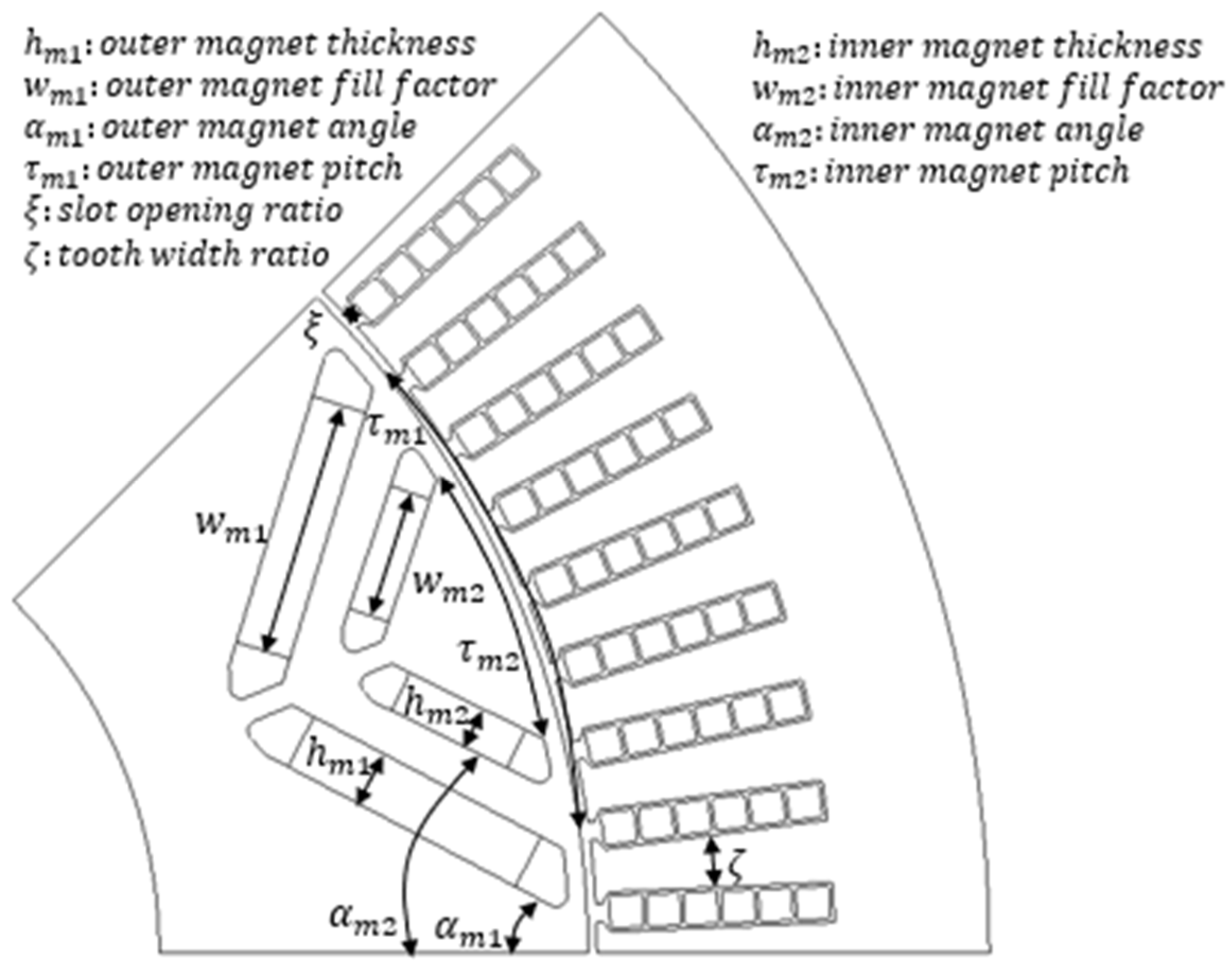
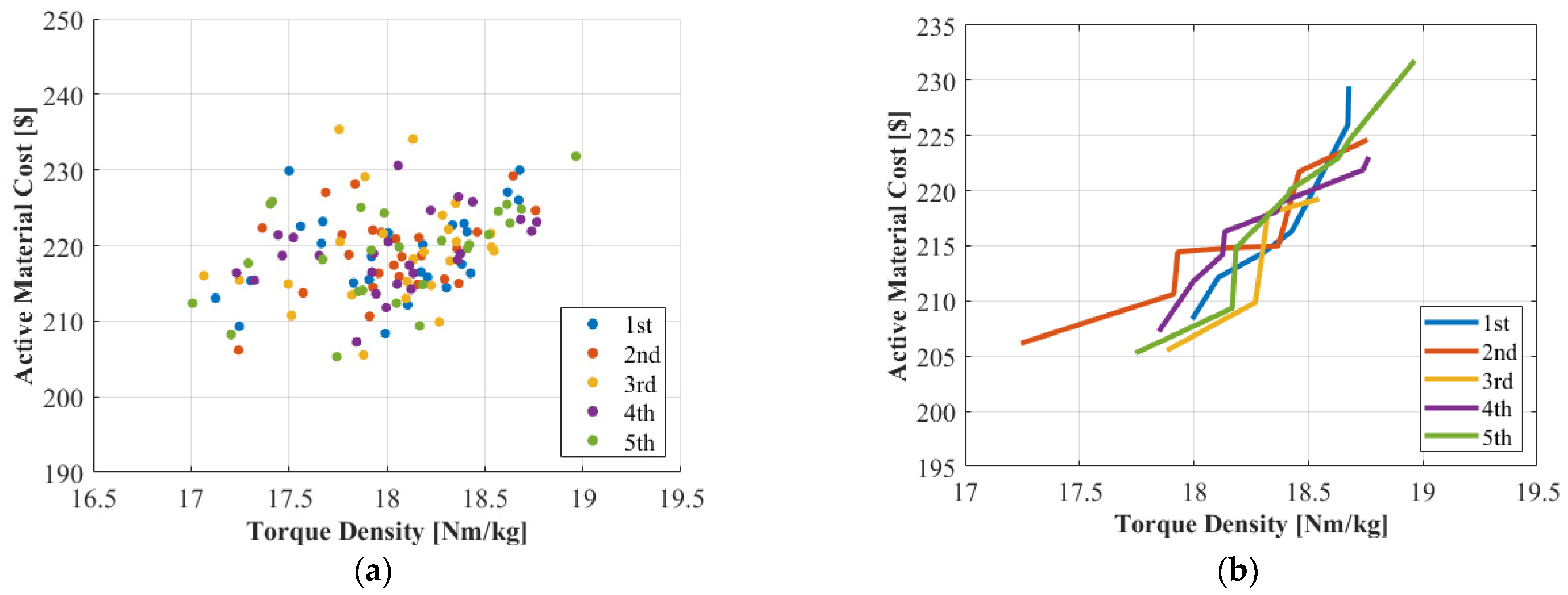
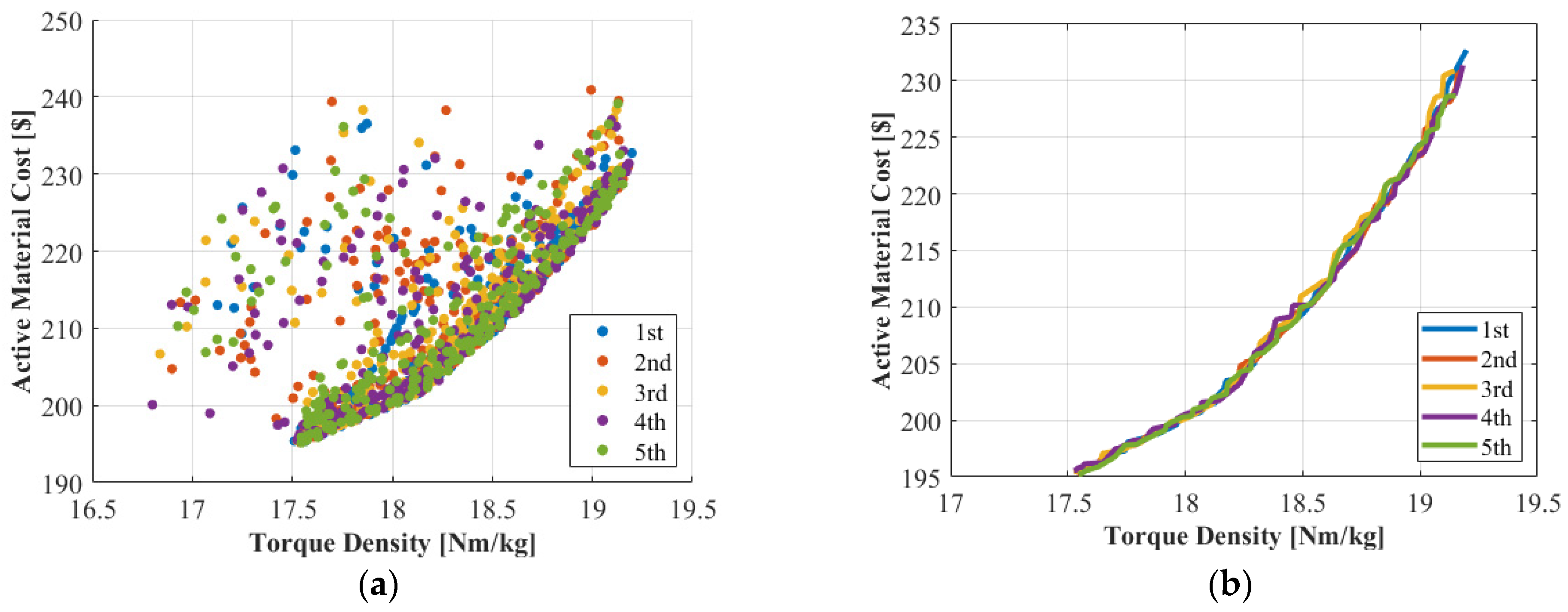
3. EPS Motor Design
4. Design Optimization
| minimize: | 1. −(Tpk/mtotal) [Nm/kg] |
| 2. Ploss [W] | |
| 3. Tcog [Nm] | |
| subject to: | 1. Active material cost ≤ $20 |
| 2. Tripple ≤ 4% |
5. Prototype Machine and Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bianchi, N.; Bolognani, S. Design techniques for reducing the cogging torque in surface-mounted PM motors. IEEE Trans. Ind. Appl. 2002, 38, 1259–1265. [Google Scholar] [CrossRef]
- Bianchi, N.; Pre, M.D.; Bolognani, S. Design of a fault-tolerant IPM motor for electric power steering. IEEE Trans. Veh. Technol. 2006, 55, 1102–1111. [Google Scholar] [CrossRef]
- Jang, J.; Cho, S.G.; Lee, S.J.; Kim, K.S.; Kim, J.M.; Hong, J.P.; Lee, T.H. Reliability-Based Robust Design Optimization with Kernel Density Estimation for Electric Power Steering Motor Considering Manufacturing Uncertainties. IEEE Trans. Magn. 2015, 51, 8001904. [Google Scholar] [CrossRef]
- Naidu, M.; Gopalakrishnan, S.; Nehl, T.W. Fault-Tolerant Permanent Magnet Motor Drive Topologies for Automotive X-By-Wire Systems. IEEE Trans. Ind. Appl. 2010, 46, 841–848. [Google Scholar] [CrossRef]
- Uler, G.F.; Mohammed, O.A.; Koh, C.-S. Design optimization of electrical machines using genetic algorithms. IEEE Trans. Magn. 1995, 31, 2008–2011. [Google Scholar] [CrossRef]
- Gao, J.; Sun, H.; He, L.; Dong, Y.; Zheng, Y. Optimization design of Switched Reluctance Motor based on Particle Swarm Optimization. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011; pp. 1–5. [Google Scholar] [CrossRef]
- Mutluer, M.; Bilgin, O. Design optimization of PMSM by particle swarm optimization and genetic algorithm. In Proceedings of the 2012 International Symposium on Innovations in Intelligent Systems and Applications, Trabzon, Turkey, 2–4 July 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Duan, Y.; Harley, R.G.; Habetler, T.G. Comparison of Particle Swarm Optimization and Genetic Algorithm in the design of permanent magnet motors. In Proceedings of the 2009 IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009; pp. 822–825. [Google Scholar] [CrossRef]
- Murata, T.; Ishibuchi, H. MOGA: Multi-objective genetic algorithms. In Proceedings of the 1995 IEEE International Conference on Evolutionary Computation, Perth, WA, Australia, 29 November–1 December 1995; pp. 289–294. [Google Scholar] [CrossRef]
- Li, Y.; Lei, G.; Bramerdorfer, G.; Peng, S.; Sun, X.; Zhu, J. Machine Learning for Design Optimization of Electromagnetic Devices: Recent Developments and Future Directions. Appl. Sci. 2021, 11, 1627. [Google Scholar] [CrossRef]
- Choi, M.; Choi, G.; Bramerdorfer, G.; Marth, E. Systematic Development of a Multi-Objective Design Optimization Process Based on a Surrogate-Assisted Evolutionary Algorithm for Electric Machine Applications. Energies 2023, 16, 392. [Google Scholar] [CrossRef]
- Taran, N.; Ionel, D.M.; Dorrell, D.G. Two-Level Surrogate-Assisted Differential Evolution Multi-Objective Optimization of Electric Machines Using 3-D FEA. IEEE Trans. Magn. 2018, 54, 8107605. [Google Scholar] [CrossRef]
- Gao, Y.; Yang, T.; Bozhko, S.; Wheeler, P.; Dragičević, T. Filter Design and Optimization of Electromechanical Actuation Systems Using Search and Surrogate Algorithms for More-Electric Aircraft Applications. IEEE Trans. Transp. Electrif. 2020, 6, 1434–1447. [Google Scholar] [CrossRef]
- Gu, J.; Hua, W.; Yu, W.; Zhang, Z.; Zhang, H. Surrogate Model-Based Multiobjective Optimization of High-Speed PM Synchronous Machine: Construction and Comparison. IEEE Trans. Transp. Electrif. 2023, 9, 678–688. [Google Scholar] [CrossRef]
- Yoo, C.-H. A New Multi-Modal Optimization Approach and Its Application to the Design of Electric Machines. IEEE Trans. Magn. 2018, 54, 8202004. [Google Scholar] [CrossRef]
- Jackson, D.; Belakaria, S.; Cao, Y.; Doppa, J.R.; Lu, X. Machine Learning Enabled Design Automation and Multi-Objective Optimization for Electric Transportation Power Systems. IEEE Trans. Transp. Electrif. 2022, 8, 1467–1481. [Google Scholar] [CrossRef]
- Gupta, S.; Biswas, P.K.; Debnath, S.; Ghosh, A.; Babu, T.S.; Zawbaa, H.M.; Kamel, S. Metaheuristic Optimization Techniques Used in Controlling of an Active Magnetic Bearing System for High-Speed Machining Application. IEEE Access 2023, 11, 12100–12118. [Google Scholar] [CrossRef]
- Eason, J.; Cremaschi, S. Adaptive sequential sampling for surrogate model generation with artificial neural networks. Comput. Chem. Eng. 2014, 68, 220–232. [Google Scholar] [CrossRef]
- Fushiki, T. Estimation of prediction error by using K-fold cross-validation. Stat. Comput. 2011, 21, 137–146. [Google Scholar] [CrossRef]
- Meckesheimer, M.; Booker, A.J.; Barton, R.R.; Simpson, T.W. Computationally inexpensive metamodel assessment strategies. AIAA J. 2002, 40, 2053–2060. [Google Scholar] [CrossRef]
- Jiang, C.; Cai, X.; Qiu, H.; Gao, L.; Li, P. A two-stage support vector regression assisted sequential sampling approach for global metamodeling. Struct. Multidiscip. Optim. 2018, 58, 1657–1672. [Google Scholar] [CrossRef]
- Fuhg, J.N.; Fau, A.; Nackenhorst, U. State-of-the-Art and Comparative Review of Adaptive Sampling Methods for Kriging. Arch. Comput. Methods Eng. 2021, 28, 2689–2747. [Google Scholar] [CrossRef]
- Liu, H.; Xu, S.; Wang, X.; Wu, J.; Song, Y. A global optimization algorithm for simulation-based problems via the extended DIRECT scheme. Eng. Optim. 2015, 47, 1441–1458. [Google Scholar] [CrossRef]
- Burke, J.V.; Curtis, F.E.; Lewis, A.S.; Overton, M.L.; Simões, L.E.A. Gradient Sampling Methods for Nonsmooth Optimization. arXiv 2018. [Google Scholar] [CrossRef]
- Sóbester, A.; Leary, S.J.; Keane, A.J. On the design of optimization strategies based on global response surface approximation models. J. Glob. Optim. 2005, 33, 31–59. [Google Scholar] [CrossRef]
- Kleijnen, J.P.C.; Van Beers, W.C.M. Application-driven sequential designs for simulation experiments: Kriging metamodeling. J. Oper. Res. Soc. 2004, 55, 876–883. [Google Scholar] [CrossRef]
- Liu, H.; Xu, S.; Ma, Y.; Chen, X.; Wang, X. An Adaptive Bayesian Sequential Sampling Approach for Global Metamodeling. J. Mech. Des. 2016, 138, 011404. [Google Scholar] [CrossRef]
- Nuchitprasittichai, A.; Cremaschi, S. An algorithm to determine sample sizes for optimization with artificial neural networks. AIChE J. 2013, 59, 805–812. [Google Scholar] [CrossRef]
- Makondo, N.; Folarin, A.L.; Zitha, S.N.; Remy, S.L. An Analysis of Reinforcement Learning for Malaria Control. arXiv 2021. [Google Scholar] [CrossRef]
- Choi, M.; Choi, G. Investigation, and Mitigation of AC Losses in IPM Machines with Hairpin Windings for EV Applications. Energies 2021, 14, 8034. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E. Initialisation Approaches for Population-Based Metaheuristic Algorithms: A Comprehensive Review. Appl. Sci. 2022, 12, 896. [Google Scholar] [CrossRef]
- EL-Refaie, A.M. Fractional-Slot Concentrated-Windings Synchronous Permanent Magnet Machines: Opportunities and Challenges. IEEE Trans. Ind. Electron. 2010, 57, 107–121. [Google Scholar] [CrossRef]
- Cros, J.; Viarouge, P. Synthesis of high performance PM motors with concentrated windings. IEEE Trans. Energy Convers. 2002, 17, 248–253. [Google Scholar] [CrossRef]
- Choi, G.; Jahns, T.M. Analysis and Design Recommendations to Mitigate Demagnetization Vulnerability in Surface PM Synchronous Machines. IEEE Trans. Ind. Appl. 2018, 54, 1292–1301. [Google Scholar] [CrossRef]


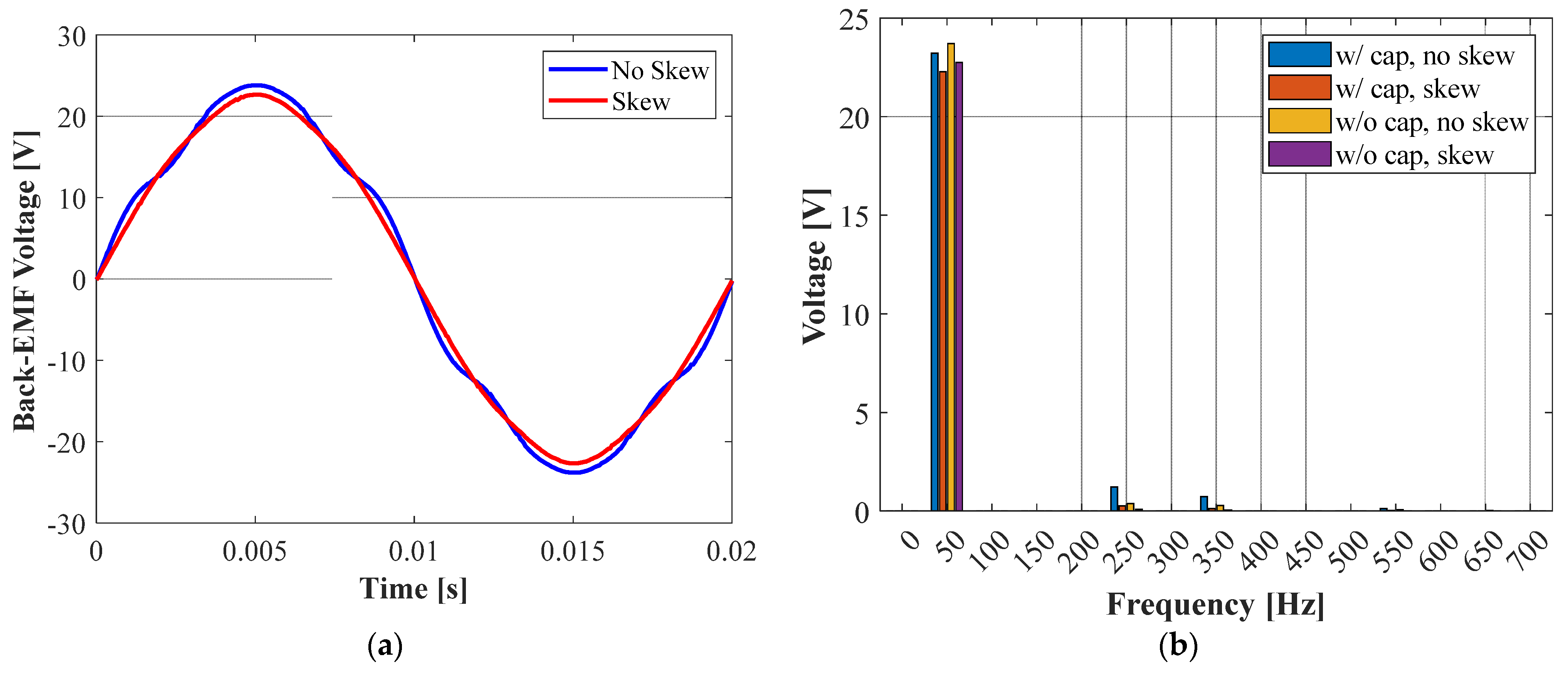
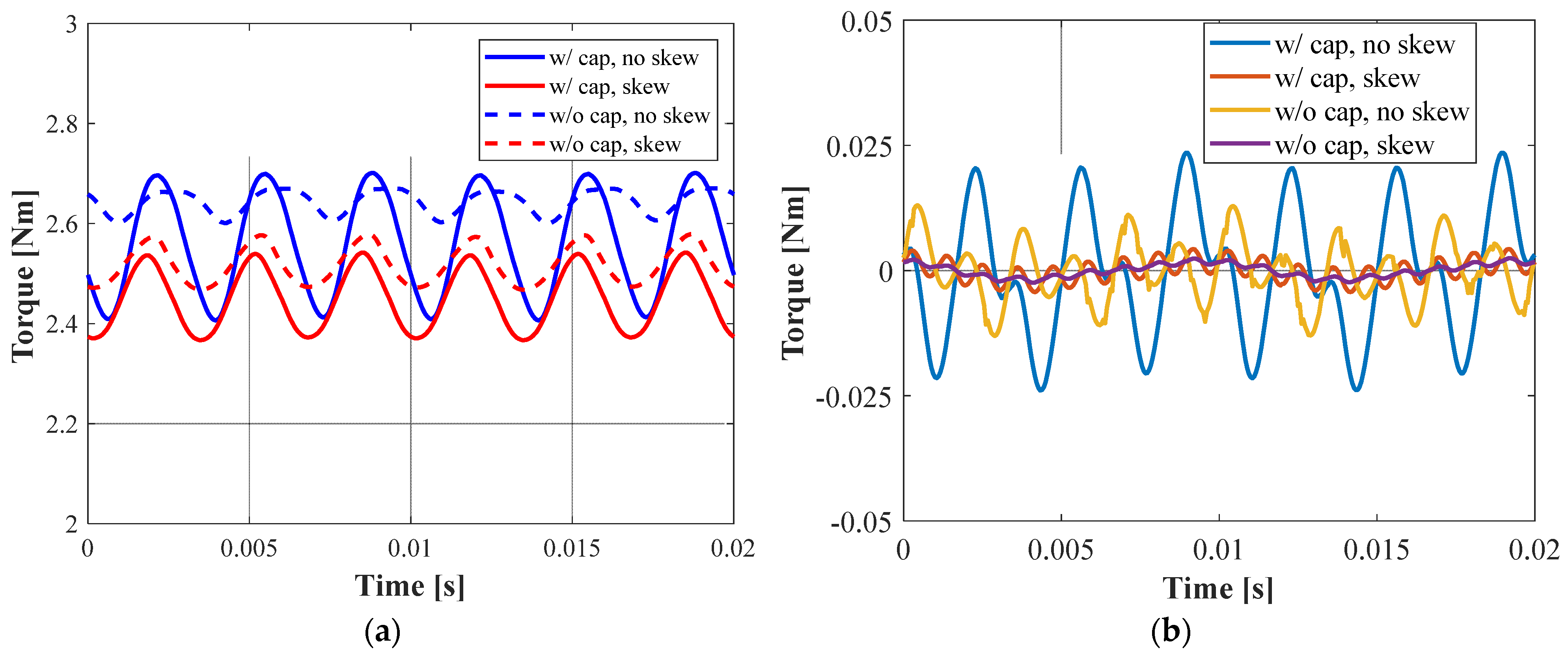
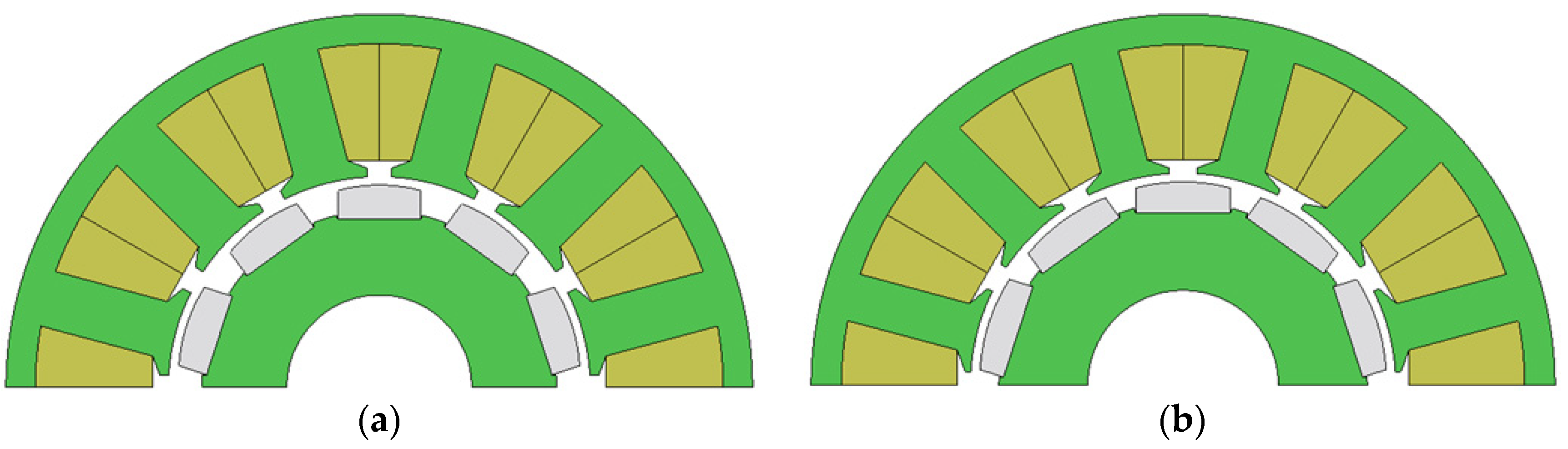



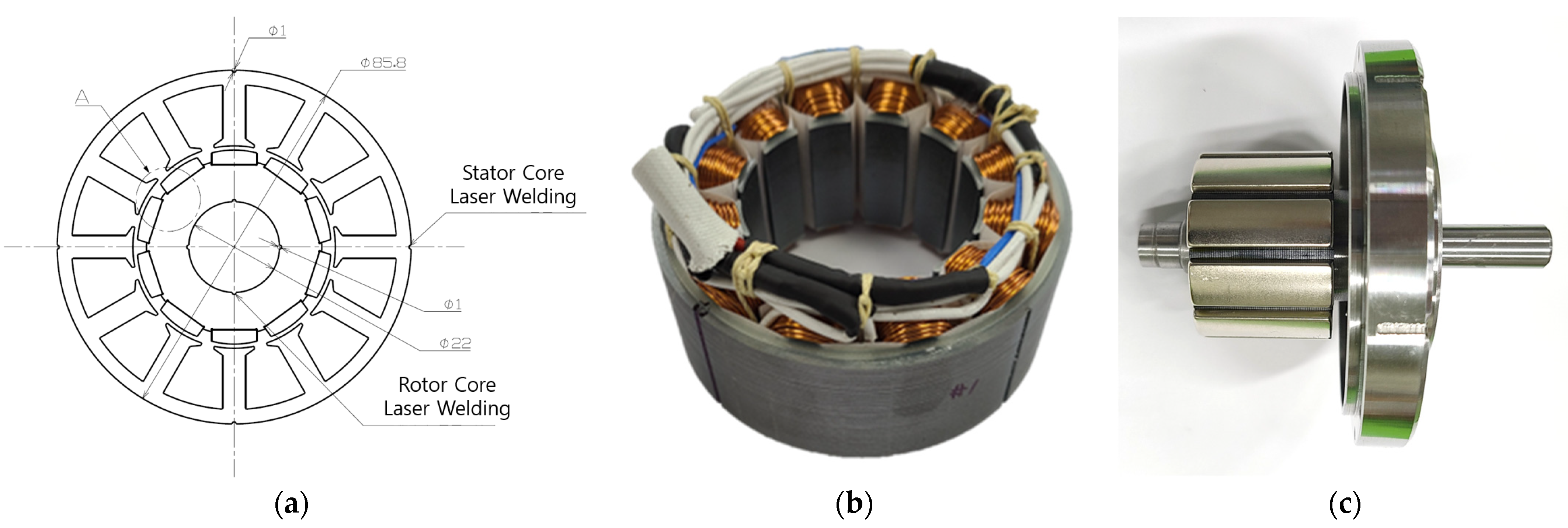

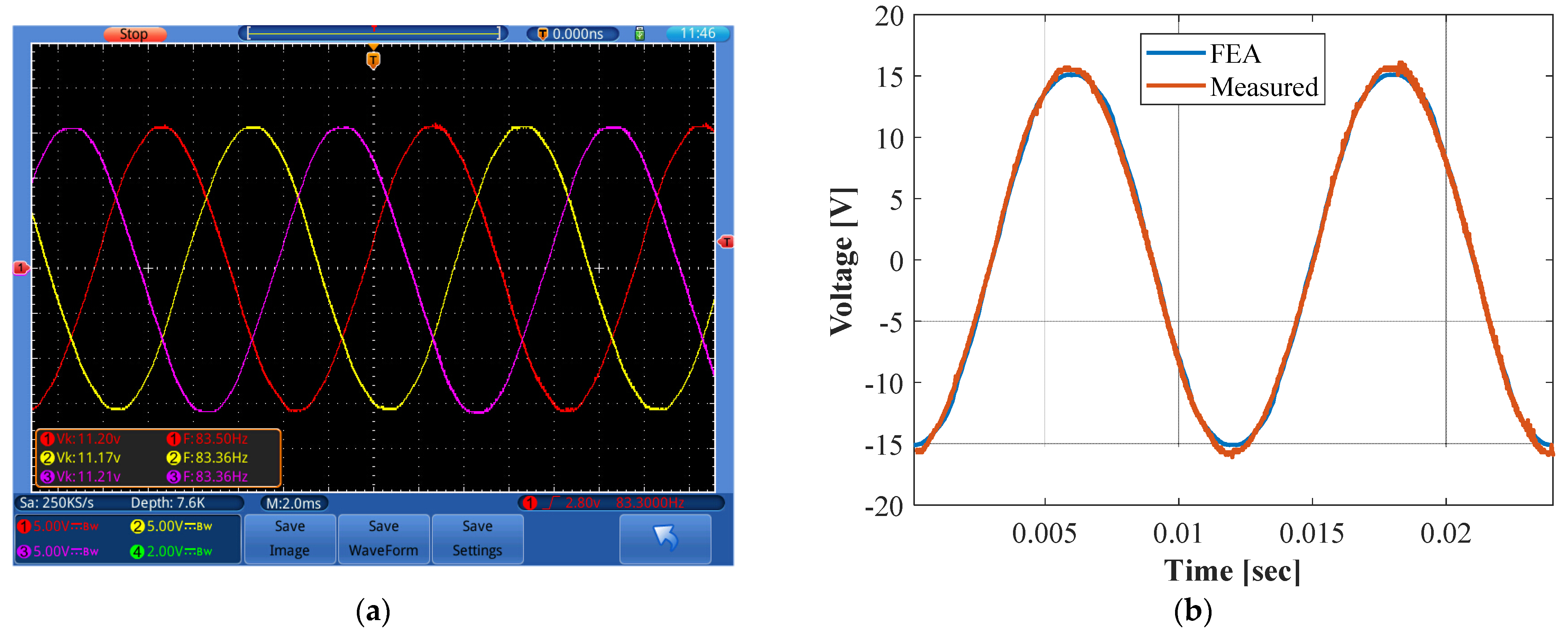
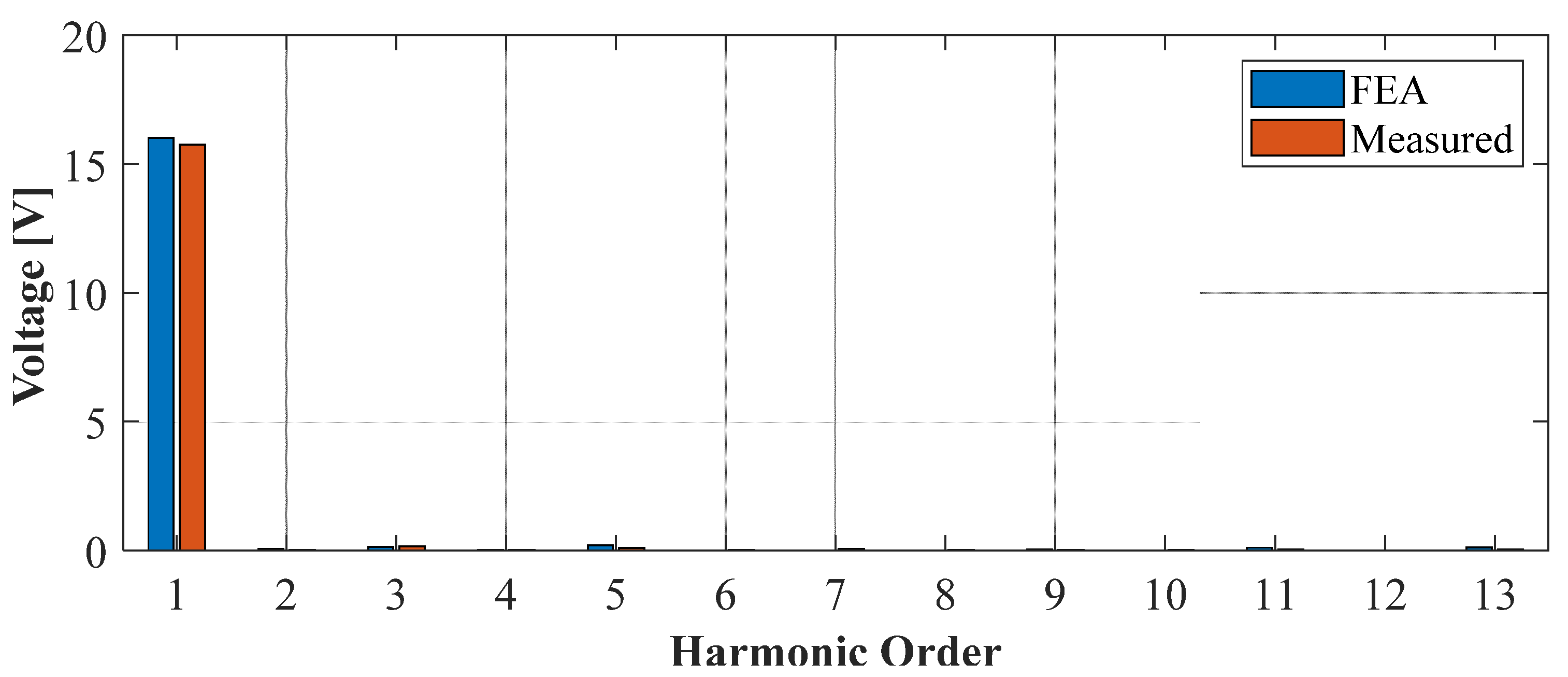
| Parameter | Value |
|---|---|
| Slot/Pole | 72/8 |
| Peak current density | 25 Arms/mm2 |
| Maximum current | 400 Arms |
| Airgap length | 0.75 mm |
| Rotor outer diameter | 150 mm |
| Stator outer diameter | mm |
| Stack length | 90 mm |
| Parameter | Design 1 | Design 2 |
|---|---|---|
| Slot/Pole | 9/6 | 12/10 |
| DC bus voltage | 48 V | |
| Rated current | 7.57 Arms | |
| Stator diameter | 86 mm | 85 mm |
| Rotor diameter | 44 mm | 47 mm |
| Stack length | 37 mm | 36 mm |
| Series turns | 105 | 100 |
| # of parallel circuit | 3 | 2 |
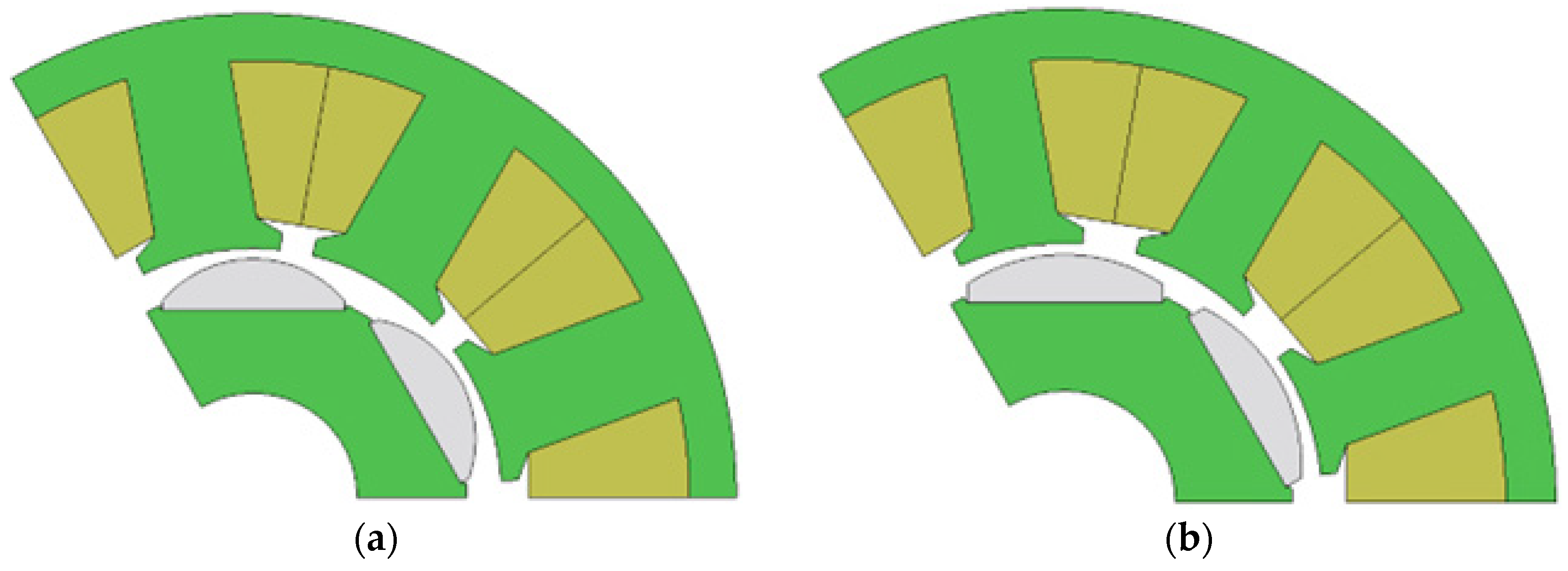
| Rotor skew | Yes | No |
| Current density | 6.54 Arms/mm2 | 6.36 Arms/mm2 |
| Operating Point | Torque [Nm] | Speed [r/min] | Power [W] |
|---|---|---|---|
| Point 1 | 1.9 | 790 | 157 |
| Point 2 | 1.1 | 1750 | 202 |
| Design Parameter | Symbol | Range | |
|---|---|---|---|
| Min | Max | ||
| Magnet arc eccentricity radius | rec | 22.5 mm | 15.5 mm |
| Magnet width ratio | τpm | 0.85 | 0.6 |
| Magnet thickness | hpm | 4 mm | 3 mm |
| Slot opening ratio | bo | 0.55 | 0.35 |
| Slot width ratio | bs | 0.55 | 0.35 |
| Tooth-tip thickness | htt | 2.4 mm | 1.2 mm |
| Torque Density [Nm/kg] | Cogging Torque [mNm] | Torque Ripple [%] | Losses [W] | Cost [$] | |
|---|---|---|---|---|---|
| Before opt. | 1.31 | 7.41 | 2.17 | 64.94 | 20.83 |
| After opt. | 1.48 | 6.62 | 2.94 | 63.94 | 19.20 |
| Difference [%] | +12.98 | −10.66 | +35.48 | −1.54 | −8.83 |
| Torque Density [Nm/kg] | Cogging Torque [mNm] | Torque Ripple [%] | Losses [W] | Cost [$] | |
|---|---|---|---|---|---|
| Before opt. | 1.71 | 40.12 | 2.08 | 54.58 | 17.48 |
| After opt. | 1.80 | 6.33 | 2.69 | 55.66 | 16.75 |
| Difference [%] | +5.23 | −84.19 | +29.44 | +1.98 | −4.21 |
| Design Parameter | Symbol | Design 1 | Design 2 | ||
|---|---|---|---|---|---|
| Before | After | Before | After | ||
| Magnet arc eccentricity radius [mm] | rec | 16 | 16 | 16.5 | 21.4 |
| Magnet width ratio [-] | τpm | 0.85 | 0.85 | 0.85 | 0.85 |
| Magnet thickness [mm] | hpm | 4.00 | 4.13 | 4.00 | 3.53 |
| Slot opening ratio [-] | bo | 0.35 | 0.41 | 0.40 | 0.41 |
| Slot width ratio [-] | bs | 0.40 | 0.48 | 0.40 | 0.40 |
| Tooth-tip thickness [mm] | htt | 1.70 | 1.41 | 0.90 | 0.67 |
| Torque Density [Nm/kg] | Cogging Torque [mNm] | Torque Ripple [%] | Losses [W] | Cost [$] | Rotor Skew | |
|---|---|---|---|---|---|---|
| Design 1 (9-slot/6-pole) | 1.48 | 6.62 | 2.94 | 63.94 | 19.20 | O |
| Design 2 (12-slot/10-pole) | 1.80 (+22%) | 6.33 (−4%) | 2.69 (−9%) | 55.66 (−13%) | 16.75 (−13%) | X |
| Test Type | Phase-a | Phase-b | Phase-c | Average |
|---|---|---|---|---|
| Experiment | 11.24 Vrms | 11.24 Vrms | 11.21 Vrms | 11.23 Vrms |
| FEA | 11.20 Vrms | 11.20 Vrms | 11.20 Vrms | 11.20 Vrms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, G.; Jang, G.-H.; Choi, M.; Kang, J.; Kang, Y.G.; Kim, S. Optimal Design of a Surface Permanent Magnet Machine for Electric Power Steering Systems in Electric Vehicle Applications Using a Gaussian Process-Based Approach. Actuators 2024, 13, 13. https://doi.org/10.3390/act13010013
Choi G, Jang G-H, Choi M, Kang J, Kang YG, Kim S. Optimal Design of a Surface Permanent Magnet Machine for Electric Power Steering Systems in Electric Vehicle Applications Using a Gaussian Process-Based Approach. Actuators. 2024; 13(1):13. https://doi.org/10.3390/act13010013
Chicago/Turabian StyleChoi, Gilsu, Gwan-Hui Jang, Mingyu Choi, Jungmoon Kang, Ye Gu Kang, and Sehwan Kim. 2024. "Optimal Design of a Surface Permanent Magnet Machine for Electric Power Steering Systems in Electric Vehicle Applications Using a Gaussian Process-Based Approach" Actuators 13, no. 1: 13. https://doi.org/10.3390/act13010013
APA StyleChoi, G., Jang, G.-H., Choi, M., Kang, J., Kang, Y. G., & Kim, S. (2024). Optimal Design of a Surface Permanent Magnet Machine for Electric Power Steering Systems in Electric Vehicle Applications Using a Gaussian Process-Based Approach. Actuators, 13(1), 13. https://doi.org/10.3390/act13010013







