Analytical and Experimental Study of Key Performance of Helicopter Rotor Torsion–Tension Straps

Abstract

As a crucial component of rotor systems, tension and torsion (TT) straps, recognized for their compact structure, have been adopted in advanced helicopters such as the SB > 1, EC145, and Mi-26. This paper presents an analytical investigation and experimental study on the key performance of TT straps. A method for rapidly evaluating the performance of the torsional deformation segment was developed. The size parameters and material properties of the torsional deformation segment that greatly influence the torsional stiffness and the stress distributions of TT straps were comprehensively identified and clearly investigated. Moreover, an experimental study of four cases of TT straps was carried out to verify the influence of the torsional deformation segment length, material, and connector segment structure on TT strap performance. The experimental results confirm that the rapid evaluation method provides high accuracy in assessing the stiffness and stress performance of TT straps, with deviations in stiffness less than 10%. The correlation between the calculated stress and shear forces and the experimental failure modes of the connector segments validates the effectiveness of the method in capturing key parameters. This research provides a theoretical and practical basis for designing critical key parameters of TT straps, facilitating a dramatic reduction in performance assessment time from days to hours and enabling the immediate identification of enhancement strategies. This accelerates the design process, thereby contributing to enhanced design efficiency and reduced costs.

1. Introduction

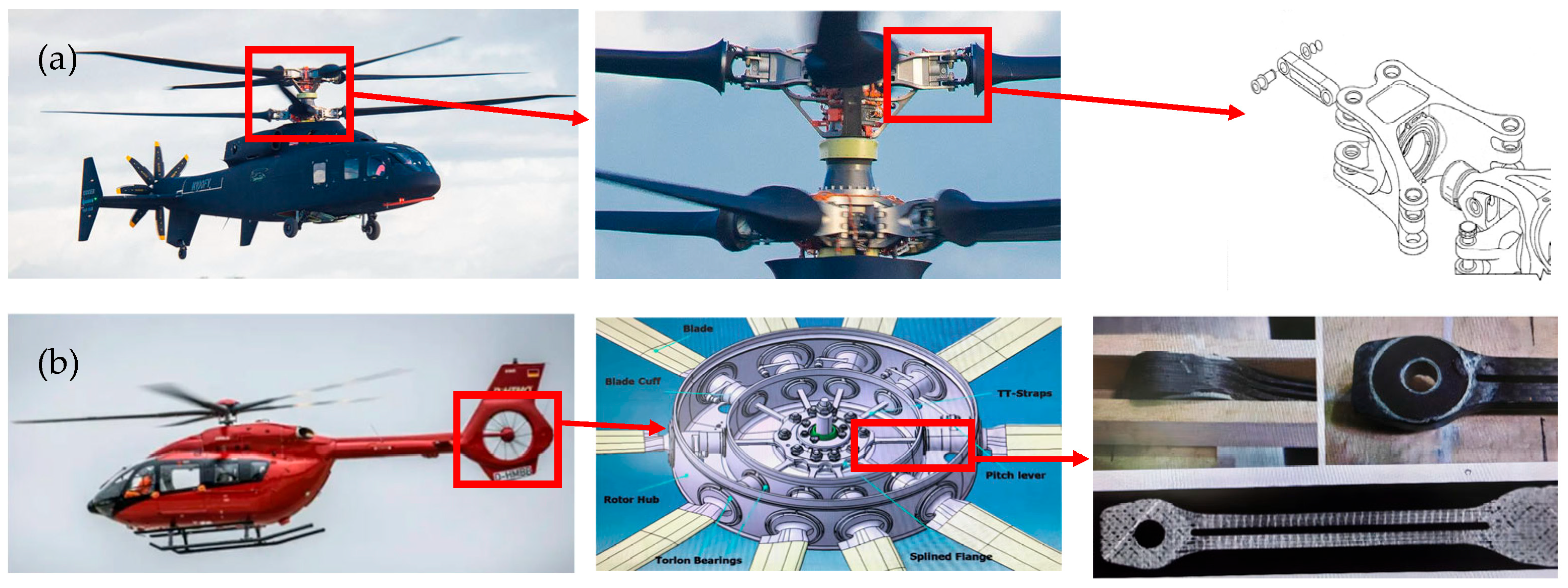
TT straps have been extensively applied in the rotor systems of various helicopters, such as the heavy-lift Mi-26, the Sikorsky compound coaxial helicopter SB > 1 (Figure 1a), the Bell XV-15 tilt rotor research aircraft, and the Airbus H120 and H145 [1,2]. The TT strap predominantly connects the rotor blade to the hub, allowing blade feathering while reacting to the centrifugal load [3]. Moreover, the TT strap improves the load handling capacity of the axial hinges in rotor hubs, simplifying the hub structure.

All prominent companies engaged in the research and development of high-performance TT straps, such as LORD, Airbus, and Mil Moscow Helicopter Plant, have decades of development experience and have released multiple generations of products. The fourth generation of a carbon fiber TT strap currently applied to the H145 tail rotor was developed by Airbus, and it is well known that this is the most advanced TT strap product [4]. The TT strap of the Mi-26 helicopter rotor is known as the largest product and can transmit the largest centrifugal force. It is worth noting that the TT strap has become a subject of intellectual property protection for major helicopter companies [5,6,7].

The mechanical performance of TT straps is a key aspect of their functionality. Over the past two decades, there has been relatively limited research in the literature focusing on the key performance metrics of the TT strap, such as its torsional stiffness, deformation, and load-bearing capacity. Elif Ahci-Ezg [8] explored structural design methodologies for these components in a study of the H145 Fenestron tail rotor TT strip (Figure 1b). In this research, the dimensions of the connection area were determined using a set of specific formulas. For the torsional deformation segment, parameters such as the number of layers, width, and thickness were optimized via Hyperstudy. However, during the TT strap design process, the slotting at the torsional deformation segment still depended on experience. Hongjin Xiong [9] created a simulation model using finite element software. The stiffness and stress distribution of a composite material TT strap were analyzed. The accuracy of the established model was confirmed through experimental testing.

Previous studies on the key performance characteristics of TT straps have relied on software for sensitivity analysis or the direct application of optimization software for deriving structural parameters. However, these methods have often demonstrated limited efficiency in assessing the performance of TT straps and have not enabled the comprehensive analysis of the correlation between key performance characteristics and critical design parameters, such as the materials, dimensions, and load-bearing capacities of the connection segment in relation to torsional stiffness and stress. In this work, a theoretical and experimental investigation of the key performance of TT straps was conducted. The torsional response of a TT strap under a specified torque was calculated, the relationship between key design parameters and performance was illustrated, a rapid evaluation method for the performance of the torsional deformation segment was established, and an analytical investigation into the key parameters influencing the TT strap performance was performed. Finally, further experimental research was carried out to examine the impacts of critical parameters such as the length, material, and structure of the connector segments through four design cases.

2. Rapid Evaluation Method for Key Performance Characteristics

This study focused on a typical TT strap using filament winding composites, aiming to establish a method for rapidly evaluating key aspects of their performance. These TT straps feature two rigid connecting segments and a flexible torsional deformation segment, composed of either a single layer or multiple layers of strap elements [10,11]. At the torsional deformation segment, strap elements with more than two layers are not interconnected, while the connecting segments utilize glass fiber fabric layers for bonding.

The structural characteristics of the strap elements include unidirectional composite laminates wound around resin or rubber filler blocks, which are then fitted within metal bushings (Figure 2).

This research was centered on the design requirements for the mechanical performance of TT straps, with the specific aim of ensuring that, under centrifugal force F_c, their torsional stiffness remains below a designated threshold, while also allowing for the maximum pitch angle alteration of the rotor blades. The mechanical performance of these straps is critically influenced by the parameters of the torsional deformation segment, which consists of multiple cuboids. A primary objective of this section is the development of a computational model to evaluate the torsional stiffness and stress distribution within these cuboids. The connection segment is responsible for bearing the loads generated by the torsional deformation segment, with its load-bearing capacity being one of the key parameters. However, other design parameters, such as the dimensions, have a relatively minor impact on the mechanical performance. Given the complexity of stresses and the diversity of configurations within the connecting segments, an accurate assessment of the load-bearing capacity using purely parametric methods presents challenges, necessitating targeted experimental research.

This section presents the detailed construction process of the rapid evaluation model for the mechanical performance of the torsional deformation segment of TT straps. Initially, in two coordinate systems, the displacement method is utilized to decompose the complex deformation of each rectangular section in the torsional deformation segment into a superposition of multiple simpler deformations: (1) free torsion; (2) warping-constrained torsion; (3) eccentric bending; and (4) additional deformation due to centrifugal forces. Subsequently, relationships between each simple deformation and the applied torque are established. Section 2.2 specifically focuses on the formulation process for the expression of additional torque due to eccentric bending in rectangles, taking into account the centrifugal force. Following this, by superimposing these expressions for simple deformations, an overall torque balance equation is derived. Finally, by solving this equation, a set of expressions is presented in Section 2.3, which intuitively demonstrates how the materials, structural parameters, and centrifugal force parameters influence the stiffness and stress distribution of TT straps.

Based on the derived expressions, this study enables the performance of the specific design parameters to be evaluated, leading to the identification of key parameters. In Section 3, analytical calculations regarding the design of critical parameters for TT straps are presented, enabling the relationship between the performance of TT straps and these parameters to be examined. The goal is to offer a more detailed theoretical foundation for the design of essential parameters of TT straps. The research approach adopted in this study is illustrated in Figure 3.

2.1. Coordinate Systems

The method is described within the following two coordinate systems:

The torsional center coordinate system: Its origin, denoted as O_t, is located at the starting end face of the torsional deformation segment. The x_t-axis coincides with the torsional center axis, and the z_t-axis is parallel to the axis of the bushing hole.

The centroid coordinate system of any cuboid: Its origin, O_ci, is at the starting end face of the torsional deformation segment, with its x_ci-axis aligning with the centroid axis of the cuboid. It is important to note that the centroid coordinate system can be obtained by translating the torsional center coordinate system (Figure 4).

2.2. Additional Torque Caused by Centrifugal Forces

This section provides a detailed analysis of the additional torque due to centrifugal forces under two states: free torsion and eccentrically constrained torsion. Here, the constraint refers to the restriction of warping and bending deformations at both ends of the torsional deformation segment, assuming that the connecting segments are rigid. The deformations under free torsion and constrained torsion are depicted in Figure 5. A segment of length dx on the torsional deformation segment was selected for in-depth analysis. To simplify the analysis, a small-angle assumption was employed. That is, sin(dθ) is approximately equal to dθ, where dθ represents the relative torsional deformation angle between two cross-sections of the infinitesimal element.

We analyzed the deviation angle between the centrifugal tensile stress σ_xFc and the coordinates (y, z) of a microelement, which possesses an area of dydz, within the torsional center coordinate system following torsional deformation. In the initial state, without torsional deformation, the microelement’s edges are aligned with the centrifugal force direction. However, when torsional deformation is introduced, shear-induced deformation prompts a deviation of the microelement’s edges from their original orientation, characterized by an angle of dθ. This phenomenon results in a relative displacement, denoted as dl₁, of the microelement’s opposing end surfaces in the y_t–z_t plane. Subsequently, the normal stress σ_xFc is bifurcated into two distinct components: one aligned with the deformation direction and the other, σ₁, aligned along dl₁’s direction (Figure 5a). The analysis proceeds to compute the torque M(σ₁) engendered by σ₁. Integrating this torque across the microelement’s entire cross-section enables the determination of the supplementary torque necessary to counteract the centrifugal force during torsional deformation.

Furthermore, under eccentrically constrained torsion conditions, a cuboid not only undergoes torsion around its centroid but also experiences bending and deflection deformations along its centroid axis. The exertion of centrifugal force notably modifies the cuboid’s bending stiffness and then increases the additional torsional stiffness.

2.3. Analytical Calculation Formulas

(1)

Torque expression

The first part of this section elucidates the torque calculation for a cuboid during torsional deformation. Neglecting the influence of body forces ensures that the total torque along the x_t-axis of the cuboid remains constant. The displacement method was employed to model the deformation distribution of the cuboid, dividing it into four parts: free torsion, warping-constrained deformation, eccentric bending deformation, and additional deformation due to centrifugal force. Given the deformation θ(L) at both ends of the cuboid around the x_t-axis, the following four torques were solved: the torque M_θ due to free torsion, the additional torque M_tφ caused by the torsional warping constraint, the additional torque M_tlz and M_tly resulting from eccentric bending, and the additional torque M_Fc generated by centrifugal force.

The free torsion torque M_θ of the cuboid was determined using a formula derived from fitting a table [12] based on different width-to-thickness ratios. The computation for M_θ is given below:

$${\mathrm{M}}_{\theta }=\theta \prime \left(x\right)\mathrm{G}{b}^4(\frac{a}{b}-0.63)/3$$

(1)

where x is the spatial coordinate along the x_t direction. $\theta \prime \left(x\right)$ denotes the derivative of $\theta \left(x\right)$ with respect to x, where $\theta \left(x\right)$ is the distribution of the torsional angle for the analyzed cuboid. G represents the shear modulus of the material, and $a$ and $b$ are the width and thickness of the cuboid, respectively.

The warping constraint torque M_tφ for a rectangular cross-section is an approximate solution obtained by neglecting the n > 1 terms of the warping function [12]. M_tφ can be calculated as follows:

$${\mathrm{M}}_{\mathrm{t}\phi }\approx -\left(1-e^{\left(1-\frac{a}{b}\right)}\right)\frac{\mathrm{E}{a}^3{b}^3}{{\left(12\right)}^2}\theta ‴\left(x\right)$$

(2)

where E denotes the tensile modulus in the fiber direction, and $\theta ‴\left(x\right)$ represents the third derivative of $\theta \left(x\right)$ with respect to x.

The additional torque resulting from eccentric bending and denoted by M_tlz can be expressed as follows:

$${\mathrm{M}}_{\mathrm{t}{l}_z}=-\mathrm{E}\frac{a^{3}b}{12}\theta ‴\left(x\right){l_z}^2$$

(3)

where $l_z$ represents the deviation of the centroid of the analyzed cuboid from the torsional center along the z_t-axis direction.

The additional torque resulting from eccentric bending and denoted by M_tly can be calculated as follows:

$${\mathrm{M}}_{\mathrm{t}{l}_y}=-\mathrm{E}\frac{b^{3}a}{12}\theta ‴\left(x\right){l_y}^2$$

(4)

where $l_y$ denotes the deviation of the centroid of the analyzed cuboid from the torsional center along the y_t-axis direction.

The formula of M_Fc is outlined below:

$${\mathrm{M}}_{\mathrm{F}\mathrm{c}}=\frac{{\mathrm{F}}_{\mathrm{c}}}{{\mathrm{A}}_{\mathrm{\Sigma }}}\left(l_z^2+\frac{b^2}{12}+l_y^2+\frac{a^2}{12}\right)ab\theta \prime \left(x\right)$$

(5)

where ${\mathrm{F}}_{\mathrm{c}}$ symbolizes the centrifugal force, while ${\mathrm{A}}_{\mathrm{\Sigma }}$ signifies the total cross-sectional area of the torsional deformation segment.

Through the superposition of five torque equations, the equilibrium expression for the total torque M_t is derived.

$${{\mathrm{M}}_{\mathrm{t}}=\mathrm{M}}_{\theta }+{\mathrm{M}}_{\mathrm{t}\phi }+{\mathrm{M}}_{\mathrm{t}{l}_z}+{\mathrm{M}}_{\mathrm{t}{l}_y}+{\mathrm{M}}_{\mathrm{F}\mathrm{c}}$$

(6)

The equation governing the total torque M_t is formulated as a second-order differential equation with constant coefficients with respect to $\theta \prime \left(x\right)$. By meticulously addressing the boundary conditions at both extremities of the torsional deformation segment, an analytical solution for $\theta \left(x\right)$ can be derived for any prescribed M_t. The general solution is as follows:

$$\theta \left(x\right)=\frac{{\mathrm{M}}_{\mathrm{t}}\left[-\frac{1}{\mathrm{K}}\sinh \left(\mathrm{K}x\right)+\frac{\cosh \left(\mathrm{K}\mathrm{L}\right)-1}{\mathrm{Ksinh}\left(\mathrm{K}\mathrm{L}\right)}\cosh \left(\mathrm{K}x\right)+x-\frac{\cosh \left(\mathrm{K}\mathrm{L}\right)-1}{\mathrm{Ksinh}\left(\mathrm{K}\mathrm{L}\right)}\right]}{\frac{\mathrm{G}{b}^4\left(\frac{a}{b}-0.63\right)}{3}+\frac{1}{{\mathrm{A}}_{\mathrm{\Sigma }}}{\mathrm{F}}_{\mathrm{c}}\left(l_z^2+\frac{b^2}{12}+l_y^2+\frac{a^2}{12}\right)ab}$$

(7)

where

$$\mathrm{K}=\sqrt{\frac{\mathrm{G}{b}^4(\frac{a}{b}-0.63)/3+\frac{1}{{\mathrm{A}}_{\mathrm{\Sigma }}}{\mathrm{F}}_{\mathrm{c}}\left(l_z^2+\frac{b^2}{12}+l_y^2+\frac{a^2}{12}\right)ab}{\left[\frac{1}{12}\left(l_z^{2}b{a}^3+l_y^{2}a{b}^3\right)+\left(1-e^{\left(1-\frac{a}{b}\right)}\right)\frac{a^3{b}^3}{{\left(12\right)}^2}\right]\mathrm{E}}}$$

where $\sinh \left(\mathrm{K}x\right)$ and $\cosh \left(\mathrm{K}x\right)$ represent the hyperbolic sine and hyperbolic cosine functions, respectively.

(2)

Calculation formulas for torsional stiffness

The second part of this section describes the calculation formulas for various torsional stiffnesses, which serve as part of the rapid evaluation method.

D_θ denotes the free torsional stiffness of the cross-section of the cuboid, and it can be calculated as follows:

$${\mathrm{D}}_{\theta }=\mathrm{G}{b}^4(\frac{a}{b}-0.63)/3$$

(8)

D_Fc refers to the additional torsional stiffness induced by the centrifugal force in the cross-section of the cuboid, and it can be calculated as follows:

$${\mathrm{D}}_{\mathrm{F}\mathrm{c}}=\frac{{\mathrm{F}}_{\mathrm{c}}}{{\mathrm{A}}_{\mathrm{\Sigma }}}\left(l_z^2+\frac{b^2}{12}+l_y^2+\frac{a^2}{12}\right)ab$$

(9)

DL_θ represents the overall free torsional stiffness of the analyzed cuboid. The expression proceeds as follows:

$${\mathrm{DL}}_{\theta }=\mathrm{G}{b}^4(\frac{a}{b}-0.63)/3\mathrm{L}$$

(10)

where L denotes the length of the torsional deformation segment.

D_LΣ denotes the overall torsional stiffness of the analyzed cuboid. The expression proceeds as follows:

$${\mathrm{D}}_{\mathrm{L}\mathrm{\Sigma }}=\frac{\frac{\mathrm{G}{b}^4\left(\frac{a}{b}-0.63\right)}{3}+\frac{1}{{\mathrm{A}}_{\mathrm{\Sigma }}}{\mathrm{F}}_{\mathrm{c}}\left(l_z^2+\frac{b^2}{12}+l_y^2+\frac{a^2}{12}\right)ab}{\left[-\frac{1}{\mathrm{K}}\sinh \left(\mathrm{K}\mathrm{L}\right)+\frac{\cosh \left(\mathrm{K}\mathrm{L}\right)-1}{\mathrm{Ksinh}\left(\mathrm{K}\mathrm{L}\right)}\cosh \left(\mathrm{K}\mathrm{L}\right)+\mathrm{L}-\frac{\cosh \left(\mathrm{K}\mathrm{L}\right)-1}{\mathrm{Ksinh}\left(\mathrm{K}\mathrm{L}\right)}\right]}$$

(11)

(3)

Stress and shear force calculation formulas.

The third part of this section presents the calculation formulas for determining the distribution of tensile stress ${\mathrm{\sigma }}_x(x,y,z)$, shear stresses ${\mathrm{\tau }}_{xy}(x,y,z)$ and ${\mathrm{\tau }}_{xz}(x,y,z)$, and shear force ${\mathrm{F}}_1$ at the end surface of the cuboid due to eccentric torsional bending. Additionally, it provides the formula for calculating the shear stress ${\mathrm{\tau }}_1$ induced by the shear force ${\mathrm{F}}_1$. These equations constitute an integral part of the rapid evaluation method.

The calculation formula for the normal stress ${\mathrm{\sigma }}_{x\mathrm{F}\mathrm{c}}$ induced by the centrifugal force is as follows:

$${\mathrm{\sigma }}_{x\mathrm{F}\mathrm{c}}=\frac{{\mathrm{F}}_{\mathrm{c}}}{{\mathrm{A}}_{\mathrm{\Sigma }}}$$

(12)

The formula for calculating the shear stress distribution is derived by omitting the terms with n > 1 from the warping function [12] when dealing with the torsion of a rectangular cross-sectioned bar.

$${\mathrm{\tau }}_{xy}(x,y,z)=-2\mathrm{G}\theta \prime \left(x\right)b\left[\frac{z}{b}-\frac{4}{{\pi }^2}\frac{\cosh \frac{\mathrm{\pi }}{b}(y-l_y)}{\cosh \left(\frac{\mathrm{\pi }a}{2b}\right)}\sin \frac{\mathrm{\pi }}{b}(z-l_z)-\frac{4}{9{\pi }^2}\frac{\cosh \frac{3\mathrm{\pi }}{b}(y-l_y)}{\cosh \left(\frac{3\mathrm{\pi }a}{2b}\right)}\sin \frac{3\mathrm{\pi }}{b}(z-l_z)\right]$$

(13)

$${\mathrm{\tau }}_{xz}(x,y,z)=-\frac{8\mathrm{G}\theta \prime \left(x\right)b}{{\pi }^2}\left[\frac{\sinh \frac{\mathrm{\pi }}{b}(y-l_y)}{\cosh \left(\frac{\mathrm{\pi }a}{2b}\right)}\cos \frac{\mathrm{\pi }}{b}(z-l_z)-\frac{1}{9}\frac{\sinh \frac{3\mathrm{\pi }}{b}(y-l_y)}{\cosh \left(\frac{3\mathrm{\pi }a}{2b}\right)}\cos \frac{3\mathrm{\pi }}{b}(z-l_z)\right]$$

(14)

The tensile stress distribution ${\mathrm{\sigma }}_x(x,y,z)$ can be calculated as follows:

$${\mathrm{\sigma }}_x(x,y,z)\approx \mathrm{E}\theta ″\left(x\right)\left[-(z-l_z)(y-l_y)+\frac{8b^2}{{\pi }^3}(\frac{\sinh \frac{\mathrm{\pi }}{b}(y-l_y)}{\cosh \left(\frac{\mathrm{\pi }a}{2b}\right)}\sin \frac{\mathrm{\pi }}{b}(z-l_z)-\frac{1}{9}\frac{\sinh \frac{3\mathrm{\pi }}{b}(y-l_y)}{\cosh \left(\frac{3\mathrm{\pi }a}{2b}\right)}\sin \frac{3\mathrm{\pi }}{b}(z-l_z))+l_y(z-l_z)-l_z(y-l_y)\right]$$

(15)

The shear force ${\mathrm{F}}_1$ can be calculated as follows:

$${\mathrm{F}}_1=\frac{{\mathrm{D}}_{\mathrm{L}\mathrm{\Sigma }}\theta \left(L\right)-{\mathrm{DL}}_{\theta }}{2\sqrt{l_y^2+l_z^2}}$$

(16)

where θ(L) represents the relative torsional angle at both ends of the torsional deformation segment.

The shear stress ${\mathrm{\tau }}_1$ can be calculated as follows:

$${\mathrm{\tau }}_1=\frac{{\mathrm{F}}_1}{ab}$$

(17)

The rapid evaluation method for assessing the performance of TT straps in this article comprises the three aforementioned sets of calculation formulas. These equations form the foundation for the subsequent analytical investigation of key parameter design aspects.

3. Analytical Study of the Key Performance

This section presents an analytical study of the key design parameters of TT straps based on the rapid performance evaluation method described in Section 2.3 and the structural parameters of the TT strap presented in [9]. The structural parameters of the TT strap in [9] are as follows: three-layer strap elements, 16.2 mm wide, 8.8 mm thick, with 276 mm long torsional deformation segments made of 3232A/S4C10-800 glass-fiber-reinforced unidirectional resin composite. This material has a tensile modulus E of 50 GPa and a shear modulus G of 4.9 GPa.

Central to the design requirements of the TT straps is their mechanical performance. Taking the TT straps of tail rotors, tail propellers, and tilt-rotor aircraft as examples, this section analyzes the key design parameters and their related mechanical performance design requirements.

(1)

Under prescribed centrifugal forces ${\mathrm{F}}_{\mathrm{c}}$, the torsional stiffness ${\sum }_{i=1}^{\mathrm{n}}{\mathrm{D}}_{\mathrm{L}\mathrm{\Sigma }i}$ should remain within predefined limits ${\mathrm{D}}_{\mathrm{limit}}$.

(2)

The torsional deformation must prevent structural failure at the maximum torsional angle. It should keep the maximal stress ${\mathrm{\sigma }}_{x\mathrm{F}\mathrm{c}}+\mathrm{Max}\left[{\mathrm{\sigma }}_x\right(x,y,z\left)\right]$ below the tensile stress threshold ${\mathrm{\sigma }}_{\mathrm{Max}}$ of the material under the specified centrifugal force and maximum torsion. Additionally, the shear stress ${\mathrm{\tau }}_{xy}(x,y,z)$ and ${\mathrm{\tau }}_{xz}(x,y,z)$ should stay within the shear strength limit ${\mathrm{\tau }}_{\mathrm{M}\mathrm{a}\mathrm{x}}$ of the material. The shear force ${\mathrm{F}}_1$ should not exceed the structural load-bearing capacity of the connecting segments.

(3)

The dimensional parameters should comply with the specified spatial constraints.

The parameters ${\mathrm{\sigma }}_{x\mathrm{F}\mathrm{c}}$, $\mathrm{Max}\left[{\mathrm{\sigma }}_x\right(x,y,z\left)\right]$, ${\tau }_{xy}(x,y,z)$, ${\tau }_{xz}(x,y,z)$, ${\mathrm{D}}_{\mathrm{L}\mathrm{\Sigma }i}$, and ${\mathrm{F}}_1$, pivotal in these design requirements, can be efficiently calculated using Formulas (12), (15), (13), (14), (11), and (16), respectively. These calculations facilitate the formulation of tailored adjustment plans to meet the specific design criteria.

Based on the parameters outlined in [9], this section presents an analytical study of the key parameter design of TT straps, utilizing relevant equations:

(1)

Equation (12) reveals the key design parameters for tensile stress ${\mathrm{\sigma }}_{x\mathrm{F}\mathrm{c}}$. When the tensile stress ${\mathrm{\sigma }}_{x\mathrm{F}\mathrm{c}}$ generated by centrifugal force becomes excessive, it can be mitigated by enhancing the cross-sectional area of the torsional deformation segment. Additionally, materials with a higher tensile stress limit can be employed to augment the load-bearing capacity.

(2)

Equation (15) reveals that the key design parameters affecting the maximum additional tensile stress $\mathrm{Max}\left[{\mathrm{\sigma }}_x\right(x,y,z\left)\right]$ due to torsion include E, $l_z$, $l_y$, $a$, $b$, $\theta ″\left(x\right)$, and L. To reduce excessive stress induced by torsion, the following measures can be adopted:

Firstly, materials with a lower modulus of elasticity in the direction of tension can be selected.

Secondly, the number of cuboids can be increased to reduce the width $a$ and thickness $b$. $a \mathrm{and} b$ are also the maximum values of 2$(z-l_z\mathrm{i})$ and 2$(y-l_y)$, respectively. Figure 6a illustrates the variations in ${\mathrm{\sigma }}_x\left(x,y,z\right)$ with $a \mathrm{and} b$, where the total cross-sectional area ${\mathrm{A}}_{\mathrm{\Sigma }}$ of the torsional deformation segment is kept constant. This approach is exemplified in the TT straps by Lord Corporation and the use of metal wire winding in the main rotor TT straps of the Mi-26, resulting in the torsional deformation segment consisting of numerous blocks with a very small width $a$ and thickness $b$.

Thirdly, all cuboids in the torsional deformation segment can be concentrated towards the center of torsion, reducing the distance from the centroid ($l_z$, $l_y$) of all cuboids to the center of torsion. Figure 6b illustrates the variation in ${\mathrm{\sigma }}_x(x,y,z)$ with changes in $l_z$ and $l_y$. This approach is exemplified in the carbon fiber torsion–tension straps of the H145 and the main rotor TT straps of the Mi-26.

Fourthly, the length of the torsional deformation segment (L) can be increased to reduce the maximum value of $\theta ″\left(x\right)$, as depicted in Figure 6c.

Lastly, a gradient reinforcement approach can be employed to alter the distribution of torsional $\theta ″\left(x\right)$ rigidity, reducing the maximum value at both ends of the torsional deformation segment. Figure 6d demonstrates the distribution pattern of $\theta ″\left(x\right)$. This strategy is implemented in the H145, where a gradually thickening transition segment is introduced between the torsional deformation and the connecting segments.

(3)

Equations (13) and (14) elucidate the essential design parameters for shear stress ${\tau }_{xy}(x,y,z)$ and ${\tau }_{xz}(x,y,z)$, represented as G, a, b, and L. These formulas are straightforward and do not necessitate illustrative analytical calculations demonstrations or charts. In instances where the additional shear stress due to torsion is significant, several strategies can be employed to mitigate this stress:

Firstly, the selection of materials with a lower shear modulus $\mathrm{G}$, such as rubber-based composite materials, can effectively decrease the torsional additional shear stress.

Secondly, increasing the number of segments in the design can effectively reduce the shear stress values for each segment. This method is exemplified by the tail rotor TT straps in the H145.

Another effective strategy is to increase the length of the torsional deformation segment L, which contributes to a reduction in the torsional rate $\theta \prime \left(x\right)$.

• Equation (11) identifies the key design parameters influencing the overall torsional stiffness ${\sum }_{i=1}^{\mathrm{n}}{\mathrm{D}}_{\mathrm{L}\mathrm{\Sigma }i}$, including E, G, $l_z$, $l_y$, $a$, $b$, L, ${\mathrm{A}}_{\mathrm{\Sigma }}$, and n. To address instances of excessive overall torsional stiffness, the following strategies can be implemented:

Firstly, opting for materials with a lower shear modulus G can effectively decrease the free torsional stiffness.

Secondly, employing materials with a lower tensile modulus E can aid in minimizing the torsional bending stiffness.

Thirdly, increasing the number of cuboids can lead to a reduction in both the width and thickness of each cuboid, thereby diminishing the free torsional stiffness and torsional bending stiffness. Figure 7a depicts the variations in torsional stiffness with changes in the width and thickness.

Fourthly, designing the cross-section to converge towards the torsional center can decrease both the moment of inertia and the radius of gyration, subsequently reducing both the torsional bending stiffness and the centrifugal additional stiffness. Figure 7b shows the variation in torsional stiffness ${\sum }_{i=1}^{\mathrm{n}}{\mathrm{D}}_{\mathrm{L}\mathrm{\Sigma }i}$ with $l_z$ and $l_y$.

Fifthly, elongating the torsional deformation section (L) serves to minimize the torsional angle per unit length, thereby reducing the overall torsional stiffness. Figure 7c demonstrates how torsional stiffness ${\sum }_{i=1}^{\mathrm{n}}{\mathrm{D}}_{\mathrm{L}\mathrm{\Sigma }i}$ varies with changes in L.

(5)

Equation (16) delineates the critical design parameters for the shear force ${\mathrm{F}}_1$ transmitted to the connection segment, encompassing E, G, $l_z$, $l_y$, $a$, $b$, L, ${\mathrm{A}}_{\mathrm{\Sigma }}$, n, and the structure of the connecting segment. To mitigate large shear forces at both ends of the torsional deformation segment, several strategies can be employed:

Firstly, the overall torsional stiffness can be reduced as described previously.

Secondly, the load-bearing capacity of the connecting segment structure can be enhanced by selecting materials with superior shear resistance.

Thirdly, modifying the connecting segment structure can improve its load-bearing ability.

In summary, the tension–torsion bar’s key design parameters include E, G, $l_z$, $l_y$, $a$, $b$, L, ${\mathrm{A}}_{\mathrm{\Sigma }}$, ${\mathrm{\sigma }}_{\mathrm{Max}}$, ${\mathrm{\tau }}_{\mathrm{Max}}$, n, and the structure of the connecting segment. Both the length of the torsional deformation segment (L) and the material properties are of paramount importance. Accordingly, the authors of this study embarked on experimental research to examine the impact of varying lengths of the deformation segment (L) and material properties. While each key performance metric can be quantitatively assessed using the formulas outlined in Section 2.3, quantitatively describing the load-bearing capacity of the connecting segment structure remains challenging. As a result, this study incorporates experimental research to evaluate the load-bearing capacity of different connecting segment structures.

4. Experimental Design and Procedure

The experimental research presented in this work includes the following components:

(1)

Stiffness and stress tests on TT straps were conducted to validate the accuracy of the rapid performance evaluation method. Specifically, strain tests were performed on the TT strap in Case 2.

(2)

Aiming to examine the effect of the critical parameter, the length of the torsional deformation segment L, TT straps with varying lengths of this segment were designed and tested for stiffness comparison, covering Cases 1, 2, and 3. Additionally, TT straps made from two different materials were compared to assess the influence of material on the overall torsional stiffness, involving Cases 3 and 4. Lastly, because it is challenging to parametrically quantify the load-bearing capacity of the connecting segment structure, the experimental analysis of the load-bearing capacities of various connecting segment structures was explored. The connecting segments in Cases 1, 2, and 3 were sequentially reinforced to enhance the resistance to shear forces ${\mathrm{F}}_1$. The framework of this chapter is illustrated in Figure 8.

4.1. The Design Process of Key Parameters for the Test Specimen

An experimental design was implemented based on a TT strap configured to undergo a 35° twist under a centrifugal force of 400,000 N. In this design, the length of the TT strap at the torsional deformation segment is limited to 300 mm, with a maximum height of 35 mm. The overall torsional stiffness of the TT strap is kept within a defined threshold of 35 Nm/°.

(1)

The design inputs are specified as:

The centrifugal force ${\mathrm{F}}_{\mathrm{c}}$ is 400,000 N;

The maximum torsional angle of the blades ${\theta L}_{max}$ is 35°.

(2)

The design requirements are mathematically expressed as follows:

$${\mathrm{\sigma }}_{x\mathrm{F}\mathrm{c}}+\mathrm{Max}\left[{\mathrm{\sigma }}_x\right(x,y,z\left)\right]\le {\mathrm{\sigma }}_{\mathrm{Max}}$$

(18)

$${{\mathrm{\tau }}_{xy}(x,y,z)\le \mathrm{\tau }}_{\mathrm{Max}},{{\mathrm{\tau }}_{xz}(x,y,z)\le \mathrm{\tau }}_{\mathrm{Max}}$$

(19)

$$\sum _{i=1}^{\mathrm{n}}{\mathrm{D}}_{\mathrm{L}\mathrm{\Sigma }i}\le 35 \mathrm{N}\mathrm{m}/°$$

(20)

$${\mathrm{F}}_1<\mathrm{the}\mathrm{load-bearing}\mathrm{capacity}\mathrm{of}\mathrm{the}\mathrm{connecting}\mathrm{segment}$$

(21)

$$\mathrm{L} < 300 \mathrm{mm}, \mathrm{n}b\le 35 \mathrm{mm}$$

(22)

(3)

The initial structural input parameters required for the test specimen are as follows:

E: Material tensile modulus;

G: Material shear modulus;

$l_z$: Distance from the centroid of the cuboid to the torsion center along the z_t-direction;

$l_y$: Distance from the centroid of the cuboid to the torsion center along the y_t-direction;

$a$: Width of the cross-section of the cuboids;

$b$: Thickness of the cross-section of the cuboids;

L: Length of the torsional deformation segment;

${\mathrm{A}}_{\mathrm{\Sigma }}$: Total cross-sectional area of the torsional deformation segment;

${\mathrm{\sigma }}_{\mathrm{Max}}$: Material tensile strength limit;

${\mathrm{\tau }}_{\mathrm{Max}}$: Material shear strength limit;

n: Number of subdivisions in the cross-section of the torsional deformation segment.

(4)

Initial structural parameter determination:

The internal diameter of the bushing was determined to be 28 mm, with a wall thickness of 2 mm, based on centrifugal force and the metal’s shear resistance. Materials with a high tensile strain limit, such as glass-fiber-reinforced composite materials and Kevlar-reinforced rubber composite materials, were selected based on Equation (13). For Cases 1 to 3, the TT straps were made out of 3232A/S4C10-800 glass-fiber-reinforced resin-based composite material without a weft band, featuring a tensile modulus E of 50 GPa, a shear modulus G of 4.9 GPa, a tensile limit ${\mathrm{\sigma }}_{\mathrm{Max}}$ of 1500 MPa, and a shear strength limit ${\mathrm{\tau }}_{\mathrm{Max}}$ of 90 MPa. Case 4 used Kevlar-fiber-reinforced rubber composite material with a modulus E of 70 GPa and a shear modulus of 0.05 GPa.

Considering a safety margin of 1× as per Equation (12), the typical sectional area ${\mathrm{A}}_{\mathrm{\Sigma }}$ was ensured to be no less than 533 mm², with a preliminary set value of 600 mm. Given the outer diameter of the bushing and the height constraints of the TT strap, the initial width $a$ of the cuboids was set to 10 mm. The number of subdivisions in the typical section’s cross-section was initially set to 2, and the thickness $b$ of cuboids was 30 mm. Consequently, the distances from the centroid of the cuboid to the torsion center $l_z$ and $l_y$ were preliminarily determined to be 0 and 25 mm, respectively. The length of the TT strap’s typical segment L was preliminarily set to 300 mm, considering the length constraints, the dimensions of the bushing, and the width of the strap element.

Using these preliminary parameters and following the key performance design method outlined in Section 3, the key parameters were adjusted to meet design requirements, excluding the load-bearing capacity of the connecting segment, which is typically assessed through experimentation due to the complexity and diversity of stresses and configurations in the connecting segment.

4.2. Design Results for the Test Specimens

During the experimental process, different configurations of the length of the torsional deformation segment L, different materials, and different connecting segment structures were planned on four test specimens to evaluate their influence on the key performances.

(1)

Design results of the torsional deformation segment

The parameter design results of the torsional deformation segment of the four schemes are shown in

Table 1. Design results of the torsional deformation segment of Cases 1 to 4.

Name	L (mm)	Materials	Layers of Strap Elements	$\mathit{b}\left(\mathbf{mm}\right)$	$\mathit{a}$ (mm)	${\mathit{l}}_{\mathit{y}}$$\left(\mathbf{mm}\right)$	Lbh (mm)
Case 1	296	3232A/S4C10-800	3	8.8	16.2	27.1	350
Case 2	276
Case 3	256
Case 4	256	Kevlar-reinforced rubber composite material	1	30

.

Here, L_bh is the distance between two bushing holes.

The calculation results for the four schemes are presented in

Table 2. Calculation results of specimens subjected to a 400,000 N centrifugal force and a torsional angle of 35°.

Name	$\mathrm{Max}\left[{\mathbf{\sigma }}_{\mathit{x}}\right(\mathit{x},\mathit{y},\mathit{z}\left)\right]$/MPa	$\mathrm{Max}\left[{\mathbf{\tau }}_{\mathit{x}\mathit{y}}\right(\mathit{x},\mathit{y},\mathit{z})$$,{\mathbf{\tau }}_{\mathit{x}\mathit{z}}(\mathit{x},\mathit{y},\mathit{z})$]/MPa	${\mathbf{F}}_1$/N	${\sum }_{\mathit{i}=1}^{\mathbf{n}}{\mathbf{D}}_{\mathbf{L}\mathbf{\Sigma }\mathit{i}}$/(Nm/deg)	${\mathbf{\sigma }}_{\mathit{x}\mathbf{F}\mathbf{c}}$/MPa
Case 1	952	78	2.7 × 105	27	467
Case 2	1034	84	2.9 × 105	30	467
Case 3	1131	90	3.2 × 105	33	467
Case 4	Approach zero	Approach zero	2.1 × 105	21.5	411

. These results indicate that all four schemes generally meet the design requirements. However, it is noted that the tensile stress in Case 3 slightly exceeded the material’s tensile strength limit.

(2)

Design of the connecting segment

During the experimental process, different structures of the connecting segment were planned on Cases 1 to 3 to evaluate their capacity to withstand shear forces ${\mathrm{F}}_1$ induced by eccentric torsional bending. Specifically, this involved the following:

(1)

The load-bearing capacity was enhanced in Case 2 compared to Case 1 by increasing the length of the glass fabric layers in the connection segment by 10 mm and adding two additional layers.

(2)

Compared to Case 2, the length of the glass fabric layers was increased by an additional 10 mm, and the number of layers was increased by 12. Furthermore, an I-shaped bushing was utilized in Case 3, which converts part of the shear force in the connection segment into compressive stress, thereby further enhancing its load-bearing capacity.

The key detailed structures of the connection segment of the three schemes are presented in

Table 3. The key detailed structures of the four schemes.

Name	Design or Physical Features	Bushing Type	Fabric Layers	${\mathbf{D}}_{\mathbf{ib}} \left(\mathbf{mm}\right)$	${\mathbf{D}}_{\mathbf{ob}} \left(\mathbf{mm}\right)$
Case 1		Straight bushing	Length of 27 mm 4 layers	28	38
Case 2		Straight bushing	Length of 37 mm 6 layers
Case 3		I-shaped bushing	Length of 47 mm 18 layers

. Here, D_ib is the internal diameter of the bushing, and D_ob is the external diameter of the bushing.

4.3. Experimental Procedure and Equipment

The clamping method for the test specimens is as follows:

(1)

One connecting segment was fixed to the load-bearing wall.

(2)

The other connecting segment was connected to the centrifugal force and torque-loading end.

The experimental setup is illustrated in Figure 9. During the experiment, an angle measurement sensor and a torque sensor were both installed at the loading end. The loading system utilized the MTS Flextest 100 coordinated load control system, which is capable of outputting both the torque and torsional angle.

Eight tensile test strain sensors (labeled S01–S08) were arranged on the TT strap, as shown in Figure 10.

The tests for stiffness and torsional capacity were conducted separately. First, the stiffness tests were performed for Cases 1 to 4. After the stiffness tests were complete, the torsional capacity tests were carried out for Cases 1 to 3.

The stiffness test was conducted as follows:

(1)

Initially, torsional displacement was applied in the absence of centrifugal force, commencing from 0° and incrementing in one direction by 1° up to 12°. Subsequently, the displacement was reversed, decreasing by 1° back to 0°.

(2)

The centrifugal force was applied, starting from 0 and increasing by increments of 10,000 N up to a maximum of 170,000 N. At this centrifugal force, torsional displacement was again applied as in Step 1, followed by unloading.

(3)

The final step involved progressively increasing the centrifugal force from 0 in 10,000 N increments until reaching up to 270,000 N. Under this force, torsional displacement was applied as per Step 1 and then unloaded.

Considering the potential impact of the loading speed and frequency on the occurrence of jumping resonance in experimental testing, as noted in [13], in this experiment, we adopted a slow loading approach. Data collection was initiated only after ensuring that the measurement points required for data acquisition remained stable for a sufficient period. Each of these steps was replicated three times. The choice of the maximum angle in stiffness testing aimed to mitigate the influence of the installation gaps and to avert potential damage to the TT straps during testing.

The torsional capability testing comprised the following steps:

(1)

The centrifugal force was incrementally increased from 0 by 10,000 N intervals until it reached up to 400,000 N, and this load was sustained for 3 s.

(2)

With the centrifugal force constant, torsional angular displacement was then applied, escalating in 1° increments until either specimen failure or a torsional angle of 50° was achieved.

(3)

In the event of no failure in the second step, the torsional angle was maintained at 50°, and the centrifugal force was further increased in 10,000 N increments until specimen failure occurred.

5. Experimental Results and Analysis

5.1. Verification of the Rapid Evaluation Method

This section presents the data analysis results from the stiffness testing experiments. Figure 11 depicts the overall torsional stiffness with the torsional angle for the TT strap in Case 2. Figure 11a shows the torsional moment M_t measured in the loading system under no centrifugal force condition, and Figure 11b illustrates these parameters under a centrifugal force of 170,000 N.

Figure 12 demonstrates the variations in the test results of the overall torsional stiffness of Case 2 with centrifugal force and compares them with the calculation results from the rapid evaluation method.

To minimize the impacts of connection gaps and large torsion nonlinear effects, the overall torsional stiffness of the specimen was calculated by dividing the torsional moment measured at a 12° torsional deformation by the torsional angle.

The experimental results indicate that the torsional moment of the TT strap varies approximately linearly with the torsional angle, and the overall torsional stiffness shows an approximately linear increase with the rise in centrifugal force. There is good consistency between the overall torsional stiffness and the calculation results.

Figure 13 shows the variations in strain for the strain sensors S01–S06 and S08 on the TT strap under 0 N and 170,000 N centrifugal forces, respectively. The data from the S07 are anomalous and are not presented. The figures suggest that the relationship between the strain and torsional angle is essentially linear.

Figure 14 reveals the relationship between the strain values measured at each test point and the calculation results obtained using the rapid evaluation method described in Section 2. It can be observed that the trends in the data from the test points are consistent with the analytical calculations. The congruence between the test points and calculated values ranges between 10% and 30%, with somewhat dispersed results. This dispersion could be attributed to the significant stress variations at the measurement points. Considering the tolerance in the placement of the sensors, the tolerance range for the strain sensor placement in the y_t-direction was 3 mm. Within this tolerance range, the analytical calculations predicted strains at the positions of S01, S04, S05, and S06 to be between 1000 με and 1900 με, as shown in Figure 14a,b. The experimental results are distributed between 1000 με and 1800 με, indicating a relatively high accuracy in the strain predictions made by the rapid evaluation method.

5.2. Experimental Results for the Influence of L

This section presents the variations in the overall torsional stiffness of the TT strap with the length L of the torsional deformation segment, along with a comparison with the analytical calculation results obtained using the rapid evaluation method:

Under both 0 N and 170,000 N centrifugal force conditions, the overall torsional stiffness of the TT strap demonstrated an approximately linear change with a reduction in the length of the typical torsional segment. Notably, a shorter length of the torsional typical segment resulted in the TT strap having greater overall torsional stiffness. The computational results derived from the rapid evaluation method exhibit good consistency with the experimental data, as illustrated in Figure 15.

Figure 16 presents the computational results of the torsional deformation distribution in the torsional deformation segment under the same torque but varying centrifugal forces. The presence of centrifugal force increased the torsional stiffness of the torsional deformation segment, altering its torsional behavior.

5.3. Test Results for the Impact of Different Materials

Due to the relatively low torsional stiffness without centrifugal force in Case 4 and the limited linearity between the torque and torsional angular displacement under the current testing equipment’s precision, it was not possible to obtain definitive results. Thus, the test results are presented within a range smaller than 1.

Table 4. Computational and test results of torsional stiffness for Cases 3 and 4.

Name		${\sum }_{\mathit{i}=1}^{\mathbf{n}}{\mathbf{D}}_{\mathbf{L}\mathbf{\Sigma }\mathit{i}}$ under Fc = 0 N	${\sum }_{\mathit{i}=1}^{\mathbf{n}}{\mathbf{D}}_{\mathbf{L}\mathbf{\Sigma }\mathit{i}}$ under Fc = 170,000 N
	Computational result	8.4 Nm/°	19 Nm/°
Case 3	Test result	8.55 Nm/°	19.02 Nm/°
	Deviation	1.8%	0.1%
	Computational result	<1 Nm/°	9 Nm/°
Case 4	Test result	0.5 Nm/°	9.67 Nm/°
	Deviation	/	7.4%

displays the overall torsional stiffness test results and the analytical calculations for Cases 3 and 4:

The comparative experimental results demonstrate that, in the stiffness tests for Cases 3 and 4, a reduction in the material’s shear modulus led to a decrease in the overall torsional stiffness under 0 N centrifugal force. However, the change in the material had a negligible impact on the increase in the torsional stiffness induced by centrifugal force. The computational results obtained through the rapid evaluation method show good consistency with the experimental data, with deviations within 10%.

5.4. Load-Bearing Capacity Tests of Different Connecting Structures

The results of the torsional capability tests are as follows:

(1)

Under a centrifugal force of 400,000 N, the specimen in Case 1 fractured at a torsional angle of 21°.

(2)

Under the same centrifugal force, the specimen in Case 2 fractured at 30°.

(3)

When the centrifugal force was increased to 450,000 N, the specimen in Case 3 exhibited bending failure at a torsional angle of 50°.

As depicted in Figure 17, the failure modes of the TT straps are presented. Specifically, Figure 17a provides a detailed description of Case 1. Figure 17b,c display the overall condition and detailed view of the failure locations for Cases 2 and 3, respectively, post-testing. The specific details are as follows:

Figure 17a presents the failure scenario of Case 1: Initially, a longitudinal fracture occurred, as shown in the left image, followed by the transverse fracture depicted in the right image, with the damage concentrated on one side. The longitudinal opening originated from torsional shear fracture, while the transverse fracture was a result of tensile failure. The undamaged sides also exhibited multiple cracks along the fiber direction. The cause of the longitudinal fracture is the insufficient length and quantity of glass fabric layers in the two connecting segments, leading to a weaker resistance to the shear force F₁. The mechanism of this failure is shown in Figure 18a, where the boxed area indicates the surface where the shear force F₁ and a portion of the centrifugal force F_c were transferred to the bushing.

Figure 17b illustrates the failure of Case 2, with the damage location being similar to that in Case 1. However, there are more evident fiber-direction cracks and fiber separation near the fracture. Compared to Case 1, Case 2 could withstand larger torsional angles under the same centrifugal force, attributed to the increased quantity and length of glass fabric layers in Case 2. Thus, the connecting segment in Case 2 had a stronger capability to withstand the shear force F₁, resulting in a better torsional deformation capacity. However, at larger angles, increased normal stress caused some fibers to break.

As shown in Figure 17c, Case 3 did not crack but bent at the transition area between the typical and connecting segments. Compared to Case 2, Case 3 could withstand larger torsional angles under greater centrifugal forces due to two reinforcement measures in the connecting segment: one was the use of more and longer glass fabric layers, and the other was the replacement of a straight bushing with an I-shaped bushing. Therefore, as shown in Figure 18b, when the torsional angle was no greater than 30°, the F₁ that was transferred to the stress concentration area around the hole was converted into compressive stress. Compared to withstanding shear stress, the wound beams exhibited better performance under compressive stress.

The experimental results comprehensively validate the accuracy of the rapid evaluation method proposed in this study in terms of stiffness and stress, confirming its effectiveness in capturing key parameters. Furthermore, the potential application of this method in engineering practice has been further affirmed. Additionally, this method is significant for shortening the design cycle and reducing costs, promising to become a powerful tool in the field of structural analysis and design.

6. Conclusions

This study carried out an analytical and experimental investigation into the key performance design of TT straps. The initial phase involved deriving a general solution for the torsional response of the TT strap under specified torque, leading to the development of calculation formulas that clearly link key parameters with performance. Consequently, a rapid evaluation method for the performance of the torsional deformation segment was established. Further, this study provides an in-depth analysis of the crucial design parameters for the TT strap, coupled with a practical case study showcasing the method’s application in design. To assess the influence of variables such as the length, material, and connecting segment structure on the TT strap’s performance, four torsion bars were meticulously designed and rigorously tested. The conclusions drawn are as follows:

The experimental findings robustly corroborate the precision of the rapid assessment method introduced in this research, particularly concerning stiffness and stress, thereby validating its efficacy in capturing key parameters.

An experimental investigation into the load-bearing capacities of the connecting segments was conducted. This study elucidated the failure mechanisms in three distinct connecting segment designs of TT straps and their correlations with the shear force F₁ as assessed by the rapid evaluation method. This method significantly contributes to enhancing the optimization of connecting segment configurations.

The outcomes of this research provide a practical, rapid evaluation method for key performance evaluation and valuable experimental insights for the expedited design of TT straps in engineering applications. This approach not only fosters enhanced design efficiency and cost-effectiveness but also offers a pertinent reference for the performance evaluation and optimization of various structural components.