Optimization Design of Magnetically Suspended Control and Sensitive Gyroscope Deflection Channel Controller Based on Neural Network Inverse System
Abstract
:1. Introduction
2. MSCSG System Principles and Modeling
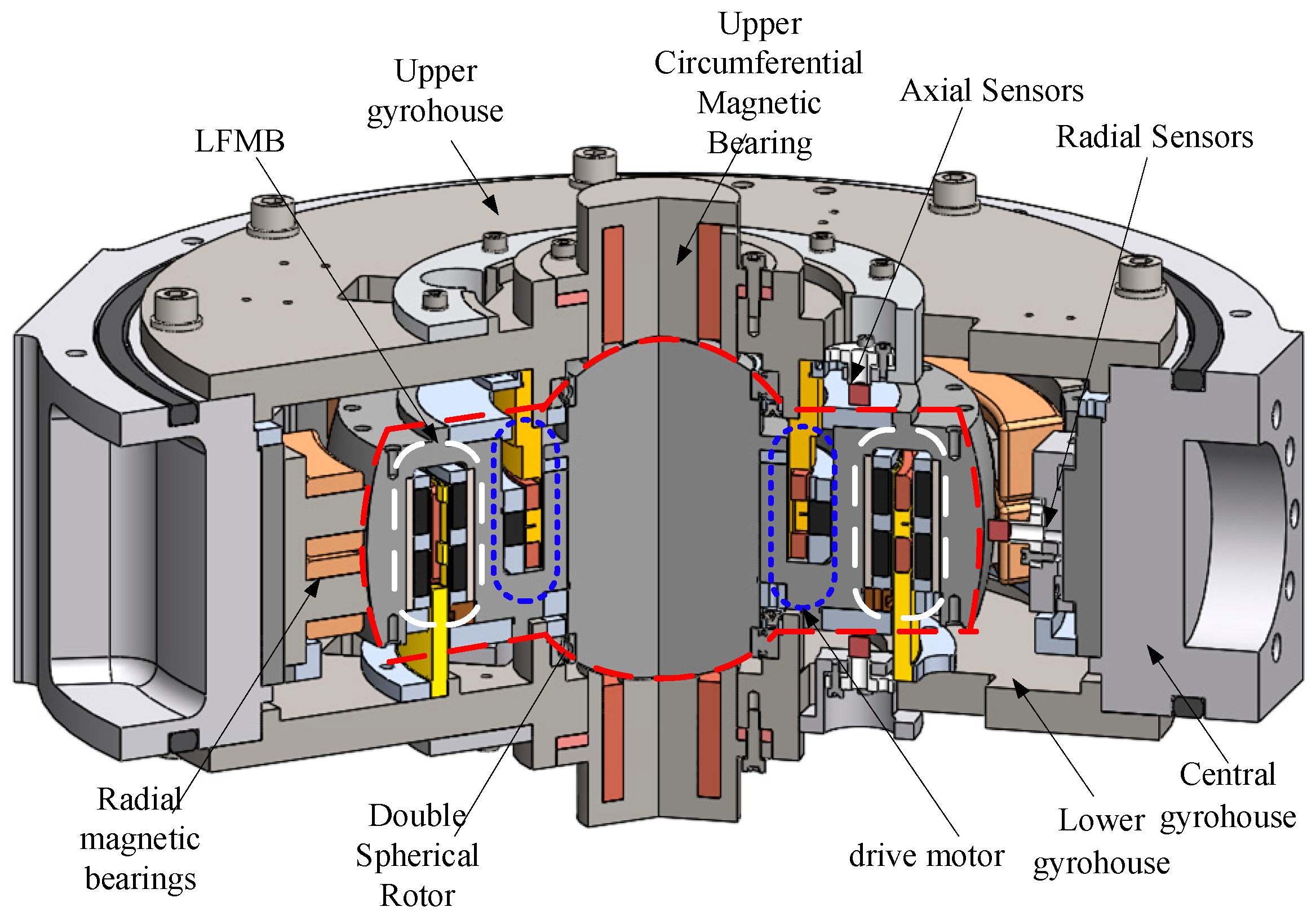
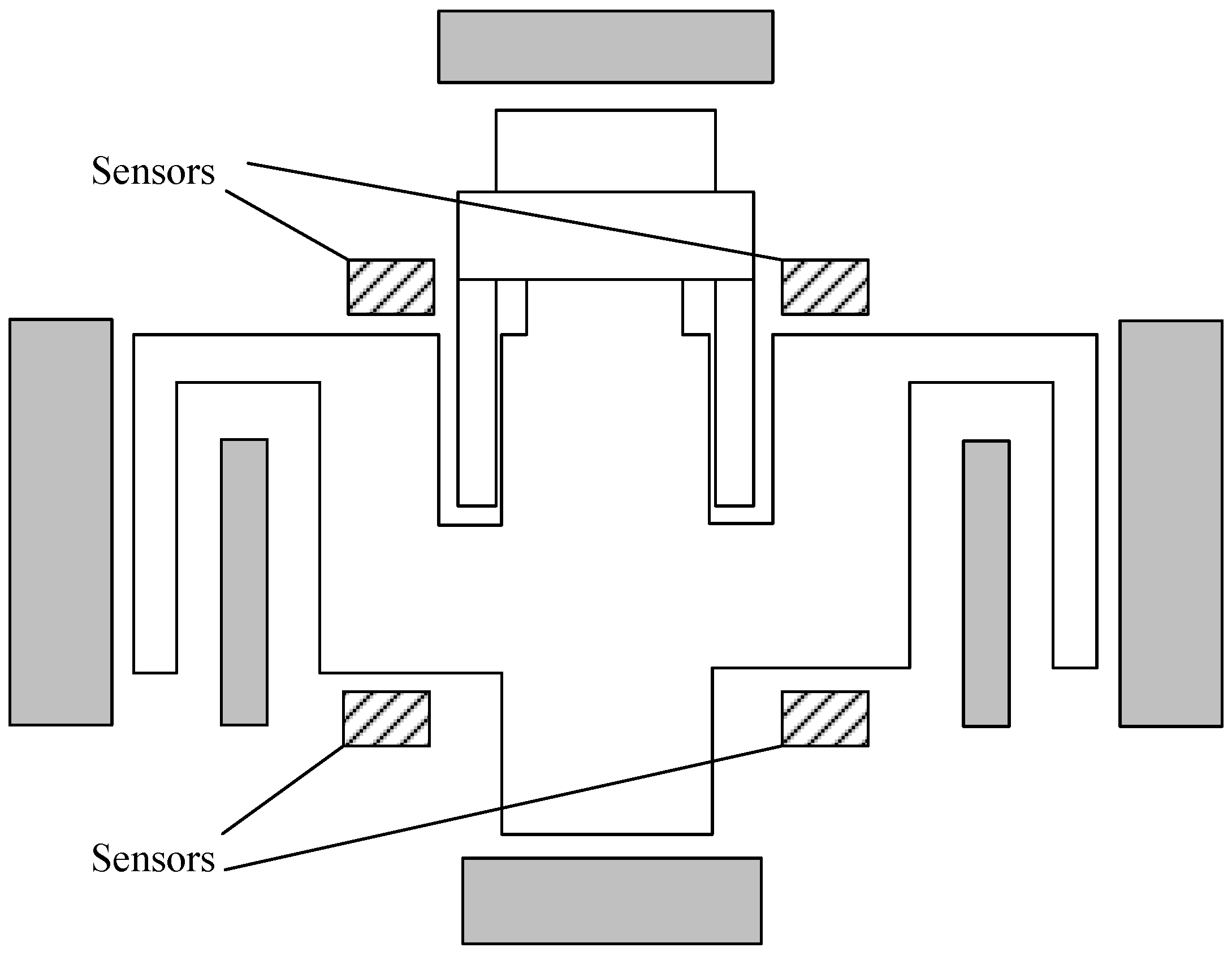
2.1. MSCSG Structure and Principle
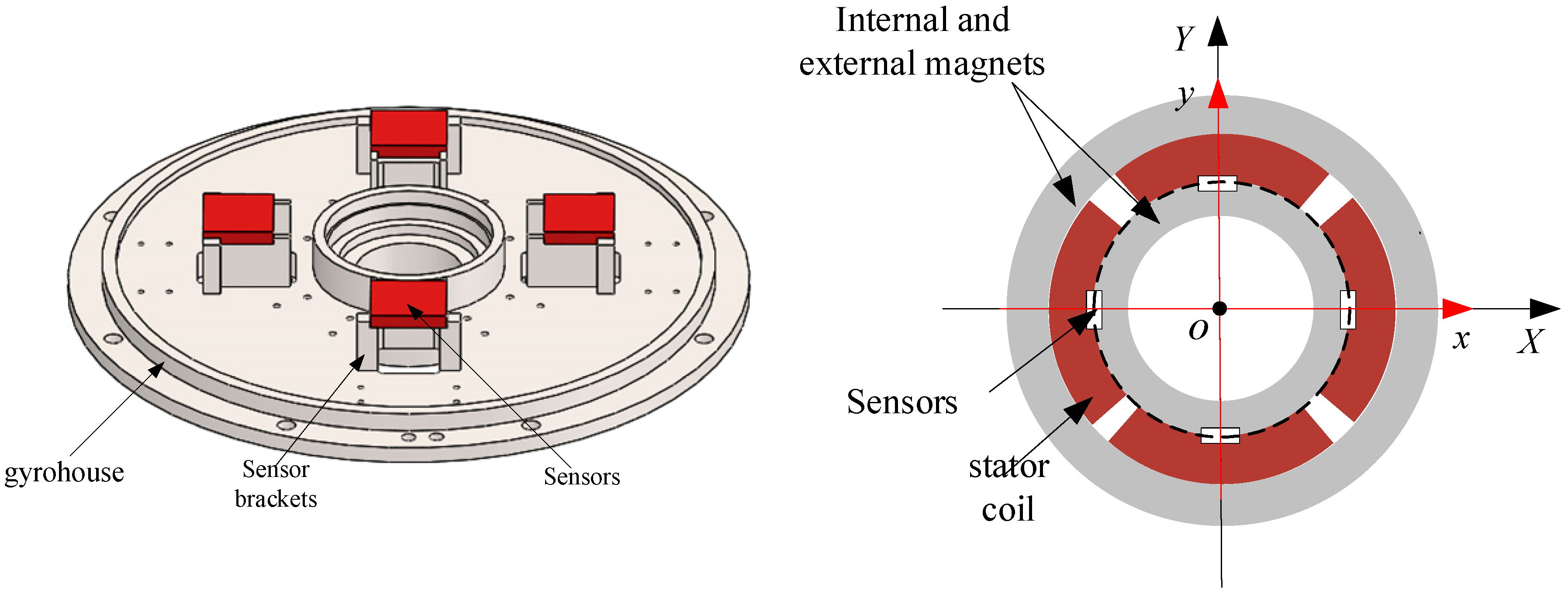
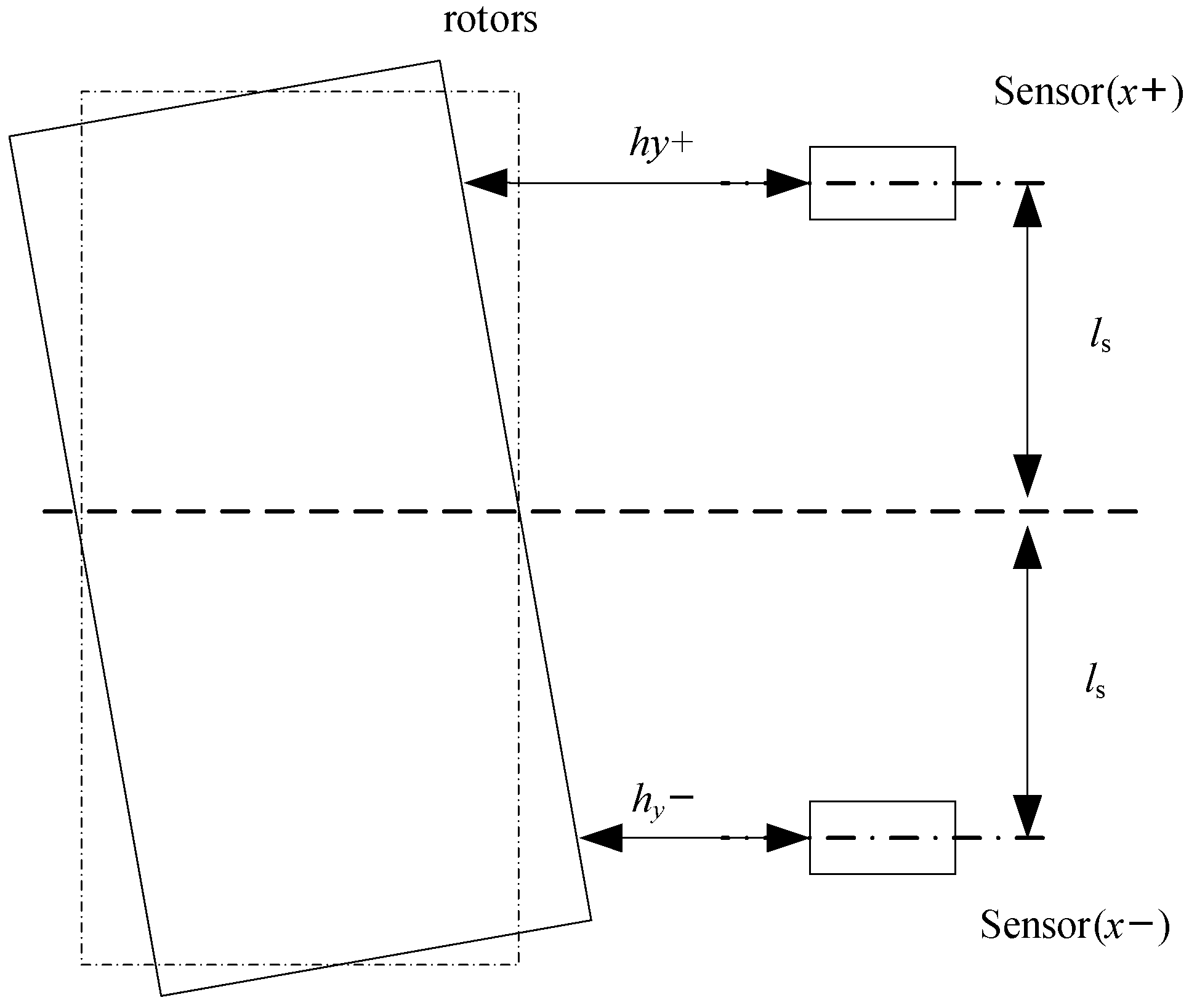
2.2. Sensor Principle
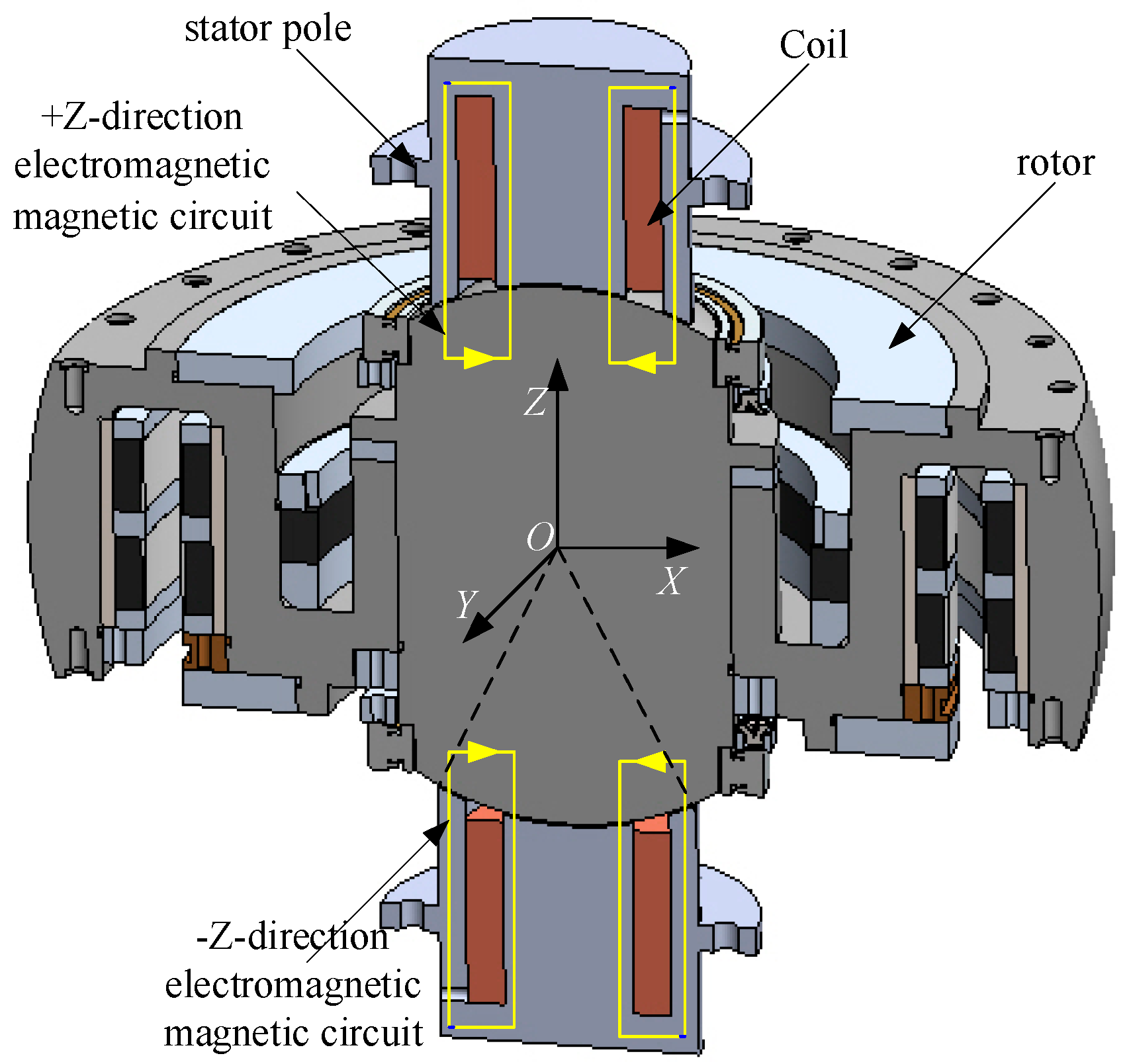
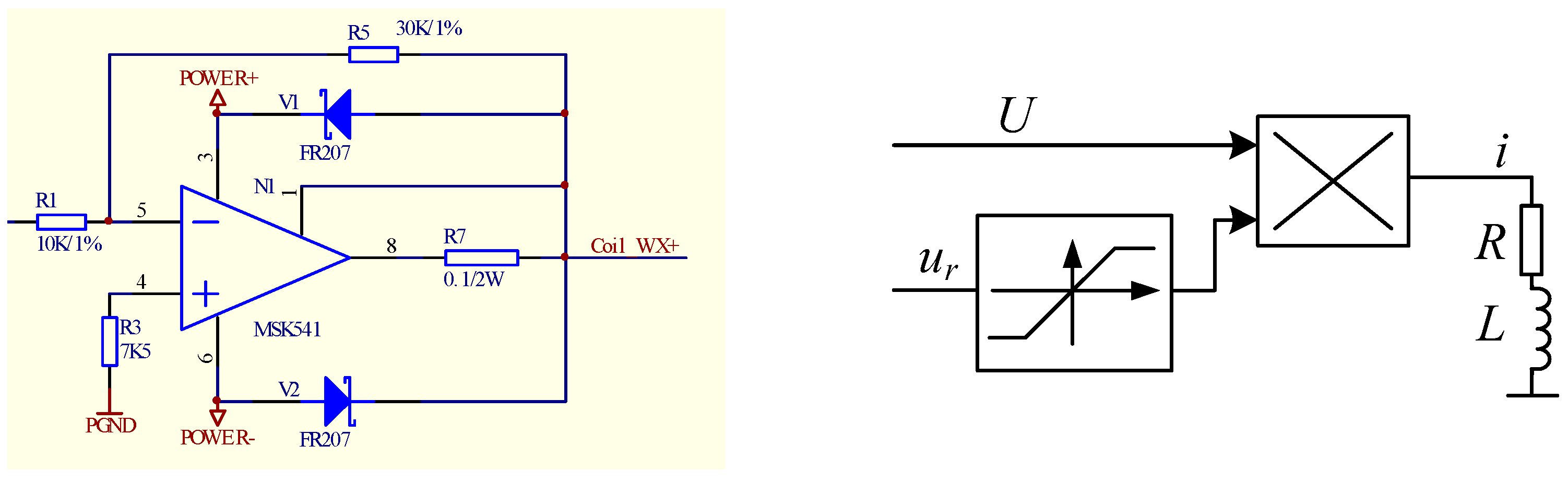
2.3. Power Amplifier Principle Analysis and Modeling
3. MSCSG Deflection Channel Decoupling
4. Controller Design
5. Simulation Analysis
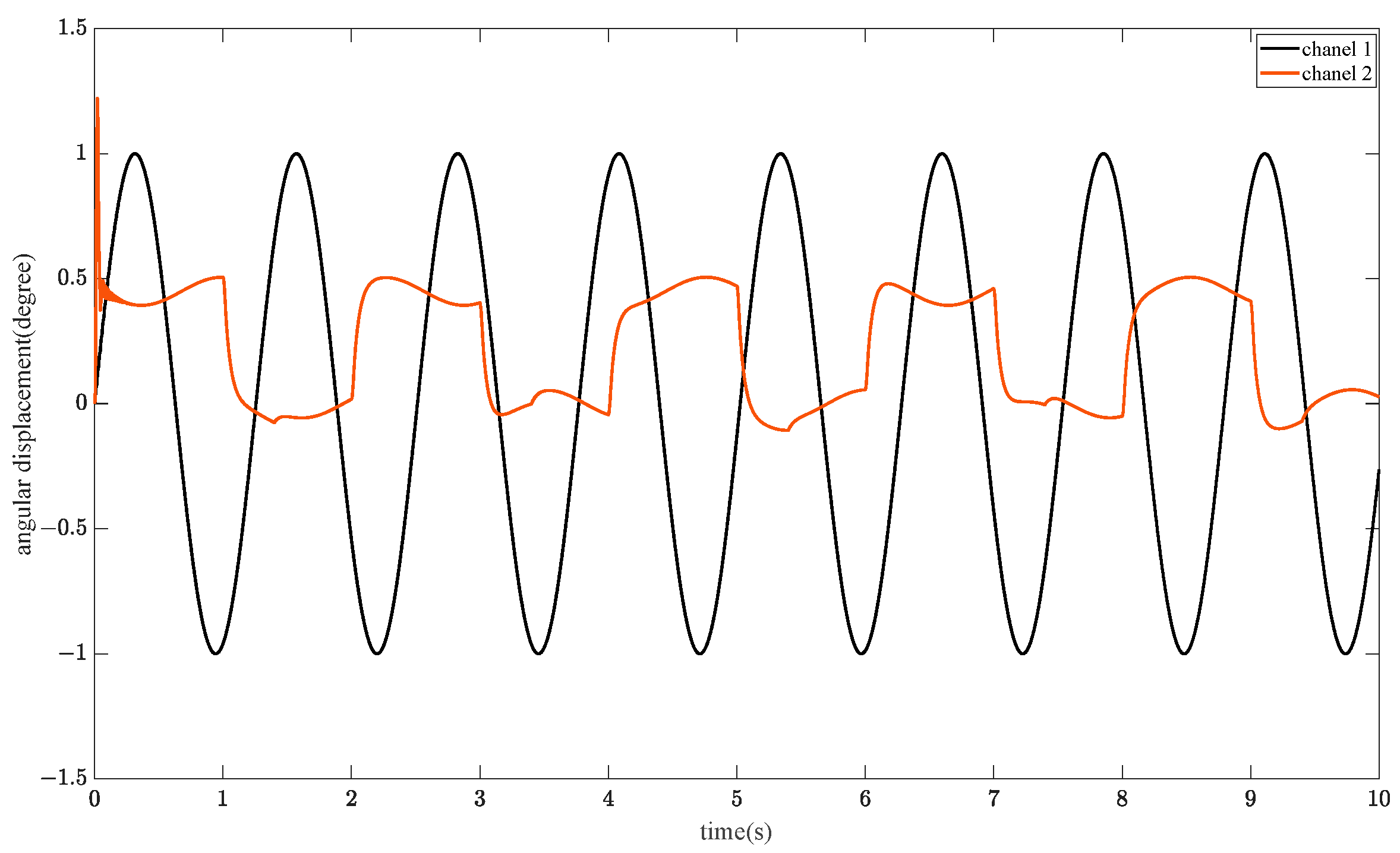
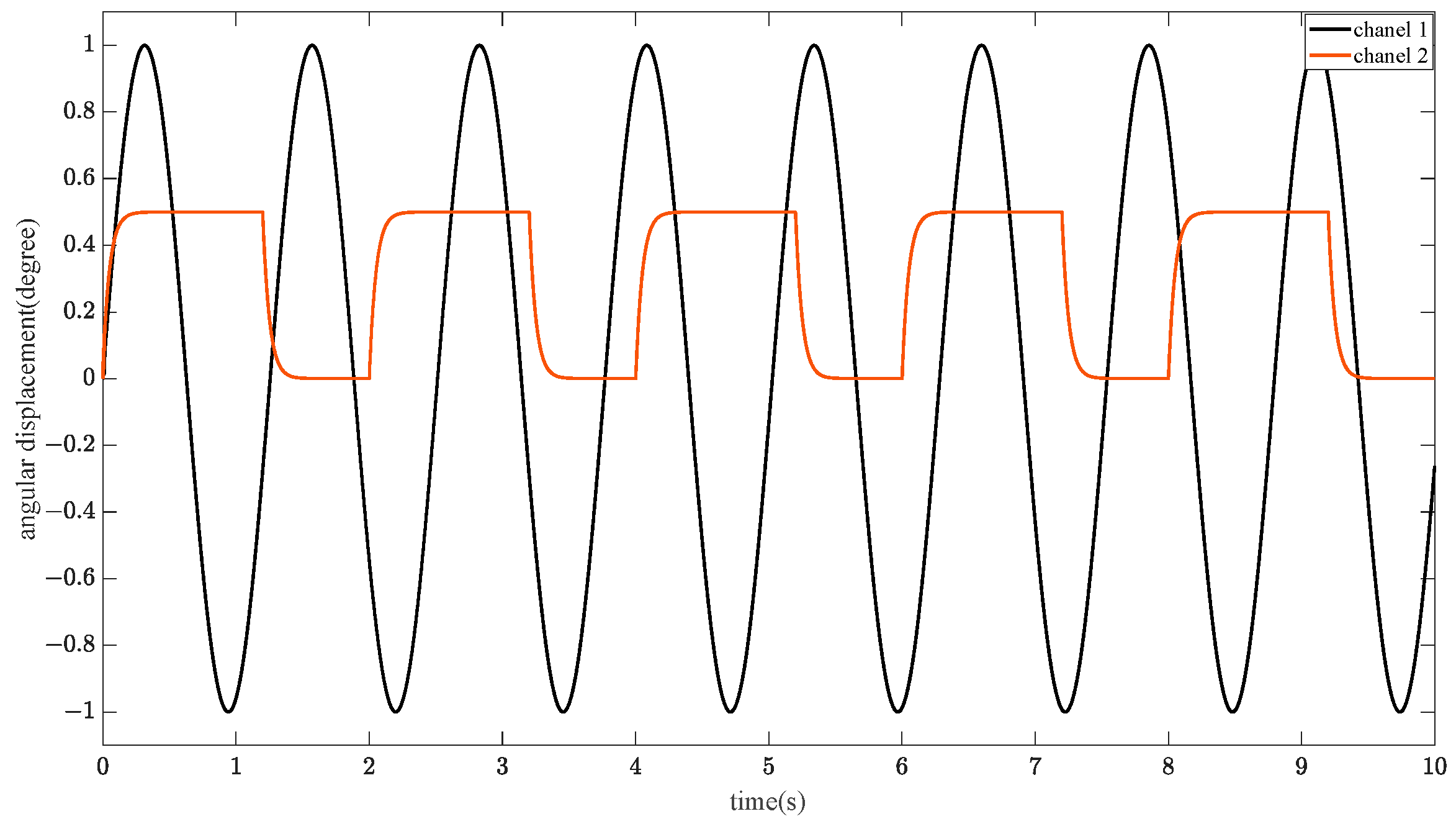
5.1. Simulation Analysis of Decoupling Capability
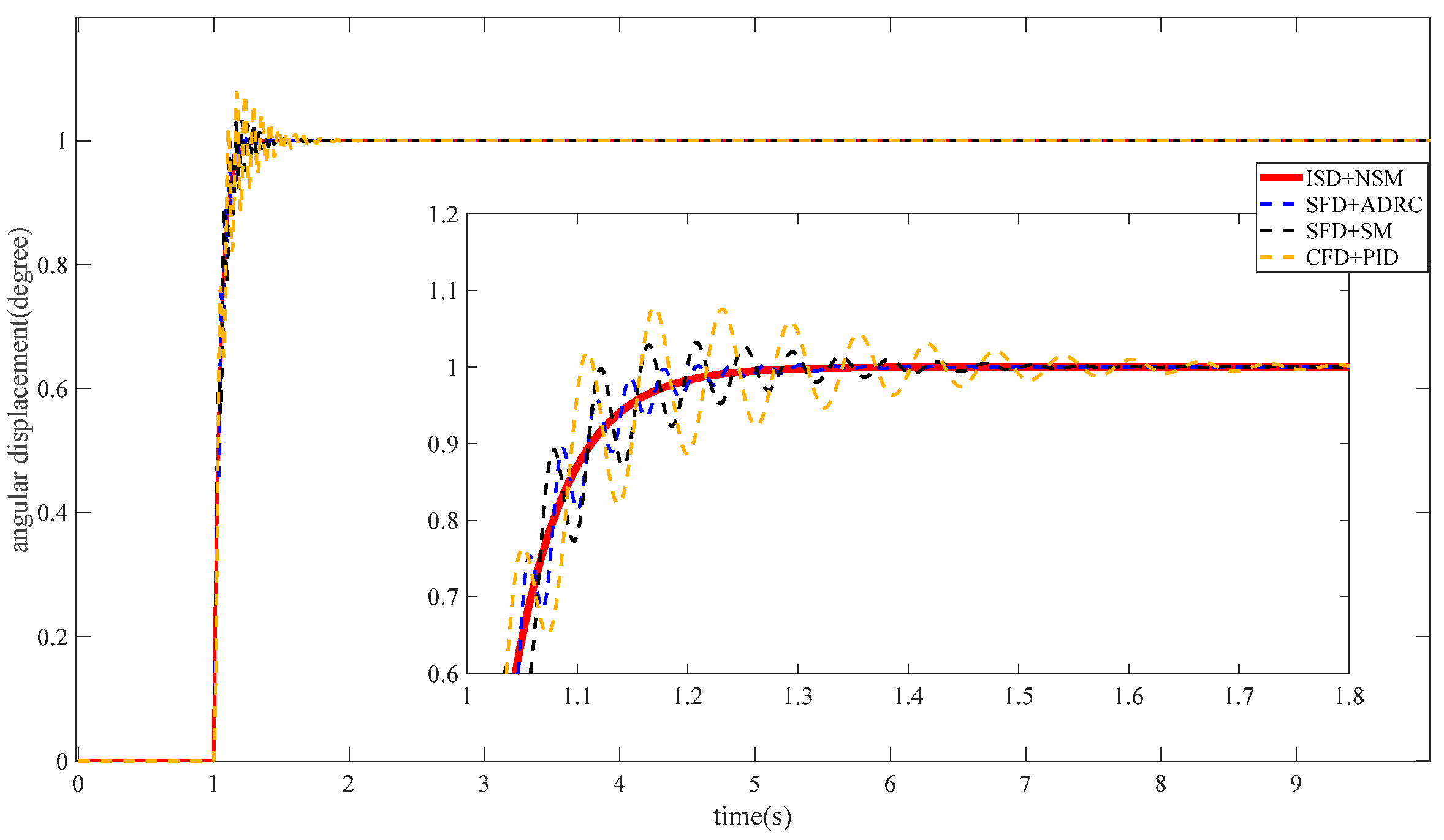
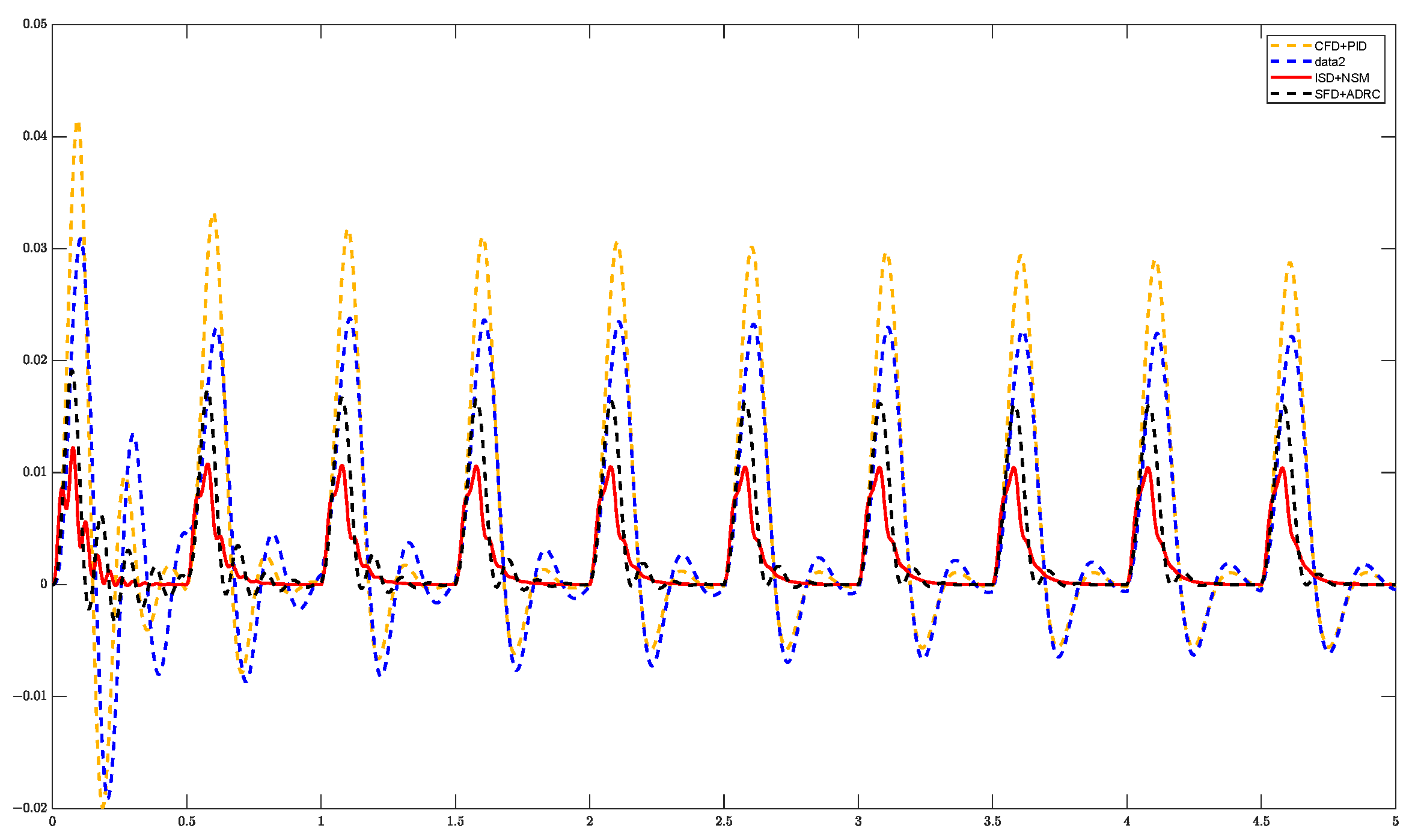
5.2. Anti-Interference Capability Analysis
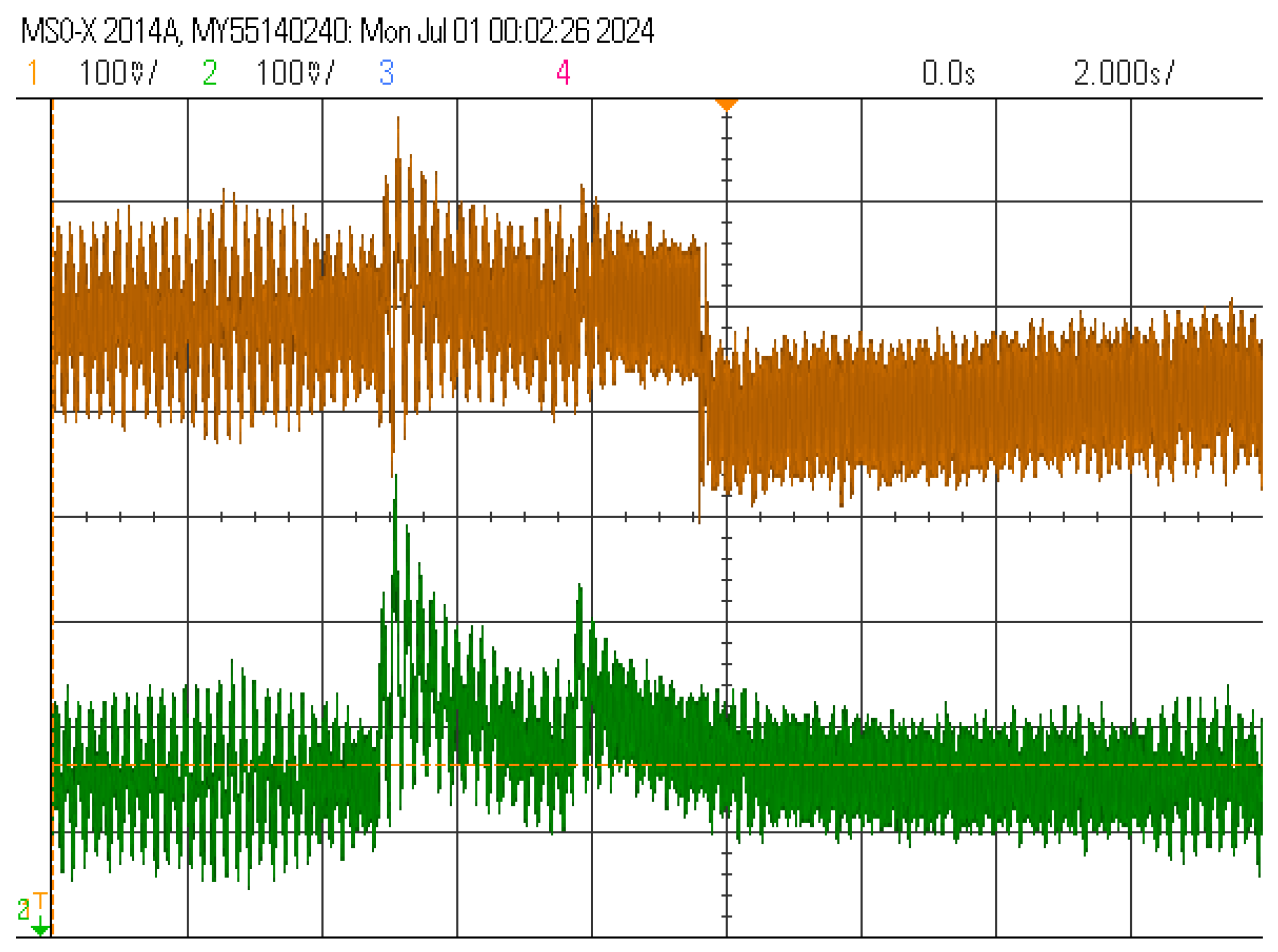
6. Experimental Verification
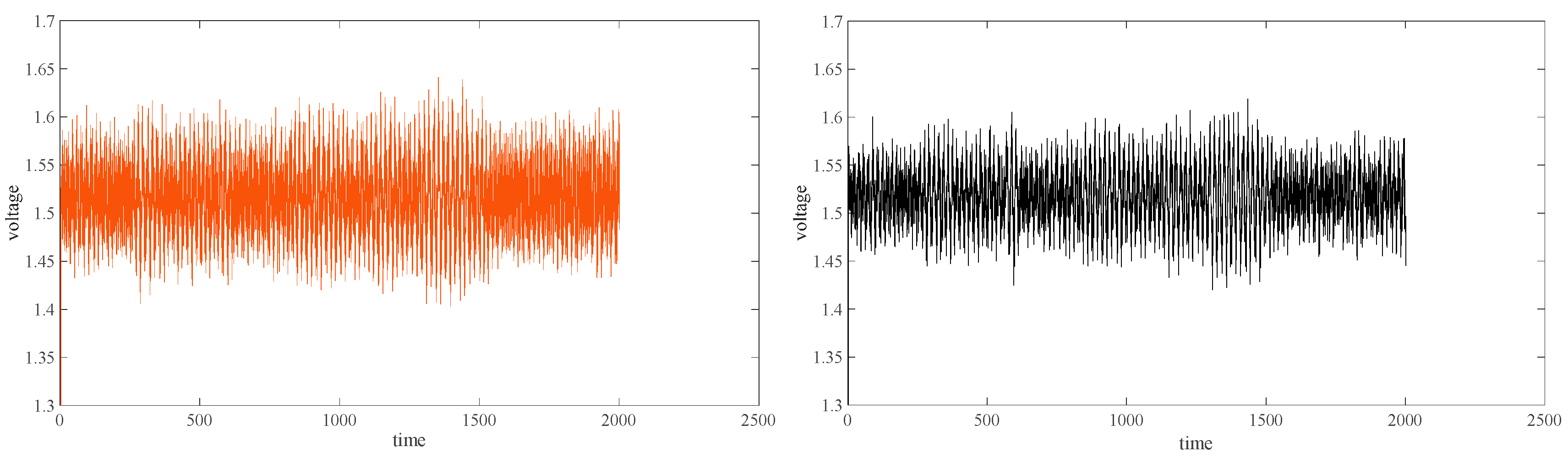
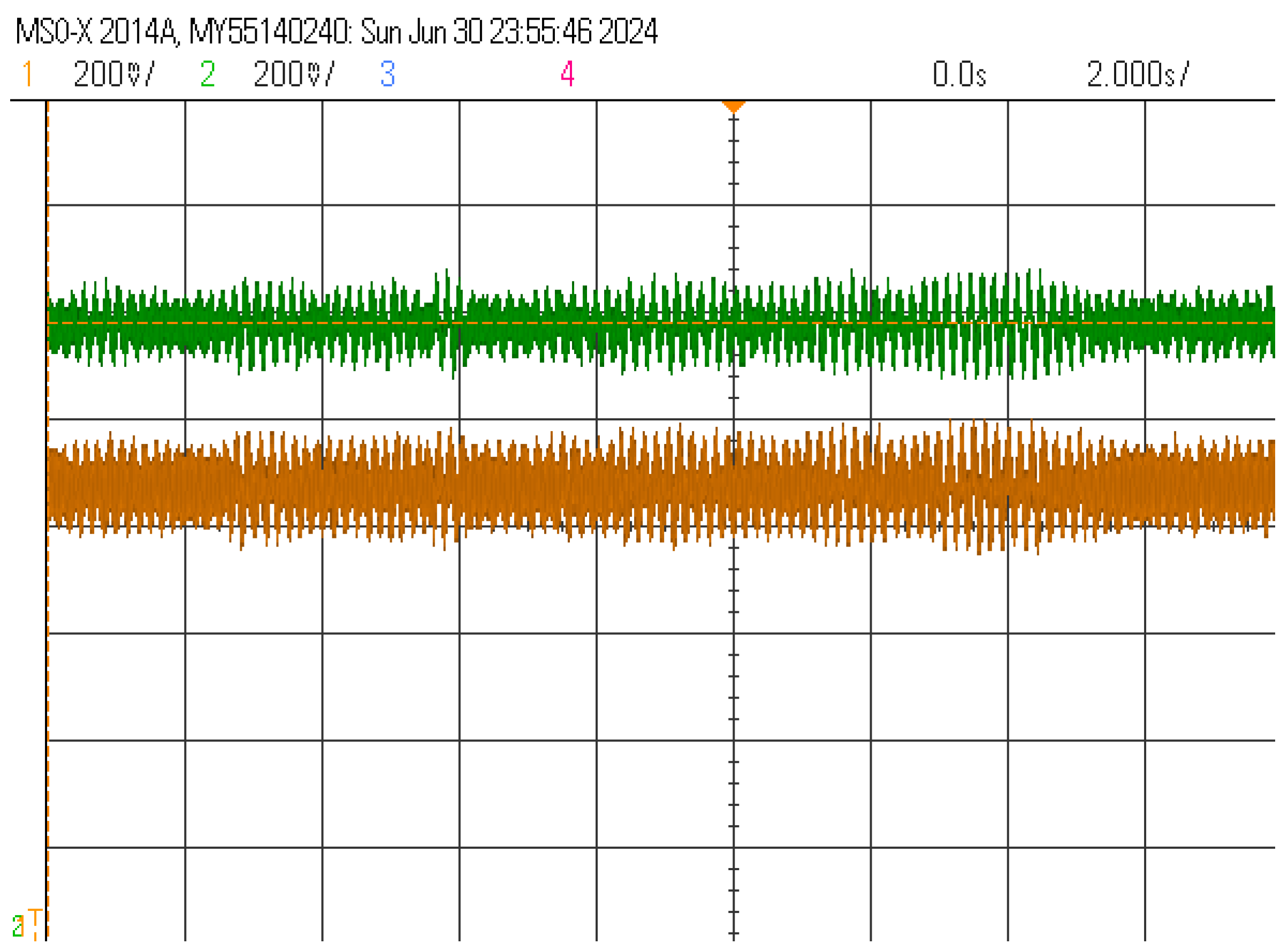
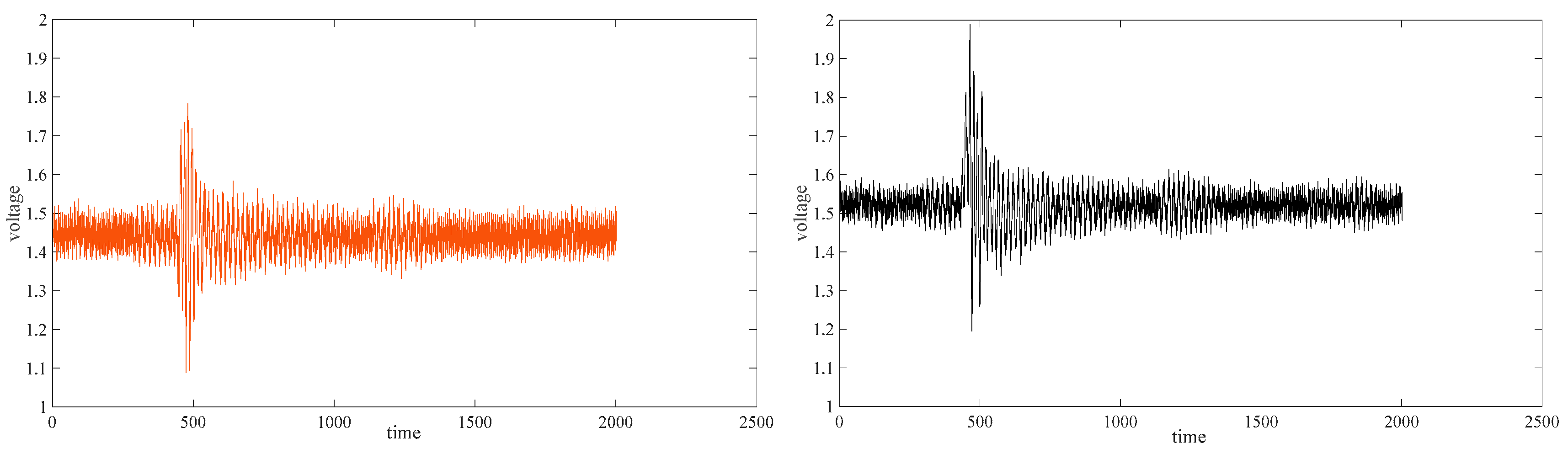
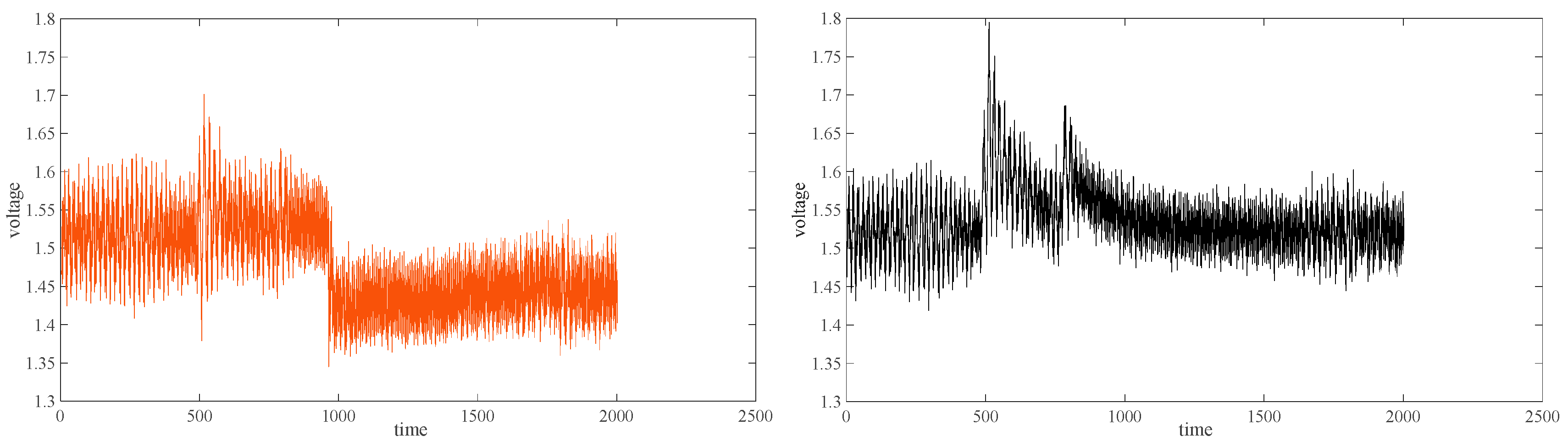
6.1. Experimental Verification of Decoupling Performance
6.2. Verification of Anti-Interference Performance
7. Conclusions
- For the structure and working principle of MSCSG, establish a two-degree-of-freedom deflection channel model, and the equations show that there is a serious coupling between the two deflection channels; model and analyse the power amplifier, and equate it to an inertial link. Design the inverse system decoupling method, and use the fuzzy method to improve the RBF neural network to compensate the uncertain perturbation and residual coupling term; design the adaptive sliding mode controller, and based on the Lyapunov stability criterion, the controller is proved to converge.
- Simulation analysis shows that the method designed in this paper, relative to the traditional method, has a large improvement in decoupling effect and anti-jamming performance; the validity of this method is subsequently verified by experiments.
- The main principle of the fuzzy RBF neural network designed in this paper is to use the abstraction ability of the fuzzy method to the natural language to correct the sliding mode controller and improve the dynamic quality; in the actual experiments, the rules of the fuzzy method are set up by ourselves according to the accumulation of experience in the previous many experiments, which may not be the optimal rules, but the introduction of the learning ability of the RBF neural network to correct the fuzzy control’s subordinate degree function and fuzzy rules, which solves the subjectivity caused by fuzzy control relying too much on the empirical basis. In brief, it means that the fuzzy rules can be gradually narrowed down by correcting the fuzzy rules one by one while keeping the parameters of the RBF neural network unchanged; on the contrary, after optimising the rule intervals, the parameters of the RBF neural network can be corrected again until the experimental results are better.
- In the future, the fuzzy rules and RBF neural network can be derived in the more underlying logic, and strive to introduce adaptive methods into the two, parameter optimisation and rule correction on the form of indicators to reflect the use of optimisation methods to find the optimal parameters and rules.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, S.-F.; Qin, C.; Xu, A.-P.; Xu, Z.-B. Research on the Reverse Sliding Mode Control Strategy of Photoelectric Tracking Rotary Table; Electronics Optics & Control: Changchun, China, 2023. [Google Scholar]
- Ning, X.; Han, B.-C.; Fang, J.-C. Disturbance Observer Based Decoupling Method of Double-gimbaled Variable Speed Control Moment Gyroscope. J. Mech. Eng. 2017, 53, 52–59. [Google Scholar] [CrossRef]
- Jiang, C. Research on Control Strategy of Turntable Servo System Based on RBF Neural Network. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2022. [Google Scholar]
- Lin, Z.-C. Research on the Control System of Maglev Dual-Stage Inertially Stabilized Platform. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2015. [Google Scholar]
- Xia, C.; Cai, Y.; Ren, Y.; Wu, D.; Wang, Y. Feedforward decoupling and internal model control for rotor of magnetically suspended control and sensing gyroscope. J. Beijing Univ. Aeronaut. Astronaut. 2018, 44, 480–488. [Google Scholar]
- Ren, Y.; Chen, X.; Cai, Y.; Wang, W.; Liu, Q. Adaptive robust sliding mode simultaneous control of spacecraft attitude and micro-vibration based on magnetically suspended control and sensitive gyro. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2020, 234, 2197–2210. [Google Scholar] [CrossRef]
- Yin, Z.; Cai, Y.; Ren, Y. Decoupled active disturbance rejection control method for magnetically suspended rotor based on state feedback. J. Beijing Univ. Aeronaut. Astronaut. 2021, 48, 1210–1221. [Google Scholar]
- Li, L.; Ren, Y.; Chen, X.; Wang, W. Design of MSCSG control system based on ADRC and RBF neural network. J. Beijing Univ. Aeronaut. Astronaut. 2020, 46, 1966–1972. [Google Scholar]
- Su, X.; Yang, X.; Xu, Y. Fuzzy adaptive terminal sliding mode control based on recurrent neural network compensation for a maglev system. Eng. Appl. Artif. Intell. 2023, 124, 106588. [Google Scholar] [CrossRef]
- Zhang, J.; Mei, X.; Zhang, D.; Jiang, G.D.; Liu, Q. Application of decoupling fuzzy sliding mode control with active disturbance rejection for MIMO magnetic levitation system. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 227, 213–229. [Google Scholar] [CrossRef]
- Mao, W.-L.; Chu, C.-T. Modeless Magnetic Bearing System Tracking Using an Adaptive Fuzzy Hermite Neural Network Method. IEEE Sens. J. 2019, 19, 5904–5915. [Google Scholar] [CrossRef]
- Jiang, C.; Zhu, H.; Wang, H. Decoupling Control of Outer Rotor Coreless Bearingless Permanent Magnet Synchronous Generator Based on Fuzzy Neural Network Inverse System. IEEE Trans. Transp. Electrif. 2023, 9, 3908–3917. [Google Scholar] [CrossRef]
- Qiu, Z.; Chen, S. Vibration control of a translational coupled double flexible beam system using sliding mode neural network fuzzy control. Trans. Inst. Meas. Control 2022, 44, 2246–2288. [Google Scholar] [CrossRef]
- Li, Z. Neural network identifier-based dynamic decoupling control of a novel permanent magnet spherical actuator. Int. J. Model. Identif. Control 2011, 13, 162–170. [Google Scholar] [CrossRef]
- Bai, C.; Chen, J.; Ren, Z.; Li, Q.D.; Xiong, Z.H. Adaptive decoupling control of hypersonic vehicle using fuzzy-neural network observer. Proc. Inst. Mech. Eng. Part G (J. Aerosp. Eng.) 2016, 230, 1216–1223. [Google Scholar] [CrossRef]
- Huang, Z.; Zhu, J.; Shao, J.; Wei, Z.; Tang, J. Recurrent neural network based high-precision position compensation control of magnetic levitation system. Sci. Rep. 2022, 12, 11435. [Google Scholar] [CrossRef] [PubMed]
- Fatemimoghadam, A.; Toshani, H.; Manthouri, M. Control of magnetic levitation system using recurrent neural network-based adaptive optimal backstepping strategy. Trans. Inst. Meas. Control 2020, 42, 2382–2395. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, Z.; Zhang, J.; Yin, L. Research on PID Controller in Active Magnetic Levitation Based on Particle Swarm Optimization Algorithm. Open Autom. Control Syst. J. 2015, 7, 1870–1874. [Google Scholar]
- Chen, S.-C.; Nguyen, V.-S.; Le, D.-K.; Nam, N.T.H. Nonlinear Control of an Active Magnetic Bearing System Achieved Using a Fuzzy Control with Radial Basis Function Neural Network. J. Appl. Math. 2014, 2014, 272391. [Google Scholar] [CrossRef]
- Chiang, G.-K.; Chu, C.-T.; Lin, T.-C. Adaptive sliding mode recurrent fuzzy neural network estimator in magnetic bearing system. Appl. Mech. Mater. 2014, 543–547, 1487–1491. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, H.; Wu, M.; Zhang, W. Active Disturbance Rejection Decoupling Control for Three-Degree-of- Freedom Six-Pole Active Magnetic Bearing Based on BP Neural Network. IEEE Trans. Appl. Supercond. 2020, 30, 3603505. [Google Scholar] [CrossRef]
- Supreeth, D.K.; Bekinal, S.I.; Shivamurthy, R.C. Optimization of Radial Electrodynamic Bearing Using Artificial Neural Network. IEEE Access 2024, 12, 67957–67970. [Google Scholar] [CrossRef]














| Parameters | Value |
|---|---|
| Jx/(kg·m2) | 0.0097 |
| Jz/(kg·m2) | 0.0287 |
| Jy/(kg·m2) | 0.0097 |
| L/m | 0.1158 |
| B/(T) | 0.35 |
| D/(mm) | 12 |
| Parameters | Value |
|---|---|
| η | 0.3 |
| α | 0.5 |
| γ | 10 |
| η | 0.1 |
| ci | [−2 −1 0 1 2] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, F.; Wang, W.; Yu, C.; Wang, S.; Zhang, W. Optimization Design of Magnetically Suspended Control and Sensitive Gyroscope Deflection Channel Controller Based on Neural Network Inverse System. Actuators 2024, 13, 302. https://doi.org/10.3390/act13080302
Chen F, Wang W, Yu C, Wang S, Zhang W. Optimization Design of Magnetically Suspended Control and Sensitive Gyroscope Deflection Channel Controller Based on Neural Network Inverse System. Actuators. 2024; 13(8):302. https://doi.org/10.3390/act13080302
Chicago/Turabian StyleChen, Feiyu, Weijie Wang, Chunmiao Yu, Shengjun Wang, and Weian Zhang. 2024. "Optimization Design of Magnetically Suspended Control and Sensitive Gyroscope Deflection Channel Controller Based on Neural Network Inverse System" Actuators 13, no. 8: 302. https://doi.org/10.3390/act13080302
APA StyleChen, F., Wang, W., Yu, C., Wang, S., & Zhang, W. (2024). Optimization Design of Magnetically Suspended Control and Sensitive Gyroscope Deflection Channel Controller Based on Neural Network Inverse System. Actuators, 13(8), 302. https://doi.org/10.3390/act13080302








