Time Integrated Flux Analysis: Exploiting the Concentration Measurements Directly for Cost-Effective Metabolic Network Flux Analysis
Abstract
:1. Introduction
2. Methods
2.1. Metabolic Time Integrated Flux Analysis
2.2. Time-Integrated Flux Balance/Variability Analysis
2.3. Sparse Time Integrated Flux Balance/Variability Analysis
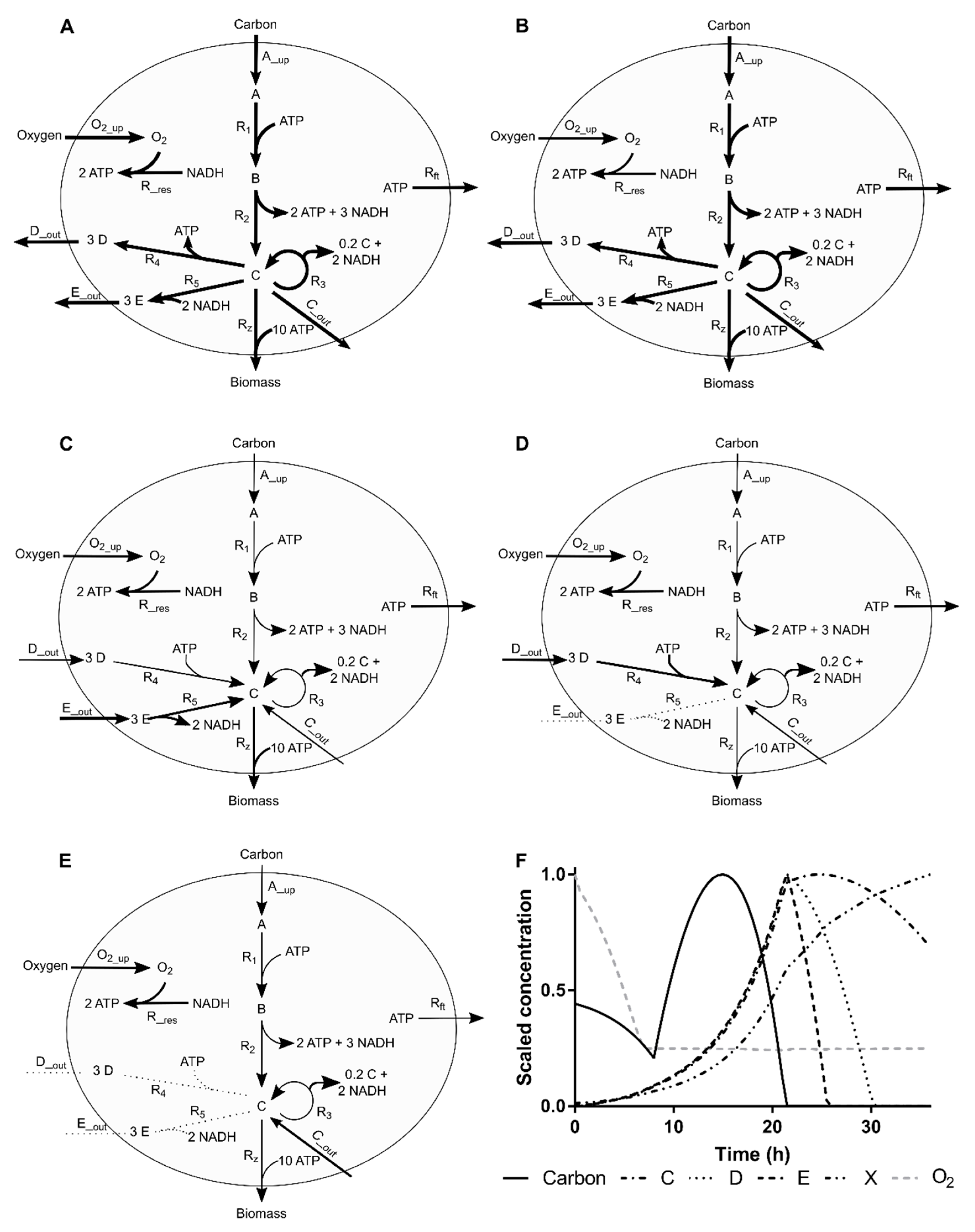
2.4. Simulation Case I
2.4.1. Process Operation
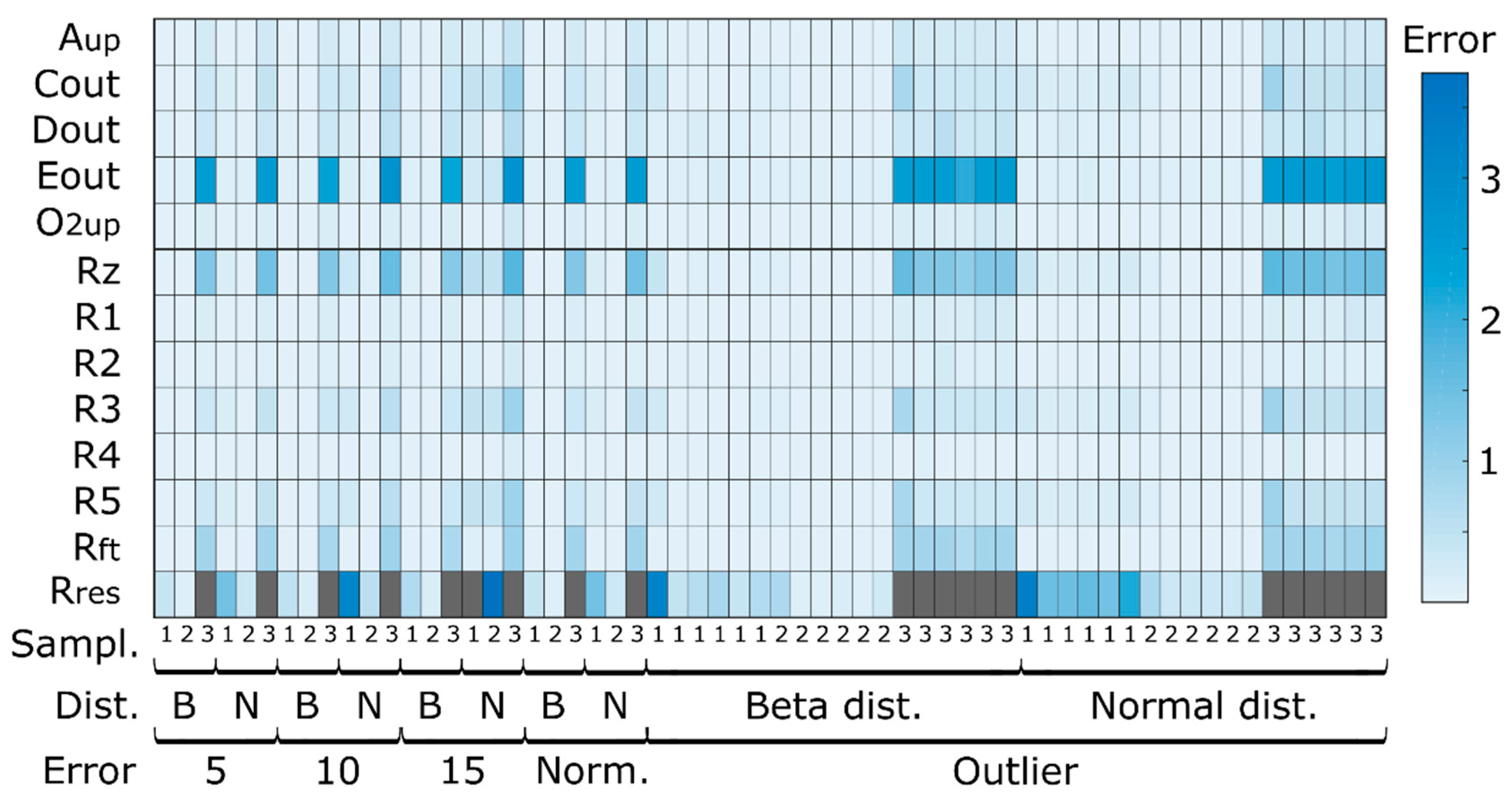
2.4.2. Simulated Sampling Strategies and Noise Levels
2.5. Simulation Case II
2.5.1. Simulated Sampling Strategies and Noise Levels
2.5.2. Test Cases (Measured and Estimated Fluxes; Irreversible Reactions)
2.6. Experimental Case
3. Results
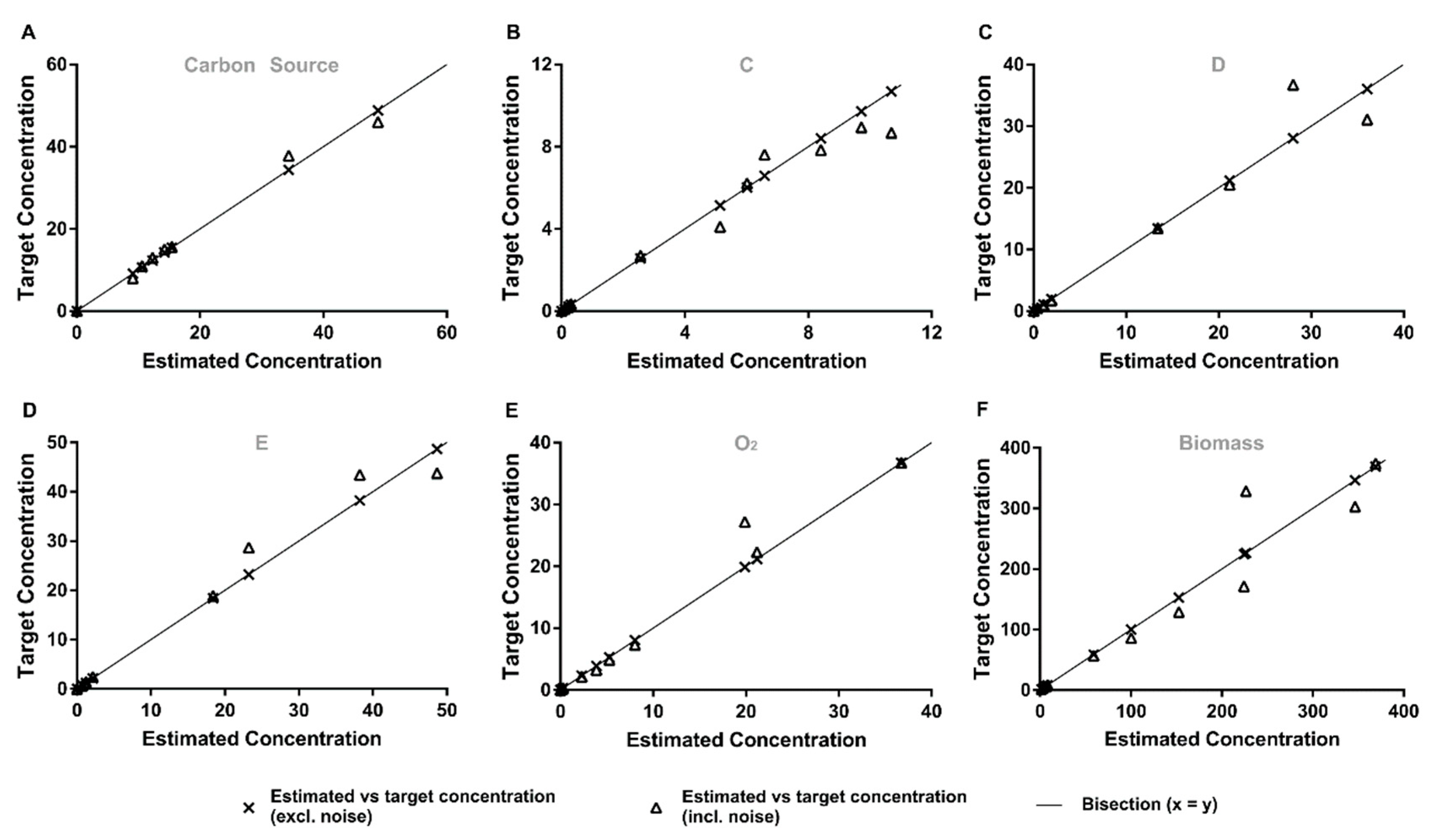
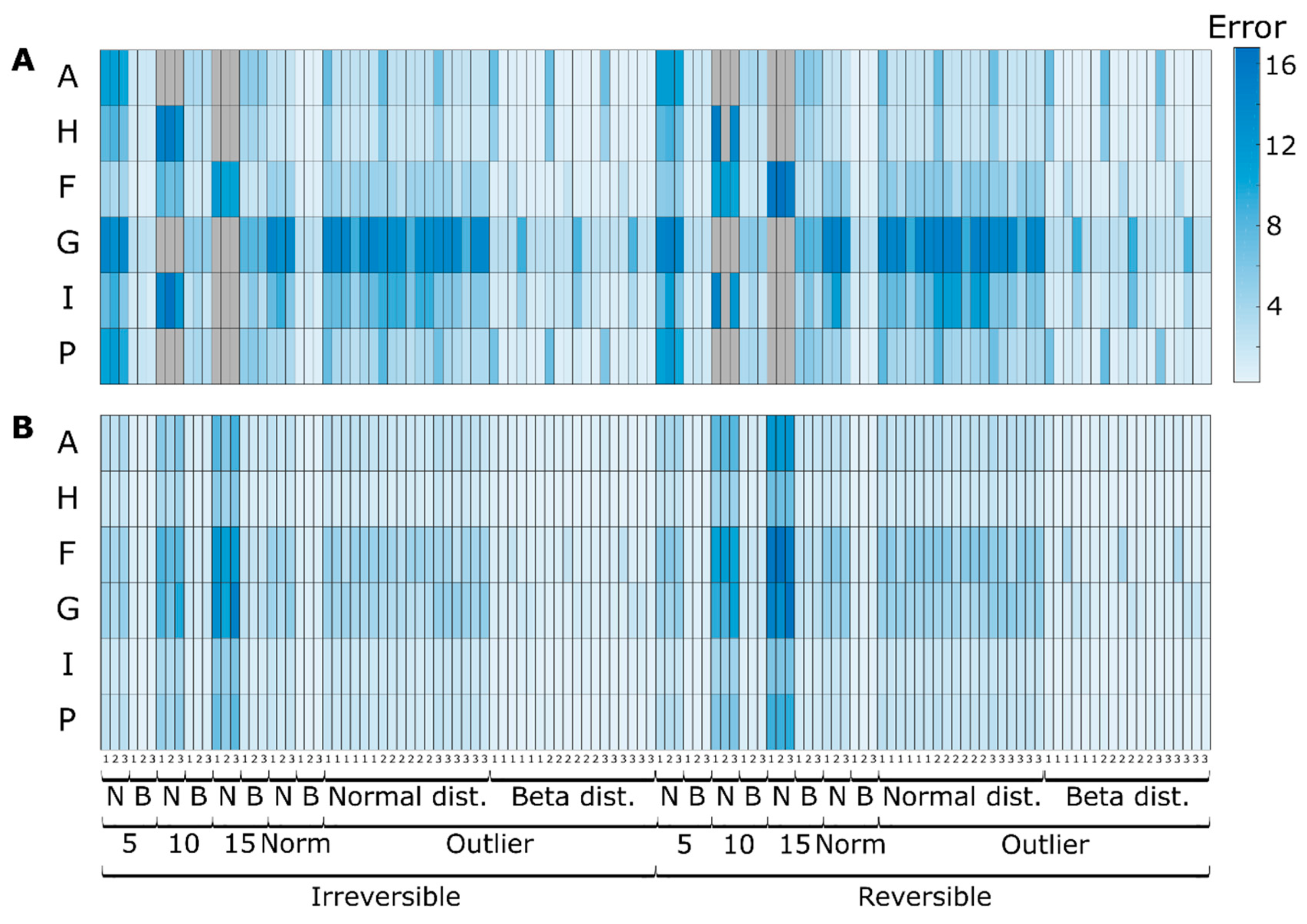
3.1. Simulation Case I
3.1.1. Quantitative Performance Assessment
3.1.2. Qualitative Performance Assessment
3.1.3. Comparison with MFA and Derivative Approach for Flux Estimation
3.2. Simulation Case II
3.2.1. Effect of Redundancy
3.2.2. Effect of Irreversibility Constrains
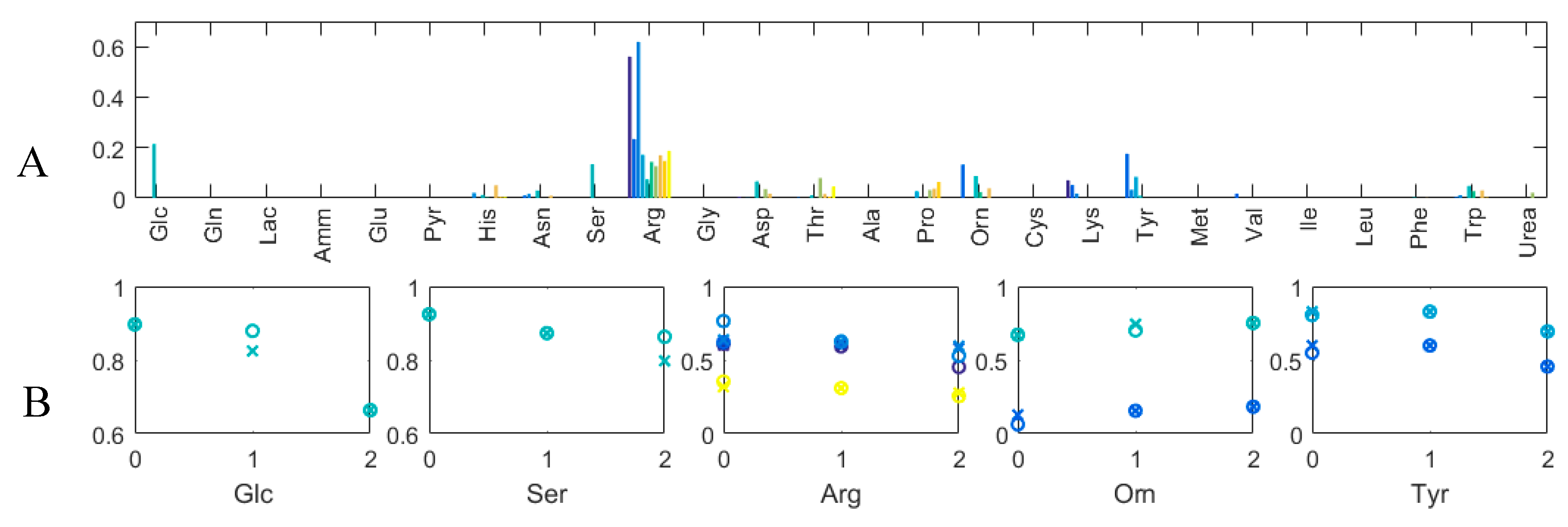
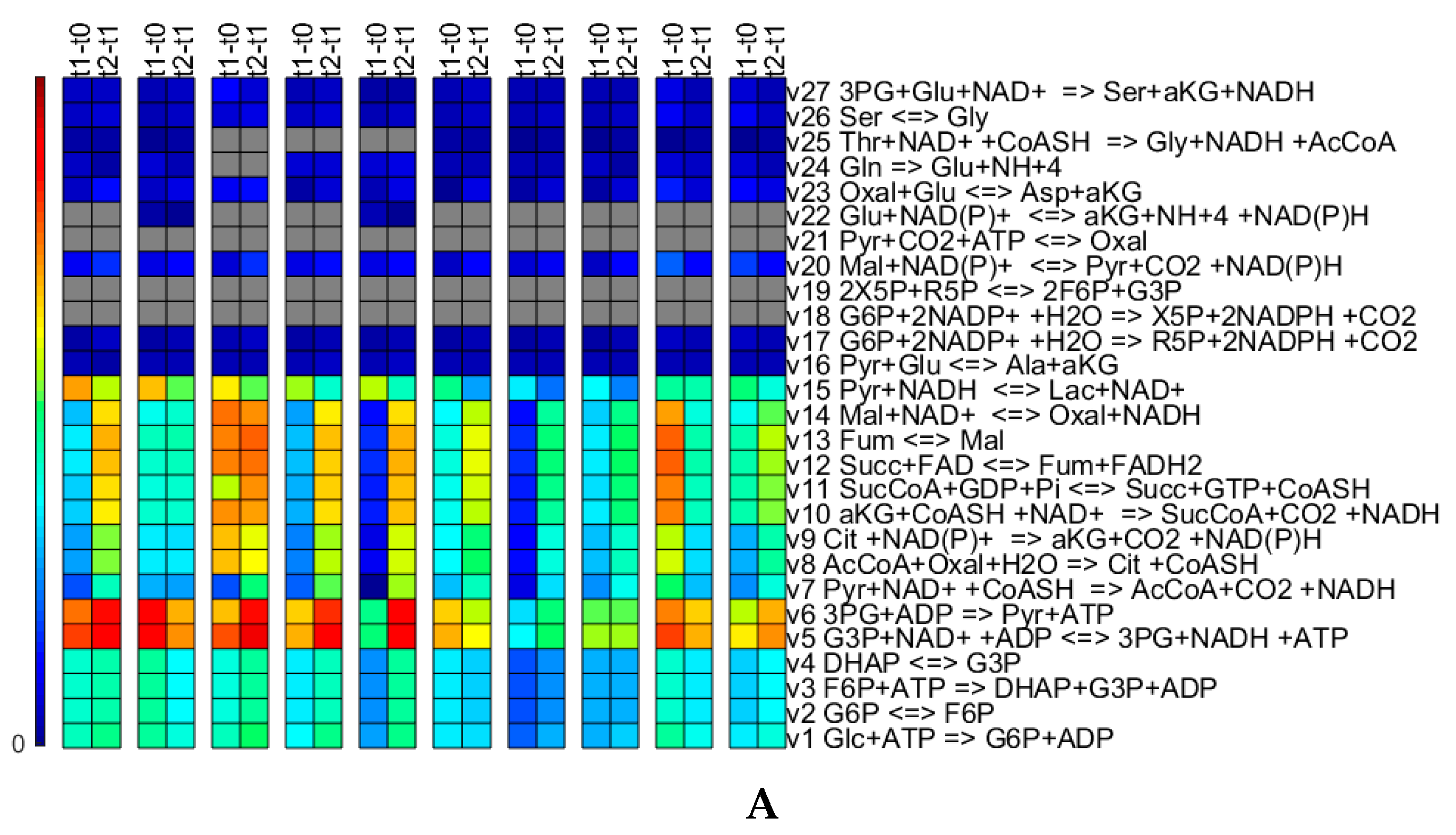
3.3. Experimental Case
3.3.1. Quantitative Performance Assessment
3.3.2. Qualitative Performance Assessment
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A. Simulation Case I
Appendix A.1. Network Topology
Appendix A.2. Simulated Kinetics
| Variable/Parameter | Value | Comment |
|---|---|---|
| (initial) | 1 L | initial conditions |
| (initial) | 2 | |
| (initial) | 0.004 | |
| (initial) | 15 | |
| 200 | feed characterization | |
| 0.05 L/h | After 8 h of fermentation | |
| PARAMETERS | ||
| 0.005 | Controlled at 20% | |
| 0.05 | ||
| 0.1 | ||
| 0.04 | ||
| 0.1 | ||
| 0.07 | ||
| 0.1 | ||
| 0.06 | ||
| 0.1 | ||
| 0.01 | ||
| 0.1 | ||
| 0.04 | ||
| 0.2 | ||
| 0.2 | ||
| 0.1 | ||
| 0.01 | ||
| 0.0028 |
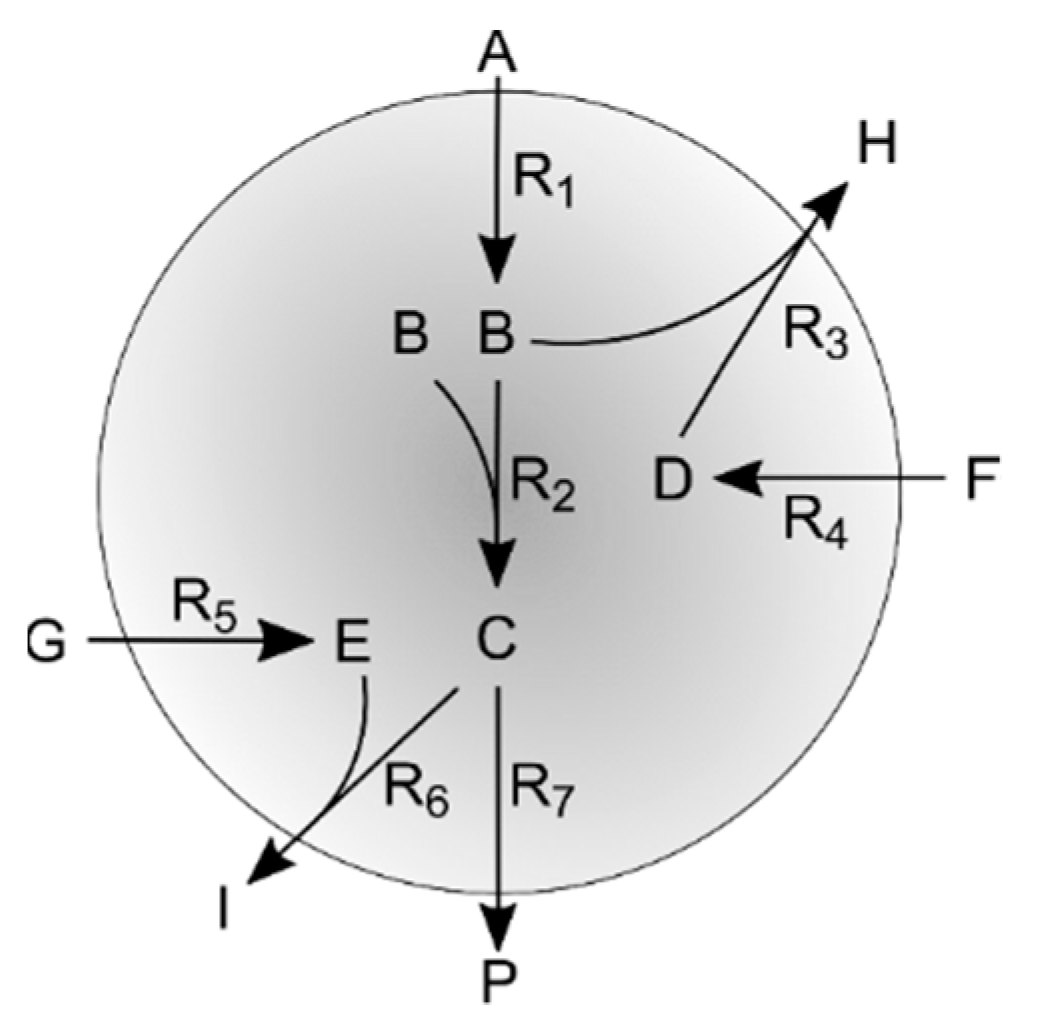
Appendix B. Simulation Case II
Appendix B. Network Topology and Simulation Kinetics
References and Note
- Stephanopoulos, G. Metabolic Fluxes and Metabolic Engineering. Metab. Eng. 1999, 1, 1–11. [Google Scholar] [CrossRef]
- Lewis, N.E.; Nagarajan, H.; Palsson, B.O. Constraining the metabolic genotype-phenotype relationship using a phylogeny of in silico methods. Nat. Rev. Microbiol. 2012, 10, 291. [Google Scholar] [CrossRef]
- Bordbar, A.; Monk, J.M.; King, Z.A.; Palsson, B.O. Constraint-based models predict metabolic and associated cellular functions. Nat. Rev. Genet. 2014, 15, 107. [Google Scholar] [CrossRef]
- Otero, J.M.; Nielsen, J. Industrial systems biology. Biotechnol. Bioeng. 2010, 105, 439–460. [Google Scholar] [CrossRef] [PubMed]
- Quek, L.E.; Dietmair, S.; Kraemer, J.O.; Nielsen, L.K. Metabolic flux analysis in mammalian cell culture. Metab. Eng. 2010, 12, 1611–1671. [Google Scholar] [CrossRef] [PubMed]
- Antoniewicz, M.R. Methods and advances in metabolic flux analysis: A mini-review. J. Ind. Microbiol. Biotechnol. 2015, 42, 317–325. [Google Scholar] [CrossRef] [PubMed]
- Orth, J.D.; Thiele, I.; Palsson, B.Ø. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245. [Google Scholar] [CrossRef]
- Raman, K.; Chandra, N. Flux balance analysis of biological systems: Applications and challenges. Brief. Bioinform. 2009, 10, 435–449. [Google Scholar] [CrossRef]
- Gudmundsson, S.; Thiele, I. Computationally efficient flux variability analysis. BMC Bioinform. 2010, 11, 489. [Google Scholar] [CrossRef]
- Satterfield, C.N. Chemical reaction engineering, Octave Levenspiel, Wiley, New York (1972). 578 pages. $16.95. AIChE J 1973, 19, 206–207. [Google Scholar] [CrossRef]
- Ozturk, S.S.; Palsson, B.Ø. Effect of initial cell density on hybridoma growth, metabolism, and monoclonal antibody production. J. Biotechnol. 1990, 16, 259–278. [Google Scholar] [CrossRef]
- Brendel, M.; Bonvin, D.; Marquardt, W. Incremental identification of kinetic models for homogeneous reaction systems. Chem. Eng. Sci. 2006, 61, 5404–5420. [Google Scholar] [CrossRef]
- Swain, P.S.; Stevenson, K.; Leary, A.; Montano-Gutierrez, L.F.; Clark, I.B.N.; Vogel, J.; Pilizota, T. Inferring time derivatives including cell growth rates using Gaussian processes. Nat. Commun. 2016, 7, 13766. [Google Scholar] [CrossRef] [PubMed]
- Willis, M.J.; von Stosch, M. Simultaneous parameter identification and discrimination of the nonparametric structure of hybrid semi-parametric models. Comput. Chem. Eng. 2017, 104, 366–376. [Google Scholar] [CrossRef]
- Leighty, R.W.; Antoniewicz, M.R. Dynamic metabolic flux analysis (DMFA): A framework for determining fluxes at metabolic non-steady state. Metab. Eng. 2011, 13, 745–755. [Google Scholar] [CrossRef]
- Liu, Y.; Gunawan, R. Parameter estimation of dynamic biological network models using integrated fluxes. BMC Syst. Biol. 2014, 8, 127. [Google Scholar] [CrossRef]
- Klamt, S.; Schuster, S.; Gilles, E.D. Calculability analysis in underdetermined metabolic networks illustrated by a model of the central metabolism in purple nonsulfur bacteria. Biotechnol. Bioeng. 2002, 77, 734–751. [Google Scholar] [CrossRef]
- Heirendt, L.; Arreckx, S.; Pfau, T.; Mendoza, S.N.; Richelle, A.; Heinken, A.; Haraldsdottir, H.S.; Wachowiak, J.; Keating, S.M.; Vlasov, V. Creation and analysis of biochemical constraint-based models using the COBRA Toolbox v3.0. Nat. Protoc. 2019, 14, 639–702. [Google Scholar] [CrossRef]
- Willis, M.J.; von Stosch, M. L0-constrained regression using mixed integer linear programming. Chemom. Intell. Lab. Syst. 2017, 165, 29–37. [Google Scholar] [CrossRef]
- Edwards, J.S.; Ramakrishna, R.; Palsson, B.O. Characterizing the metabolic phenotype: A phenotype phase plane analysis. Biotechnol. Bioeng. 2002, 77, 27–36. [Google Scholar] [CrossRef]
- Abbate, T.; Dewasme, L.; Vande Wouwer, A.; Bogaerts, P. Adaptive flux variability analysis of HEK cell cultures. Comput. Chem. Eng. 2019, 106633. [Google Scholar] [CrossRef]
- Bayer, B.; Sissolak, B.; Duerkop, M.; von Stosch, M.; Striedner, G. The shortcomings of accurate rate estimations in cell cultivation processes and a solution for precise and robust process modeling. Bioprocess Biosyst. Eng. 2019, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Material not intended for publication: aAbbate, T.; aDewasme, L.; aVande Wouwer, A.; bDumas, P. aAutomatic Control Laboratory, University of Mons and bCVDS, TRD, GSK Biologicals. Materials and Methods similar to those used in [21]. 2019.




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Portela, R.M.C.; Richelle, A.; Dumas, P.; von Stosch, M. Time Integrated Flux Analysis: Exploiting the Concentration Measurements Directly for Cost-Effective Metabolic Network Flux Analysis. Microorganisms 2019, 7, 620. https://doi.org/10.3390/microorganisms7120620
Portela RMC, Richelle A, Dumas P, von Stosch M. Time Integrated Flux Analysis: Exploiting the Concentration Measurements Directly for Cost-Effective Metabolic Network Flux Analysis. Microorganisms. 2019; 7(12):620. https://doi.org/10.3390/microorganisms7120620
Chicago/Turabian StylePortela, Rui M. C., Anne Richelle, Patrick Dumas, and Moritz von Stosch. 2019. "Time Integrated Flux Analysis: Exploiting the Concentration Measurements Directly for Cost-Effective Metabolic Network Flux Analysis" Microorganisms 7, no. 12: 620. https://doi.org/10.3390/microorganisms7120620
APA StylePortela, R. M. C., Richelle, A., Dumas, P., & von Stosch, M. (2019). Time Integrated Flux Analysis: Exploiting the Concentration Measurements Directly for Cost-Effective Metabolic Network Flux Analysis. Microorganisms, 7(12), 620. https://doi.org/10.3390/microorganisms7120620




