Fifty Generations of Amitosis: Tracing Asymmetric Allele Segregation in Polyploid Cells with Single-Cell DNA Sequencing
Abstract
1. Introduction
2. Materials and Methods
2.1. Paramecium Strain and Culture Conditions
2.2. Experiment Outline
2.3. DNA Isolation and Sequencing
2.4. Amplification Biases of MDA-Based Whole-Genome Amplification
2.5. Data Preprocessing and Calculation of IES Retention Scores
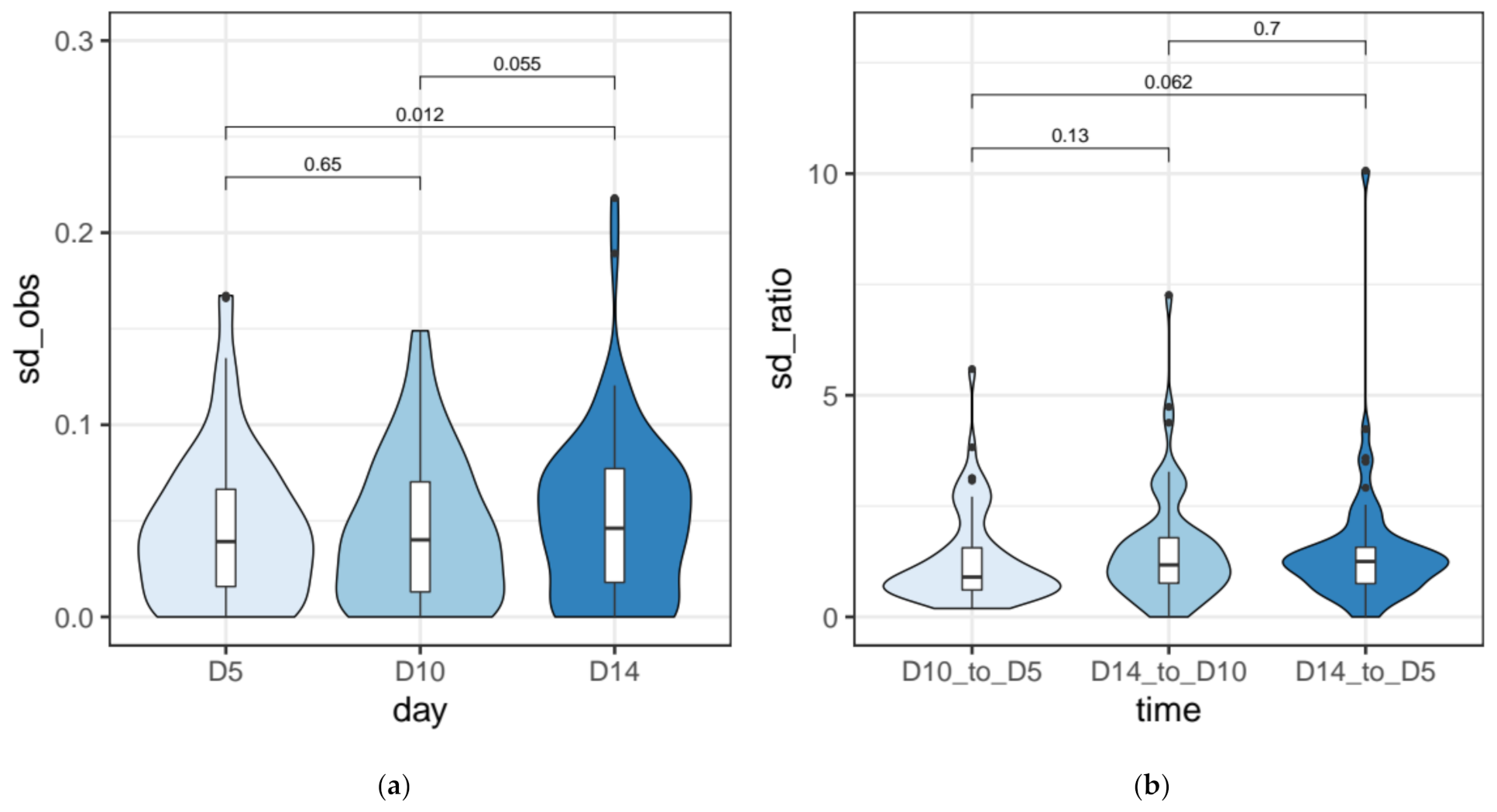
2.6. Quantification of the Measurement Error for IRS Estimates
2.7. Quantification of IES Dropout
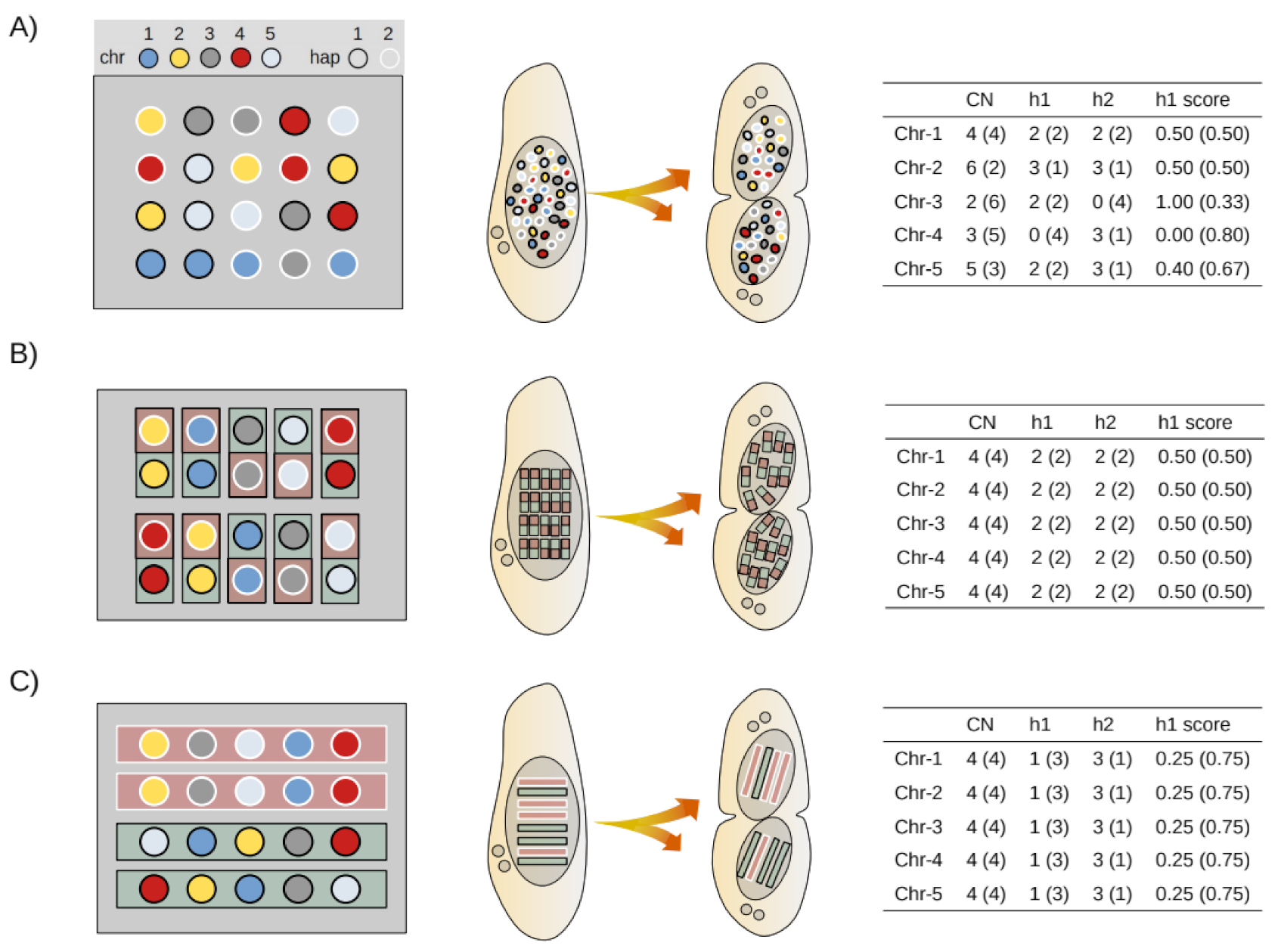
2.8. Mathematical Modeling of Somatic Assortment
2.9. Bioinformatic Simulation of Somatic Assortment
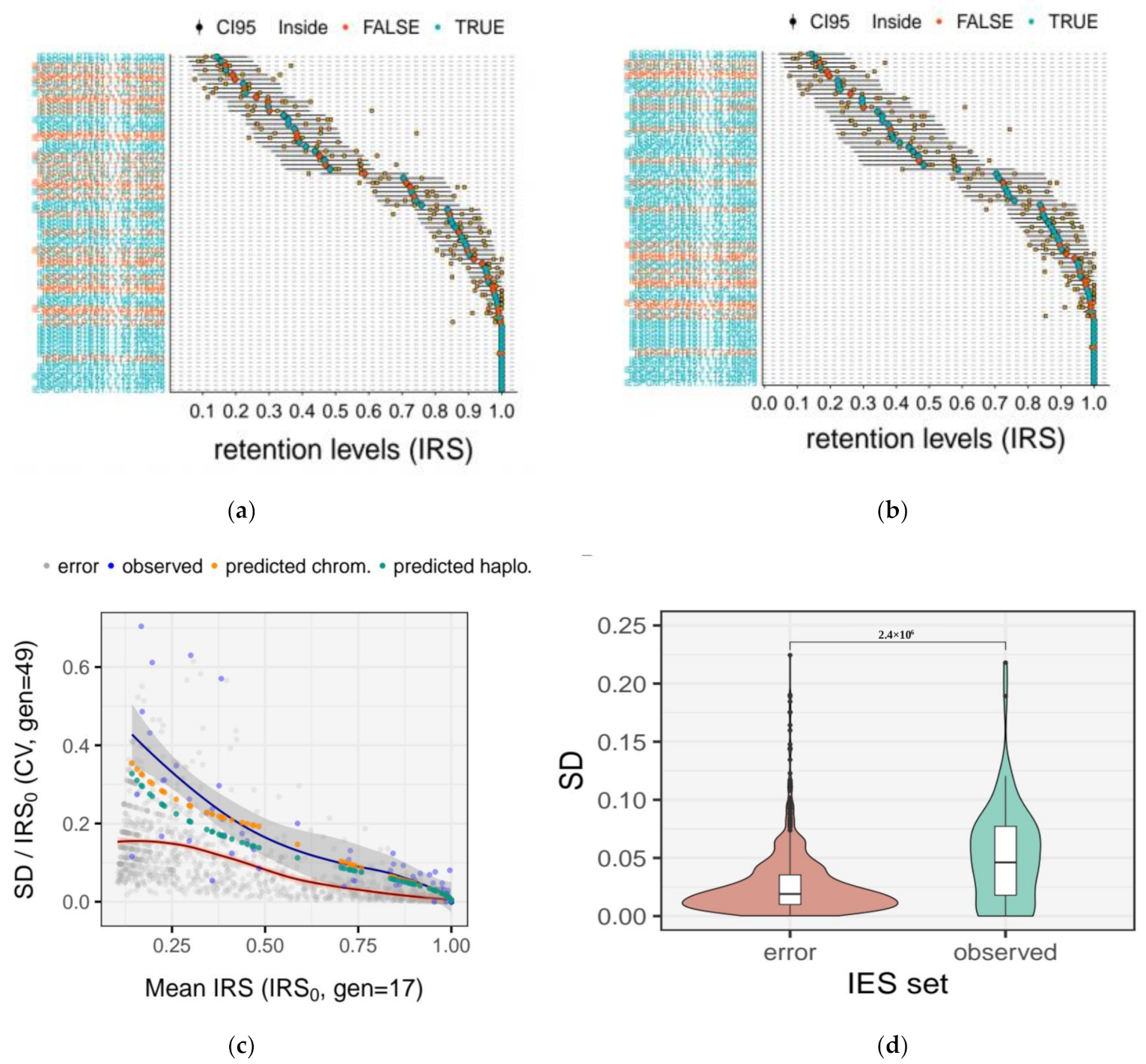
2.10. Experimental Estimates of Somatic Assortment
2.11. Simulation of Retention Levels and Confidence Intervals
2.12. Code Availability
3. Results
3.1. Single-Cell DNA Sequencing of the Paramecium Somatic Genome
3.2. Detection of AT-Rich Germline Sequences in the Paramecium Somatic Genome
3.3. IES Retention Levels across the First ~50 Amitotic Divisions Post Self-Fertilization
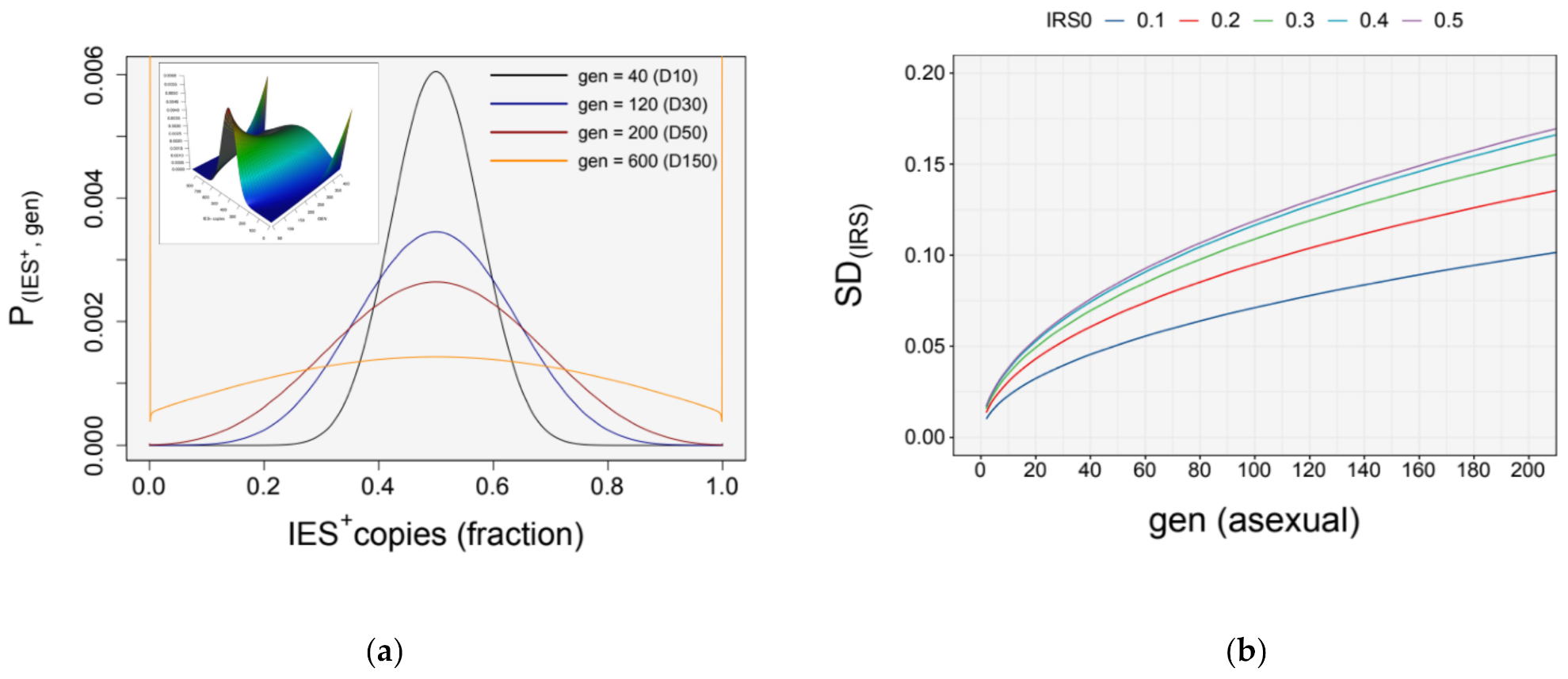
3.4. Simulation of Somatic Assortment
3.5. Somatic Assortment in Paramecium: Comparing Theoretical and Empirical Observations
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Assumptions
- The ploidy of the somatic nucleus, k, is assumed to be 860 (C).
- The total number of segregating units in the nucleus, N, is conserved, and amounts to 2 × k (1720) after DNA replication.
- Each daughter cell receives an equal number of copies, k, at each cell division.
- The number of successes is a natural number ranging from 0 to k.
- The process operates in a selection-free environment.
- 6.
- We assumed 115 somatic chromosomes (Chr)
- 7.
- The total number of segregating units, N, is conserved and amounts to 2 × k × Chr (197,800) after DNA replication.
- 8.
- Each daughter cell receives an equal number of copies, N/2, at each cell division.
- 9.
- The number of successes is a natural number ranging from 0 to N/2.
Appendix A.2. Mathematics
Appendix A.3. Rate of Somatic Assortment
Appendix A.4. Rate of Loss of Heterozygosity
References
- Child, C.M. Studies on the relation between amitosis and mitosis. Biol. Bull. 1907, 12, 89–114. [Google Scholar] [CrossRef]
- Conklin, E.G. Mitosis and amitosis. Biol. Bull. 1917, 33, 396–436. [Google Scholar] [CrossRef][Green Version]
- Pfitzer, P. Amitosis: A Historical Misinterpretation? Pathol. Res. Pract. 1980, 167, 292–300. [Google Scholar] [CrossRef]
- Flemming, W. Ueber Theilung und Kernformen bei Leukocyten, und über deren Attractionssphären. Arch. Für Mikrosk. Anat. 1891, 37, 249–298. [Google Scholar] [CrossRef]
- Macklin, C.C. Amitosis in cells growing in vitro. Biol. Bull. 1916, 30, 445–466. [Google Scholar] [CrossRef]
- Nakahara, W. Preliminary note on the nuclear division in the adipose cells of insects. Anat. Rec. 1917, 13, 81–86. [Google Scholar] [CrossRef]
- Lucchetta, E.M.; Ohlstein, B. Amitosis of Polyploid Cells Regenerates Functional Stem Cells in the Drosophila Intestine. Cell Stem Cell 2017, 20, 609–620.e6. [Google Scholar] [CrossRef] [PubMed]
- Miller, R.H. Amitosis and Endocytogenesis in the Fruit of Malus sylvestris. Ann. Bot. 1980, 46, 567–575. [Google Scholar] [CrossRef]
- Yiquan, C.; Binkung, W. A Study on Amitosis of the Nucleus of the Mammalian Cell. Cells Tissues Organs 1986, 127, 69–76. [Google Scholar] [CrossRef]
- Kuhn, E.M.; Therman, E.; Susman, B. Amitosis and endocycles in early cultured mouse trophoblast. Placenta 1991, 12, 251–261. [Google Scholar] [CrossRef]
- ORIAS, E. Evolution of Amitosis of the Ciliate Macronucleus: Gain of the Capacity to Divide. J. Protozool. 1991, 38, 217–221. [Google Scholar] [CrossRef] [PubMed]
- Fox, D.T.; Duronio, R.J. Endoreplication and polyploidy: Insights into development and disease. Development 2013, 140, 3–12. [Google Scholar] [CrossRef] [PubMed]
- Zielke, N.; Edgar, B.A.; DePamphilis, M.L. Endoreplication. Cold Spring Harb. Perspect. Biol. 2013, 5, a012948. [Google Scholar] [CrossRef] [PubMed]
- Schoenfelder, K.P.; Fox, D.T. The expanding implications of polyploidy. J. Cell Biol. 2015, 209, 485–491. [Google Scholar] [CrossRef]
- Erenpreisa, J.; Salmina, K.; Huna, A.; Kosmacek, E.A.; Cragg, M.S.; Ianzini, F.; Anisimov, A.P. Polyploid tumour cells elicit paradiploid progeny through depolyploidizing divisions and regulated autophagic degradation. Cell Biol. Int. 2011, 35, 687–695. [Google Scholar] [CrossRef]
- Duncan, A.W.; Taylor, M.H.; Hickey, R.D.; Hanlon Newell, A.E.; Lenzi, M.L.; Olson, S.B.; Finegold, M.J.; Grompe, M. The ploidy conveyor of mature hepatocytes as a source of genetic variation. Nature 2010, 467, 707–710. [Google Scholar] [CrossRef] [PubMed]
- Duncan, A.W.; Hanlon Newell, A.E.; Bi, W.; Finegold, M.J.; Olson, S.B.; Beaudet, A.L.; Grompe, M. Aneuploidy as a mechanism for stress-induced liver adaptation. J. Clin. Investig. 2012, 122, 3307–3315. [Google Scholar] [CrossRef]
- Lyn, D.H. Phylum CILIOPHORA—Conjugating, Ciliated Protists with Nuclear Dualism. In The Ciliated Protozoa; Lyn, D.H., Ed.; Springer: Dordrecht, The Netherlands, 2010; pp. 89–120. [Google Scholar]
- Beale, G.H.; Preer Jr., J. R. Micronuclei and Macronuclei. In Paramecium: Genetics and epigenetics; CRC Press: Boca Raton, FL, USA, 2008; pp. 139–149. ISBN 9780415257855. [Google Scholar]
- Woodard, J.; Gelber, B.; Swift, H. Nucleoprotein changes during the mitotic cycle in Paramecium aurelia. Exp. Cell Res. 1961, 23, 258–264. [Google Scholar] [CrossRef]
- Preer, J.R.; Preer, L.B. The Size of Macronuclear DNA and Its Relationship to Models for Maintaining Genic Balance*†. J. Protozool. 1979, 26, 14–18. [Google Scholar] [CrossRef]
- Eisen, J.A.; Coyne, R.S.; Wu, M.; Wu, D.; Thiagarajan, M.; Wortman, J.R.; Badger, J.H.; Ren, Q.; Amedeo, P.; Jones, K.M.; et al. Macronuclear Genome Sequence of the Ciliate Tetrahymena thermophila, a Model Eukaryote. PLoS Biol. 2006, 4, e286. [Google Scholar] [CrossRef]
- Hamilton, E.P.; Kapusta, A.; Huvos, P.E.; Bidwell, S.L.; Zafar, N.; Tang, H.; Hadjithomas, M.; Krishnakumar, V.; Badger, J.H.; Caler, E.V.; et al. Structure of the germline genome of Tetrahymena thermophila and relationship to the massively rearranged somatic genome. Elife 2016, 5. [Google Scholar] [CrossRef]
- Orias, E.; Flacks, M. Macronuclear genetics of Tetrahymena. I. Random distribution of macronuclear gene copies in T. pyriformis, syngen 1. Genetics 1975, 79, 187–206. [Google Scholar] [CrossRef]
- Doerder, F.P.; Deak, J.C.; Lief, J.H. Rate of phenotypic assortment in Tetrahymena thermophila. Dev. Genet. 1992, 13, 126–132. [Google Scholar] [CrossRef] [PubMed]
- Berger, J.D.; Schmidt, H.J. Regulation of macronuclear DNA content in Paramecium tetraurelia. J. Cell Biol. 1978, 76, 116–126. [Google Scholar] [CrossRef] [PubMed]
- Spring, K.J.; Pham, S.; Zufall, R.A. Chromosome Copy Number Variation and Control in the Ciliate Chilodonella uncinata. PLoS ONE 2013, 8, e56413. [Google Scholar] [CrossRef][Green Version]
- Brito, P.H.; Guilherme, E.; Soares, H.; Gordo, I. Mutation accumulation in Tetrahymena. BMC Evol. Biol. 2010, 10, 354. [Google Scholar] [CrossRef] [PubMed]
- Xu, K.; Doak, T.G.; Lipps, H.J.; Wang, J.; Swart, E.C.; Chang, W.J. Copy number variations of 11 macronuclear chromosomes and their gene expression in Oxytricha trifallax. Gene 2012, 505, 75–80. [Google Scholar] [CrossRef]
- Bell, G. Isolation cultures. In Sex and Death in Protozoa; Cambridge University Press: Cambridge, UK, 1989; pp. 13–22. [Google Scholar]
- Merriam, E.V.; Bruns, P.J. Phenotypic assortment in Tetrahymena thermophila: Assortment kinetics of antibiotic-resistance markers, tsA, death, and the highly amplified rDNA locus. Genetics 1988, 120, 389–395. [Google Scholar] [CrossRef]
- Nanney, D.L.; Preparata, R.M. Genetic Evidence Concerning the Structure of the Tetrahymena thermophila Macronucleus*†. J. Protozool. 1979, 26, 2–9. [Google Scholar] [CrossRef]
- Arnaiz, O.; Mathy, N.; Baudry, C.; Malinsky, S.; Aury, J.M.; Denby Wilkes, C.; Garnier, O.; Labadie, K.; Lauderdale, B.E.; Le Mouël, A.; et al. The Paramecium Germline Genome Provides a Niche for Intragenic Parasitic DNA: Evolutionary Dynamics of Internal Eliminated Sequences. PLoS Genet. 2012, 8. [Google Scholar] [CrossRef]
- Guérin, F.; Arnaiz, O.; Boggetto, N.; Denby Wilkes, C.; Meyer, E.; Sperling, L.; Duharcourt, S.; Wilkes, C.D.; Meyer, E.; Sperling, L.; et al. Flow cytometry sorting of nuclei enables the first global characterization of Paramecium germline DNA and transposable elements. BMC Genom. 2017, 18, 327. [Google Scholar] [CrossRef]
- Duharcourt, S.; Betermier, M. Programmed Rearrangement in Ciliates: Paramecium. Microbiol. Spectr. 2014, 2. [Google Scholar] [CrossRef]
- Vitali, V.; Hagen, R.; Catania, F. Environmentally induced plasticity of programmed DNA elimination boosts somatic variability in Paramecium tetraurelia. Genome Res. 2019, 29, 1693–1704. [Google Scholar] [CrossRef] [PubMed]
- Duret, L.; Cohen, J.; Jubin, C.; Dessen, P.; Goût, J.F.; Mousset, S.; Aury, J.M.; Jaillon, O.; Noël, B.; Arnaiz, O.; et al. Analysis of sequence variability in the macronuclear DNA of Paramecium tetraurelia: A somatic view of the germline. Genome Res. 2008, 18, 585–596. [Google Scholar] [CrossRef]
- Catania, F.; McGrath, C.L.; Doak, T.G.; Lynch, M. Spliced DNA Sequences in the Paramecium Germline: Their Properties and Evolutionary Potential. Genome Biol. Evol. 2013, 5, 1200–1211. [Google Scholar] [CrossRef] [PubMed]
- Hagen, R.; Vitali, V.; Catania, F. Cross-Generational Effects and Non-random Developmental Response to Temperature Variation in Paramecium. Front. Cell Dev. Biol. 2020, 8, 1169. [Google Scholar] [CrossRef]
- Huang, L.; Ma, F.; Chapman, A.; Lu, S.; Xie, X.S. Single-Cell Whole-Genome Amplification and Sequencing: Methodology and Applications. Annu. Rev. Genom. Hum. Genet. 2015, 16, 79–102. [Google Scholar] [CrossRef]
- Pinard, R.; de Winter, A.; Sarkis, G.J.; Gerstein, M.B.; Tartaro, K.R.; Plant, R.N.; Egholm, M.; Rothberg, J.M.; Leamon, J.H. Assessment of whole genome amplification-induced bias through high-throughput, massively parallel whole genome sequencing. BMC Genom. 2006, 7, 216. [Google Scholar] [CrossRef]
- Sabina, J.; Leamon, J.H. Bias in whole genome amplification: Causes and considerations. In Whole Genome Amplification: Methods and Protocols, Methods in Molecular Biology; Humana Press Inc.: New York, NY, USA, 2015; Volume 1347, pp. 15–41. [Google Scholar]
- Maurer-Alcalá, X.X.; Knight, R.; Katz, L.A. Exploration of the germline genome of the ciliate chilodonella uncinata through single-cell omics (Transcriptomics and genomics). Mbio 2018, 9. [Google Scholar] [CrossRef] [PubMed]
- Börgstrom, E.; Paterlini, M.; Mold, J.E.; Frisen, J.; Lundeberg, J. Comparison of whole genome amplification techniques for human single cell exome sequencing. PLoS ONE 2017, 12, e0171566. [Google Scholar] [CrossRef]
- Van Der Plaetsen, A.S.; Deleye, L.; Cornelis, S.; Tilleman, L.; Van Nieuwerburgh, F.; Deforce, D. STR profiling and copy number variation analysis on single, preserved cells using current Whole Genome Amplification methods. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef]
- Deleye, L.; Tilleman, L.; Van Der Plaetsen, A.S.; Cornelis, S.; Deforce, D.; Van Nieuwerburgh, F. Performance of four modern whole genome amplification methods for copy number variant detection in single cells. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef]
- de Bourcy, C.F.A.; De Vlaminck, I.; Kanbar, J.N.; Wang, J.; Gawad, C.; Quake, S.R. A Quantitative Comparison of Single-Cell Whole Genome Amplification Methods. PLoS ONE 2014, 9, e105585. [Google Scholar] [CrossRef] [PubMed]
- Luquette, L.J.; Bohrson, C.L.; Sherman, M.A.; Park, P.J. Identification of somatic mutations in single cell DNA-seq using a spatial model of allelic imbalance. Nat. Commun. 2019, 10, 1–14. [Google Scholar] [CrossRef]
- Meier, A.; Fricke, E.; Fisch, E.; Baedker, S.; Wedler, H.; Korfhage, C. Genomic Analysis of Individual Cells by NGS and Real-Time PCR. Available online: www.qiagen.com/at/resources/resourcedetail?id=e97d2c8b-98be-4ef7-be78-2c0c5f414cf3&lang=en, (accessed on 8 September 2021).
- Lasken, R.S.; Egholm, M. Whole genome amplification: Abundant supplies of DNA from precious samples or clinical specimens. Trends Biotechnol. 2003, 21, 531–535. [Google Scholar] [CrossRef] [PubMed]
- Videvall, E. Plasmodium parasites of birds have the most AT-rich genes of eukaryotes. Microb. Genom. 2018, 4. [Google Scholar] [CrossRef] [PubMed]
- Beisson, J.; Bétermier, M.; Bré, M.H.; Cohen, J.; Duharcourt, S.; Duret, L.; Kung, C.; Malinsky, S.; Meyer, E.; Preer, J.R.; et al. Maintaining clonal paramecium tetraurelia cell lines of controlled age through daily reisolation. Cold Spring Harb. Protoc. 2010, 5, pdb–prot5361. [Google Scholar] [CrossRef] [PubMed]
- Taylor, C.V.; van Wagtendonk, W.J. Growth studies of colpoda duodenaria in the absence of other living organisms. J. Cell. Comp. Physiol. 1941, 17, 349–353. [Google Scholar] [CrossRef]
- Li, H.; Handsaker, B.; Wysoker, A.; Fennell, T.; Ruan, J.; Homer, N.; Marth, G.; Abecasis, G.; Durbin, R. The Sequence Alignment/Map format and SAMtools. Bioinformatics 2009. [Google Scholar] [CrossRef]
- Aury, J.-M.; Jaillon, O.; Duret, L.; Noel, B.; Jubin, C.; Porcel, B.M.; Ségurens, B.; Daubin, V.; Anthouard, V.; Aiach, N.; et al. Global trends of whole-genome duplications revealed by the ciliate Paramecium tetraurelia. Nature 2006, 444, 171–178. [Google Scholar] [CrossRef]
- Frampton, M.; Houlston, R. Generation of Artificial FASTQ Files to Evaluate the Performance of Next-Generation Sequencing Pipelines. PLoS ONE 2012, 7, e49110. [Google Scholar] [CrossRef]
- R Core Team, R. A Language and Environment for Statistical Computing 2020; R Foundation for Statistical Computing: Vienna, Austria. Available online: https://www.R-project.org/ (accessed on 8 September 2021).
- Langmead, B.; Trapnell, C.; Pop, M.; Salzberg, S.L. Ultrafast and memory-efficient alignment of short DNA sequences to the human genome. Genome Biol. 2009, 10, R25. [Google Scholar] [CrossRef]
- Denby Wilkes, C.; Arnaiz, O.; Sperling, L. ParTIES: A toolbox for Paramecium interspersed DNA elimination studies. Bioinformatics 2016, 32, 599–601. [Google Scholar] [CrossRef]
- Preer, J.R. Quantitative predictions of random segregation models of the ciliate macronucleus. Genet. Res. 1976, 27, 227–238. [Google Scholar] [CrossRef]
- Nyberg, D. Are macronuclear subunits in Paramecium functionally diploid? Genet. Res. 1976, 27, 239–248. [Google Scholar] [CrossRef]
- Sonneborn, T.M. Recent Advances in the Genetics of Paramecium and Euplotes. Adv. Genet. 1947, 1, 263–358. [Google Scholar] [CrossRef] [PubMed]
- Swart, E.C.; Bracht, J.R.; Magrini, V.; Minx, P.; Chen, X.; Zhou, Y.; Khurana, J.S.; Goldman, A.D.; Nowacki, M.; Schotanus, K.; et al. The Oxytricha trifallax Macronuclear Genome: A Complex Eukaryotic Genome with 16,000 Tiny Chromosomes. PLoS Biol. 2013, 11, e1001473. [Google Scholar] [CrossRef]
- Wickert, S.; Nangle, L.; Shevel, S.; Orias, E. Tetrahymena macronuclear genome mapping: Colinearity of macronuclear coassortment groups and the micronuclear map on chromosome 1L. Genetics 2000, 154, 1155–1167. [Google Scholar] [CrossRef] [PubMed]
- Wong, L.; Klionsky, L.; Wickert, S.; Merriam, V.; Orias, E.; Hamilton, E.P. Autonomously replicating macronuclear DNA pieces are the physical basis of genetic coassortment groups in Tetrahymena thermophila. Genetics 2000, 155, 1119–1125. [Google Scholar] [CrossRef] [PubMed]
- Takagi, Y.; Nobuoka, T.; Doi, M. Clonal lifespan of Paramecium tetraurelia: Effect of selection on its extension and use of fissions for its determination. J. Cell Sci. 1987, 88 Pt 1, 129–138. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; West, J.A.; Zufall, R.A.; Azevedo, R.B.R. Amitosis confers benefits of sex in the absence of sex to Tetrahymena. bioRxiv 2019, 794735. [Google Scholar]
- Zufall, R.A.; McGrath, C.L.; Muse, S.V.; Katz, L.A. Genome architecture drives protein evolution in ciliates. Mol. Biol. Evol. 2006, 23, 1681–1687. [Google Scholar] [CrossRef][Green Version]
- Lage, J.M.; Leamon, J.H.; Pejovic, T.; Hamann, S.; Lacey, M.; Dillon, D.; Segraves, R.; Vossbrinck, B.; González, A.; Pinkel, D.; et al. Whole genome analysis of genetic alterations in small DNA samples using hyperbranched strand displacement amplification and array-CGH. Genome Res. 2003, 13, 294–307. [Google Scholar] [CrossRef] [PubMed]
- Nanney, D.L. Mating Tactics and Ecogenetic Strategies. In Experimental Ciliatology: An Introduction to Genetic and Developmental Analysis in Ciliates; John Wiley & Sons, Inc.: New York, NY, USA, 1980; pp. 85–94. ISBN 0471060089. [Google Scholar]
- Catania, F.; Wurmser, F.; Potekhin, A.A.; Przyboś, E.; Lynch, M. Genetic diversity in the Paramecium aurelia species complex. Mol. Biol. Evol. 2009, 26, 421–431. [Google Scholar] [CrossRef] [PubMed]
- Johri, P.; Krenek, S.; Marinov, G.K.; Doak, T.G.; Berendonk, T.U.; Lynch, M. Population Genomics of Paramecium Species. Mol. Biol. Evol. 2017, 34, 1194–1216. [Google Scholar] [CrossRef]
- Gilley, D.; Blackburn, E.H. Lack of telomere shortening during senescence in Paramecium. Proc. Natl. Acad. Sci. USA 1994, 91, 1955–1958. [Google Scholar] [CrossRef] [PubMed]
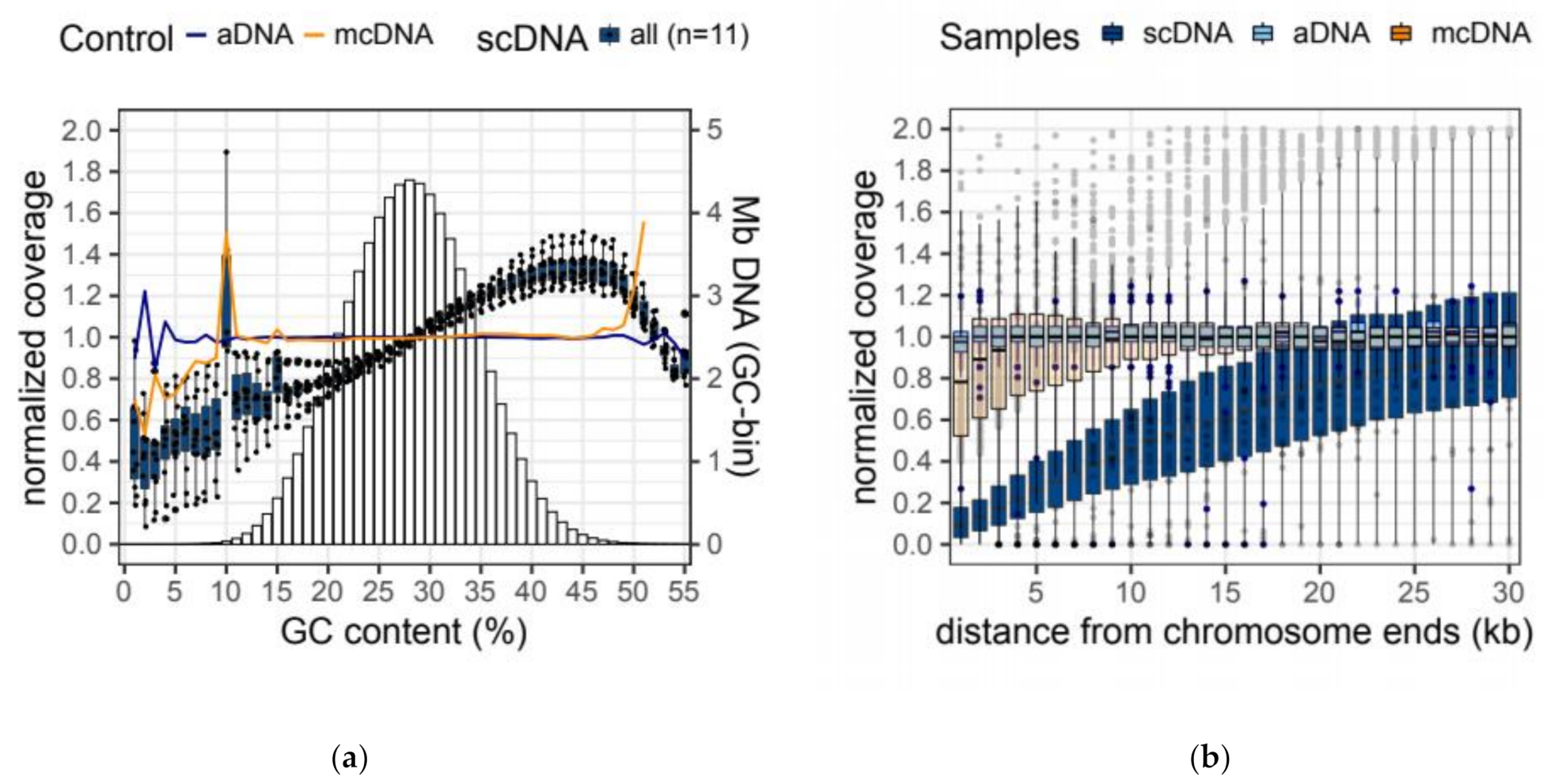

| Sample | GC Bias | Terminal Bias | ||||
|---|---|---|---|---|---|---|
| Coverage | Coverage | |||||
| bGC | 16th perc. (22% GC) | 84th perc. (34% GC) | bTer | 1 kb away | 30 kb away | |
| aDNA | 0.001 | 0.999 | 1.000 | 0.006 | 0.981 | 1.007 |
| mcDNA | −0.009 | 0.985 | 1.010 | 0.059 | 0.830 | 1.000 |
| scDNA | 0.163 ± 0.059 | 0.811 ± 0.043 | 1.160 ± 0.036 | 0.321 ± 0.025 | 0.140 ± 0.024 | 1.037 ± 0.029 |
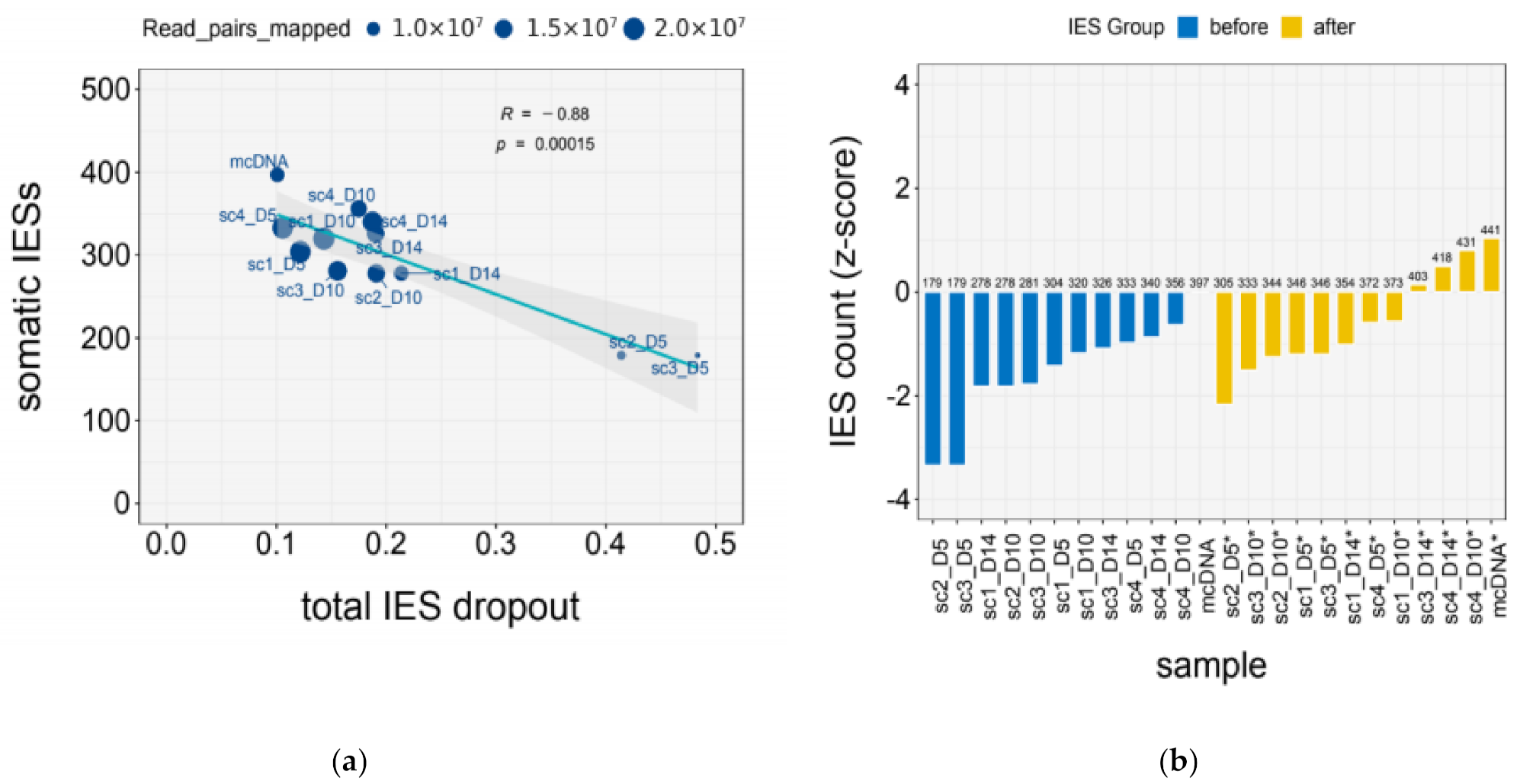
| Sample | Mapped (M) | IES Dropout | |||
|---|---|---|---|---|---|
| Total | Terminal | GC | Residual | ||
| mcDNA | 10.92 | 0.10 | 0.05 | 0.00 | 0.06 |
| scDNA_1x | 11.29 ± 3.62 | 0.28 ± 0.14 | 0.11 ± 0.02 | 0.11 ± 0.09 | 0.06 ± 0.02 |
| scDNA_2x | 19.67 ± 0.51 | 0.12 ± 0.02 | 0.08 ± 0.01 | 0.02 ± 0.01 | 0.03 ± 0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vitali, V.; Rothering, R.; Catania, F. Fifty Generations of Amitosis: Tracing Asymmetric Allele Segregation in Polyploid Cells with Single-Cell DNA Sequencing. Microorganisms 2021, 9, 1979. https://doi.org/10.3390/microorganisms9091979
Vitali V, Rothering R, Catania F. Fifty Generations of Amitosis: Tracing Asymmetric Allele Segregation in Polyploid Cells with Single-Cell DNA Sequencing. Microorganisms. 2021; 9(9):1979. https://doi.org/10.3390/microorganisms9091979
Chicago/Turabian StyleVitali, Valerio, Rebecca Rothering, and Francesco Catania. 2021. "Fifty Generations of Amitosis: Tracing Asymmetric Allele Segregation in Polyploid Cells with Single-Cell DNA Sequencing" Microorganisms 9, no. 9: 1979. https://doi.org/10.3390/microorganisms9091979
APA StyleVitali, V., Rothering, R., & Catania, F. (2021). Fifty Generations of Amitosis: Tracing Asymmetric Allele Segregation in Polyploid Cells with Single-Cell DNA Sequencing. Microorganisms, 9(9), 1979. https://doi.org/10.3390/microorganisms9091979






