An Improved Approach to Automated Measurement of Body Condition Score in Dairy Cows Using a Three-Dimensional Camera System
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
Statistical Analyses
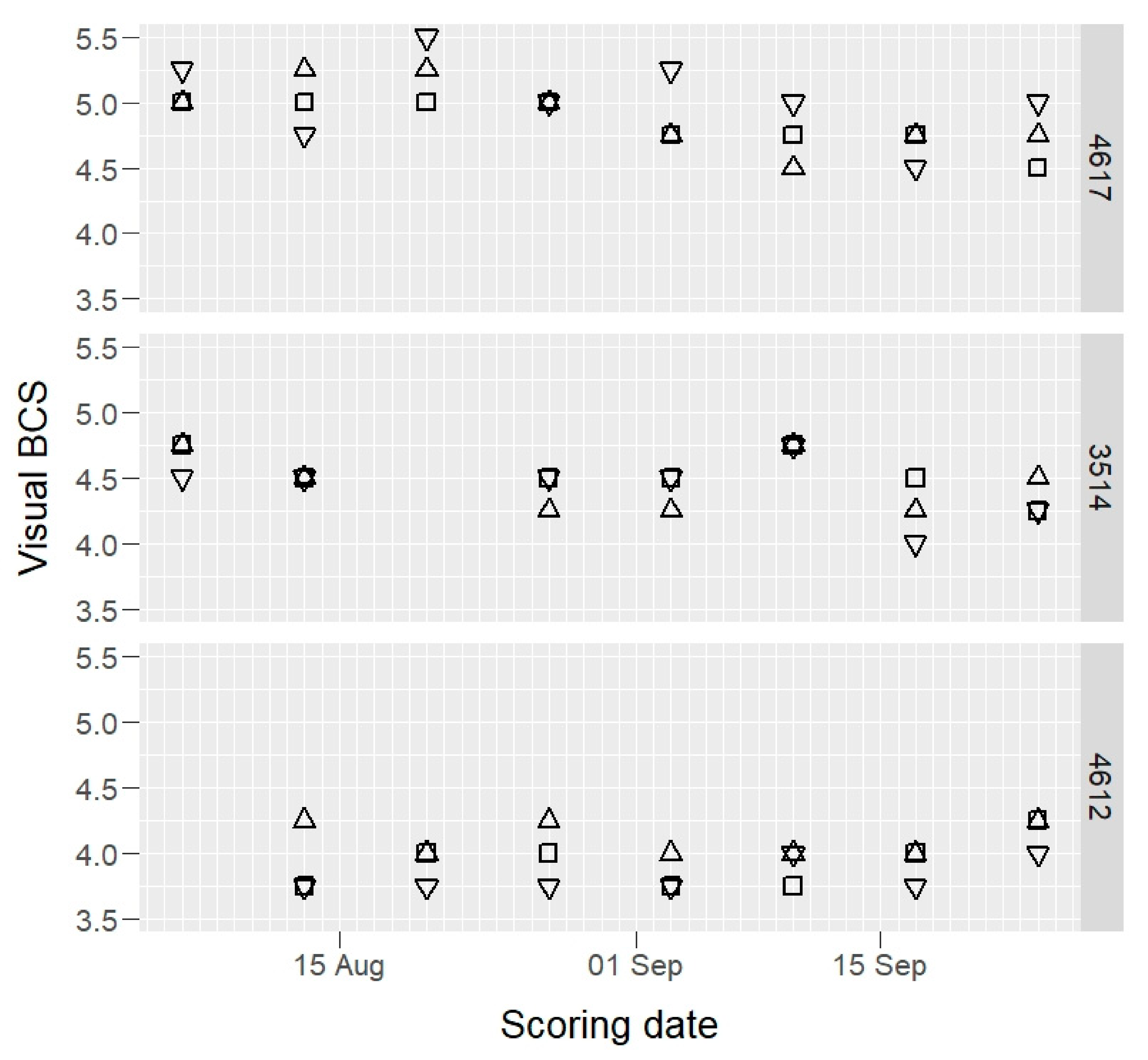
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bewley, J.M.; Schutz, M.M. REVIEW: An Interdisciplinary Review of Body Condition Scoring for Dairy Cattle. Prof. Anim. Sci. 2008, 24, 507–529. [Google Scholar] [CrossRef] [Green Version]
- Roche, J.R.; Friggens, N.C.; Kay, J.K.; Fisher, M.W.; Stafford, K.J.; Berry, D.P. Invited review: Body condition score and its association with dairy cow productivity, health, and welfare. J. Dairy Sci. 2009, 92, 5769–5801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carvalho, P.D.; Souza, A.H.; Amundson, M.C.; Hackbart, K.S.; Fuenzalida, M.J.; Herlihy, M.M.; Ayres, H.; Dresch, A.R.; Vieira, L.M.; Guenther, J.N.; et al. Relationships between fertility and postpartum changes in body condition and body weight in lactating dairy cows. J. Dairy Sci. 2014, 97, 3666–3683. [Google Scholar] [CrossRef] [Green Version]
- Manriquez, D.; Thatcher, W.W.; Santos, J.E.P.; Chebel, R.C.; Galvão, K.N.; Schuenemann, G.M.; Bicalho, R.C.; Gilbert, R.O.; Rodriguez-Zas, S.; Seabury, C.M.; et al. Effect of body condition change and health status during early lactation on performance and survival of Holstein cows. J. Dairy Sci. 2021, 104, 12785–12799. [Google Scholar] [CrossRef] [PubMed]
- Wildman, E.E.; Jones, G.M.; Wagner, P.E.; Boman, R.L.; Troutt, H.F., Jr.; Lesch, T.N. A dairy cow body condition scoring system and its relationship to selected production characteristics. J. Dairy Sci. 1982, 65, 495–501. [Google Scholar] [CrossRef]
- Earle, D.F. A guide to scoring dairy cow condition. J. Agric. 1976, 74, 228–231. [Google Scholar]
- Macdonald, K.A.; Roche, J.R. Condition Scoring Made Easy. Condition Scoring Dairy Herds, 1st ed.; Dexcel Ltd.: Hamilton, New Zealand, 2004; ISBN 0-476-00217-6. [Google Scholar]
- Roche, J.R.; Dillon, P.G.; Stockdale, C.R.; Baumgard, L.H.; VanBaale, M.J. Relationships among international body condition scoring systems. J. Dairy Sci. 2004, 87, 3076–3079. [Google Scholar] [CrossRef] [Green Version]
- Qiao, Y.; Kong, H.; Clark, C.; Lomax, S.; Su, D.; Eiffert, S.; Sukkarieh, S. Intelligent perception for cattle monitoring: A review for cattle identification, body condition score evaluation, and weight estimation. Comput. Electron. Agric. 2021, 185, 106143. [Google Scholar] [CrossRef]
- Mullins, I.L.; Truman, C.M.; Campler, M.R.; Bewley, J.M.; Costa, J.H.C. Validation of a commercial automated body condition scoring system on a commercial dairy farm. Animals 2019, 9, 287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mandel, J.; Stiehler, R.D. Sensitivity—A criterion for the comparison of methods of test. J. Res. Natl. Bur. Stand. 1954, 53, 155–159. [Google Scholar] [CrossRef]
- Cleveland, W.S. Robust Locally Weighted Regression and Smoothing Scatterplots. J. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley: Reading, MA, USA, 1977. [Google Scholar]
- Lin, L.I. A Concordance Correlation Coefficient to Evaluate Reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar] [CrossRef] [PubMed]
- Altman, D.G.; Bland, J.M. Measurement in medicine: The analysis of method comparison studies. Statistician 1983, 32, 307–317. [Google Scholar] [CrossRef]
- Hannah, M.C.; Giri, K.; Albornoz, R.I.; Gourley, C.J.P.; Awty, I.M.; Wales, W.J. Sensitivity by variance components—A flexible criterion for comparison of measurement methods. 2021. in preparation. [Google Scholar]
- Galwey, N.W. Introduction to Mixed Modelling, beyond Regression and Analysis of Variance, 2nd ed.; John Wiley & Sons: Chichester, UK, 2014. [Google Scholar]
- Kristensen, E.; Dueholm, L.; Vink, D.; Andersen, J.E.; Jakobsen, E.B.; Illum-Nielsen, S.; Petersen, F.A.; Enevoldsen, C. Within- and across-person uniformity of body condition scoring in Danish Holstein cattle. J. Dairy Sci. 2006, 89, 3721–3728. [Google Scholar] [CrossRef]
- Francq, B.G.; Govaerts, B. How to regress and predict in a Bland-Altman plot? Review and contribution based on tolerance intervals and correlated-errors-in-variables models. Stat. Med. 2016, 35, 2328–2358. [Google Scholar] [CrossRef] [PubMed]
- Martins, B.M.; Mendes, A.L.C.; Silva, L.F.; Moreira, T.R.; Costa, J.H.C.; Rotta, P.P.; Chizzotti, M.L.; Marcondes, M.I. Estimating body weight, body condition score, and type traits in dairy cows using three dimensional cameras and manual body measurements. Livest. Sci. 2020, 236, 104054. [Google Scholar] [CrossRef]



| Model Parameters | Raw Camera | Refined Camera | Visual Scoring |
|---|---|---|---|
| Mean BCS | 4.50 | 4.49 | 4.44 |
| Variance components (×10−2): | |||
| Week () | 1.70 | 1.90 | 1.00 |
| Animal () | 3.75 | 4.63 | 7.36 |
| Camera (), or Scorer ) | 0.00 | 0.00 | 0.04 |
| Week.Day | 0.05 | 0.04 | |
| Week.Animal ( | 0.52 | 0.77 | 0.94 |
| Week.Camera (), or Week.Scorer () | 0.00 | 0.00 | 0.22 |
| Animal.Camera (), or Animal.Scorer () | 0.14 | 0.06 | 0.56 |
| Week.Day.Milking ( | 0.00 | 0.00 | |
| Week.Day.Animal ( | 0.00 | 0.06 | |
| Week.Day.Camera ( | 0.00 | 0.00 | |
| Week.Animal.Camera ( | 0.00 | 0.00 | |
| Week.Day.Milking.Animal ( | 0.00 | 0.12 | |
| Week.Day.Milking.Camera( | 0.02 | 0.03 | |
| Week.Day.Animal.Camera ( | 0.092 | 0.00 | |
| Week.Day.Milking.Animal.Camera ( | 0.00 | 0.00 | |
| Residual ( | 2.18 | 0.62 | 1.86 |
| Summary Statistics | Raw Camera | Refined Camera | Visual Scoring |
|---|---|---|---|
| For change within animal over time: | |||
| Actual SD, , (BCS) | 0.149 | 0.164 | 0.139 |
| Error SD, , (BCS) | 0.041 | 0.026 | 0.083 |
| Sensitivity, | 3.6 | 6.2 | 1.7 |
| Relative Sensitivity, RS, of camera to visual scoring | 2.1 | 3.7 | |
| Rate of change in BCS, β, (BCS/Month) | −0.18 | −0.19 | −0.17 |
| Time to detect BCS change of , (Days) | 21 | 12 | 44 |
| For differences between animals at the same week: | |||
| Actual SD, , (BCS) | 0.207 | 0.232 | 0.288 |
| Error SD, , (BCS) | 0.048 | 0.030 | 0.090 |
| Sensitivity | 4.3 | 7.8 | 3.2 |
| Relative Sensitivity, RS, of camera to visual scoring | 1.3 | 2.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albornoz, R.I.; Giri, K.; Hannah, M.C.; Wales, W.J. An Improved Approach to Automated Measurement of Body Condition Score in Dairy Cows Using a Three-Dimensional Camera System. Animals 2022, 12, 72. https://doi.org/10.3390/ani12010072
Albornoz RI, Giri K, Hannah MC, Wales WJ. An Improved Approach to Automated Measurement of Body Condition Score in Dairy Cows Using a Three-Dimensional Camera System. Animals. 2022; 12(1):72. https://doi.org/10.3390/ani12010072
Chicago/Turabian StyleAlbornoz, Rodrigo I., Khageswor Giri, Murray C. Hannah, and William J. Wales. 2022. "An Improved Approach to Automated Measurement of Body Condition Score in Dairy Cows Using a Three-Dimensional Camera System" Animals 12, no. 1: 72. https://doi.org/10.3390/ani12010072
APA StyleAlbornoz, R. I., Giri, K., Hannah, M. C., & Wales, W. J. (2022). An Improved Approach to Automated Measurement of Body Condition Score in Dairy Cows Using a Three-Dimensional Camera System. Animals, 12(1), 72. https://doi.org/10.3390/ani12010072






