Population Dynamics of American Bullfrog (Lithobates catesbeianus) and Implications for Control
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
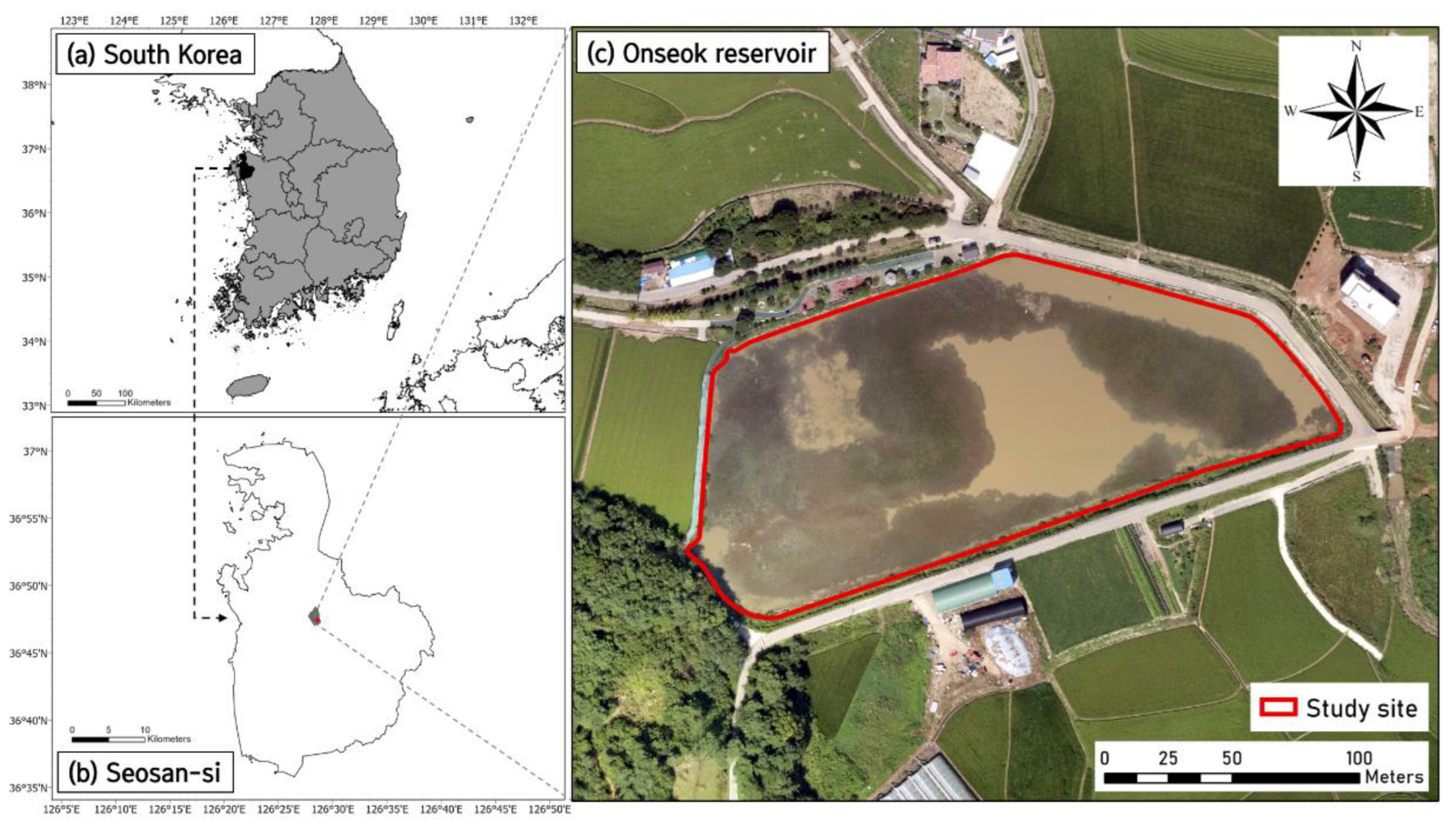
2.1. Study Site
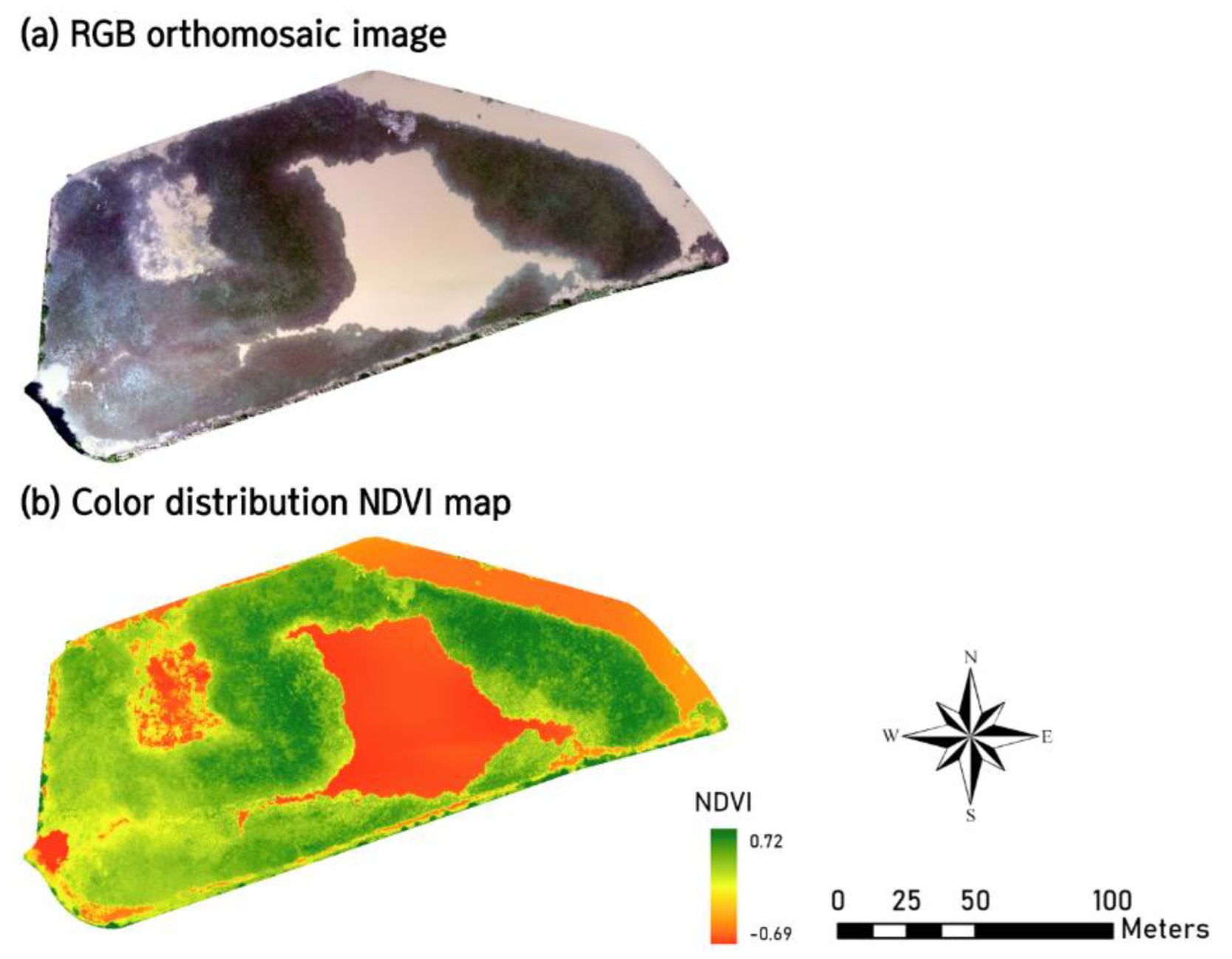
2.2. Collecting Environmental Data
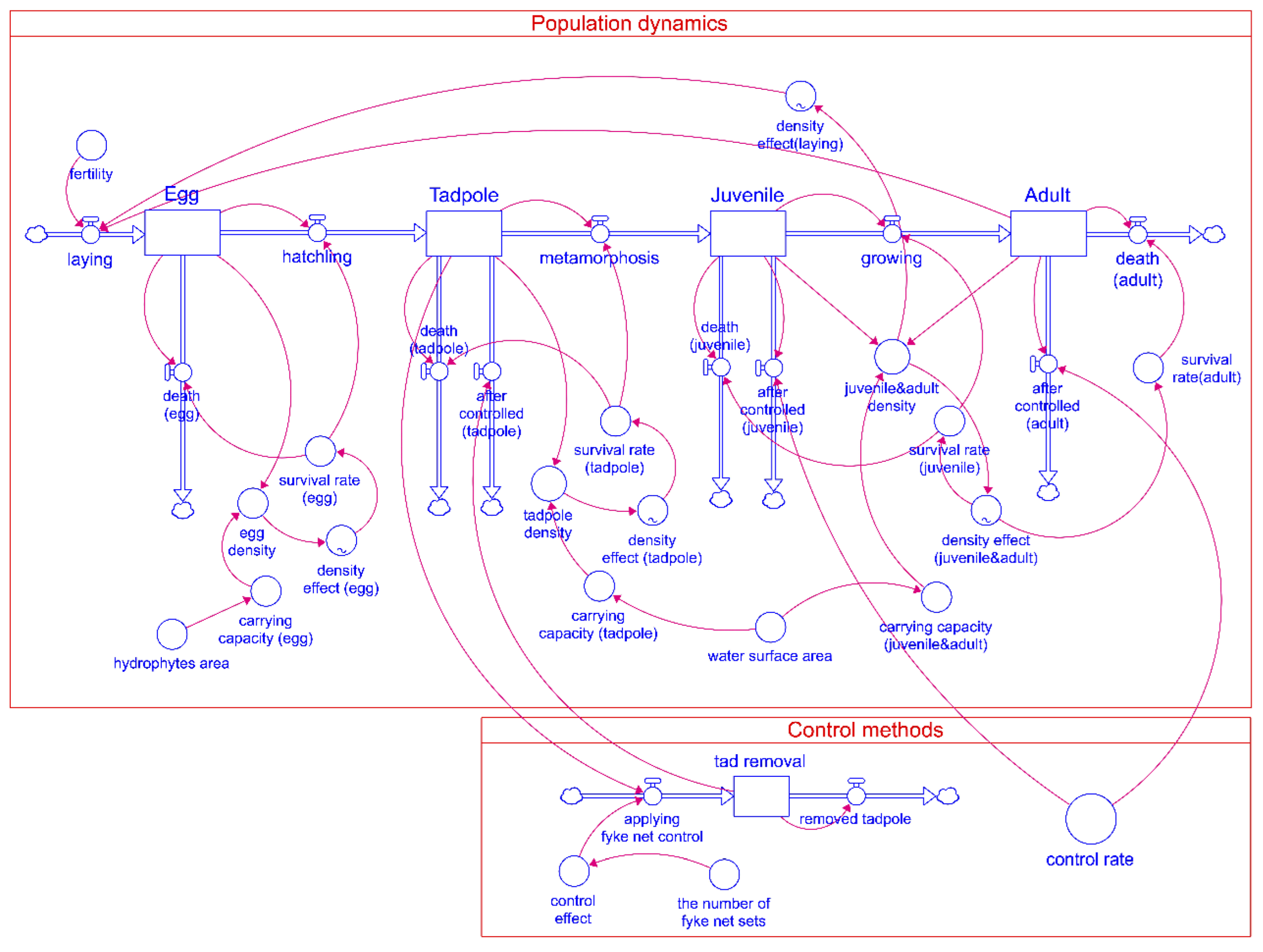
2.3. Dynamic Population Model for L. catesbeianus
2.4. Model Implementation
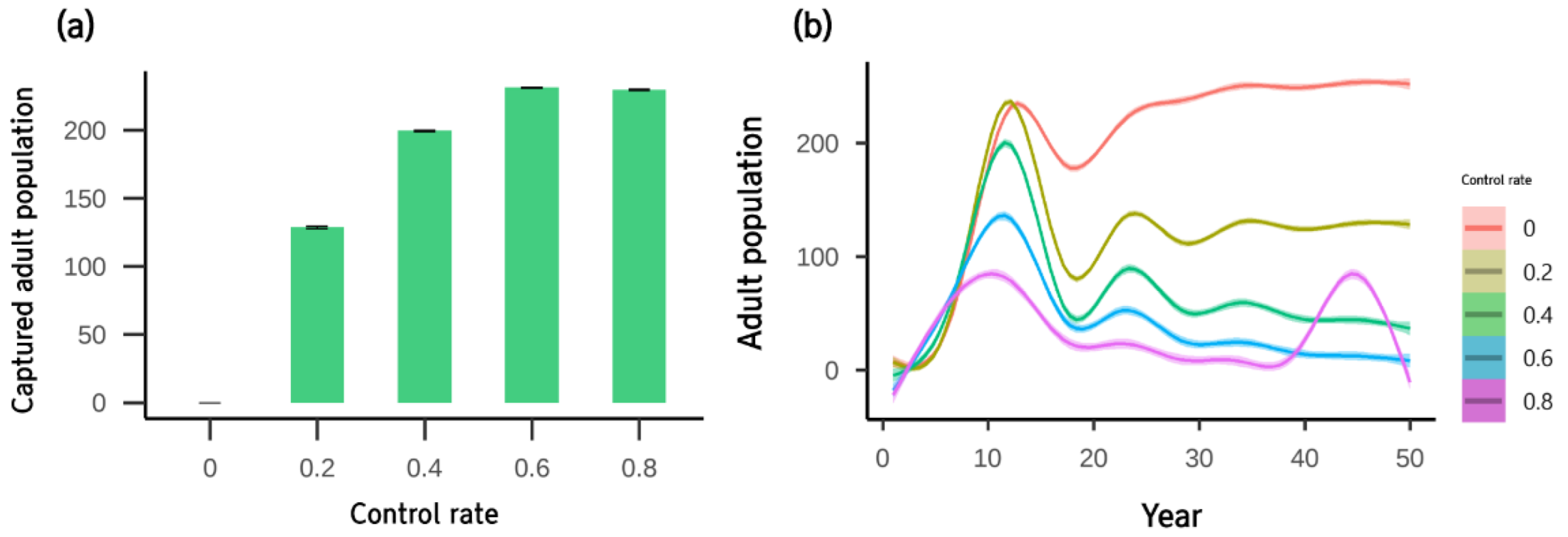
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- U.S. Congress, Office of Technology and Assessment. Harmful Non-Indigenous Species in the United States; U.S. Government Printing Office: Washington, DC, USA, 1993.
- Hoddle, M.S. Restoring Balance: Using Exotic Species to Control Invasive Exotic Species. Conserv. Biol. 2004, 18, 38–49. [Google Scholar] [CrossRef] [Green Version]
- MacDougall, A.S.; Turkington, R. Are invasive species the drivers or passengers of change in degraded ecosystems? Ecology 2005, 86, 42–55. [Google Scholar] [CrossRef] [Green Version]
- Burdyshaw, C. Detailed Discussion of the Laws Concerning Invasive Species. In Animal Law Information; Animal Legal & Historical Center, Michigan State University College of Law: East Lansing, MI, USA, 2011. [Google Scholar]
- Lowe, S.; Browne, M.; Boudjelas, S.; De Poorter, M. 100 of the World’s Worst Invasive Alien Species: A Selection from the Global Invasive Species Database; The Invasive Species Specialist Group (ISSG): Auckland, New Zealand, 2000. [Google Scholar]
- Lever, C. Naturalized Reptiles and Amphibians of the World; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Ficetola, G.F.; Thuiller, W.; Miaud, C. Prediction and Validation of the Potential Global Distribution of a Problematic Alien Invasive Species—The American Bullfrog. Divers. Distrib. 2007, 13, 476–485. [Google Scholar] [CrossRef]
- Garner, T.W.J.; Perkins, M.W.; Govindarajulu, P.; Seglie, D.; Walker, S.; Cunningham, A.A.; Fisher, M.C. The Emerging Amphibian Pathogen Batrachochytrium Dendrobatidis Globally Infects Introduced Populations of the North American Bullfrog, Rana Catesbeiana. Biol. Lett. 2006, 2, 455–459. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, H.; Baek, T.; Speare, R.; Webb, R.; Park, S.; Kim, T.; Lasater, K.; Shin, S.; Son, S.; Park, J.; et al. First Detection of the Amphibian Chytrid Fungus Batrachochytrium Dendrobatidis in Free-Ranging Populations of Amphibians on Mainland Asia: Survey in South Korea. Dis. Aquat. Org. 2009, 86, 9–13. [Google Scholar] [CrossRef] [Green Version]
- Wei, Y.; Xu, K.; Zhu, D.; Chen, X.; Wang, X. Early-Spring Survey for Batrachochytrium Dendrobatidis in Wild Rana Dybowskii in Heilongjiang Province, China. Dis. Aquat. Org. 2010, 92, 241–244. [Google Scholar] [CrossRef]
- Flecker, A.S.; Feifarek, B.P.; Taylor, B.W. Ecosystem Engineering by a Tropical Tadpole: Density-Dependent Effects on Habitat Structure and Larval Growth Rates. Copeia 1999, 1999, 495. [Google Scholar] [CrossRef]
- Pryor, G.S. Growth Rates and Digestive Abilities of Bullfrog Tadpoles (Rana Catesbeiana) Fed Algal Diets. J. Herpetol. 2003, 37, 560–566. [Google Scholar] [CrossRef]
- Kraus, F. Alien Reptiles and Amphibians: A Scientific Compendium and Analysis; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Snow, N.P.; Witmer, G. American Bullfrogs as Invasive Species: A Review of the Introduction, Subsequent Problems, Management Options, and Future Directions. In Proceedings of the 24th Vertebrate Pest Conference, Sacramento, CA, USA, 22–25 February 2010; Timm, R.M., Fagerstone, K.A., Eds.; University of California, Davis: Davis, CA, USA, 2010; pp. 86–89. [Google Scholar]
- Borzée, A.; Kosch, T.A.; Kim, M.; Jang, Y. Introduced Bullfrogs Are Associated with Increased Batrachochytrium Dendrobatidis Prevalence and Reduced Occurrence of Korean Treefrogs. PLoS ONE 2017, 12, e0177860. [Google Scholar]
- Kim, H.K. Biology of the Bullfrog (Rana Catesbeiana). J. Korean Res. Inst. Better Living (Ewha Womans Univ.) 1972, 8, 67–92. [Google Scholar]
- Oh, H.; Hong, C. Current Conditions of Habitat for Rana Catesbeiana and Trachemys Scripta Elegans Imported to Jeju-Do, Including Proposed Management Plans. Korean J. Environ. Ecol. 2007, 21, 311–317. (In Korean) [Google Scholar]
- National Institute of Ecology. Information on Alien Species in Korea (I); National Institute of Ecology: Seocheon, Korea, 2014; p. 246. (In Korean)
- Kil, J.H.; Hwang, S.M.; Lee, D.H.; Kim, D.E.; Kim, Y.H.; Lee, C.W.; Kim, H.M.; Kim, M.J.; Kim, J.M.; Oh, K.J. Alien Species in Korea; National Institute of Environmental Research: Incheon, Korea, 2011; p. 138. (In Korean) [Google Scholar]
- Park, D.; Min, M.S.; Lasater, K.; Song, J.Y.; Suh, J.H.; Son, S.H.; Kaplan, R. Conservation of Amphibians in South Korea. In Amphibian Biology, Conservation of Amphibians of the Eastern Hemisphere; Das, I., Heatwole, H., Eds.; Pelagic Publishing: Exeter, UK, 2014; Volume 11, pp. 52–88. [Google Scholar]
- Groffen, J.; Kong, S.; Jang, Y.; Borzée, A. The Invasive American Bullfrog (Lithobates Catesbeianus) in the Republic of Korea: History and Recommendations for Population Control. Manag. Biol. Invasion 2019, 10, 517–535. [Google Scholar] [CrossRef] [Green Version]
- Ministry of Environment. Identification of Alien Animals Introduced and Ecosystem Risk Classification Study in Korea; Ministry of Environment: Gwacheon, Korea, 2006; p. 254. (In Korean)
- Ministry of Environment. A Study on the Monitoring System and Management Plan for Invasive Alien Species; Ministry of Environment: Gwacheon, Korea, 2006; p. 219. (In Korean)
- Adams, M.J.; Pearl, C.A. Problems and Opportunities Managing Invasive Bullfrogs: Is There Any Hope? In Biological Invaders in Inland Waters: Profiles, Distribution, and Threats; Gherardi, F., Ed.; Springer: Dordrecht, The Netherlands, 2007; pp. 679–693. [Google Scholar]
- Kim, D.B.; Koo, A.K. A Study on the Current Status and Improvement of Ecosystem Disturbance Species. J. Environ. Policy Adm. 2021, 29, 59–81. (In Korean) [Google Scholar]
- Cecil, S.G.; Just, J.J. Survival Rate, Population Density and Development of a Naturally Occurring Anuran Larvae (Rana Catesbeiana). Copeia 1979, 1979, 447. [Google Scholar] [CrossRef]
- Schwalbe, C.R.; Rosen, P.C. Preliminary Report on Effect of Bullfrogs in Wetland Herpetofaunas in Southeastern Arizona. In Management of Amphibians, Reptiles, and Small Mammals in North America; Szaro, R.C., Severson, K.E., Patton, D.R., Eds.; General Technical Report (RM-166); US Department of Agriculture, Forest Service: Fort Collins, CO, USA, 1988; pp. 166–173. [Google Scholar]
- Govindarajulu, P.; Altwegg, R.; Anholt, B.R. Matrix Model Investigation of Invasive Species Control: Bullfrogs on Vancouver Island. Ecol. Appl. 2005, 15, 2161–2170. [Google Scholar] [CrossRef] [Green Version]
- Giovanelli, J.G.; Haddad, C.F.; Alexandrino, J. Predicting the Potential Distribution of the Alien Invasive American Bullfrog (Lithobates Catesbeianus) in Brazil. Biol. Invasions 2008, 10, 585–590. [Google Scholar] [CrossRef]
- Sibly, R.M.; Hone, J. Population Growth Rate and Its Determinants: An Overview. Phil. Trans. R. Soc. Lond. B 2002, 357, 1153–1170. [Google Scholar] [CrossRef]
- Schaub, M.; Abadi, F. Integrated Population Models: A Novel Analysis Framework for Deeper Insights into Population Dynamics. J. Ornithol. 2011, 152, 227–237. [Google Scholar] [CrossRef] [Green Version]
- Dennis, B.; Desharnais, R.A.; Cushing, J.M.; Costantino, R.F. Nonlinear Demographic Dynamics: Mathematical Models, Statistical Methods, and Biological Experiments. Ecol. Monogr. 1995, 65, 261–282. [Google Scholar] [CrossRef]
- Ramsey, D.S.; Parkes, J.; Morrison, S.A. Quantifying Eradication Success: The Removal of Feral Pigs from Santa Cruz Island, California. Conserv. Biol. 2009, 23, 449–459. [Google Scholar] [CrossRef]
- Davis, A.J.; Hooten, M.B.; Miller, R.S.; Farnsworth, M.L.; Lewis, J.; Moxcey, M.; Pepin, K.M. Inferring Invasive Species Abundance Using Removal Data from Management Actions. Ecol. Appl. 2016, 26, 2339–2346. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Davis, A.J.; Farrar, R.; Jump, B.; Hall, P.; Guerrant, T.; Pepin, K.M. An Efficient Method of Evaluating Multiple Concurrent Management Actions on Invasive Populations. Ecol. Appl. 2022, 32, e2623. [Google Scholar] [CrossRef] [PubMed]
- Dolbeer, R.A. Population Dynamics: The Foundation of Wildlife Damage Management for the 21st Century. In Proceedings of the Vertebrate Pest Conference, Costa Mesa, CA, USA, 2–5 March 1998; Volume 18, pp. 2–11. [Google Scholar]
- Cohen-Cline, H.; Turkheimer, E.; Duncan, G.E. Access to green space, physical activity and mental health: A twin study. J. Epidemiol. Community Health 2015, 69, 523–529. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gandhi, G.M.; Parthiban, B.S.; Thummalu, N.; Christy, A. Ndvi: Vegetation change detection using remote sensing and gis—A case study of Vellore District. Procedia Comput. Sci. 2015, 57, 1199–1210. [Google Scholar] [CrossRef]
- Fatemi, M.; Narangifard, M. Monitoring LULC changes and its impact on the LST and NDVI in District 1 of Shiraz City. Arab. J. Geosci. 2019, 12, 127. [Google Scholar] [CrossRef]
- Medeiros, C.I.; Both, C.; Kaefer, I.L.; Cechin, S.Z. Reproductive Phenology of the American Bullfrog in Subtropical Brazil: Photoperiod as a Main Determinant of Seasonal Activity. An. Acad. Bras. Ciênc. 2016, 88, 1909–1921. [Google Scholar] [CrossRef] [Green Version]
- Lemenkova, P. Detection of Vegetation Coverage in Urban Agglomeration of Brussels by NDVI Indicator Using ECognition Software and Remote Sensing Measurements. In Proceedings of the 3rd Int’l Conference “GIS and Remote Sensing. GIS Day”, Tsaghkadzor, Armenia, 17–19 November 2014; Manandyan, H., Ed.; Print Way: Tsaghkadzor, Armenia, 2014; pp. 112–119. [Google Scholar]
- Ministry of Environment. Guidebook for Invasive Alien Wild Animals and Plants; Ministry of Environment: Gwacheon, Korea, 2009; p. 127. (In Korean)
- Verhulst, P.F. Notice Sur La Loi Que La Population Suit Dans Son Accroissement. Corresp. Math. Phys. 1838, 10, 113–117. [Google Scholar]
- Louette, G. Use of a native predator for the control of an invasive amphibian. Wildl. Res. 2012, 39, 271–278. [Google Scholar] [CrossRef]
- Ford, A. Modeling the Environment, 2nd ed.; Island Press: Washington, DC, USA, 2010; pp. 99–115. [Google Scholar]
- Ford, A. System Dynamics Models of Environment, Energy and Climate Change. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2009; pp. 9014–9034. [Google Scholar]
- Howell, P.E.; Muths, E.; Sigafus, B.H.; Hossack, B.R. Survival Estimates for the Invasive American Bullfrog. Amphib.-Reptil. 2020, 41, 559–564. [Google Scholar] [CrossRef]
- Louette, G.; Devisscher, S.; Adriaens, T. Control of Invasive American Bullfrog Lithobates Catesbeianus in Small Shallow Water Bodies. Eur. J. Wildl. Res. 2013, 59, 105–114. [Google Scholar] [CrossRef] [Green Version]
- Bury, R.B.; Whelan, J.A. Ecology and Management of the Bullfrog; US Department of the Interior, Fish and Wildlife Service: Washington, DC, USA, 1985.
- Bøhn, T.; Sandlund, O.T.; Amundsen, P.A.; Primicerio, R. Rapidly Changing Life History during Invasion. Oikos 2004, 106, 138–150. [Google Scholar] [CrossRef]
- Aldridge, D.; Ockendon, N.; Rocha, R.; Smith, R.K.; Sutherland, W.J. Some Aspects of Control of Freshwater Invasive Species. In What Works in Conservation 2020; Sutherland, W.J., Dicks, L.V., Ockendon, N., Smith, R.K., Eds.; Open Book Publishers: Cambridge, UK, 2020. [Google Scholar]
- Doubledee, R.A.; Muller, E.B.; Nisbet, R.M. Bullfrogs, Disturbance Regimes, and the Persistence of California Red-Legged Frogs. J. Wildl. Manag. 2003, 67, 424–438. [Google Scholar] [CrossRef]
- McIntire, K.M.; Juliano, S.A. How can mortality increase population size? A test of two mechanistic hypotheses. Ecology 2018, 99, 1660–1670. [Google Scholar] [CrossRef] [PubMed]
- Newman, R.A. Ecological constraints on amphibian metamorphosis: Interactions of temperature and larval density with responses to changing food level. Oecologia 1998, 115, 9–16. [Google Scholar] [CrossRef]
- Loman, J. Density regulation in tadpoles of Rana temporaria: A full pond field experiment. Ecology 2004, 85, 1611–1618. [Google Scholar] [CrossRef]
- Pardini, E.A.; Drake, J.M.; Chase, J.M.; Knight, T.M. Complex Population Dynamics and Control of the Invasive Biennial Alliaria Petiolata (Garlic Mustard). Ecol. Appl. 2009, 19, 387–397. [Google Scholar] [CrossRef]
- Juliano, S.A. Population Dynamics. J. Am. Mosq. Control Assoc. 2007, 23, 265–275. [Google Scholar] [CrossRef]
- Rosen, P.C.; Schwalbe, C.R. Bullfrogs: Introduced Predators in Southwestern Wetlands. In Our Living Resources: A Report to the Nation on the Distribution, Abundance, and Health of US Plants, Animals, and Ecosystems; US Department of the Interior, National Biological Service: Washington, DC, USA, 1995; pp. 452–454. [Google Scholar]
- Guibert, S.; Dejean, T.; Hippolyte, S. Le Parc Naturel Regional Périgord-Limousin: Territoire d’expérimentation et d’innovation Par La Mise En Place d’un Programme d’éradication de La Grenouille Taureau (Lithobates Catesbeianus) Associé à Un Programme de Recherche Sur Les Maladies Émergentes Des Amphibiens. EPOPS: La Revue des Naturalistes du Limousin 2010, 1, 5–24. [Google Scholar]
- Mack, R.N.; Simberloff, D.; Lonsdale, W.M.; Evans, H.; Clout, M.; Bazzaz, F.A. Biotic Invasions: Causes, Epidemiology, Global consequences, and Control. Ecol. Appl. 2000, 10, 22. [Google Scholar] [CrossRef]
- Altwegg, R.; Reyer, H.U. Patterns of Natural Selection on Size at Metamorphosis in Water Frogs. Evolution 2003, 57, 872–882. [Google Scholar] [CrossRef]



| Model Sector | Parameter | Description | References |
|---|---|---|---|
| Population Dynamics | Population size | The population at each stage in the life cycle of L. catesbeianus | - |
| Survival rate | The rate of survival is affected by the density effect in developing to the next stage | [28], [47] | |
| Fertility | The number of maximum eggs produced by female L. catesbeianus | [14] | |
| Carrying capacity | Maximum population size at each stage in the life cycle of the American bullfrog in the Onseok reservoir | [27], [48] | |
| Control methods | Control rate | Rate of removed individuals to total population at each juvenile and adult stage | - |
| The number of double fyke net sets | The number of the double fyke net set used to control | - | |
| Control effect | The control efficiency of the double fyke net set | [48] |
| Control Method | Intensity | Population | ||
|---|---|---|---|---|
| Mean | SE | Range | ||
| No control | - | 242 | 0.76 | 137 |
| The number of double fyke net sets | 1 | 173 | 0.50 | 91 |
| 2 | 150 | 0.41 | 66 | |
| 3 | 136 | 0.41 | 74 | |
| 4 | 128 | 0.42 | 97 | |
| 5 | 125 | 0.46 | 126 | |
| Control rate | 0.2 | 127 | 0.32 | 54 |
| 0.4 | 56 | 0.46 | 69 | |
| 0.6 | 24 | 0.42 | 62 | |
| 0.8 | 26 | 1.04 | 154 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, B.; Kim, I.; Choi, K.; Cho, W.; Ko, D.W. Population Dynamics of American Bullfrog (Lithobates catesbeianus) and Implications for Control. Animals 2022, 12, 2827. https://doi.org/10.3390/ani12202827
Chang B, Kim I, Choi K, Cho W, Ko DW. Population Dynamics of American Bullfrog (Lithobates catesbeianus) and Implications for Control. Animals. 2022; 12(20):2827. https://doi.org/10.3390/ani12202827
Chicago/Turabian StyleChang, Byungwoo, Inyoo Kim, Kwanghun Choi, Wonhee Cho, and Dongwook W. Ko. 2022. "Population Dynamics of American Bullfrog (Lithobates catesbeianus) and Implications for Control" Animals 12, no. 20: 2827. https://doi.org/10.3390/ani12202827
APA StyleChang, B., Kim, I., Choi, K., Cho, W., & Ko, D. W. (2022). Population Dynamics of American Bullfrog (Lithobates catesbeianus) and Implications for Control. Animals, 12(20), 2827. https://doi.org/10.3390/ani12202827






