Climate Spaces and Cliffs: A Novel Bovine Thermodynamic and Mass Balances Model
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. The Niche Mapper Computer Model
2.2. The Dairy Niche Mapper Model
2.3. Niche Mapper Validations
2.4. Validation Methods for Dairy Niche Mapper (DNM)C
2.5. Metabolic Chamber Simulations
2.6. Climate Effects on Cows in Confinement
2.7. Experimental Design and Sensitivity Analyses for Global Locations, Body Size and Diet Effects on Milk Production Using the Yates Algorithm [48,49]
2.8. Global Simulations for Dairy Animals Outdoors
3. Results
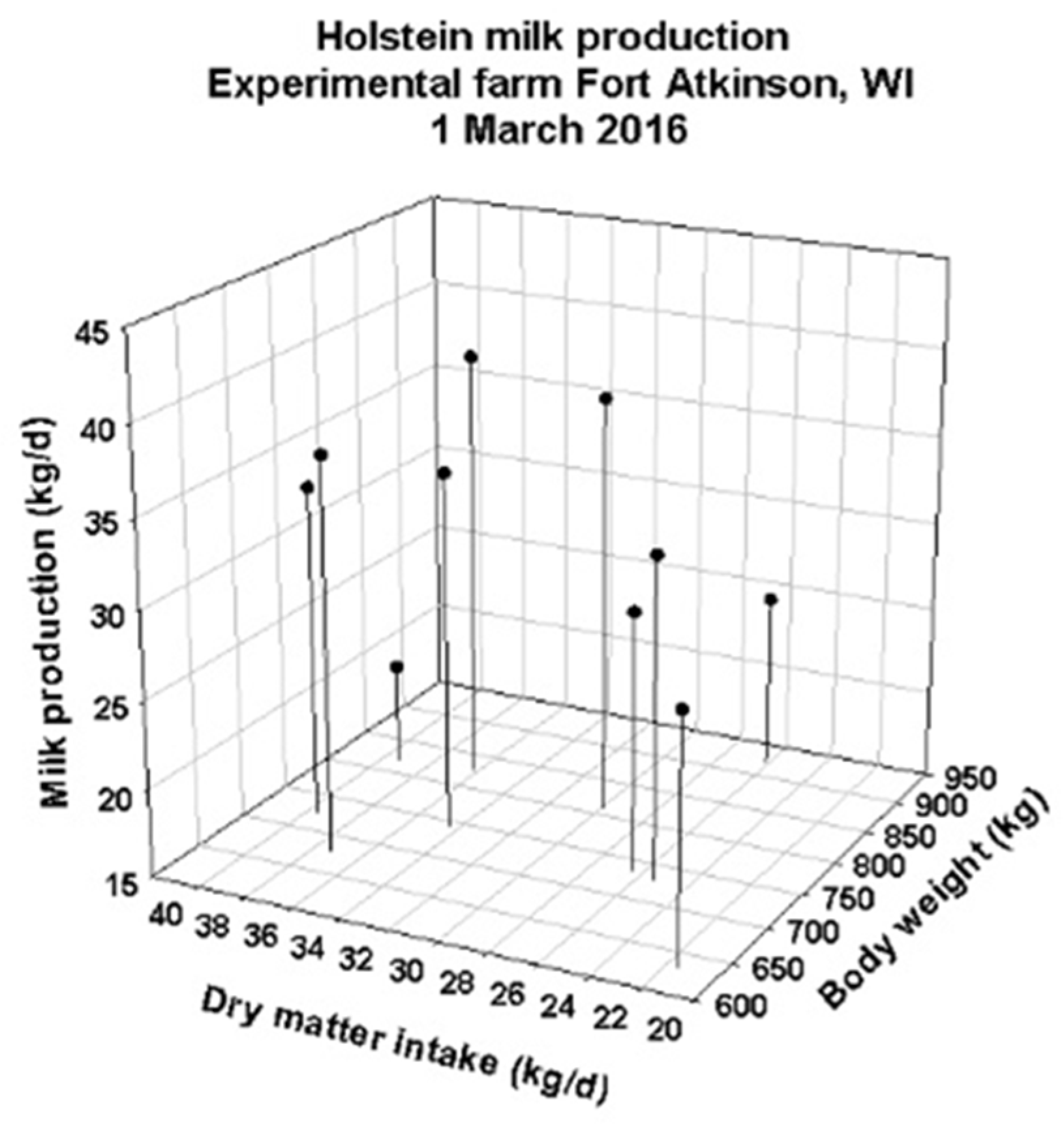
3.1. DNM Validations Using Data from an Experimental Dairy Barn
3.2. DNM Validation Using Peer-Reviewed Literature Data
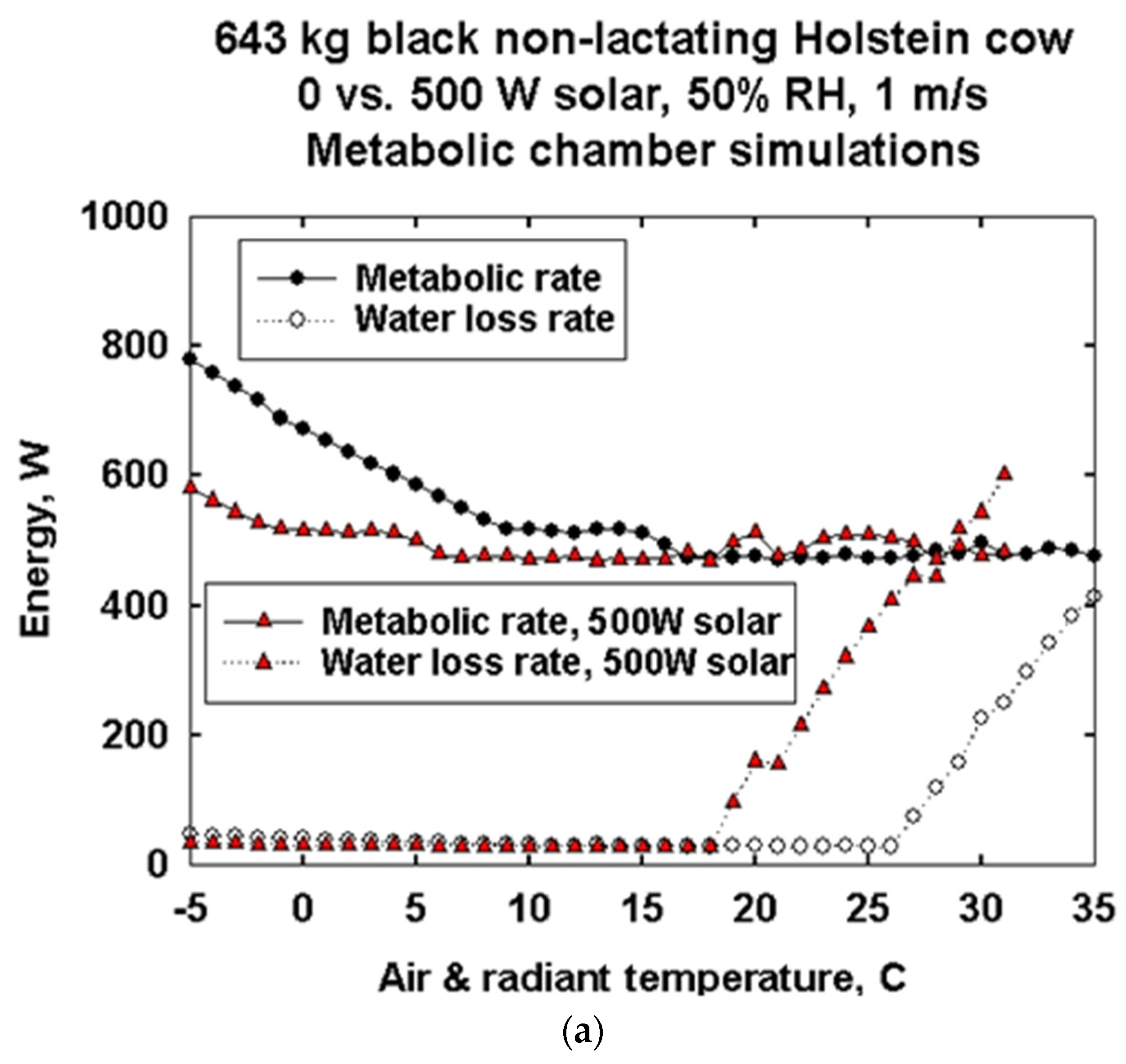
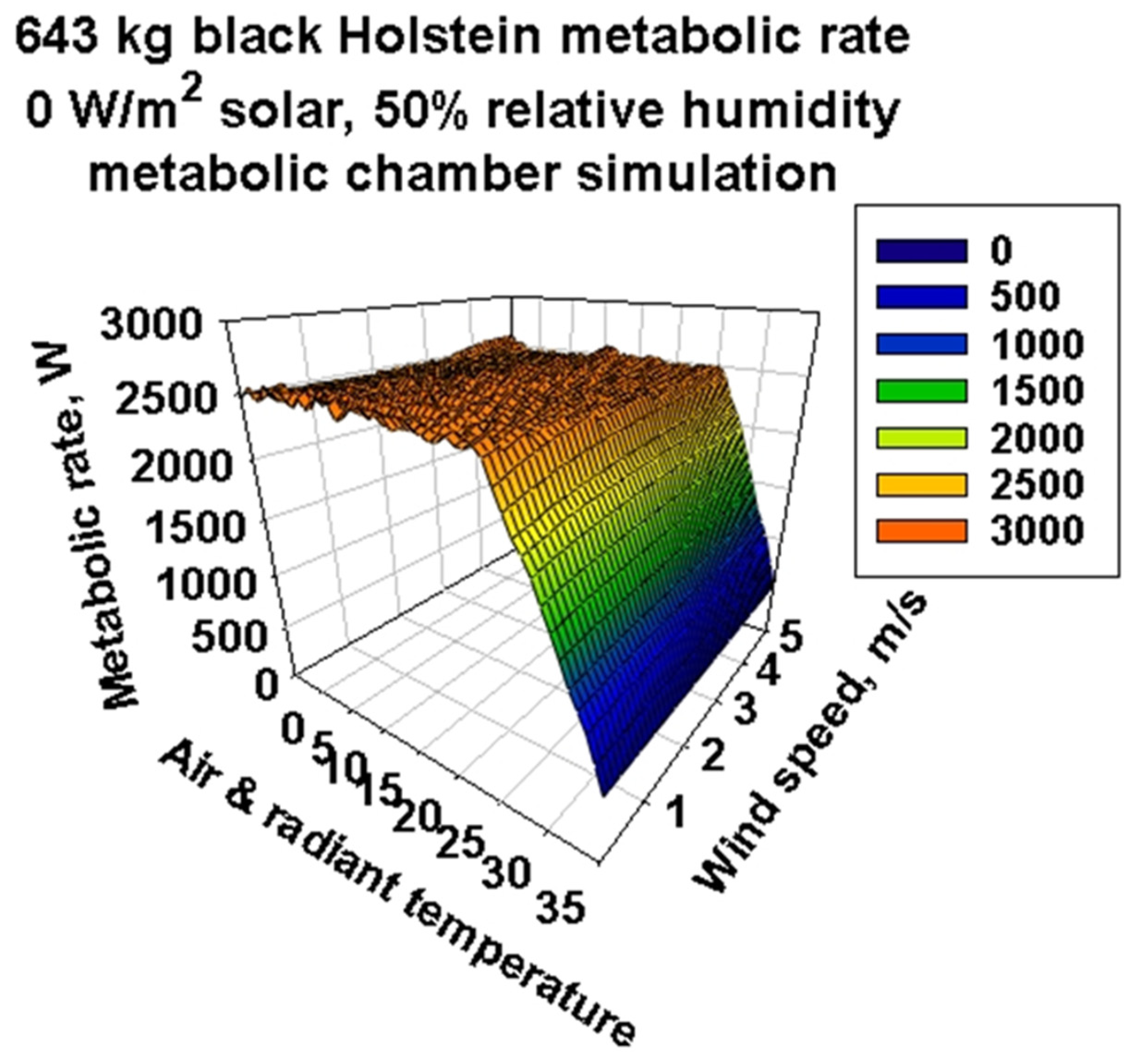
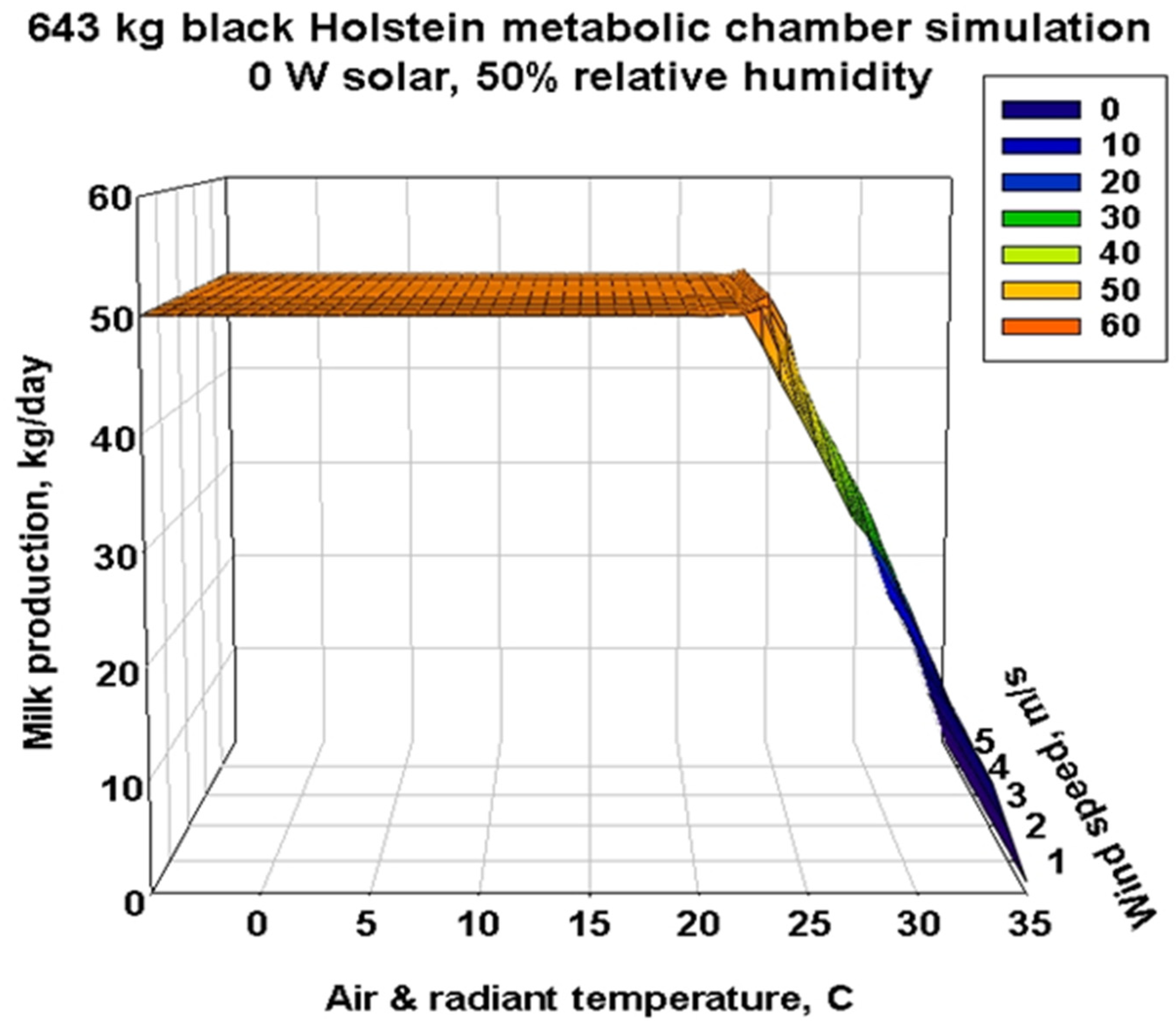
3.3. Metabolic Chamber Simulations
4. Discussion
4.1. General Summary
4.2. Some Limitations and Caveats
5. Conclusions
- DNM can define the climate spaces and climate cliffs where target milk production levels are or are not feasible. The climate cliff precipices and their slopes show where and how fast heat stress prevents achieving milk production and even survival. DNM provides an improved quantitative understanding of the multidimensional nonlinear interactions of climate variation and dairy bovine characteristics for current and future milk production as well as feed and water needs for grazing and confinement dairy operations. DNM outputs include feasible activity times, milk production and water and feed needs for different-sized Holstein cows on high-grain (confinement feeding) versus high-forage (grazing feeding) diets at three arbitrary north latitudes, 12°, 30° and 60°, for North and Central America and Asia.
- Trade-offs in climate, location, body size and diet type as main and interactive effects on cow feed and water needs and the capacity to produce animal products for human consumption are illustrated. Relocation efforts and selection or crossbreeding for smaller animal size are needed for grazing dairy animals, especially in low-elevation tropical and subtropical regions to maintain or increase production capabilities as climates continue to warm.
- Selection of smaller sized and high production efficiency cows may be more suitable for tropical and subtropical regions, because these cows can ameliorate some of the effects of climate warming at low elevations.
- Temperature, body size and, to a lesser extent, wind speed, relative humidity, solar radiation and haircoat color affect the ability to produce milk at targeted levels for cows. It is clear that it is possible, by adjusting cow morphological and physiological properties and behavioral traits, in combination with modifications of land use and management practices, e.g., season of calving and utilizing bioinformatics-biophysical computational models, to rapidly advance our understanding of better options for maintaining and improving dairy production globally in the face of the current escalating global climate crisis.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Porter, W.P.; Gates, D.M. Thermodynamic equilibria of animals with environment. Ecol. Monogr. 1969, 39, 227–244. [Google Scholar] [CrossRef]
- Berman, A. Influence of Some Factors on the Relative Evaporation Rate from the Skin of Cattle. Nature 1957, 179, 1256. [Google Scholar] [CrossRef]
- Gebremedhin, K.G.; Cramer, C.O.; Porter, W.P. Predictions and Measurements of Heat Production and Food and Water Requirements of Holstein Calves in Different Environments. Trans. ASAE 1981, 24, 0715–0720. [Google Scholar] [CrossRef]
- Ramírez-Rivera, E.J.; Rodríguez-Miranda, J.; Huerta-Mora, I.R.; Cárdenas-Cágal, A.; Juárez-Barrientos, J.M. Tropical milk production systems and milk quality: A review. Trop. Anim. Health Prod. 2019, 51, 1295–1305. [Google Scholar] [CrossRef] [PubMed]
- Campbell-Staton, S.C.; Walker, R.H.; Rogers, S.A.; De León, J.; Landecker, H.; Porter, W.; Mathewson, P.D.; Long, R.A. Physiological costs of undocumented human migration across the southern United States border. Science 2021, 374, 1496–1500. [Google Scholar] [CrossRef]
- Rogers, S.A.; Robbins, C.T.; Mathewson, P.D.; Carnahan, A.M.; van Manen, F.T.; Haroldson, M.A.; Porter, W.P.; Rogers, T.R.; Soule, T.; Long, R.A. Thermal constraints on energy balance, behaviour and spatial distribution of grizzly bears. Funct. Ecol. 2021, 35, 398–410. [Google Scholar] [CrossRef]
- Verzuh, T.L.; Rogers, S.A.; Mathewson, P.D.; May, A.; Porter, W.P.; Class, C.; Knox, L.; Cufaude, T.; Hall, L.E.; Long, R.A.; et al. Behavioral responses of a large, heat-sensitive mammal to climatic variation at multiple spatial scales. J. Anim. Ecol. 2022, 92, 619–634. [Google Scholar] [CrossRef]
- Appuhamy, J.; Judy, J.; Kebreab, E.; Kononoff, P. Prediction of drinking water intake by dairy cows. J. Dairy Sci. 2016, 99, 7191–7205. [Google Scholar] [CrossRef] [PubMed]
- Neves, S.F.; Silva, M.C.F.; Miranda, J.M.; Stilwell, G.; Cortez, P.P. Predictive Models of Dairy Cow Thermal State: A Review from a Technological Perspective. Vet. Sci. 2022, 9, 416. [Google Scholar] [CrossRef] [PubMed]
- St-Pierre, N.R.; Cobanov, B.; Schnitkey, G. Economic Losses from Heat Stress by US Livestock Industries1. J. Dairy Sci. 2003, 86, E52–E77. [Google Scholar] [CrossRef]
- Key, N.; Sneeringer, S.; Marquardt, D. Climate Change, Heat Stress, and US Dairy Production; United States Department of Agriculture: Washington, DC, USA, 2014.
- USDA. Dairy Cattle Management Practices in the United States; USDA–APHIS–VS–CEAH–NAHMS, Tech. Rep.; USDA: Washington, DC, USA, 2014; update in 2016.
- Hashimoto, T.; Horikawa, D.D.; Saito, Y.; Kuwahara, H.; Kozuka-Hata, H.; Shin-i, T.; Minakuchi, Y.; Ohishi, K.; Motoyama, A.; Aizu, T.; et al. Extremotolerant tardigrade genome and improved radiotolerance of human cultured cells by tardigrade-unique protein. Nat. Commun. 2016, 7, 12808. [Google Scholar] [CrossRef] [PubMed]
- Hoegh-Guldberg, O.; Bindi, M.; Allen, M. Impacts of 1.5 °C Global Warming on Natural and Human Systems. In Global Warming of 1.5 °C: An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; IPCC: Geneva, Switzerland, 2018. [Google Scholar]
- IPCC. Climate Change 2007: The Physical Science Basis: Summary for Policymakers; IPCC: Geneva, Switzerland, 2007. [Google Scholar]
- IPCC-AR6. Available online: https://www.ipcc.ch/assessment-report/ar6/ (accessed on 6 September 2023).
- Sillmann, J.; Kharin, V.V.; Zhang, X.; Zwiers, F.W.; Bronaugh, D. Climate extremes indices in the CMIP5 multimodel ensemble: Part 1. Model evaluation in the present climate. J. Geophys. Res. Atmos. 2013, 118, 1716–1733. [Google Scholar] [CrossRef]
- Willett, K.M.; Gillett, N.P.; Jones, P.D.; Thorne, P.W. Attribution of observed surface humidity changes to human influence. Nature 2007, 449, 710–712. [Google Scholar] [CrossRef] [PubMed]
- Klinedinst, P.L.; Wilhite, D.A.; Hahn, G.L.; Hubbard, K.G. The potential effects of climate change on summer season dairy cattle milk production and reproduction. Clim. Chang. 1993, 23, 21–36. [Google Scholar] [CrossRef]
- Nesamvuni, E.; Lekalakala, R.; Norris, D.; Ngambi, J. Effects of climate change on dairy cattle, South Africa. Afr. J. Agric. Res. 2012, 7, 3867–3872. [Google Scholar] [CrossRef]
- Garner, J.B.; Douglas, M.; Williams, S.R.O.; Wales, W.J.; Marett, L.C.; DiGiacomo, K.; Leury, B.J.; Hayes, B.J. Responses of dairy cows to short-term heat stress in controlled-climate chambers. Anim. Prod. Sci. 2017, 57, 1233–1241. [Google Scholar] [CrossRef]
- Wildridge, A.M.; Thomson, P.C.; Garcia, S.C.; John, A.J.; Jongman, E.C.; Clark, C.E.; Kerrisk, K.L. Short communication: The effect of temperature-humidity index on milk yield and milking frequency of dairy cows in pasture-based automatic milking systems. J. Dairy Sci. 2018, 101, 4479–4482. [Google Scholar] [CrossRef]
- Thornton, P.K.; van de Steeg, J.; Notenbaert, A.; Herrero, M. The impacts of climate change on livestock and livestock systems in developing countries: A review of what we know and what we need to know. Agric. Syst. 2009, 101, 113–127. [Google Scholar] [CrossRef]
- Ji, B.; Banhazi, T.; Perano, K.; Ghahramani, A.; Bowtell, L.; Wang, C.; Li, B. A review of measuring, assessing and mitigating heat stress in dairy cattle. Biosyst. Eng. 2020, 199, 4–26. [Google Scholar] [CrossRef]
- Mathewson, P.D.; Porter, W.P.; Barrett, L.; Fuller, A.; Henzi, S.P.; Hetem, R.S.; Young, C.; McFarland, R. Field data confirm the ability of a biophysical model to predict wild primate body temperature. J. Therm. Biol. 2020, 94, 102754. [Google Scholar] [CrossRef]
- Porter, W.; Munger, J.; Stewart, W.; Budaraju, S.; Jaeger, J. Endotherm Energetics—From a Scalable Individual-Based Model to Ecological Applications. Aust. J. Zool. 1994, 42, 125–162. [Google Scholar] [CrossRef]
- Dudley, P.N.; Bonazza, R.; Porter, W.P. Consider a Non-Spherical Elephant: Computational Fluid Dynamics Simulations of Heat Transfer Coefficients and Drag Verified Using Wind Tunnel Experiments. J. Exp. Zool. Part A Ecol. Genet. Physiol. 2013, 319, 319–327. [Google Scholar] [CrossRef]
- Mathewson, P.D.; Porter, W.P. Simulating Polar Bear Energetics during a Seasonal Fast Using a Mechanistic Model. PLoS ONE 2013, 8, e72863. [Google Scholar]
- Gebremedhin, K.; Hillman, P.; Lee, C.; Collier, R.; Willard, S.; Arthington, J.; Brown-Brandl, T. Sweating Rates of Dairy and Feedlot Cows under Stressful Thermal Environments. In Proceedings of the Livestock Environment VIII, Iguassu Falls, Brazil, 31 August–4 September 2008; ASABE: St. Joseph, MI, USA, 2008; p. 108. [Google Scholar]
- Wood, P.D.P. Algebraic Model of the Lactation Curve in Cattle. Nature 1967, 216, 164–165. [Google Scholar] [CrossRef]
- Whittemore, C.T. Lactation of the Dairy Cow; Longman Group Ltd.: Harlow, UK, 1980. [Google Scholar]
- Bernard, J. Milk production and composition responses to the source of protein supplements in diets containing wheat middlings. J. Dairy Sci. 1997, 80, 938–942. [Google Scholar] [CrossRef] [PubMed]
- Jewell, K.A.; McCormick, C.A.; Odt, C.L.; Weimer, P.J.; Suen, G. Ruminal bacterial community composition in dairy cows is dynamic over the course of two lactations and correlates with feed efficiency. Appl. Environ. Microbiol. 2015, 81, 4697–4710. [Google Scholar] [CrossRef]
- Heinrichs, A.J.; Wells, S.; Hurd, H.; Hill, G.; Dargatz, D. The national dairy heifer evaluation project: A profile of heifer management practices in the United States. J. Dairy Sci. 1994, 77, 1548–1555. [Google Scholar] [CrossRef]
- Tucker, C.B.; MacNeil, M.; Webster, A.; Tucker, C.B.; MacNeil, M.; Webster, A. Guide for the Care and Use of Agricultural Animals in Research and Teaching. 2020. Available online: https://www.adsa.org/Portals/0/SiteContent/docs/AgGuide4th/Ag_Guide_4th_ed.pdf (accessed on 14 May 2023).
- Anzures-Olvera, F.; Véliz, F.G.; De Santiago, A.; García, J.E.; Mellado, J.; Macías-Cruz, U.; Avendaño-Reyes, L.; Mellado, M. The impact of hair coat color on physiological variables, reproductive performance and milk yield of Holstein cows in a hot environment. J. Therm. Biol. 2019, 81, 82–88. [Google Scholar] [CrossRef]
- Becerril, C.M.; Wilcox, C.J.; Lawlor, T.J.; Wiggans, O.R.; Webb, D.W. Effects of Percentage of White Coat Color on Holstein Production and Reproduction in a Subtropical Environment1. J. Dairy Sci. 1993, 76, 2286–2291. [Google Scholar] [CrossRef]
- New, M.; Lister, D.; Hulme, M.; Makin, I. A high-resolution data set of surface climate over global land areas. Clim. Res. 2002, 21, 1–25. [Google Scholar] [CrossRef]
- Idso, S.B.; Jackson, R.D. Thermal radiation from the atmosphere. J. Geophys. Res. 1969, 74, 5397–5403. [Google Scholar] [CrossRef]
- Porter, W.P.; Mitchell, J.W.; Beckman, W.A.; DeWitt, C.B. Behavioral implications of mechanistic ecology. Oecologia 1973, 13, 1–54. [Google Scholar] [CrossRef]
- Kearney, M.R.; Munns, S.L.; Moore, D.; Malishev, M.; Bull, C.M. Field tests of a general ectotherm niche model show how water can limit lizard activity and distribution. Ecol. Monogr. 2018, 88, 672–693. [Google Scholar] [CrossRef]
- Mathewson, P.D.; Moyer-Horner, L.; Beever, E.A.; Briscoe, N.J.; Kearney, M.; Yahn, J.M.; Porter, W.P. Mechanistic variables can enhance predictive models of endotherm distributions: The American pika under current, past, and future climates. Glob. Chang. Biol. 2016, 23, 1048–1064. [Google Scholar] [CrossRef]
- Wang, Y.; Widga, C.; Graham, R.W.; McGuire, J.L.; Porter, W.; Wårlind, D.; Williams, J.W. Caught in a bottleneck: Habitat loss for woolly mammoths in central North America and the ice-free corridor during the last deglaciation. Glob. Ecol. Biogeogr. 2020, 30, 527–542. [Google Scholar] [CrossRef]
- Natori, Y.; Porter, W.P. Model of Japanese serow (Capricornis crispus) energetics predicts distribution on Honshu, Japan. Ecol. Appl. 2007, 17, 1441–1459. [Google Scholar] [CrossRef]
- Berman, A. Nychthemeral and seasonal patterns of thermoregulation in cattle. Aust. J. Agric. Res. 1968, 19, 181–189. [Google Scholar] [CrossRef]
- Chen, J.M.; Schütz, K.E.; Tucker, C.B. Cooling cows efficiently with sprinklers: Physiological responses to water spray. J. Dairy Sci. 2015, 98, 6925–6938. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Gao, H.; Gebremedhin, K.G.; Bjerg, B.S.; Van Os, J.; Tucker, C.B.; Zhang, G. A predictive model of equivalent temperature index for dairy cattle (ETIC). J. Therm. Biol. 2018, 76, 165–170. [Google Scholar] [CrossRef]
- Box, G.E.P.; Hunter, J.S. The 2 k—P Fractional Factorial Designs. Technometrics 1961, 3, 311–351. [Google Scholar] [CrossRef]
- Box, G.E.P.; Hunter, W.G.; Hunter, J.S. Statistics for Experimenters; John Wiley and Sons: New York, NY, USA, 1978. [Google Scholar]
- Steadman, R.G. The Assessment of Sultriness. Part I: A Temperature-Humidity Index Based on Human Physiology and Clothing Science. J. Appl. Meteorol. 1979, 18, 861–873. [Google Scholar] [CrossRef]
- Bohmanova, J.; Misztal, I.; Cole, J.B. Temperature-Humidity Indices as Indicators of Milk Production Losses due to Heat Stress. J. Dairy Sci. 2007, 90, 1947–1956. [Google Scholar] [CrossRef]
- Kowalski, G.; Mitchell, J. An analytical and experimental investigation of the heat transfer mechanisms within fibrous media. Am. Soc. Mech. Eng. 1979, 1, 7. [Google Scholar]
- Dawson, T.J.; Webster, K.N.; Maloney, S.K. The fur of mammals in exposed environments; do crypsis and thermal needs necessarily conflict? The polar bear and marsupial koala compared. J. Comp. Physiol. B 2014, 184, 273–284. [Google Scholar] [CrossRef] [PubMed]
- Fisher, A.D.; Roberts, N.; Bluett, S.J.; Verkerk, G.A.; Matthews, L.R. Effects of shade provision on the behaviour, body temperature and milk production of grazing dairy cows during a New Zealand summer. N. Z. J. Agric. Res. 2008, 51, 99–105. [Google Scholar] [CrossRef]







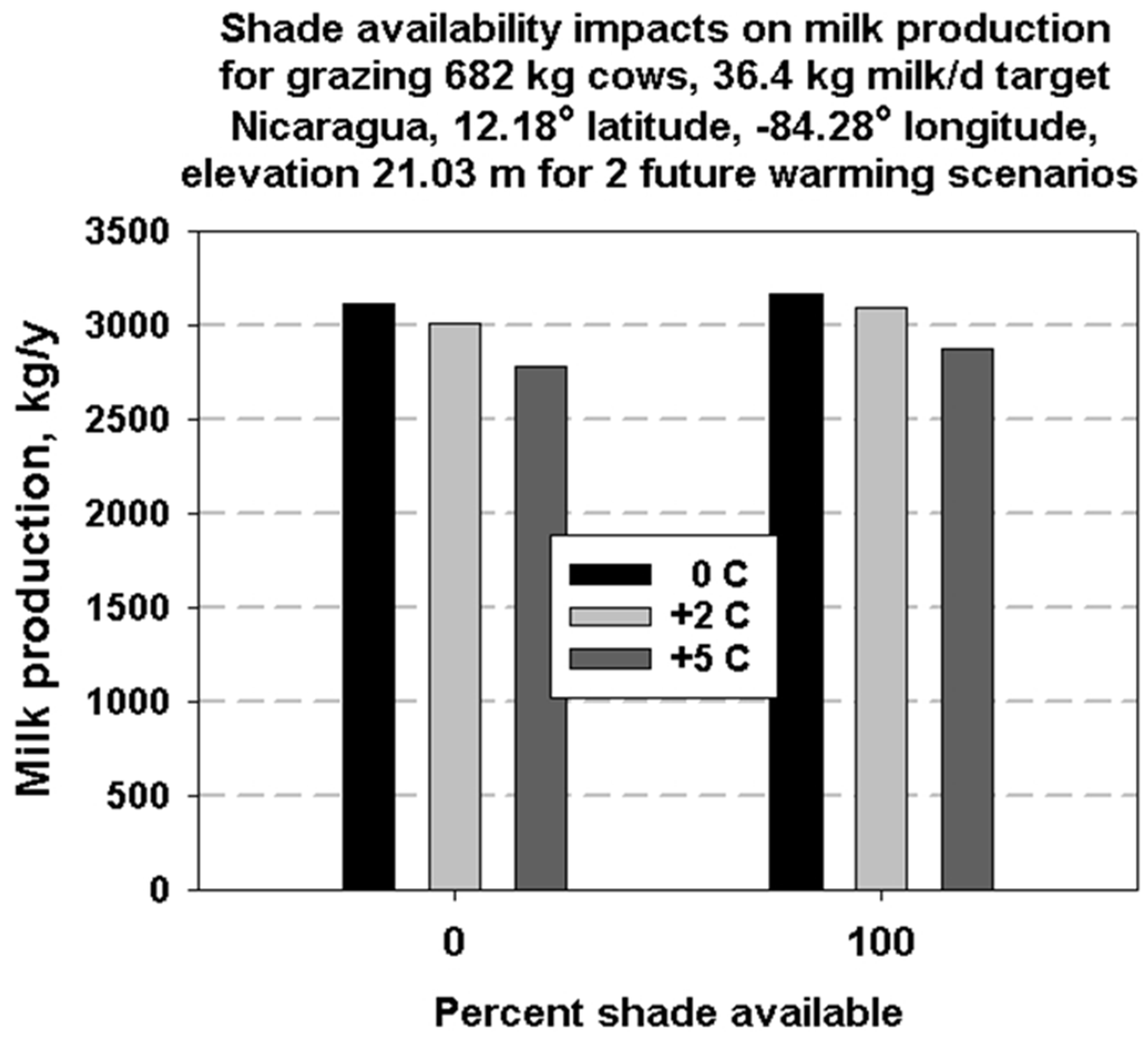

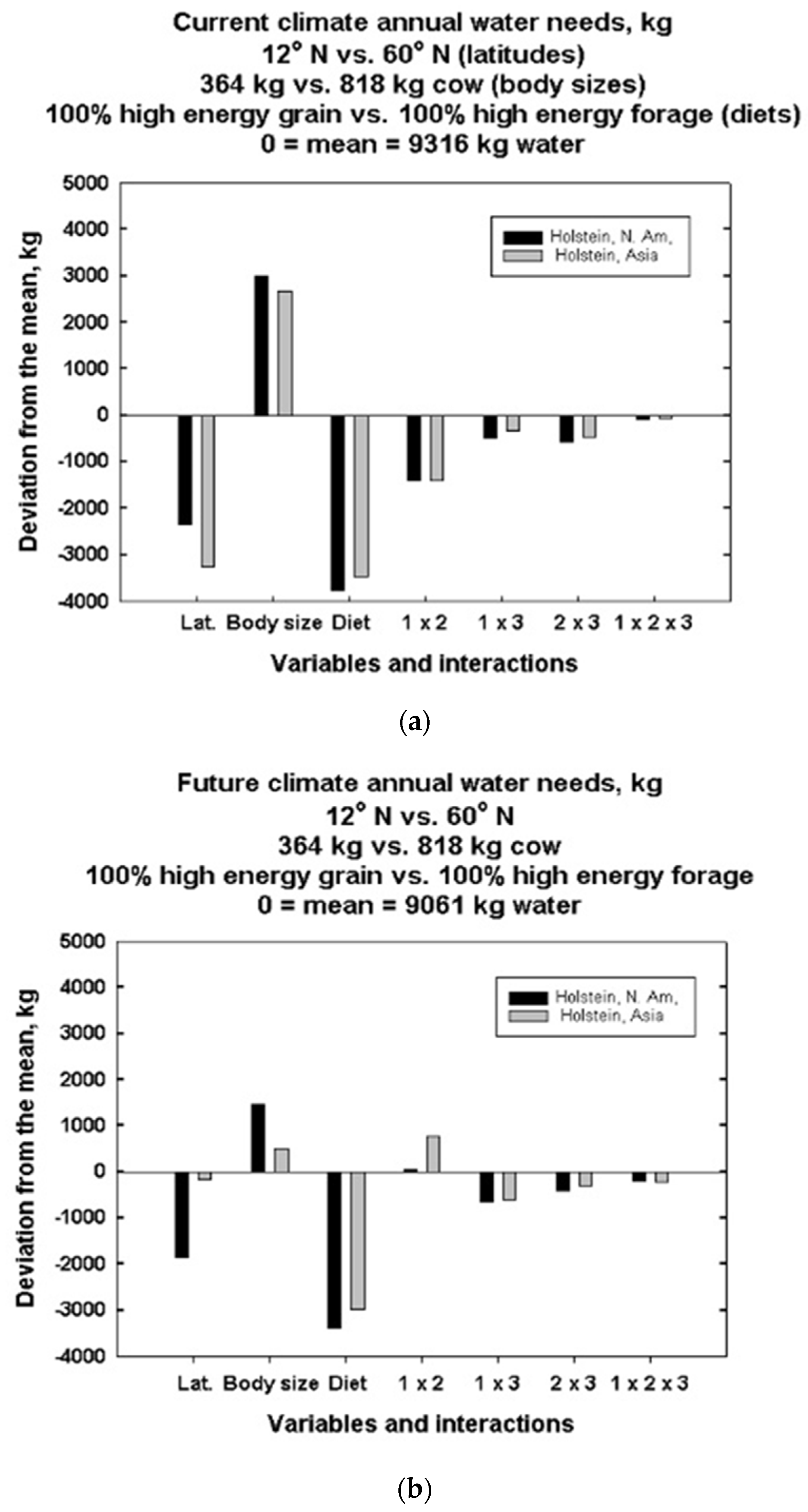
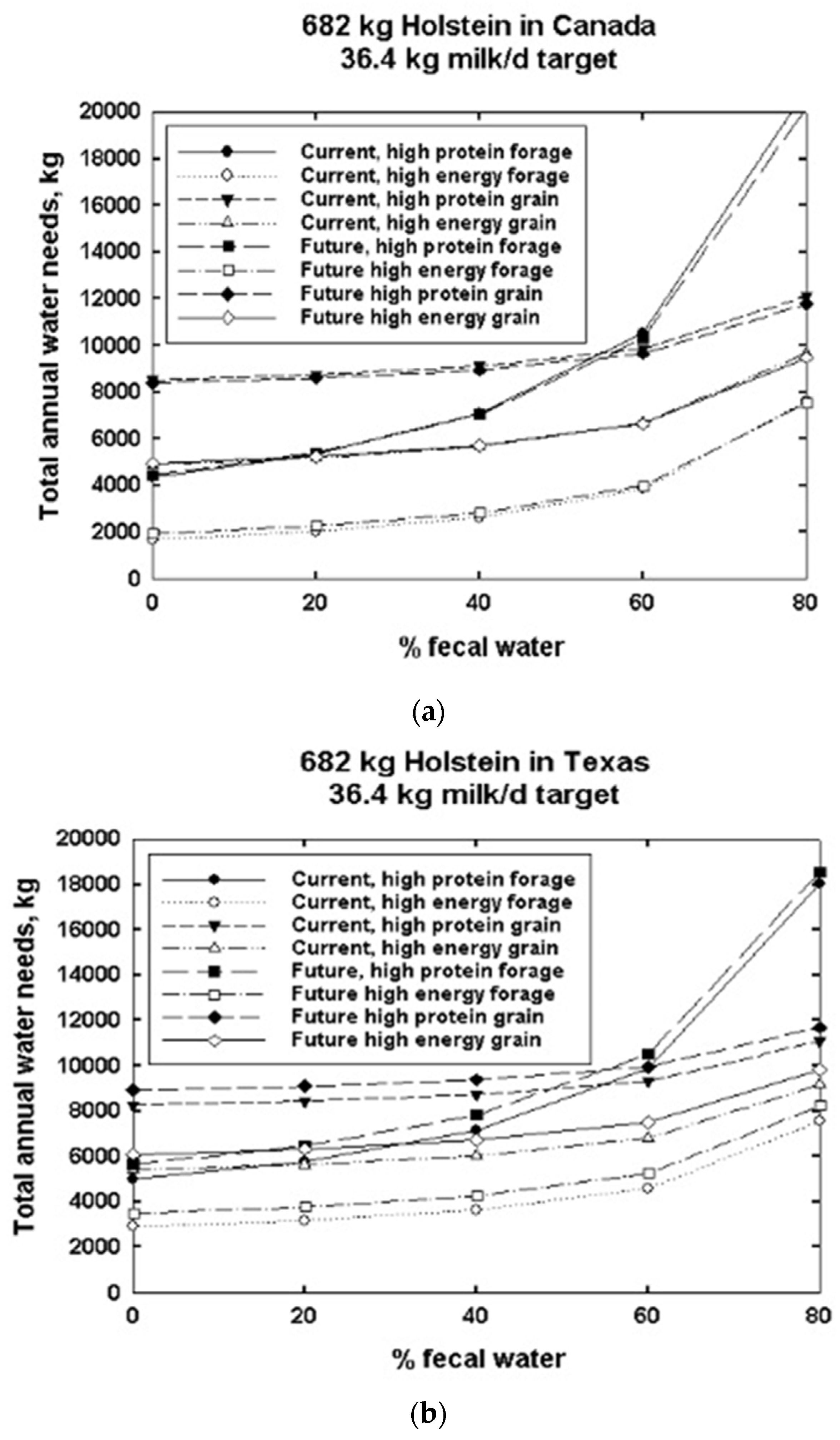
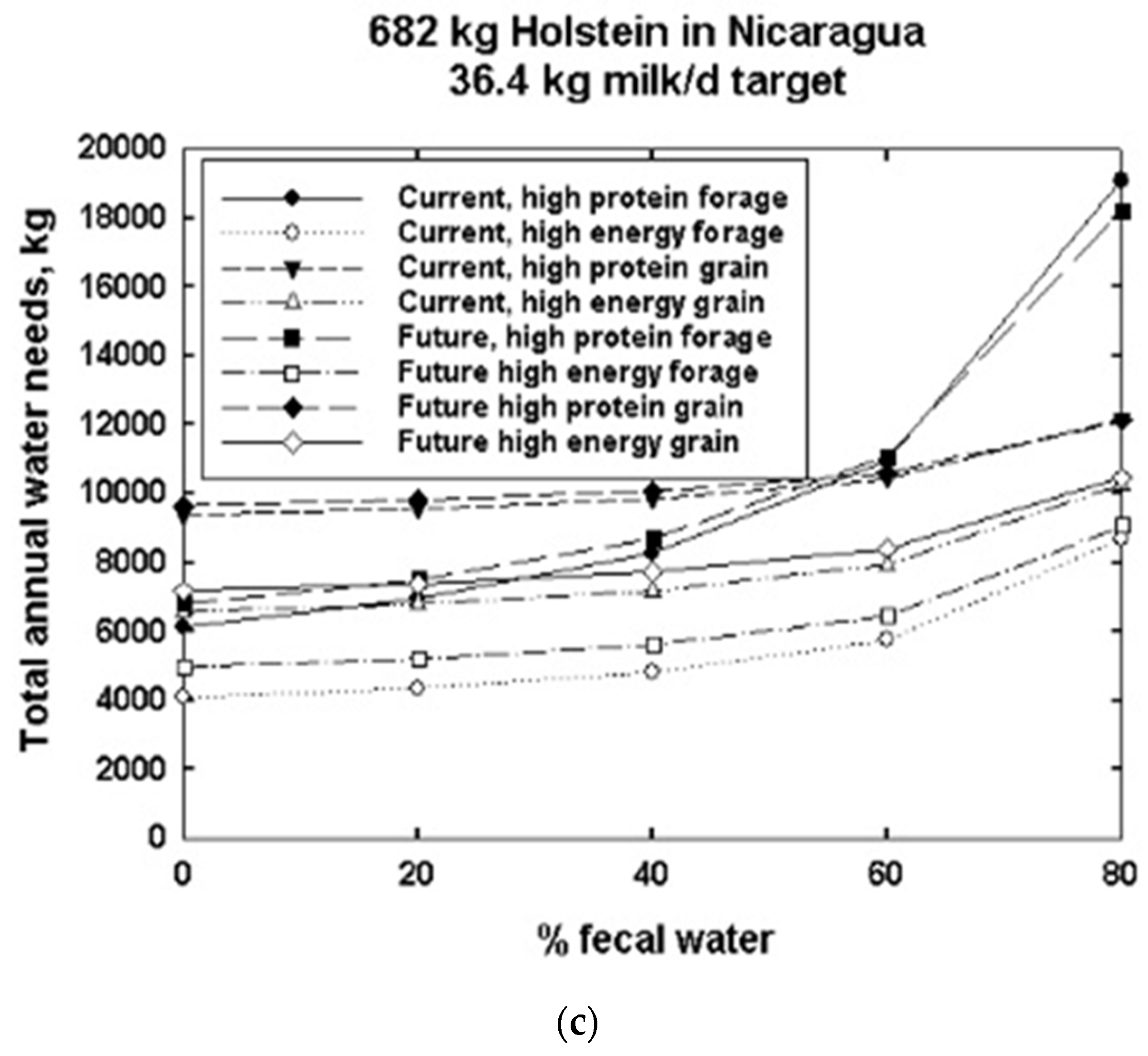
| Input | References | |
|---|---|---|
| Animal Attributes | ||
| Height (cm) | 147.3 | Our measurements |
| Fur depth (cm) | 0.336 | Our measurements |
| Hair length (cm) | 0.635 | Our measurements |
| Weight (kg) | 682 | Assumed value |
| Calving month | 9 | Assumed value |
| Calving day | 5 | Assumed value |
| Shade available | Yes | Assumed value |
| Fur reflectivity %, % of total skin | ||
| Black | 16, 50 | Our measurement, assumed % portion |
| White | 48, 50 | Our measurement, assumed % portion |
| Brown or Red | 40, 0 | Our measurement, assumed % portion |
| Tan | 45, 0 | Our measurement, assumed % portion |
| % Fecal water | 80. | Our measurements |
| Location and Elevation | ||
| Latitude (deg) | 12.03 | niche-mapper.com/Global Climate Extractor |
| Longitude (deg) | 123.77 | niche-mapper.com/Global Climate Extractor |
| Elevation (m) | 27.72 | niche-mapper.com/Global Climate Extractor |
| Milk Production | ||
| Maximum Expected Milk (kg) | 36.4 | From typical Holstein production range |
| % Milk fat | 3.2 | From typical Holstein production range |
| % Milk protein | 3.5 | From typical Holstein production range |
| Barn Usage | No | |
| Summer Diet | ||
| High-Protein Forage (HPF) | 100 | Assumed diet % value |
| High-Energy Forage (HEF) | 0 | Assumed diet % value |
| High-Protein Grain (HPG) | 0 | Assumed diet % value |
| High-Energy Grain (HEG) | 0 | Assumed diet % value |
| Winter Diet | ||
| High-Protein Forage | 100 | Assumed diet % value |
| High-Energy Forage | 0 | Assumed diet % value |
| High-Protein Grain | 0 | Assumed diet % value |
| High-Energy Grain | 0 | Assumed diet % value |
| 23 Full Factorial Design Levels with Center Replicate—Holsteins | |||
|---|---|---|---|
| Variable | Low (−) | Center (0) | High (+) |
| Latitude (degrees N) | 12° Philippines | 30° China | 60° Russia |
| Size (kg) | 364 | 818 | 1273 |
| Diet (% energy diet type) | 100% HEG | 50/50 HEG/HEF | 100% HEF |
| Location | ||||||
|---|---|---|---|---|---|---|
| Milk Production, kg/y (Body Size, kg) | Philippines | China | Russia | Nicaragua | Texas | Canada |
| Current Milk (364 kg) | 6864 | 7008 | 7008 | 6897 | 6967 | 7008 |
| Future Milk (364 kg) | 5669 | 6988 | 7008 | 5753 | 6921 | 7008 |
| Current Milk (818 kg) | 6576 | 7008 | 7008 | 6630 | 6967 | 7008 |
| Future Milk (818 kg) | 4506 | 6915 | 7008 | 4494 | 6670 | 7008 |
| Current Milk (1273 kg) | 5659 | 6970 | 7008 | 5729 | 6886 | 7008 |
| Future Milk (1273 kg) | 2496 | 6503 | 7008 | 2236 | 6272 | 7008 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Porter, W.P.; Bertz, A.E.; Mathewson, P.D.; Solorzano, L.C.; Dudley, P.N.; Bonazza, R.; Gebremedhin, K.G. Climate Spaces and Cliffs: A Novel Bovine Thermodynamic and Mass Balances Model. Animals 2023, 13, 3043. https://doi.org/10.3390/ani13193043
Porter WP, Bertz AE, Mathewson PD, Solorzano LC, Dudley PN, Bonazza R, Gebremedhin KG. Climate Spaces and Cliffs: A Novel Bovine Thermodynamic and Mass Balances Model. Animals. 2023; 13(19):3043. https://doi.org/10.3390/ani13193043
Chicago/Turabian StylePorter, Warren P., Alexa E. Bertz, Paul D. Mathewson, Luis C. Solorzano, Peter N. Dudley, Riccardo Bonazza, and Kifle G. Gebremedhin. 2023. "Climate Spaces and Cliffs: A Novel Bovine Thermodynamic and Mass Balances Model" Animals 13, no. 19: 3043. https://doi.org/10.3390/ani13193043
APA StylePorter, W. P., Bertz, A. E., Mathewson, P. D., Solorzano, L. C., Dudley, P. N., Bonazza, R., & Gebremedhin, K. G. (2023). Climate Spaces and Cliffs: A Novel Bovine Thermodynamic and Mass Balances Model. Animals, 13(19), 3043. https://doi.org/10.3390/ani13193043






