Prediction of Body Mass of Dairy Cattle Using Machine Learning Algorithms Applied to Morphological Characteristics
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Ethical Procedures
2.2. Data Collection
2.3. Statistical Analysis
2.3.1. Data Normality Analysis
2.3.2. Data Correlation Analysis
2.3.3. Regression Analysis
2.4. Development of ANN
2.4.1. Dense Neural Network (Multi-Layer Perceptron)
2.4.2. Hyperparameters
2.5. Support Vector Regression (SVR)
3. Results and Discussion
3.1. Results of the Data Normality Analysis
3.2. Results of Data Correlation Analysis
3.3. Linear Regression Results
3.4. Multiple Linear Regression Results
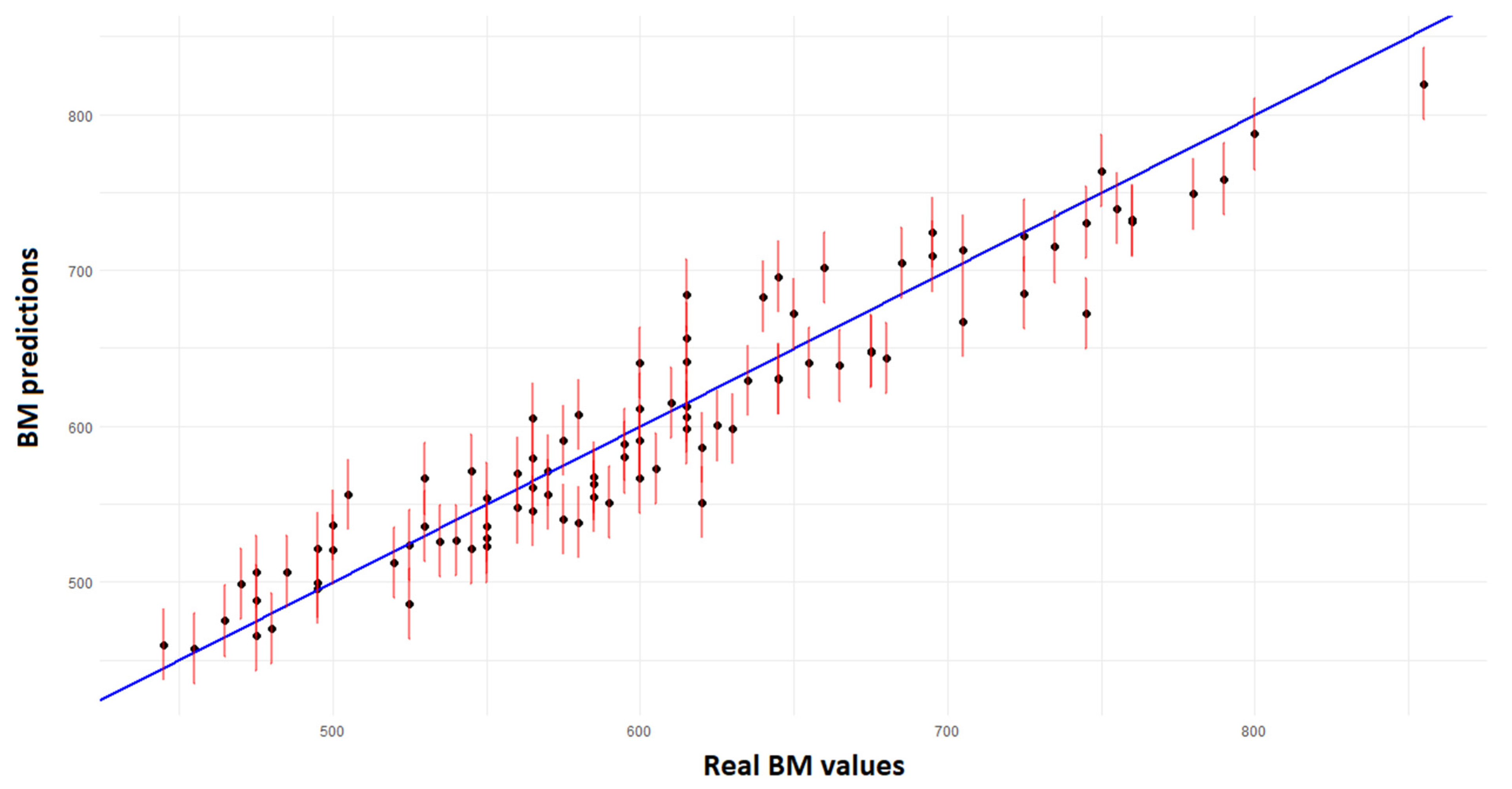
3.5. Neural Network Results
3.6. Support Vector Regression (SVR) Results
3.7. Comparison Between Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- National Academies of Sciences, Engineering, and Medicine. Nutrient Requirements of Dairy Cattle: Eighth Revised Edition; The National Academies Press: Washington, DC, USA, 2021.
- Contreras-Govea, F.E.; Cabrera, V.E.; Armentano, L.E.; Shaver, R.D.; Crump, P.M.; Beede, D.K.; VandeHaar, M.J. Constraints for nutritional grouping in Wisconsin and Michigan dairy farms. J. Dairy Sci. 2015, 98, 1336–1344. [Google Scholar] [PubMed]
- Raboisson, D.; Mounié, M.; Maigné, E. Diseases, reproductive performance, and changes in milk production associated with subclinical ketosis in dairy cows: A meta-analysis and review. J. Dairy Sci. 2014, 97, 7547–7563. [Google Scholar] [PubMed]
- Cainzos, J.M.; Andreu-Vazquez, C.; Guadagnini, M.; Rijpert-Duvivier, A.; Duffield, T. A systematic review of the cost of ketosis in dairy cattle. J. Dairy Sci. 2022, 105, 6175–6195. [Google Scholar] [CrossRef] [PubMed]
- VandeHaar, M.J.; Armentano, L.E.; Weigel, K.; Spurlock, D.M.; Tempelman, R.J.; Veerkamp, R. Harnessing the genetics of the modern dairy cow to continue improvements in feed efficiency. J. Dairy Sci. 2016, 99, 4941–4954. [Google Scholar] [CrossRef]
- Weber, V.A.D.M.; Weber, F.D.L.; Gomes, R.D.C.; Oliveira Junior, A.D.S.; Menezes, G.V.; Abreu, U.G.P.D.; Belete, N.A.d.S.; Pistori, H. Prediction of Girolando cattle weight by means of body measurements extracted from images. Rev. Bras. Zootec. 2020, 49, e20190110. [Google Scholar]
- Gomes, R.A.; Monteiro, G.R.; Assis, G.J.F.; Busato, K.C.; Ladeira, M.M.; Chizzotti, M.L. Estimating body weight and body composition of beef cattle trough digital image analysis. J. Anim. Sci. 2016, 94, 5414–5422. [Google Scholar]
- Ma, W.; Qi, X.; Sun, Y.; Gao, R.; Ding, L.; Wang, R.; Peng, C.; Zhang, J.; Wu, J.; Xu, Z.; et al. Computer Vision-Based Measurement Techniques for Livestock Body Dimension and Weight: A Review. Agriculture 2024, 14, 306. [Google Scholar] [CrossRef]
- Paputungan, U.; Hakim, L.; Ciptadi, G.; Lapian, H.F.N. The estimation accuracy of live weight from metric body measurements in Ongole grade cows. J. Indones. Trop. Anim. Agric. 2013, 38, 149–155. [Google Scholar]
- Paputungan, U.; Hakim, L.; Ciptadi, G.; Lapian, H.F.N. Application of body volume formula for predicting live weight in Ongole crossbred cows. Int. J. Livest. Prod. 2015, 6, 35–40. [Google Scholar]
- Lukuyu, M.N.; Gibson, J.P.; Savage, D.B.; Duncan, A.J.; Mujibi, F.D.N.; Okeyo, A.M. Use of body linear measurements to estimate liveweight of crossbred dairy cattle in smallholder farms in Kenya. SpringerPlus 2016, 5, 1–14. [Google Scholar]
- Franco, M.D.O.; Marcondes, M.I.; Campos, J.M.D.S.; Freitas, D.R.D.; Detmann, E.; Valadares Filho, S.D.C. Evaluation of body weight prediction Equations in growing heifers. Acta Scientiarum. Anim. Sci. 2017, 39, 201–206. [Google Scholar]
- Bewley, J. Precision dairy farming: Advanced analysis solutions for future profitability. In Proceedings of the First North American Conference on Precision Dairy Management, Toronto, ON, Canada, 2–5 March 2010; Volume 16. [Google Scholar]
- de Oliveira, F.M.; Ferraz, G.A.E.S.; André, A.L.G.; Santana, L.S.; Norton, T.; Ferraz, P.F.P. Digital and Precision Technologies in Dairy Cattle Farming: A Bibliometric Analysis. Animals 2024, 14, 1832. [Google Scholar] [CrossRef] [PubMed]
- Lathuilière, S.; Mesejo, P.; Alameda-Pineda, X.; Horaud, R. A comprehensive analysis of deep regression. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 2065–2081. [Google Scholar] [PubMed]
- Enevoldsen, C.; Kristensen, T. Estimation of body weight from body size measurements and body condition scores in dairy cows. J. Dairy Sci. 1997, 80, 1988–1995. [Google Scholar]
- Heinrichs, A.J.; Rogers, G.W.; Cooper, J.B. Predicting body weight and wither height in Holstein heifers using body measurements. J. Dairy Sci. 1992, 75, 3576–3581. [Google Scholar]
- Gruber, L.; Ledinek, M.; Steininger, F.; Fuerst-Waltl, B.; Zottl, K.; Royer, M.; Krimberger, K.; Mayerhofer, M.; Egger-Danner, C. Body weight prediction using body size measurements in Fleckvieh, Holstein, and Brown Swiss dairy cows in lactation and dry periods. Arch. Anim. Breed. 2018, 61, 413–424. [Google Scholar]
- Ruchay, A.; Kober, V.; Dorofeev, K.; Kolpakov, V.; Miroshnikov, S. Accurate body measurement of live cattle using three depth cameras and non-rigid 3-D shape recovery. Comput. Electron. Agric. 2020, 179, 105821. [Google Scholar]
- Ruchay, A.; Kober, V.; Dorofeev, K.; Kolpakov, V.; Dzhulamanov, K.; Kalschikov, V.; Guo, H. Comparative analysis of machine learning algorithms for predicting live weight of Hereford cows. Comput. Electron. Agric. 2022, 195, 106837. [Google Scholar]
- Le Cozler, Y.; Allain, C.; Xavier, C.; Depuille, L.; Caillot, A.; Delouard, J.M.; Delattre, L.; Luginbuhl, T.; Faverdin, P. Volume and surface area of Holstein dairy cows calculated from complete 3D shapes acquired using a high-precision scanning system: Interest for body weight estimation. Comput. Electron. Agric. 2019, 165, 104977. [Google Scholar]
- Miller, G.A.; Hyslop, J.J.; Barclay, D.; Edwards, A.; Thomson, W.; Duthie, C.A. Using 3D imaging and machine learning to predict liveweight and carcass characteristics of live finishing beef cattle. Front. Sustain. Food Syst. 2019, 3, 30. [Google Scholar]
- Wang, Z.; Shadpour, S.; Chan, E.; Rotondo, V.; Wood, K.M.; Tulpan, D. ASAS-NANP SYMPOSIUM: Applications of machine learning for livestock body weight prediction from digital images. J. Anim. Sci. 2021, 99, skab022. [Google Scholar] [PubMed]
- Ozkaya, S.; Bozkurt, Y. The relationship of parameters of body measures and body weight by using digital image analysis in pre-slaughter cattle. Arch. Anim. Breed. 2008, 51, 120–128. [Google Scholar] [CrossRef]
- Tasdemir, S.; Urkmez, A.; Inal, S. Determination of body measurements on the Holstein cows using digital image analysis and estimation of live weight with regression analysis. Comput. Electron. Agric. 2011, 76, 189–197. [Google Scholar]
- Martins, B.M.; Mendes, A.L.C.; Silva, L.F.; Moreira, T.R.; Costa, J.H.C.; Rotta, P.P.; Chizzotti, M.L.; Marcondes, M.I. Estimating body weight, body condition score, and type traits in dairy cows using three dimensional cameras and manual body measurements. Livest. Sci. 2020, 236, 104054. [Google Scholar]
- Ozkaya, S.; Neja, W.; Krezel-Czopek, S.; Oler, A. Estimation of bodyweight from body measurements and determination of body measurements on Limousin cattle using digital image analysis. Anim. Prod. Sci. 2015, 56, 2060–2063. [Google Scholar]
- Massey Jr, F.J. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar]
- Berger, V.W.; Zhou, Y. Kolmogorov–smirnov test: Overview. In Wiley Statsref: Statistics Reference Online; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar]
- Zar, J.H. Spearman rank correlation. Encycl. Biostat. 2005, 7. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Ben-David, S. Understanding Machine Learning: From Theory to Algorithms; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Niazian, M.; Sadat-Noori, S.A.; Abdipour, M.; Tohidfar, M.; Mortazavian, S.M.M. Image processing and artificial neural network-based models to measure and predict physical properties of embryogenic callus and number of somatic embryos in ajowan (Trachyspermum ammi (L.) Sprague). Vitr. Cell. Dev. Biol. Plant 2018, 54, 54–68. [Google Scholar]
- Passos, D.; Mishra, P. A tutorial on automatic hyperparameter tuning of deep spectral modelling for regression and classification tasks. Chemom. Intell. Lab. Syst. 2022, 223, 104520. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Chok, N.S. Pearson’s versus Spearman’s and Kendall’s Correlation Coefficients for Continuous Data. Doctoral Dissertation, University of Pittsburgh, Pittsburgh, PA, USA, 2010. [Google Scholar]
- Mukaka, M.M. A guide to appropriate use of correlation coefficient in medical research. Malawi Med. J. 2012, 24, 69–71. [Google Scholar] [PubMed]
- Pereira, M.N.; Júnior, N.M.; Oliveira, R.C.; Salvati, G.G.S.; Pereira, R.A.N. Methionine precursor effects on lactation performance of dairy cows fed raw or heated soybeans. J. Dairy Sci. 2021, 104, 2996–3007. [Google Scholar] [PubMed]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; Volume 2, pp. 1–758. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R.; Taylor, J. Linear Regression. In An Introduction to Statistical Learning. Springer Texts in Statistics; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Alin, A. Multicollinearity. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 370–374. [Google Scholar]
- Daoud, J.I. Multicollinearity and regression analysis. J. Phys. Conf. Ser. 2017, 949, 012009. [Google Scholar]
- Alonso, J.; Castañón, Á.R.; Bahamonde, A. Support Vector Regression to predict carcass weight in beef cattle in advance of the slaughter. Comput. Electron. Agric. 2013, 91, 116–120. [Google Scholar] [CrossRef]
- Heinrichs, A.J.; Heinrichs, B.S.; Jones, C.M.; Erickson, P.S.; Kalscheur, K.F.; Nennich, T.D.; Heins, B.J.; Cardoso, F.C. Verifying Holstein heifer heart girth to body weight prediction equations. J. Dairy Sci. 2017, 100, 8451–8454. [Google Scholar]
- Rigatti, S.J. Random forest. J. Insur. Med. 2017, 47, 31–39. [Google Scholar]
- Liu, H.; Reibman, A.R.; Boerman, J.P. Feature extraction using multi-view video analytics for dairy cattle body weight estimation. Smart Agric. Technol. 2023, 6, 100359. [Google Scholar]




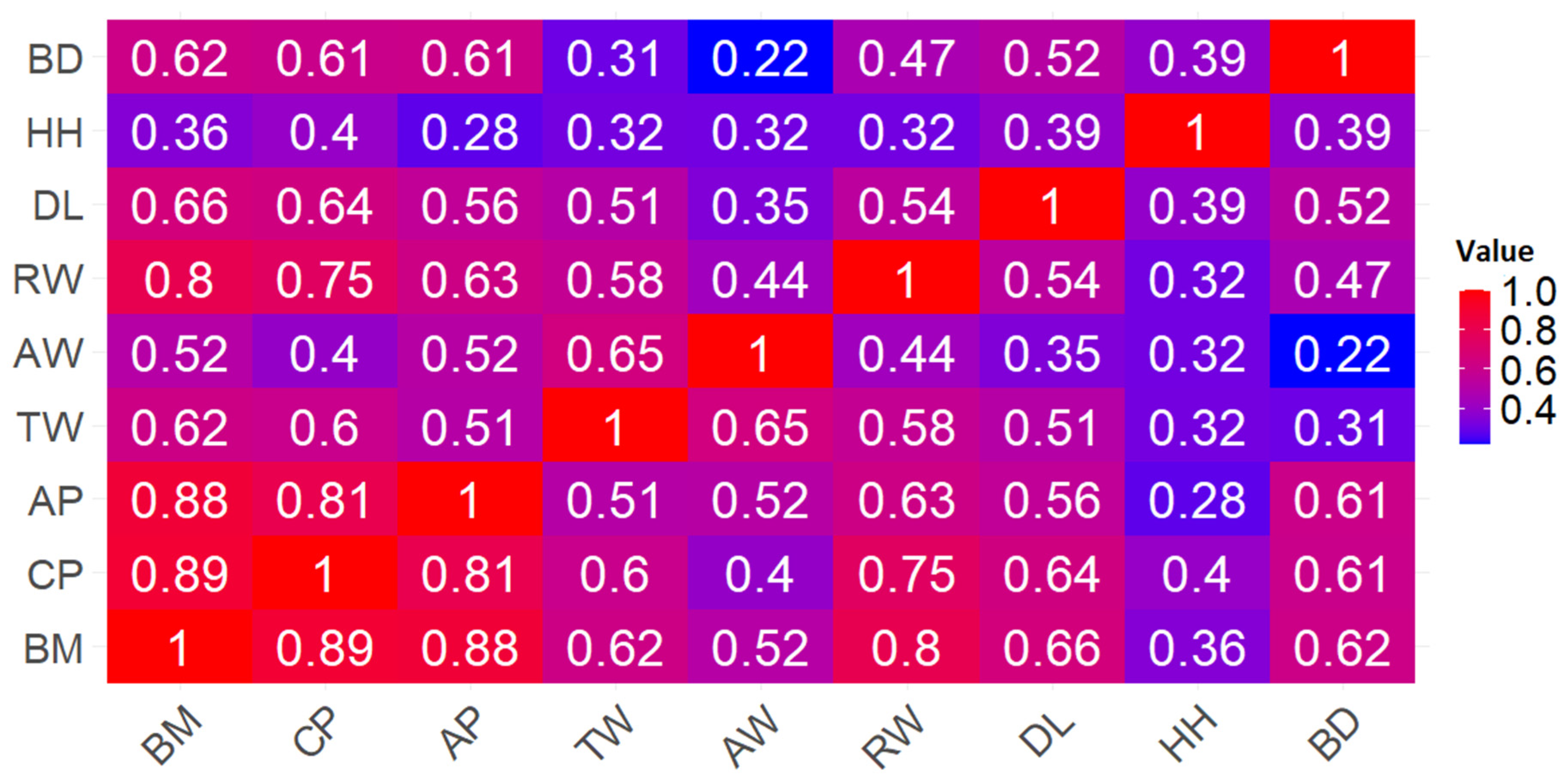
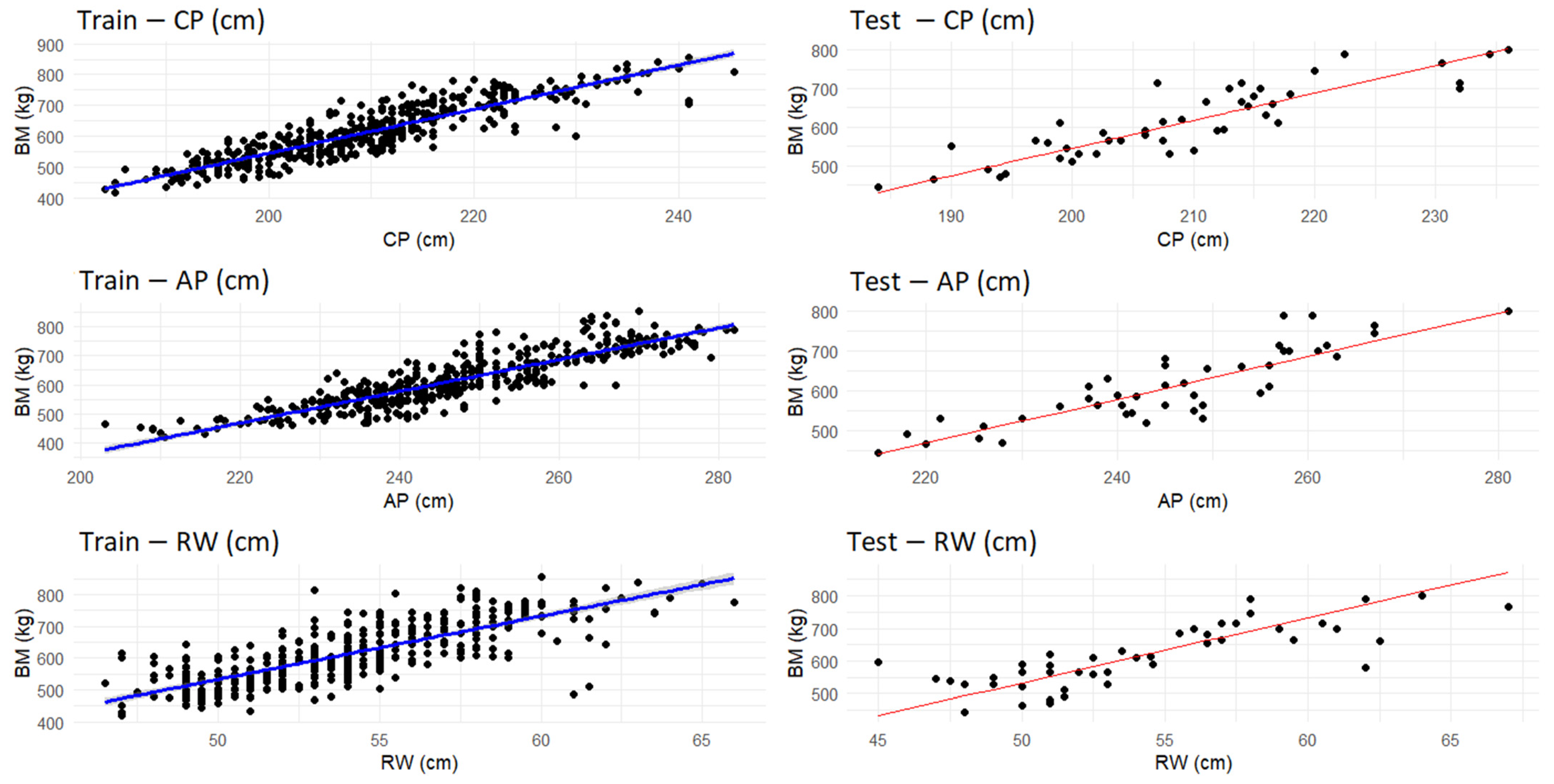

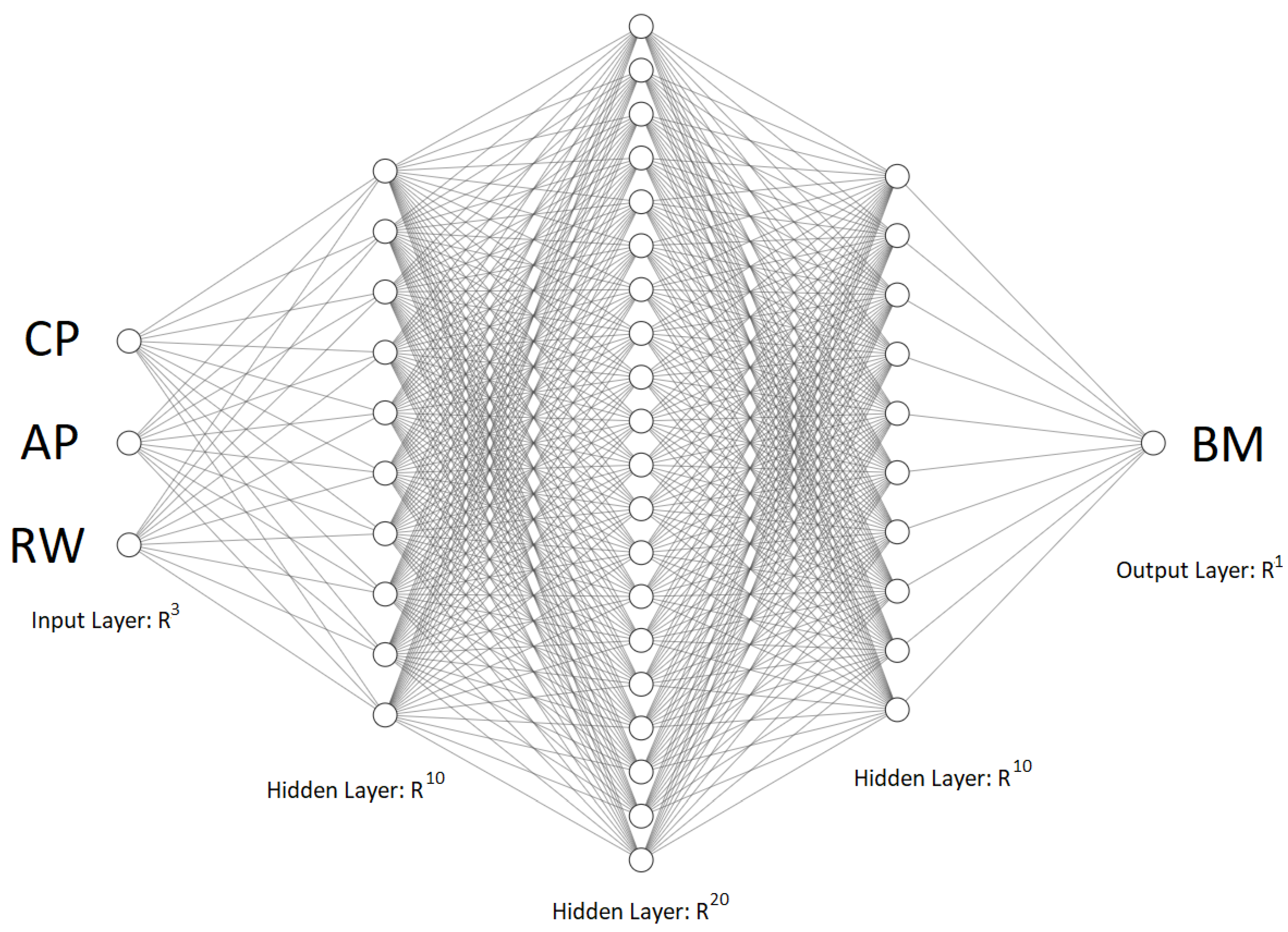

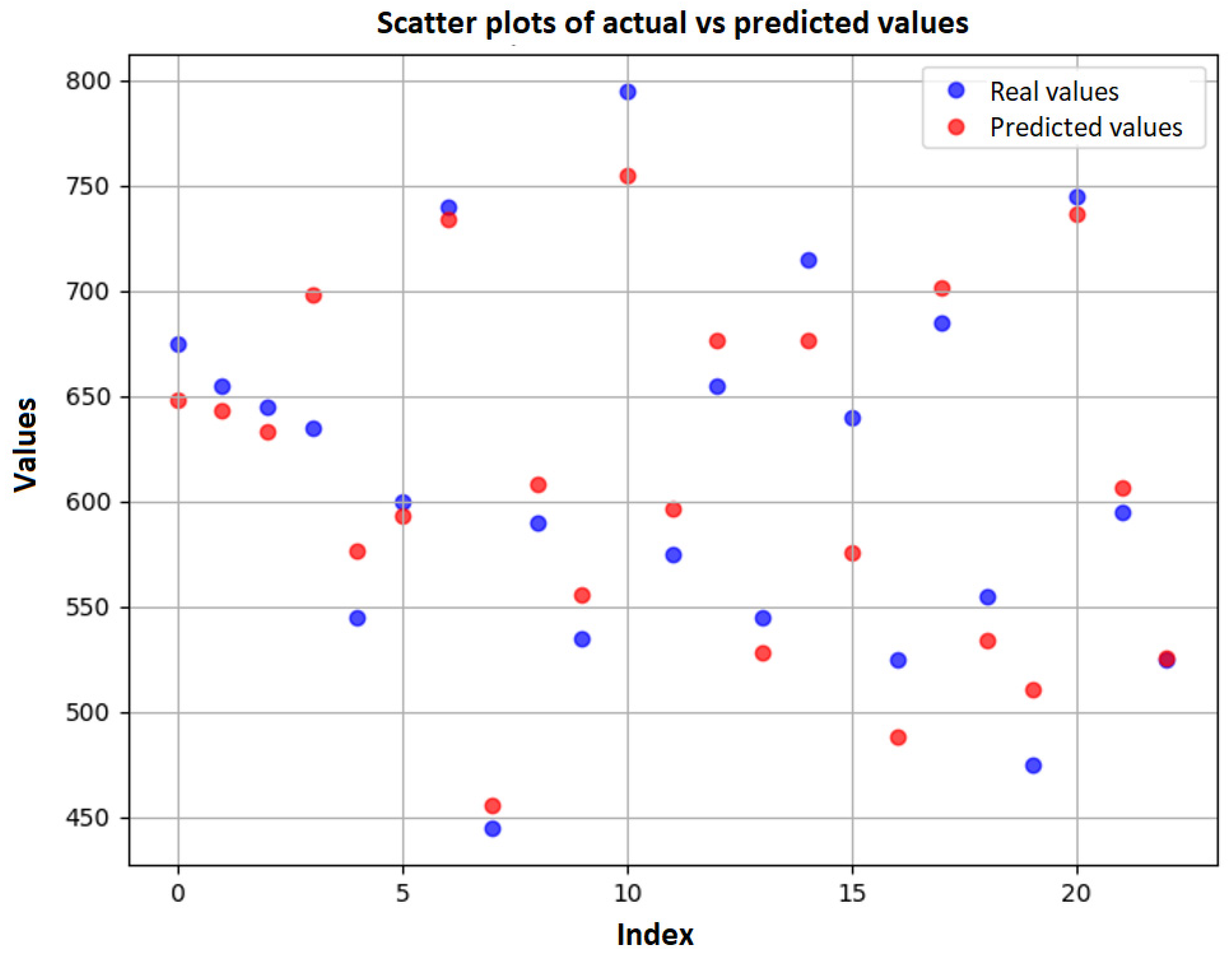
| Variable | D¹ | p-Value2 | Conclusion |
|---|---|---|---|
| BM | 0.071943 | 0.01624 | Not Normal (p < 0.05) |
| CP | 0.055219 | 0.1173 | Normal (p > 0.05) |
| AP | 0.054523 | 0.126 | Normal (p > 0.05) |
| TW | 0.06787 | 0.02758 | Not Normal (p < 0.05) |
| AW | 0.040716 | 0.4238 | Normal (p > 0.05) |
| RW | 0.081225 | 0.004329 | Not Normal (p < 0.05) |
| DL | 0.052554 | 0.1532 | Normal (p > 0.05) |
| HH | 0.052619 | 0.1523 | Normal (p > 0.05) |
| BD | 0.061925 | 0.05652 | Not Normal (p < 0.05) |
| Model | Train R2 | Test | ||
|---|---|---|---|---|
| R2 | MAE | RMSE | ||
| Model CP | 0.7953 | 0.7763 | 33.42 | 43.69 |
| Model AP | 0.7682 | 0.7656 | 34.23 | 44.72 |
| Model RW | 0.6062 | 0.5484 | 48.04 | 62.08 |
| Variable | Estimate | p-Value | Significance Level |
|---|---|---|---|
| CP | 2.8999 | <2 × 10−16 | <0.001 |
| AP | 2.6445 | <2 × 10−16 | <0.001 |
| RW | 6.3471 | <2 × 10−16 | <0.001 |
| Model | Train R2 | Test | ||
|---|---|---|---|---|
| R2 | MAE | RMSE | ||
| Multiple Model 1 (CP + AP + RW) | 0.8959 | 0.9067 | 22.29 | 28.00 |
| Variable | Estimate | p-Value | Significance Level |
|---|---|---|---|
| CP | 2.7509 | <2 × 10−16 | <0.001 |
| AP | 2.3619 | <2 × 10−16 | <0.001 |
| TW | 0.8203 | 0.0636 | Not significant |
| AW | 0.6406 | 0.1471 | <0.1 |
| RW | 5.6785 | <2 × 10−16 | <0.001 |
| DL | 0.3929 | 0.2054 | <0.1 |
| HH | −0.8360 | 0.0222 | <0.05 |
| BD | 0.7616 | 0.1424 | <0.1 |
| Model | Train R2 | Test | ||
|---|---|---|---|---|
| R2 | MAE | RMSE | ||
| Multiple Model 2 (All Variables) | 0.8997 | 0.9063 | 22.20 | 28.05 |
| Type of Optimizer | Number of Epochs | Topology | Batch Size |
|---|---|---|---|
| RMSprop | 5000 | 3-10-20-10-1 | 8 |
| Model | Train R2 | Test | ||
|---|---|---|---|---|
| R2 | MAE | RMSE | ||
| ANN MLP | 0.9139 | 0.9125 | 21.97 | 25.86 |
| Model | Train R2 | Test | ||
|---|---|---|---|---|
| R2 | MAE | RMSE | ||
| SVR | 0.9160 | 0.9046 | 22.81 | 27.41 |
| Model | Train R2 | Test | ||
|---|---|---|---|---|
| R2 | MAE | RMSE | ||
| Model CP | 0.7953 | 0.7763 | 33.42 | 43.69 |
| Model AP | 0.7682 | 0.7656 | 34.23 | 44.72 |
| Model RW | 0.6062 | 0.5484 | 48.04 | 62.08 |
| Multiple Model 1 (CP + AP + RW) | 0.8959 | 0.9067 | 22.29 | 28.00 |
| Multiple Model 2 (All Variables) | 0.8997 | 0.9063 | 22.20 | 28.05 |
| Artificial Neural Network | 0.9139 | 0.9125 | 21.97 | 25.86 |
| SVR Model | 0.9159 | 0.9046 | 22.81 | 27.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Oliveira, F.M.; Ferraz, P.F.P.; Ferraz, G.A.e.S.; Pereira, M.N.; Barbari, M.; Rossi, G. Prediction of Body Mass of Dairy Cattle Using Machine Learning Algorithms Applied to Morphological Characteristics. Animals 2025, 15, 1054. https://doi.org/10.3390/ani15071054
de Oliveira FM, Ferraz PFP, Ferraz GAeS, Pereira MN, Barbari M, Rossi G. Prediction of Body Mass of Dairy Cattle Using Machine Learning Algorithms Applied to Morphological Characteristics. Animals. 2025; 15(7):1054. https://doi.org/10.3390/ani15071054
Chicago/Turabian Stylede Oliveira, Franck Morais, Patrícia Ferreira Ponciano Ferraz, Gabriel Araújo e Silva Ferraz, Marcos Neves Pereira, Matteo Barbari, and Giuseppe Rossi. 2025. "Prediction of Body Mass of Dairy Cattle Using Machine Learning Algorithms Applied to Morphological Characteristics" Animals 15, no. 7: 1054. https://doi.org/10.3390/ani15071054
APA Stylede Oliveira, F. M., Ferraz, P. F. P., Ferraz, G. A. e. S., Pereira, M. N., Barbari, M., & Rossi, G. (2025). Prediction of Body Mass of Dairy Cattle Using Machine Learning Algorithms Applied to Morphological Characteristics. Animals, 15(7), 1054. https://doi.org/10.3390/ani15071054










