A Comparative Study of Optimizing Genomic Prediction Accuracy in Commercial Pigs
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Ethics Statement
2.2. Experimental Animals and Phenotypic Data
2.3. Genotyping and Imputation
2.4. Genetic Parameter Estimation
2.5. Statistical Models
2.5.1. GBLUP
2.5.2. ssGBLUP
2.5.3. Bayesian Models
2.6. Genomic Prediction Accuracy and Bias
3. Results
3.1. Statistical Phenotypes and Estimation of Heritability
3.2. Prediction Accuracy of Seven Statistical Models
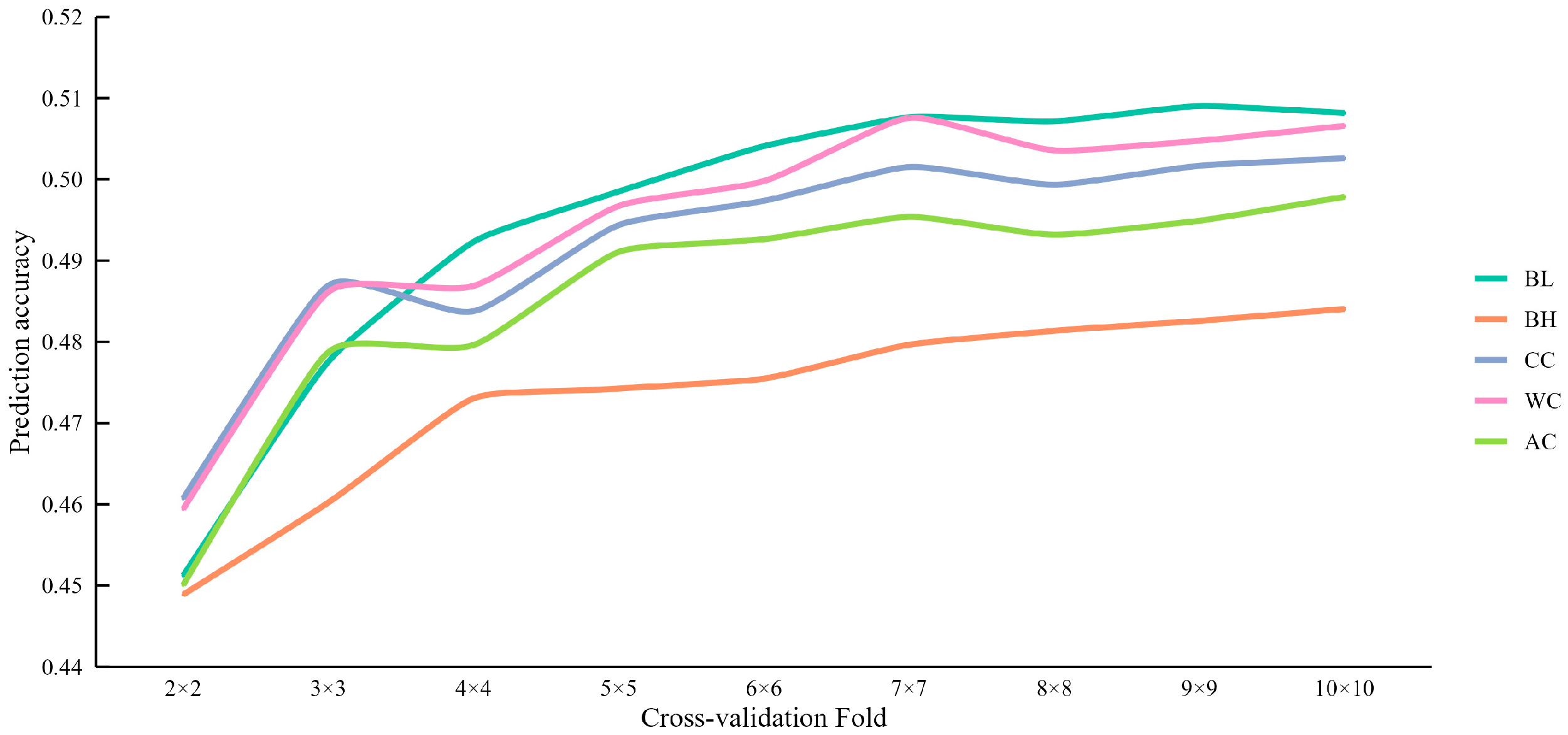
3.3. Prediction Accuracy of Different Cross-Validation Folds
3.4. Estimated Heritability of SNPs and INDELs from WGS
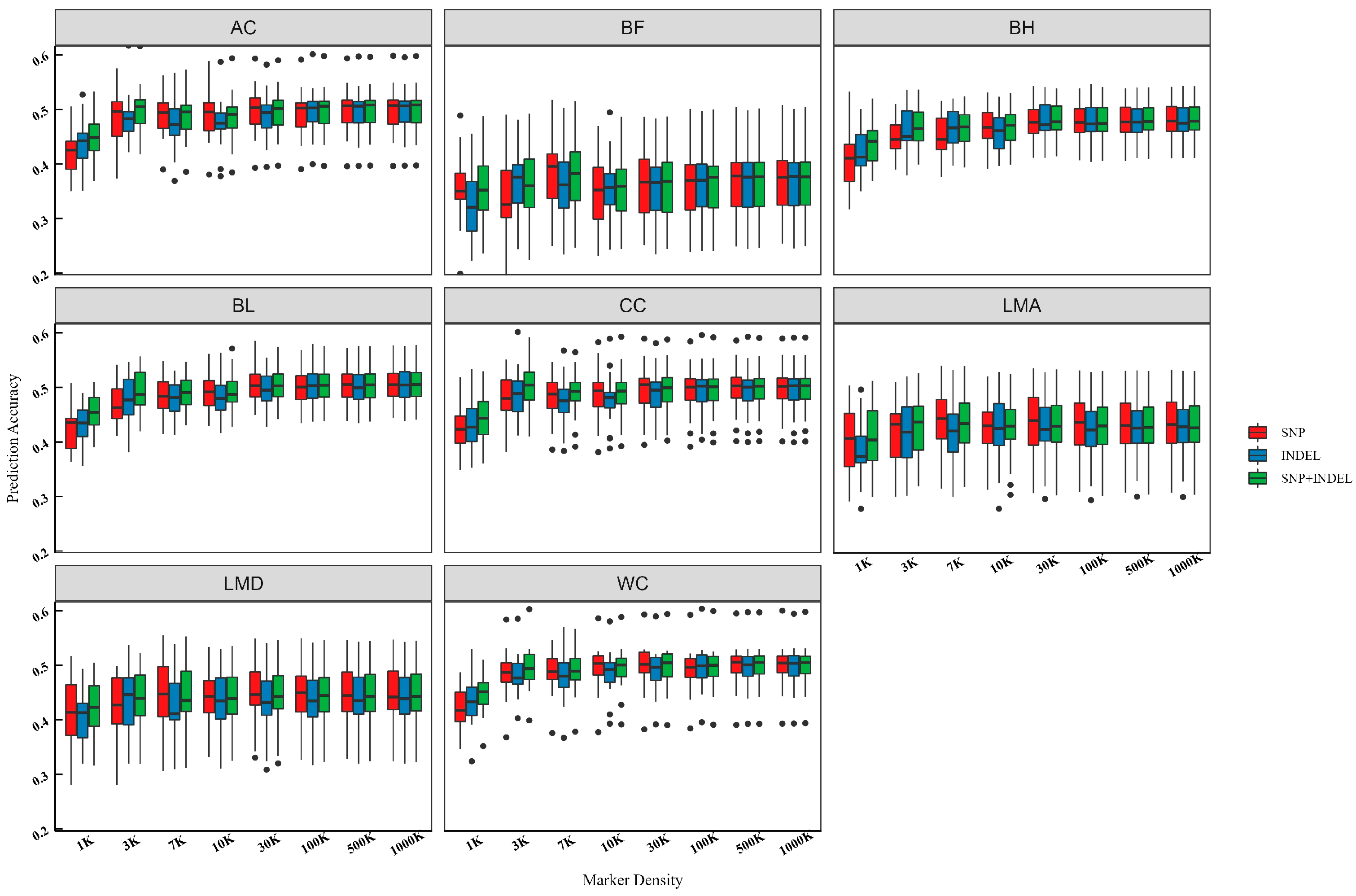
3.5. Prediction Accuracy of SNPs and INDELs from WGS
4. Discussion
4.1. Model Performance and Trait Architecture
4.2. Factors Affecting the Accuracy of Genomic Prediction
4.3. Implications for Pig Breeding
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Abdominal circumference |
| BF | Backfat thickness |
| BH | Body height |
| BL | Body length |
| BLUP | Best Linear Unbiased Prediction |
| CC | Chest circumference |
| GWAS | Genome-wide association study |
| GBLUP | Genomic Best Linear Unbiased Prediction |
| GEBV | Genomic estimated breeding value |
| GP | Genomic prediction |
| h2 | Heritability |
| INDEL | Insertion and deletion |
| LD | Linkage disequilibrium |
| LMA | Loin muscle area |
| LMD | Loin muscle depth |
| MAF | Minor allele frequency |
| MCMC | Markov chain Monte Carlo theory |
| QTL | Quantitative trait loci |
| RRBLUP | Ridge Regression Best Linear Unbiased Prediction |
| SNP | Single-nucleotide polymorphism |
| ssGBLUP | Single-step Genomic Best Linear Unbiased Prediction |
| LASSO | Least absolute shrinkage and selection operator |
| WC | Waist circumference |
| WGS | Whole genome sequence |
References
- Meuwissen, T.H.; Hayes, B.J.; Goddard, M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef]
- Hayes, B.J.; Cogan, N.O.I.; Pembleton, L.W.; Goddard, M.E.; Wang, J.; Spangenberg, G.C.; Forster, J.W.; Rognli, O.A. Prospects for genomic selection in forage plant species. Plant Breed. 2013, 132, 133–143. [Google Scholar] [CrossRef]
- Sonesson, A.K.; Meuwissen, T.H. Testing strategies for genomic selection in aquaculture breeding programs. Genet. Sel. Evol. 2009, 41, 37. [Google Scholar] [CrossRef] [PubMed]
- Habier, D.; Fernando, R.L.; Dekkers, J.C.M. The Impact of Genetic Relationship Information on Genome-Assisted Breeding Values. Genetics 2007, 177, 2389–2397. [Google Scholar] [CrossRef] [PubMed]
- Christensen, O.F.; Lund, M.S. Genomic prediction when some animals are not genotyped. Genet. Sel. Evol. 2010, 42, 2. [Google Scholar] [CrossRef] [PubMed]
- Whittaker, J.C.; Thompson, R.; Denham, M.C. Marker-assisted selection using ridge regression. Genet. Res. 2000, 75, 249–252. [Google Scholar] [CrossRef]
- Goddard, M.E.; Hayes, B.J. Genomic selection. J. Anim. Breed. Genet. 2007, 124, 323–330. [Google Scholar] [CrossRef]
- De los Campos, G.; Gianola, D.; Rosa, G.J.; Weigel, K.A.; Crossa, J. Semi-parametric genomic-enabled prediction of genetic values using reproducing kernel Hilbert spaces methods. Genet. Res. 2010, 92, 295–308. [Google Scholar] [CrossRef]
- Maenhout, S.; De Baets, B.; Haesaert, G.; Van Bockstaele, E. Support vector machine regression for the prediction of maize hybrid performance. Theor. Appl. Genet. 2007, 115, 1003–1013. [Google Scholar] [CrossRef]
- Svetnik, V.; Liaw, A.; Tong, C.; Culberson, J.C.; Sheridan, R.P.; Feuston, B.P. Random forest: A classification and regression tool for compound classification and QSAR modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef]
- Kristensen, P.S.; Jahoor, A.; Andersen, J.R.; Cericola, F.; Orabi, J.; Janss, L.L.; Jensen, J. Genome-Wide Association Studies and Comparison of Models and Cross-Validation Strategies for Genomic Prediction of Quality Traits in Advanced Winter Wheat Breeding Lines. Front. Plant Sci. 2018, 9, 69. [Google Scholar] [CrossRef]
- Zhang, H.; Yin, L.; Wang, M.; Yuan, X.; Liu, X. Factors Affecting the Accuracy of Genomic Selection for Agricultural Economic Traits in Maize, Cattle, and Pig Populations. Front. Genet. 2019, 10, 189. [Google Scholar] [CrossRef] [PubMed]
- Misztal, I.; Tsuruta, S.; Lourenco, D.; Aguilar, I.; Legarra, A.; Vitezica, Z. Manual for BLUPF90 Family of Programs; University of Georgia: Athens, GA, USA, 2014. [Google Scholar]
- Ozsensoy, Y.; Sahin, S. Comparison of different DNA isolation methods and use of dodecyle trimethyl ammonium bromide (DTAB) for the isolation of DNA from meat products. J. Adv. Vet. Anim. Res. 2016, 3, 368. [Google Scholar] [CrossRef]
- Ding, R.; Yang, M.; Wang, X.; Quan, J.; Zhuang, Z.; Zhou, S.; Li, S.; Xu, Z.; Zheng, E.; Cai, G.; et al. Genetic Architecture of Feeding Behavior and Feed Efficiency in a Duroc Pig Population. Front. Genet. 2018, 9, 220. [Google Scholar] [CrossRef]
- Purcell, S.; Neale, B.; Todd-Brown, K.; Thomas, L.; Ferreira, M.A.; Bender, D.; Maller, J.; Sklar, P.; de Bakker, P.I.; Daly, M.J.; et al. PLINK: A tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 2007, 81, 559–575. [Google Scholar] [CrossRef]
- Ding, R.; Savegnago, R.; Liu, J.; Long, N.; Tan, C.; Cai, G.; Zhuang, Z.; Wu, J.; Yang, M.; Qiu, Y.; et al. The SWine IMputation (SWIM) haplotype reference panel enables nucleotide resolution genetic mapping in pigs. Commun. Biol. 2023, 6, 577. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Lee, S.H.; Goddard, M.E.; Visscher, P.M. GCTA: A Tool for Genome-wide Complex Trait Analysis. Am. J. Hum. Genet. 2011, 88, 76–82. [Google Scholar] [CrossRef]
- VanRaden, P.M. Efficient methods to compute genomic predictions. J. Dairy. Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef]
- Aguilar, I.; Misztal, I.; Johnson, D.L.; Legarra, A.; Tsuruta, S.; Lawlor, T.J. Hot topic: A unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score. J. Dairy. Sci. 2010, 93, 743–752. [Google Scholar] [CrossRef]
- Kjetsa, M.V.; Gjuvsland, A.B.; Nordbo, O.; Grindflek, E.; Meuwissen, T. Accuracy of genomic prediction of maternal traits in pigs using Bayesian variable selection methods. J. Anim. Breed. Genet. 2022, 139, 654–665. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Q.; Ding, X. Advances in genomic selection in domestic animals. Chin. Sci. Bull. 2011, 56, 2655–2663. [Google Scholar] [CrossRef][Green Version]
- Pérez, P.; de los Campos, G. Genome-Wide Regression and Prediction with the BGLR Statistical Package. Genetics 2014, 198, 483–495. [Google Scholar] [CrossRef]
- Park, T.; Casella, G. The Bayesian Lasso. J. Am. Stat. Assoc. 2008, 103, 681–686. [Google Scholar] [CrossRef]
- Erbe, M.; Hayes, B.J.; Matukumalli, L.K.; Goswami, S.; Bowman, P.J.; Reich, C.M.; Mason, B.A.; Goddard, M.E. Improving accuracy of genomic predictions within and between dairy cattle breeds with imputed high-density single nucleotide polymorphism panels. J. Dairy. Sci. 2012, 95, 4114–4129. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, Z.; Wu, J.; Qiu, Y.; Ruan, D.; Ding, R.; Xu, C.; Zhou, S.; Zhang, Y.; Liu, Y.; Ma, F.; et al. Improving the accuracy of genomic prediction for meat quality traits using whole genome sequence data in pigs. J. Anim. Sci. Biotechnol. 2023, 14, 67. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Zhang, J.; Jiang, Y.; Gao, H.; Tang, S.; Mi, S.; Yu, F.; Meng, Q.; Xiao, W.; Zhang, Q.; et al. Genomic prediction for growth and reproduction traits in pig using an admixed reference population. J. Anim. Sci. 2017, 95, 3415. [Google Scholar] [CrossRef]
- Christensen, O.F.; Madsen, P.; Nielsen, B.; Ostersen, T.; Su, G. Single-step methods for genomic evaluation in pigs. Animal 2012, 6, 1565–1571. [Google Scholar] [CrossRef]
- Gao, H.; Christensen, O.F.; Madsen, P.; Nielsen, U.S.; Zhang, Y.; Lund, M.S.; Su, G. Comparison on genomic predictions using three GBLUP methods and two single-step blending methods in the Nordic Holstein population. Genet. Sel. Evol. 2012, 44, 8. [Google Scholar] [CrossRef]
- Luan, T.; Woolliams, J.A.; Lien, S.; Kent, M.; Svendsen, M.; Meuwissen, T.H. The accuracy of Genomic Selection in Norwegian red cattle assessed by cross-validation. Genetics 2009, 183, 1119–1126. [Google Scholar] [CrossRef]
- Daetwyler, H.D.; Pong-Wong, R.; Villanueva, B.; Woolliams, J.A. The impact of genetic architecture on genome-wide evaluation methods. Genetics 2010, 185, 1021–1031. [Google Scholar] [CrossRef]
- Do, C.-H.; Park, C.-H.; Wasana, N.; Choi, J.-G.; Park, S.-B.; Kim, S.-D.; Cho, G.-H.; Lee, D.-H. Genetic and phenotypic relationships of live body measurement traits and carcass traits in crossbred pigs of Korea. Korean J. Agric. Sci. 2014, 41, 229–236. [Google Scholar] [CrossRef]
- Zhou, L.; Ji, J.; Peng, S.; Zhang, Z.; Fang, S.; Li, L.; Zhu, Y.; Huang, L.; Chen, C.; Ma, J. A GWA study reveals genetic loci for body conformation traits in Chinese Laiwu pigs and its implications for human BMI. Mamm. Genome 2016, 27, 610–621. [Google Scholar] [CrossRef]
- Song, H.; Zhang, J.; Zhang, Q.; Ding, X. Using Different Single-Step Strategies to Improve the Efficiency of Genomic Prediction on Body Measurement Traits in Pig. Front. Genet. 2018, 9, 730. [Google Scholar] [CrossRef]
- Lo, L.L.; McLaren, D.G.; McKeith, F.K.; Fernando, R.L.; Novakofski, J. Genetic analyses of growth, real-time ultrasound, carcass, and pork quality traits in Duroc and Landrace pigs: II. Heritabilities and correlations. J. Anim. Sci. 1992, 70, 2387–2396. [Google Scholar] [CrossRef]
- Cleveland, M.A.; Hickey, J.M.; Forni, S. A common dataset for genomic analysis of livestock populations. G3 2012, 2, 429–435. [Google Scholar] [CrossRef] [PubMed]
- de Roos, A.P.; Hayes, B.J.; Goddard, M.E. Reliability of genomic predictions across multiple populations. Genetics 2009, 183, 1545–1553. [Google Scholar] [CrossRef] [PubMed]
- Combs, E.; Bernardo, R. Accuracy of Genomewide Selection for Different Traits with Constant Population Size, Heritability, and Number of Markers. Plant Genome 2013, 6. [Google Scholar] [CrossRef]
- Hayes, B.J.; Macleod, A.; Daetwyler, H.D.; Veerkamp, R.F.; Tassell, C.P.V.; Gredler, B.; Druet, T.; Bagnato, A.; Vilkki, J.; Koning, D.J.D. Genomic Prediction from Whole Genome Sequence in Livestock: The 1000 Bull Genomes Project. 2014. Available online: https://hal.science/hal-01193911/document (accessed on 13 June 2024).
- van Binsbergen, R.; Calus, M.P.; Bink, M.C.; van Eeuwijk, F.A.; Schrooten, C.; Veerkamp, R.F. Genomic prediction using imputed whole-genome sequence data in Holstein Friesian cattle. Genet. Sel. Evol. 2015, 47, 71. [Google Scholar] [CrossRef]
- Zhang, C.; Kemp, R.A.; Stothard, P.; Wang, Z.; Boddicker, N.; Krivushin, K.; Dekkers, J.; Plastow, G. Genomic evaluation of feed efficiency component traits in Duroc pigs using 80K, 650K and whole-genome sequence variants. Genet. Sel. Evol. 2018, 50, 14. [Google Scholar] [CrossRef]

| Trait | N 9 | Mean (±SD) 10 | Min 11 | Max 12 | C.V./% 13 | h2 (±SE) 14 |
|---|---|---|---|---|---|---|
| BL (cm) 1 | 1494 | 123.70 ± 7.14 | 101.00 | 145.00 | 5.77 | 0.52 ± 0.02 |
| BH (cm) 2 | 1494 | 64.60 ± 3.64 | 51.00 | 78.00 | 5.63 | 0.49 ± 0.02 |
| CC (cm) 3 | 1494 | 112.24 ± 8.16 | 88.00 | 140.00 | 7.27 | 0.48 ± 0.02 |
| WC (cm) 4 | 1494 | 110.45 ± 8.79 | 84.00 | 140.00 | 7.96 | 0.49 ± 0.02 |
| AC (cm) 5 | 1494 | 121.34 ± 8.59 | 94.00 | 150.00 | 7.08 | 0.48 ± 0.02 |
| BF(mm) 6 | 650 | 11.40 ± 3.08 | 5.50 | 20.80 | 27.07 | 0.39 ± 0.02 |
| LMA(cm2) 7 | 650 | 40.36 ± 7.29 | 20.25 | 59.10 | 18.05 | 0.42 ± 0.02 |
| LMD (mm) 8 | 650 | 53.18 ± 6.69 | 33.23 | 69.10 | 12.56 | 0.45 ± 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Liu, Y.; Zhang, Y.; Zhuang, Z.; Huang, J.; Luan, M.; Zhao, X.; Dong, L.; Ye, J.; Yang, M.; et al. A Comparative Study of Optimizing Genomic Prediction Accuracy in Commercial Pigs. Animals 2025, 15, 966. https://doi.org/10.3390/ani15070966
Chen X, Liu Y, Zhang Y, Zhuang Z, Huang J, Luan M, Zhao X, Dong L, Ye J, Yang M, et al. A Comparative Study of Optimizing Genomic Prediction Accuracy in Commercial Pigs. Animals. 2025; 15(7):966. https://doi.org/10.3390/ani15070966
Chicago/Turabian StyleChen, Xiaojian, Yiyi Liu, Yuling Zhang, Zhanwei Zhuang, Jinyan Huang, Menghao Luan, Xiang Zhao, Linsong Dong, Jian Ye, Ming Yang, and et al. 2025. "A Comparative Study of Optimizing Genomic Prediction Accuracy in Commercial Pigs" Animals 15, no. 7: 966. https://doi.org/10.3390/ani15070966
APA StyleChen, X., Liu, Y., Zhang, Y., Zhuang, Z., Huang, J., Luan, M., Zhao, X., Dong, L., Ye, J., Yang, M., Zheng, E., Cai, G., Yang, J., Wu, Z., & Liu, L. (2025). A Comparative Study of Optimizing Genomic Prediction Accuracy in Commercial Pigs. Animals, 15(7), 966. https://doi.org/10.3390/ani15070966





