Experimental and Numerical Investigation of a Dissipative Connection for the Seismic Retrofit of Precast RC Industrial Sheds
Abstract
:1. Introduction
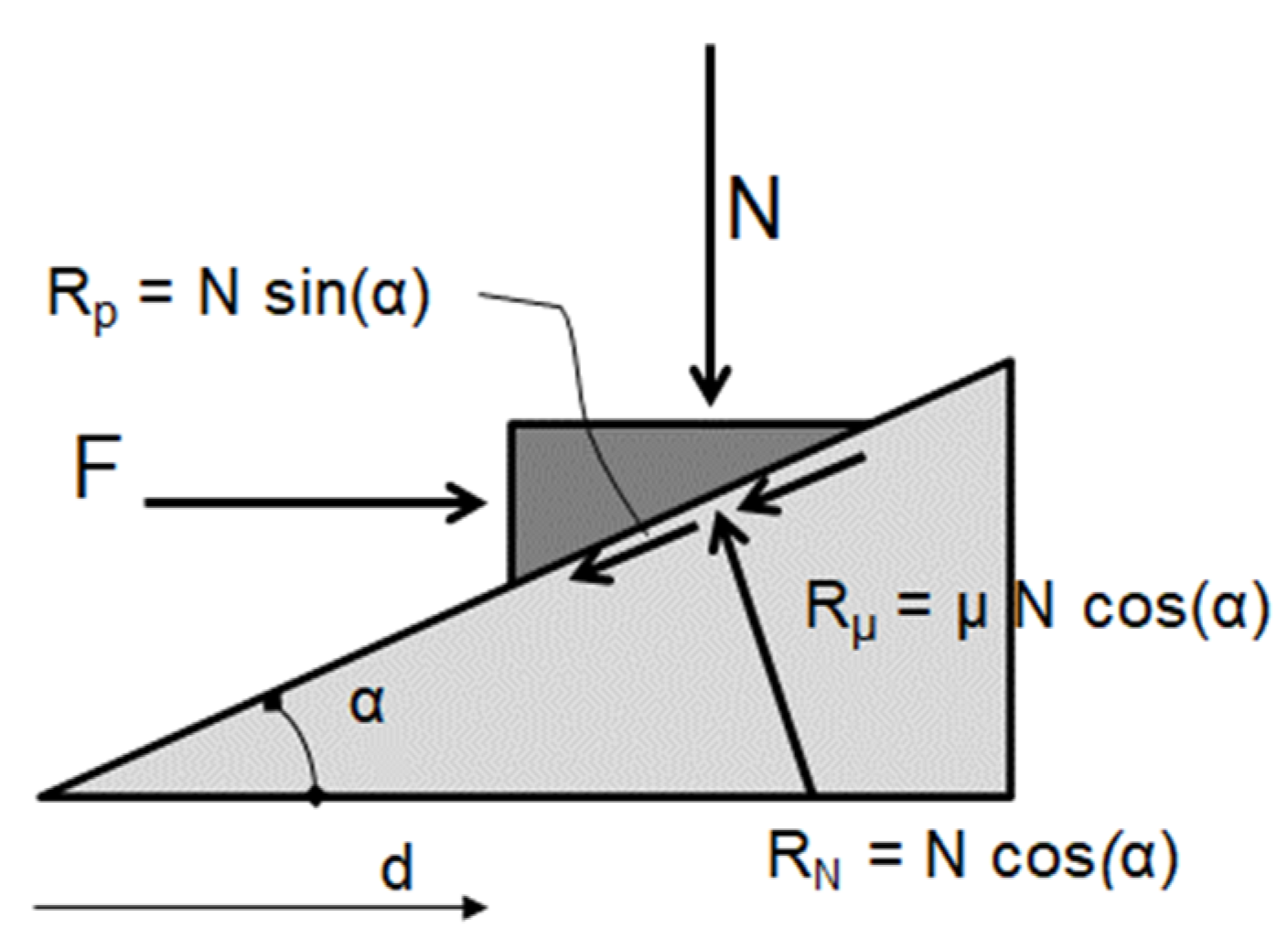
2. Principle of the Dissipative Connection System
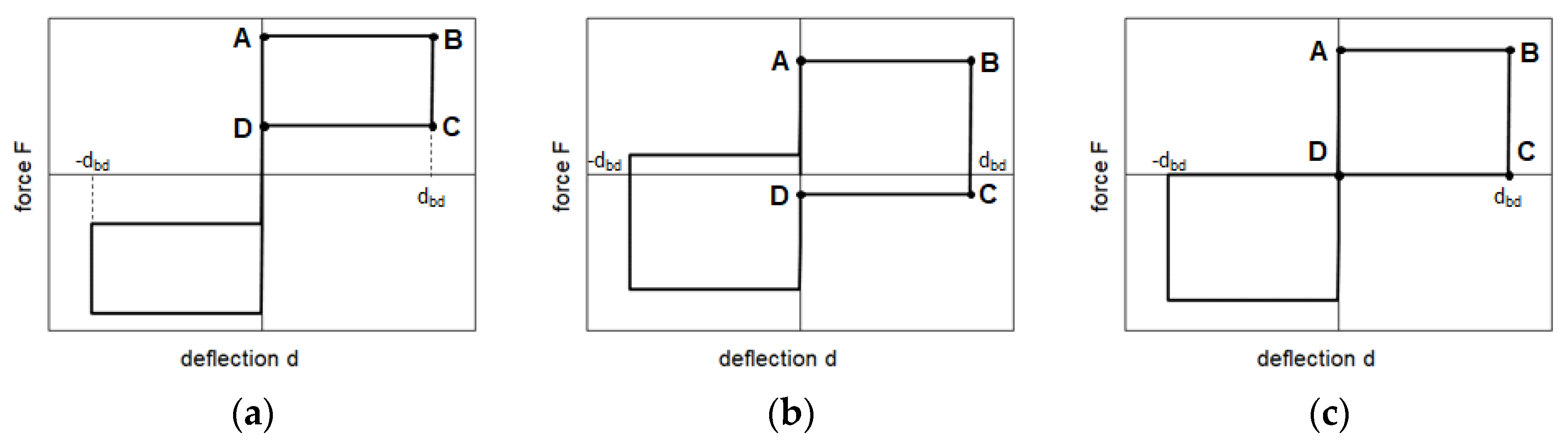
- If µ < tan(α), the curve has the shape shown in Figure 3a: when sign(d) and sign(V) have different signs, sin(α) > µ cos(α) and the recentering force due to gravity prevails on the friction term. The device has a fair recentering behavior and naturally tends to return to the origin at the end of the seismic shake. Moreover, for a given angle α, this design choice limits the shear force on the top of the columns, but reduces the amount of dissipated energy, which is proportional to µ, and therefore increases the displacement;
- If µ > tan(α), the curve has the shape shown in Figure 3b: the friction shear force prevails over the restoring force due to the slope, which hampers the recentering capability of the connection. For a given angle α, this choice increases the shear force on the top of the columns, but reduces the maximum displacement by increasing the dissipation;
- If µ = tan(α), the curve has the shape shown in Figure 3c, corresponding to an elastic-perfectly plastic behavior. When sign(d) and sign(V) have different signs, sin(α) = µ cos(α) and the device has no inherent recentering capacity; however, it does not develop any resistance to an external recentering action, which can be due to, e.g., small vibrations occurring during the coda stage of the ground motion. For a given angle α, this solution is likely to represent the best trade-off to control both maximum forces and displacements, and is implemented in the design of the DCS.
3. Materials and Methods
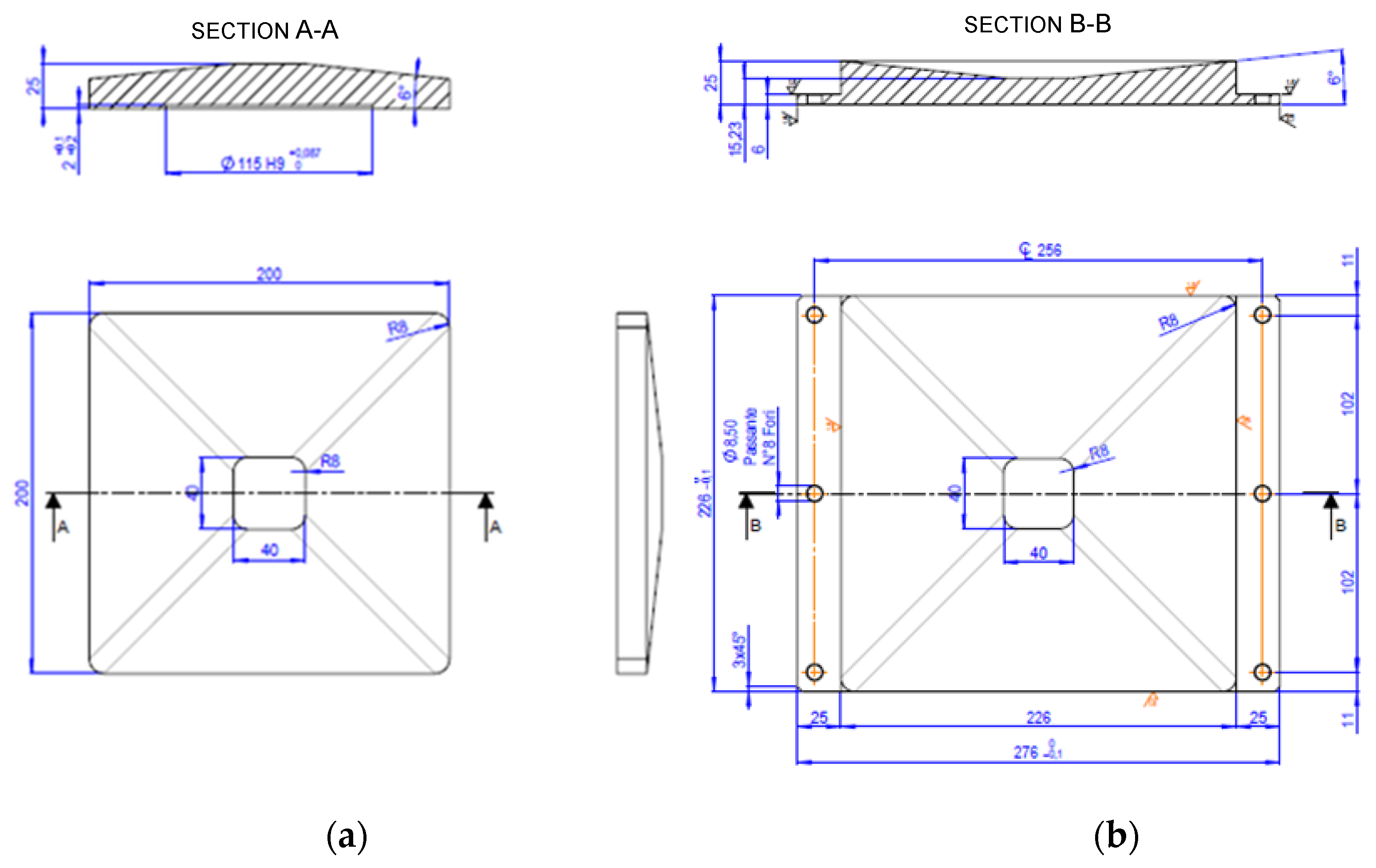
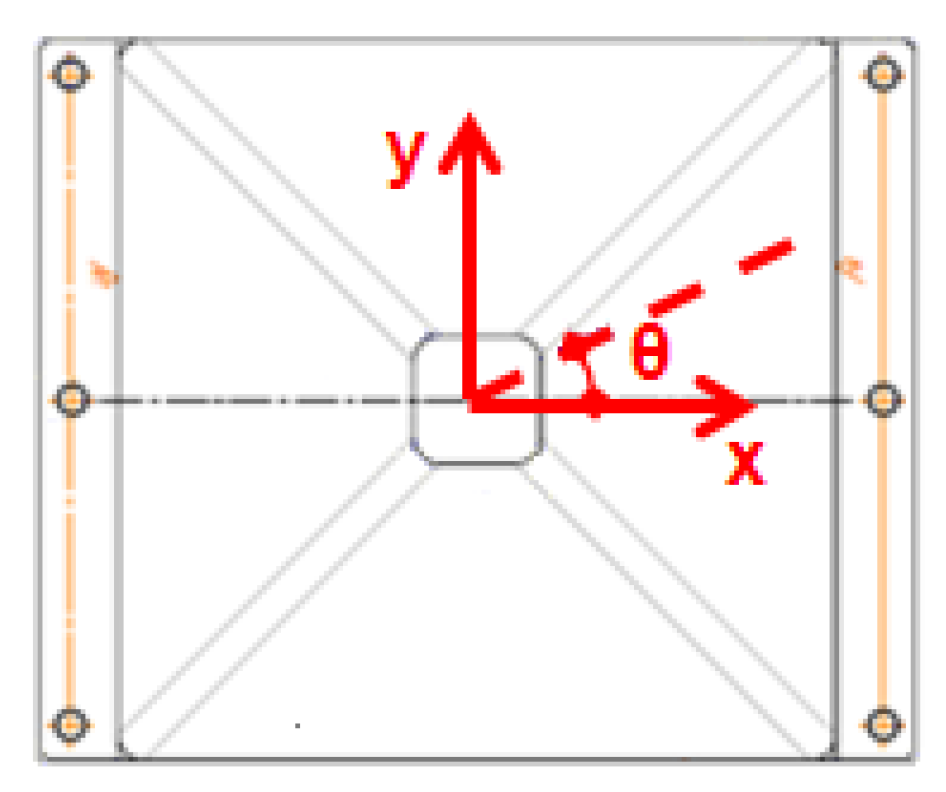
3.1. Experimental Investigation
3.2. Numerical Investigation
- For the DCS, the force—deflection curve evaluated experimentally on the prototype was scaled up to the full size of the device; the hysteretic behavior was modelled by assigning a pivot hysteresis type, with hysteresis parameters: α1 = α2 = 1010;β1 = β 2 = 0; η = 1 (in the present framework, parameters α1 and α2 define the slope of the elastic branch of the load—deflection curve in either direction of loading, β1 and β2 define the force at zero displacement for unloading towards either positive or negative forces, respectively, and 0 ≤ η ≤ 1 defines the amount of degradation of the elastic slopes after plastic deformation, where η = 1 means no degradation);
- For the beam-to-column pure friction connection, a constant friction coefficient μcc = 0.30, coupled to an isotropic hysteresis type, was assigned (it must be noted that, to be conservative, one half of the concrete-to-concrete friction coefficient recommended in Eurocode 8 [36] for smooth surfaces was adopted).
4. Results
4.1. Experimental Results
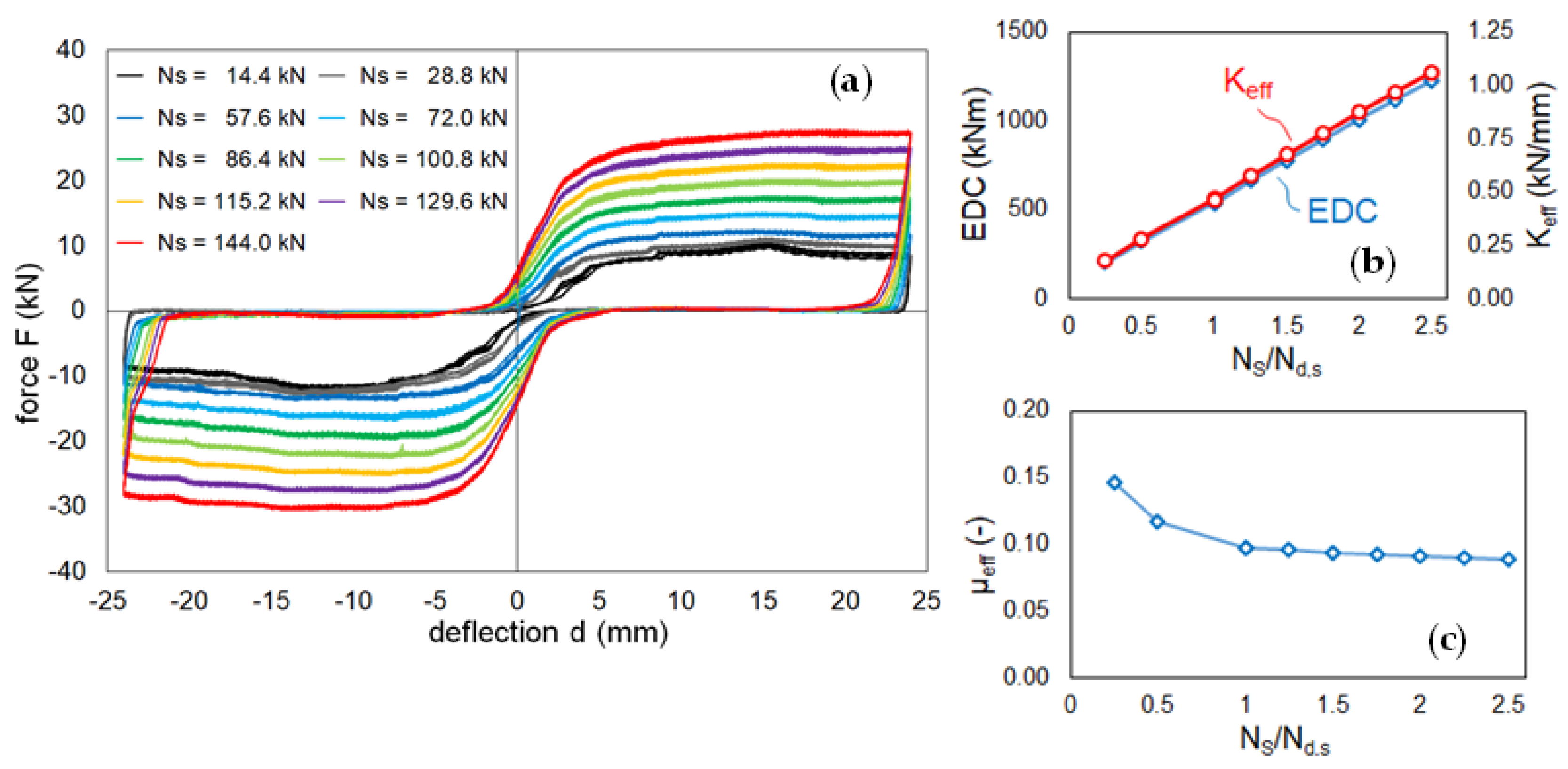
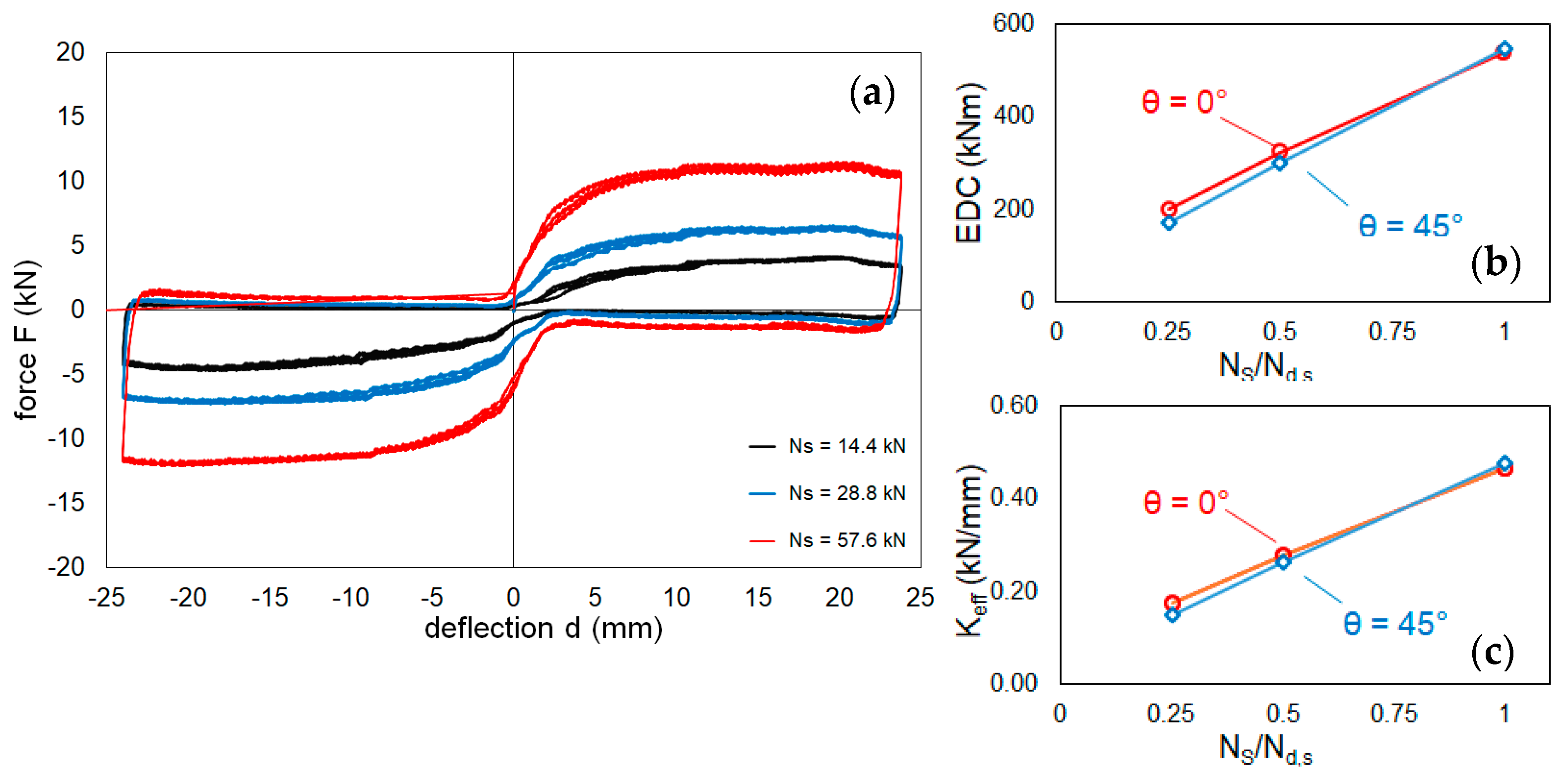
- For small deflections, the force follows an almost proportional relationship with the displacement; this behavior is ascribed to the elastic deflection of the plates and the fixtures, before sliding is triggered between the mating surfaces of the convex and concave plates;
- When the frictional resistance is exceeded, sliding is activated, and the response of the device is characterized by an almost constant force regardless of the deflection; in this phase the horizontal force of the system matches the theoretical value calculated according to Equation (1);
- As the deflection exceeds a certain threshold d*, a shallow decrease of the horizontal force is noticed; when d = d* the convex plate reaches the boundary of the concave plate, and for larger deflections the actual contact area between the mating surfaces of the two plates decreases, increasing the contact pressure, which in turn affects the coefficient of friction;
- During the return movement of the convex plate towards the origin the reaction force is virtually negligible; in this phase the restoring force due to the sloped surface and the friction force have opposite signs and balance each other, providing a null (or very small) resistance.
- Effective stiffness:
- Effective coefficient of friction:
4.2. Numerical Results
5. Conclusions
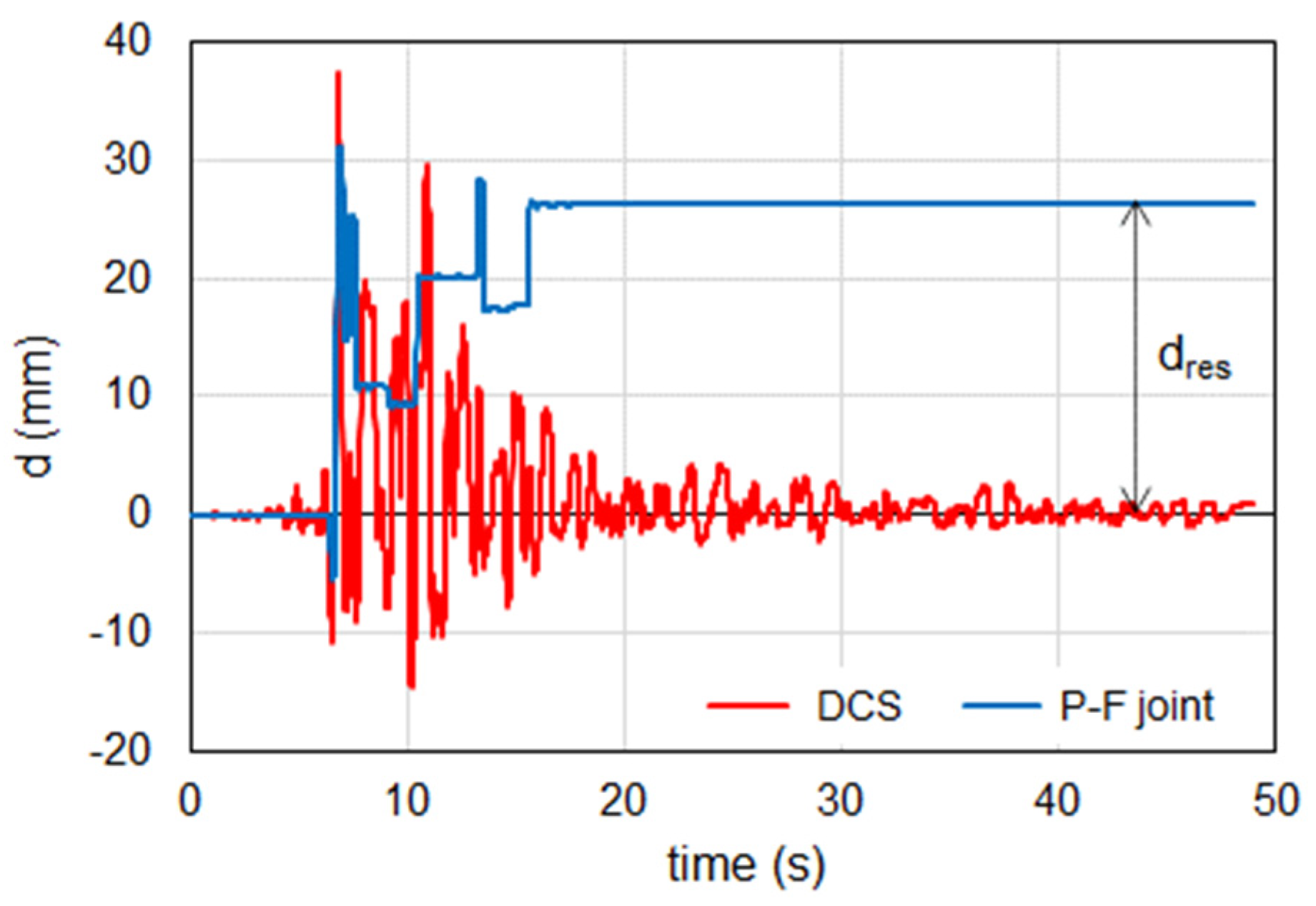
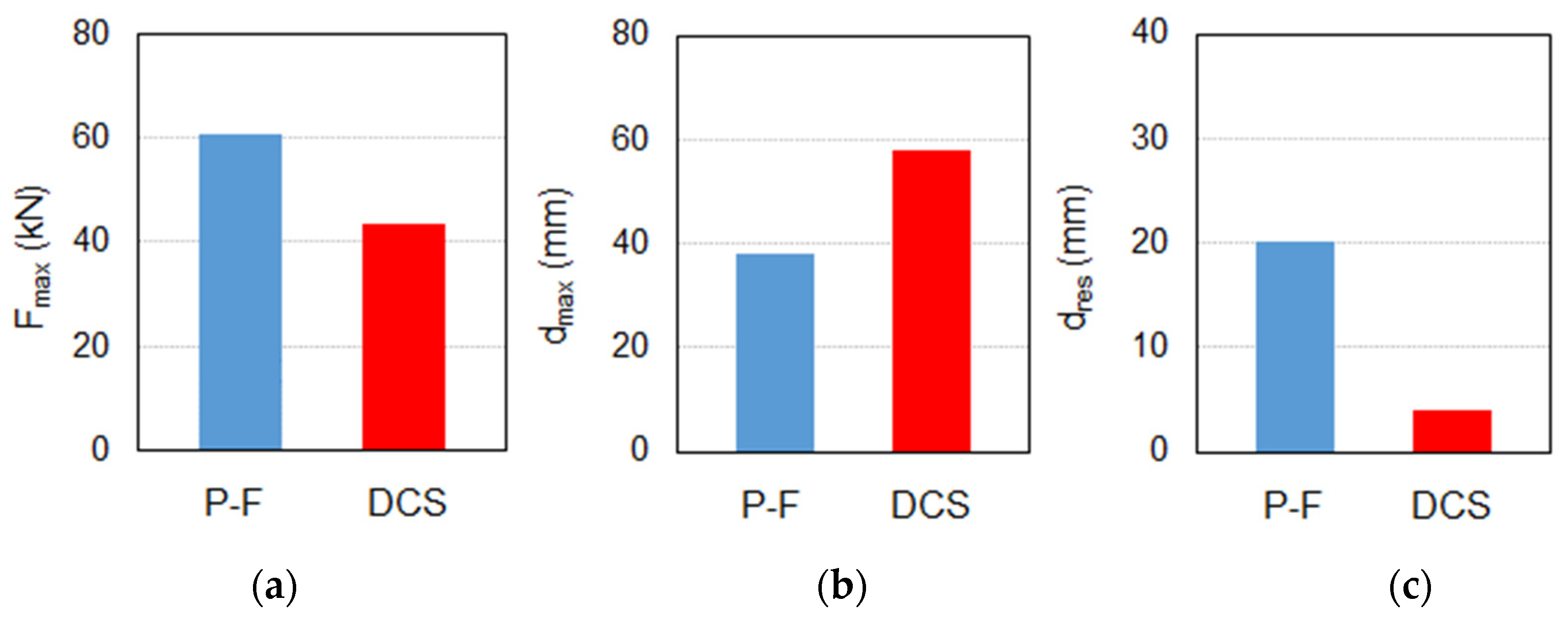
- The force-displacement curve shows, after an initial elastic response, a constant force when the convex plate moves away from the center, and a negligible reaction when the convex plate returns towards the origin; the force, which is governed by the properties (slope angle and friction) of the sliding surfaces, increases linearly with the vertical load on the support but is scarcely affected by the velocity;
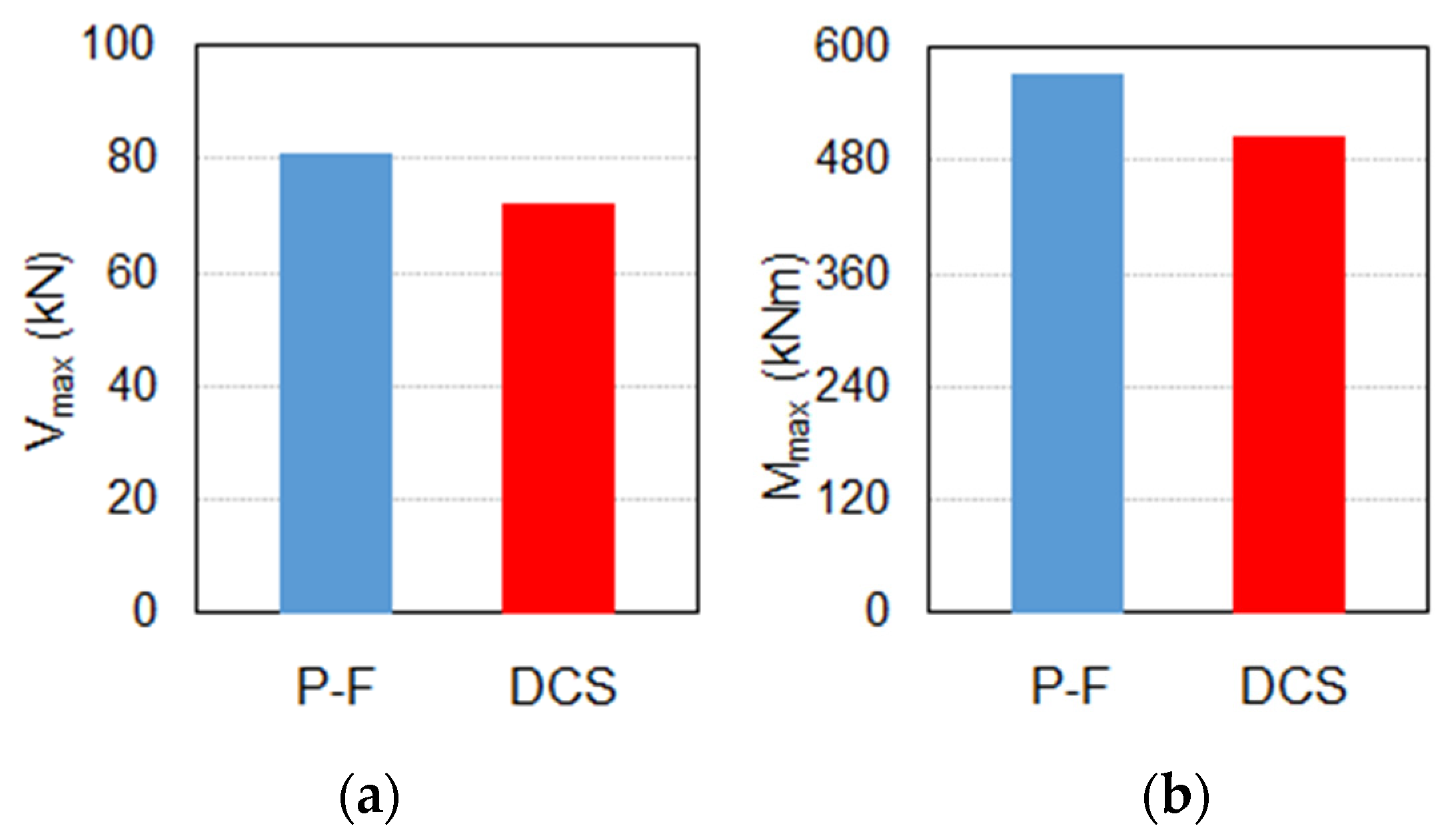
- Non-linear dynamic analyses proved the effectiveness of the DCS to control the relative displacements at the beam-to-column joint, and the maximum shear force transmitted to the column head, thereby limiting internal forces and moments within the columns;
- Owing to a certain restoring capacity provided by assuming μ = tan(α), the DCS was able to control the residual displacement at the end of the ground motion within small values (1/15 of the maximum displacement, in the examined case), thereby limiting the accrual of displacements during sequences of earthquake, which can hamper the capability of the structure to withstand aftershocks.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Belleri, A.; Brunesi, E.; Nascimbene, R.; Pagani, M.; Riva, P. Seismic performance of precast industrial facilities following major earthquakes in the Italian territory. J. Perform. Constr. Facil. 2015, 29, 04014135. [Google Scholar] [CrossRef] [Green Version]
- Belleri, A.; Torquati, M.; Riva, P.; Nascimbene, R. Vulnerability assessment and retrofit solutions of precast industrial structures. Earthq. Struct. 2015, 8, 801–820. [Google Scholar] [CrossRef]
- Bosio, M.; Belleri, A.; Riva, P.; Marini, A. Displacement-based simplified seismic loss assessment of Italian precast buildings. J. Earthq. Eng. 2020, 24, 60–81. [Google Scholar] [CrossRef]
- Artioli, E.; Battaglia, R.; Tralli, A. Effects of 2012 Emilia earthquake on industrial buildings of early ‘900 on the Po river line. Eng. Struct. 2013, 56, 1220–1233. [Google Scholar] [CrossRef]
- Magliulo, G.; Fabbrocino, G.; Manfredi, G. Seismic assessment of existing precast industrial buildings using static and dynamic nonlinear analyses. Eng. Struct. 2008, 30, 2580–2588. [Google Scholar] [CrossRef]
- Liberatore, L.; Sorrentino, L.; Liberatore, D.; Decanini, L.D. Failure of industrial structures induced by the Emilia (Italy) 2012 earthquakes. Eng. Fail. Anal. 2013, 34, 629–647. [Google Scholar] [CrossRef]
- Belleri, A.; Moaveni, B.; Restrepo, J.I. Damage assessment through structural identification of a three-story large-scale precast concrete structure. Earthq. Eng. Struct. Dyn. 2014, 43, 61–76. [Google Scholar] [CrossRef]
- Brunesi, E.; Nascimbene, R.; Bolognini, D.; Bellotti, D. Experimental investigation of the cyclic response of reinforced precast concrete framed structures. PCI J. 2015, 2, 57–79. [Google Scholar] [CrossRef]
- Batalha, N.; Rodrigues, H.; Varum, H. Seismic performance of RC precast industrial buildings—Learning with the past earthquakes. Innov. Infrastruct. Solut. 2018, 4, 4. [Google Scholar] [CrossRef]
- Casotto, C.; Silva, V.; Crowley, H.; Nascimbene, R.; Pinho, R. Seismic fragility of Italian RC precast industrial structures. Eng. Struct. 2015, 94, 122–136. [Google Scholar] [CrossRef]
- Demartino, C.; Vanzi, I.; Monti, G.; Sulpizio, C. Precast industrial buildings in Southern Europe: Loss of support at frictional beam-to-column connections under seismic actions. Bull. Earthq. Eng. 2016, 16, 259–294. [Google Scholar] [CrossRef]
- Italian Building Code. Technical Recommendations for Design, Execution and Testing of Precast Buildings—D.M. 3/12/1987; Italian Building Code: Rome, Italy, 1987. (In Italian) [Google Scholar]
- Italian Building Code. Technical Recommendations for Buildings—D.M. 14/01/2008; Italian Building Code: Rome, Italy, 2008. (In Italian) [Google Scholar]
- Mazza, F.; Mazza, M. Seismic retrofitting of gravity-loads designed r.c. framed buildings combining CFRP and hysteretic damped braces. Bull. Earthq. Eng. 2019, 17, 3423–3445. [Google Scholar] [CrossRef]
- Bournas, D.A.; Negro, P.; Taucer, F.F. Performance of industrial buildings during the Emilia earthquakes in Northern Italy and recommendations for their strengthening. Bull. Earthq. Eng. 2014, 12, 2383–2404. [Google Scholar] [CrossRef]
- Martinelli, P.; Mulas, M.G. An innovative passive control technique for industrial precast frames. Eng. Struct. 2010, 32, 1123–1132. [Google Scholar] [CrossRef]
- Javidan, M.M.; Nasab, M.S.E.; Kim, J. Full-scale tests of two-story RC frames retrofitted with steel plate multi-slit dampers. Steel Comp. Struct. 2021, 39, 645–664. [Google Scholar] [CrossRef]
- Javidan, M.M.; Kim, J. Steel hysteretic column dampers for seismic retrofit of soft-first-story structures. Steel Compos. Struct. 2020, 37, 259–272. [Google Scholar] [CrossRef]
- Belleri, A.; Marini, A.; Riva, P.; Nascimbene, R. Dissipating and re-centring devices for portal-frame precast structures. Eng. Struc. 2017, 150, 736–745. [Google Scholar] [CrossRef]
- Javidan, M.M.; Kim, J. Seismic retrofit of soft-first-story structures using rotational friction dampers. J. Struct. Eng. 2019, 145, 04019162. [Google Scholar] [CrossRef]
- Sonda, D.; Pollini, A.; Cossu, M. Seismic retrofit of an industrial building using damping devices. Struct. Eng. Int. 2020, 30, 53–63. [Google Scholar] [CrossRef]
- Dal Lago, B.; Naveed, M.; Tornaghi, M.L. Tension-only ideal dissipative bracing for the seismic retrofit of precast industrial buildings. Bull. Earthq. Eng. 2021, 19, 4503–4532. [Google Scholar] [CrossRef]
- Morelli, F.; Piscini, A.; Salvatore, W. Seismic retrofit of an industrial structure through an innovative self-centering hysteretic damper: Modelling, analysis and optimization. In Proceedings of the ECCOMAS 2016 VII European Congress on Computational Methods in Applied Sciences and Engineering, Crete, Greece, 5–10 June 2016. [Google Scholar]
- Quaglini, V.; Gandelli, E.; Dubini, P.; Limongelli, M.P. Total displacement of curved surface sliders under nonseismic and seismic actions: A parametric study. Struct. Control Health Monit. 2017, 24, e2031. [Google Scholar] [CrossRef]
- Decanini, L.; Gavarini, C.; Mollaioli, F. Some remarks on the Umbria-Marche earthquakes of 1997. Europ. Earthq. Eng. 2000, 3, 18–48. [Google Scholar]
- Huang, Y.; Wu, J.P.; Zhang, T.Z.; Zhang, D.N. Relocation of the M 8.0 Wenchuan earthquake and its aftershock sequence. Sci. China Ser. D-Earth Sci. 2008, 51, 1703–1711. [Google Scholar] [CrossRef]
- Di Sarno, L.; Elnashai, A.S.; Manfredi, G. Assessment of RC columns subjected to horizontal and vertical ground motions recorded during the 2009 L’Aquila (Italy) earthquake. Eng. Struct. 2011, 33, 1514–1535. [Google Scholar] [CrossRef]
- Di Sarno, L.; Yenidogan, C.; Erdik, M. Field evidence and numerical investigation of the Mw = 7.1 October 23 Van, Tabanli and the Mw > 5.7 November Earthquakes of 2011. Bull. Earthq. Eng. 2013, 11, 313–346. [Google Scholar] [CrossRef]
- Motosaka, M.; Mitsuji, K. Building damage during the 2011 off the Pacific coast of Tohoku Earthquake. Soils Found. 2012, 52, 929–944. [Google Scholar] [CrossRef] [Green Version]
- Carydis, P.; Castiglioni, C.; Lekkas, E.; Kostaki, I.; Lebesis, N.; Drei, A. The Emilia Romagna, May 2012 earthquake sequence. The influence of the vertical earthquake component and related geoscientific and engineering aspects. Int. J. Earthq. Eng. 2012, 29, 31–58. [Google Scholar]
- Mari, L.; Quaglini, V.; Pettorruso, C.; Bruschi, E. Experimental and numerical assessment of isolation seismic device for retrofit of industrial shed. In Proceedings of the COMPDYN 2021 and 8th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Athens, Greece, 27–30 June 2021. [Google Scholar]
- Harris, H.G.; Sabnis, G. Structural Modeling and Experimental Techniques, 2nd ed.; CRC Press LLC: Boca Raton, FL, USA, 1999. [Google Scholar]
- Italian Building Code. Technical Recommendations for Buildings—D.M. 17/02/2018; Italian Building Code: Rome, Italy, 2018. (In Italian) [Google Scholar]
- SAP2000. Analysis Reference, Volume 1; Computer and Structures Inc.: Berkeley, CA, USA, 1997. [Google Scholar]
- ASCE/SEI 41-13. Seismic Evaluation and Retrofit of Existing Buildings; American Society of Civil Engineers: Reston, VA, USA, 2014. [Google Scholar]
- EN 1998-1. Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings; CEN European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Andrawes, B.; DesRoches, R. Unseating prevention for multiple frame bridges using superelastic devices. Smart Mater. Struct. 2005, 14, S60–S67. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures, 5th ed.; Pearson: London, UK, 2017. [Google Scholar]
- Iervolino, I.; Galasso, C.; Cosenza, E. REXEL: Computer aided record selection for code-based seismic structural analysis. Bull. Earthq. Eng. 2010, 8, 339–362. [Google Scholar] [CrossRef]
- Ambraseys, N.; Smit, P.; Sigbjornsson, R.; Suhadolc, P.; Margaris, B. Internet-Site for European Strong-Motion Data, European Commission, Research-Directorate General, Environment and Climate Programme. Available online: http://www.isesd.cv.ic.ac.uk/ESD/ (accessed on 24 November 2021).


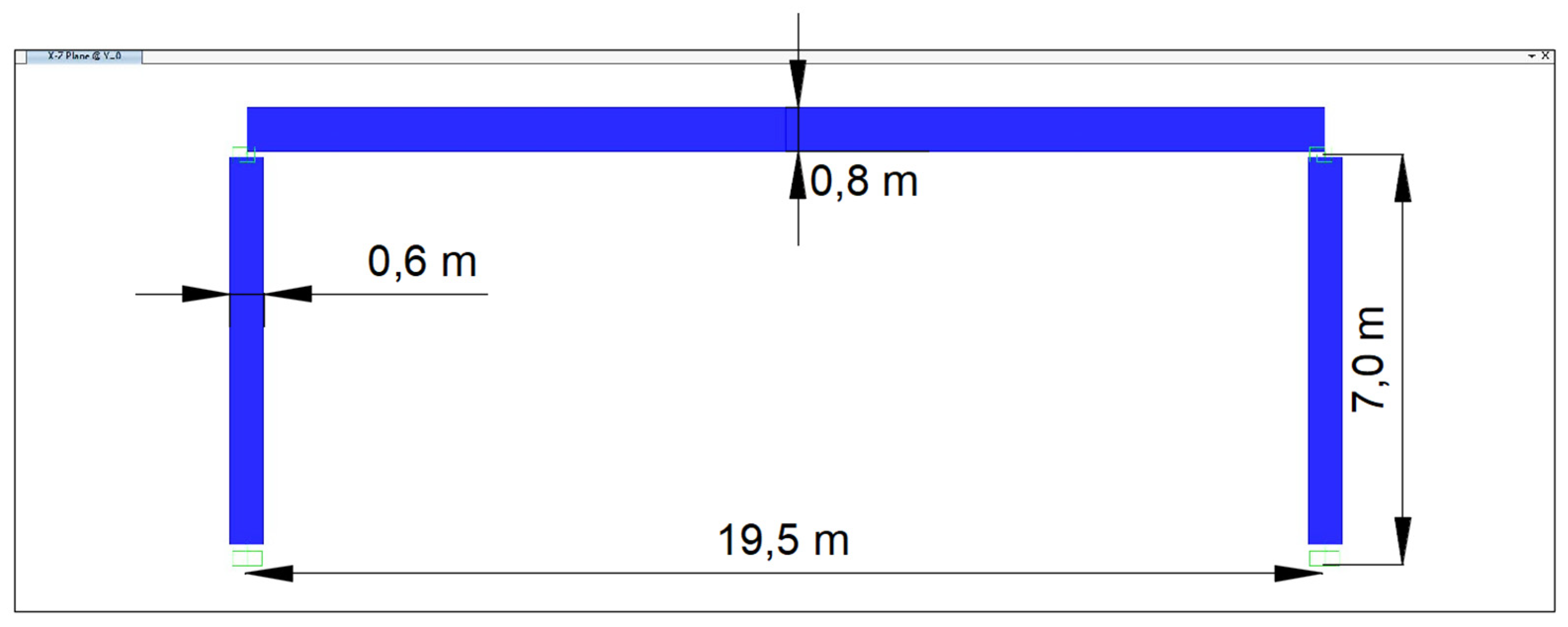



| Quantity | Dimension | Scale Factor |
|---|---|---|
| Length | [L] | SL = 0.4 |
| Elastic Modulus | [F] [L]−2 | SE = 1.0 |
| Force | [F] | SF = (SL)2 = 0.16 |
| Pressure | [F] [L]−2 | Sp = 1.0 |
| Displacement | [L] | Sd = 0.4 |
| Time | [T] | ST = (SL)1/2 = 0.6324 |
| Velocity | [L] [T]−1 | SV = (SL)1/2 = 0.6324 |
| Frequency | [T]−1 | Sf = (SL)−1/2 = 1.5811 |
| ID | NS [kN] | dS [mm] | VS [mm/s] | θ [°] | n [#] |
|---|---|---|---|---|---|
| Static Test (S) | |||||
| S1 | 14.4 | 24 | 0.672 | 0 | 3 |
| S2 | 28.8 | 24 | 0.672 | 0 | 3 |
| S3 | 57.6 | 24 | 0.672 | 0 | 3 |
| S4 | 72.0 | 24 | 0.672 | 0 | 3 |
| S5 | 86.4 | 24 | 0.672 | 0 | 3 |
| S6 | 100.8 | 24 | 0.672 | 0 | 3 |
| S7 | 115.2 | 24 | 0.672 | 0 | 3 |
| S8 | 129.6 | 24 | 0.672 | 0 | 3 |
| S9 | 144.0 | 24 | 0.672 | 0 | 3 |
| Dynamic Test (D) | |||||
| D1a | 28.8 | 24 | 3.36 | 0 | 5 |
| D1b | 28.8 | 24 | 6.72 | 0 | 5 |
| D1c | 28.8 | 24 | 16.8 | 0 | 5 |
| D1d | 28.8 | 24 | 33.6 | 0 | 5 |
| D2a | 57.6 | 24 | 3.36 | 0 | 20 |
| Static Test with Rotation (R) | |||||
| R1 | 14.4 | 24 | 0.672 | 45 | 3 |
| R2 | 28.8 | 24 | 0.672 | 45 | 3 |
| R3 | 57.6 | 24 | 0.672 | 45 | 3 |
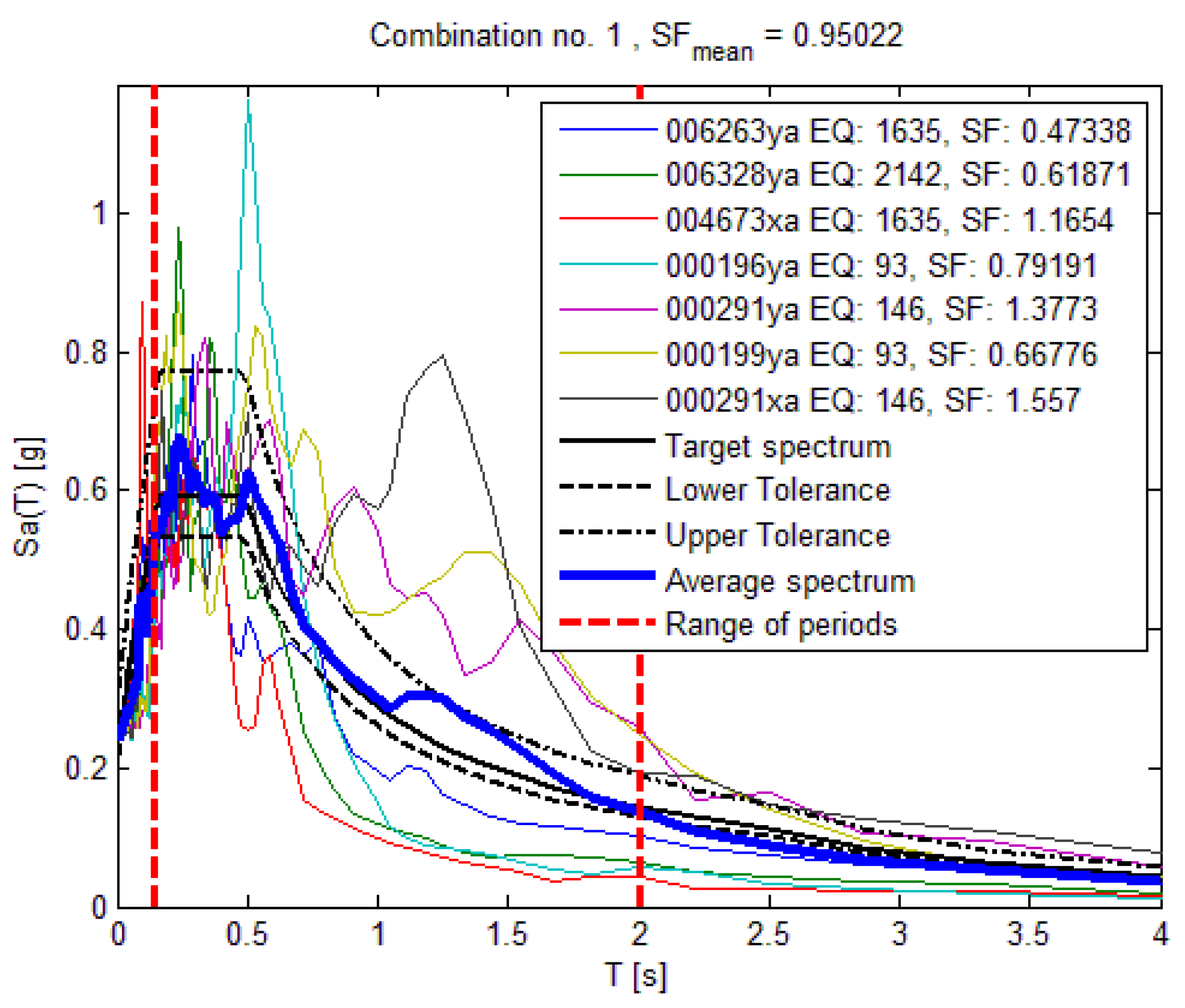
| Record | Waveform | EQ | Mw (-) | Rep (-) | PGA (m/s2) | PGV (m/s) | SF |
|---|---|---|---|---|---|---|---|
| South Iceland | 6263ya | 1635 | 6.5 | 7 | 5.018 | 0.498 | 0.473 |
| South Iceland (aftershock) | 6328ya | 2142 | 6.4 | 12 | 3.839 | 0.202 | 0.619 |
| South Iceland | 4673xa | 1635 | 6.5 | 15 | 2.038 | 0.122 | 1.165 |
| Montenegro | 196ya | 93 | 6.9 | 25 | 2.997 | 0.253 | 0.792 |
| Campano Lucano | 291ya | 146 | 6.9 | 16 | 1.725 | 0.275 | 1.377 |
| Montenegro | 199 | 93 | 6.9 | 16 | 3.557 | 0.520 | 0.668 |
| Campano Lucano | 291xa | 146 | 6.9 | 16 | 1.526 | 0.271 | 1.557 |
| Mean | 6.71 | 15.3 | 2.958 | 0.306 | 0.950 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quaglini, V.; Pettorruso, C.; Bruschi, E.; Mari, L. Experimental and Numerical Investigation of a Dissipative Connection for the Seismic Retrofit of Precast RC Industrial Sheds. Geosciences 2022, 12, 25. https://doi.org/10.3390/geosciences12010025
Quaglini V, Pettorruso C, Bruschi E, Mari L. Experimental and Numerical Investigation of a Dissipative Connection for the Seismic Retrofit of Precast RC Industrial Sheds. Geosciences. 2022; 12(1):25. https://doi.org/10.3390/geosciences12010025
Chicago/Turabian StyleQuaglini, Virginio, Carlo Pettorruso, Eleonora Bruschi, and Luca Mari. 2022. "Experimental and Numerical Investigation of a Dissipative Connection for the Seismic Retrofit of Precast RC Industrial Sheds" Geosciences 12, no. 1: 25. https://doi.org/10.3390/geosciences12010025
APA StyleQuaglini, V., Pettorruso, C., Bruschi, E., & Mari, L. (2022). Experimental and Numerical Investigation of a Dissipative Connection for the Seismic Retrofit of Precast RC Industrial Sheds. Geosciences, 12(1), 25. https://doi.org/10.3390/geosciences12010025







