Temperature Dependence of the Dielectric Constant on the Lunar Surface Based on Mini-RF and Diviner Observations
Abstract
1. Introduction
2. Studied Data and Methods
2.1. Lunar Remote-Sensing Data Used in This Study
2.1.1. Mini-RF Data
2.1.2. Diviner Brightness Temperature Data
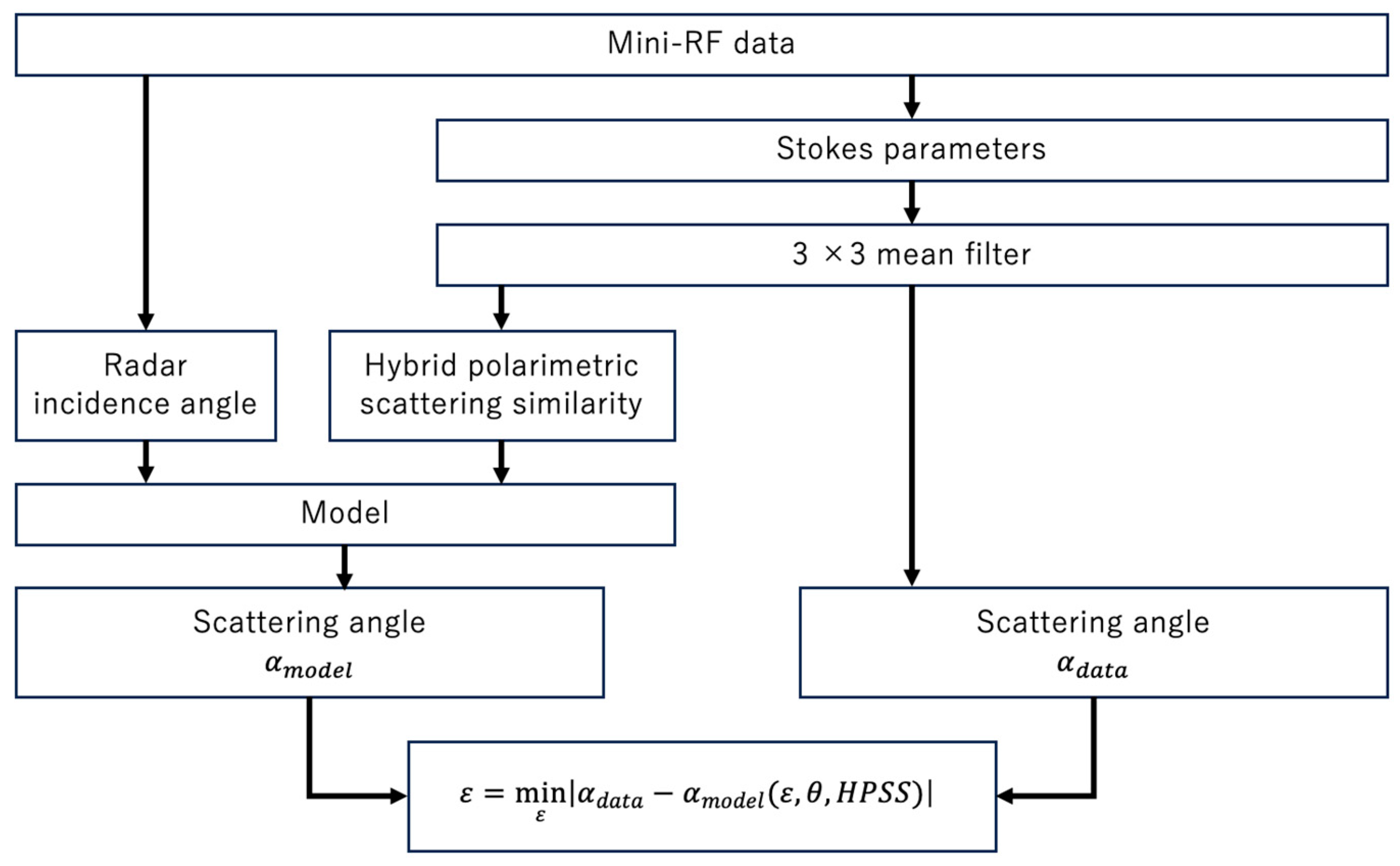
2.2. The Method for Estimating the Dielectric Constant
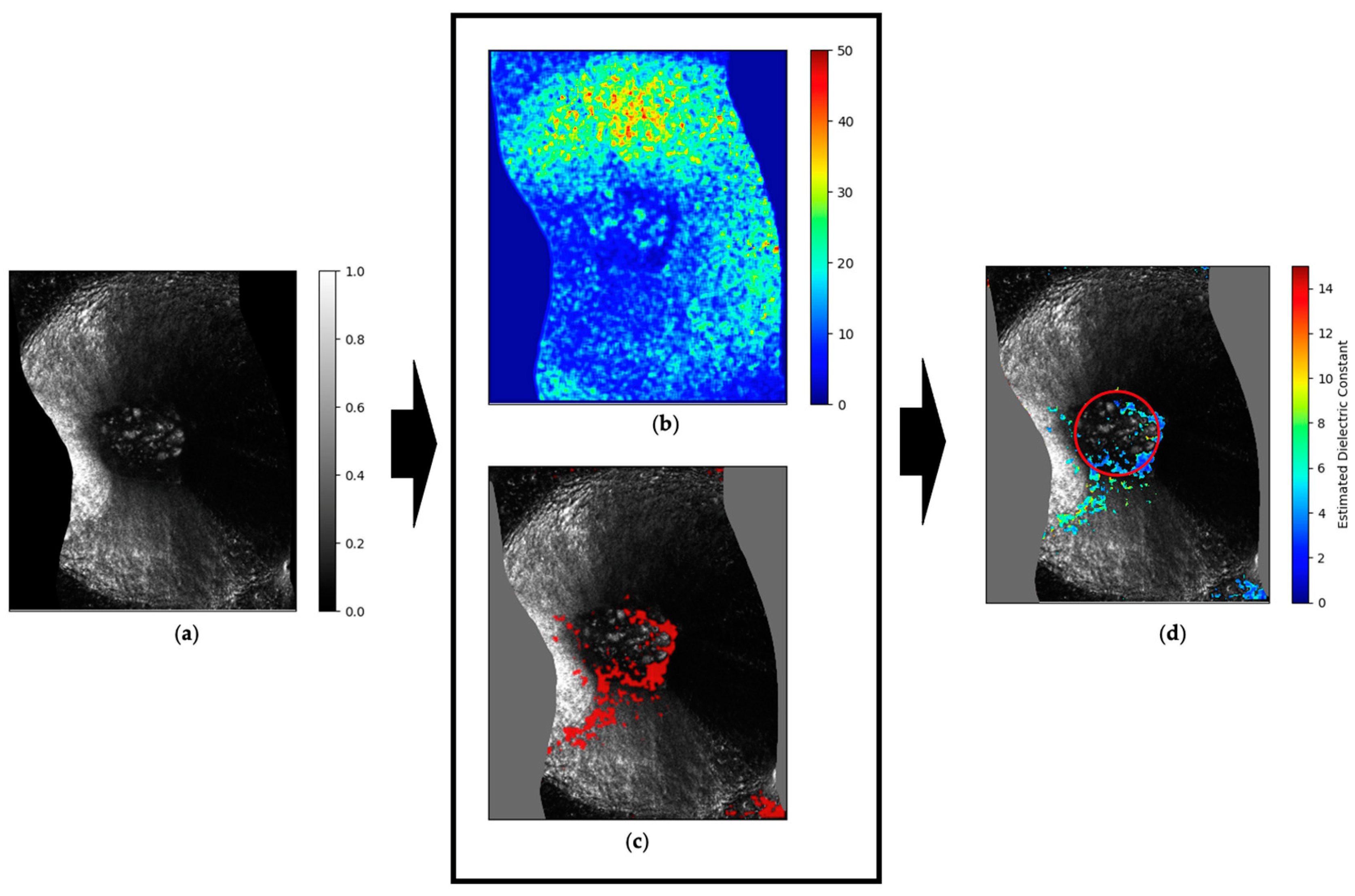
2.3. Analysis of a Crater Floor in the North Polar Region
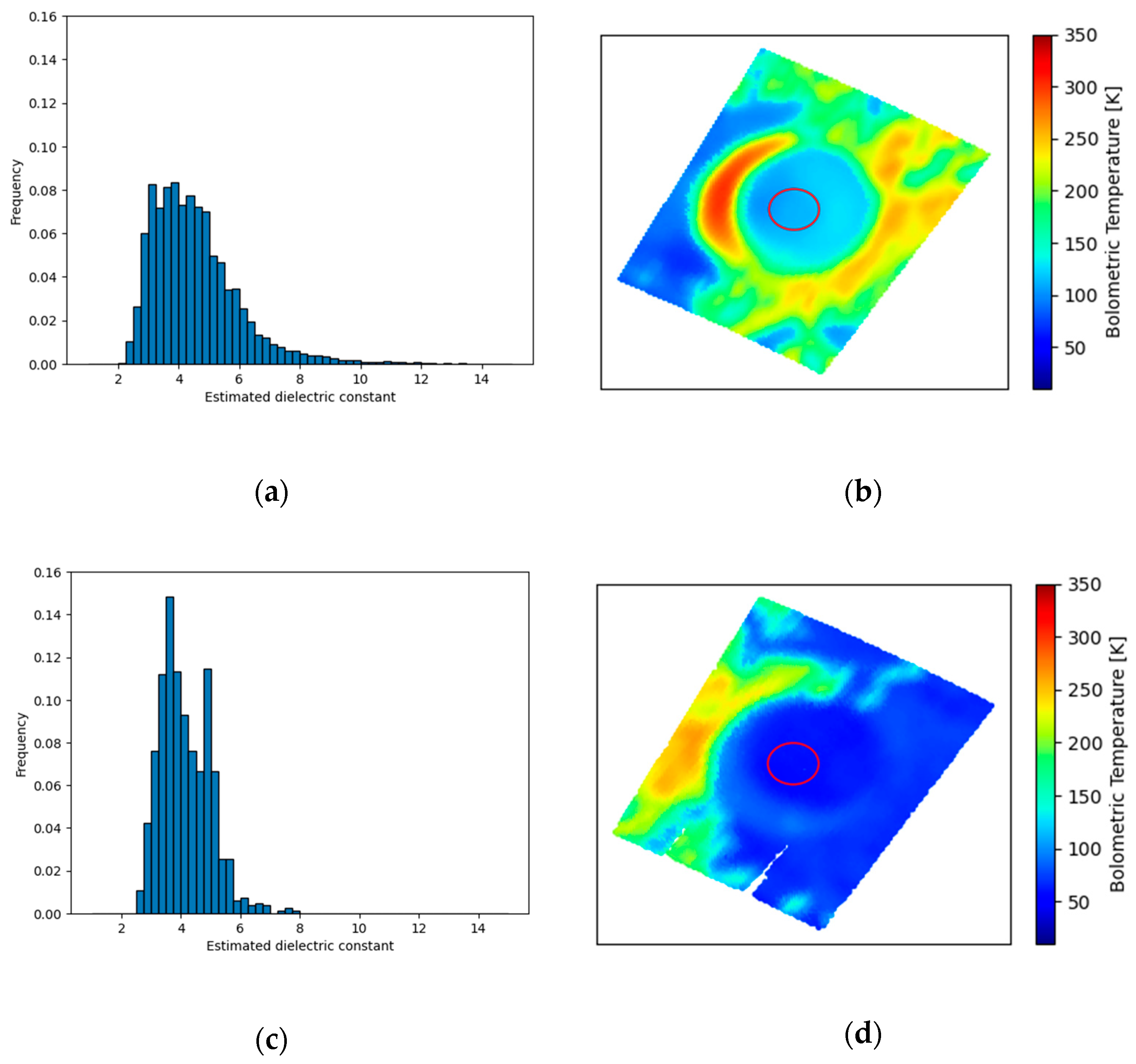
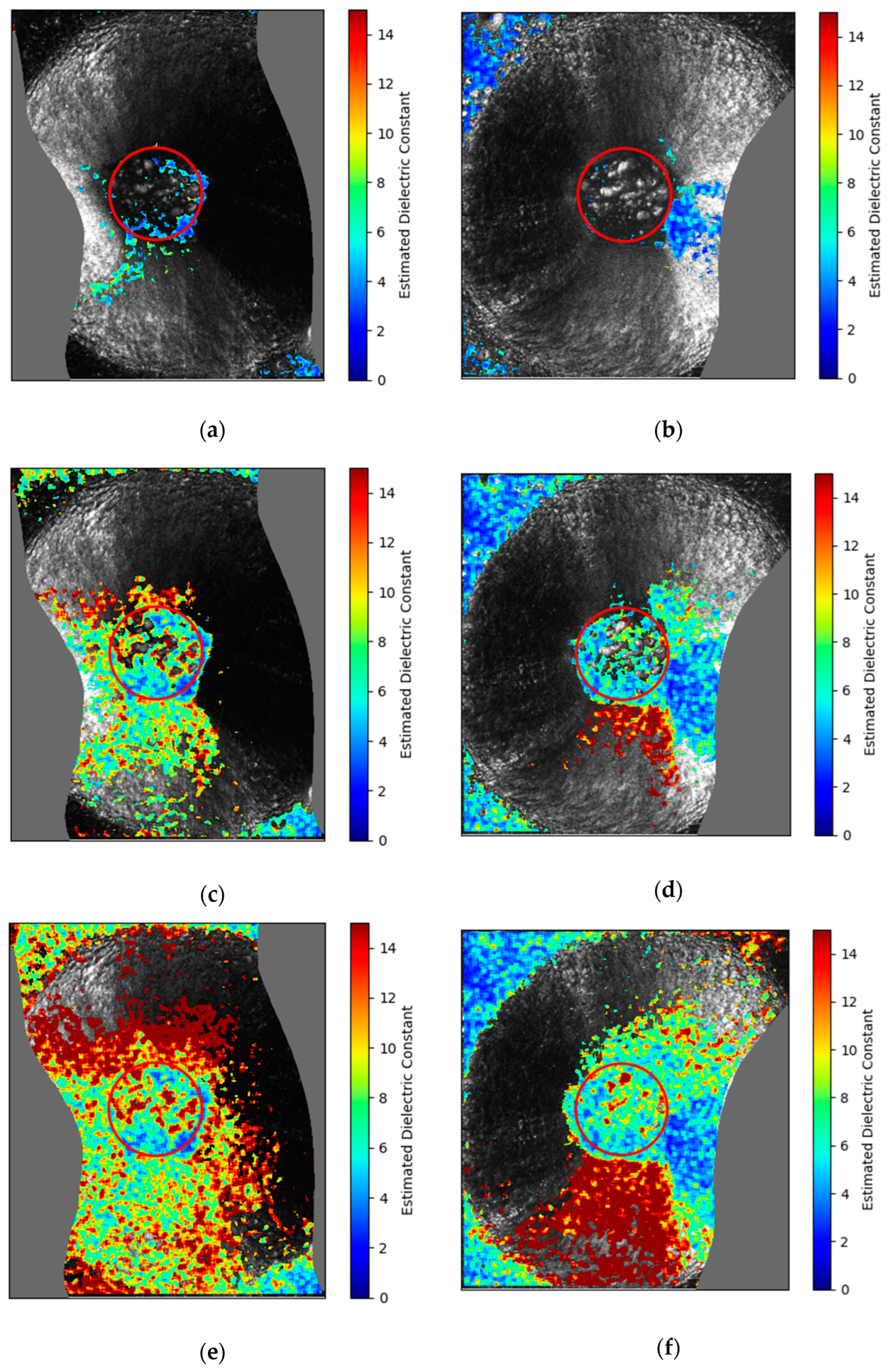
3. Results
4. Discussion
4.1. Temperature Dependence of the Dielectric Constant
4.2. The Threshold of the HPSS Parameter
4.3. Difference in Observation Depth between Mini-RF and Diviner
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Spudis, P.D.; Bussey, D.B.J.; Baloga, S.M.; Cahill, J.T.S.; Glaze, L.S.; Patterson, G.W.; Raney, R.K.; Thompson, T.W.; Thomson, B.J.; Ustinov, E.A. Evidence for water ice on the moon: Results for anomalous polar craters from the LRO Mini-RF imaging radar. J. Geophys. Res. Planets 2013, 118, 2016–2029. [Google Scholar] [CrossRef]
- Ishiyama, K.; Kumamoto, A.; Ono, T.; Yamaguchi, Y.; Haruyama, J.; Ohtake, M.; Katoh, Y.; Terada, N.; Oshigami, S. Estimation of the permittivity and porosity of the lunar uppermost basalt layer based on observations of impact craters by SELENE. J. Geophys. Res. Planets 2013, 118, 1453–1467. [Google Scholar] [CrossRef]
- Su, Y.; Wang, R.; Deng, X.; Zhang, Z.; Zhou, J.; Xiao, Z.; Ding, C.; Li, Y.; Dai, S.; Ren, X.; et al. Hyperfine Structure of Regolith Unveiled by Chang’E-5 Lunar Regolith Penetrating Radar. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Olhoeft, G.R.; Strangway, D.W. Dielectric Properties of First 100 Meters of Moon. Earth Planet. Sci. Lett. 1975, 24, 394–404. [Google Scholar] [CrossRef]
- Kobayashi, M.; Miyamoto, H.; Pál, B.D.; Niihara, T.; Takemura, T. Laboratory measurements show temperature-dependent permittivity of lunar regolith simulants. Earth Planets Space 2023, 75, 8. [Google Scholar] [CrossRef]
- Gao, Y.; Dang, Y.; Lu, P.; Hou, W.; Zhao, F.; Wang, B.; Yu, W.; Wang, R. Investigating the dielectric properties of lunar surface regolith fines using Mini-RF SAR data. ISPRS J. Photogramm. Remote Sens. 2023, 197, 56–70. [Google Scholar] [CrossRef]
- Singh, A.; Sharma, A.; Kumar, S.; Chang, L.; Vashishtha, A.; Raj, R.; Agrawal, S.; Chauhan, P. Dielectric characterization and polarimetric analysis of lunar north polar crater Hermite-A using Chandrayaan-1 Mini-SAR, Lunar Reconnaissance Orbiter (LRO) Mini-RF, and Chandrayaan-2 DFSAR data. Adv. Space Res. 2022, 70, 4030–4055. [Google Scholar] [CrossRef]
- Kumar, A.; Kochar, I.M.; Pandey, D.K.; Das, A.; Putrevu, D.; Kumar, R.; Panigrahi, R.K. Dielectric Constant Estimation of Lunar Surface Using Mini-RF and Chandrayaan-2 SAR Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–8. [Google Scholar] [CrossRef]
- Williams, J.; Greenhagen, B.T.; Paige, D.A.; Schorghofer, N.; Sefton-Nash, E.; Hayne, P.O.; Lucey, P.G.; Siegler, M.A.; Aye, K.M. Seasonal Polar Temperatures on the Moon. J. Geophys. Res. Planets 2019, 124, 2505–2521. [Google Scholar] [CrossRef]
- Raney, R.K.; Spudis, P.D.; Bussey, B.; Crusan, J.; Jensen, J.R.; Marinelli, W.; McKerracher, P.; Neish, C.; Palsetia, M.; Schulze, R.; et al. The Lunar Mini-RF Radars: Hybrid Polarimetric Architecture and Initial Results. Proc. IEEE 2011, 99, 808–823. [Google Scholar] [CrossRef]
- Nozette, S.; Spudis, P.; Bussey, B.; Jensen, R.; Raney, K.; Winters, H.; Lichtenberg, C.L.; Marinelli, W.; Crusan, J.; Gates, M.; et al. The Lunar Reconnaissance Orbiter Miniature Radio Frequency (Mini-RF) Technology Demonstration. Space Sci. Rev. 2010, 150, 285–302. [Google Scholar] [CrossRef]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: New York, NY, USA, 2009. [Google Scholar]
- Paige, D.A.; Foote, M.C.; Greenhagen, B.T.; Schofield, J.T.; Calcutt, S.; Vasavada, A.R.; Preston, D.J.; Taylor, F.W.; Allen, C.C.; Snook, K.J.; et al. The Lunar Reconnaissance Orbiter Diviner Lunar Radiometer Experiment. Space Sci. Rev. 2010, 150, 125–160. [Google Scholar] [CrossRef]
- Paige, D.A.; Siegler, M.A.; Zhang, J.A.; Hayne, P.O.; Foote, E.J.; Bennett, K.A.; Vasavada, A.R.; Greenhagen, B.T.; Schofield, J.T.; McCleese, D.J.; et al. Diviner Lunar Radiometer Observations of Cold Traps in the Moon’s South Polar Region. Science 2010, 330, 479–482. [Google Scholar] [CrossRef]
- Hajnsek, I.; Pottier, E.; Cloude, S.R. Inversion of surface parameters from polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 2003, 41, 727–744. [Google Scholar] [CrossRef]
- Ponnurangam, G.G.; Jagdhuber, T.; Hajnsek, I.; Rao, Y.S. Soil Moisture Estimation Using Hybrid Polarimetric SAR Data of RISAT-1. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2033–2049. [Google Scholar] [CrossRef]
- Yushkova, O.V.; Kibardina, I.N. Dielectric Properties of Lunar Surface. Sol. Syst. Res. 2017, 51, 121–126. [Google Scholar] [CrossRef]
- Eke, V.R.; Bartram, S.A.; Lane, D.A.; Smith, D.; Teodoro, L.F. Lunar polar craters—Icy, rough or just sloping? Icarus 2014, 241, 66–78. [Google Scholar] [CrossRef][Green Version]
- Fassett, C.I.; Bramson, A.M.; Cahill, J.T.S.; Harris, C.P.; Morgan, G.A.; Neish, C.D.; Nypaver, C.A.; Patterson, G.W.; Rivera-Valentin, E.; Taylor, P.A.; et al. Improved Orthorectification and Empirical Reduction of Topographic Effects in Monostatic Mini-RF S-band Observations of the Moon. Planet. Sci. J. 2024, 5, 4. [Google Scholar] [CrossRef]
- Campbell, B.A. High circular polarization ratios in radar scattering from geologic targets. J. Geophys. Res. Planets 2012, 117, E6. [Google Scholar] [CrossRef]
- Bandfield, J.L.; Ghent, R.R.; Vasavada, A.R.; Paige, D.A.; Lawrence, S.J.; Robinson, M.S. Lunar surface rock abundance and regolith fines temperatures derived from LRO Diviner Radiometer data. J. Geophys. Res. Planets 2011, 116, E12. [Google Scholar] [CrossRef]
- Hayne, P.O.; Bandfield, J.L.; Siegler, M.A.; Vasavada, A.R.; Ghent, R.R.; Williams, J.; Greenhagen, B.T.; Aharonson, O.; Elder, C.M.; Lucey, P.G.; et al. Global Regolith Thermophysical Properties of the Moon From the Diviner Lunar Radiometer Experiment. J. Geophys. Res. Planets 2017, 122, 2371–2400. [Google Scholar] [CrossRef]
- Cloude, S.R.; Goodenough, D.G.; Chen, H. Compact Decomposition Theory. IEEE Geosci. Remote Sens. Lett. 2012, 9, 28–32. [Google Scholar] [CrossRef]
- Heggy, E.; Palmer, E.M.; Thompson, T.W.; Thomson, B.J.; Patterson, G.W. Bulk composition of regolith fines on lunar crater floors: Initial investigation by LRO/Mini-RF. Earth Planet. Sci. Lett. 2020, 541, 116274. [Google Scholar] [CrossRef]

| Local Time at Crater Floor <hour> 1 | Mini-RF Data | Season | Diviner Data |
|---|---|---|---|
| 18.01 (evening) | lsz_04556_1cd_xku_82n149_v1 2 | summer | pcp_avg_tbol_poln_sum_ltim71_240 4 |
| pcp_avg_tbol_poln_sum_ltim73_240 4 | |||
| 6.47 (morning) | lsz_04751_1cd_xku_82n152_v1 3 | winter | pcp_avg_tbol_poln_win_ltim27_240 5 |
| Local Time <hour> 1 | Tbol [K] 2 | Average | Std 3 | Median |
|---|---|---|---|---|
| 18.01 (summer evening) | 109.2 | 4.53 | 1.43 | 4.28 |
| 6.47 (winter morning) | 58.7 | 4.14 | 0.84 | 3.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, C.; Miyamoto, H.; Kobayashi, M. Temperature Dependence of the Dielectric Constant on the Lunar Surface Based on Mini-RF and Diviner Observations. Geosciences 2024, 14, 101. https://doi.org/10.3390/geosciences14040101
Sun C, Miyamoto H, Kobayashi M. Temperature Dependence of the Dielectric Constant on the Lunar Surface Based on Mini-RF and Diviner Observations. Geosciences. 2024; 14(4):101. https://doi.org/10.3390/geosciences14040101
Chicago/Turabian StyleSun, Chenhao, Hideaki Miyamoto, and Makito Kobayashi. 2024. "Temperature Dependence of the Dielectric Constant on the Lunar Surface Based on Mini-RF and Diviner Observations" Geosciences 14, no. 4: 101. https://doi.org/10.3390/geosciences14040101
APA StyleSun, C., Miyamoto, H., & Kobayashi, M. (2024). Temperature Dependence of the Dielectric Constant on the Lunar Surface Based on Mini-RF and Diviner Observations. Geosciences, 14(4), 101. https://doi.org/10.3390/geosciences14040101








