Cenozoic Carbon Dioxide: The 66 Ma Solution
Abstract
1. Introduction
2. Sources and Methods
2.1. Data Sources
2.2. Henry’s Law Constants for 35.1‰ Salinity Sea Water
2.3. Seawater Ions for 35.1‰ Salinity
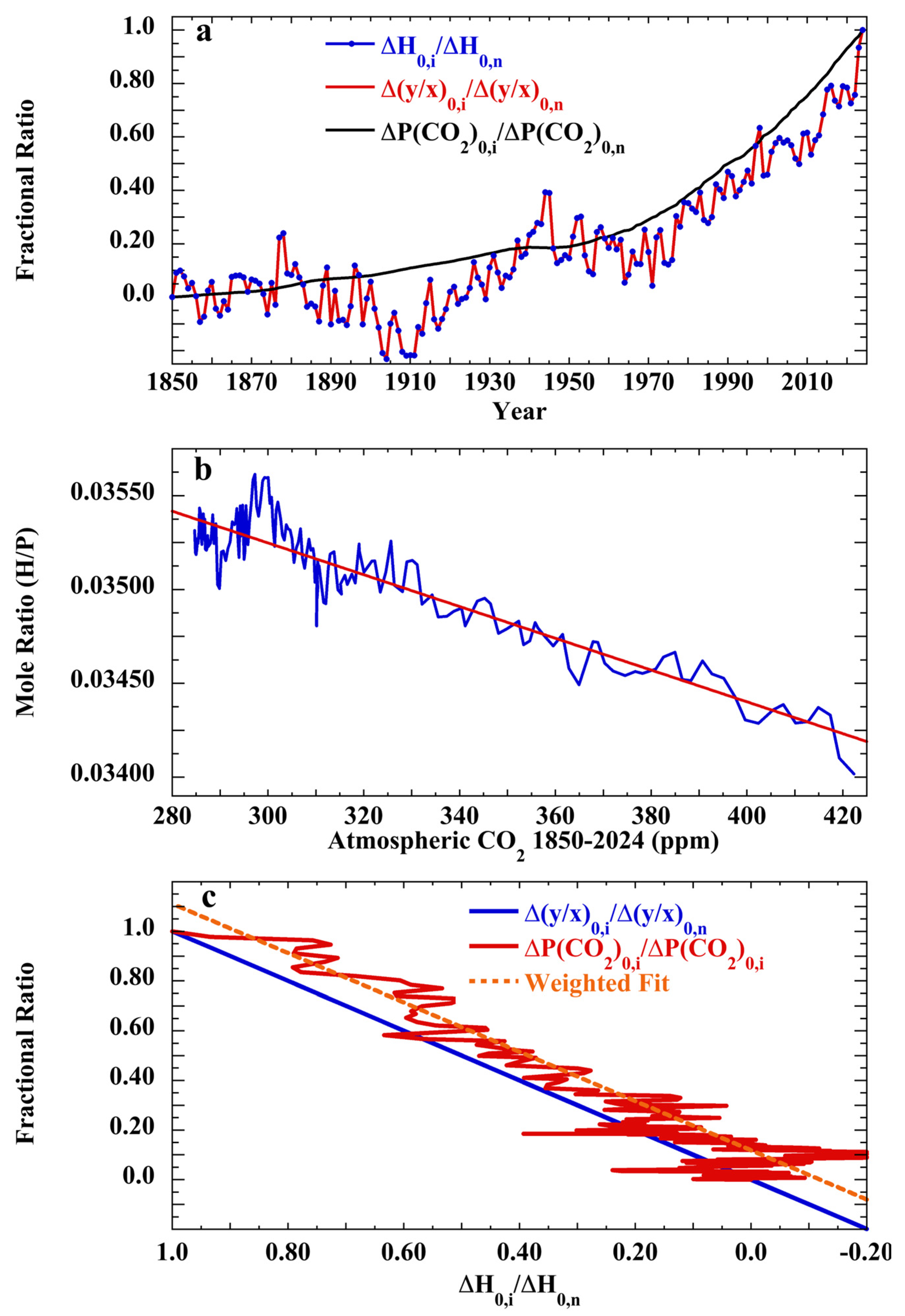
2.4. Weighting for the Least Squares Fit, ΔHi/ΔHn vs. ΔP(CO2)i/ΔP(CO2)n
2.5. Data Analysis
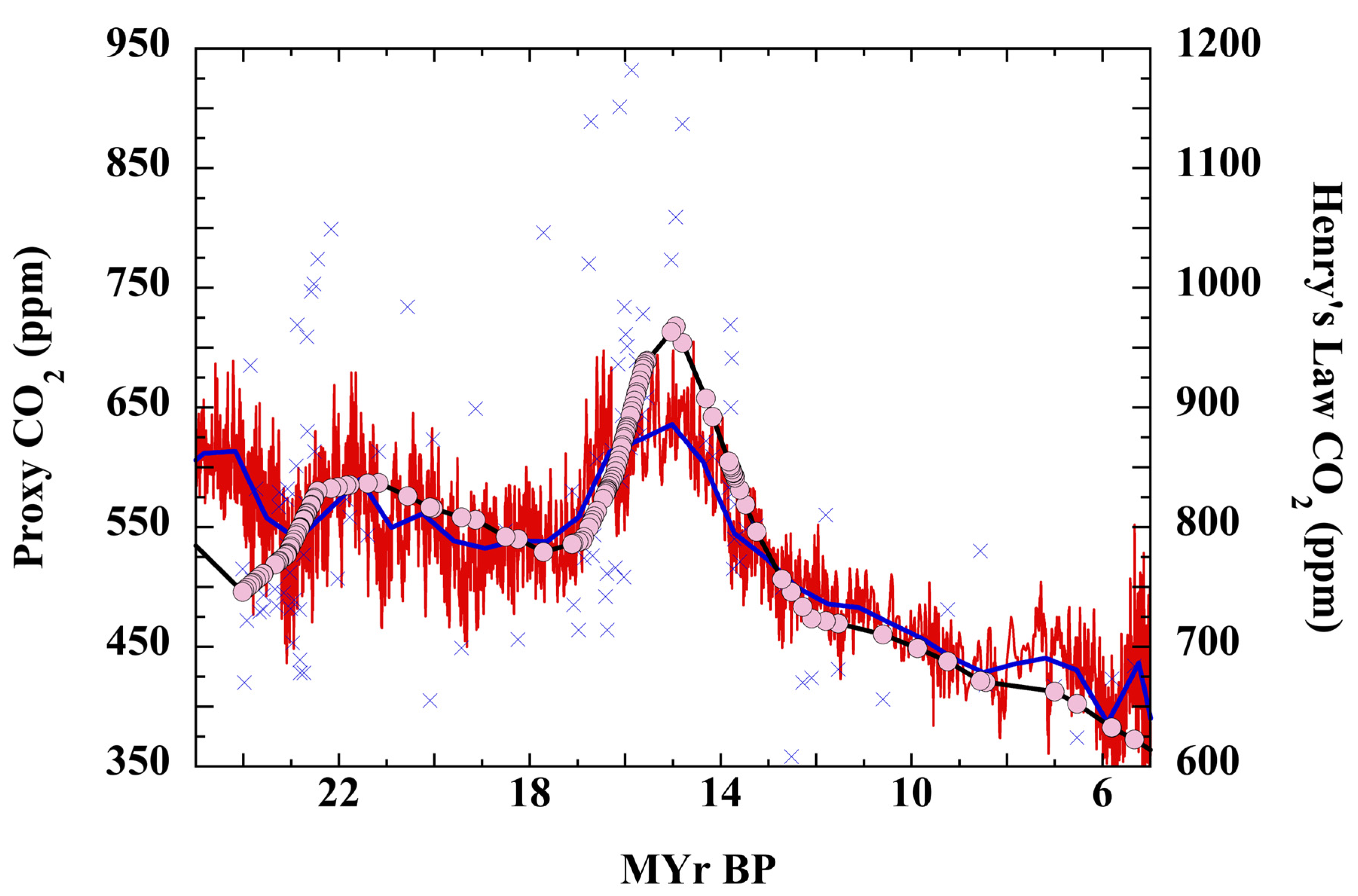
3. Results
3.1. Schumpe Parameters, the Sechenov Equation, and Henry’s Law for CO2 in Seawater
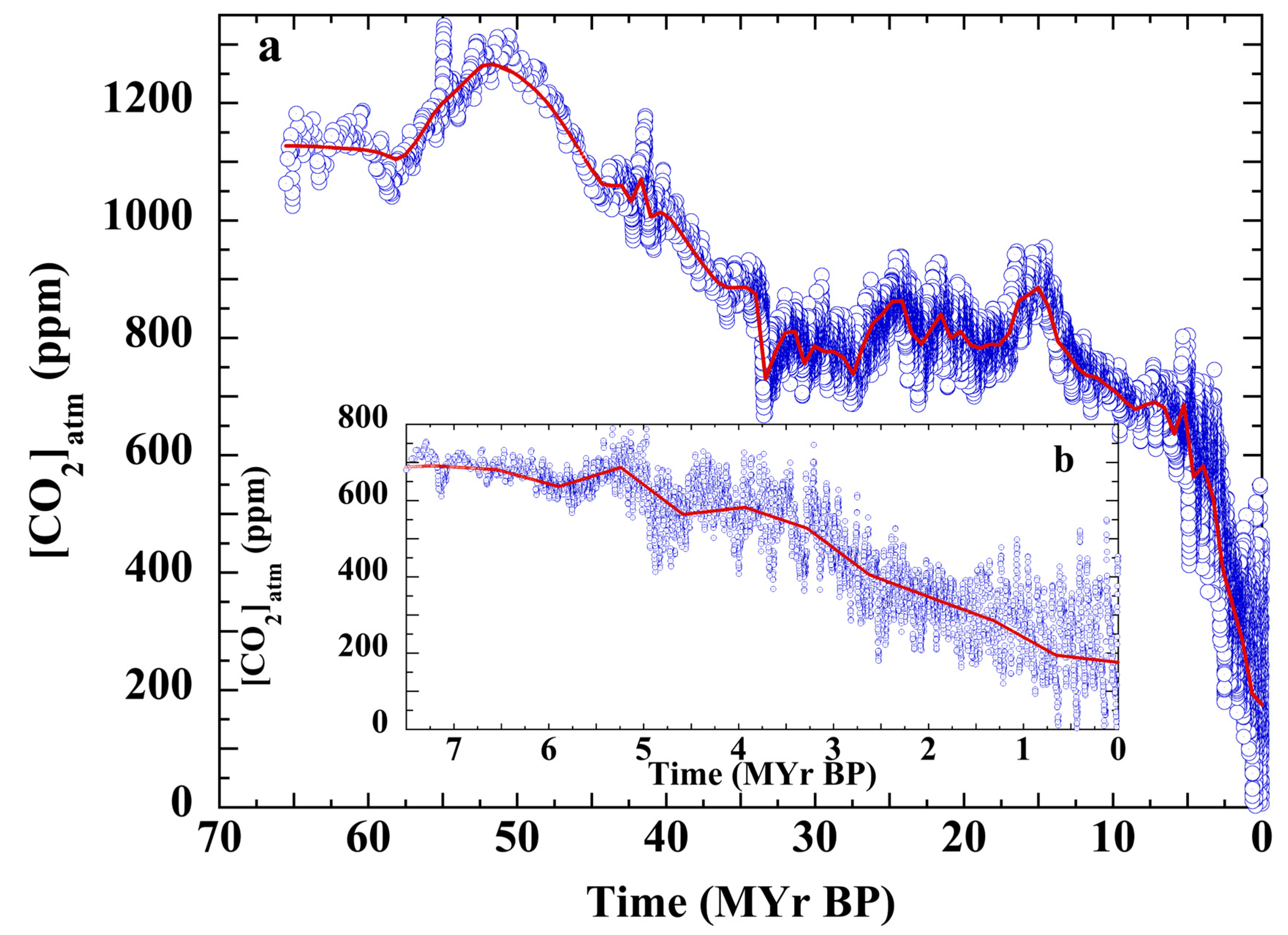
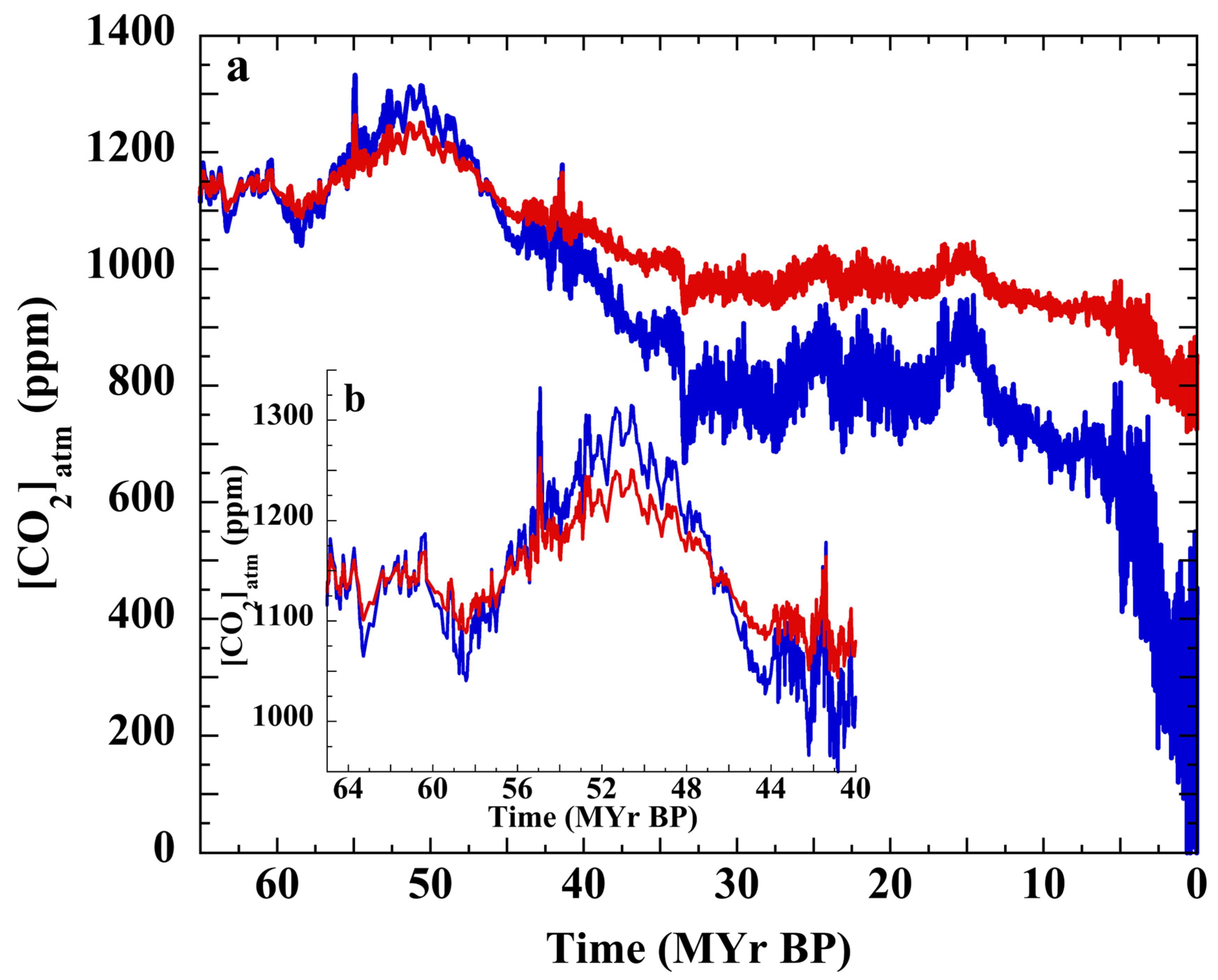
3.2. Henry’s Law Estimation of Cenozoic CO2
3.3. Empirical Test of Henry’s Law Ratios
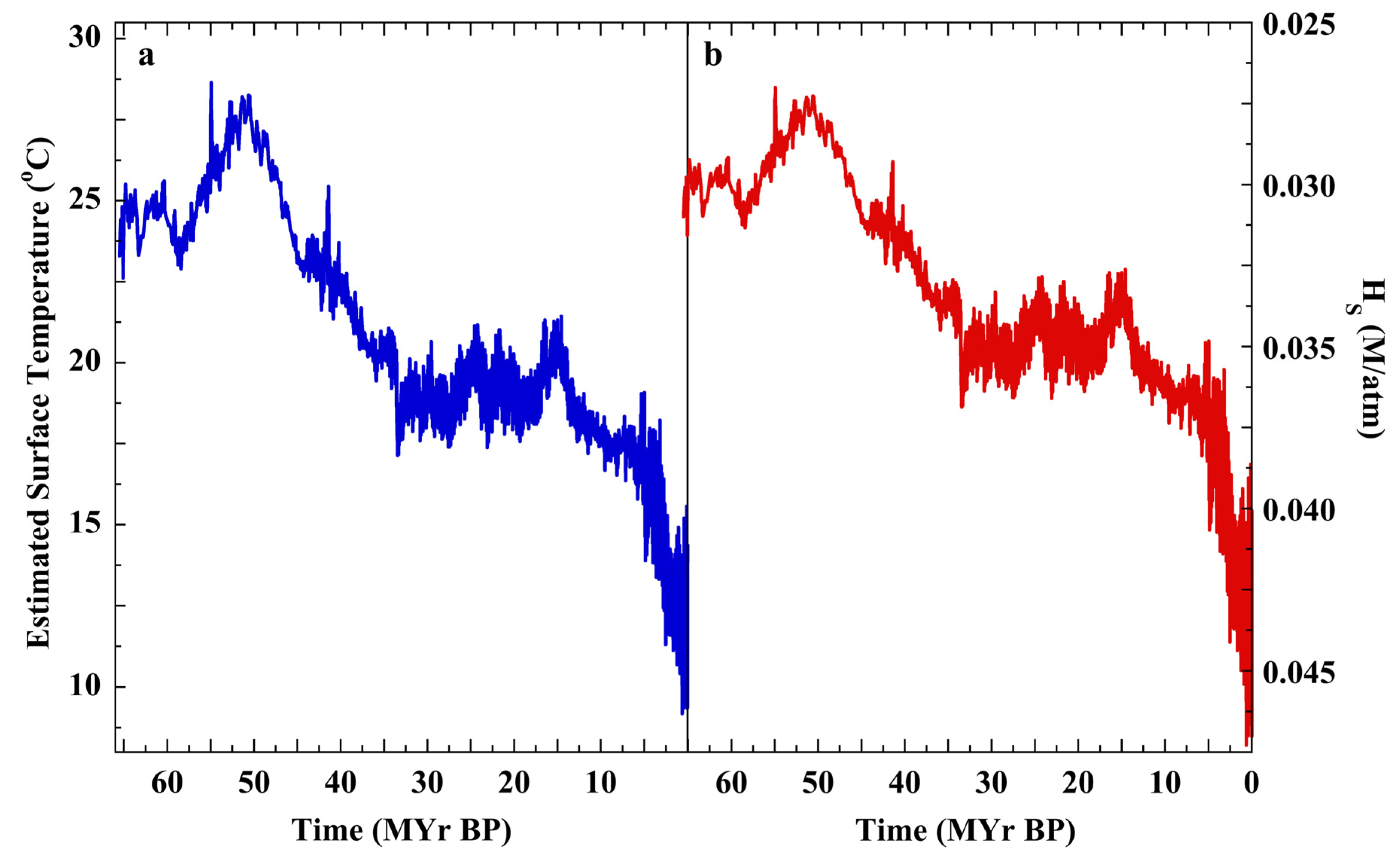
3.4. The Null Hypothesis, SST, and Cenozoic CO2
3.5. Basaltic Flood Magmatism and Ocean Heating
3.6. The Null Hypothesis and Trends in Cenozoic P(CO2)
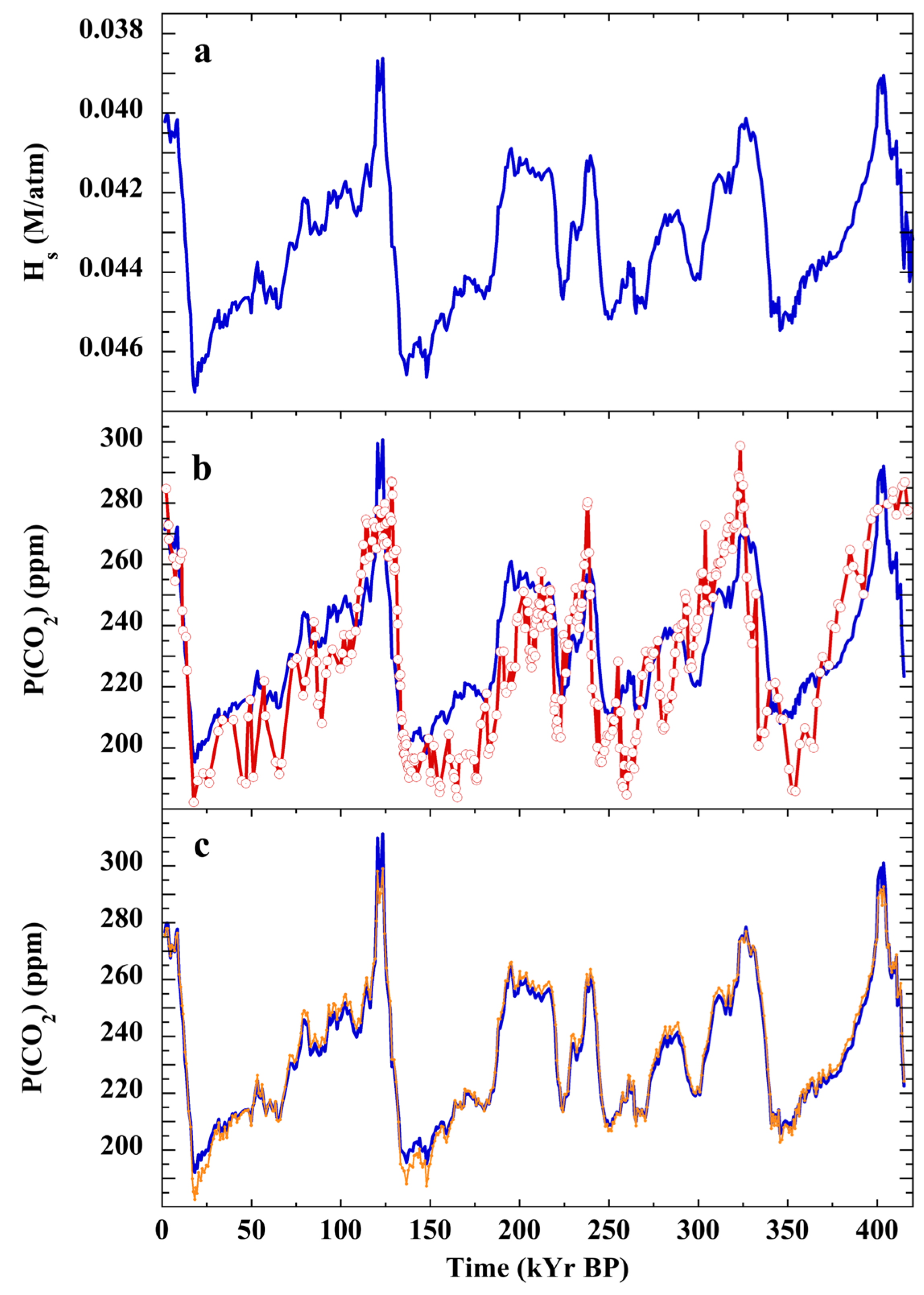
3.7. Testing the Null Hypothesis: Atmospheric CO2 over the Cenozoic
3.8. The PETM and Cenozoic P(CO2)
4. Discussion
4.1. The Null Hypothesis
4.2. The Paleocene–Eocene Thermal Maximum (PETM)
4.3. The Miocene Climate Optimum
4.4. Pleistocene and Holocene
5. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pearson, P.N.; Palmer, M.R. Atmospheric carbon dioxide over the past 60 million years. Nature 2000, 406, 695–699. [Google Scholar] [CrossRef] [PubMed]
- Rae, J.W.B.; Zhang, Y.G.; Liu, X.; Foster, G.L.; Stoll, H.M.; Whiteford, R.D. Atmospheric CO2 over the Past 66 Million Years from Marine Archives. Annu. Rev. Earth Planet. Sci. 2021, 49, 609–641. [Google Scholar] [CrossRef]
- Raitzsch, M.; Bijma, J.; Bickert, T.; Schulz, M.; Holbourn, A.; Kučera, M. Atmospheric carbon dioxide variations across the middle Miocene climate transition. Clim. Past 2021, 17, 703–719. [Google Scholar] [CrossRef]
- Wang, Y.; Momohara, A.; Wang, L.; Lebreton-Anberrée, J.; Zhou, Z. Evolutionary History of Atmospheric CO2 during the Late Cenozoic from Fossilized Metasequoia Needles. PLoS ONE 2015, 10, e0130941. [Google Scholar] [CrossRef] [PubMed]
- Westerhold, T.; Marwan, N.; Drury, A.J.; Liebrand, D.; Agnini, C.; Anagnostou, E.; Barnet, J.S.K.; Bohaty, S.M.; De Vleeschouwer, D.; Florindo, F.; et al. An astronomically dated record of Earth’s climate and its predictability over the last 66 million years. Science 2020, 369, 1383–1387. [Google Scholar] [CrossRef]
- Zachos, J.C.; Dickens, G.R.; Zeebe, R.E. An early Cenozoic perspective on greenhouse warming and carbon-cycle dynamics. Nature 2008, 451, 279–283. [Google Scholar] [CrossRef]
- Zhang, Y.G.; Pagani, M.; Liu, Z.; Bohaty, S.M.; DeConto, R. A 40-million-year history of atmospheric CO2. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20130096. [Google Scholar] [CrossRef]
- Royer, D.L. 6.11—Atmospheric CO2 and O2 During the Phanerozoic: Tools, Patterns, and Impacts, in Treatise on Geochemistry, 2nd ed.; Holland, H.D., Turekian, K.K., Eds.; Elsevier: Oxford, UK, 2014; pp. 251–267. [Google Scholar]
- Guillermic, M.; Misra, S.; Eagle, R.; Tripati, A. Atmospheric CO2 estimates for the Miocene to Pleistocene based on foraminiferal δ11B at Ocean Drilling Program Sites 806 and 807 in the Western Equatorial Pacific. Clim. Past 2022, 18, 183–207. [Google Scholar] [CrossRef]
- Herbert, T.D.; Dalton, C.A.; Liu, Z.; Salazar, A.; Si, W.; Wilson, D.S. Tectonic degassing drove global temperature trends since 20 Ma. Science 2022, 377, 116–119. [Google Scholar] [CrossRef]
- Kasbohm, J.; Schoene, B. Rapid eruption of the Columbia River flood basalt and correlation with the mid-Miocene climate optimum. Sci. Adv. 2018, 4, eaat8223. [Google Scholar] [CrossRef]
- Schaller, M.F.; Fung, M.K. The extraterrestrial impact evidence at the Palaeocene–Eocene boundary and sequence of environmental change on the continental shelf. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2018, 376, 20170081. [Google Scholar] [CrossRef] [PubMed]
- Kelly, D.C.; Zachos, J.C.; Bralower, T.J.; Schellenberg, S.A. Enhanced terrestrial weathering/runoff and surface ocean carbonate production during the recovery stages of the Paleocene-Eocene thermal maximum. Paleoceanography 2005, 20. [Google Scholar] [CrossRef]
- Mejía, L.M.; Méndez-Vicente, A.; Abrevaya, L.; Lawrence, K.T.; Ladlow, C.; Bolton, C.; Cacho, I.; Stoll, H. A diatom record of CO2 decline since the late Miocene. Earth Planet. Sci. Lett. 2017, 479, 18–33. [Google Scholar] [CrossRef]
- Stoll, H.M.; Shimizu, N.; Archer, D.; Ziveri, P. Coccolithophore productivity response to greenhouse event of the Paleocene–Eocene Thermal Maximum. Earth Planet. Sci. Lett. 2007, 258, 192–206. [Google Scholar] [CrossRef]
- McKay, D.I.A.; Tyrrell, T.; Wilson, P.A. Global carbon cycle perturbation across the Eocene-Oligocene climate transition. Paleoceanography 2016, 31, 311–329. [Google Scholar] [CrossRef]
- Basak, C.; Martin, E.E. Antarctic weathering and carbonate compensation at the Eocene–Oligocene transition. Nat. Geosci. 2013, 6, 121–124. [Google Scholar] [CrossRef]
- Beerling, D.J.; Taylor, L.L.; Bradshaw, C.D.C.; Lunt, D.J.; Valdes, P.J.; Banwart, S.A.; Pagani, M.; Leake, J.R. Ecosystem CO2 starvation and terrestrial silicate weathering: Mechanisms and global-scale quantification during the late Miocene. J. Ecol. 2012, 100, 31–41. [Google Scholar] [CrossRef]
- A Bestland, E. Weathering flux and CO2 consumption determined from palaeosol sequences across the Eocene–Oligocene transition. Palaeogeogr. Palaeoclim. Palaeoecol. 2000, 156, 301–326. [Google Scholar] [CrossRef]
- Chen, Z.; Ding, Z.; Yang, S.; Zhang, C.; Wang, X. Increased precipitation and weathering across the Paleocene-Eocene Thermal Maximum in central China. Geochem. Geophys. Geosystems 2016, 17, 2286–2297. [Google Scholar] [CrossRef]
- Dutkiewicz, A.; Müller, R.D.; Cannon, J.; Vaughan, S.; Zahirovic, S. Sequestration and subduction of deep-sea carbonate in the global ocean since the Early Cretaceous. Geology 2018, 47, 91–94. [Google Scholar] [CrossRef]
- Goddéris, Y.; Donnadieu, Y. A sink- or a source-driven carbon cycle at the geological timescale? Relative importance of palaeogeography versus solid Earth degassing rate in the Phanerozoic climatic evolution. Geol. Mag. 2019, 156, 355–365. [Google Scholar] [CrossRef]
- John, C.M.; Banerjee, N.R.; Longstaffe, F.J.; Sica, C.; Law, K.R.; Zachos, J.C. Clay assemblage and oxygen isotopic constraints on the weathering response to the Paleocene-Eocene thermal maximum, east coast of North America. Geology 2012, 40, 591–594. [Google Scholar] [CrossRef]
- Kump, L.R.; Brantley, S.L.; Arthur, M.A. Chemical Weathering, Atmospheric CO2, and Climate. Annu. Rev. Earth Planet. Sci. 2000, 28, 611–667. [Google Scholar] [CrossRef]
- Passchier, S.; Krissek, L.A. Oligocene–Miocene Antarctic continental weathering record and paleoclimatic implications, Cape Roberts drilling Project, Ross Sea, Antarctica. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2008, 260, 30–40. [Google Scholar] [CrossRef]
- Penman, D.E. Silicate weathering and North Atlantic silica burial during the Paleocene-Eocene Thermal Maximum. Geology 2016, 44, 731–734. [Google Scholar] [CrossRef]
- Penman, D.E.; Turner, S.K.; Sexton, P.F.; Norris, R.D.; Dickson, A.J.; Boulila, S.; Ridgwell, A.; Zeebe, R.E.; Zachos, J.C.; Cameron, A.; et al. An abyssal carbonate compensation depth overshoot in the aftermath of the Palaeocene–Eocene Thermal Maximum. Nat. Geosci. 2016, 9, 575–580. [Google Scholar] [CrossRef]
- Von Strandmann, P.A.E.P.; Jones, M.T.; West, A.J.; Murphy, M.J.; Stokke, E.W.; Tarbuck, G.; Wilson, D.J.; Pearce, C.R.; Schmidt, D.N. Lithium isotope evidence for enhanced weathering and erosion during the Paleocene-Eocene Thermal Maximum. Sci. Adv. 2021, 7, eabh4224. [Google Scholar] [CrossRef]
- Pollard, D.; Kump, L.; Zachos, J. Interactions between carbon dioxide, climate, weathering, and the Antarctic ice sheet in the earliest Oligocene. Glob. Planet. Chang. 2013, 111, 258–267. [Google Scholar] [CrossRef]
- Ramos, E.J.; Breecker, D.O.; Barnes, J.D.; Li, F.; Gingerich, P.D.; Loewy, S.L.; Satkoski, A.M.; Baczynski, A.A.; Wing, S.L.; Miller, N.R.; et al. Swift Weathering Response on Floodplains during the Paleocene-Eocene Thermal Maximum. Geophys. Res. Lett. 2022, 49, e2021GL097436. [Google Scholar] [CrossRef]
- Li, G.; Ji, J.; Chen, J.; Kemp, D.B. Evolution of the Cenozoic carbon cycle: The roles of tectonics and CO2 fertilization. Glob. Biogeochem. Cycles 2009, 23, GB1009. [Google Scholar] [CrossRef]
- Wallmann, K. Controls on the cretaceous and cenozoic evolution of seawater composition, atmospheric CO2 and climate. Geochim. Cosmochim. Acta 2001, 65, 3005–3025. [Google Scholar] [CrossRef]
- Hansen, J.; Sato, M.; Russell, G.; Kharecha, P. Climate sensitivity, sea level and atmospheric carbon dioxide. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120294. [Google Scholar] [CrossRef] [PubMed]
- E Hansen, J.; Sato, M.; Simons, L.; Nazarenko, L.S.; Sangha, I.; Kharecha, P.; Zachos, J.C.; von Schuckmann, K.; Loeb, N.G.; Osman, M.B.; et al. Global warming in the pipeline. Oxf. Open Clim. Chang. 2023, 3, kgad008. [Google Scholar] [CrossRef]
- Anagnostou, E.; John, E.H.; Edgar, K.M.; Foster, G.L.; Ridgwell, A.; Inglis, G.N.; Pancost, R.D.; Lunt, D.J.; Pearson, P.N. Changing atmospheric CO2 concentration was the primary driver of early Cenozoic climate. Nature 2016, 533, 380–384. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, B.J.; Brentnall, S.J.; Anderson, C.W.; Berner, R.A.; Beerling, D.J. Atmospheric carbon dioxide linked with Mesozoic and early Cenozoic climate change. Nat. Geosci. 2008, 1, 43–48. [Google Scholar] [CrossRef]
- Glikson, A. Cenozoic mean greenhouse gases and temperature changes with reference to the Anthropocene. Glob. Change Biol. 2016, 22, 3843–3858. [Google Scholar] [CrossRef]
- Royer, D.L.; Pagani, M.; Beerling, D.J. Geobiological constraints on Earth system sensitivity to CO2 during the Cretaceous and Cenozoic. Geobiology 2012, 10, 298–310. [Google Scholar] [CrossRef]
- Pagani, M.; Arthur, M.A.; Freeman, K.H. Miocene evolution of atmospheric carbon dioxide. Paleoceanography 1999, 14, 273–292. [Google Scholar] [CrossRef]
- Mackay, D.; Shiu, W.Y. A critical review of Henry’s law constants for chemicals of environmental interest. J. Phys. Chem. Ref. Data 1981, 10, 1175–1199. [Google Scholar] [CrossRef]
- Staudinger, J.; Roberts, P.V. A critical review of Henry’s law constants for environmental applications. Crit. Rev. Environ. Sci. Technol. 1996, 26, 205–297. [Google Scholar] [CrossRef]
- Clever, H.L. An Evaluation of the Solubility of Carbon Dioxide in Aqueous Electrolyte Solutions. In IUPAC-NIST Solubility Database: NIST Standard Reference Database 106; Scharlin, P., Ed.; 1996, Office of Data and Informatics of the National Institute of Standards and Technology (NIST); Material Measurement Laboratory (MML): Washington, DC, USA, 2023; 94p. [Google Scholar]
- Sander, R. Compilation of Henry’s law constants (version 5.0.0) for water as solvent. Atmos. Chem. Phys. 2023, 23, 10901–12440. [Google Scholar] [CrossRef]
- Abbatt, J.D.P. Section 5. Heterogeneous Processes, in Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies; Burkholder, J.B., Sander, S.P., Eds.; JPL Publication No., 19-5; Jet Propulsion Laboratory: Pasadena, CA, USA, 2019. [Google Scholar]
- Scharlin, P.; Cargill, R.W. Carbon Dioxide in Water and Aqueous Electrolyte Solutions; Lorimer, J.W., Ed.; IUPAC Solubility Data Series; International Union of Pure and Applied Chemistry: Oxford, UK, 1996; Volume 62, pp. xviii + 383. [Google Scholar]
- Sazonov, V.P.; Shaw, D.G. Solubility System: Carbon dioxide with Electrolyte and Water, in IUPAC-NIST Solubility Database: NIST Standard Reference Database 106, Volume 62; Scharlin, P., Ed.; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Weiss, R. Carbon dioxide in water and seawater: The solubility of a non-ideal gas. Mar. Chem. 1974, 2, 203–215. [Google Scholar] [CrossRef]
- Kozdon, R.; Kelly, D.C.; Kita, N.T.; Fournelle, J.H.; Valley, J.W. Planktonic foraminiferal oxygen isotope analysis by ion microprobe technique suggests warm tropical sea surface temperatures during the Early Paleogene. Paleoceanography 2011, 26, PA3206. [Google Scholar] [CrossRef]
- Gaskell, D.E.; Huber, M.; O’brien, C.L.; Inglis, G.N.; Acosta, R.P.; Poulsen, C.J.; Hull, P.M. The latitudinal temperature gradient and its climate dependence as inferred from foraminiferal δ18O over the past 95 million years. Proc. Natl. Acad. Sci. USA 2022, 119. [Google Scholar] [CrossRef] [PubMed]
- Bernard, S.; Daval, D.; Ackerer, P.; Pont, S.; Meibom, A. Burial-induced oxygen-isotope re-equilibration of fossil foraminifera explains ocean paleotemperature paradoxes. Nat. Commun. 2017, 8, 1134. [Google Scholar] [CrossRef]
- Lüthi, D.; Le Floch, M.; Bereiter, B.; Blunier, T.; Barnola, J.-M.; Siegenthaler, U.; Raynaud, D.; Jouzel, J.; Fischer, H.; Kawamura, K.; et al. High-resolution carbon dioxide concentration record 650,000–800,000 years before present. Nature 2008, 453, 379–382. [Google Scholar] [CrossRef]
- Lüthi, D.; Le Floch, M.; Bereiter, B.; Blunier, T.; Barnola, J.-M.; Siegenthaler, U.; Raynaud, D.; Jouzel, J.; Fischer, H.; Kawamura, K.; et al. EPICA Dome C Ice Core Terminations I and II Air Isotopes and CO2 Data. 2013; This Dataset Gathers Published and New Data of d15N, d18Oatm and CO2 from the EPICA Dome C Ice Core over Terminations I and II. Available online: https://www.ncei.noaa.gov/pub/data/paleo/icecore/antarctica/epica_domec/edc2013d18oatm.txt (accessed on 23 March 2024).
- EEA. Trends in Atmospheric Concentrations of CO2 (ppm), CH4 (ppb) and N2O (ppb), between 1800 and 2017. Data Visualizations 2024. Available online: https://www.eea.europa.eu/data-and-maps/daviz/atmospheric-concentration-of-carbon-dioxide-5/download.table (accessed on 28 March 2024).
- Wu, B.; Woodward, M.D.; Nishio, S.; Olivieri, A.; Rojas, L.P.; van Rijsbergen, M.; Derradji-Aouat, A. Fresh Water and Seawater Properties. In 26th International Towing Tank Conference; ITCC Association: Rio de Janeiro, Brazil, 2011. [Google Scholar]
- Carroll, J.J.; Slupsky, J.D.; Mather, A.E. The Solubility of Carbon Dioxide in Water at Low Pressure. J. Phys. Chem. Ref. Data 1991, 20, 1201–1209. [Google Scholar] [CrossRef]
- Pawlowicz, R. Key Physical Variables in the Ocean: Temperature, Salinity, and Density. Nat. Educ. Knowl. 2013, 4, 13. Available online: https://www.nature.com/scitable/knowledge/library/key-physical-variables-in-the-ocean-temperature-102805293/ (accessed on 28 August 2024).
- Millero, F.J. The Partial Molal Volumes of Ions in Seawater1. Limnol. Oceanogr. 1969, 14, 376–385. [Google Scholar] [CrossRef]
- Xian, P.; Ji, B.; Bian, S.; Zong, J.; Zhang, T. Influence of Differences in the Density of Seawater on the Measurement of the Underwater Gravity Gradient. Sensors 2023, 23, 714. [Google Scholar] [CrossRef]
- Puigdomenech, I. Medusa: Chemical Equilibrium Software. 2004. Available online: https://www.kth.se/che/medusa/downloads-1.386254 (accessed on 28 August 2024).
- Bijl, P.K.; Schouten, S.; Sluijs, A.; Reichart, G.-J.; Zachos, J.C.; Brinkhuis, H. Early Palaeogene temperature evolution of the southwest Pacific Ocean. Nature 2009, 461, 776–779. [Google Scholar] [CrossRef]
- Huang, B.; Thorne, P.W.; Banzon, V.F.; Boyer, T.; Chepurin, G.; Lawrimore, J.H.; Menne, M.J.; Smith, T.M.; Vose, R.S.; Zhang, H.-M. Extended Reconstructed Sea Surface Temperature, Version 5 (ERSSTv5): Upgrades, Validations, and Intercomparisons. J. Clim. 2017, 30, 8179–8205. [Google Scholar] [CrossRef]
- Huang, B. NOAA Extended Reconstructed Sea Surface Temperature (ERSST), Version 5.202402. 2017. Available online: https://www.ncei.noaa.gov/products/extended-reconstructed-sst (accessed on 2 April 2024).
- Kennedy, J.J.; Rayner, N.A.; Atkinson, C.P.; Killick, R.E. An Ensemble Data Set of Sea Surface Temperature Change From 1850: The Met Office Hadley Centre HadSST.4.0.0.0 Data Set. J. Geophys. Res. Atmos. 2019, 124, 7719–7763. [Google Scholar] [CrossRef]
- Ronov, A.B. The Distribution of Basalts, Andesites, and Rhyolites on the Continents and Continental Margins and in the Oceans. Int. Geol. Rev. 1985, 27, 1276–1284. [Google Scholar] [CrossRef]
- Ernst, R.E.; Bond, D.P.G.; Zhang, S.-H.; Buchan, K.L.; Grasby, S.E.; Youbi, N.; Bilali, H.E.; Bekker, A.; Doucet, L.S. Large Igneous Province Record through Time and Implications for Secular Environmental Changes and Geological Time-Scale Boundaries. In Large Igneous Provinces; American Geophysical Union and John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2021; pp. 1–26. [Google Scholar]
- Percival, L.M.E.; Matsumoto, H.; Callegaro, S.; Erba, E.; Kerr, A.C.; Mutterlose, J.; Suzuki, K. Cretaceous large igneous provinces: From volcanic formation to environmental catastrophes and biological crises. Geol. Soc. Lond. Spéc. Publ. 2024, 544, sp544–sp2023. [Google Scholar] [CrossRef]
- White, R.S.; McKenzie, D. Magmatism at rift zones: The generation of volcanic continental margins and flood basalts. J. Geophys. Res. 1989, 94, 7685–7729. [Google Scholar] [CrossRef]
- Saunders, A.D.; Fitton, J.F.; Kerr, A.C. The North Atlantic Igneous Province. In Large Igneous Provinces: Continental, Oceanic and Planetary Flood Volcanism; Mahoney, J.J., Coffin, M.F., Eds.; American Geophysical Union Monograph: Washington, DC, USA, 1997; pp. 45–93. [Google Scholar]
- Eldholm, O.; Grue, K. North Atlantic volcanic margins: Dimensions and production rates. J. Geophys. Res. 1994, 99, 2955–2968. [Google Scholar] [CrossRef]
- Eldholm, O.; Myhre, A.M.; Thiede, J. Cenozoic Tectono-Magmatic Events in the North Atlantic: Potential Paleoenvironmental Implications; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Horni, J.; Hopper, J.R.; Blischke, A.; Geisler, W.H.; Stewart, M.; McDermott, K.; Judge, M.; Erlendsson, Ö.; Árting, U. Regional distribution of volcanism within the North Atlantic Igneous Province. In The NE Atlantic Region. A Reappraisal of Crustal Structure, Tectonostratigraphy and Magmatic Evolution; Péron-Pinvidic, G., Hopper, J.R., Funck, T., Stoker, M.S., Gaina, C., Doornenbal, J.C., Arting, U.E., Eds.; Geological Society, London, Special Publications: London, UK, 2017; p. SP447.18. [Google Scholar]
- Ganerød, M.; Smethurst, M.A.; Torsvik, T.H.; Prestvik, T.; Rousse, S.; McKenna, C.; Van Hinsbergen, D.J.J.; Hendriks, B.W.H. The North Atlantic Igneous Province reconstructed and its relation to the Plume Generation Zone: The Antrim Lava Group revisited. Geophys. J. Int. 2010, 182, 183–202. [Google Scholar] [CrossRef]
- Fukuyama, H. Heat of fusion of basaltic magma. Earth Planet. Sci. Lett. 1985, 73, 407–414. [Google Scholar] [CrossRef]
- Millero, F.J.; Perron, G.; Desnoyers, J.E. Heat capacity of seawater solutions from 5° to 35 °C and 0.5 to 22‰ chlorinity. J. Geophys. Res. 1973, 78, 4499–4507. [Google Scholar] [CrossRef]
- Shiklomanov, I.A. World Fresh Water Resources, in Water in Crisis: A Guide to the World’s Fresh Water Resources; Gleik, P.H., Ed.; Oxford University: New York, NY, USA, 1993; pp. xxiv, 473. [Google Scholar]
- Sparks, R.S.J.; Huppert, H.E. Density changes during the fractional crystallization of basaltic magmas: Fluid dynamic implications. Contrib. Miner. Pet. 1984, 85, 300–309. [Google Scholar] [CrossRef]
- Green, D.H.; Falloon, T.J.; Eggins, S.M.; Yaxley, G.M. Primary magmas and mantle temperatures. Eur. J. Miner. 2001, 13, 437–451. [Google Scholar] [CrossRef]
- Bouhifd, M.A.; Besson, P.; Courtial, P.; Gérardin, C.; Navrotsky, A.; Richet, P. Thermochemistry and melting properties of basalt. Contrib. Miner. Pet. 2007, 153, 689–698. [Google Scholar] [CrossRef]
- Rae, J.W.; Foster, G.L.; Schmidt, D.N.; Elliott, T. Boron isotopes and B/Ca in benthic foraminifera: Proxies for the deep ocean carbonate system. Earth Planet. Sci. Lett. 2011, 302, 403–413. [Google Scholar] [CrossRef]
- Rae, J.W.B. Boron Isotopes in Foraminifera: Systematics, Biomineralisation, and CO2 Reconstruction. In Boron Isotopes: The Fifth Element; Marschall, H., Foster, G., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 107–143. [Google Scholar]
- Rasbury, E.T.; Hemming, N.G. Boron Isotopes: A “Paleo-pH Meter” for Tracking Ancient Atmospheric CO2. Elements 2017, 13, 243–248. [Google Scholar] [CrossRef]
- Raitzsch, M.; Hönisch, B. Cenozoic boron isotope variations in benthic foraminifers. Geology 2013, 41, 591–594. [Google Scholar] [CrossRef]
- Shao, J.; Stott, L.D.; Gray, W.R.; Greenop, R.; Pecher, I.; Neil, H.L.; Coffin, R.B.; Davy, B.; Rae, J.W. Atmosphere-Ocean CO2 Exchange Across the Last Deglaciation From the Boron Isotope Proxy. Paleoceanogr. Paleoclimatology 2019, 34, 1650–1670. [Google Scholar] [CrossRef]
- Zhang, Y.G.; Pearson, A.; Benthien, A.; Dong, L.; Huybers, P.; Liu, X.; Pagani, M. Refining the alkenone-pCO2 method I: Lessons from the Quaternary glacial cycles. Geochim. Cosmochim. Acta 2019, 260, 177–191. Available online: https://www.sciencedirect.com/science/article/pii/S0016703719303813 (accessed on 22 July 2024). [CrossRef]
- Zhang, Y.G.; Henderiks, J.; Liu, X. Refining the alkenone-pCO2 method II: Towards resolving the physiological parameter ‘b’. Geochim. Cosmochim. Acta 2020, 281, 118–134. [Google Scholar] [CrossRef]
- Tanner, T.; Hernández-Almeida, I.; Drury, A.J.; Guitián, J.; Stoll, H. Decreasing Atmospheric CO2 During the Late Miocene Cooling. Paleoceanogr. Paleoclimatology 2020, 35, e2020PA003925. [Google Scholar] [CrossRef]
- Lisiecki, L.E. A benthic δ13C-based proxy for atmospheric pCO2 over the last 1.5 Myr. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Sachs, J.P.; Schneider, R.R.; Eglinton, T.I.; Freeman, K.H.; Ganssen, G.; McManus, J.F.; Oppo, D.W. Alkenones as paleoceanographic proxies. Geochem. Geophys. Geosystems 2000, 1. [Google Scholar] [CrossRef]
- Seki, O.; Foster, G.L.; Schmidt, D.N.; Mackensen, A.; Kawamura, K.; Pancost, R.D. Alkenone and boron-based Pliocene pCO2 records. Earth Planet. Sci. Lett. 2010, 292, 201–211. [Google Scholar] [CrossRef]
- Foster, G.L.; Rae, J.W. Reconstructing Ocean pH with Boron Isotopes in Foraminifera. Annu. Rev. Earth Planet. Sci. 2016, 44, 207–237. [Google Scholar] [CrossRef]
- Gaillardet, J.; Lemarchand, D. Boron in the Weathering Environment. In Boron Isotopes: The Fifth Element; Marschall, H., Foster, G., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 163–188. [Google Scholar]
- Gradstein, F.M.; Ogg, J.G. Geologic Time Scale 2004—Why, how, and where next! Lethaia 2004, 37, 175–181. [Google Scholar] [CrossRef]
- Bijl, P.K.; Houben, A.J.P.; Schouten, S.; Bohaty, S.M.; Sluijs, A.; Reichart, G.-J.; Damsté, J.S.S.; Brinkhuis, H. Transient Middle Eocene Atmospheric CO2 and Temperature Variations. Science 2010, 330, 819–821. [Google Scholar] [CrossRef]
- Schouten, S.; van der Meer, M.T.J.; Hopmans, E.C.; Rijpstra, W.I.C.; Reysenbach, A.-L.; Ward, D.M.; Damsté, J.S.S. Archaeal and bacterial glycerol dialkyl glycerol tetraether lipids in hot springs of yellowstone national park. Appl. Environ. Microbiol. 2007, 73, 6181–6191. [Google Scholar] [CrossRef]
- Tateo, F. Clay Minerals at the Paleocene–Eocene Thermal Maximum: Interpretations, Limits, and Perspectives. Minerals 2020, 10, 1073. [Google Scholar] [CrossRef]
- Martín-Martín, M.; Guerrera, F.; Tosquella, J.; Tramontana, M. Paleocene-Lower Eocene carbonate platforms of westernmost Tethys. Sediment. Geol. 2020, 404, 105674. [Google Scholar] [CrossRef]
- Li, J.; Hu, X.; Garzanti, E.; BouDagher-Fadel, M. Spatial heterogeneity in carbonate-platform environments and carbon isotope values across the Paleocene–Eocene thermal maximum (Tethys Himalaya, South Tibet). Glob. Planet. Chang. 2022, 214, 103853. [Google Scholar] [CrossRef]
- Bowen, G.J.; Zachos, J.C. Rapid carbon sequestration at the termination of the Palaeocene–Eocene Thermal Maximum. Nat. Geosci. 2010, 3, 866–869. [Google Scholar] [CrossRef]
- Bains, S.; Norris, R.D.; Corfield, R.M.; Faul, K.L. Termination of global warmth at the Palaeocene/Eocene boundary through productivity feedback. Nature 2000, 407, 171–174. [Google Scholar] [CrossRef]
- Bains, S.; Norris, R.D.; Corfield, R.; Bowen, G.J.; Gingerich, P.D.; Koch, P.L. Marine-terrestrial linkages at the Paleocene-Eocene boundary. In Causes and Consequences of Globally Warm Climates in the Early Paleogene; Geological Society of America: Boulder, CO, USA, 2003; pp. 1–9. [Google Scholar]
- Steinthorsdottir, M.; Coxall, H.K.; de Boer, A.M.; Huber, M.; Barbolini, N.; Bradshaw, C.D.; Burls, N.J.; Feakins, S.J.; Gasson, E.; Henderiks, J.; et al. The Miocene: The Future of the Past. Paleoceanogr. Paleoclimatology 2021, 36, e2020PA004037. [Google Scholar] [CrossRef]
- Yang, Y.; Ye, C.; Galy, A.; Fang, X.; Xue, Y.; Liu, Y.; Yang, R.; Zhang, R.; Han, W.; Zhang, W.; et al. Monsoon-Enhanced Silicate Weathering as a New Atmospheric CO2 Consumption Mechanism Contributing to Fast Late Miocene Global Cooling. Paleoceanogr. Paleoclimatology 2021, 36, e2020PA004008. [Google Scholar] [CrossRef]
- Pélissié, T.; Orliac, M.J.; Antoine, P.O.; Biot, V.; Escarguel, G. Beyond Eocene and Oligocene Epochs: The Causses du Quercy Geopark and the Grande Coupure. Geoconservation Res. 2023, 4, 573–585. [Google Scholar] [CrossRef]
- Kürschner, W.M.; Kvaček, Z.; Dilcher, D.L. The impact of Miocene atmospheric carbon dioxide fluctuations on climate and the evolution of terrestrial ecosystems. Proc. Natl. Acad. Sci. USA 2008, 105, 449–453. [Google Scholar] [CrossRef]
- Barker, P.; Thomas, E. Origin, signature and palaeoclimatic influence of the Antarctic Circumpolar Current. Earth-Sci. Rev. 2004, 66, 143–162. [Google Scholar] [CrossRef]
- Crowley, T.J. The geologic record of climatic change. Rev. Geophys. 1983, 21, 828–877. [Google Scholar] [CrossRef]
- Culberson, C.H.; Pytkowicz, R.M. Ionization of water in seawater. Mar. Chem. 1973, 1, 309–316. [Google Scholar] [CrossRef]
- Bauska, T.K.; Joos, F.; Mix, A.C.; Roth, R.; Ahn, J.; Brook, E.J. Links between atmospheric carbon dioxide, the land carbon reservoir and climate over the past millennium. Nat. Geosci. 2015, 8, 383–387. [Google Scholar] [CrossRef]
- Teng, H.; Masutani, S.; Kinoshita, C.; Nihous, G. Solubility of CO2 in the ocean and its effect on CO2 dissolution. Energy Convers. Manag. 1996, 37, 1029–1038. [Google Scholar] [CrossRef]
- Tachikawa, K.; Vidal, L.; Sonzogni, C.; Bard, E. Glacial/interglacial sea surface temperature changes in the Southwest Pacific ocean over the past 360ka. Quat. Sci. Rev. 2009, 28, 1160–1170. [Google Scholar] [CrossRef]
- Hoffman, J.S.; Clark, P.U.; Parnell, A.C.; He, F. Regional and global sea-surface temperatures during the last interglaciation. Science 2017, 355, 276–279. [Google Scholar] [CrossRef] [PubMed]
- Cuffey, K.M.; Clow, G.D.; Steig, E.J.; Buizert, C.; Fudge, T.J.; Koutnik, M.; Waddington, E.D.; Alley, R.B.; Severinghaus, J.P. Deglacial temperature history of West Antarctica. Proc. Natl. Acad. Sci. USA 2016, 113, 14249–14254. [Google Scholar] [CrossRef] [PubMed]
- He, T.; Kemp, D.B.; Li, J.; Ruhl, M. Paleoenvironmental changes across the Mesozoic–Paleogene hyperthermal events. Glob. Planet. Chang. 2023, 222, 104058. [Google Scholar] [CrossRef]
- Rampino, M.R.; Caldeira, K.; Rodriguez, S. Cycles of ∼32.5 My and ∼26.2 My in correlated episodes of continental flood basalts (CFBs), hyper-thermal climate pulses, anoxic oceans, and mass extinctions over the last 260 My: Connections between geological and astronomical cycles. Earth-Sci. Rev. 2023, 246, 104548. [Google Scholar] [CrossRef]
- O’Brien, C.L.; Robinson, S.A.; Pancost, R.D.; Damsté, J.S.S.; Schouten, S.; Lunt, D.J.; Alsenz, H.; Bornemann, A.; Bottini, C.; Brassell, S.C.; et al. Cretaceous sea-surface temperature evolution: Constraints from TEX86 and planktonic foraminiferal oxygen isotopes. Earth-Sci. Rev. 2017, 172, 224–247. [Google Scholar] [CrossRef]
- Moriya, K. Development of the Cretaceous Greenhouse Climate and the Oceanic Thermal Structure. Paléontol. Res. 2011, 15, 77–88. [Google Scholar] [CrossRef]
- Huber, B.T.; MacLeod, K.G.; Watkins, D.K.; Coffin, M.F. The rise and fall of the Cretaceous Hot Greenhouse climate. Glob. Planet. Chang. 2018, 167, 1–23. [Google Scholar] [CrossRef]
- Hoffman, P.F.; Schrag, D.P. The snowball Earth hypothesis: Testing the limits of global change. Terra Nova 2002, 14, 129–155. [Google Scholar] [CrossRef]
- Joseph, A. Chapter 2—Geological timeline of significant events on Earth. In Water Worlds in the Solar System; Joseph, A., Ed.; Elsevier: Amsterdam, The Netherlands, 2023; pp. 55–114. [Google Scholar]
- Dutkiewicz, A.; Merdith, A.S.; Collins, A.S.; Mather, B.; Ilano, L.; Zahirovic, S.; Müller, R.D. Duration of Sturtian “Snowball Earth” glaciation linked to exceptionally low mid-ocean ridge outgassing. Geology 2024, 52, 292–296. [Google Scholar] [CrossRef]
- Parmentola, J. Celestial Mechanics and Estimating the Termination of the Holocene Warm Period. Sci. Clim. Chang. 2023, 3, 392–395. [Google Scholar] [CrossRef]
- Lindzen, R.S.; Pan, W. A note on orbital control of equator-pole heat fluxes. Clim. Dyn. 1994, 10, 49–57. [Google Scholar] [CrossRef]
- Wunsch, C. The spectral description of climate change including the 100 ky energy. Clim. Dyn. 2003, 20, 353–363. [Google Scholar] [CrossRef]
- Petit, J.R.; Jouzel, J.; Raynaud, D.; Barkov, N.I.; Barnola, J.M.; Basile, I.; Bender, M.; Chappellaz, J.; Davis, M.; Delaygue, G.; et al. Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica. Nature 1999, 399, 429–436. [Google Scholar] [CrossRef]


| Salt | NaCl | KCl | MgCl2 | MgSO4 | CaSO4 |
|---|---|---|---|---|---|
| Molality | 0.472 | 0.0103 | 0.0336 | 0.0196 | 8.82 × 10−3 |
| g/kg | 27.58 | 0.766 | 3.19 | 2.36 | 1.20 |
| Molarity | 0.456 | 0.0100 | 0.0324 | 0.0190 | 8.85 × 10−3 |
| Total mole fraction | 8.716 × 10−3 | 1.902 × 10−4 | 6.205 × 10−4 | 3.620 × 10−4 | 1.629 × 10−5 |
| Mole fraction of salts | 0.867 | 0.0189 | 0.0617 | 0.0360 | 0.0162 |
| Anion | Schumpe hi | Cation | Schumpe hi |
|---|---|---|---|
| Cl− | 0.0318 | Na+ | 0.1143 |
| 0.1117 | K+ | 0.0922 | |
| Mg2+ | 0.1694 | ||
| Ca2+ | 0.1762 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frank, P. Cenozoic Carbon Dioxide: The 66 Ma Solution. Geosciences 2024, 14, 238. https://doi.org/10.3390/geosciences14090238
Frank P. Cenozoic Carbon Dioxide: The 66 Ma Solution. Geosciences. 2024; 14(9):238. https://doi.org/10.3390/geosciences14090238
Chicago/Turabian StyleFrank, Patrick. 2024. "Cenozoic Carbon Dioxide: The 66 Ma Solution" Geosciences 14, no. 9: 238. https://doi.org/10.3390/geosciences14090238
APA StyleFrank, P. (2024). Cenozoic Carbon Dioxide: The 66 Ma Solution. Geosciences, 14(9), 238. https://doi.org/10.3390/geosciences14090238







