Unraveling the Spatio-Temporal Evolution of the Ranchería Delta (Riohacha, Colombia): A Multi-Period Analysis Using GIS
Abstract
1. Introduction
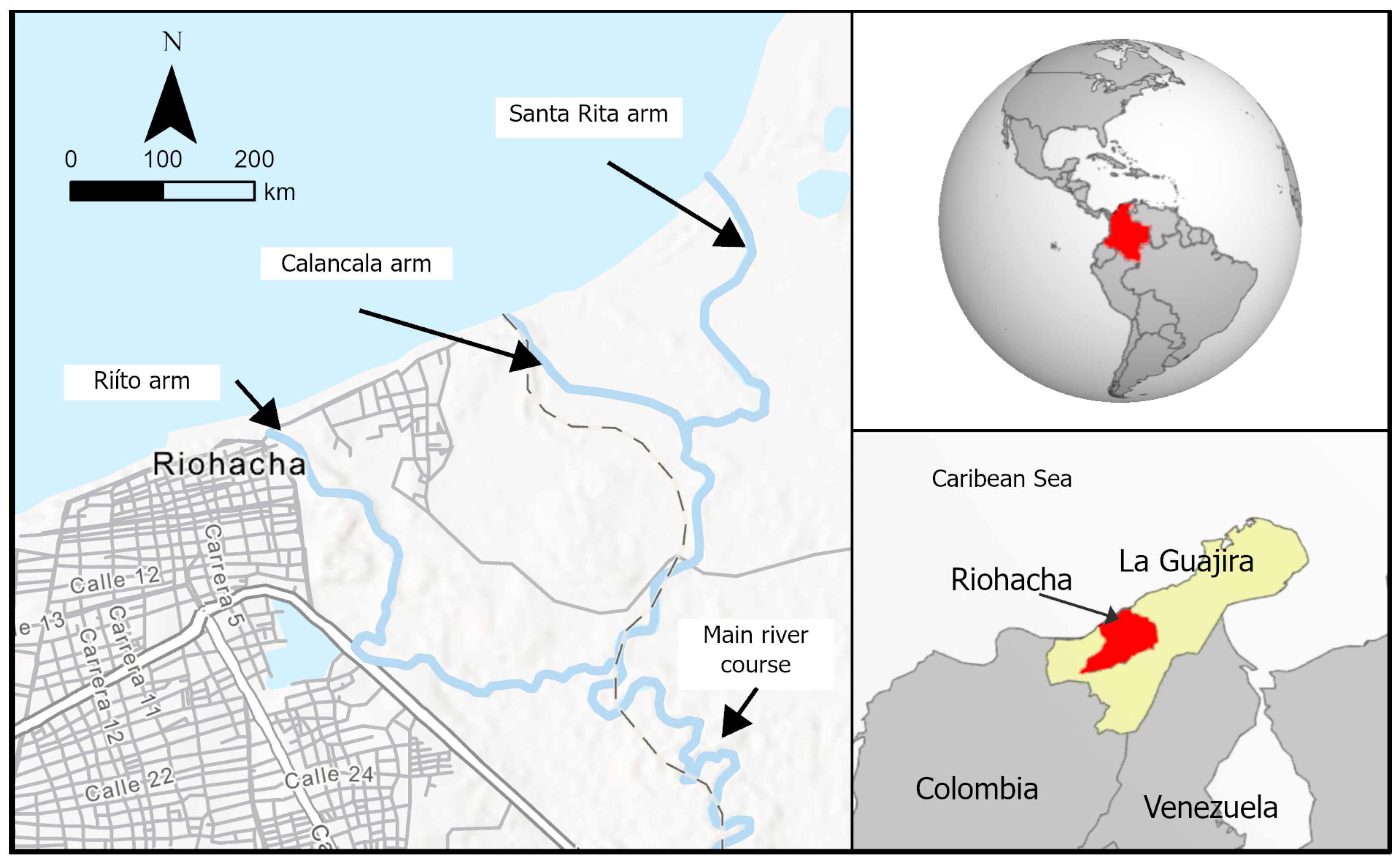
2. Study Site Description
3. Methodology
3.1. Image Acquisition and Preprocessing
3.2. Reprojecting and Spatial Accuracy
3.3. Shoreline Profiling
3.4. Baseline Construction and Data Structuring
3.5. Casting Transects
3.6. Temporal Trends in Shoreline Change Metrics: Multi-Period Statistical Analysis (2003–2023)
4. Results
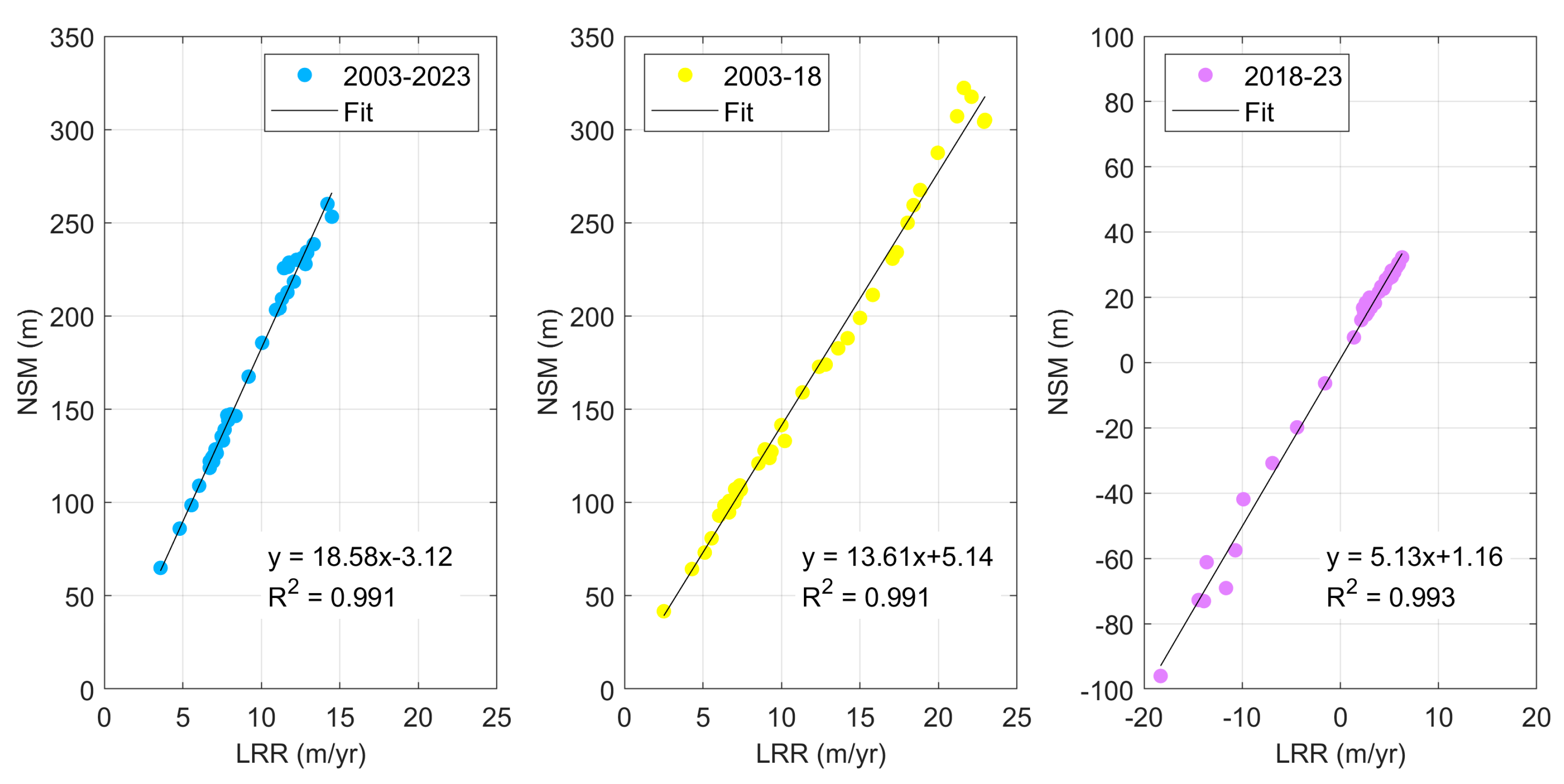
4.1. Shoreline Change Metrics: Trends in Accretion and Erosion
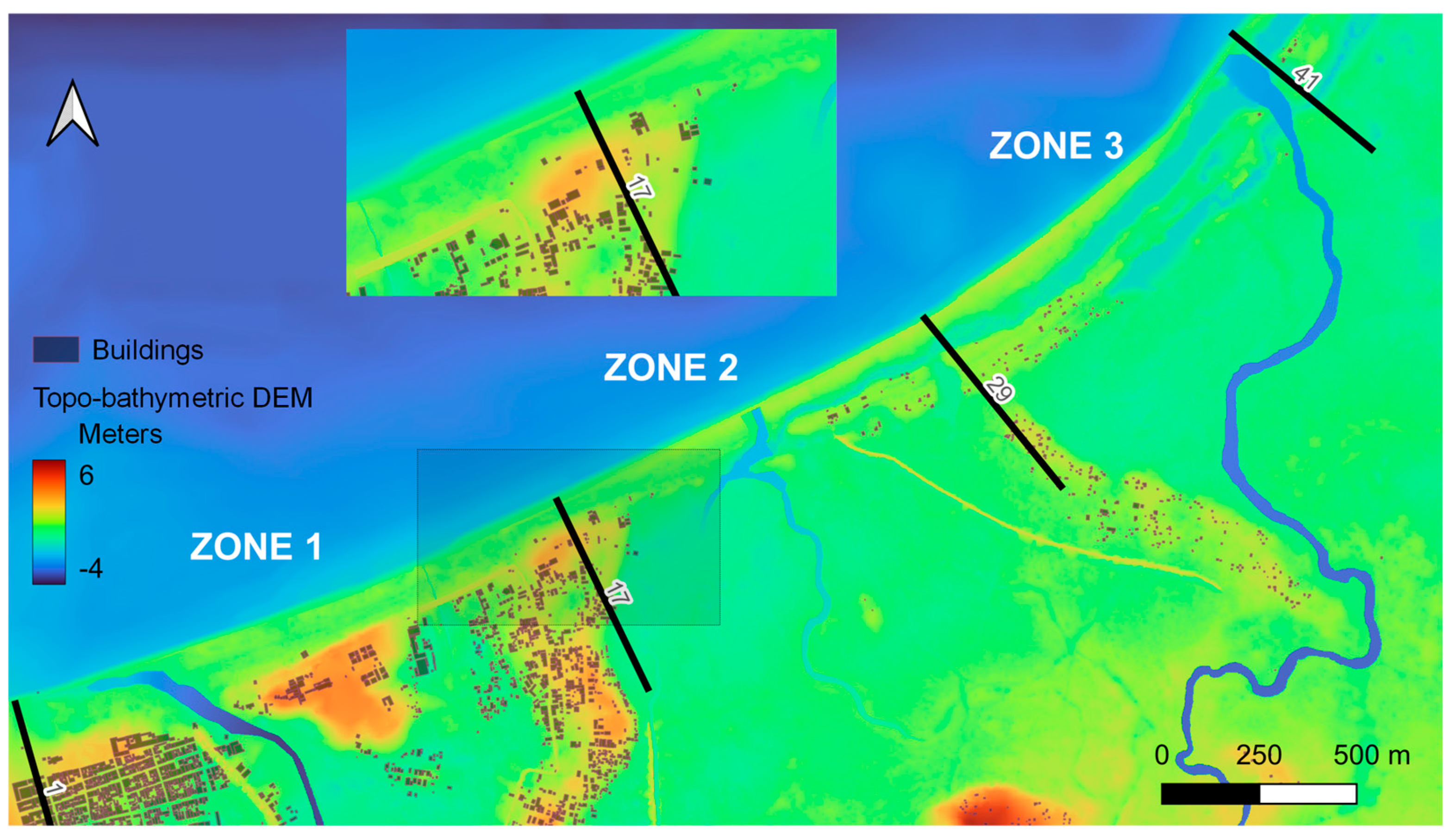
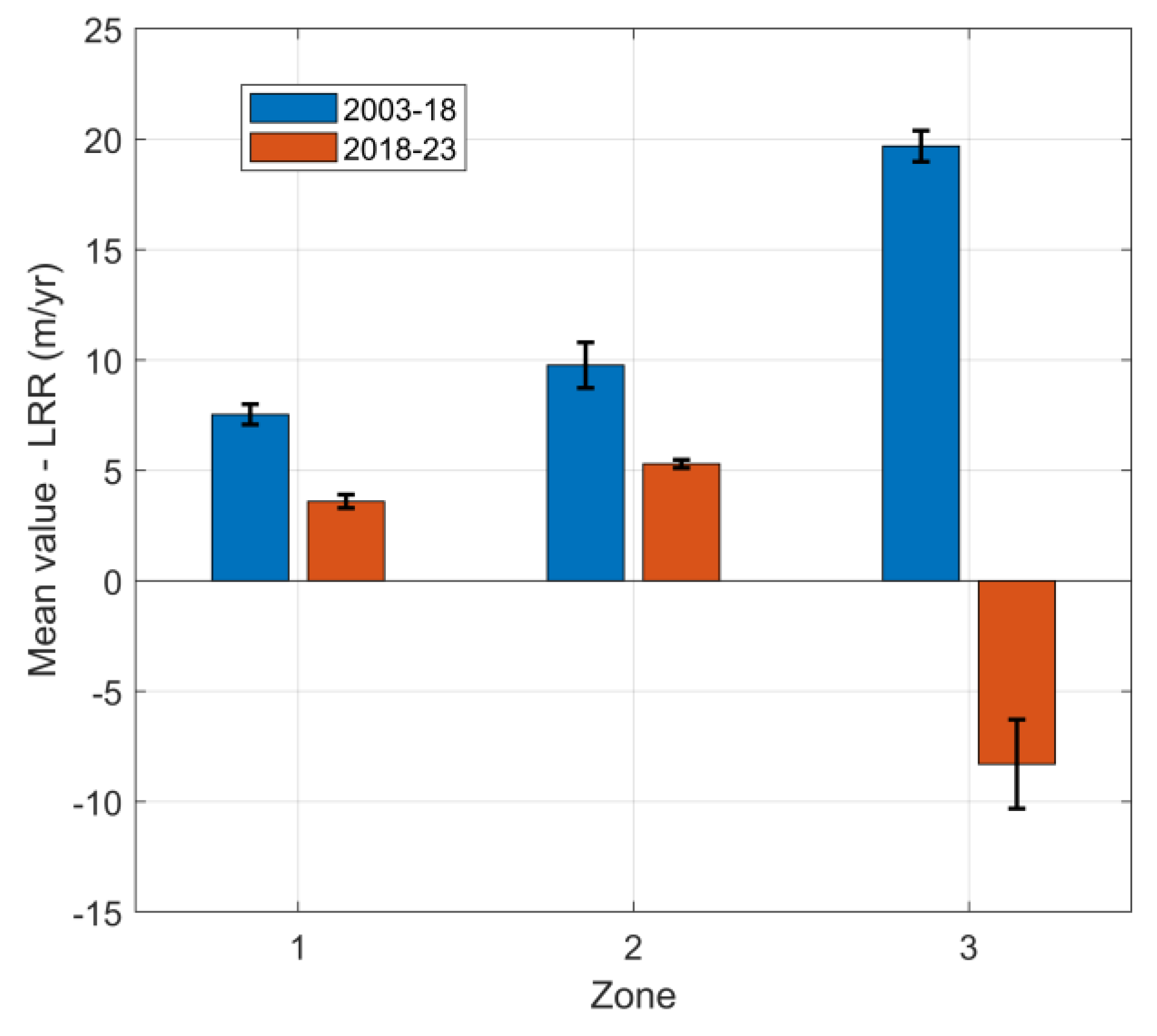
4.2. Spatial and Temporal Patterns of Shoreline Change and Statistical Significance
4.2.1. Net Shoreline Movement (NSM)
4.2.2. Linear Regression Rate (LRR)
4.3. Shoreline Future Predictions
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- The United Nation’s Ocean Conference Factsheet: People and Oceans. Available online: https://sustainabledevelopment.un.org/content/documents/Ocean_Factsheet_People.pdf (accessed on 8 January 2025).
- Restrepo, J.D. Deltas de Colombia: Morfodinámica y Vulnerabilidad Ante el Cambio Global; Universidad EAFIT: Medellín, Colombia, 2008. [Google Scholar]
- Nienhuis, J.H.; Ashton, A.D.; Edmonds, D.A.; Hoitink, A.J.F.; Kettner, A.J.; Rowland, J.C.; Törnqvist, T.E. Global-Scale Human Impact on Delta Morphology Has Led to Net Land Area Gain. Nature 2020, 577, 514–518. [Google Scholar] [CrossRef] [PubMed]
- Abd-Elhamid, H.F.; Zeleňáková, M.; Barańczuk, J.; Gergelova, M.B.; Mahdy, M. Historical Trend Analysis and Forecasting of Shoreline Change at the Nile Delta Using RS Data and GIS with the DSAS Tool. Remote Sens. 2023, 15, 1737. [Google Scholar] [CrossRef]
- Akdeniz, H.B.; İnam, Ş. Spatio-Temporal Analysis of Shoreline Changes and Future Forecasting: The Case of Küçük Menderes Delta, Türkiye. J. Coast. Conserv. 2023, 27, 34. [Google Scholar] [CrossRef]
- Dominguez, J.M.L.; Guimarães, J.K. Effects of Holocene Climate Changes and Anthropogenic River Regulation in the Development of a Wave-Dominated Delta: The São Francisco River (Eastern Brazil). Mar. Geol. 2021, 435, 106456. [Google Scholar] [CrossRef]
- Rahman, M.K.; Crawford, T.W.; Islam, M.S. Shoreline Change Analysis along Rivers and Deltas: A Systematic Review and Bibliometric Analysis of the Shoreline Study Literature from 2000 to 2021. Geosciences 2022, 12, 410. [Google Scholar] [CrossRef]
- Apostolopoulos, D.; Nikolakopoulos, K. A Review and Meta-Analysis of Remote Sensing Data, GIS Methods, Materials and Indices Used for Monitoring the Coastline Evolution over the Last Twenty Years. Eur. J. Remote Sens. 2021, 54, 240–265. [Google Scholar] [CrossRef]
- Gopinath, G.; Thodi, M.F.C.; Surendran, U.P.; Prem, P.; Parambil, J.N.; Alataway, A.; Al-Othman, A.A.; Dewidar, A.Z.; Mattar, M.A. Long-Term Shoreline and Islands Change Detection with Digital Shoreline Analysis Using RS Data and GIS. Water 2023, 15, 244. [Google Scholar] [CrossRef]
- Hossen, M.F.; Sultana, N. Shoreline Change Detection Using DSAS Technique: Case of Saint Martin Island, Bangladesh. Remote Sens. Appl. 2023, 30, 100943. [Google Scholar] [CrossRef]
- Mishra, M.; Sudarsan, D.; Kar, D.; Naik, A.K.; Das, P.P.; Santos, C.A.G.; Silva, R.M. The Development and Research Trend of Using Dsas Tool for Shoreline Change Analysis: A Scientometric Analysis. J. Urban Environ. Eng. 2020, 14, 69–77. [Google Scholar] [CrossRef]
- Ford, M. Shoreline Changes on an Urban Atoll in the Central Pacific Ocean: Majuro Atoll, Marshall Islands. J. Coast. Res. 2012, 279, 11–22. [Google Scholar] [CrossRef]
- Hugenholtz, C.; Brown, O.; Walker, J.; Barchyn, T.E.; Nesbit, P.; Kucharczyk, M.; Myshak, S. Spatial Accuracy of UAV-Derived Orthoimagery and Topography: Comparing Photogrammetric Models Processed with Direct Geo-Referencing and Ground Control Points. Geomatica 2016, 70, 21–30. [Google Scholar] [CrossRef]
- Parelius, E.J. A Review of Deep-Learning Methods for Change Detection in Multispectral Remote Sensing Images. Remote Sens. 2023, 15, 2092. [Google Scholar] [CrossRef]
- Castedo, R.; de la Vega-Panizo, R.; Fernández-Hernández, M.; Paredes, C. Measurement of Historical Cliff-Top Changes and Estimation of Future Trends Using GIS Data between Bridlington and Hornsea—Holderness Coast (UK). Geomorphology 2015, 230, 146–160. [Google Scholar] [CrossRef]
- Chowdhury, P.; Lakku, N.K.G.; Lincoln, S.; Seelam, J.K.; Behera, M.R. Climate Change and Coastal Morphodynamics: Interactions on Regional Scales. Sci. Total Environ. 2023, 899, 166432. [Google Scholar] [CrossRef]
- Himmelstoss, E.A.; Henderson, R.E.; Kratzmann, M.G.; Farris, A.S. Digital Shoreline Analysis System (DSAS); User Guide; U.S. Geological Survey: Woods Hole, MA, USA, 2021; pp. 1–104. [Google Scholar]
- Eteh, D.R.; Paaru, M.; Egobueze, F.E.; Okpobiri, O. Utilizing Machine Learning and DSAS to Analyze Historical Trends and Forecast Future Shoreline Changes Along the River Niger, Niger Delta. Water Conserv. Sci. Eng. 2024, 9, 91. [Google Scholar] [CrossRef]
- Gharnate, A.; Taouali, O.; Mhammdi, N. Shoreline Change Assessment of the Moroccan Atlantic Coastline Using DSAS Techniques. J. Coast. Res. 2024, 40, 418–435. [Google Scholar] [CrossRef]
- Azizan, N.N.; Abdul Rahim, H.; Adnan, N.A.; Razali, R.; Mohd, F.A.; Ariffin, E.H. Assessment of Shoreline Changes at Northern Selangor Coast, Malaysia Using Digital Shoreline Analysis System (DSAS). J. Adv. Geospat. Sci. Technol. 2024, 4, 79–103. [Google Scholar]
- Coca, O.; Ricaurte-Villota, C. Regional Patterns of Coastal Erosion and Sedimentation Derived from Spatial Autocorrelation Analysis: Pacific and Colombian Caribbean. Coasts 2022, 2, 125–151. [Google Scholar] [CrossRef]
- Oñate, V.; Orejarena-Rondón, A.F.; Restrepo, J.C. A Simple Approach to the Risk Assessment of Strategic Infrastructure on the Colombian Caribbean Coast. J. Coast. Res. 2024, 40, 749–767. [Google Scholar] [CrossRef]
- Rangel-Buitrago, N.G.; Anfuso, G.; Williams, A.T. Coastal Erosion along the Caribbean Coast of Colombia: Magnitudes, Causes and Management. Ocean. Coast. Manag. 2015, 114, 129–144. [Google Scholar] [CrossRef]
- Stéphan, P.; Blaise, E.; Suanez, S.; Fichaut, B.; Autret, R.; Floc’h, F.; Cuq, V.; Le Dantec, N.; Ammann, J.; David, L.; et al. Long, Medium, and Short-Term Shoreline Dynamics of the Brittany Coast (Western France). J. Coast. Res. 2019, 88, 89. [Google Scholar] [CrossRef]
- Andrade, C.A.; Barton, E.D. The Guajira Upwelling System. Cont. Shelf Res. 2005, 25, 1003–1022. [Google Scholar] [CrossRef]
- Instituto Geográfico Agustín Codazzi (IGAC). Estudio General de Suelos y Zonificación de Tierras del Departamento de la Guajira; Imprenta Nacional de Colombia: Bogotá, Colombia, 2009. [Google Scholar]
- Urrego, L.E.; Correa-Metrio, A.; González-Arango, C. Colombian Caribbean Mangrove Dynamics: Anthropogenic and Environmental Drivers. Boletín Soc. Geológica Mex. 2018, 70, 133–145. [Google Scholar] [CrossRef]
- IDEAM & Instituto de Hidrológico Meteorología y Estudios Ambientales Boletín Condiciones Hidrometeorológicas. Available online: https://www.ideam.gov.co/sala-de-prensa/boletines/Bolet%C3%ADn-de-Condiciones-Hidrometeorol%C3%B3gicas-Actuales%2C-Alertas-y-Pron%C3%B3sticos-%28BCH%29 (accessed on 14 February 2024).
- INVEMAR. Climatologie de la Vitesse et la Direction des Vents Pour la Mer Territoriale Sous Juridiction Colombienne 8° a 19° N–69° a 84° W. Atlas ERS 1 et 2 et Quickscat, Colombie. CNRS–UMRS 8591; Instituto de Investigaciones Marinas y Costeras: Santa Marta, Colombia, 2006. [Google Scholar]
- Restrepo, J.C.; Otero, L.; Casas, A.C.; Henao, A.; Gutiérrez, J. Shoreline Changes between 1954 and 2007 in the Marine Protected Area of the Rosario Island Archipelago (Caribbean of Colombia). Ocean. Coast. Manag. 2012, 69, 133–142. [Google Scholar] [CrossRef]
- Puerta Silva, C.; Carmona Castillo, S. How Do Environmental Impact Assessments Fail to Prevent Social Conflict? Government Technologies in a Dam Project in Colombia. J. Polit. Ecol. 2020, 27, 1072–1091. [Google Scholar] [CrossRef]
- Google Earth Pro Google Earth Pro. Available online: http://www.earth.google.com (accessed on 9 January 2024).
- Environmental Systems Research Institute Inc. ArcGIS Pro, Version 3.1.3; [Software]; Environmental Systems Research Institute: Redlands, CA, USA, 2023. [Google Scholar]
- Fernández-Hernández, M.; Calvo, A.; Iglesias, L.; Castedo, R.; Ortega, J.J.; Diaz-Honrubia, A.J.; Mora, P.; Costamagna, E. Anthropic Action on Historical Shoreline Changes and Future Estimates Using GIS: Guadarmar del Segura (Spain). Appl. Sci. 2023, 13, 9792. [Google Scholar] [CrossRef]
- Ghorai, D.; Mahapatra, M. Extracting Shoreline from Satellite Imagery for GIS Analysis. Remote Sens. Earth Syst. Sci. 2020, 3, 13–22. [Google Scholar] [CrossRef]
- Topah, E.B.; Salleh, S.A.; Rahim, H.A.; Adnan, N.A. Mapping of Coastline Changes in Mangrove Forest Using Digital Shoreline Analyst System (DSAS). IOP Conf. Ser. Earth Environ. Sci. 2022, 1067, 012036. [Google Scholar] [CrossRef]
- Environmental Systems Research Institute. ArcGIS Desktop: Release 10.5; Environmental Systems Research Institute: Redlands, CA, USA, 2016. [Google Scholar]
- Apostolopoulos, D.N.; Avramidis, P.; Nikolakopoulos, K.G. Estimating Quantitative Morphometric Parameters and Spatiotemporal Evolution of the Prokopos Lagoon Using Remote Sensing Techniques. J. Mar. Sci. Eng. 2022, 10, 931. [Google Scholar] [CrossRef]
- Manno, G.; Lo Re, C.; Basile, M.; Ciraolo, G. A New Shoreline Change Assessment Approach for Erosion Management Strategies. Ocean. Coast. Manag. 2022, 225, 106226. [Google Scholar] [CrossRef]
- Natesan, U.; Parthasarathy, A.; Vishnunath, R.; Kumar, G.E.J.; Ferrer, V.A. Monitoring Longterm Shoreline Changes along Tamil Nadu, India Using Geospatial Techniques. Aquat. Procedia 2015, 4, 325–332. [Google Scholar] [CrossRef]
- Sabour, S.; Brown, S.; Nicholls, R.J.; Haigh, I.D.; Luijendijk, A.P. Multi-Decadal Shoreline Change in Coastal Natural World Heritage Sites—A Global Assessment. Environ. Res. Lett. 2020, 15, 104047. [Google Scholar] [CrossRef]
- Miller, J.N.; Miller, J.C.; Miller, R.D. Statistics and Chemometrics for Analytical Chemistry, 7th ed.; Pearson Education: Essex, UK, 2018. [Google Scholar]
- The MathWorks Inc. MATLAB Version: 23.2.0.2515942 (R2023b) Update 7; The MathWorks Inc.: Natick, MA, USA, 2023. [Google Scholar]
- Tukey, J.W. The Collected Works of John W. Tukey; Taylor & Francis: Abingdon, UK, 1984. [Google Scholar]
- Şenol, H.İ.; Kaya, Y.; Yiğit, A.Y.; Yakar, M. Extraction and Geospatial Analysis of the Hersek Lagoon Shoreline with Sentinel-2 Satellite Data. Surv. Rev. 2024, 56, 367–382. [Google Scholar] [CrossRef]
- Escobar Villanueva, J.R.; Pérez-Montiel, J.I.; Nardini, A.G.C. DEM Generation Incorporating River Channels in Data-Scarce Contexts: The “Fluvial Domain Method”. Hydrology 2025, 12, 33. [Google Scholar] [CrossRef]
- Kazi, H.; Karabulut, M. Monitoring the Shoreline Changes of the Göksu Delta (Türkiye) Using Geographical Information Technologıes and Predictions for the near Future. Int. J. Geogr. Geogr. Educ. 2023, 329–352. [Google Scholar] [CrossRef]
- Urrego, L.E.; Correa-Metrio, A.; González, C.; Castaño, A.R.; Yokoyama, Y. Contrasting Responses of Two Caribbean Mangroves to Sea-Level Rise in the Guajira Peninsula (Colombian Caribbean). Palaeogeogr. Palaeoclim. Palaeoecol. 2013, 370, 92–102. [Google Scholar] [CrossRef]
- Beleño, S.; Molina-Bolívar, E.L.; Y Jiménez, G.; Luz, E.; Molina-Bolívar, G.; Jiménez-Pitre, I. Riesgos Relacionados Con el Cambio Climático de la Flora y Fauna Asociada a Bosques de Manglar en el Caribe Colombiano. Intropica 2022, 17, 290–300. [Google Scholar]
- Molina-Bolívar, G.E.; Nava Ferrer, M.L.; Jiménez Pitre, I.A. Water Physicochemical Variables in the Rancheria River Delta, La Guajira, Colombia. Cienc. Desarro. 2020, 11, 21–32. [Google Scholar] [CrossRef]
- Lage, A.F.; Robertson, K.G. Morfodinámica del Litoral Caribe y Amenazas Naturales. Cuad. Geogr. Rev. Colomb. Geogr. 2001, 10, 1–35. [Google Scholar]
- Rangel-Buitrago, N.; Williams, A.T.; Anfuso, G. Hard Protection Structures as a Principal Coastal Erosion Management Strategy along the Caribbean Coast of Colombia. A Chronicle of Pitfalls. Ocean. Coast. Manag. 2018, 156, 58–75. [Google Scholar] [CrossRef]
- Esteban-Cantillo, O.J.; Clerici, N.; Avila-Diaz, A.; Quesada, B. Historical and Future Extreme Climate Events in Highly Vulnerable Small Caribbean Islands. Clim. Dyn. 2024, 62, 7233–7250. [Google Scholar] [CrossRef]
- Bernet, M.; Torres Acosta, L. Rising Sea Level and Increasing Tropical Cyclone Frequency Are Threatening the Population of San Andrés Island, Colombia, Western Caribbean. BSGF-Earth Sci. Bull. 2022, 193, 4. [Google Scholar] [CrossRef]




| Category | Shoreline Change Rate Intervals | Shoreline Rate Classification |
|---|---|---|
| 1 | LRR < −2 | Very high erosion |
| 2 | −2 < LRR < −1 | High erosion |
| 3 | −1 < LRR < 0 | Moderate erosion |
| 4 | LRR = 0 | Stable |
| 5 | 0 < LRR < 1 | Moderate accretion |
| 6 | 1 < LRR < 2 | High accretion |
| 7 | LRR > 2 | Very high accretion |
| Statistics | 2003–2018 | 2018–2023 | 2003–2023 |
|---|---|---|---|
| Total number of transect | 41 | 41 | 41 |
| NSM (m) | |||
| Average | 165.71 | 4.50 | 170.21 |
| Minimum | 41.66 | −95.91 | 64.92 |
| Maximum | 322.33 | 32.26 | 260.08 |
| Standard Deviation | 80.13 | 35.87 | 53.30 |
| EPR (m/yr) | |||
| Average | 11.05 | 0.84 | 8.37 |
| Minimum | 2.78 | −17.98 | 3.19 |
| Maximum | 21.49 | 6.05 | 12.79 |
| Standard Deviation | 5.34 | 6.72 | 2.62 |
| LRR (m/yr) | |||
| Average | 11.79 | 0.65 | 9.33 |
| Minimum | 2.51 | −18.31 | 3.58 |
| Maximum | 22.96 | 6.29 | 14.49 |
| Standard Deviation | 5.86 | 6.97 | 2.86 |
| LR2 | |||
| Average | 0.94 | 0.76 | 0.91 |
| Minimum | 0.65 | 0.18 | 0.57 |
| Maximum | 0.99 | 1 | 0.98 |
| Standard Deviation | 0.06 | 0.21 | 0.09 |
| Erosion Transects, Number | 0 (0%) | 10 (24%) | 0 (0%) |
| Accretion Transects, Number | 41 (100%) | 31 (76%) | 41 (100%) |
| Overall trend of the period | Accretion | Accretion | Accretion |
| Source | Sum of Squares | Degrees of Freedom | Mean Sum of Squares | F | p-Value |
|---|---|---|---|---|---|
| Period | 5.89 × 105 | 1 | 5.89 × 105 | 686.97 | 8.27 × 10−40 |
| Zone | 3.79 × 104 | 2 | 1.89 × 104 | 22.11 | 2.71 × 10−8 |
| Period:Zone | 2.05 × 105 | 2 | 1.03 × 105 | 119.65 | 3.31 × 10−24 |
| Error | 6.51 × 104 | 76 | 8.57 × 102 | ||
| Total | 8.41 × 105 | 81 |
| Source | Sum of Squares | Degrees of Freedom | Mean Sum of Squares | F | p-Value |
|---|---|---|---|---|---|
| Period | 2.97 × 103 | 1 | 2.97 × 103 | 267.84 | 0 |
| Zone | 6.52 × 101 | 2 | 3.26 × 101 | 2.94 | 0.0591 |
| Period:Zone | 2.41 × 103 | 2 | 1.20 × 103 | 108.45 | 0 |
| Error | 8.43 × 102 | 76 | 1.11 × 101 | ||
| Total | 5.86 × 103 | 81 |
| Source of Variation | Lower Limit | Upper Limit | p-Value |
|---|---|---|---|
| Zone 1 (2003–2018) vs. Zone 1 (2018–2023) | 0.49 | 7.37 | 0.0157 |
| Zone 1 (2003–2018) vs. Zone 2 (2003–2018) | −1.40 | 5.87 | 0.4746 |
| Zone 1 (2003–2018) vs. Zone 2 (2018–2023) | −5.87 | 1.40 | 0.4743 |
| Zone 1 (2003–2018) vs. Zone 3 (2003–2018) | 8.43 | 15.87 | 1.62 × 10−13 |
| Zone 1 (2003–2018) vs. Zone 3 (2018–2023) | −19.55 | −12.11 | 6.06 × 10−19 |
| Zone 1 (2018–2023) vs. Zone 2 (2003–2018) | 2.53 | 9.81 | 6.01 × 10−5 |
| Zone 1 (2018–2023) vs. Zone 2 (2018–2023) | −1.93 | 5.33 | 0.7455 |
| Zone 1 (2018–2023) vs. Zone 3 (2003–2018) | 12.37 | 19.81 | 2.58 × 10−19 |
| Zone 1 (2018–2023) vs. Zone 3 (2018–2023) | −15.61 | −8.17 | 4.00 × 10−13 |
| Zone 2 (2003–2018) vs. Zone 2 (2018–2023) | 0.65 | 8.29 | 0.0125 |
| Zone 2 (2003–2018) vs. Zone 3 (2003–2018) | 6.02 | 13.82 | 1.90 × 10−9 |
| Zone 2 (2003–2018) vs. Zone 3 (2018–2023) | −21.96 | −14.16 | 6.37 × 10−21 |
| Zone 2 (2018–2023) vs. Zone 3 (2003–2018) | 10.49 | 18.29 | 7.13 × 10−16 |
| Zone 2 (2018–2023) vs. Zone 3 (2018–2023) | −17.50 | −9.69 | 9.55 × 10−15 |
| Zone 3 (2003–2018) vs. Zone 3 (2018–2023) | 24.01 | 31.96 | 1.60 × 10−34 |
| Transect | Future Change (in Meters) for the 2003–2023 LRR Data | Future Change (in Meters) for the 2018–2023 LRR Data |
|---|---|---|
| 30 | 129.2 | 43.9 |
| 31 | 133.3 | 13.8 |
| 32 | 128.1 | −15.6 |
| 33 | 122.5 | −44.1 |
| 34 | 117.7 | −69.2 |
| 35 | 114.4 | −98.8 |
| 36 | 116.9 | −136.2 |
| 37 | 129 | −144.4 |
| 38 | 144.9 | −116.5 |
| 39 | 142.1 | −107 |
| 40 | 127.4 | −139 |
| 41 | 113.1 | −183.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández-Hernández, M.; Iglesias, L.; Villanueva, J.R.E.; Castedo, R. Unraveling the Spatio-Temporal Evolution of the Ranchería Delta (Riohacha, Colombia): A Multi-Period Analysis Using GIS. Geosciences 2025, 15, 95. https://doi.org/10.3390/geosciences15030095
Fernández-Hernández M, Iglesias L, Villanueva JRE, Castedo R. Unraveling the Spatio-Temporal Evolution of the Ranchería Delta (Riohacha, Colombia): A Multi-Period Analysis Using GIS. Geosciences. 2025; 15(3):95. https://doi.org/10.3390/geosciences15030095
Chicago/Turabian StyleFernández-Hernández, Marta, Luis Iglesias, Jairo R. Escobar Villanueva, and Ricardo Castedo. 2025. "Unraveling the Spatio-Temporal Evolution of the Ranchería Delta (Riohacha, Colombia): A Multi-Period Analysis Using GIS" Geosciences 15, no. 3: 95. https://doi.org/10.3390/geosciences15030095
APA StyleFernández-Hernández, M., Iglesias, L., Villanueva, J. R. E., & Castedo, R. (2025). Unraveling the Spatio-Temporal Evolution of the Ranchería Delta (Riohacha, Colombia): A Multi-Period Analysis Using GIS. Geosciences, 15(3), 95. https://doi.org/10.3390/geosciences15030095







