Accuracy Assessment of Deep Learning Based Classification of LiDAR and UAV Points Clouds for DTM Creation and Flood Risk Mapping
Abstract
:1. Introduction
1.1. Data Sources to Obtain Digital Elevation Models (DEMs) for Flood Modelling
1.2. DEM Generation from Point Clouds
2. Study Area and Data
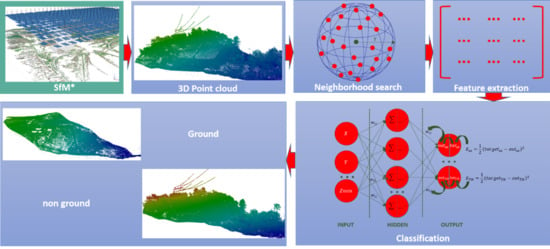
3. Methods
- (1)
- LiDAR point cloud: calculation of the contextual information for each point by considering the spatial arrangement of all points inside the local neighborhood,
- (2)
- LiDAR point cloud: feature extraction,
- (3)
- LiDAR point cloud: calibration and supervised classification (ground and non-ground points) using the deep back propagation neural network (BPNN)
- (4)
- Accuracy assessment of the LiDAR point cloud classification
- (5)
- Application to the UAV data
- Create the UAV point clouds (from overlapping images and using the SfM algorithm)
- UAV point cloud: feature extraction (the same as (2))
- UAV point cloud: calibration and supervised classification (ground and non-ground points) using the deep back propagation neural network (BPNN) (the same as (3))
- Accuracy assessment of the UAV point cloud classification (the same as (4))
- (6)
- Accuracy assessment of the LiDAR and UAV derived DEMs
- (7)
- Flood risk assessment using the created DEM.
3.1. Point Cloud Generation using SfM Algorithm (UAV Data)
3.2. Neighborhood Search and Feature Extraction (UAV and LIDAR Point Clouds)
3.3. Classification of the UAV and LIDAR Point Clouds Using a Back Propagation Neural Network (BPNN)
3.4. Accuracy Assessment
3.4.1. Point Cloud Classification
3.4.2. Point Cloud and DEM Accuracy
3.5. Flood Risk Assessment
4. Results
4.1. Point Cloud Classification
4.2. Spatial Variability of UAV and LiDAR DEM Accuracy
4.3. Accuracy of UAV and LiDAR Point Clouds (C2C Method)
4.4. Flood Risk Assessment
5. Discussion
5.1. Convenience of using Imbalanced or Balanced Datasets for Point Cloud Classification
5.2. Effect of the Land Cover Class on the Algorithm Performance and Elevation Accuracy
5.3. Suitability of the Proposed Method to Produce DEM from UAV and LiDAR Data
5.4. Usability of the LiDAR and UAV SfM DEM in Flood Risk Mapping
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- CRED; UNISDR. The Human Cost of Weather Related Disasters 1995–2015. Available online: https://reliefweb.int/sites/reliefweb.int/files/resources/COP21_WeatherDisastersReport_2015_FINAL.pdf (accessed on 17 May 2019).
- Directive 2007/60/EC of the European Parliament and of the Council on the Assessment and Management of Flood Risks. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32007L0060&from=EN (accessed on 25 May 2018).
- Ogania, J.L.; Puno, G.R.; Alivio, M.B.T.; Taylaran, J.M.G. Effect of digital elevation model’s resolution in producing flood hazard maps. Glob. J. Environ. Sci. Manag. 2019, 5, 95–106. [Google Scholar]
- Saksena, S.; Merwade, V. Incorporating the effect of DEM resolution and accuracy for improved flood inundation mapping. J. Hydrol. 2015, 530, 180–194. [Google Scholar] [CrossRef] [Green Version]
- EXCIMAP (European Exchange Circle on Flood Mapping). Handbook on Good Practice for Flood Mapping in Europe. 29–30 November 2007. Available online: http://ec.europa.eu/environment/water/flood_risk/flood_atlas/pdf/handbook_goodpractice.pdf (accessed on 25 May 2019).
- Rulebook for Determining Methodology for Flood Vulnerability and Flood Risk Mapping. Available online: http://www.rdvode.gov.rs/doc/dokumenta/podzak/Pravilnik%20o%20metodologiji%20za%20karte%20ugrozenosti%20i%20karte%20rizika%20od%20polava.pdf (accessed on 1 July 2019).
- Jovanović, M.; Prodanović, D.; Plavšić, J.; Rosić, N. Problemi pri izradi karata ugroženosti od poplava. Vodoprivreda 2014, 46, 3–13. [Google Scholar]
- Jakovljević, G.; Govedarica, M. Water Body Extraction and Flood Risk Assessment Using LiDAR and Open Data. In Climate Change Adaptation in Eastern Europe: Managing Risks and Building Resilience to Climate Change; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Noh, S.J.; Lee, J.; Lee, S.; Kawaike, K.; Seo, D. Hyper-resolution 1D-2D urban flood modelling using LiDAR data and hybrid parallelization. Environ. Model. Softw. 2018, 103, 131–145. [Google Scholar] [CrossRef]
- Shen, D.; Qian, T.; Chen, W.; Chi, Y.; Wang, J. A Quantitative Flood-Related Building Damage Evaluation Method Using Airborne LiDAR Data and 2-D Hydraulic Model. Water 2019, 11, 987. [Google Scholar] [CrossRef]
- Smith, M.W.; Carrivick, J.L.; Quincey, D.J. Structure from motion photogrammetry in physical geography, Prog. Phys. Geogr. 2015, 1–29. [Google Scholar] [CrossRef]
- Eltner, A.; Kaiser, A.; Castillo, C.; Rock, G.; Neugirg, F.; Abellán, A. Image-based surface reconstruction in geomorphometry-merits, limits and developments. Earth Surf. Dyn. 2016, 4, 359–389. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. Structure-from-motion’ photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Gebrehiwot, A.; Hashemi-Beni, L.; Thompson, G.; Kordjamshidi, P.; Langan, T. Deep Convolutional Neural Network for Flood Extent Mapping Using Unmanned Aerial Vehicles Data. Sensor 2019, 19, 1486. [Google Scholar] [CrossRef]
- Hashemi-Beni, L.; Jones, J.; Thompson, G.; Johnson, C.; Gebrehiwot, A. Challenges and Opportunities for UAV-Based Digital Elevation Model Generation for Flood-Risk Management: A Case of Princeville, North Caroline. Sensor 2018, 18, 3843. [Google Scholar] [CrossRef] [PubMed]
- Schumann, G.J.P.; Muhlhausen, J.; Andreadis, K. Rapid Mapping of Small-Scale River-Floodplain Envronments Using UAV SfM Supports Classical Theoru. Remote Sens. 2019, 11, 982. [Google Scholar] [CrossRef]
- Govedarica, M.; Jakovljević, G.; Álvarez-Taboada, F. Flood risk assessment based on LiDAR and UAV points clouds and DEM. In Remote Sensing for Agriculture, Ecosystems, and Hydrology XX; SPIE: Berlin, Germany, 2018. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Z.; Peterson, J.; Chandra, S. The Effect of LiDAR Data Density on DEM Accuracy. 2007. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.458.4833&rep=rep1&type=pdf (accessed on 30 June 2019).
- Asal, F.F. Evaluating the effects of reduction in LiDAR data on the visual and statistical characteristics of the created Digital Elevation Models. In Proceedings of the 2016 XXIII ISPRS Congress, Prague, Czech Republic, 12–19 July 2016. [Google Scholar]
- Liu, X.; Zhang, Z.; Peterson, J.; Chandra, S. The effect of LiDAR data density on DEM accuracy. In Proceedings of the International Congress on Modelling and Simulation (MODSIM07), Christchurch, New Zealand, 2007; pp. 1363–1369. [Google Scholar]
- Thomas, I.A.; Jordan, P.; Shine, O.; Fenton, O.; Mellander, P.E.; Dunlop, P.; Murphy, P.N.C. Defining optimal DEM resolutions and point densities for modelling hydrologically sensitive areas in agricultural catchments dominated by microtopography. Int. J. Appl. Earth Obs. Geoinf. 2017, 54, 38–52. [Google Scholar] [CrossRef] [Green Version]
- Rashidi, P.; Rastiveis, H. Extraction of ground points from LiDAR data based on slope and progressive window thresholding (SPWT). Earth Obs. Geomat. Eng. EOGE 2018, 1, 36–44. [Google Scholar] [CrossRef]
- Axelsson, P. DEM generation from laser scanner data using adaptive TIN models. Int. Arch. Photogramm. Remote Sens. 2000, 33, 110–117. [Google Scholar]
- Hu, X.; Yuan, Y. Deep-Learning-Based Classification for DTM Extraction from ALS Point Cloud. Remote Sens. 2016, 8, 730. [Google Scholar] [CrossRef]
- Rizaldy, A.; Persello, C.; Gevaert, C.; Elberink, S.O.; Vosselman, G. Ground and Multi-Class Classification of Airborne Laser Scanner Point Clouds Using Fully Convolutional Networks. Remote Sens. 2018, 10, 1723. [Google Scholar] [CrossRef]
- Sofman, B.; Bagnell, J.A.; Stentz, A.; Vandapel, N. Terrain Classification from Aerial Data to Support Ground Vehicle Navigation. 2006. Available online: https://pdfs.semanticscholar.org/e94d/f03ec54e1c5b42c4ac50d4c8667d2e8cad6a.pdf?_ga=2.53795883.2092844519.1558797131-1702618147.1556638397 (accessed on 2 May 2019).
- Qi, C.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Pont Sets for 3D Classification and Segmentation. arXiv 2017, arXiv:1612.00593v2. [Google Scholar]
- Hackel, T.; Wegner, J.D.; Schindler, K. Fast semantic segmentation of the 3D point clouds with strongly varying density. In Proceedings of the 2016 XXIII ISPRS Congress, Prague, Czech Republic, 12–19 July 2016. [Google Scholar]
- Becker, C.; Hano, N.; Rosonskaya, E.; d’Angelo, E.; Strecha, C. Classification of Aerial photogrammetric 3D point clouds. arXiv 2017, arXiv:1705.08374v1. [Google Scholar]
- Turner, D.; Lucieer, A.; Watson, C. An Automated Technique for Generating Georectified Mosaics from Ultra-High Resolution Unmanned Aerial Vehicle (UAV) Imagery, Based on Structure from Motion (SfM) Point Clouds. Remote Sens. 2012, 4, 1392–1410. [Google Scholar] [CrossRef] [Green Version]
- Filin, S.; Pfeofer, N. Neighborhood systems for airborne laser data. Photogramm. Eng. Remote Sens. 2005, 71, 743–755. [Google Scholar] [CrossRef]
- Weinmann, M.; Mallet, C.; Jutzi, N. Involving different neighborhood types for the analysis of low-level geometric 2D and 3D features and their relevance for point cloud classification. In Proceedings of the 37. Wissenschaftlich-Technische Jahrestagung der DGPF, Würzburg, Germany, 08–10 March 2017; Kersten, T.P., Ed.; German Society for Photogrammetry, Remote Sensing and Geoinformatics: Hamburg, Germany, 2017. [Google Scholar]
- Friedman, J.H.; Bentley, J.L.; Finkel, R.A. An algorithm for finding best matches in logarithmic expected time. ACM Trans. Math. Softw. 1977, 3, 209–226. [Google Scholar] [CrossRef]
- Maneewongvatana, M.; Mount, D. Analysis of Approximate Nearest Neighbor Searching with Clusterd Point Sets. arXiv 1999, arXiv:cs/9901013v1. [Google Scholar]
- Alsmadi, M.; Omar, K.; Noah, S. Back Propagation Algorithm: The Best Algorithm among the Multi-layer Perceptron Algorithm. Int. J. Comput. Sci. Netw. Secur. 2009, 9, 378–383. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2015, arXiv:1412.6980v9. [Google Scholar]
- Kubat, M.; Matwin, S. Addressing the curse of imbalanced training sets: One-sided selection. In Proceedings of the 14th International Conference on Machine Learning (ICML), Nashville, TN, USA, 8–12 July 1997; pp. 179–186. [Google Scholar]
- sklearn. preprocessing. StandardScaler. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html (accessed on 1 June 2019).
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Bekkar, M.; Kheliouane Djemaa, H.; Akrouf Alitouche, T. Evaluation Measure for Models Assessment over Imbalanced Data Sets. J. Inf. Eng. Appl. 2013, 3, 27–38. [Google Scholar]
- CloudCompare. Available online: https://www.cloudcompare.org/ (accessed on 5 June 2019).
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanners. Application to the Rangitikei canyon. J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]
- Chen, C.; Liaw, A.; Breiman, L. Using Random Forest to Learn Imbalanced Data. Available online: https://statistics.berkeley.edu/tech-reports/666 (accessed on 21 July 2019).
- Dal Pozzolo, A.; Caelen, O.; Bontempi, G. When is undersampling effective in unbalanced classification tasks. In Machine Learning and Knowledge Discovery in Databases; Springer: Berlin, Germany, 2015. [Google Scholar]
- Dal Pozzolo, A.; Caelen, O.; Johnson, R.A.; Bontempi, G. Calibrating probability with under sampling for unbalanced classification. In Proceedings of the IEEE Symposium Series on Computational Intelligence, Cape Town, South Africa, 7–10 December 2015. [Google Scholar]
- Sun, Y.; Wong, A.K.; Kamel, M.S. Classification of imbalanced data: A review. Int. J. Pattern Recognit. Artif. Intell. 2009, 23, 687–719. [Google Scholar] [CrossRef]
- Japkowicz, N.; Stephen, S. The class imbalance problem: A systematic study. Intell. Data Anal. J. 2002, 6, 429–450. [Google Scholar] [CrossRef]
- Salach, A.; Bakula, K.; Pilarska, M.; Ostrowski, W.; Gorski, K.; Kurczynski, Z. Accuracy Assessment of Point Clouds from LiDAR and Dense Image Matching Acquired Using the UAV Platform for DTM Creation. ISPRS Int. J. Geo-Inf. 2018, 7, 342. [Google Scholar] [CrossRef]
- Kavzgoul, T. Increasing the accuracy of neural network classification using refined training data. Environ. Model. Softw. 2009, 24, 850–858. [Google Scholar] [CrossRef]






| Area | Type | Number of Points | Ground [%] | Non Ground [%] |
|---|---|---|---|---|
| A | Validation | 2,804,726 | 23.2 | 76.7 |
| B | Validation | 4,419,520 | 17.8 | 82.2 |
| C | Algorithm calibration | 3,801,412 | 8.1 | 91.9 |
| D | Algorithm calibration | 1,811,545 | 23.6 | 76.4 |
| Type | Title 2 |
|---|---|
| LiDAR | LMS-Q680i-Full Waveform Analysis with settable frequency up to 400,000 Hz, with field of view of 60°, and a divergence of 0.5 mrad beam; Class 3R |
| Navigation system | IGI CCNS5 + Aerocontrol (positioning and navigation unit data storage); Inertial Measurement Unit (IMU) IIf (inertial unit—400 HZ); GPS a 2 HZ (Novatel antenna 12-channel L1/L2). |
| Camera | n.1 Metric Camera Digicam-H39 (39 Mpixels) |
| Thermal Camera | Variocam thermal sensor system with a detector of 1024 × 768 pixels and the spectral range from 7.5 to 14 μm. |
| Image Resolution [MP] | Number of GCP | Attitude of Image Capture [m] | Forward Overlap [%] | Side Overlap [%] | Ground Resolution [cm pix−1] |
|---|---|---|---|---|---|
| 42 | 13 | 150 | 70 | 70 | 2.7 |
| Precision | Recall | F1-score | OA [%] | |||
|---|---|---|---|---|---|---|
| Test | BU | Non-ground | 0.90 | 0.89 | 0.89 | 89.53 |
| Ground | 0.89 | 0.90 | 0.90 | |||
| BO | Non-ground | 0.92 | 0.86 | 0.89 | 89.77 | |
| Ground | 0.88 | 0.93 | 0.90 | |||
| BOU | Non-ground | 0.90 | 0.92 | 0.91 | 89.68 | |
| Ground | 0.88 | 0.86 | 0.87 | |||
| Imbalanced | Non-ground | 0.92 | 0.98 | 0.96 | 93.37 | |
| Ground | 0.89 | 0.71 | 0.79 | |||
| Validation | BU | Non-ground | 0.99 | 0.56 | 0.72 | 64.80 |
| Ground | 0.37 | 0.97 | 0.52 | |||
| BO | Non-ground | 0.95 | 0.51 | 0.66 | 60.81 | |
| Ground | 0.36 | 0.93 | 0.52 | |||
| BOU | Non-ground | 0.93 | 0.58 | 0.71 | 64.52 | |
| Ground | 0.38 | 0.85 | 0.53 | |||
| Imbalanced | Non-ground | 0.93 | 0.97 | 0.95 | 92.20 | |
| Ground | 0.86 | 0.72 | 0.78 |
| LiDAR | UAV | |||
|---|---|---|---|---|
| RMSE [m] | MAE [m] | RMSE [m] | MAE [m] | |
| All classes | 0.25 | 0.05 | 0.59 | −0.28 |
| Water | 0.37 | 0.09 | 1.70 | −1.11 |
| High vegetation | 0.20 | 0.03 | 1.00 | −0.39 |
| Medium vegetation | 0.19 | 0.04 | 0.51 | −0.26 |
| Low vegetation | 0.19 | 0.04 | 0.23 | −0.21 |
| Bare land | 0.20 | 0.03 | 0.25 | −0.18 |
| Built up areas | 0.27 | 0.06 | 0.28 | −0.27 |
| Absolute Distance along Z axis [m] | Number of Points Lidar | Percent Lidar [%] | Number of Points UAV | Percent UAV [%] |
|---|---|---|---|---|
| –5.12 to –4 | 0 | 0 | 2129 | 0.0282 |
| –4 to –3 | 0 | 0 | 1610 | 0.0213 |
| –3 to –2 | 0 | 0 | 11,462 | 0.1517 |
| –2 to –1 | 8 | 0.0005 | 19,712 | 0.2608 |
| –1 to –0.5 | 52 | 0.0036 | 275,648 | 3.6471 |
| –0.25 to –0.5 | 292 | 0.0203 | 680,829 | 9.0079 |
| –0.1 to –0.25 | 600 | 0.0418 | 789,888 | 10.4509 |
| –0.1 to –0.05 | 1330 | 0.0925 | 440,820 | 5.8324 |
| –0.05 to –0.01 | 14,105 | 0.9816 | 242,428 | 3.2075 |
| –0.01 to 0 | 1,303,374 | 90.7021 | 0 | 0 |
| 0 to 0.01 | 67,085 | 4.6685 | 360,129 | 4.7648 |
| 0.01 to 0.05 | 43,076 | 2.9976 | 274,241 | 3.6284 |
| 0.05 to 0.1 | 5367 | 0.3735 | 400,257 | 5.2957 |
| 0.1 to 0.25 | 1056 | 0.0734 | 2,119,942 | 28.0486 |
| 0.25 to 0.5 | 279 | 0.0194 | 1,283,580 | 16.9828 |
| 0.5 to 1 | 176 | 0.0122 | 580,283 | 6.9696 |
| 1 to 2 | 47 | 0.0032 | 128,656 | 1.5211 |
| 2 to 3 | 109 | 0.0076 | 12,980 | 0.1585 |
| 3 to 4 | 26 | 0.0018 | 1778 | 0.0226 |
| 4 to 4.18 | 1 | 0.0002 | 0 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jakovljevic, G.; Govedarica, M.; Alvarez-Taboada, F.; Pajic, V. Accuracy Assessment of Deep Learning Based Classification of LiDAR and UAV Points Clouds for DTM Creation and Flood Risk Mapping. Geosciences 2019, 9, 323. https://doi.org/10.3390/geosciences9070323
Jakovljevic G, Govedarica M, Alvarez-Taboada F, Pajic V. Accuracy Assessment of Deep Learning Based Classification of LiDAR and UAV Points Clouds for DTM Creation and Flood Risk Mapping. Geosciences. 2019; 9(7):323. https://doi.org/10.3390/geosciences9070323
Chicago/Turabian StyleJakovljevic, Gordana, Miro Govedarica, Flor Alvarez-Taboada, and Vladimir Pajic. 2019. "Accuracy Assessment of Deep Learning Based Classification of LiDAR and UAV Points Clouds for DTM Creation and Flood Risk Mapping" Geosciences 9, no. 7: 323. https://doi.org/10.3390/geosciences9070323
APA StyleJakovljevic, G., Govedarica, M., Alvarez-Taboada, F., & Pajic, V. (2019). Accuracy Assessment of Deep Learning Based Classification of LiDAR and UAV Points Clouds for DTM Creation and Flood Risk Mapping. Geosciences, 9(7), 323. https://doi.org/10.3390/geosciences9070323