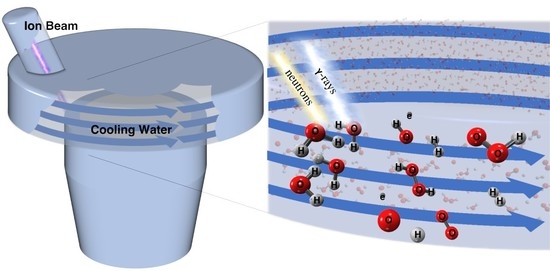
Preliminary Assessment of Radiolysis for the Cooling Water System in the Rotating Target of SORGENTINA-RF
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. A Simplified Model Calculation
3.2. Refined Model Numerical Simulations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DR | Dose rate |
| MCNP | Monte Carlo N-Particle Transport Code |
| FENDL | Fusion Evaluated Nuclear Data Library |
| IBED PHTS | Integrated blanket edge localized mode coils and divertor primary heat transfer system |
| THC | Threshold hydrogen concentration |
References
- Pietropaolo, A.; Contessa, G.M.; Farini, M.; Fonnesu, N.; Marinari, R.; Moro, F.; Rizzo, A.; Scaglione, S.; Terranova, N.; Utili, M.; et al. SORGENTINA-RF project: Fusion neutrons for 99Mo medical radioisotope. Eur. Phys. J. Plus 2021, 136, 1140. [Google Scholar]
- Lister, D.; Uchida, S. Determining water chemistry conditions in nuclear reactor coolants. J. Nucl. Sci. Technol. 2015, 52, 451–466. [Google Scholar]
- Lorenzetto, P.; Bjergbakke, E.; Hickel, B. Water radiolysis under NET conditions. Fusion Eng. Des. 1991, 17, 165–270. [Google Scholar] [CrossRef]
- Karditsas, P.J. Water radiolysis in fusion neutron environments. Fusion Eng. Des. 2011, 86, 2701–2704. [Google Scholar] [CrossRef]
- Giambartolomei, G.; Pesetti, A.; Raucci, M.; Aquaro, D. Effect of non-condensable gas in steam condensation at sub-atmospheric pressure condition. J. Phys. Conf. Ser. 2021, 2177, 012019. [Google Scholar] [CrossRef]
- Petrov, A.Y.; Macdonald, D.; Engelhardt, G. Assessment of Radiolysis in Tokamak Cooling Water System of ITER Fusion Reactor. In Proceedings of the 21st International Conference on Water Chemistry in Nuclear Reactor Systems, San Francisco, CA, USA, 9–14 September 2018. [Google Scholar]
- Swiatla-Wojcik, D.; Buxton, G.V. Modeling of radiation spur processes in water at temperatures up to 300 °C. J. Phys. Chem. 1995, 99, 011464–11471. [Google Scholar] [CrossRef]
- Fan, Z.; Cao, X.; Tong, L.; Muroya, Y.; Whitaker, G.; Momeni, M.; Lin, M. An improved method for modelling coolant radiolysis in ITER. Fusion Eng. Des. 2018, 127, 91–98. [Google Scholar]
- Doyle, P.; Bartels, D. Python script for homogeneous aqueous chemical reaction analysis and associated data related to radiolysis simulations. Data Brief 2020, 31, 105734. [Google Scholar] [CrossRef] [PubMed]
- Ershov, B.G.; Gordeev, A.V. A model for radiolysis of water and aqueous solutions of H2, H2O2 and O2. Radiat. Phys. Chem. 2008, 77, 928–935. [Google Scholar] [CrossRef]
- Mancini, A. (ENEA—Department of Fusion and Technologies for Nuclear Safety and Security, Rome, Italy). Private communication, 2022.
- Mckinney, G. MCNP—A General Monte Carlo Code n-Particle Transport Code, Version 5; X-5 Monte Carlo Team; LA-UR-03-1987; Los Alamos National Laboratory: Los Alamos, NM, USA, 2005. [Google Scholar]
- FENDL-3.1d: Fusion Evaluated Nuclear Data Library Ver.3.1d. Available online: https://www-nds.iaea.org/fendl/ (accessed on 15 February 2022).
- White, W.C. Photoatomic Data Library MCPLIB04: A New Photoatomic Library Based on Data from ENDF/B-VI Release 8; LAUR-03-1019; Los Alamos National Laboratory: Los Alamos, NM, USA, 2003. [Google Scholar]
- Elliot, A.J.; Bartels, D.M. The Reaction Set, Rate Constants and g-Values for the Simulation of the Radiolysis of Light Water over the Range 20 Deg to 350 Deg C Based on Information Available in 2008; AECL–153-127160-450-001; Atomic Energy of Canada Limited: Mississauga, ON, Canada, 2009. [Google Scholar]
- Doyle, P.; Sun, K.; Snead, L.; Katoh, Y.; Bartels, D.; Zinkle, S.; Raiman, S. The effects of neutron and ionizing irradiation on the aqueous corrosion of SiC. J. Nucl. Mater. 2020, 536, 152190. [Google Scholar] [CrossRef]
- Yakabuskie, P.A. The Influence of Long-Term Gamma-Radiation and Initially Dissolved Chemicals on Aqueous Kinetics and Interfacial Processes. Ph.D. Thesis, The University of Western Ontario, London, ON, Canada, 2015. [Google Scholar]
- Milinchuk, V.K.; Klinshpont, E.R.; Belozerov, V.I.; Khavroshina, I.S.; Sadikov, E.I. The tansformation of the oxide coatings of aluminum by imitation factors of nuclear power plants. Nucl. Eng. Technol. 2016, 2, 209–213. [Google Scholar] [CrossRef]
- Kanjana, K.; Ampornrat, P.; Channuie, J. Gamma-radiation-induced corrosion of aluminum alloy: Low dose effect. J. Phys. Conf. Ser. 2017, 860, 012041. [Google Scholar] [CrossRef]
- Godart, P.; Fischman, J.; Seto, K.A.; Hart, D. Hydrogen production from aluminum-water reactions subject to varied pressures and temperatures. Int. J. Hydrogen Energy 2019, 44, 11448–11458. [Google Scholar] [CrossRef]
- Lertnaisat, P.; Katsumura, Y.; Mukai, S.; Umehara, R.; Shimizu, Y.; Suzuki, M. Simulation of the inhibition of water α-radiolysis via H2 addition. J. Nucl. Sci. Technol. 2014, 51, 1087–1095. [Google Scholar] [CrossRef]










| No. | Reaction | k (M s) |
|---|---|---|
| 1 | ·OH + H2 →·H + H2O | 9.37 × 10 |
| 2 | · OH + H → HO2 · + OH− | 1.32 × 10 |
| 3 | · OH + H2O2 → HO2 · + H2O | 5.04 × 10 |
| 4 | · OH + → O2 + OH− | 1.40 × 10 |
| 5 | · OH + HO2· → O2 + H2O | 1.05 × 10 |
| 6 | · OH + ·OH → H2O2 | 7.86 × 10 |
| 7 | · OH + | 5.26 × 10 |
| 8 | ·H + O2 → HO2· | 3.68 × 10 |
| 9 | ·H + → H | 3.51 × 10 |
| 10 | ·H + HO2· → H2O2 | 3.51 × 10 |
| 11 | ·H + H2O2 → ·OH + H2O | 1.65 × 10 |
| 12 | ·H + ·OH → H2O | 1.23 × 10 |
| 13 | ·H + ·H → H2 | 1.37 × 10 |
| 14 | 3.39 × 10 | |
| 15 | 3.01 × 10 | |
| 16 | 3.51 × 10 | |
| 17 | 4.38 × 10 | |
| 18 | 2.16 × 10 | |
| 19 | 3.96 × 10 | |
| 20 | 1.37 × 1010 | |
| 21 | 1.41 × 10 | |
| 22 | 1.96 × 10 | |
| 23 | 9.02 | |
| 24 | 1.23 × 10 s | |
| 25 | 7.89 × 10 | |
| 26 | 0.0624 s | |
| 27 | 3.51 × 10 | |
| 28 | 2.46 × 10 | |
| 29 | 1.89 × 10 s | |
| 30 | ·H + OH− → | 5.74 × 10 |
| 31 | 0.526 | |
| 32 | 39 |
| G(e) | G(H) | G(·H) | G(·OH) | G(HO) | G(HO) | |
|---|---|---|---|---|---|---|
| Neutron | 1.39 | 0.70 | 0.54 | 1.74 | 0.76 | 0.03 |
| Gamma | 2.91 | 0.46 | 0.65 | 3.17 | 0.65 | 0.00 |
| Simulation conditions | Values |
|---|---|
| DR | 0.04148 Gy/s |
| DR | 0.74878 Gy/s |
| Temperature | 60 °C |
| Pressure | 0.3 bar |
| Initial pH | 6.5/7/7.5 |
| Time | 1 year |
| pH 6.5 | pH 7 | pH 7.5 | |
|---|---|---|---|
| 2.29 × 10 M | 8.07 × 10 M | 4.24 × 10 M | |
| 9.32 × 10 M | 1.42 × 10 M | 7.25 × 10 M | |
| 3.15 × 10 M | 7.32 × 10 M | 1.34 × 10 M | |
| 3.11 × 10 M | 3.48 × 10 M | 6.52 × 10 M | |
| 1.57 × 10 M | 4.29 × 10 M | 2.83 × 10 M | |
| 1.07 × 10 M | 1.83 × 10 M | 3.53 × 10 M | |
| 1.15 × 10 M | 1.23 × 10 M | 2.35 × 10 M | |
| 7.64 × 10 M | 1.25 × 10 M | 7.95 × 10 M | |
| 6.5–6.7 | 7.0–7.3 | 7.5–7.8 |
| [H] = 0 µM | [H] = 1 µM | [H] = 10 µM | [H] = 100 µM | |
|---|---|---|---|---|
| 2.29 × 10 M | 1.46 × 10 M | 2.13 × 10 M | 2.22 × 10 M | |
| 9.32 × 10 M | 2.42 × 10 M | 3.22 × 10 M | 3.31 × 10 M | |
| 3.11 × 10 M | 1.17 × 10 M | 7.36 × 10 M | 7.15 × 10 M | |
| 1.57 × 10 M | 1.73 × 10 M | 3.67 × 10 M | 2.74 × 10 M | |
| 1.07 × 10 M | 2.92 × 10 M | 6.68 × 10 M | 5.13 × 10 M | |
| 1.15 × 10 M | 1.27 × 10 M | 2.68 × 10 M | 2.00 × 10 M | |
| 7.64 × 10 M | 2.42 × 10 M | 1.02 × 10 M | 9.14 × 10 M | |
| 6.5–7 | 6.5–7 | 6.5–7 | 6.5–7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sartorio, C.; Angiolini, M.; Flammini, D.; Pietropaolo, A.; Agostini, P.; Alberghi, C.; Candido, L.; Capogni, M.; Capone, M.; Cataldo, S.; et al. Preliminary Assessment of Radiolysis for the Cooling Water System in the Rotating Target of SORGENTINA-RF. Environments 2022, 9, 106. https://doi.org/10.3390/environments9080106
Sartorio C, Angiolini M, Flammini D, Pietropaolo A, Agostini P, Alberghi C, Candido L, Capogni M, Capone M, Cataldo S, et al. Preliminary Assessment of Radiolysis for the Cooling Water System in the Rotating Target of SORGENTINA-RF. Environments. 2022; 9(8):106. https://doi.org/10.3390/environments9080106
Chicago/Turabian StyleSartorio, Camillo, Massimo Angiolini, Davide Flammini, Antonino Pietropaolo, Pietro Agostini, Ciro Alberghi, Luigi Candido, Marco Capogni, Mauro Capone, Sebastiano Cataldo, and et al. 2022. "Preliminary Assessment of Radiolysis for the Cooling Water System in the Rotating Target of SORGENTINA-RF" Environments 9, no. 8: 106. https://doi.org/10.3390/environments9080106
APA StyleSartorio, C., Angiolini, M., Flammini, D., Pietropaolo, A., Agostini, P., Alberghi, C., Candido, L., Capogni, M., Capone, M., Cataldo, S., Contessa, G. M., D’Arienzo, M., Del Dotto, A., Diamanti, D., Dongiovanni, D., Farini, M., Ferrari, P., Fiore, A., Fonnesu, N., ... Zummo, G., on behalf of the SRF-Collaboration. (2022). Preliminary Assessment of Radiolysis for the Cooling Water System in the Rotating Target of SORGENTINA-RF. Environments, 9(8), 106. https://doi.org/10.3390/environments9080106