A Perspective on Supplier Selection and Order Allocation: Literature Review
Abstract
1. Introduction
2. Organization of the Related Literature
2.1. Problem Category
2.1.1. Literature Reviews
2.1.2. Deterministic Optimization Models
2.1.3. Uncertain Optimization Models
2.2. Operations Research Techniques
3. Observations
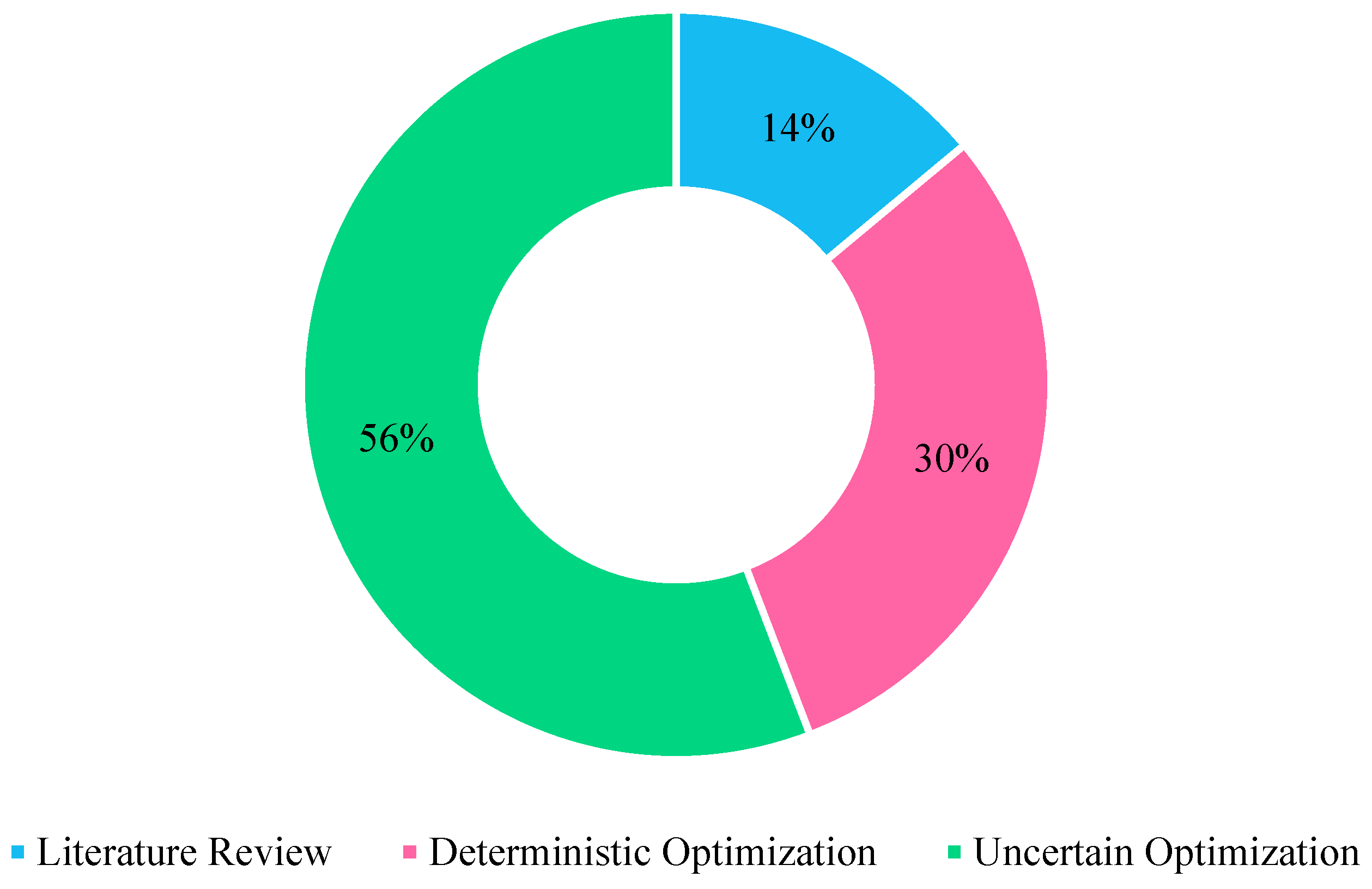
3.1. The Most Popular Category
3.2. The Most Popular Source of Uncertainty
3.3. Common Objective Functions
3.4. Most and Least Popular Techniques
3.5. Popular Applications
3.6. The List of Publications
3.7. Classification of the Articles Based on Year
4. Discussion and Conclusions
- (i)
- Simultaneously consider multiple sources of uncertainty in the objective function. Many papers focused on one factor for uncertainty and used that as a basis to help determine their fuzzy or stochastic model. In real cases, multiple factors should be measured under uncertainty and incorporated into the optimization models.
- (ii)
- Increased research on SSOA in the healthcare industry other than how it relates to manufacturing equipment. Sudden events like COVID-19 show how disruptive events can significantly impact the supply of medical supplies and staff to meet in-hospital care. SSOA can be used to improve existing hospital systems that can prevent short staffing and insufficient medical supply in predictable and unpredictable situations.
- (iii)
- Overall, more research should be conducted in the field of supplier selection and as a result, extra literature reviews can be written. Many papers cover the topics on solely supplier selection or order allocation. Increasing studies on SSOA can provide a more comprehensive view of the topic of SSOA and the implementation of its techniques in real-world situations.
- (iv)
- There are several future opportunities to explore the applications of data science techniques, such as machine learning methods in SSOA. For instance, neural networks can be combined (e.g., Yang et al. (2008a, 2008b); Zhang et al. 2005).
Author Contributions
Funding
Conflicts of Interest
References
- Ahmad, Md. Tanweer, Mohammad Firouz, and Sandeep Mondal. 2022. Robust supplier-selection and order-allocation in two-echelon supply networks: A parametric tolerance design approach. Computers and Industrial Engineering 171: 108394. [Google Scholar] [CrossRef]
- Alejo-Reyes, Avelina, Abraham Mendoza, and Elias Olivares-Benitez. 2021. A heuristic method for the supplier selection and order quantity allocation problem. Applied Mathematical Modelling 90: 1130–42. [Google Scholar] [CrossRef]
- Ali, Hassan, and Jingwen Zhang. 2023. A fuzzy multi-objective decision-making model for global green supplier selection and order allocation under quantity discounts. Expert Systems with Applications 225: 120119. [Google Scholar] [CrossRef]
- Arabsheybani, Amir, and Alireza Khasmeh Arshadi. 2021. Robust and resilient supply chain network design considering risks in food industry: Flavour industry in Iran. International Journal of Management Science and Engineering Management 16: 197–208. [Google Scholar] [CrossRef]
- Araújo, Lavínia Maria Mendes, Caio Souto Maior, Isis Didier Lins, and Marcio Moura. 2023. Technology selection and ranking: Literature review and current applications in oil and gas industry. Geoenergy Science and Engineering 226: 211771. [Google Scholar] [CrossRef]
- Bai, Chunguang, Qingyun Zhu, and Joseph Sarkis. 2022. Supplier portfolio selection and order allocation under carbon neutrality: Introducing a “Cool”ing model. Computers and Industrial Engineering 170: 108335. [Google Scholar] [CrossRef]
- Beiki, Hossein, Mohammad Seyedhosseini, Vadim Ponkratov, Angelina Olegovna Zekiy, and Sergei Anatolyevich Ivanov. 2021. Addressing a sustainable supplier selection and order allocation problem by an integrated approach: A case of automobile manufacturing. Journal of Industrial and Production Engineering 38: 239–53. [Google Scholar] [CrossRef]
- Chauhan, Vinod Kumar, Stephen Mak, Ajith Kumar Parlikad, Muhannad Alomari, Linus Casassa, and Alexandra Brintrup. 2023. Real-time large-scale supplier order assignments across two-tiers of a supply chain with penalty and dual-sourcing. Computers and Industrial Engineering 176: 108928. [Google Scholar] [CrossRef]
- de Oliveira, Maiquiel Schmidt, Vilmar Steffen, Antonio Carlos de Francisco, and Flavio Trojan. 2023. Integrated data envelopment analysis, multi-criteria decision making, and cluster analysis methods: Trends and perspectives. Decision Analytics Journal 8: 100271. [Google Scholar] [CrossRef]
- Dobos, Imre, and Gyöngyi Vörösmarty. 2021. Green supplier selection using a common weights analysis of DEA and EOQ types of order allocation. Managerial and Decision Economics 42: 612–21. [Google Scholar] [CrossRef]
- Ebrahim Qazvini, Zahra, Alireza Haji, and Hassan Mina. 2021. A fuzzy solution approach to supplier selection and order allocation in green supply chain considering the location-routing problem. Scientia Iranica 28: 446–64. [Google Scholar] [CrossRef]
- Esmaeili-Najafabadi, Elham, Nader Azad, and Mohammad Saber Fallah Nezhad. 2021. Risk-averse supplier selection and order allocation in the centralized supply chains under disruption risks. Expert Systems with Applications 175: 114691. [Google Scholar] [CrossRef]
- Esteso, Ana, M. M. E. Alemany, and Angel Ortiz. 2023. Sustainable agri-food supply chain planning through multi-objective optimisation. Journal of Decision Systems, 1–25. [Google Scholar] [CrossRef]
- Feng, Yuqiang, Yanju Chen, and Yankui Liu. 2022. Optimising two-stage robust supplier selection and order allocation problem under risk-averse criterion. International Journal of Production Research 61: 6356–80. [Google Scholar] [CrossRef]
- Firouzi, Fatameh, and Omid Jadidi. 2021. Multi-objective model for supplier selection and order allocation problem with fuzzy parameters. Expert Systems with Applications 180: 115129. [Google Scholar] [CrossRef]
- Goodarzi, Fariba, Vahid Abdollahzadeh, and Masoomeh Zeinalnezhad. 2022. An integrated multi-criteria decision-making and multi-objective optimization framework for green supplier evaluation and optimal order allocation under uncertainty. Decision Analytics Journal 4: 100087. [Google Scholar] [CrossRef]
- Hamdi, Faiza, Laila Messaoudi, and Jalel Euchi. 2023. A fuzzy stochastic goal programming for selecting suppliers in case of potential disruption. Journal of Industrial and Production Engineering 40: 677–91. [Google Scholar] [CrossRef]
- Hosseini, Zahra Sadat, Simme Douwe Flapper, and Mohammadali Pirayesh. 2022. Sustainable supplier selection and order allocation under demand, supplier availability and supplier grading uncertainties. Computers and Industrial Engineering 165: 107811. [Google Scholar] [CrossRef]
- Hu, Shaolung, Zhijie Sasha Dong, and Benjamin Lev. 2022. Supplier selection in disaster operations management: Review and research gap identification. Socio-Economic Planning Sciences 82: 101302. [Google Scholar] [CrossRef]
- Islam, Samiul, Saman Hassanzadeh Amin, and Leslie J. Wardley. 2021. Machine learning and optimization models for supplier selection and order allocation planning. International Journal of Production Economics 242: 108315. [Google Scholar] [CrossRef]
- Islam, Samiul, Saman Hassanzadeh Amin, and Leslie J. Wardley. 2022. Supplier selection and order allocation planning using predictive analytics and multi-objective programming. Computers and Industrial Engineering 174: 108825. [Google Scholar] [CrossRef]
- Islam, Samiul, Saman Hassanzadeh Amin, and Leslie. J. Wardley. 2023. A Supplier Selection and Order Allocation Planning Framework by Integrating Deep Learning, Principal Component Analysis, and Optimization Techniques. Expert Systems with Applications 235: 121121. [Google Scholar] [CrossRef]
- Jamalnia, Aboozar, Yu Gong, and Kannan Govindan. 2022. Sub-supplier’s sustainability management in multi-tier supply chains: A systematic literature review on the contingency variables, and a conceptual framework. International Journal of Production Economics 225: 108671. [Google Scholar] [CrossRef]
- Kaur, Harpreet, and Surya Prakash Singh. 2021. Multi-stage hybrid model for supplier selection and order allocation considering disruption risks and disruptive technologies. International Journal of Production Economics 231: 107830. [Google Scholar] [CrossRef]
- Liaqait, Raja Awais, Salman Warsi, Mujtaba Agha, Taiba Zahid, and Till Becker. 2022. A multi-criteria decision framework for sustainable supplier selection and order allocation using multi-objective optimization and fuzzy approach. Engineering Optimization 54: 928–48. [Google Scholar] [CrossRef]
- Liu, Dengzhou, and Zhongkai Li. 2021. Joint decision-making of product family configuration and order allocation by coordinating suppliers under disruption risks. Journal of Engineering Design 32: 213–46. [Google Scholar] [CrossRef]
- Masudin, Ilyas, Sabila Zahra Umamy, Al-Imron Cynthia Novel, and Restuputri Dian. 2022. Green procurement implementation through supplier selection: A bibliometric review. Cogent Engineering 9: 2119686. [Google Scholar] [CrossRef]
- Mirzaee, Hossein, Hamed Samarghandi, and Keith Willoughby. 2023. A robust optimization model for green supplier selection and order allocation in a closed-loop supply chain considering cap-and-trade mechanism. Expert Systems with Applications 228: 120423. [Google Scholar] [CrossRef]
- Mohammed, Ahmed, Chunguang Bai, Nabil Channouf, Teejan Al Ahmed, and Shaymaa Maher Mohamed. 2023. G-resilient multi-tier supplier selection and order allocation in food industry: A hybrid methodology. International Journal of Systems Science: Operations and Logistics 10: 2195055. [Google Scholar] [CrossRef]
- Mohammed, Ahmed, Irina Harris, Anthony Soroka, Mohamed Naim, Tim Ramjaun, and Morteza Yazdani. 2021. Gresilient supplier assessment and order allocation planning. Annals of Operations Research 296: 335–62. [Google Scholar] [CrossRef]
- Nasr, Arash Khalili, Madjid Tavana, Behrouz Alavi, and Hassan Mina. 2021. A novel fuzzy multi-objective circular supplier selection and order allocation model for sustainable closed-loop supply chains. Journal of Cleaner Production 287: 124994. [Google Scholar] [CrossRef]
- Nayeri, Sina, Mohammed Amin Khoei, Mohammed Reza Rouhani-Tazangi, Mohssen GhanavatiNejad, Mohammad Rahmani, and Erfan Babaee Tirkolaee. 2023. A data-driven model for sustainable and resilient supplier selection and order allocation problem in a responsive supply chain: A case study of the healthcare system. Engineering Applications of Artificial Intelligence 124: 106511. [Google Scholar] [CrossRef]
- Nguyen, Van Hop. 2023. A hierarchical heuristic algorithm for multi-objective order allocation problem subject to supply uncertainties. Journal of Industrial and Production Engineering 40: 343–59. [Google Scholar] [CrossRef]
- Sarfaraz, Amir Homayoun, Amir Karbassi Yazdi, Peter Wanke, Elaheh Ashtari Nezhad, and Raheleh Sadat Hosseini. 2022. A novel hierarchical fuzzy inference system for supplier selection and performance improvement in the oil and gas industry. Journal of Decision Systems 32: 356–83. [Google Scholar] [CrossRef]
- Sharifi, Ebrahim, Liping Fang, and Saman Hassanzadeh Amin. 2023. A novel two-stage multi-objective optimization model for sustainable soybean supply chain design under uncertainty. Sustainable Production and Consumption 40: 297–317. [Google Scholar] [CrossRef]
- Spyridonidou, Sofia, and Dimitra G. Vagiona. 2023. A systematic review of site-selection procedures of PV and CSP technologies. Energy Reports 9: 2947–79. [Google Scholar] [CrossRef]
- Sun, Yulin, Simon Cong Guo, and Xueping Li. 2022. An order-splitting model for supplier selection and order allocation in a multi-echelon supply chain. Computers and Operations Research 137: 105515. [Google Scholar] [CrossRef]
- Ventura, Jose A., Kevin A. Bunn, Bárbara Venegas Venegas, and Lisha Duan. 2021. A coordination mechanism for supplier selection and order quantity allocation with price-sensitive demand and finite production rates. International Journal of Production Economics 233: 108007. [Google Scholar] [CrossRef]
- Wu, Chong, Jing Gao, and David Barnes. 2022. Sustainable partner selection and order allocation for strategic items: An integrated multi-stage decision-making model. International Journal of Production Research 61: 1076–100. [Google Scholar] [CrossRef]
- Yang, Xinying, Gong Gong, and Yuan Tian. 2008a. Optimal game theory in complicated virtual-modeling and CGF decision-making with multi-granularities. Presented at the 2008 International Conference on Smart Manufacturing Application, Goyangi, Republic of Korea, April 9–11; Piscataway: IEEE, pp. 95–99. [Google Scholar]
- Yang, Xinying, Guanghong Gong, Yuan Tian, and Xiaoxia Yu. 2008b. Generalized optimal game theory in virtual decision-makings. Presented at the 2008 Chinese Control and Decision Conference, Yantai, China, July 2–4; Piscataway: IEEE, pp. 1960–64. [Google Scholar]
- Yang, Yi, and Chen Peng. 2023. A prediction-based supply chain recovery strategy under disruption risks. International Journal of Production Research 61: 7670–84. [Google Scholar] [CrossRef]
- Yousefi, Samuel, Mustafa Jahangoshai Rezaee, and Maghsud Solimanpur. 2021. Supplier selection and order allocation using two-stage hybrid supply chain model and game-based order price. Operational Research 21: 553–88. [Google Scholar] [CrossRef]
- Zaretalab, Arash, Mani Sharifi, Pedram Pourkarim Guilani, Sharareh Taghipour, and Seyed Taghi Akhavan Niaki. 2022. A multi-objective model for optimizing the redundancy allocation, component supplier selection, and reliable activities for multi-state systems. Reliability Engineering and System Safety 222: 108394. [Google Scholar] [CrossRef]
- Zhang, Ping, Xinying Yang, and Zongji Chen. 2005. Neural network gain scheduling design for large envelope curve flight control law. Journal of Beijing University of Aeronautics and Astronautics 31: 604–8. [Google Scholar]
- Zhang, Yueran, Zhanwen Niu, Yaqing Zuo, and Chao-Chao Liu. 2023. Two-stage hybrid model for supplier selection and order allocation considering cyber risk. INFOR: Information Systems and Operational Research 61: 530–58. [Google Scholar] [CrossRef]
| Source of Uncertainty | References |
|---|---|
| Availability/Selection | Firouzi and Jadidi (2021); Feng et al. (2022) |
| Cost | Mirzaee et al. (2023); Mohammed et al. (2023) |
| Supplier | Hosseini et al. (2022); Nasr et al. (2021) |
| Decision-makers | Wu et al. (2022) |
| Delivery time | Mirzaee et al. (2023); Nguyen (2023) |
| Demand | Arabsheybani and Arshadi (2021); Ebrahim Qazvini et al. (2021); Hamdi et al. (2023); Hosseini et al. (2022); Islam et al. (2022); Islam et al. (2023); Islam et al. (2021); Kaur and Singh (2021); Liaqait et al. (2022); Mirzaee et al. (2023); Goodarzi et al. (2022); Mohammed et al. (2023); Sharifi et al. (2023); Zhang et al. (2023) |
| Disruptions/Event-based | Liu and Li (2021); Nayeri et al. (2023); Yang and Peng (2023); Zhang et al. (2023) |
| Processing time | Arabsheybani and Arshadi (2021) |
| Quality (defect rate) | Nguyen (2023) |
| Prices | Sharifi et al. (2023) |
| Quantity discount | Ali and Zhang (2023) |
| Resource utilization | Mirzaee et al. (2023) |
| Techniques | References |
|---|---|
| Analytical Hierarchical Process (AHP) | Mohammed et al. (2021); Nasr et al. (2021) |
| Analytical Network Process (ANP) | Nasr et al. (2021) |
| Backtracking Algorithm | Liu and Li (2021) |
| Bargaining Game | Yousefi et al. (2021) |
| Best–Worst Method (BWM) | Wu et al. (2022) |
| BWM-ER (Best–Worst Method-Evidential Reasoning) | Hosseini et al. (2022) |
| Bi-level Programming Model | Liu and Li (2021) |
| Bi-objective Mixed-Integer Programming | Yang and Peng (2023) |
| Chebyshev Multi-Choice Goal Programming with Utility Function (CMCGP-UF) | Nayeri et al. (2023) |
| Common Weights Model | Dobos and Vörösmarty (2021) |
| Conditional Value-at-Risk (CVaR) | Esmaeili-Najafabadi et al. (2021) |
| Differential Evolution | Alejo-Reyes et al. (2021) |
| Data Envelopment Analysis (DEA) | Dobos and Vörösmarty (2021); Kaur and Singh (2021); Yousefi et al. (2021) |
| Dynamic Programming | Hosseini et al. (2022); Nguyen (2023) |
| Economic Order Quantity (EOQ) | Ventura et al. (2021) |
| Fuzzy Analytical Hierarchy Process (FAHP) | Arabsheybani and Arshadi (2021); Ali and Zhang (2023); Ebrahim Qazvini et al. (2021); Kaur and Singh (2021); Zhang et al. (2023) |
| Fuzzy BWM | Goodarzi et al. (2022); Nasr et al. (2021) |
| Fuzzy Compromise Programming | Ali and Zhang (2023); Nguyen (2023) |
| Fuzzy-Delphi | Goodarzi et al. (2022) |
| Fuzzy Goal Programming | Nasr et al. (2021) |
| Fuzzy Multi-Objective Mixed-Integer Linear Programming | Liaqait et al. (2022); Mohammed et al. (2023) |
| Fuzzy Multi-Objective Optimization based on Ratio Analysis (MOORA) | Arabsheybani and Arshadi (2021) |
| Fuzzy Robust Stochastic (FRS) Optimization | Nayeri et al. (2023) |
| Fuzzy Sets Theory | Firouzi and Jadidi (2021); Sarfaraz et al. (2022) |
| Fuzzy Stochastic BWM | Nayeri et al. (2023) |
| Fuzzy Stochastic Goal Programming | Hamdi et al. (2023) |
| Fuzzy SWOT (Strengths, Weaknesses, Opportunities, Threats) | Islam et al. (2022) |
| Genetic Algorithm (GA) | Chauhan et al. (2023); Liu and Li (2021) |
| Global Criterion Method (GCM) | Yousefi et al. (2021) |
| Gray Correlation TOPSIS (GC-TOPSIS) | Goodarzi et al. (2022) |
| Language Entropy Weight Method | Beiki et al. (2021) |
| Light-Gradient Boosted Machine (LGBM) | Islam et al. (2023) |
| Long-Short-Term Memory (LSTM) | Islam et al. (2022); Islam et al. (2023) |
| Mixed-Integer Linear Programming (MILP) | Feng et al. (2022); Islam et al. (2023); Nguyen (2023) |
| Mixed-Integer Nonlinear Programming (MINLP) | Ahmad et al. (2022); Alejo-Reyes et al. (2021); Esmaeili-Najafabadi et al. (2021); Sun et al. (2022); Ventura et al. (2021) |
| Mixed Integer Programming (MIP) | Chauhan et al. (2023); Firouzi and Jadidi (2021); Kaur and Singh (2021); Zhang et al. (2023) |
| Multi-Criteria Decision Making (MCDM) | Goodarzi et al. (2022) |
| Multi-Objective Evolutionary Algorithm based on Decomposition (MOEA/D) | Zaretalab et al. (2022) |
| Multi-Objective Linear Programming (MOLP) | Ali and Zhang (2023) |
| Multi-Objective Mixed-Integer Linear Programming (MOMILP) | Bai et al. (2022); Ebrahim Qazvini et al. (2021); Goodarzi et al. (2022); Islam et al. (2022); Nasr et al. (2021) |
| Multi-Objective Mixed-Integer Nonlinear Programming (MOMILP) | Yousefi et al. (2021) |
| Multi-Objective Optimization | Esteso et al. (2023) |
| Multi-Objective Programming (MOP) | Beiki et al. (2021); Islam et al. (2021); Mohammed et al. (2021) |
| Multi-Stage Decision-Making Framework | Nayeri et al. (2023) |
| Non-Dominated Sorting Genetic Algorithm Type II | Zaretalab et al. (2022) |
| Order Splitting | Sun et al. (2022) |
| Particle Swarm Optimisation (PSO) | Alejo-Reyes et al. (2021); Esmaeili-Najafabadi et al. (2021); Wu et al. (2022) |
| Polyhedral and Box Ambiguity Sets | Feng et al. (2022) |
| Principal Component Analysis (PCA) | Islam et al. (2023) |
| Product Family Configuration and Order Allocation (PCOA) | Liu and Li (2021) |
| Relational Regressor Chain | Islam et al. (2021) |
| Seasonal Autoregressive Integrated Moving Average (SARIMA) | Islam et al. (2023); Nayeri et al. (2023) |
| Shannon Entropy | Sarfaraz et al. (2022) |
| Stochastic Mixed-Integer Linear Programming | Islam et al. (2021) |
| Stochastic Programming | Hosseini et al. (2022); Sharifi et al. (2023) |
| Taguchi Loss Function (TLF) | Wu et al. (2022) |
| Taguchi Method of Tolerance Design (TMTD) | Ahmad et al. (2022) |
| Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) | Mohammed et al. (2021); Wu et al. (2022); Zhang et al. (2023) |
| Trapezoidal Fuzzy BWM | Sharifi et al. (2023) |
| Trapezoidal Fuzzy Numbers | Wu et al. (2022) |
| Two-stage Distributionally Robust (DR) Mean-CVaR model | Feng et al. (2022) |
| Value-at-Risk (VaR) | Esmaeili-Najafabadi et al. (2021) |
| Weight additive function | Firouzi and Jadidi (2021) |
| Objective Functions | References | |
|---|---|---|
| Single-objective | Min total cost for first and second echelon | Ahmad et al. (2022) |
| Min total cost per time unit (ordering, purchasing, inventory, transportation costs) | Alejo-Reyes et al. (2021) | |
| Min cost of machining parts as per requirements (proportion and supplier) | Chauhan et al. (2023) | |
| Max sum of inequalities | Dobos and Vörösmarty (2021) | |
| Max expected total profit | Sun et al. (2022) | |
| Max supply chain profit (cost per time unit, purchasing, ordering, inventory holding, and supplier managerial costs) | Ventura et al. (2021) | |
| Min supply chain costs | Zhang et al. (2023) | |
| Multi-objective | (5) Min overall procurement costs, min number of defective items, min delivery lateness rate (from supplier location to buyer destination), min total greenhouse gas emissions, min overall foreign transportation risks | Ali and Zhang (2023) |
| (2) Max profit, max total value of supply chain resiliency | Arabsheybani and Arshadi (2021) | |
| (4) Max purchasing quantity, min purchasing cost, min investment cost, carbon neutrality | Bai et al. (2022) | |
| (3) Min total cost, min carbon emissions, max procurement value | Beiki et al. (2021) | |
| (2) Min total costs of chain, max value of purchases from qualified suppliers | Ebrahim Qazvini et al. (2021) | |
| (2) Min total annual expected supply chain costs (including annual expected costs of the buyer and annual expected cost of the suppliers), min CVaR | Esmaeili-Najafabadi et al. (2021) | |
| (5) Max economic profits, min waste, unsatisfied demand, max sold crops and their freshness, min farmers’ perception of economic injustice | Esteso et al. (2023) | |
| (4) Cost of contracting main suppliers, cost of contracting backup suppliers, min sum of purchasing and transportation cost, worst-case mean-CVaR value of the second-stage cost | Feng et al. (2022) | |
| (4) Min cost and late delivery, total monetary cost, number of defective units, number of units delivered late | Firouzi and Jadidi (2021) | |
| (2) Max order value based on selected supplier’s weights, max total value of purchase, min total cost (variable purchase cost, transport costs, order fixed costs, inventory control cost, and penalty costs) | Goodarzi et al. (2022) | |
| Min cost (fixed cost, purchasing cost, and shortage cost), max sum of membership functions | Hamdi et al. (2023) | |
| (2) Max total value of purchase (TVP), min total cost of purchase (TCP) | Hosseini et al. (2022) | |
| (2) Min total cost (cost of different meat types, requisition costs, holding costs), max on-time delivery of meat | Islam et al. (2023) | |
| (5) Min total cost (purchasing, holding, and ordering costs), max weight of suppliers, min supplier carbon footprint, max supplier rates of on-time delivery, min supplier defect rates | Islam et al. (2022) | |
| (5) Min total cost, max on-time delivery, min damage rates, min carbon emissions | Islam et al. (2021) | |
| (5) Max total output, min total cost of procurement (unit price, ordering cost, transportation, total risk, holding cost) | Kaur and Singh (2021) | |
| (2) Max total value of purchase (TVP), min total cost of purchase (TCP) | Hosseini et al. (2022) | |
| (2) Min total cost (cost of different meat types, requisition costs, holding costs), max on-time delivery of meat | Islam et al. (2023) | |
| (5) Min total cost (purchasing, holding, and ordering costs), max weight of suppliers, min supplier carbon footprint, max supplier rates of on-time delivery, min supplier defect rates | Islam et al. (2022) | |
| (5) Min total cost, max on-time delivery, min damage rates, min carbon emissions | Islam et al. (2021) | |
| (5) Max total output, min total cost of procurement (unit price, ordering cost, transportation, total risk, holding cost) | Kaur and Singh (2021) | |
| (5) Min cost (purchasing, ordering, inventory holding, transportation, transfer, and customs clearance cost), min total travel time, min carbon emission (i.e., from ship, rail, road), min noise pollution), max total value of sustainable purchasing | Liaqait et al. (2022) | |
| (2) Min cost module instance, max lowest quantity of module instance | Liu and Li (2021) | |
| (3) Min related costs (purchasing, transportation, operating costs), min transportation time, max g-resilient performance (purchasing value) | Mohammed et al. (2023) | |
| (3) Min related costs, min environmental impact, max of resilience purchasing | Mohammed et al. (2021) | |
| (4) Min total cost of chain, min undesired environmental effect, max employment created, min lost sales, max procurement value from sustainable suppliers | Nasr et al. (2021) | |
| (4) Min total costs (fixed cost of supplier contract making, fixed cost for building manufacturing sites, fixed cost of using manufacturing technologies, procurement costs, production costs, shortage costs, extra capacity costs, transport costs), min greenhouse gas emissions from production and transport activities, max created jobs, max scores of suppliers | Nayeri et al. (2023) | |
| (3) Min total cost (procurement cost, requisition cost, and holding cost), min total rejected material, min total raw material quantity from late delivery | Nguyen (2023) | |
| (2) Min operator, max operator | Sarfaraz et al. (2022) | |
| (4) Max total profit, max job opportunities, max supplier’s sustainability, min carbon emissions | Sharifi et al. (2023) | |
| (5) Min total cost, min total carbon emissions, min total social value, min total defect rate, min total supplier value | Wu et al. (2022) | |
| (3) Max production capacity, max and min estimated cost and estimated service level | Yang and Peng (2023) | |
| (2) Min total supply chain annual cost, max overall supplier efficiency | Yousefi et al. (2021) | |
| (2) Min total cost (technical activities, planning activities, procurement costs), max system availabilities | Zaretalab et al. (2022) |
| Journal | Number of Papers | |||
|---|---|---|---|---|
| LR | DO | UO | Total | |
| Applied Mathematical Modelling | 1 | 1 | ||
| Annals of Operations Research | 1 | 1 | ||
| Computers & Industrial Engineering | 3 | 2 | 5 | |
| Computers & Operations Research | 1 | 1 | ||
| Cogent Engineering | 1 | 1 | ||
| Decision Analytics Journal | 1 | 1 | 2 | |
| Energy Reports | 1 | 1 | ||
| Engineering Applications of Artificial Intelligence | 1 | 1 | ||
| Engineering Optimization | 1 | 1 | ||
| Expert Systems with Applications | 1 | 4 | 5 | |
| Geoenergy Science and Engineering | 1 | 1 | ||
| Information Systems and Operational Research | 1 | 1 | ||
| International Journal of Management Science and Engineering Management | 1 | 1 | ||
| International Journal of Production Economics | 1 | 1 | 2 | 4 |
| International Journal of Production Research | 3 | 3 | ||
| International Journal of Systems Science | 1 | 1 | ||
| Journal of Cleaner Production | 1 | 1 | ||
| Journal of Decision Systems | 1 | 1 | 2 | |
| Journal of Engineering Design | 1 | 1 | ||
| Journal of Industrial and Production Engineering | 1 | 2 | 3 | |
| Managerial and Decision Economics | 1 | 1 | ||
| Operational Research | 1 | 1 | ||
| Reliability Engineering and System Safety | 1 | 1 | ||
| Scientia Iranica | 1 | 1 | ||
| Socio-Economic Planning Sciences | 1 | 1 | ||
| Sustainable Production and Consumption | 1 | 1 | ||
| Total | 6 | 13 | 24 | 43 |
| Number of Articles | ||||
|---|---|---|---|---|
| Year | LR | DO | UO | Total |
| 2021 | 0 | 7 | 7 | 14 |
| 2022 | 3 | 4 | 7 | 14 |
| 2023 | 3 | 2 | 10 | 15 |
| Total | 6 | 13 | 24 | 43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.; Amin, S.H.; Shah, B. A Perspective on Supplier Selection and Order Allocation: Literature Review. Adm. Sci. 2024, 14, 206. https://doi.org/10.3390/admsci14090206
Nguyen T, Amin SH, Shah B. A Perspective on Supplier Selection and Order Allocation: Literature Review. Administrative Sciences. 2024; 14(9):206. https://doi.org/10.3390/admsci14090206
Chicago/Turabian StyleNguyen, Trish, Saman Hassanzadeh Amin, and Bharat Shah. 2024. "A Perspective on Supplier Selection and Order Allocation: Literature Review" Administrative Sciences 14, no. 9: 206. https://doi.org/10.3390/admsci14090206
APA StyleNguyen, T., Amin, S. H., & Shah, B. (2024). A Perspective on Supplier Selection and Order Allocation: Literature Review. Administrative Sciences, 14(9), 206. https://doi.org/10.3390/admsci14090206






