Feasibility Study on Grouting Compactness Detection in Sleeves Using Piezoelectric Transducers
Abstract
:1. Introduction
2. Detection Method of Piezoceramic Transducer
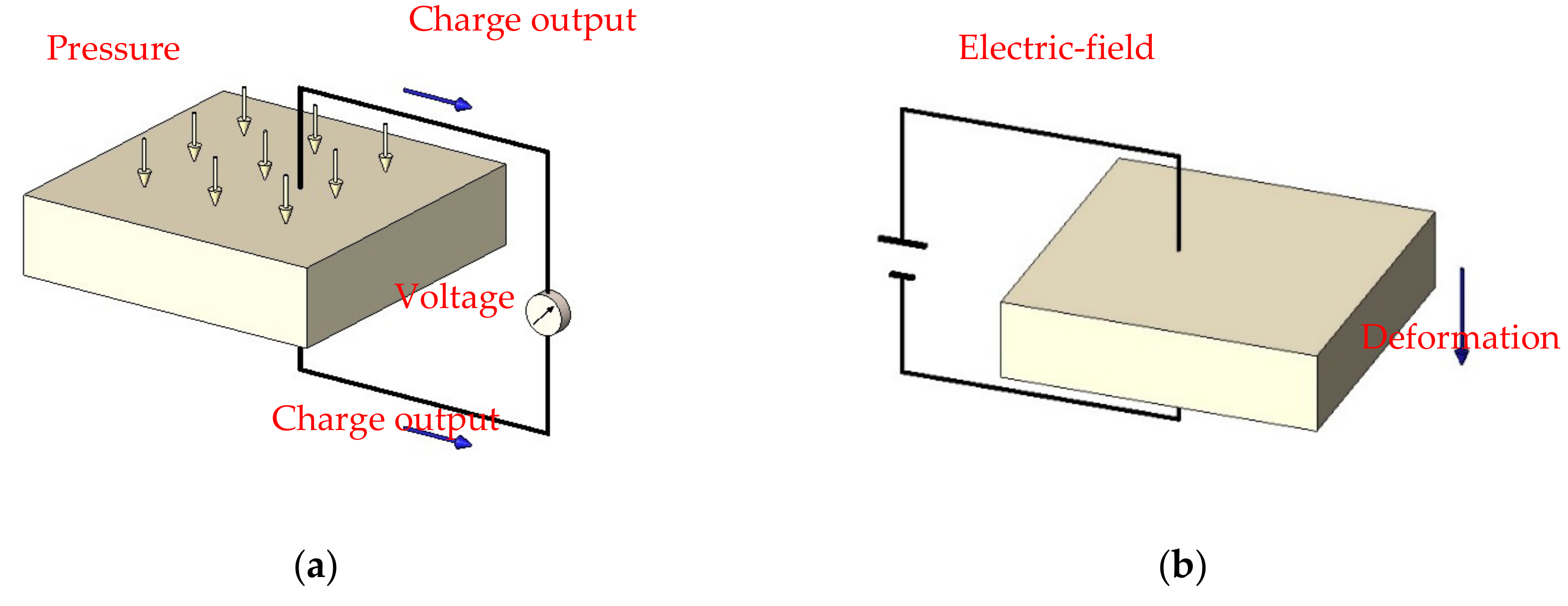
2.1. Piezoelectric Effect
2.2. Wavelet Packet Energy Method
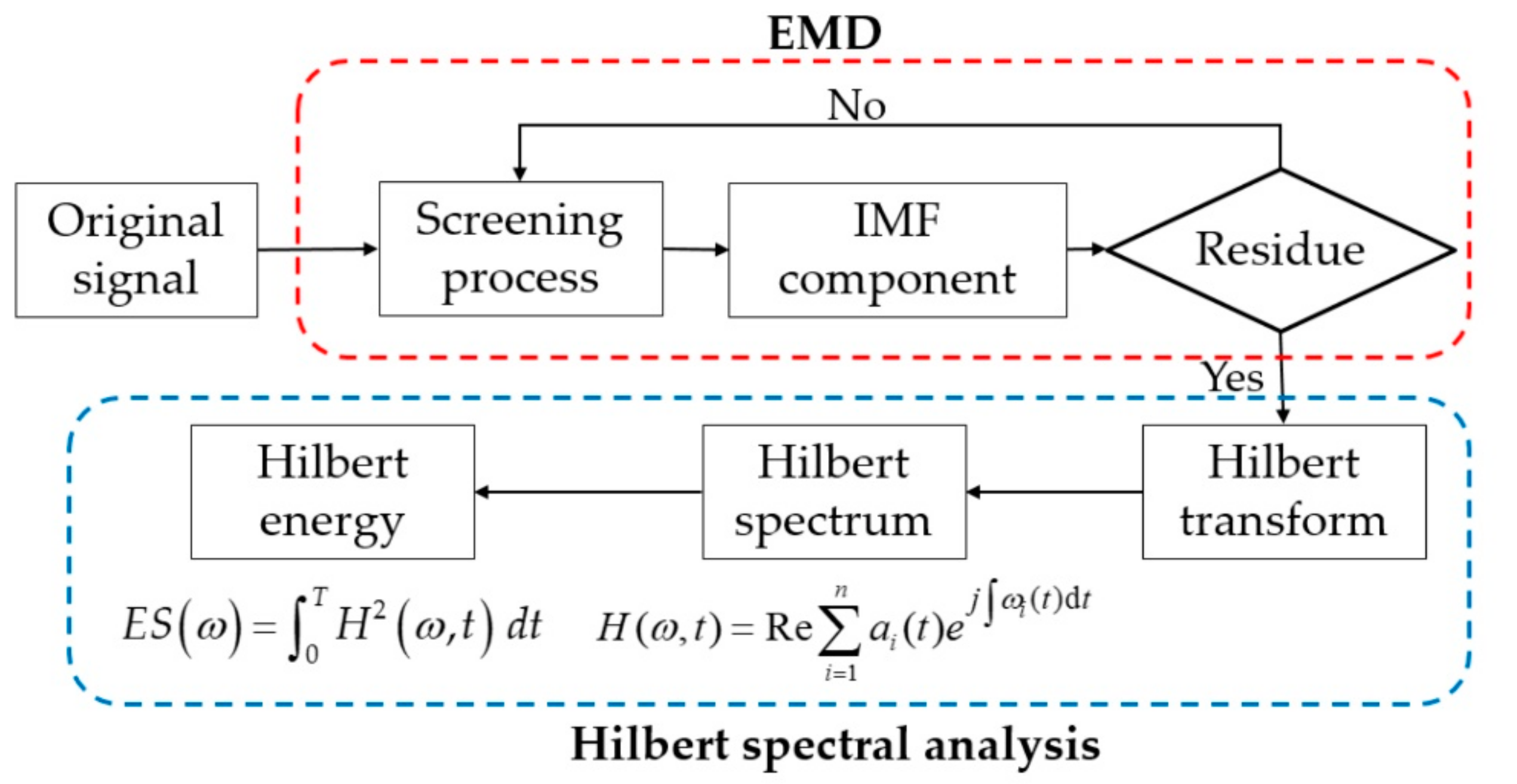
2.3. Hilbert-Huang Transform Method
3. Experimental Setup
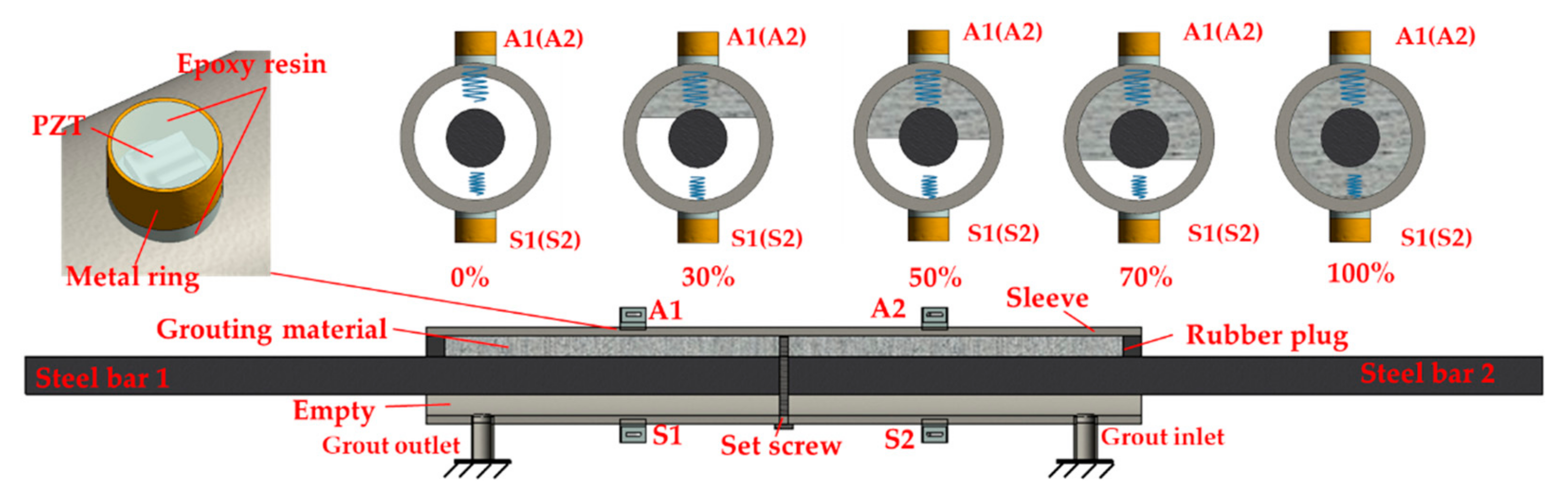
3.1. Specimen Fabrication
3.2. Grouting Compactness Detection of Sleeves
4. Test Results and Discussion
4.1. Preliminary Processing of Signals
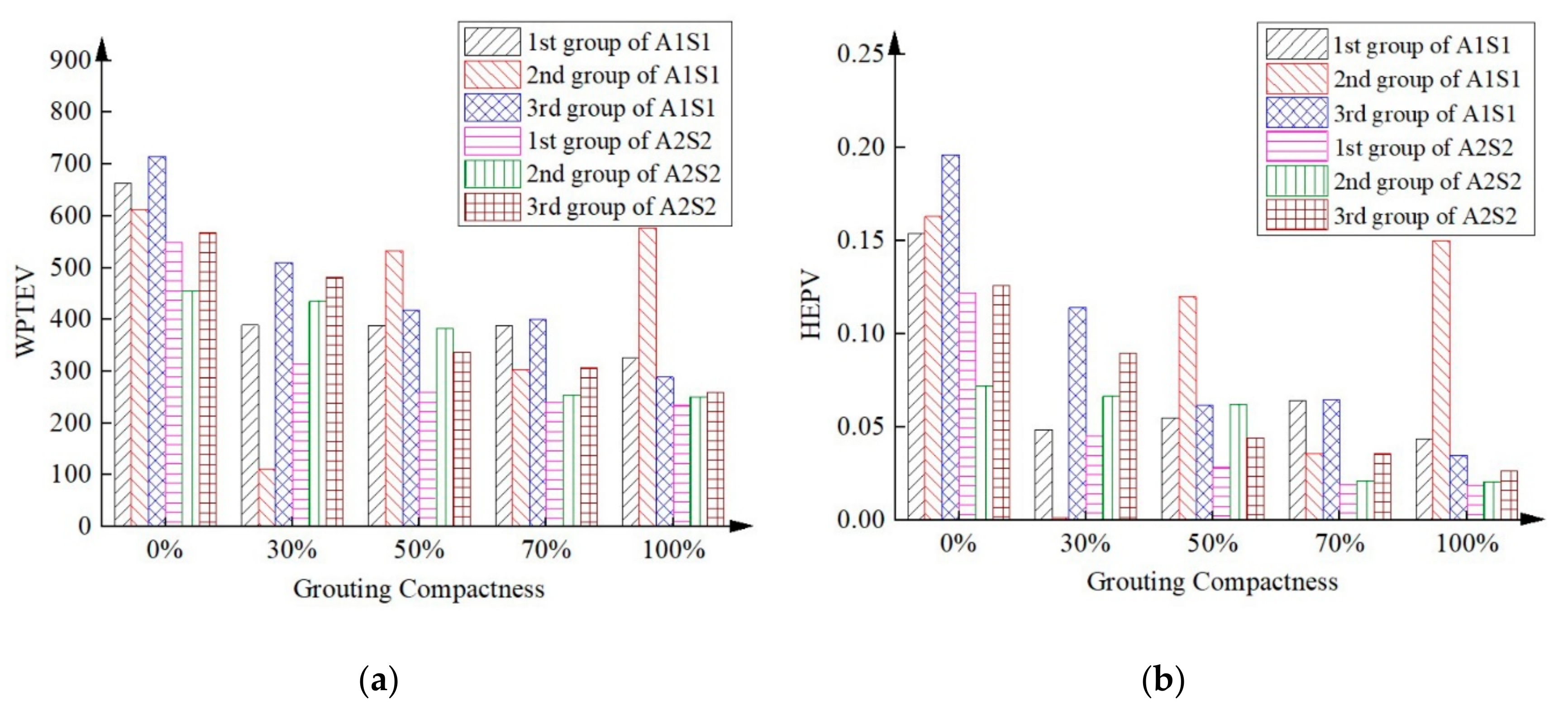
4.2. Grouting Compactness Detection Based on WPE Method
4.3. Grouting Compactness Detection Based on HHT Method
4.4. Grouting Compactness Detection Result and Discussion
5. Conclusion and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Ling, J.H.; Rahman, A.B.A.; Ibrahim, I.S.; Hamid, Z.A. Tensile capacity of grouted splice sleeves. Eng. Struct. 2016, 111, 285–296. [Google Scholar] [CrossRef]
- Ling, J.H.; Rahman, A.B.A.; Ibrahim, I.S.; Hamid, Z.A. Behavior of grouted pipe splice under incremental tensile load. Constr. Build. Mater. 2012, 33, 90–98. [Google Scholar] [CrossRef]
- Sayadi, A.A.; Rahman, A.B.A.; Jumaat, M.Z.B.; Johnson, A.U.; Ahmad, S. The relationship between interlocking mechanism and bond strength in elastic and inelastic segment of splice sleeve. Constr. Build. Mater. 2014, 55, 227–237. [Google Scholar] [CrossRef]
- Xu, F.; Wang, K.; Wang, S.G.; Li, W.W.; Liu, W.Q.; Du, D.S. Experimental bond behavior of deformed rebars in half-grouted sleeve connections with insufficient grouting defect. Constr. Build. Mater. 2018, 185, 264–274. [Google Scholar] [CrossRef]
- Kim, H. Bond strength of mortar-filled steel pipe splices reflecting confining effect. J. Asian Archit. Build. Eng. 2012, 11, 125–132. [Google Scholar] [CrossRef]
- Nie, D.L.; Jia, L.G.; Du, M.K.; Liu, M. Experimental study on detecting density of grouting materials for steel sleeves by using ultrasonic wave. Concrete 2014, 9, 120–123. [Google Scholar]
- Jiang, S.F.; Cai, W.X. Ultrasonic testing method of grouting sleeve compactness. J. Vib. Shock. 2018, 37, 43–49. [Google Scholar]
- Li, Z.H.; Zheng, L.L.; Chen, C.J.; Long, Z.L.; Wang, Y. Ultrasonic Detection Method for Grouted Defects in Grouted Splice Sleeve Connector Based on Wavelet Pack Energy. Sensors 2019, 19, 1642. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.L.; Wei, G.S.; Liu, Z.H.; Chen, X.D.; Wang, X.J. Detection of prefabricated shear wall grouting anchor grouting compactness based on the impact echo method. J. Yangtze U. (Nat. Sci. Ed.) 2017, 14, 26–31. [Google Scholar]
- Gao, R.D.; Li, X.M.; Zhang, F.W.; Xu, Q.F.; Wang, Z.L.; Liu, H. Experiment on detection of coupler grouting compactness based on industrial X-CT. Nondestruct. Test. 2017, 4, 12–17. [Google Scholar]
- Li, X.M.; Gao, R.D.; Xu, Q.F.; Wang, Z.L.; Zhang, F.W.; Xie, Y. Study on inspection technology for sleeve grouting connection quality of precast shear wall based on X-ray digital radiography method. Build. Struct. 2018, 48, 57–61. [Google Scholar]
- Ghafari, E.; Yuan, Y.; Wu, C.; Nantung, T.; Lu, N. Evaluation the compressive strength of the cement paste blended with supplementary cementitious materials using a piezoelectric-based sensor. Constr. Build. Mater. 2018, 171, 504–510. [Google Scholar] [CrossRef]
- Su, Y.; Han, G.S.; Amran, A.; Nantung, T.; Lu, N. Instantaneous monitoring the early age properties of cementitious materials using PZT-based electromechanical impedance (EMI) technique. Constr. Build. Mater. 2019, 225, 340–347. [Google Scholar] [CrossRef]
- Su, Y.; Kotian, R.R.; Lu, N. Energy harvesting potential of bendable concrete using polymer based piezoelectric generator. Compos. Part B Eng. 2018, 153, 124–129. [Google Scholar] [CrossRef]
- Roh, Y.S. Built in Diagnostics for Identifying an Anomaly in Plates Using Wave Scattering. Ph.D. Thesis, Stanford University, Palo Alto, CA, USA, 1999. [Google Scholar]
- Song, G.; Gu, H.; Mo, Y.L. Concrete structural health monitoring using embedded piezoceramic transducers. Smart Mater. Struct. 2007, 16, 959–968. [Google Scholar] [CrossRef] [Green Version]
- Song, G.; Gu, H.; Mo, Y.L. Smart aggregate: Multi-functional sensors for concrete structures-a tutorial and review. Smart Mater. Struct. 2008, 17, 033001. [Google Scholar] [CrossRef]
- Yen, G.G.; Lin, K.C. Wavelet packet feature extraction for vibration monitoring. IEEE Trans. Ind. Electron. 2000, 47, 650–667. [Google Scholar] [CrossRef] [Green Version]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Jiang, T.Y.; Hong, Y.; Zheng, J.B.; Wang, L.; Gu, H.C. Crack Detection of FRP-Reinforced Concrete Beam Using Embedded Piezoceramic Smart Aggregates. Sensors 2019, 19, 1979. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Li, B.; Song, G.B. Active debonding detection for large rectangular CFSTs based on wavelet packet energy spectrum with piezoceramics. J. Struct. Eng. 2012, 139, 1435–1443. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, T.; Song, G.; Gu, H.C. Active interface debonding detection of a concrete-filled steel tube with piezoelectric technologies using wavelet packet analysis. Mech. Syst. Signal. Process. 2013, 36, 7–17. [Google Scholar] [CrossRef]
- Hu, H.F.; Staszewski, W.J.; Hu, N.Q.; Jenal, R.B.; Qin, G.J. Crack detection using nonlinear acoustics and piezoceramic transducers-instantaneous amplitude and frequency analysis. Smart Mater. Struct. 2010, 19, 065017. [Google Scholar] [CrossRef]
- Hong, X.B.; Liu, Y.; Liufu, Y.H.; Lin, P.S. Debonding Detection in Hidden Frame Supported Glass Curtain Walls Using the Nonlinear Ultrasonic Modulation Method with Piezoceramic Transducers. Sensors 2018, 18, 2094. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, T.Y.; Kong, Q.Z.; Wang, W.X.; Huo, L.S.; Song, G. Monitoring of grouting compactness in a post-tensioning tendon duct using piezoceramic transducers. Sensors 2016, 16, 1343. [Google Scholar] [CrossRef] [Green Version]
- Jiang, T.Y.; Zheng, J.B.; Huo, L.S.; Song, G. Finite element analysis of grouting compactness monitoring in a post –tensioning tendon duct using piezoceramic transducers. Sensors 2017, 17, 2239. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Luo, M.; Hei, C.; Song, G. Quantitative evaluation of compactness of concrete-filled fiber-reinforced polymer tubes using piezoceramic transducers and time difference of arrival. Smart Mater. Struct. 2018, 27, 035023. [Google Scholar] [CrossRef]
- Leo, M.; Looney, D.; D’Orazio, T.; Mandic, D.P. Identification of Defective Areas in Composite Materials by Bivariate EMD Analysis of Ultrasound. IEEE Trans. Instrum. Meas. 2011, 61, 221–232. [Google Scholar] [CrossRef]
- Wu, C.; Zhou, R.Z. Nonlinear behavior analysis of structural dynamic response based on Hilbert spectrum. J. Vib. Shock 2013, 32, 70–76. [Google Scholar]
- Hong, X.B.; Liu, Y.; Lin, X.H.; Luo, Z.Q.; He, Z.W. Nonlinear ultrasonic detection method for delamination damage of lined anti-corrosion pipes using PZT transducers. Appl. Sci. 2018, 8, 2240. [Google Scholar] [CrossRef] [Green Version]
- Standards Press of China. JG/T 408-2013: Cementitious Grout for Coupler of Rebar Splicing, Ministry of Housing and Urban-Rural Development of the People’s Republic of China; Standards Press of China: Beijing, China, 2013. [Google Scholar]
- Sampath, S.; Bhattacharya, B.; Aryan, P.; Sohn, H. A Real-Time, Non-Contact Method for In-Line Inspection of Oil and Gas Pipelines Using Optical Sensor Array. Sensors 2019, 19, 3615. [Google Scholar] [CrossRef] [Green Version]





| Type | Density (g/cm3) | Coupling Factor | Dielectric Constant | Dielectric Loss | Piezoelectric Coefficient | Curie Temperature (°C) | Mechanical Quality Factor |
|---|---|---|---|---|---|---|---|
| PZT-5 | 7.6 | 0.62 | 2200 | 2 | 500 | 270 | 80 |
| Tested Property | Performance Index | Measured Value | |
|---|---|---|---|
| Fluidity/mm | Initial 30 min 1 d | ≥300 ≥260 ≥35 | 355 306 58.5 |
| Compressive strength/MPa | 3 d 28 d | ≥60 ≥85 | 90.7 122.2 |
| Rate of upright direction expansion/% | Difference between 24 and 3 h | ≥0.02 0.02–0.5 | 0.683 0.225 |
| Methods | WPTEVs | HEPVs | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Grouting compactness of sleeve | 0% | 30% | 50% | 70% | 100% | 0% | 30% | 50% | 70% | 100% | |
| Serial Number | 1st group of A1S1 | 663.23 | 388.93 | 388.43 | 388.60 | 325.43 | 0.154 | 0.0485 | 0.0551 | 0.0641 | 0.0439 |
| 2nd group of A1S1 | 611.60 | 111.81 | 533.27 | 303.12 | 577.06 | 0.163 | 0.0013 | 0.1200 | 0.0358 | 0.1500 | |
| 3rd group of A1S1 | 714.09 | 510.44 | 418.36 | 400.41 | 288.51 | 0.196 | 0.114 | 0.0616 | 0.0645 | 0.0350 | |
| 1st group of A2S2 | 549.37 | 314.57 | 259.85 | 240.05 | 234.02 | 0.122 | 0.0452 | 0.0283 | 0.0194 | 0.0188 | |
| 2nd group of A2S2 | 455.73 | 435.46 | 382.89 | 254.81 | 250.92 | 0.072 | 0.0666 | 0.0625 | 0.0212 | 0.0207 | |
| 3rd group of A2S2 | 567.11 | 481.14 | 336.66 | 306.49 | 259.84 | 0.126 | 0.0897 | 0.0443 | 0.0357 | 0.0266 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.; Yang, C.; Ma, S.; Xu, X. Feasibility Study on Grouting Compactness Detection in Sleeves Using Piezoelectric Transducers. Appl. Sci. 2020, 10, 149. https://doi.org/10.3390/app10010149
Wu C, Yang C, Ma S, Xu X. Feasibility Study on Grouting Compactness Detection in Sleeves Using Piezoelectric Transducers. Applied Sciences. 2020; 10(1):149. https://doi.org/10.3390/app10010149
Chicago/Turabian StyleWu, Chen, Chao Yang, Shenglan Ma, and Xiaoliang Xu. 2020. "Feasibility Study on Grouting Compactness Detection in Sleeves Using Piezoelectric Transducers" Applied Sciences 10, no. 1: 149. https://doi.org/10.3390/app10010149
APA StyleWu, C., Yang, C., Ma, S., & Xu, X. (2020). Feasibility Study on Grouting Compactness Detection in Sleeves Using Piezoelectric Transducers. Applied Sciences, 10(1), 149. https://doi.org/10.3390/app10010149




