Histogram Based Clustering for Nonlinear Compensation in Long Reach Coherent Passive Optical Networks
Abstract
:1. Introduction
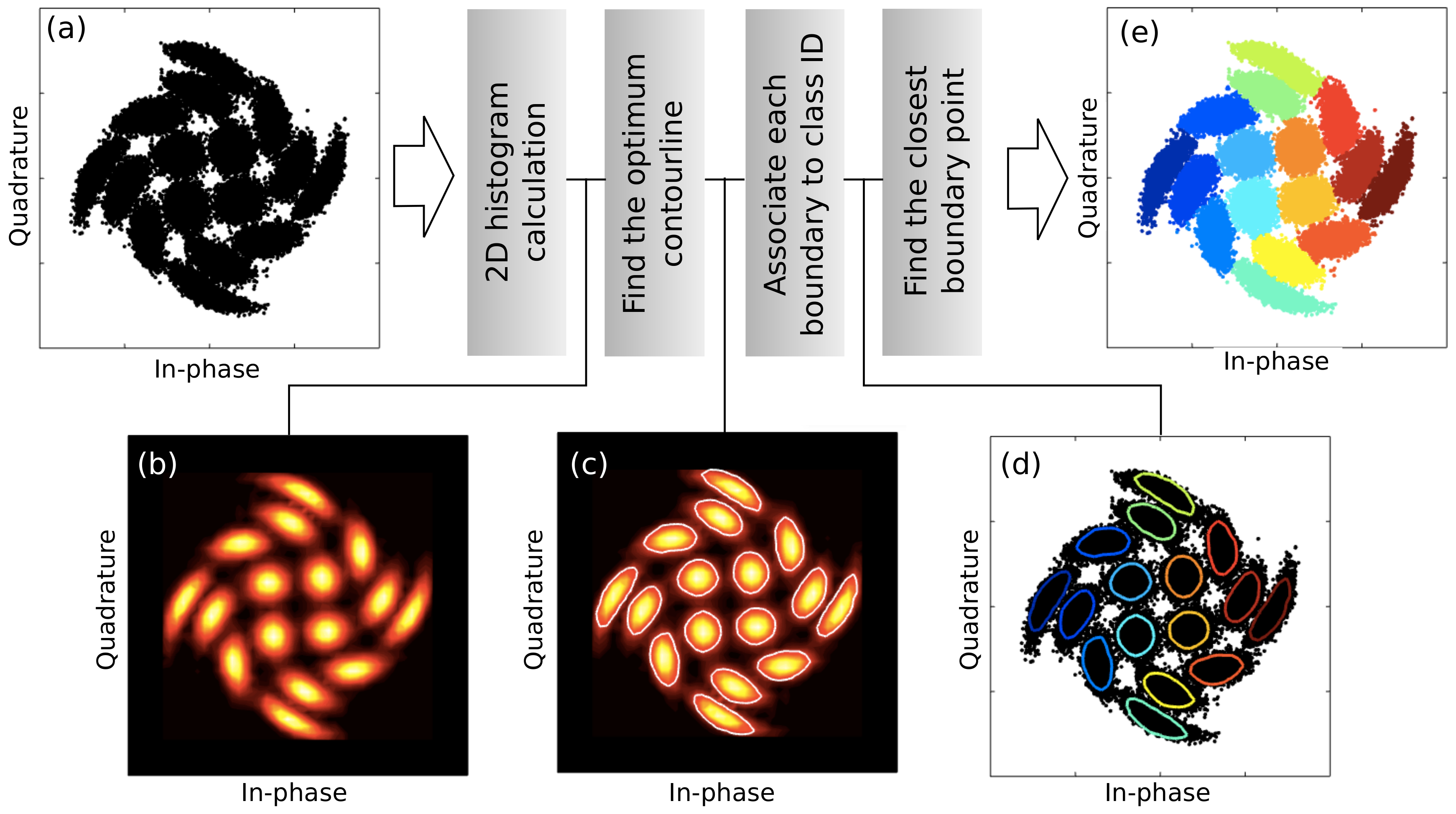
2. Histogram Based Clustering
- Calculation of the 2D histogram of the in-phase and quadrature components of the received distorted symbols.
- Find the lowest contour line in the histogram that results in M isolated islands, M being the number of clusters to be identified.
- Assign a class ID to the values of the boundary for each island.
- For each received symbol, find the closest boundary point and associate it with its class ID.
3. Simulation Setup
4. Results and Discussion
4.1. Performance Analysis
4.2. Block Size and Complexity Analysis
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PON | Passive optical network |
| LR | Long reach |
| DSP | Digital signal processor |
| SPM | Self-phase modulation |
| XPM | Cross-phase modulation |
| FWM | Four wave mixing |
| QAM | Quadrature amplitude modulation |
| DBP | Digital back-propagation |
| IVSTF | Inverse Volterra series transfer function |
| SVM | Support vector machine |
| DBSCAN | Density based spatial clustering of applications with noise |
| HBC | Histogram based clustering |
| LD | Laser diode |
| CW | Continuous-wave |
| DP-MZM | Dual parallel Mach–Zehnder modulator |
| EDFA | Erbium doped fibre amplifier |
| ASE | Amplified spontaneous emission |
| DAC | Digital to analogue converter |
| SSMF | Standard single mode fibre |
| DPT | Dynamic polarization tracker |
| ADC | Analogue-to-digital converter |
| BER | Bit error rate |
| SNR | Signal-to-noise ratio |
References
- Nesset, D. PON roadmap. IEEE/OSA J. Opt. Commun. Netw. 2017, 9, A71–A76. [Google Scholar] [CrossRef]
- Effenberger, F.J. Industrial trends and roadmap of access. J. Lightwave Technol. 2017, 35, 1142–1146. [Google Scholar] [CrossRef]
- Hsu, D.Z.; Wei, C.C.; Chen, H.Y.; Chen, J.; Yuang, M.C.; Lin, S.H.; Li, W.Y. 21 Gb/s after 100 km OFDM long reach PON transmission using a cost-effective electro-absorption modulator. Opt. Express 2010, 18, 27758–27763. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; He, J.; Chen, L. Real-time optical OFDM long reach PON system over 100 km SSMF using a directly modulated DFB laser. J. Opt. Commun. Netw. 2014, 6, 18–25. [Google Scholar] [CrossRef]
- Lavery, D.; Ionescu, M.; Makovejs, S.; Torrengo, E.; Savory, S.J. A long reach ultra-dense 10 Gbit/s WDM-PON using a digital coherent receiver. Opt. Express 2010, 18, 25855–25860. [Google Scholar] [CrossRef] [PubMed]
- Lavery, D.; Maher, R.; Millar, D.S.; Thomsen, B.C.; Bayvel, P.; Savory, S.J. Digital coherent receivers for long reach optical access networks. J. Lightwave Technol. 2013, 31, 609–620. [Google Scholar] [CrossRef]
- Liu, X.; Effenberger, F. ONU-dependent dispersion pre-compensation at OLT for high speed wide-coverage PON. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–5. [Google Scholar]
- Kikuchi, K. Fundamentals of coherent optical fibre communications. J. Lightwave Technol. 2016, 34, 157–179. [Google Scholar] [CrossRef]
- Kikuchi, K.; Tsukamoto, S. Evaluation of sensitivity of the digital coherent receiver. J. Lightwave Technol. 2008, 26, 1817–1822. [Google Scholar] [CrossRef]
- Ip, E.M.; Kahn, J.M. Fibre impairment compensation using coherent detection and digital signal processing. J. Lightwave Technol. 2009, 28, 502–519. [Google Scholar] [CrossRef]
- Vacondio, F.; Rival, O.; Simonneau, C.; Grellier, E.; Bononi, A.; Lorcy, L.; Antona, J.C.; Bigo, S. On nonlinear distortions of highly dispersive optical coherent systems. Opt. Express 2012, 20, 1022–1032. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear fibre optics. In Nonlinear Science at the Dawn of the 21st Century; Springer: Berlin, Germany, 2000; pp. 195–211. [Google Scholar]
- Gordon, J.P.; Mollenauer, L.F. Phase noise in photonic communications systems using linear amplifiers. Opt. Lett. 1990, 15, 1351–1353. [Google Scholar] [CrossRef] [PubMed]
- Lau, A.P.T.; Kahn, J.M. Signal design and detection in presence of nonlinear phase noise. J. Lightwave Technol. 2007, 25, 3008–3016. [Google Scholar] [CrossRef]
- Da Ros, F.; Sackey, I.; Elschner, R.; Richter, T.; Meuer, C.; Nölle, M.; Jazayerifar, M.; Petermann, K.; Peucheret, C.; Schubert, C. Kerr nonlinearity compensation in a 5× 28-GBd PDM 16-QAM WDM system using fibre based optical phase conjugation. In Proceedings of the 2014 The European Conference on Optical Communication (ECOC), Cannes, France, 21–25 September 2014; pp. 1–3. [Google Scholar]
- Ip, E.; Kahn, J.M. Compensation of dispersion and nonlinear impairments using digital backpropagation. J. Lightwave Technol. 2008, 26, 3416–3425. [Google Scholar] [CrossRef]
- Millar, D.S.; Makovejs, S.; Behrens, C.; Hellerbrand, S.; Killey, R.I.; Bayvel, P.; Savory, S.J. Mitigation of fibre nonlinearity using a digital coherent receiver. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1217–1226. [Google Scholar] [CrossRef]
- Pan, J.; Cheng, C.H. Nonlinear electrical predistortion and equalization for the coherent optical communication system. J. Lightwave Technol. 2011, 29, 2785–2789. [Google Scholar] [CrossRef]
- Giacoumidis, E.; Aldaya, I.; Jarajreh, M.A.; Tsokanos, A.; Le, S.T.; Farjady, F.; Jaouën, Y.; Ellis, A.D.; Doran, N.J. Volterra based reconfigurable nonlinear equalizer for coherent OFDM. IEEE Photonics Technol. Lett. 2014, 26, 1383–1386. [Google Scholar] [CrossRef]
- Alpaydin, E. Introduction to Machine Learning; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Zibar, D.; Piels, M.; Jones, R.; Schäeffer, C.G. Machine learning techniques in optical communication. J. Lightwave Technol. 2015, 34, 1442–1452. [Google Scholar] [CrossRef] [Green Version]
- Giacoumidis, E.; Lin, Y.; Wei, J.; Aldaya, I.; Tsokanos, A.; Barry, L. Harnessing machine learning for fibre-induced nonlinearity mitigation in long-haul coherent optical OFDM. Future Internet 2019, 11, 2. [Google Scholar] [CrossRef] [Green Version]
- Khan, F.N.; Lu, C.; Lau, A.P.T. Machine learning methods for optical communication systems. In Signal Processing in Photonic Communications; Optical Society of America: Washington, DC, USA, 2017; p. SpW2F-3. [Google Scholar]
- Mata, J.; De Miguel, I.; Duran, R.J.; Merayo, N.; Singh, S.K.; Jukan, A.; Chamania, M. Artificial intelligence (AI) methods in optical networks: A comprehensive survey. Opt. Switch. Netw. 2018, 28, 43–57. [Google Scholar] [CrossRef]
- Ahmad, S.T.; Kumar, K.P. Radial basis function neural network nonlinear equalizer for 16-QAM coherent optical OFDM. IEEE Photonics Technol. Lett. 2016, 28, 2507–2510. [Google Scholar] [CrossRef]
- Chen, E.; Tao, R.; Zhao, X. Channel equalization for OFDM system based on the BP neural network. In Proceedings of the 2006 8th international Conference on Signal Processing, Guilin, China, 16–20 November 2006; Volume 3. [Google Scholar]
- Jarajreh, M.A.; Giacoumidis, E.; Aldaya, I.; Le, S.T.; Tsokanos, A.; Ghassemlooy, Z.; Doran, N.J. Artificial neural network nonlinear equalizer for coherent optical OFDM. IEEE Photonics Technol. Lett. 2014, 27, 387–390. [Google Scholar] [CrossRef]
- Nguyen, T.; Mhatli, S.; Giacoumidis, E.; Van Compernolle, L.; Wuilpart, M.; Mégret, P. Fibre nonlinearity equalizer based on support vector classification for coherent optical OFDM. IEEE Photonics J. 2016, 8, 1–9. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, M.; Li, Z.; Cui, Y.; Liu, J.; Yang, Y.; Wang, H. Nonlinear decision boundary created by a machine learning based classifier to mitigate nonlinear phase noise. In Proceedings of the 2015 European Conference on Optical Communication (ECOC), Valencia, Spain, 27 September–1 October 2015; pp. 1–3. [Google Scholar]
- Giacoumidis, E.; Mhatli, S.; Nguyen, T.; Le, S.; Aldaya, I.; McCarthy, M.; Eggleton, B. Kerr-induced nonlinearity reduction in coherent optical OFDM by low complexity support vector machine regression based equalization. In Proceedings of the 2016 Optical Fibre Communications Conference and Exhibition (OFC), Anaheim, CA, USA, 20–24 March 2016; pp. 1–3. [Google Scholar]
- Zhang, J.; Chen, W.; Gao, M.; Shen, G. K-means-clustering based fibre nonlinearity equalization techniques for 64-QAM coherent optical communication system. Opt. Express 2017, 25, 27570–27580. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Yu, S.; Yang, J.; Chen, Z.; Han, Y.; Gu, W. Nonparameter nonlinear phase noise mitigation by using M-ary support vector machine for coherent optical systems. IEEE Photonics J. 2013, 5, 7800312. [Google Scholar] [CrossRef]
- Boada, R.; Borkowski, R.; Monroy, I.T. Clustering algorithms for Stokes space modulation format recognition. Opt. Express 2015, 23, 15521–15531. [Google Scholar] [CrossRef] [Green Version]
- Pakala, L.; Schmauss, B. Non-linear mitigation using carrier phase estimation and K-means clustering. In Proceedings of the Photonic Networks; 16. ITG Symposium, Leipzig, Germany, 7–8 May 2015; pp. 1–3. [Google Scholar]
- Giacoumidis, E.; Aldaya, I.; Wei, J.; Sanchez, C.; Mrabet, H.; Barry, L.P. Affinity propagation clustering for blind nonlinearity compensation in coherent optical OFDM. Proceedings of CLEO: Science and Innovations, San Jose, CA, USA, 15–17 May 2018; p. STh1C-5. [Google Scholar]
- Giacoumidis, E.; Lin, Y.; Barry, L.P. Fibre Nonlinear Compensation Using Machine Learning Clustering. In Proceedings of the 56th ICREIT conference, London, UK, 18–19 January 2019; pp. 1–4. [Google Scholar]
- Zibar, D.; Winther, O.; Franceschi, N.; Borkowski, R.; Caballero, A.; Arlunno, V.; Schmidt, M.N.; Gonzales, N.G.; Mao, B.; Ye, Y.; et al. Nonlinear impairment compensation using expectation maximization for dispersion managed and unmanaged PDM 16-QAM transmission. Opt. Express 2012, 20, B181–B196. [Google Scholar] [CrossRef] [Green Version]
- Pfau, T.; Hoffmann, S.; Noé, R. Hardware-efficient coherent digital receiver concept with feedforward carrier recovery for M-QAM constellations. J. Lightwave Technol. 2009, 27, 989–999. [Google Scholar] [CrossRef]
- Yang, J.; Werner, J.J.; Dumont, G.A. The multimodulus blind equalization and its generalized algorithms. IEEE J. Sel. Areas Commun. 2002, 20, 997–1015. [Google Scholar] [CrossRef]
- Lathi, B.P. Modern Digital and Analogue Communication Systems; Oxford University Press, Inc.: Oxford, UK, 1998. [Google Scholar]




| System Parameters | |||
|---|---|---|---|
| Laser linewidth | 0.5 MHz | Fibre lengths (L,L) | 80 km, 0–20 km |
| Laser power | 1 mW | Fibre attenuation | 0.2 dB |
| MZM insertion loss | 6 dB | Fibre chromatic dispersion | 16 ps/nm/km |
| Amplifier gain | 20 dB | Fibre PMD | 3.16 |
| Amplifier noise figure | 4 dB | Nonlinear coefficient () | 1.3·W·km |
| Attenuator | 20 dB | Fibre effective area | 80 m |
| PD thermal noise density | 10 pA/ | Electrical filter bandwidth | 10.5 GHz |
| PD responsivity | 1 W/A | Electrical RX filter order | 4 |
| Signal parameters | |||
| Modulation format | 16-QAM | No. of synchronization symbols | 64 |
| Electrical TX filter | 4th-order Bessel | Bit rate | 56 Gbps |
| Simulation parameters | |||
| Number of simulated symbols | 16,384 | Sampling rate | s−1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aldaya, I.; Giacoumidis, E.; de Oliveira, G.; Wei, J.; Pita, J.L.; Marconi, J.D.; Fagotto, E.A.M.; Barry, L.; Abbade, M.L.F. Histogram Based Clustering for Nonlinear Compensation in Long Reach Coherent Passive Optical Networks. Appl. Sci. 2020, 10, 152. https://doi.org/10.3390/app10010152
Aldaya I, Giacoumidis E, de Oliveira G, Wei J, Pita JL, Marconi JD, Fagotto EAM, Barry L, Abbade MLF. Histogram Based Clustering for Nonlinear Compensation in Long Reach Coherent Passive Optical Networks. Applied Sciences. 2020; 10(1):152. https://doi.org/10.3390/app10010152
Chicago/Turabian StyleAldaya, Ivan, Elias Giacoumidis, Geraldo de Oliveira, Jinlong Wei, Julián Leonel Pita, Jorge Diego Marconi, Eric Alberto Mello Fagotto, Liam Barry, and Marcelo Luis Francisco Abbade. 2020. "Histogram Based Clustering for Nonlinear Compensation in Long Reach Coherent Passive Optical Networks" Applied Sciences 10, no. 1: 152. https://doi.org/10.3390/app10010152
APA StyleAldaya, I., Giacoumidis, E., de Oliveira, G., Wei, J., Pita, J. L., Marconi, J. D., Fagotto, E. A. M., Barry, L., & Abbade, M. L. F. (2020). Histogram Based Clustering for Nonlinear Compensation in Long Reach Coherent Passive Optical Networks. Applied Sciences, 10(1), 152. https://doi.org/10.3390/app10010152








