Experimental and Numerical Investigation of Striker Shape Influence on the Destruction Image in Multilayered Composite after Low Velocity Impact
Abstract
:1. Introduction
2. Experimental Research
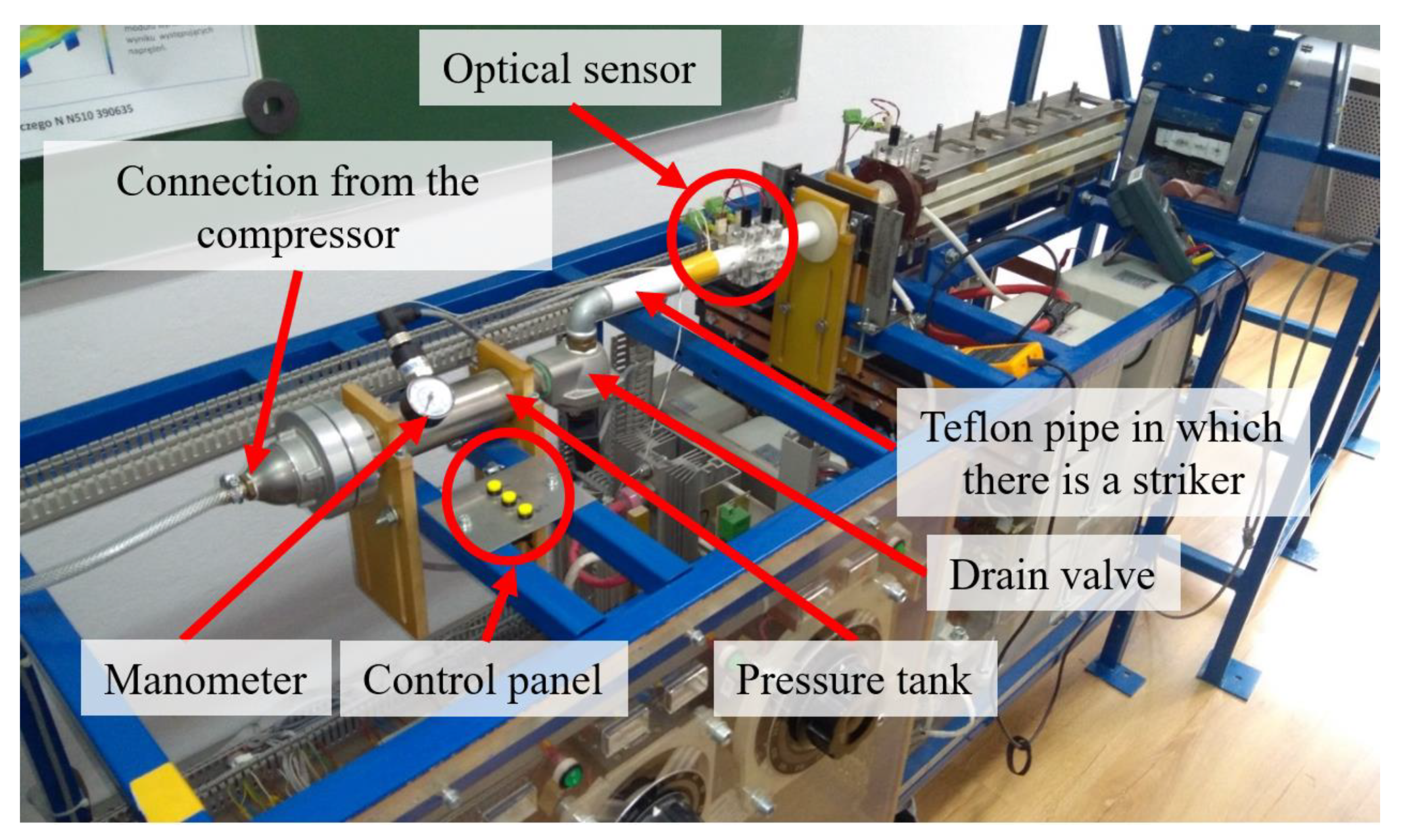
2.1. Methodology
2.2. Results
3. Numerical Research
3.1. Preparation of Numerical Model
3.2. Numerical Results
3.3. Comparison of Experimental and Numerical Research
3.4. Delamination
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
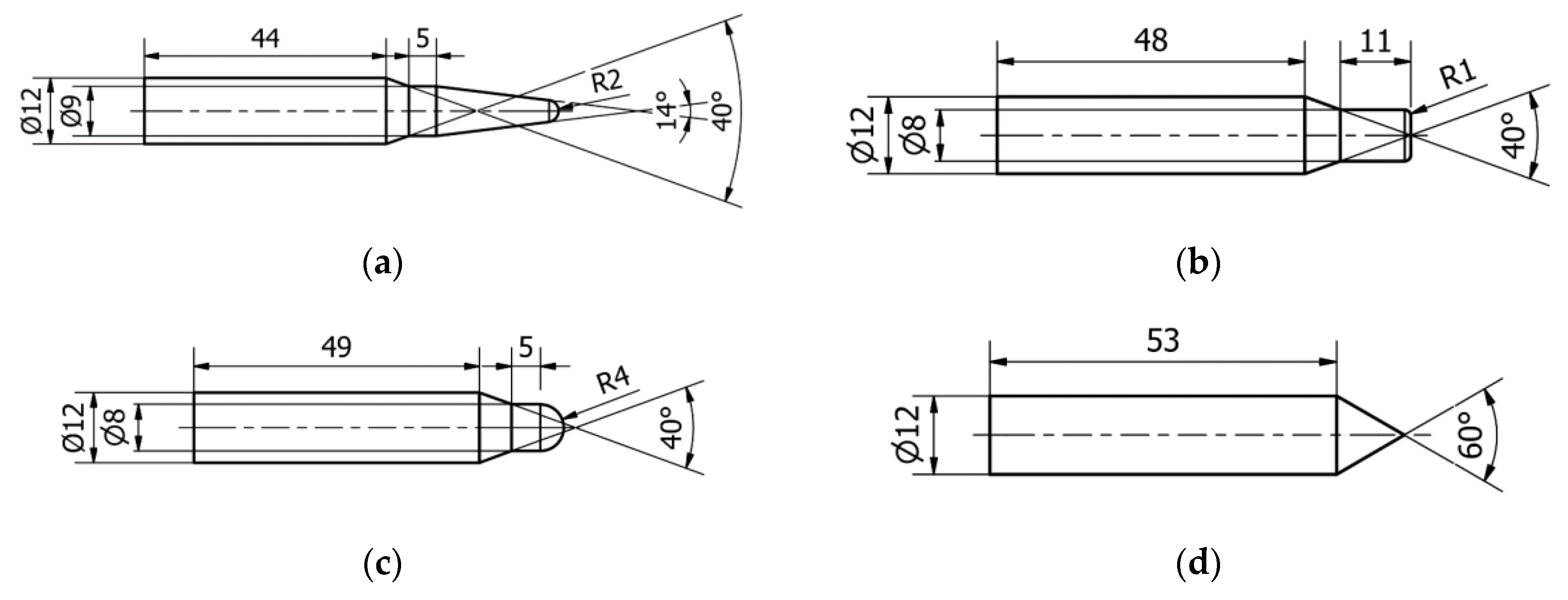
Appendix B

Appendix C




References
- Jureczko, M. Multidisciplinary Optimization of Wind Turbine Blades with Respect to Minimize Vibrations. In Recent Advances in Composite Materials for Wind Turbine Blade; Attaf, B., Ed.; The World Academic Publishing Co. Ltd.: Hong Kong, China, 2013; pp. 129–146. [Google Scholar]
- Pawlak, M. The Acceleration Severity Index in the impact of a vehicle against permanent road equipment support structures. Mech. Res. Commun. 2016, 77, 21–28. [Google Scholar] [CrossRef]
- Szymiczek, M. Selection of engineering materials on lightweight energy-intensive shields. Poly. Process. 2016, 22, 149–157. [Google Scholar]
- Chatys, R.; Kleinhofs, M.; Panich, A.; Kisiel, M. Modeling of mechanical properties of composite structures taking into account military needs. AIP Conf. Proc. 2019, 2077, 1–8. [Google Scholar] [CrossRef]
- MIL-STD-662F Military Standard: V50 Ballistic Test for Armor; Department of Defense: Washington, DC, USA, 1997.
- STANAG 4569 Protection Levels for Logistic and Light Armoured Vehicle Occupants; NATO/PFP Unclassified; NATO: Brussels, Belgium, 1998.
- Rojek, M.; Szymiczek, M.; Stabik, J.; Mężyk, A.; Jamroziak, K.; Krzystała, E.; Kurowski, J. Composite materials with the polymeric matrix applied to ballistic shields. Arch. Mater. Sci. Eng. 2013, 63, 26–35. [Google Scholar]
- Machoczek, T.; Mężyk, A.; Duda, S. Shaping the dynamic characteristics of military special vehicles. Solid State Phenom. 2016, 248, 192–203. [Google Scholar] [CrossRef]
- Krzystała, E.; Kciuk, S.; Mężyk, A. Identification of Hazards for the Crew of Special Vehicles during an Explosion; Wydawnictwo Naukowe Instytutu Technologii Eksploatacji: Gliwice, Poland, 2012. [Google Scholar]
- Jureczko, M.; Mężyk, A. Multidisciplinary optimization of wind turbine blades. In Proceedings of the Fourth European & African Conference on Wind Engineering, EACWE 4, Prague, Czech Republic, 11–15 July 2005; Naprstek, J., Ed.; Institute of Theoretical and Applied Mechanics, Academy of Sciences of the Czech Republic: Prague, Czech Republic, 2005; pp. 40–46. [Google Scholar]
- Cegła, M.; Habaj, W.; Stępniak, W.; Podgórzak, P. Hybrid ceramic-textile composite armour structures for a strengthened bulled-proof vest. Fibres Text. East. Eur. 2015, 23, 85–88. [Google Scholar]
- Lane, R.A. High performance fibers for personnel and vehicle armor systems. Putting a stop to current and future threats. Amptiac Q. 2005, 9, 3–9. [Google Scholar]
- Radziszewski, L. Final Ballistics of Small-Caliber Ammunition When Shooting at Selected Targets; Wydawnictwo Politechniki Świętokrzyskiej: Kielce, Poland, 2007. [Google Scholar]
- Czapla, T.; Wrona, J. Technology development of military applications of unmanned ground vehicles. Stud. Comput. Intell. 2013, 481, 293–309. [Google Scholar] [CrossRef]
- Nabaglo, T.; Kowal, J.; Jurkiewicz, A. Construction of a parametrized tracked vehicle model and its simulation in MSC.ADAMS program. J. Low Freq. Noise Vib. Act. Control 2013, 32, 167–173. [Google Scholar] [CrossRef] [Green Version]
- Jamroziak, K. Identification of Materials Properties in Terminal Ballistics; Oficyna Wydawnicza Politechniki Wrocławskiej: Wroclaw, Poland, 2013. [Google Scholar]
- Wersa, E.; Seweryn, A.; Szusta, J.; Rak, Z. Fatigue testing of transmission gear. Maint. Reliab. 2015, 17, 207–214. [Google Scholar] [CrossRef] [Green Version]
- Ostachowicz, W.M.; Krawczuk, M.; Palacz, M. Detection of delamination in multilayer composite beams. Key Eng. Mater. 2003, 245–246, 483–490. [Google Scholar] [CrossRef]
- Palacz, M. Spectral methods for modelling of wave propagation in structures in terms of damage detection—A review. Appl. Sci. 2018, 8, 1124. [Google Scholar] [CrossRef] [Green Version]
- Boczkowska, A.; Kapuściński, J.; Lindemann, Z.; Witemberg-Perzyk, D.; Wojciechowski, S. Composites; Oficyna Wydawnicza Politechniki Warszawskiej: Warsaw, Poland, 2000. [Google Scholar]
- Kang, T.J.; Kim, C. Impact energy absorption mechanism of largely deformable composites with different reinforcing structures. Fibers Polym. 2000, 1, 45–54. [Google Scholar] [CrossRef]
- Naik, N.K.; Shrirao, P.; Reddy, B.C.K. Ballistic impact behaviour of woven fabric composites: Formulation. Int. J. Impact Eng. 2006, 32, 1521–1552. [Google Scholar] [CrossRef]
- Hogg, P.J. Composites for ballistic applications. Proc. Compos. Process. 2003, 1–11. [Google Scholar]
- Sławski, S.; Szymiczek, M.; Domin, J. Influence of the reinforcement on the destruction image of the composites panels after applying impact load. AIP Conf. Proc. 2019, 2077, 1–10. [Google Scholar] [CrossRef]
- Fejdyś, M.; Łandwijt, M. Technical fibres reinforcing the composite material. Tech. Tex. 2010, 18, 12–22. [Google Scholar]
- Sławski, S.; Szymiczek, M.; Chmielnicki, B. Puncture resistance of epoxy-carbon composites subjected to ageing process in the thermal shock conditions. Polym. Process. 2018, 24, 52–60. [Google Scholar]
- Kaczmarczyk, J.; Kozłowska, A.; Grajcar, A.; Sławski, S. Modelling and microstructural aspects of ultra-thin sheet metal bundle cutting. Metals 2019, 9, 162. [Google Scholar] [CrossRef] [Green Version]
- Kaczmarczyk, J. Modelling of guillotine cutting of a cold-rolled steel sheet. Materials 2019, 12, 2954. [Google Scholar] [CrossRef] [Green Version]
- Xiong, X.; Xiao, Q. Meso-scale simulation of concrete based on fracture and interaction behavior. Appl. Sci. 2019, 9, 2986. [Google Scholar] [CrossRef] [Green Version]
- Cho, J.-R. A numerical evaluation of SIFs of 2-D functionally graded materials by enriched natural element method. Appl. Sci. 2019, 9, 3581. [Google Scholar] [CrossRef] [Green Version]
- Wróbel, G.; Szymiczek, M.; Kaczmarczyk, J. Influence of the structure and number of reinforcement layers on the stress state in the shells of tanks and pressure pipes. Mech. Compos. Mater. 2017, 53, 165–178. [Google Scholar] [CrossRef]
- Ochelski, S. Experimental Methods of Construction Composites Mechanics; Wydawnictwa Naukowo-Techniczne: Warsaw, Poland, 2004. [Google Scholar]
- Naik, N.K.; Ramasimha, R.; Arya, H.; Prabhu, S.V.; ShamaRao, N. Impact response and damage tolerance characteristics of glass–carbon/epoxy hybrid composite plates. Compos. Part B Eng. 2001, 32, 565–574. [Google Scholar] [CrossRef]
- Hosur, M.V.; Adbullah, M.; Jeelani, S. Studies on the low-velocity impact response of woven hybrid composites. Compos. Struct. 2005, 67, 253–262. [Google Scholar] [CrossRef]
- Ying, S.; Mengyun, T.; Zhijun, R.; Baohui, S.; Li, C. An experimental investigation on the low-velocity impact response of carbon-aramid/epoxy hybrid composite laminates. J. Reinf. Plast. Compos. 2017, 36, 422–434. [Google Scholar] [CrossRef]
- Rodríguez-Millán, M.; Ito, T.; Loya, J.A.; Olmedo, A.; Miguélez, M.H. Development of numerical model for ballistic resistance evaluation of combat helmet and experimental validation. Mater. Des. 2016, 110, 391–403. [Google Scholar] [CrossRef] [Green Version]
- Tan, L.B.; Tse, K.M.; Lee, H.P.; Tan, V.B.C.; Lim, S.P. Performance of an advanced combat helmet with different interior cushioning systems in ballistic impact: Experiments and finite element simulations. Int. J. Impact Eng. 2012, 50, 99–112. [Google Scholar] [CrossRef]
- Tham, C.Y.; Tan, V.B.C.; Lee, H.P. Ballistic impact of a KEVLAR® helmet: Experiment and simulations. Int. J. Impact Eng. 2008, 35, 304–318. [Google Scholar] [CrossRef]
- Mayer, P.; Pyka, D.; Jamroziak, K.; Pach, J.; Bocian, M. Experimental and numerical studies on ballistic laminates on the polyethylene and polypropylene matrix. J. Mech. 2019, 35, 187–197. [Google Scholar] [CrossRef]
- Bandaru, A.K.; Chavan, V.V.; Ahmad, S.; Alagirusamy, R.; Bhatnagar, N. Ballistic impact response of Kevlar® reinforced thermoplastic composite armors. Int. J. Impact Eng. 2016, 89, 1–13. [Google Scholar] [CrossRef]
- Pach, J.; Mayer, P.; Jamroziak, K.; Polak, S.; Pyka, D. Experimental analysis of puncture resistance of aramid laminates on styrene-butadiene-styrene and epoxy resin matrix for ballistic applications. Arch. Civ. Mech. Eng. 2019, 19, 1327–1337. [Google Scholar] [CrossRef]
- Reis, P.N.B.; Ferreira, J.A.M.; Zhang, Z.Y.; Benameur, T.; Richardson, M.O.W. Impact response of Kevlar composites with nanoclay enhanced epoxy matrix. Compos. Part B Eng. 2013, 46, 7–14. [Google Scholar] [CrossRef]
- Sarasini, F.; Tirillò, J.; Valente, M.; Ferrante, L.; Cioffi, S.; Iannace, S.; Sorrentino, L. Hybrid composites based on aramid and basalt woven fabrics: Impact damage modes and residual flexural properties. Mater. Des. 2013, 49, 290–302. [Google Scholar] [CrossRef]
- Gustin, J.; Joneson, A.; Mahinfalah, M.; Stone, J. Low velocity impact of combination Kevlar/carbon fiber sandwich composites. Compos. Struct. 2005, 69, 396–406. [Google Scholar] [CrossRef]
- Ulven, C.; Vaidya, U.K.; Hosur, M.V. Effect of projectile shape during ballistic perforation of VARTM carbon/epoxy composite panels. Compos. Struct. 2003, 61, 143–150. [Google Scholar] [CrossRef]
- Rodríguez Millán, M.; Moreno, C.E.; Marco, M.; Santiuste, C.; Miguélez, H. Numerical analysis of the ballistic behaviour of Kevlar® composite under impact of double-nosed stepped cylindrical projectiles. J. Reinf. Plast. Compos. 2016, 35, 124–137. [Google Scholar] [CrossRef] [Green Version]
- Mitsubishi Chemical Corporation—Information Brochure. Available online: https://www.m-chemical.co.jp/en/products/departments/mcc/cfcm/product/CFtow_Jul2018en.pdf (accessed on 25 November 2019).
- Twaron—Information Brochure. Available online: https://www.fibermaxcomposites.com/shop/datasheets/aramidFiberMDS.pdf (accessed on 25 November 2019).
- GRM Systems sp. z o. o.—Product Datasheet: Epoxy Resin LG 285 + Hardeners HG 285, HG 286, HG 287. Date of Modification: 11 April 2012. Available online: http://www.grm-systems.cz/en/epoxy (accessed on 11 April 2012).
- Kroczek, R.; Domin, J. Project of an pneumatic drive unit as initial decelerator of hybrid electromagnetic launcher. Electr. Mach. Proc. Note 2015, 108, 89–94. [Google Scholar]
- Heimbs, S.; Heller, S.; Middendorf, P.; Hähnel, F.; Weiße, J. Low velocity impact on CFRP plates with compressive preload: Test and modelling. Int. J. Impact Eng. 2009, 36, 1182–1193. [Google Scholar] [CrossRef]
- Bresciani, L.; Manes, A.; Ruggiero, A.; Iannitti, G.; Giglio, M. Experimental tests and numerical modelling of ballistic impacts against Kevlar 29 plain-woven fabrics with an epoxy matrix: Macro-homogeneous and meso-heterogeneous approaches. Compos. Part B Eng. 2016, 88, 114–130. [Google Scholar] [CrossRef]
- Manes, A.; Bresciani, L.M.; Giglio, M. Ballistic performance of multi-layered composite plates impacted by different 7.62 mm calibre projectiles. Proc. Eng. 2014, 88, 208–215. [Google Scholar] [CrossRef] [Green Version]
- Heimbs, S.; Bergmann, T.; Schueler, D.; Toso-Pentecôte, N. High velocity impact on preloaded composite plates. Compos. Struct. 2014, 111, 158–168. [Google Scholar] [CrossRef]
- Hallquist, J.O. LS-DYNA® Keyword User’s Manual Volume II; LS-DYNA R11; Livermore Software Technology Corporation: Livemore, CA, USA, 2018. [Google Scholar]
- Jackson, K.E.; Littell, J.D.; Fasanella, E.L. Simulating the impact response of composite airframe components. In Proceedings of the 13th International LS-DYNA Users Conference, Hampton, VA, USA, 8–10 June 2014; pp. 1–26. [Google Scholar]
- Cherniaev, A.; Montesano, J.; Butcher, C. Modeling the axial crush response of CFRP tubes using MAT054, MAT058 and MAT262 in LS-DYNA®. In Proceedings of the 15th International LS-DYNA® Users Conference, Detroit, MI, USA, 10–12 June 2018; pp. 1–17. [Google Scholar]
- Performance Composites Limited. Available online: http://www.performance-composites.com/carbonfibre/mechanicalproperties_2.asp (accessed on 12 September 2019).
- Dogan, F.; Hadavinia, H.; Donchev, T.; Bhonge, P. Delamination of impacted composite structures by cohesive zone interface elements and tiebreak contact. Cent. Eur. J. Eng. 2012, 2, 612–626. [Google Scholar] [CrossRef] [Green Version]
- Elmarakbi, A.M.; Nu, H.; Fukunaga, H. Finite element simulation of delamination growth in composite materials using LS-DYNA. Compos. Sci. Technol. 2009, 69, 2283–2391. [Google Scholar] [CrossRef] [Green Version]
- Muflahi, S.A.; Mohamed, G.; Hallett, S.R. Investigation of delamination modeling capabilities for thin composite structures in LS-DYNA®. In Proceedings of the 13th International LS-DYNA Users Conference, Detroit, MI, USA, 8–10 June 2014; pp. 1–14. [Google Scholar]
- Garcia, C.; Trendafilova, I.; Zucchelli, A. The effect of polycaprolactone nanofibers on the dynamic and impact behavior of glass fibre reinforced polymer composites. J. Compos. Sci. 2018, 2, 43. [Google Scholar] [CrossRef] [Green Version]
- Hallquist, J.O. LS-DYNA® Keyword User’s Manual Volume I; LS-DYNA R11; Livermore Software Technology Corporation: Livemore, CA, USA, 2018. [Google Scholar]
- Das, S.; Jagan, S.; Shaw, A.; Pal, A. Determination of inter-yarn friction and its effect on ballistic response of para-aramid woven fabric under low velocity impact. Compos. Struct. 2015, 120, 129–140. [Google Scholar] [CrossRef]
- Rao, M.; Nilakantan, G.; Keefe, M.; Powers, B.; Bogetti, T. Global/Local Modeling of Ballistic Impact onto Woven Fabrics. J. Compos. Mater. 2009, 43, 445–467. [Google Scholar] [CrossRef]
- INEOS Olefins & Polymers USA—Information Brochure. Available online: https://www.ineos.com/globalassets/ineos-group/businesses/ineos-olefins-and-polymers-usa/products/technical-information--patents/ineos-typical-engineering-properties-of-hdpe.pdf (accessed on 12 September 2019).
- Garcia, C.; Trendafilova, I. Triboelectric sensor as a dual system for impact monitoring and prediction of the damage in composite structures. NANO Energy 2019, 60, 527–535. [Google Scholar] [CrossRef] [Green Version]
- Will, M.A.; Franz, T.; Nurick, G.N. The effect of laminate stacking sequence of CFRP filament wound tubes subjected to projectile impact. Compos. Struct. 2002, 58, 259–270. [Google Scholar] [CrossRef]
- Mitrevski, T.; Marshall, I.H.; Thomson, R.S.; Jones, R. Low-velocity impacts on preloaded GFRP specimens with various impactor shapes. Compos. Struct. 2006, 76, 209–217. [Google Scholar] [CrossRef]
- Mitrevski, T.; Marshall, I.H.; Thomson, R.S.; Jones, R.; Whittingham, B. The effect of impactor shape on the impact response of composite laminates. Compos. Struct. 2005, 67, 139–148. [Google Scholar] [CrossRef]















| Parameter | Unit | Twaron 2200 | Pyrofil TR30 S |
|---|---|---|---|
| Elongation at break [%] | % | 2.9 | 1.8 |
| Tensile strength [MPa] | MPa | 2930 | 4120 |
| Tensile modulus | GPa | 102 | 235 |
| Parameter | Unit | Value |
|---|---|---|
| Flexural modulus | MPa | 2700–3300 |
| Tensile strength | MPa | 75–85 |
| Compressive strength | MPa | 130–150 |
| Elongation at break | % | 5–6.5 |
| Hardness in Shore D scale | - | 85 |
| Striker Geometry | Average Striker Velocity [m/s] | Average Kinetic Energy [J] | Average Cavity Diameter [mm] | Average Depth of Penetration [mm] |
|---|---|---|---|---|
| Conical | 30.99 | 23.5 | 5.9 | 5.1 |
| Hemispherical | 30.98 | 23.5 | 6.2 | 1.5 |
| Blunt | 30.92 | 23.4 | 7.0 | 0.1 |
| Ogival | 31.05 | 23.6 | 4.7 | 4.5 |
| Material Properties | Epoxy Resin/Carbon Fiber | Epoxy Resin/Aramid Fiber |
|---|---|---|
| Young’s modulus E1 = E2 [MPa] | 70,000 | 30,000 |
| Shear modulus G12 [MPa] | 5000 | 5000 |
| Tensile strength XT = YT [MPa] | 600 | 480 |
| Compressive strength XC = YC [MPa] | 570 | 190 |
| Shear strength S [MPa] | 90 | 50 |
| Tensile strain εXT = εYT [%] | 0.85 | 1.6 |
| Compressive strain εXC = εYC [%] | 0.8 | 0.6 |
| Shear strain εS [%] | 1.8 | 1 |
| Density [g/cm3] | 1.6 | 1.4 |
| Poisson’s Ratio | 0.1 | 0.2 |
| Young’s Modulus [MPa] | Poisson’s Ratio | Density [g/cm3] |
|---|---|---|
| 701 | 0.4 | 0.946 |
| Striker Geometry | Cavity Diameter [mm] | Depth of Penetration [mm] |
|---|---|---|
| Conical | 8 | 6 |
| Hemispherical | 6 | 2 |
| Blunt | 7.5 | 0.07 |
| Ogival | 5.5 | 4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sławski, S.; Szymiczek, M.; Kaczmarczyk, J.; Domin, J.; Duda, S. Experimental and Numerical Investigation of Striker Shape Influence on the Destruction Image in Multilayered Composite after Low Velocity Impact. Appl. Sci. 2020, 10, 288. https://doi.org/10.3390/app10010288
Sławski S, Szymiczek M, Kaczmarczyk J, Domin J, Duda S. Experimental and Numerical Investigation of Striker Shape Influence on the Destruction Image in Multilayered Composite after Low Velocity Impact. Applied Sciences. 2020; 10(1):288. https://doi.org/10.3390/app10010288
Chicago/Turabian StyleSławski, Sebastian, Małgorzata Szymiczek, Jarosław Kaczmarczyk, Jarosław Domin, and Sławomir Duda. 2020. "Experimental and Numerical Investigation of Striker Shape Influence on the Destruction Image in Multilayered Composite after Low Velocity Impact" Applied Sciences 10, no. 1: 288. https://doi.org/10.3390/app10010288
APA StyleSławski, S., Szymiczek, M., Kaczmarczyk, J., Domin, J., & Duda, S. (2020). Experimental and Numerical Investigation of Striker Shape Influence on the Destruction Image in Multilayered Composite after Low Velocity Impact. Applied Sciences, 10(1), 288. https://doi.org/10.3390/app10010288






