A Modal Perturbation Method for Eigenvalue Problem of Non-Proportionally Damped System
Abstract
1. Introduction
2. Solution Scheme of Perturbation Method
2.1. Theoretical Background
2.2. Corresponding Proportionally Damped System
2.3. Modal Perturbation Method
3. Verification with Numerical Examples
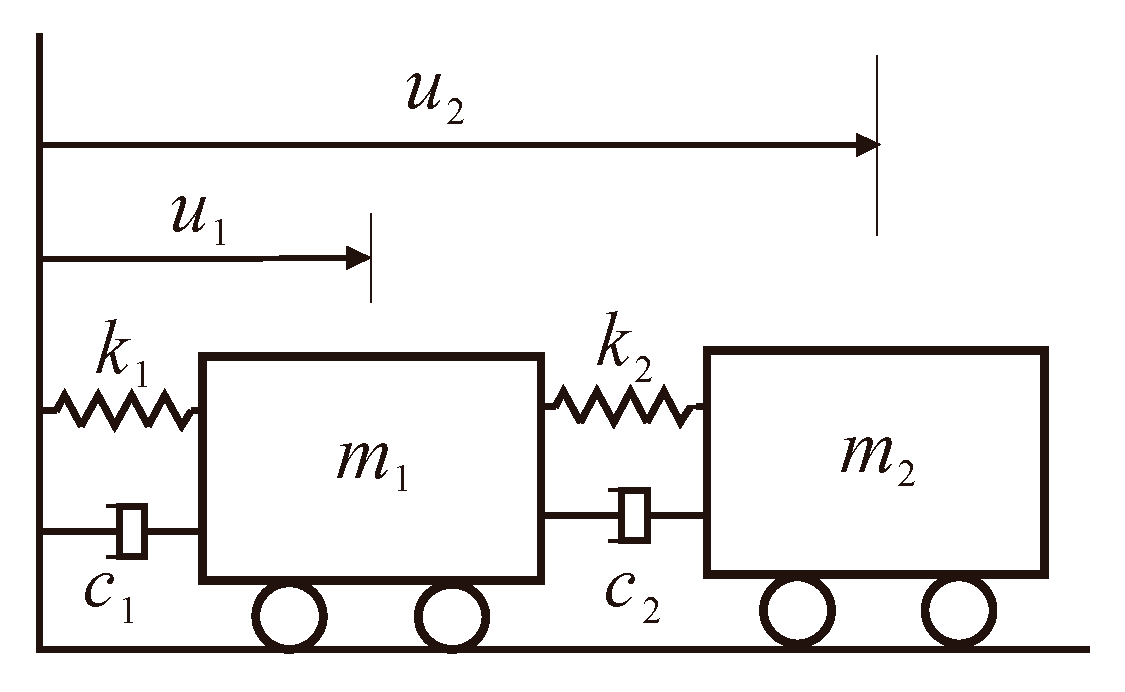
3.1. Two Degrees-Of-Freedom System
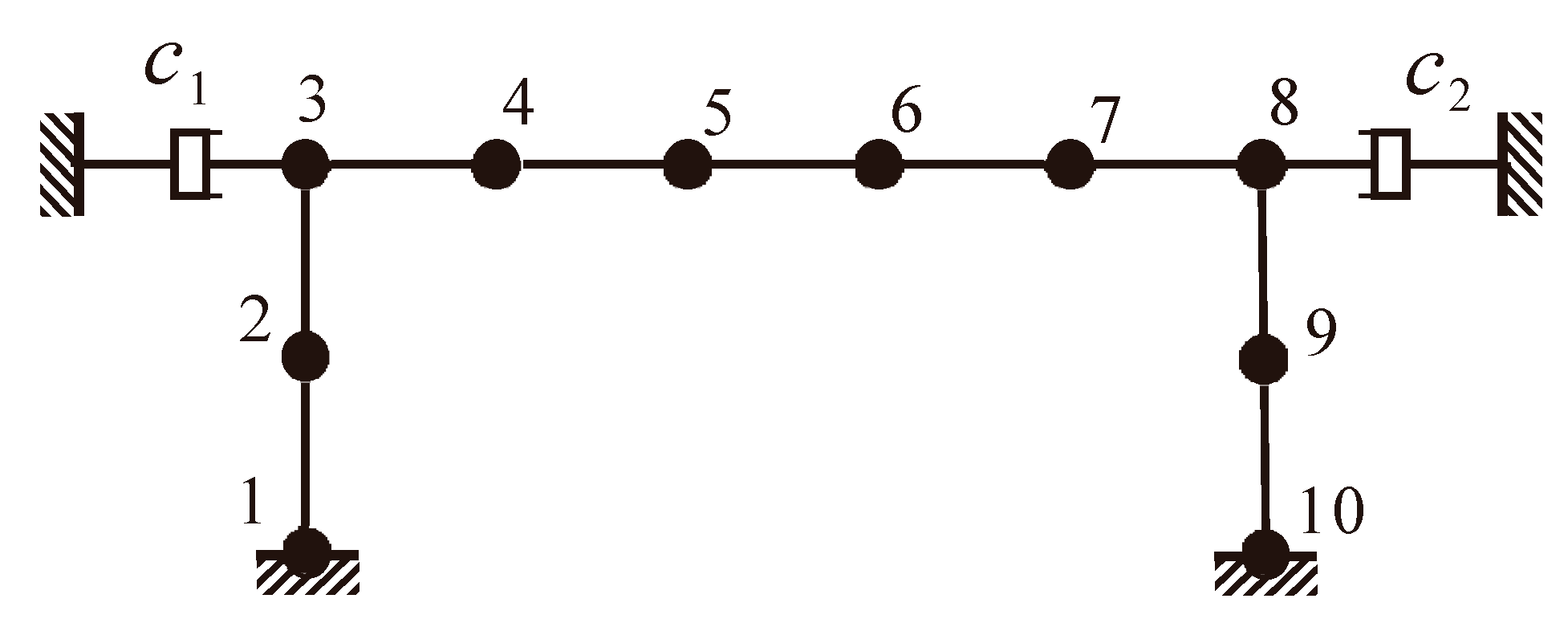
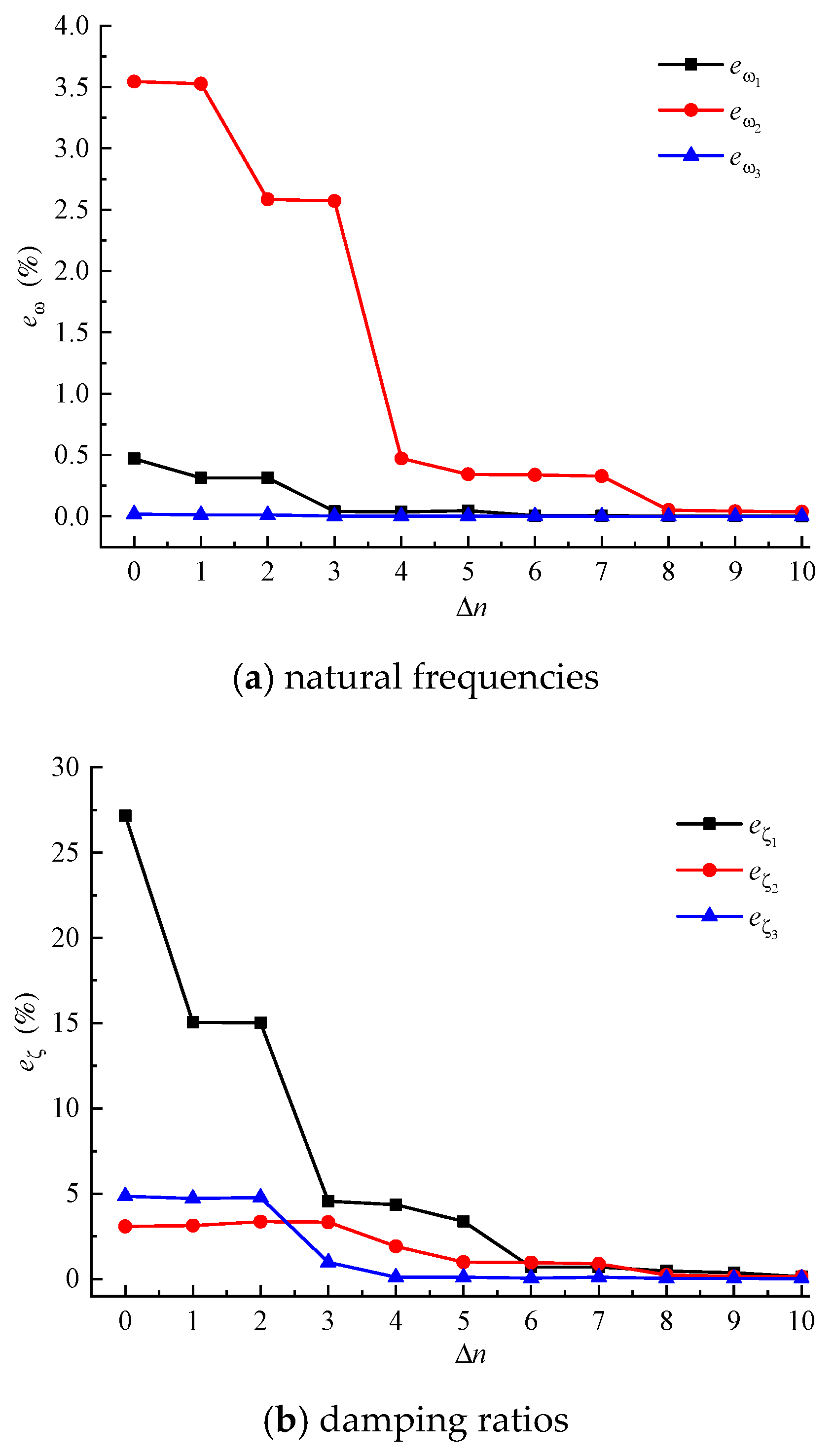
3.2. Frame with Concentrated Damper
4. Conclusions
- (1)
- The modal perturbation method transforms the characteristic equation of state space into a set of nonlinear algebraic equations by using the real mode shapes of the corresponding undamped system. The method only requires the first few lower eigenvectors of the undamped system, the calculation time is shorter than the state space method, which will simplify the solution and be convenient to solve the large system.
- (2)
- With the increase of vibration modes of the corresponding undamped system, the eigenvalues and eigenvectors monotonically converge to exact solutions. Usually j + 8 is enough to obtain sufficiently accurate natural frequencies and damping ratios. When all of the mode shapes of the undamped system are used, the modal perturbation method will obtain the exact solution.
- (3)
- The equivalent proportionally damped system is close to the non-proportionally damped system to reduce the effect of the deviation damping matrix so that the method can deal with the highly non-proportionally damped system. The method is particularly suitable for finding a few individual orders of frequency and mode for system with highly non-proportional damping.
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Cruz, C.; Miranda, E. Evaluation of soil-structure interaction effects on the damping ratios of buildings subjected to earthquakes. Soil Dyn. Earthq. Eng. 2017, 100, 183–195. [Google Scholar] [CrossRef]
- Králik, J.; Králik, J., Jr. Dynamic analysis of soil-structure interaction effects on NPP building using simplified and solid FE model of layered subsoil. J. Meas. Eng. 2019, 7, 12–19. [Google Scholar] [CrossRef]
- O’Riordan, N.J.; Almufti, I.; Lee, J.; Ellison, K.; Motamed, R. Site response analysis for dynamic soil-structure interaction and performance-based design. Proc. Inst. Civ. Eng. Geotech. Eng. 2019, 172, 76–86. [Google Scholar] [CrossRef]
- Lu, Z.; He, X.; Zhou, Y. Studies on damping behavior of vertically mixed structures with upper steel and lower concrete substructures. Struct. Des. Tall Spec. Build. 2017, 26, 1–14. [Google Scholar] [CrossRef]
- Wei, H.; Jiang, Q.; Zhi, Z. An approach to equivalent damping ratio of vertically mixed structures based on response error minimization. Soil Dyn. Earthq. Eng. 2015, 72, 119–128. [Google Scholar] [CrossRef]
- Papageorgiou, A.V.; Gantes, C.J. Equivalent modal damping ratios for concrete/steel mixed structures. Comput. Struct. 2010, 88, 1124–1136. [Google Scholar] [CrossRef]
- Losanno, D.; Londono, J.M.; Zinno, S.; Serino, G. Effective damping and frequencies of viscous damper braced structures considering the supports flexibility. Comput. Struct. 2018, 207, 121–131. [Google Scholar] [CrossRef]
- Li, Z.; Dong, H.; Wang, X.; He, M. Experimental and numerical investigations into seismic performance of timber-steel hybrid structure with supplemental dampers. Eng. Struct. 2017, 151, 33–43. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Prentice-Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Perotti, F. Analytical and numerical techniques for the dynamic analysis of non-classically damped linear systems. Soil Dyn. Earthq. Eng. 1994, 13, 197–212. [Google Scholar] [CrossRef]
- Foss, K.A. Coordinates which uncouple the equation of damped linear dynamic system. J. Appl. Mech. 1958, 25, 361–364. [Google Scholar]
- Ibrahimbegovic, A.; Wilson, E. Simple numerical algorithms for the mode superposition analysis of linear structural systems with non-proportional damping. Comput. Struct. 1989, 33, 523–531. [Google Scholar] [CrossRef]
- Cronin, D.L. Approximation for determining harmonically excited response of non-classically damped systems. J. Manuf. Sci. Eng. 1976, 98, 43–47. [Google Scholar] [CrossRef]
- Igusa, T.; Der Kiureghian, A.; Sackman, J.L. Modal decomposition method for stationary response of non-classically damping systems. J. Earthq. Eng. Struct. Dyn. 1984, 12, 121–136. [Google Scholar] [CrossRef]
- Udwadia, F.E. A note on nonproportional damping. J. Eng. Mech. 2009, 135, 1248–1256. [Google Scholar] [CrossRef][Green Version]
- Farghaly, A.A. Parametric study on equivalent damping ratio of different composite structural building systems. Int. J. Steel Struct. 2015, 15, 7–16. [Google Scholar] [CrossRef]
- Jae-Seung, H.; Chang-Soon, R. Equivalent damping ratio identification of a non-classically damped structure with vibration control system. J. Wind Eng. Inst. Korea 2017, 21, 121–126. [Google Scholar]
- Jiang, Q.; Zhou, Z.; Huang, W. Investigation on the Modal Strain Energy for Dynamic Analysis of Steel-Concrete Vertically Mixed Structures. J. Asian Archit. Build. Eng. 2015, 14, 671–678. [Google Scholar] [CrossRef]
- Ashory, M.R.; Ghasemi-Ghalebahman, A.; Kokabi, M.J. An efficient modal strain energy-based damage detection for laminated composite plates. Adv. Compos. Mater. 2017, 147–162. [Google Scholar] [CrossRef]
- Charney, F.A.; Mcnamara, R.J. Comparison of methods for computing equivalent viscous damping ratios of structures with added viscous damping. J. Struct. Eng. 2008, 134, 32–44. [Google Scholar] [CrossRef]
- Udwadia, F.E.; Esfandiari, R.S. Non-classically damped systems: An iterative approach. J. Appl. Mech. 1990, 57, 423–433. [Google Scholar] [CrossRef]
- Adhikari, S. An iterative approach for nonproportionally damped systems. Mech. Res. Commun. 2011, 38, 226–230. [Google Scholar] [CrossRef]
- Meirovitch, L.; Ryland, G., II. Response of slightly damped gyroscopic systems. J. Sound Vibr. 1979, 67, 1–19. [Google Scholar] [CrossRef]
- Singh, M.P.; Suarez, L.E. A perturbation analysis of the eigenproperties of equipment-structure systems. Nucl. Eng. Des. 1986, 97, 167–185. [Google Scholar] [CrossRef]
- Igusa, T.; Der Kiureghian, A. Dynamic characterization of two-degree-of-freedom equipment-structure systems. J. Eng. Mech. 1985, 111, 1–19. [Google Scholar] [CrossRef]
- Yang, Y.B.; Huang, W.H. Equipment-structure interaction considering the effect of torsion and base isolation. Earthq. Eng. Struct. Dyn. 1998, 27, 155–171. [Google Scholar] [CrossRef]
- Cha, P.D. Approximate eigensolutions for arbitrarily damped nearly proportional systems. J. Sound Vibr. 2005, 288, 813–827. [Google Scholar] [CrossRef]
- Lou, M.; Chen, G. Modal perturbation method and its applications in structural systems. J. Eng. Mech. 2003, 129, 935–943. [Google Scholar] [CrossRef]
- Lou, M.; Duan, Q.; Chen, G. Modal perturbation method for the dynamic characteristics of timoshenko beams. Shock Vib. 2013, 12, 425–434. [Google Scholar] [CrossRef]
- Hračov, S.; Náprstek, J. Approximate complex eigensolution of proportionally damped linear systems supplemented with a passive damper. Procedia Eng. 2017, 199, 1677–1682. [Google Scholar] [CrossRef]
- Tang, J.; Wang, W.L. Perturbation method for determining eigensolutions of weakly damped systems. J. Sound Vibr. 1995, 187, 671–681. [Google Scholar] [CrossRef]
- Chung, K.R.; Lee, C.W. Dynamic reanalysis of weakly non-proportionally damped systems. J. Sound Vibr. 1986, 111, 37–50. [Google Scholar] [CrossRef]
- Kwak, M.K. Perturbation method for the eigenvalue problem of lightly damped systems. J. Sound Vibr. 1993, 160, 351–357. [Google Scholar] [CrossRef]
- Claret, A.M.; Venancio-Filho, F. A modal superposition pseudo-force method for dynamic analysis of structural systems with non-proportional damping. Earthq. Eng. Struct. Dyn. 1991, 20, 303–315. [Google Scholar] [CrossRef]
- Chen, H.C.; Taylor R, L. Solution of viscously damped linear systems using a set of load-dependent vectors. Earthq. Eng. Struct. Dyn. 1990, 19, 653–665. [Google Scholar] [CrossRef]
| Case | Mode | Frequencies (rad/s) | ||||
|---|---|---|---|---|---|---|
| Exact | MPM | PDM | FPM [23] | FPM [27] | ||
| 1 | 1 | 7.763773 | 7.763773 | 7.629608 | 7.742608 | 7.689488 |
| 2 | 12.880336 | 12.880336 | 13.106833 | 13.441784 | 13.126397 | |
| 2 | 1 | 8.061740 | 8.061740 | 7.629608 | 7.761653 | 7.814849 |
| 2 | 12.404270 | 12.404270 | 13.106833 | 13.374905 | 13.163732 | |
| Case | Mode | Damping Ratios | ||||
|---|---|---|---|---|---|---|
| Exact | MPM | PDM | FPM [23] | FPM [27] | ||
| 1 | 1 | 0.171709 | 0.171709 | 0.172745 | 0.170224 | 0.171399 |
| 2 | 0.230342 | 0.230342 | 0.227517 | 0.221847 | 0.227178 | |
| 2 | 1 | 0.187282 | 0.187282 | 0.186851 | 0.183673 | 0.182422 |
| 2 | 0.208007 | 0.208007 | 0.203283 | 0.199209 | 0.202404 | |
| Case | Mode | MPM | FDM | FPM [23] | FPM [27] | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.237 | 1 | 0 | 0 | 1.728 | 0.603 | 0.273 | 0.865 | 0.957 | 0.181 |
| 2 | 0 | 0 | 1.758 | 1.226 | 4.359 | 3.688 | 1.910 | 1.374 | ||
| 2 | 0.708 | 1 | 0 | 0 | 5.360 | 0.230 | 3.722 | 1.927 | 3.063 | 2.595 |
| 2 | 0 | 0 | 5.664 | 2.271 | 7.825 | 4.230 | 6.123 | 2.694 | ||
| Mode | Frequencies (rad/s) | |||||
|---|---|---|---|---|---|---|
| Exact | MPM (n = 16) | MPM (n = 11) | PDM | FPM [23] | FPM [27] | |
| 1 | 7.645171 | 7.645171 | 7.645066 | 7.60922 | 7.610119 | 7.695591 |
| 2 | 9.049425 | 9.049425 | 9.045580 | 8.74224 | 8.831296 | 8.74224 |
| 3 | 12.725162 | 12.725162 | 12.725139 | 12.72513 | 12.72513 | 12.785979 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, D.; Fu, X.; Chen, Q.; Lu, P.; Tan, J. A Modal Perturbation Method for Eigenvalue Problem of Non-Proportionally Damped System. Appl. Sci. 2020, 10, 341. https://doi.org/10.3390/app10010341
Pan D, Fu X, Chen Q, Lu P, Tan J. A Modal Perturbation Method for Eigenvalue Problem of Non-Proportionally Damped System. Applied Sciences. 2020; 10(1):341. https://doi.org/10.3390/app10010341
Chicago/Turabian StylePan, Danguang, Xiangqiu Fu, Qingjun Chen, Pan Lu, and Jinpeng Tan. 2020. "A Modal Perturbation Method for Eigenvalue Problem of Non-Proportionally Damped System" Applied Sciences 10, no. 1: 341. https://doi.org/10.3390/app10010341
APA StylePan, D., Fu, X., Chen, Q., Lu, P., & Tan, J. (2020). A Modal Perturbation Method for Eigenvalue Problem of Non-Proportionally Damped System. Applied Sciences, 10(1), 341. https://doi.org/10.3390/app10010341





