Impact Performance of a Plate Structure with Coconut-Inspired Microchannels

Abstract

Very few studies have been conducted in the past to reveal the underlying mechanism that causes the high-impact performance of coconuts as a natural composite material and a structure. The goal of this study is to understand the dominant microstructures of coconuts with respect to mechanical impact. In this study, we use a high-resolution X-ray computed tomography (CT) machine in scanning the microstructures and analyzing the patterns of microchannels in coconut shells. By using the established patterns, we model a novel plate structure with coconut-inspired microchannels. Numerical simulation elucidates a significant improvement in crashworthiness. The microchannel design opens a path to further developing self-healing composites and intelligent composites with sensing elements embedded in the channels.

1. Introduction

Coconut is a natural composite product with better impact performance than human bone structures. We still do not have full knowledge about the multiscale patterns and structures of this composite. Although coconut fibers have been used in man-made composites, the underlying hierarchical structure of the coconut shell was seldom investigated. There is almost no previous effort in modeling three-dimension (3D) coconut composite patterns and structures with respect to mechanical impact behavior. This calls for an investigation on the coconut composite patterns for better impact performance.

2. Literature Review

Coconut fibers have been used as matrix reinforcement for polymers. A group of scientists [1,2,3,4,5,6,7,8] evaluated the structural characteristics and mechanical performance of coir fiber/thermoset polymer composites. Tensile and flexural strength as well as impact performance of the composites were measured. In some studies, scanning electron microscopy or X-ray dispersion analysis was used. Other researchers [9,10,11,12,13] investigated the mechanical performance of coir fiber/thermoplastic polymer composites. The chopped dust [14,15] of coir fibers or coconut shells was also used with polymers to form composites.

Gludovatz et al. [16] conducted an innovative study on the multiscale structure of coconut shells. They examined the structure of coconut shells across multiple length scales through X-ray computed tomography (CT) and focused ion-beam microscopy. Fracture toughness was investigated on the latitudinal and longitudinal planes.

Hassan et al. [17] investigated the improvement in shear strength of soft clay embedded with a single crushed coconut shell (CCS) column. An unconfined compression test was conducted to determine the shear strength. The experimental results show about 20–30% improvement in shear strength.

Schmier et al. [18] qualitatively analyzed and visualized the functional morphology of the coconut endocarp on several hierarchical levels. Based on those findings, the authors presented a more precise evaluation of the toughening mechanisms in the endocarp.

Ha et al. [19] investigated the crashworthiness characteristics of a new bio-inspired conical corrugation tubes (CCTs). They classified the deformation of CCTs into four modes. The numerical simulations indicate that the CCTs produced a smoother force–displacement relationship than straight tubes. So far, the high-impact performance of coconuts is still a mystery. The main goal of this study is to reveal the fundamental mechanism of this high-impact performance via a quantitative numerical computation. The unique contributions of this paper include:

(a)

We designed a complete set of morphological parameters to describe microchannels inside coconut shells.

(b)

A series of statistical analyses were conducted in a dimensionless way to reveal the intrinsic geometric relationships of microchannels with respect to the thickness of the coconut shells.

(c)

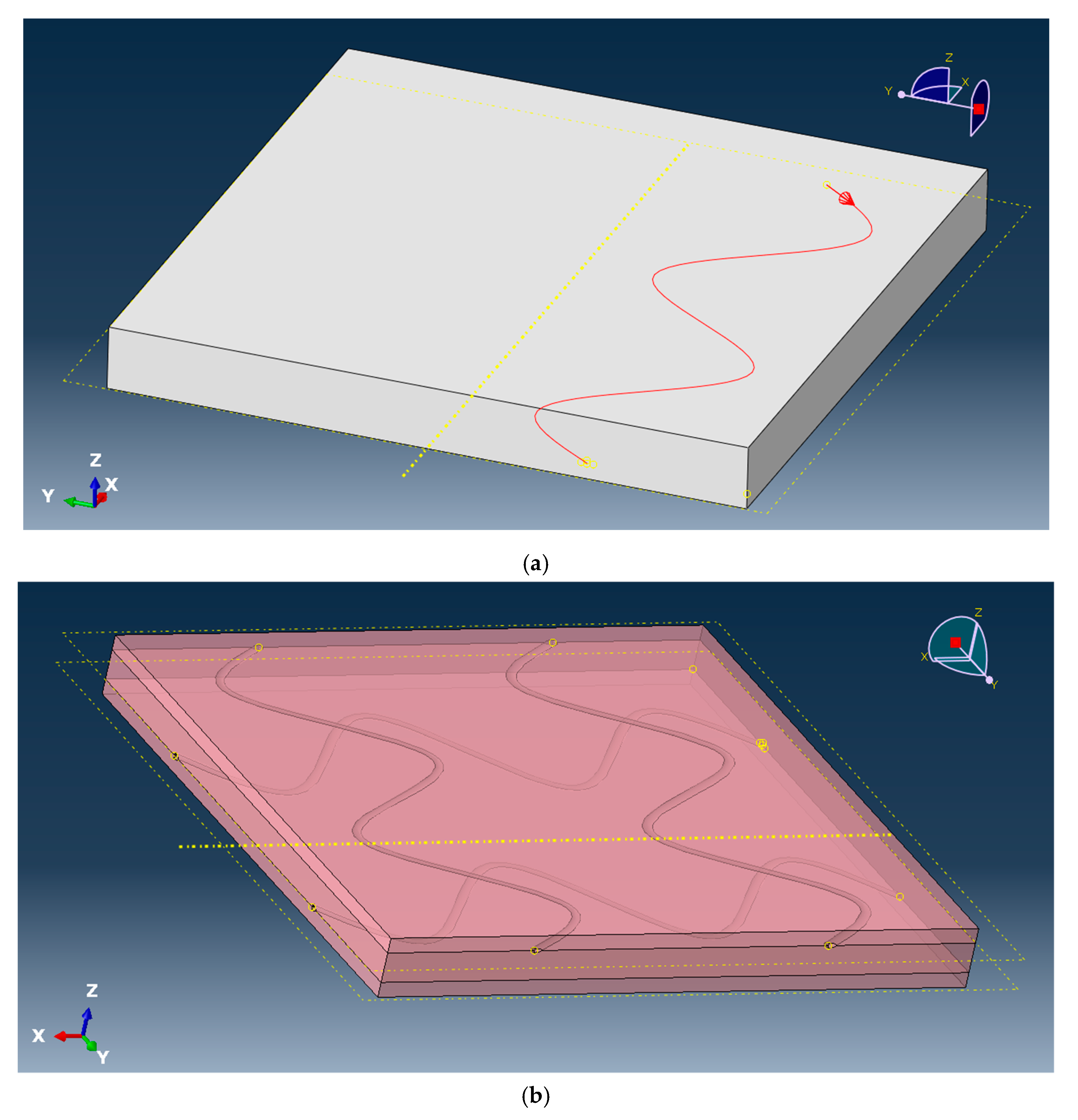
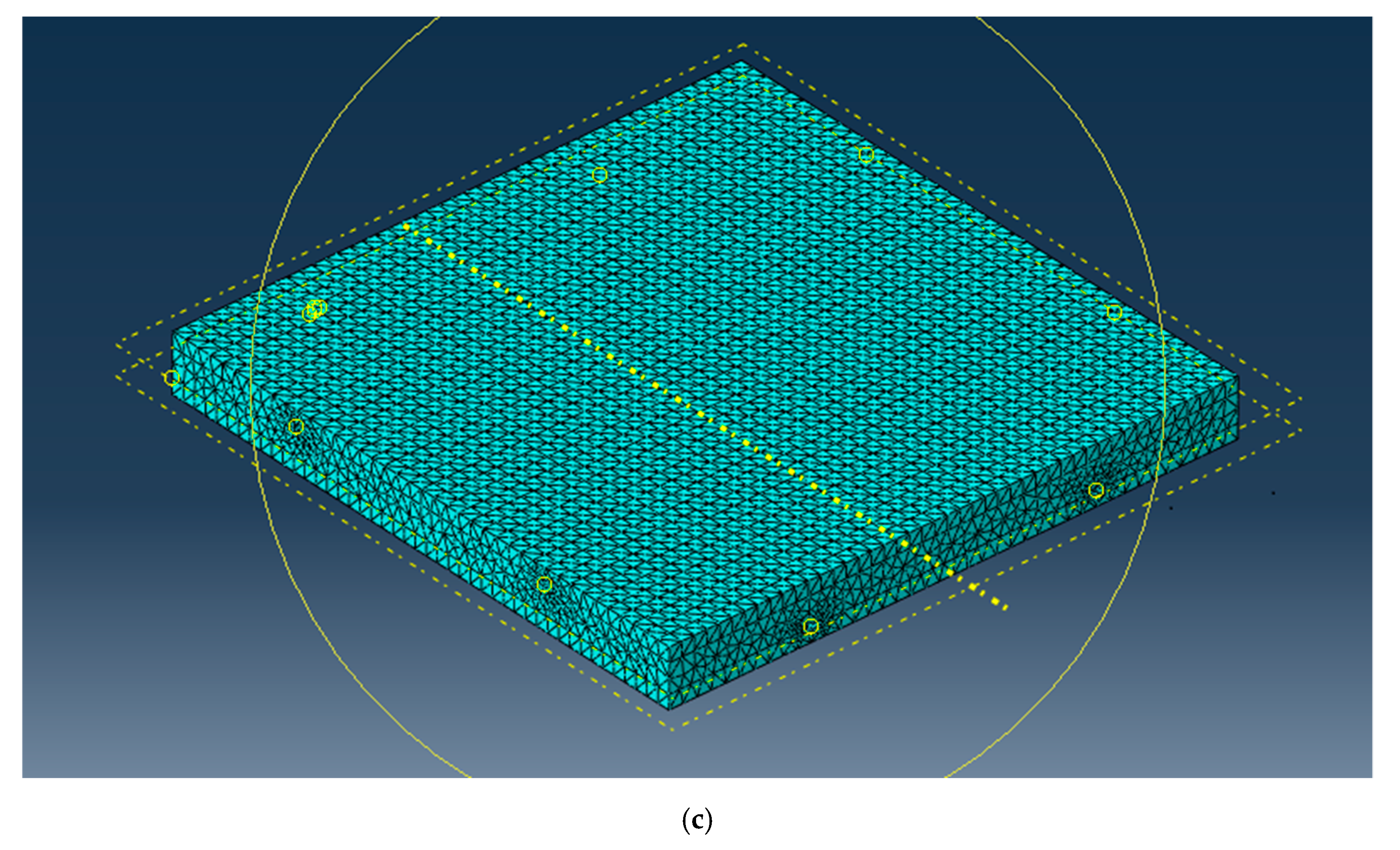
We created the first coconut-inspired plate structure with embedded microchannels.

(d)

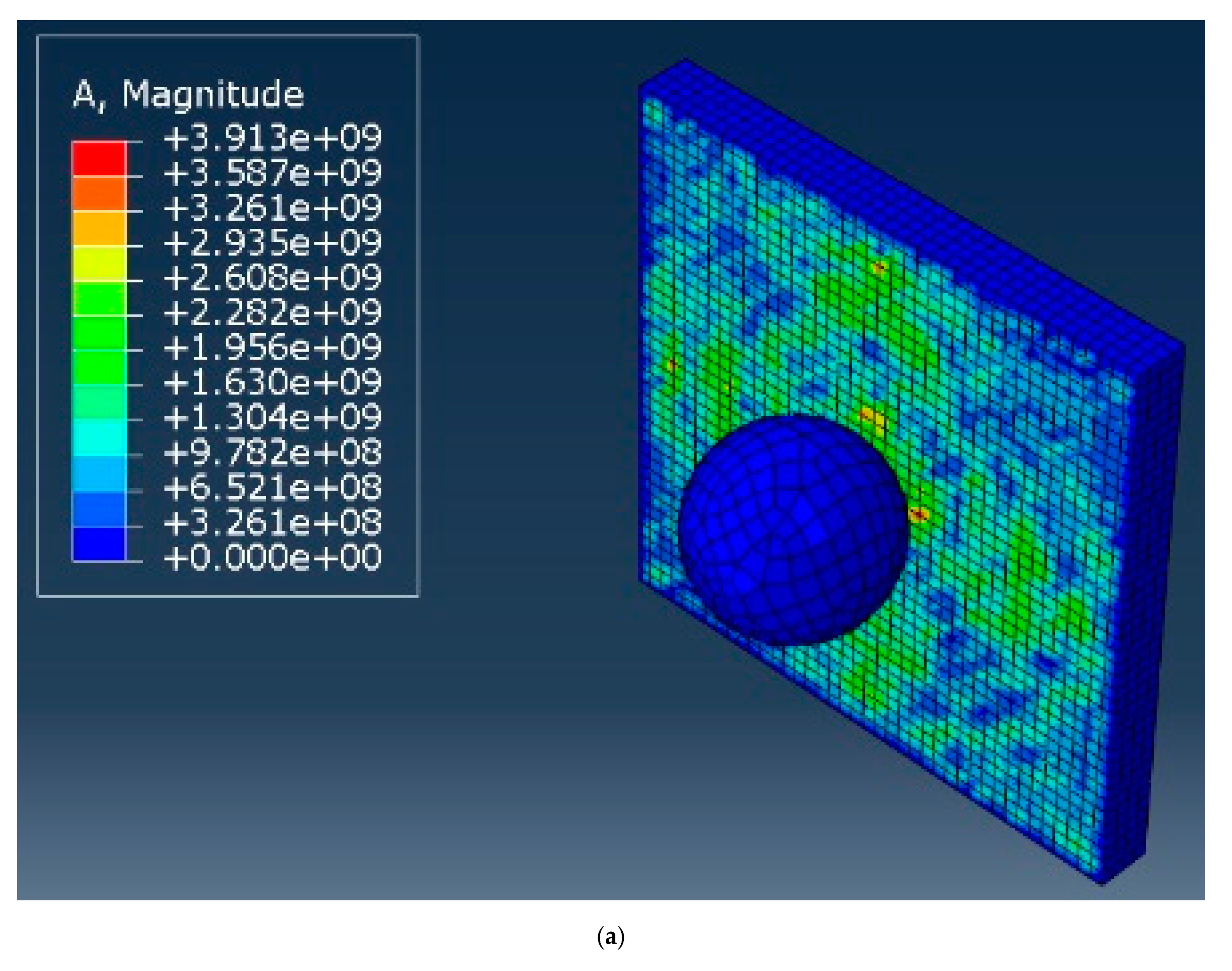
Our numerical simulations elucidate the improvement of a coconut-inspired plate in mechanical impact performance compared to the conventional plate structure.

The rest of this paper is organized as follows. In Section 3, the X-ray CT analysis of coconut shell samples is described. Next, a bio-inspired design of coconut composites is given in Section 4. Section 5 provides the results of dynamic simulation and discussion, and Section 6 is related to industrial applications of coconut composites. Some concluding remarks and future research are given in Section 7.

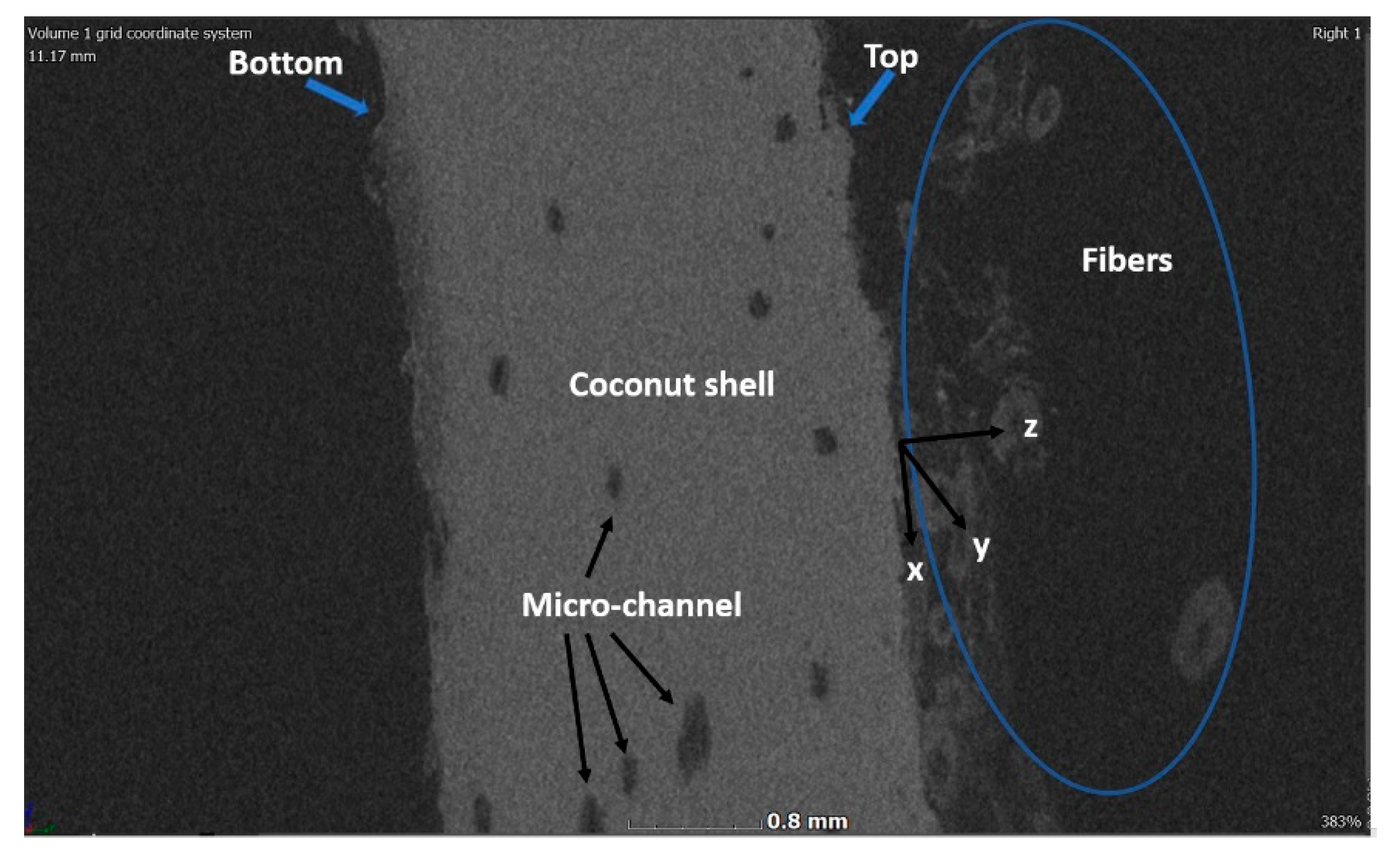
3. X-Ray CT Analysis of Coconut Shell Samples

Our approach, as shown in Figure 1, contains the following technical components: (1) microscale and mesoscale X-ray scanning of coconut specimens; (2) analysis of structures of coconut shells; (3) modeling of coconut composites; and (4) dynamic impact evaluation of crashworthiness.

An Xradia Versa 510 was used in measuring the internal structures of adult coconut shell specimens. Figure 2, Figure 3 and Figure 4 present typical camera images of the coconut sample as well as X-ray CT data. Figure 2 shows the outer layer of fibers; in Figure 3, a fixture of the X-ray CT machine and a small coconut shell specimen are given; and Figure 4 refers to CT data after volume reconstruction from two different views (perspective and top).

In this paper, we let the outward direction of surface normal at each coconut shell be the positive z-coordinate direction (Figure 5); with respect to the coconut shell, the “top” refers to the place of junction with the outer-layer fibers, and the “bottom” denotes the location next to the interior coconut meat layer. Figure 6 shows five cross-section views (i.e., top view) in different x-y planes. From this figure, the following trends can be observed at the horizontal cross-sections.

(a)

Especially at places near the top horizontal cross-section, the microchannels go vertically in the z direction (not in a horizontal plane). This helps maintain the structural integrity of coconut shells.

(b)

At the middle layers, the channels are smoothly shaped, i.e., there is no sharp corner or edge for stress concentration.

(c)

At the middle layers, the channels are not located in any particular layer. In other words, different segments of the channels stay at the different middle layers. In this way, the structural weakening due to microchannels becomes minimum.

(d)

“Horizontal Middle 1” shows (1) branching patterns, (2) small sine curve patterns, and (3) half horizontal and half vertical patterns.

(e)

“Horizontal Middle 2” demonstrates three or four branch patterns.

(f)

“Horizontal Middle 3” depicts a neural network pattern.

(g)

At places near the bottom layer, there are more segments of channels in the horizontal layer, compared to the vertical direction. This may be because the bottom layer is relatively far from the top layer where an impact force is loaded directly in an impact event.

Figure 7 demonstrates the distribution of microchannels in the side cross-sections and the top cross-sections. The following trends can be observed:

(a)

The channel density is quite uniform from the top surface to the bottom surface of the coconut shells.

(b)

The cross-sectional shape of the microchannels can be described as an ellipse.

(c)

Smaller channels tend to take a circular shape, while larger channels are of elliptical shape.

(d)

The long axis of microchannels is roughly perpendicular to the direction of surface normal of the coconut shells.

The statistical characteristics of microchannels are analyzed with respect to the following features:

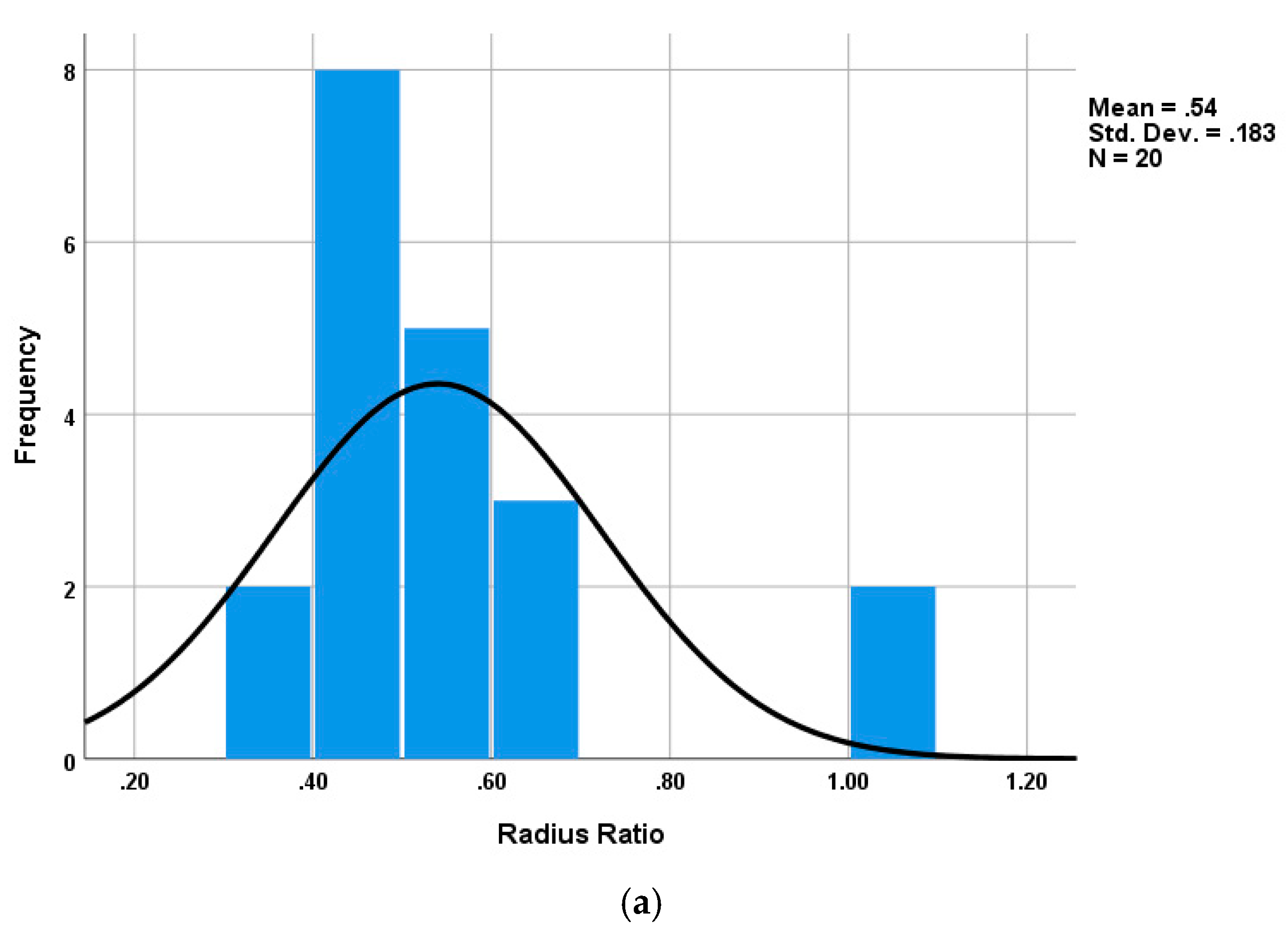
(1)

The lengths of long and short half-axes of an ellipse representing a microchannel, $r_{long}$ (mm) and $r_{short}$ (mm)

(2)

A ratio of $r_{short}$ to $r_{long}$

(3)

An average radius of a channel, $r_a=\frac{r_{short}+r_{long}}{2}$ (mm)

(4)

Thickness of coconut shell, t (mm)

(5)

A ratio of $r_a$ to t

(6)

Distance from the top surface to the location of a channel, $d_{top}$ (mm)

(7)

A ratio of $d_{top}$ to t

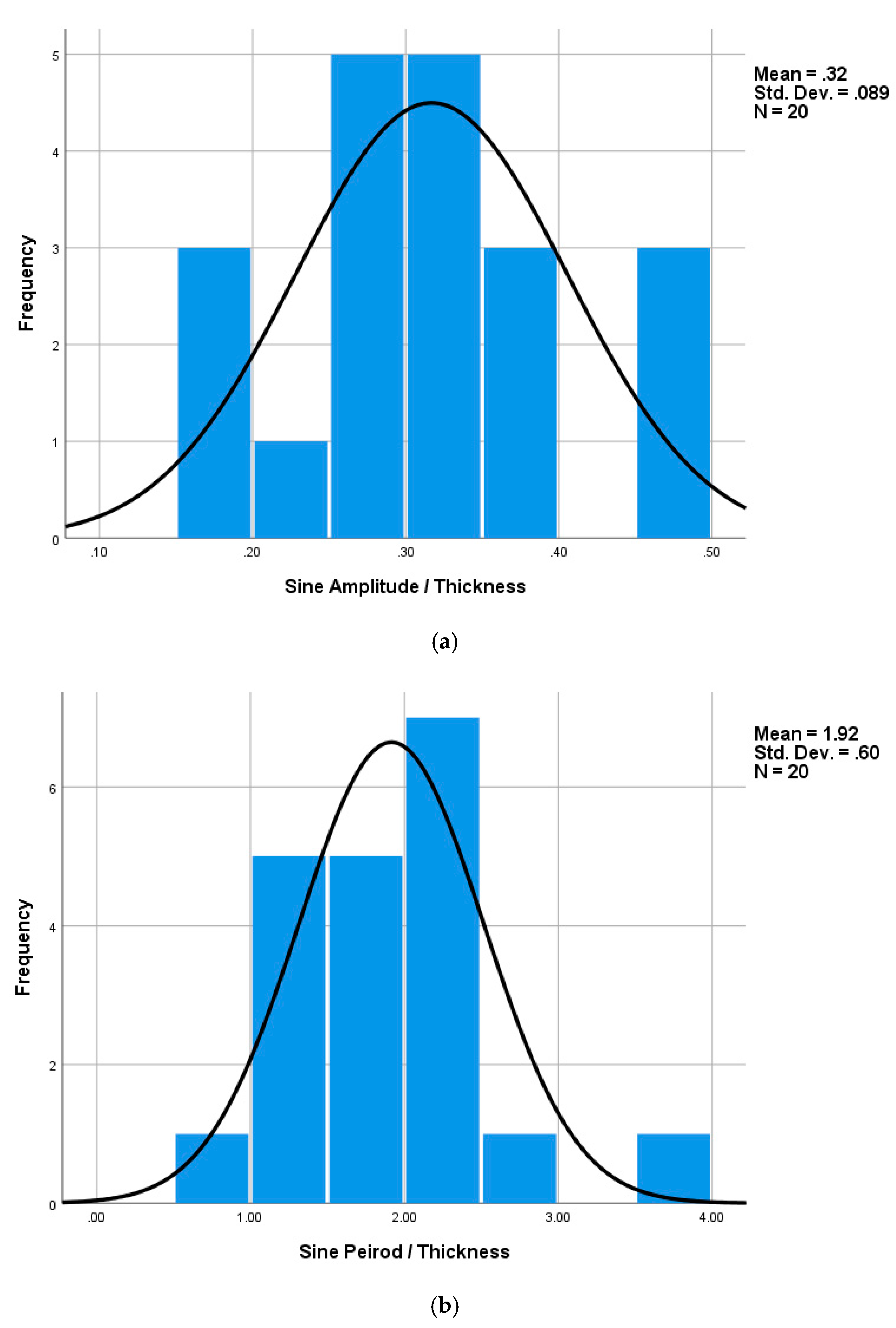
(8)

Amplitude, a (mm), and period, T (mm), of a microchannel in the form of a sine curve

(9)

A ratio of a to T

(10)

A ratio of T to t

For a circular channel, $r_{short}$ = $r_{long}$, and with respect to an elliptical channel, $r_{short}$ < $r_{long}$. The results of statistical analyses (based on approximate normal distributions) in Figure 8 indicate that the mean values of the radius ratio, $r_a$/t and $d_{top}$/t are 0.54, 0.06, and 0.58, respectively. Figure 9 indicates that the mean values of a ratio of sine amplitude and period to the shell thickness are respectively 0.32 and 1.92. $r_{short}$/$r_{long}$ = 0.54 means that the channels are of an elliptical shape and its long axis is about twice as long as its short axis; with $d_{top}/t$ = 0.06, the diameter of the microchannels is approximately 1/10th of the coconut shell thickness; when $d_{top}$/t = 0.58, it indicates that the middle layers are the center place of a distribution. Actually, the distribution in Figure 8c is more like a uniform distribution across the entire coconut thickness except at the places near the top ($d_{top}$/t = [0.0, 0.1]).

4. Bio-Inspired Design of Coconut Composites

Based on the analysis results in Section 3, we decide to use the following patterns for constructing a coconut-inspired plate: (1) radius ratio = 0.5, i.e., elliptical channels with $r_{short}$ = 0.5 $r_{long}$; (2) the ratio of $r_a$ to t = 0.05, which means that the diameter of microchannels is 1/10th of the plate thickness; (3) the distribution of microchannels follows an approximate uniform distribution, as illustrated in the right image of Figure 6; (4) the layout of each microchannel is an approximate sine curve, except at the places near the top of the plate where the channels grow vertically in the direction of plate surface normal; and (5) the long axis of each microchannel is perpendicular to the direction of the surface normal.

Figure 10 shows a design of coconut-inspired plate model based on the aforementioned patterns. The left image refers to a computer-aided design (CAD) model, and the right image is a finite element mesh. This is only one example of applying the above patterns. There are many possible designs to be derived from the aforementioned patterns, and it depends upon other scientists and engineers to explore in the future for various applications.

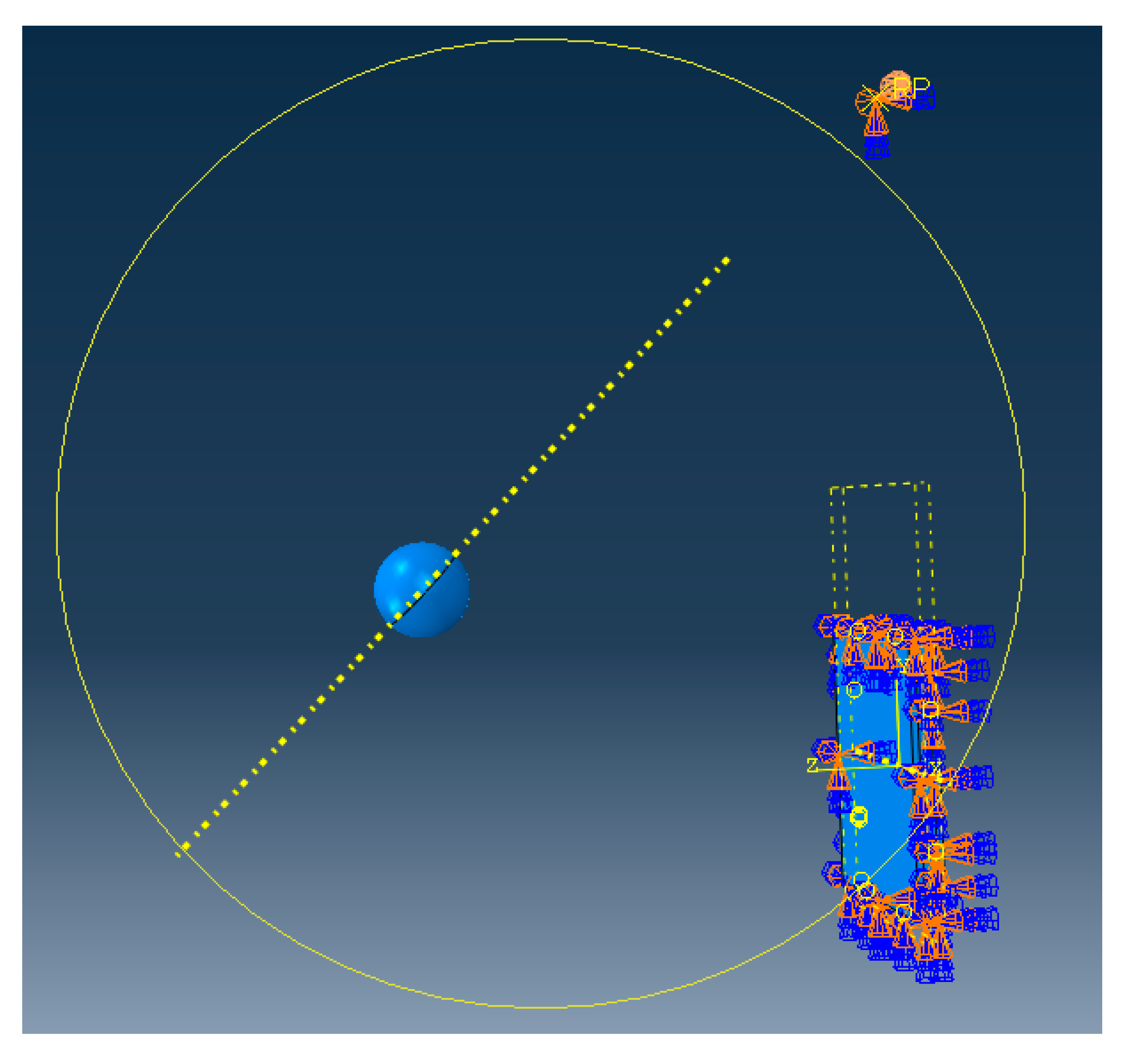
5. Dynamic Impact Simulation and Discussion

A pendulum impact test is established, as shown in Figure 11. The steel ball has a reference point as its rotational center. The displacements at the boundaries of a plate are fixed along all three coordinate directions as well as three rotational directions. The plate is oriented with its surface normal pointing horizontally. We consider a generic material for the plate with Young’s modulus = 70 GPa and Poisson’s ration = 0.34. The exact values of material parameters are not important here, because we are only interested in a comparison of impact performance. The steel ball is 45 degrees from the plate, with its initial angular velocity = 750 radians/second and its weight = 1.5 kg.

Figure 12c shows about 40% improvement in reducing the impact acceleration of a plate with coconut-inspired microchannels (Figure 10) compared to a regular plate with the same material parameters and impact setting. Figure 13 shows that the increase in strain energy and the decrease in acceleration are one underlying reason for the coconut-inspired plate to absorb more impact energy, leading to better crashworthiness, i.e., better protection to occupants if the plate serves as a protection layer. The strain energy is defined as

$$U_e=\frac{1}{2}{{\displaystyle \int }}_V^{}{\left\{\sigma \right\}}^T\left\{\epsilon \right\}dV$$

(1)

where the stress vector ${\left\{\sigma \right\}}^T=\left\{{\sigma }_{xx}{\sigma }_{yy}{\sigma }_{zz}{\sigma }_{xy}{\sigma }_{xz}{\sigma }_{yz}\right\}$ and elastic strain ${\left\{\epsilon \right\}}^T=\left\{{\epsilon }_{xx}{\epsilon }_{yy}{\epsilon }_{zz}{\epsilon }_{xy}{\epsilon }_{xz}{\epsilon }_{yz}\right\}$. V refers to the volume of the model. The material is modeled with both plastic strain and elastic strain.

6. Industrial Applications

Coconut shells have been utilized in making industrial components such as auto parts. Automakers incorporate the coconut fibers to produce useful composite components [20,21]. The auto parts include the load floor, package shelf, console armrests, structural guards, rear deck lid, applique brackets, side-door cladding, interior door panels, compartment liner, radiator end tank, and veneer.

Coconut husks was also used for making a stronger, lighter paddleboard [22]. By absorbing less epoxy than other materials, coconut fibers reduce the weight of a paddleboard with Australian brand NSP. It decreases the weight of the board by 30% and eliminates toxic materials by 40%.

7. Conclusions and Future Perspective

In this study, the following conclusions can be drawn:

(a)

We digitally uncover a network of microchannels inside coconut shells as one underlying reason for the high-impact performance of coconuts.

(b)

We designed five dimensionless ratios to describe the intrinsic geometric relation between microchannels and the thickness of coconut shells. These dimensionless parameters are scale-invariant and will therefore facilitate coconut-inspired designs.

(c)

The cross-section of microchannels is approximated by an ellipse. A series of statistical analyses reveal the mean values of microchannel morphology with respect to coconut shell thickness.

(d)

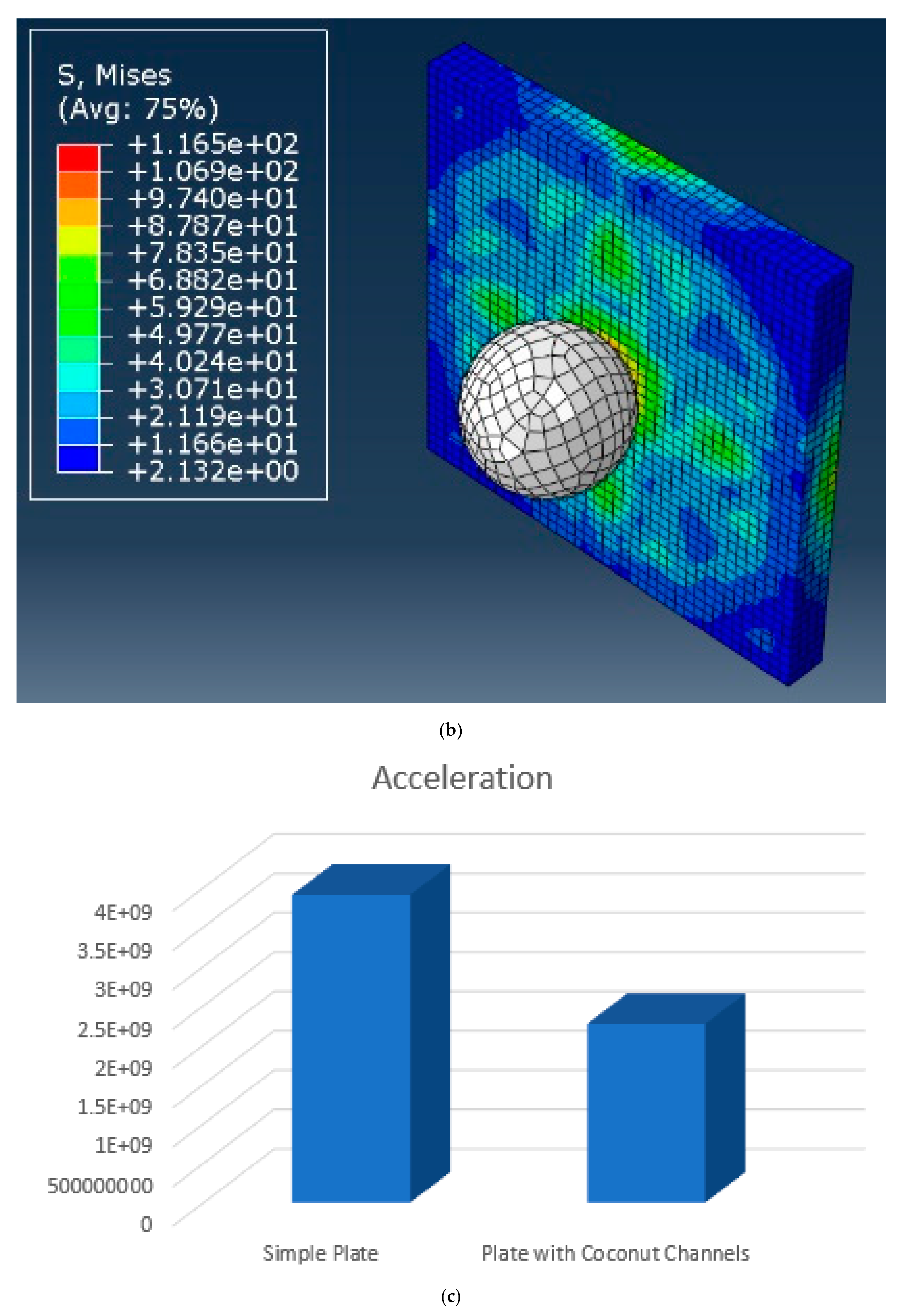
In addition, we numerically demonstrate the significant improvement (about 40%) in reducing the impact acceleration with a coconut-inspired plate. The design patterns of microchannels can be potentially applied in various applications.

The microchannels may be further utilized as the space of healing agents for self-healing composites or the space of sensing elements for intelligent composites with self-sensing capability.