Motor Vector Control Based on Speed-Torque-Current Map
Abstract
:1. Introduction
2. Electric Drive System Configuration and Main Parameters
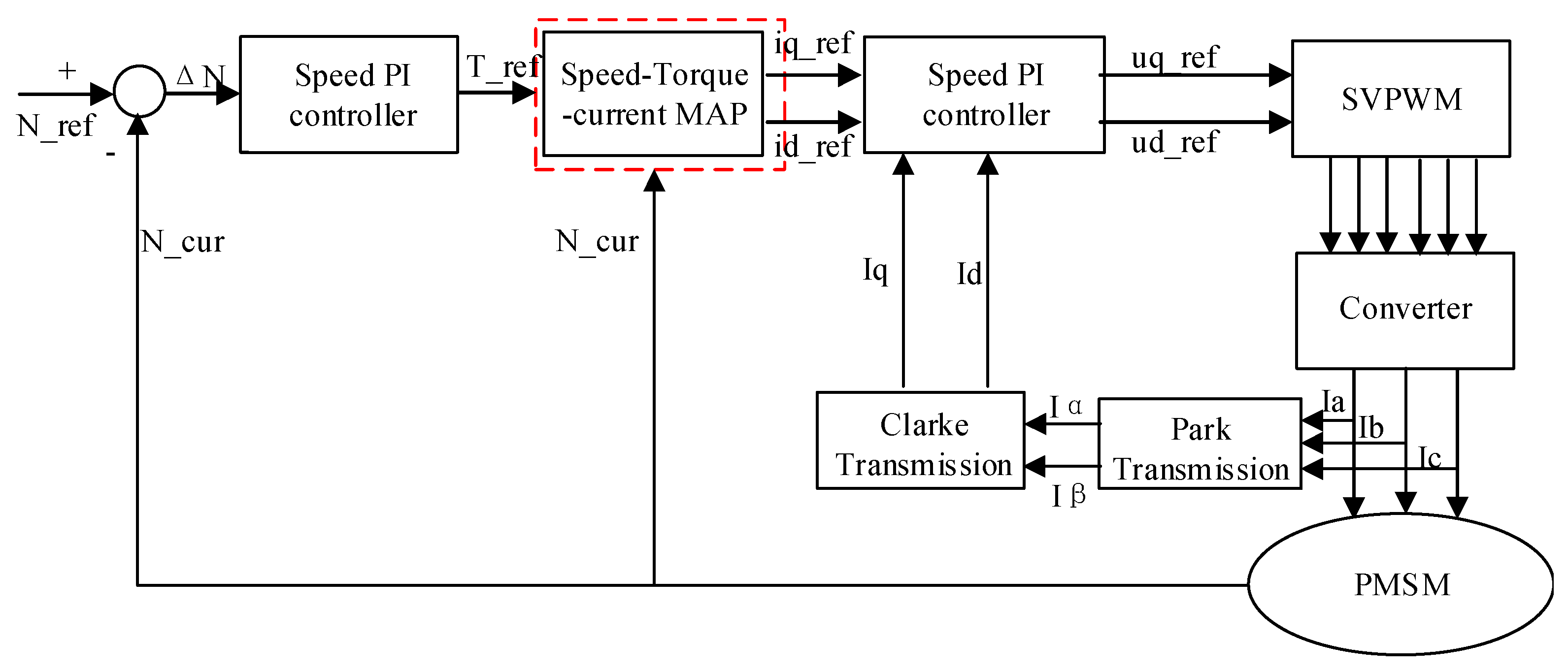
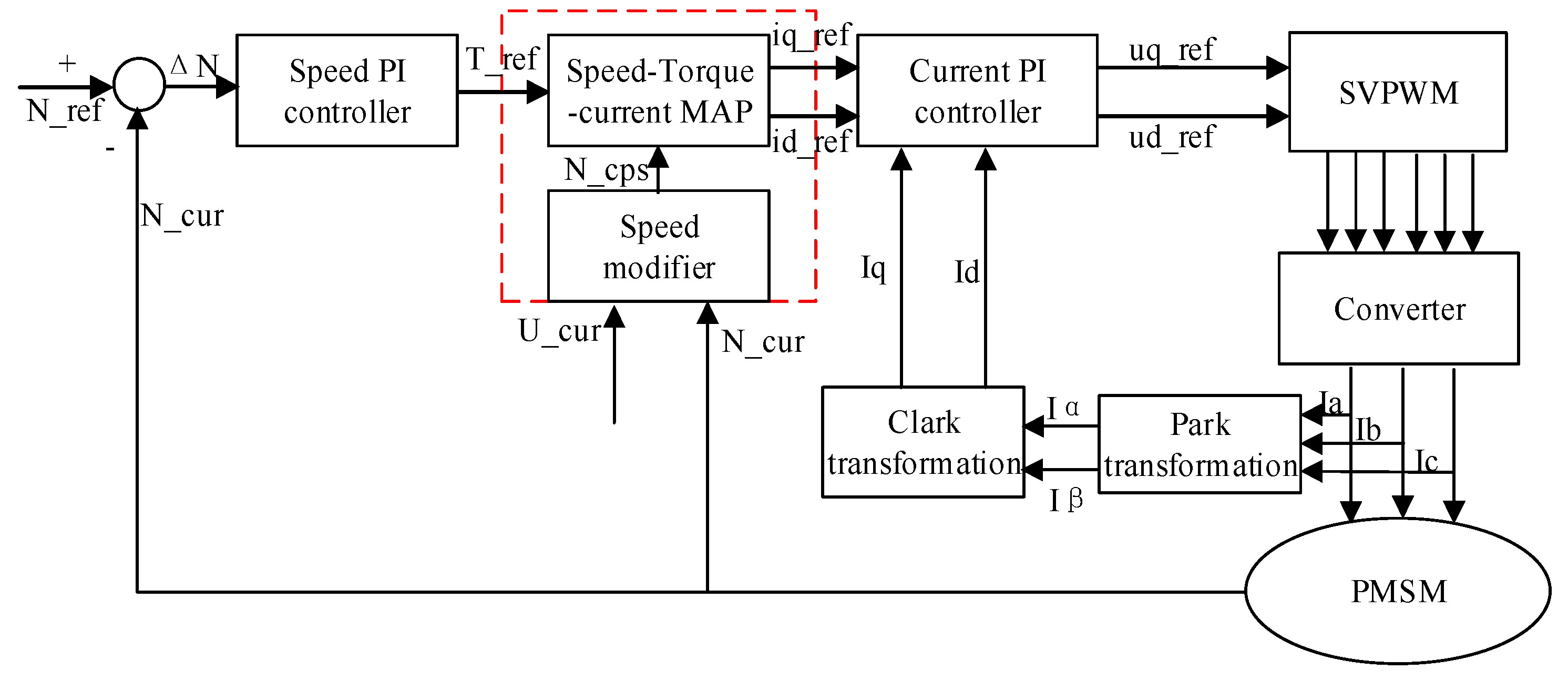
3. Motor Vector Control Strategy Based on Speed-Torque-Current Map
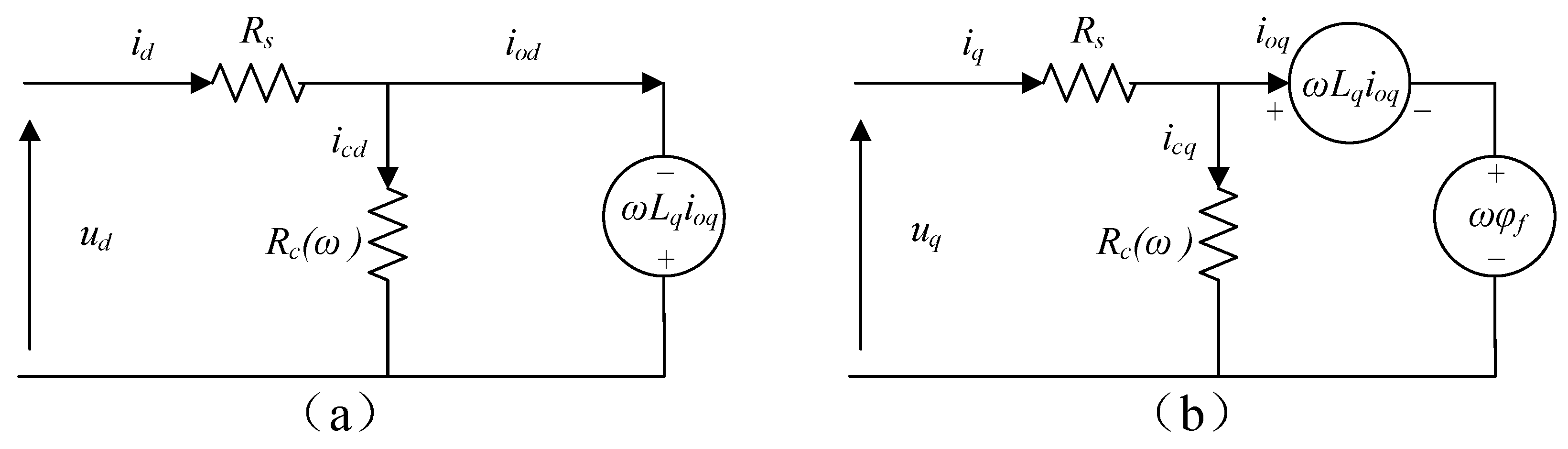
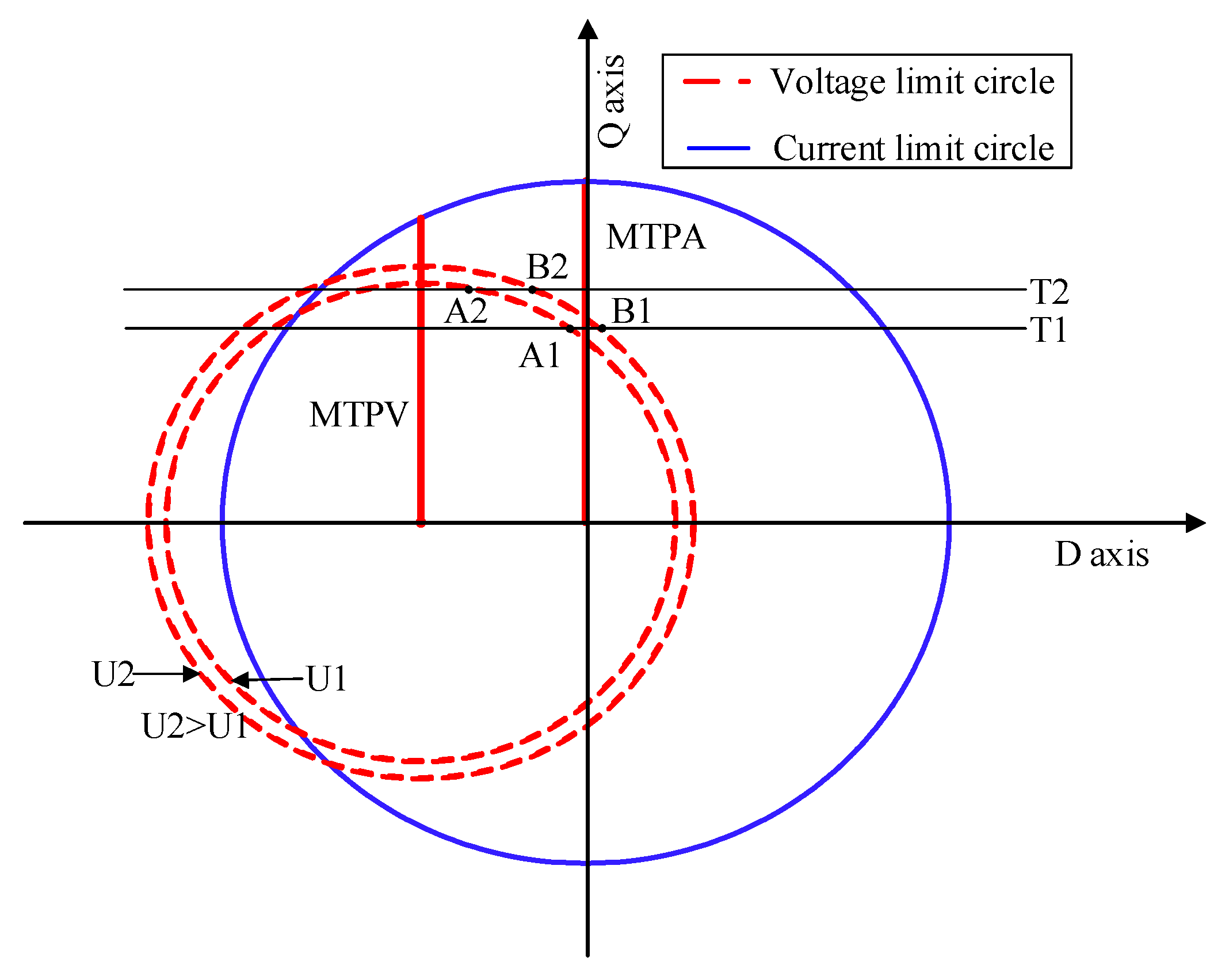
3.1. Motor Model and Operation Constraints
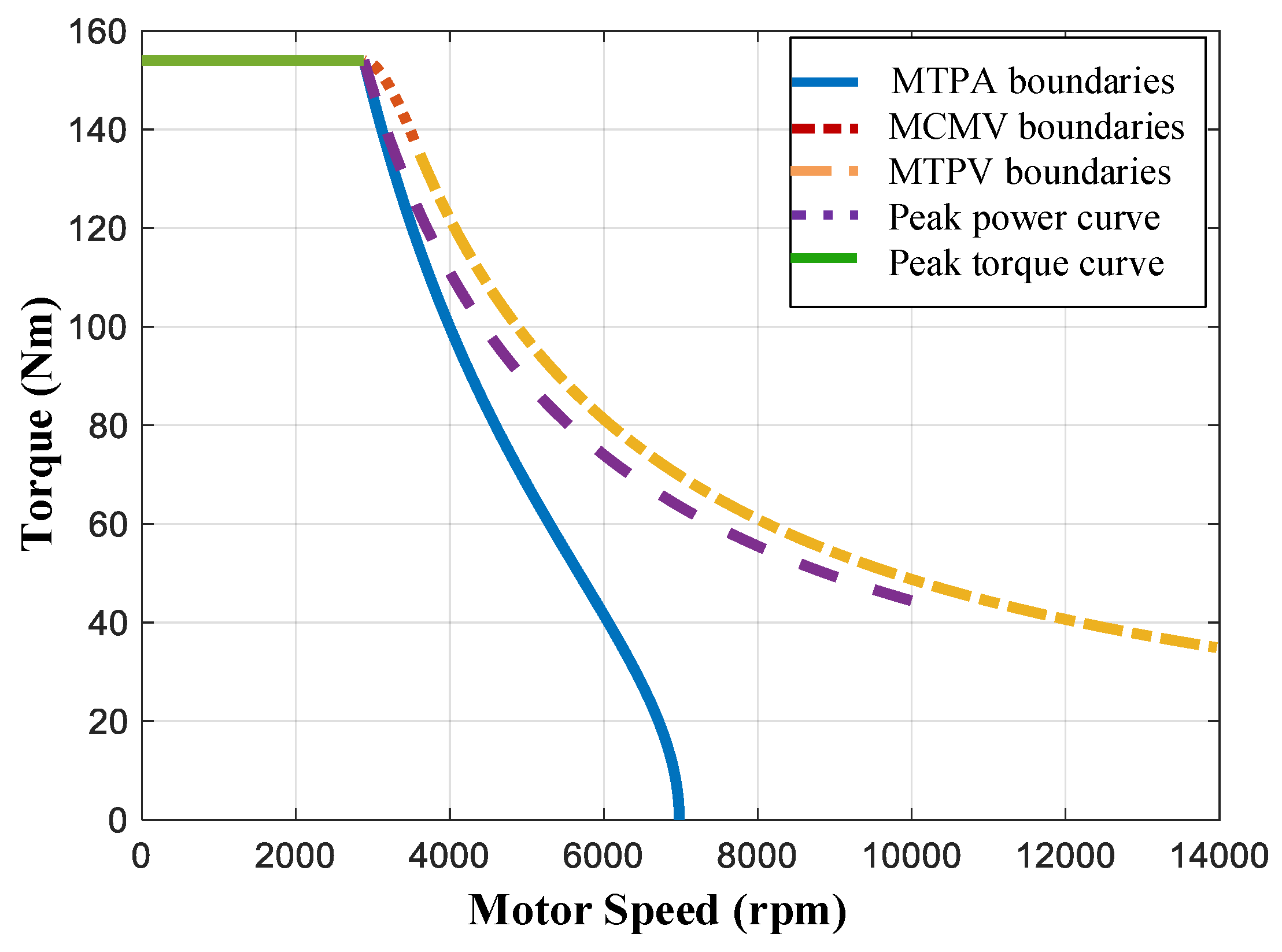
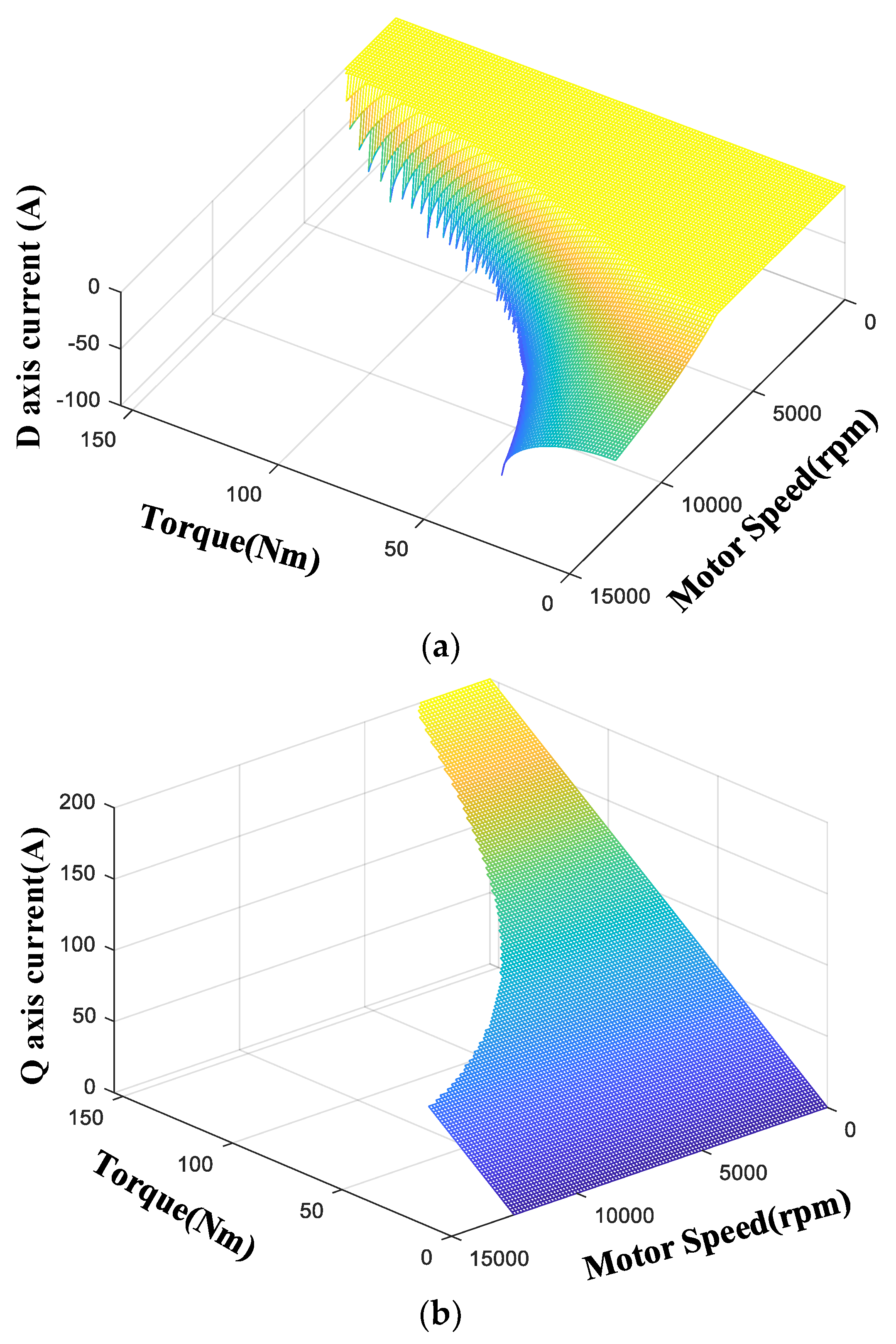
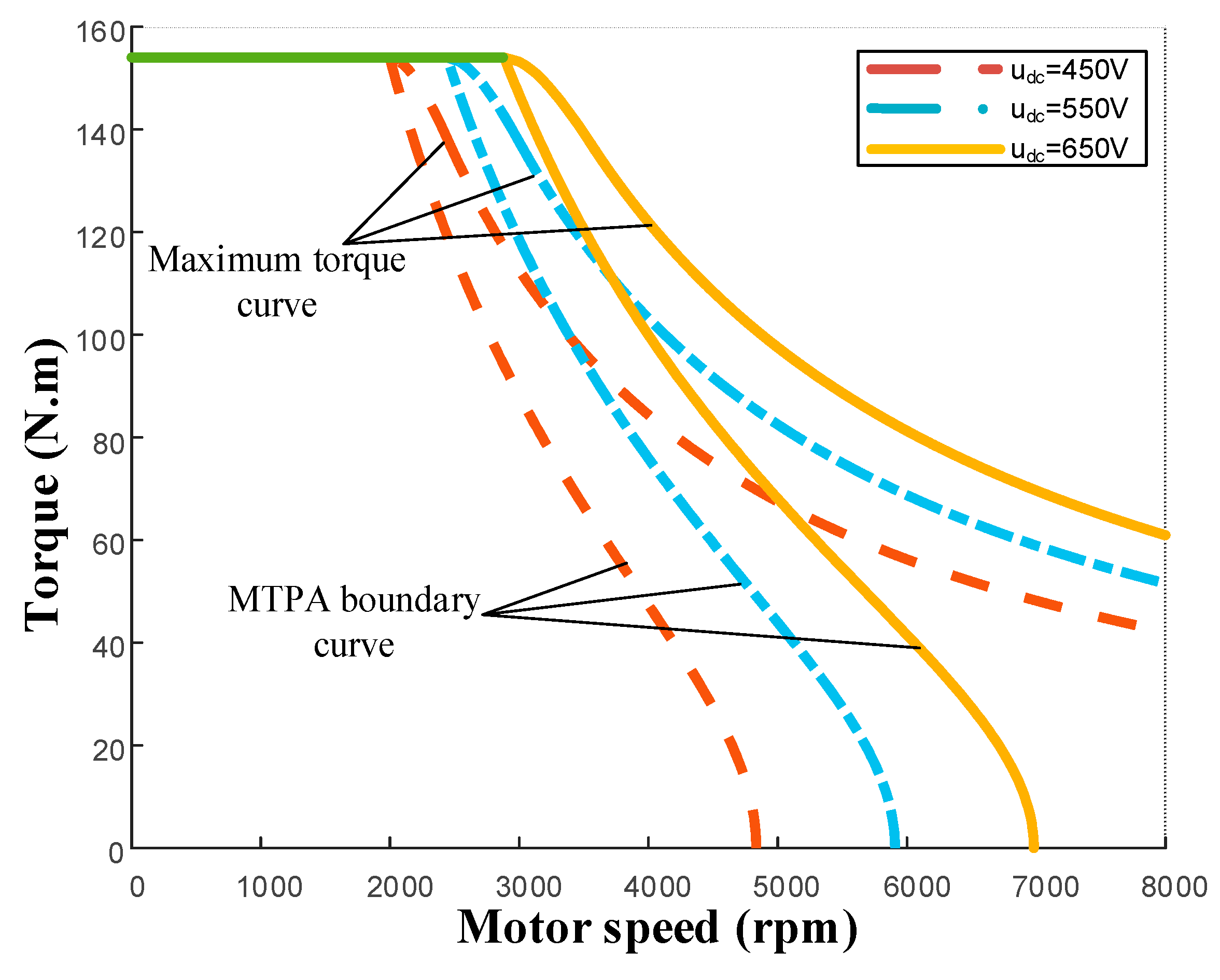
3.2. Speed-Torque-Current Map Integrated Current Control
- (a)
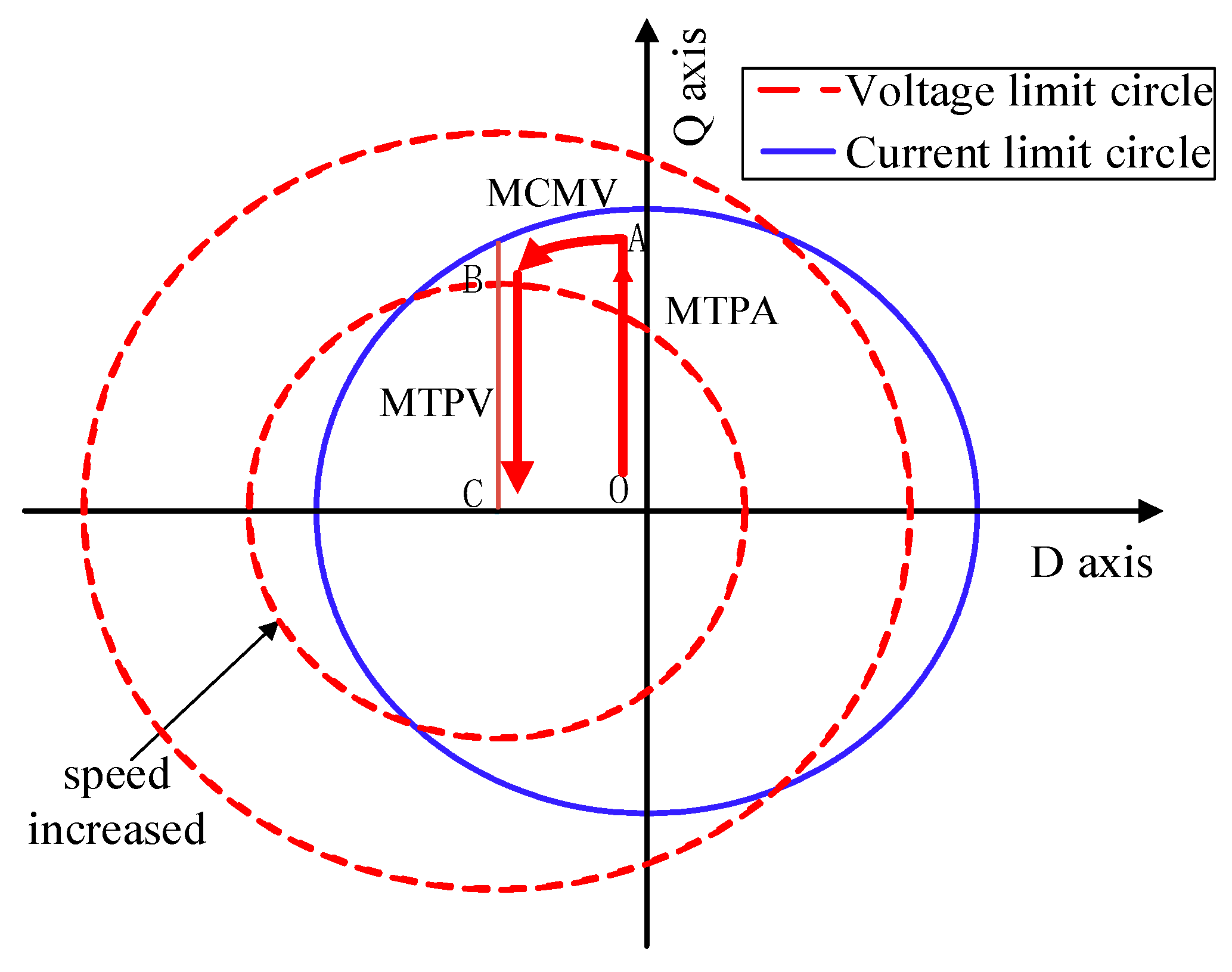
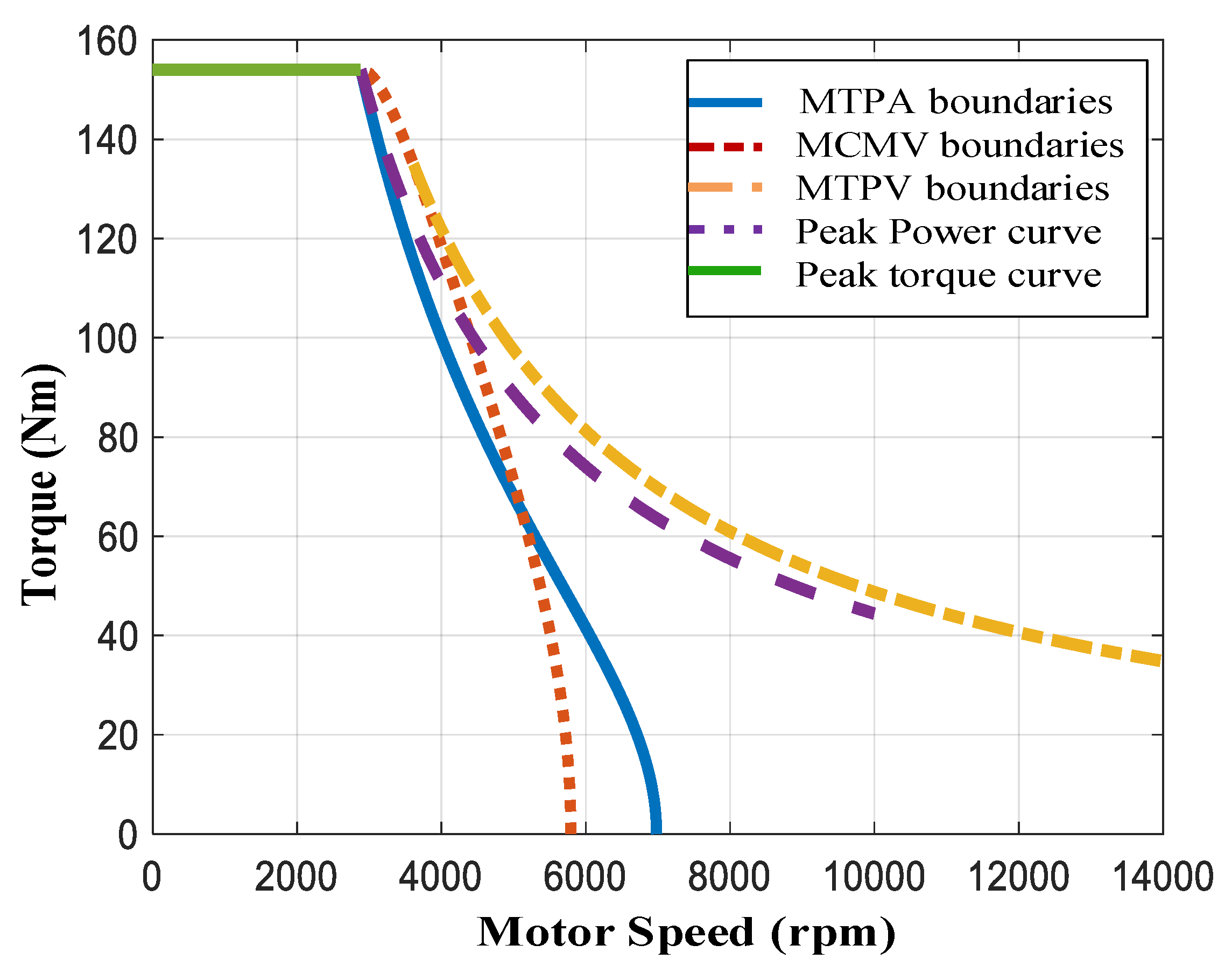
- The MTPA control strategy is adopted in the peak torque area to minimize the copper loss and iron loss.
- (b)
- In the high-torque region of the weak magnetic field, the MCMV control is adopted to transit to the MTPV control range.
- (c)
- MTPV control is used to extend the speed range of the motor in the high-speed region of the weak magnetic field.
3.3. Motor Vector Control Strategy
4. Verification of the Proposed Vector Control Strategy
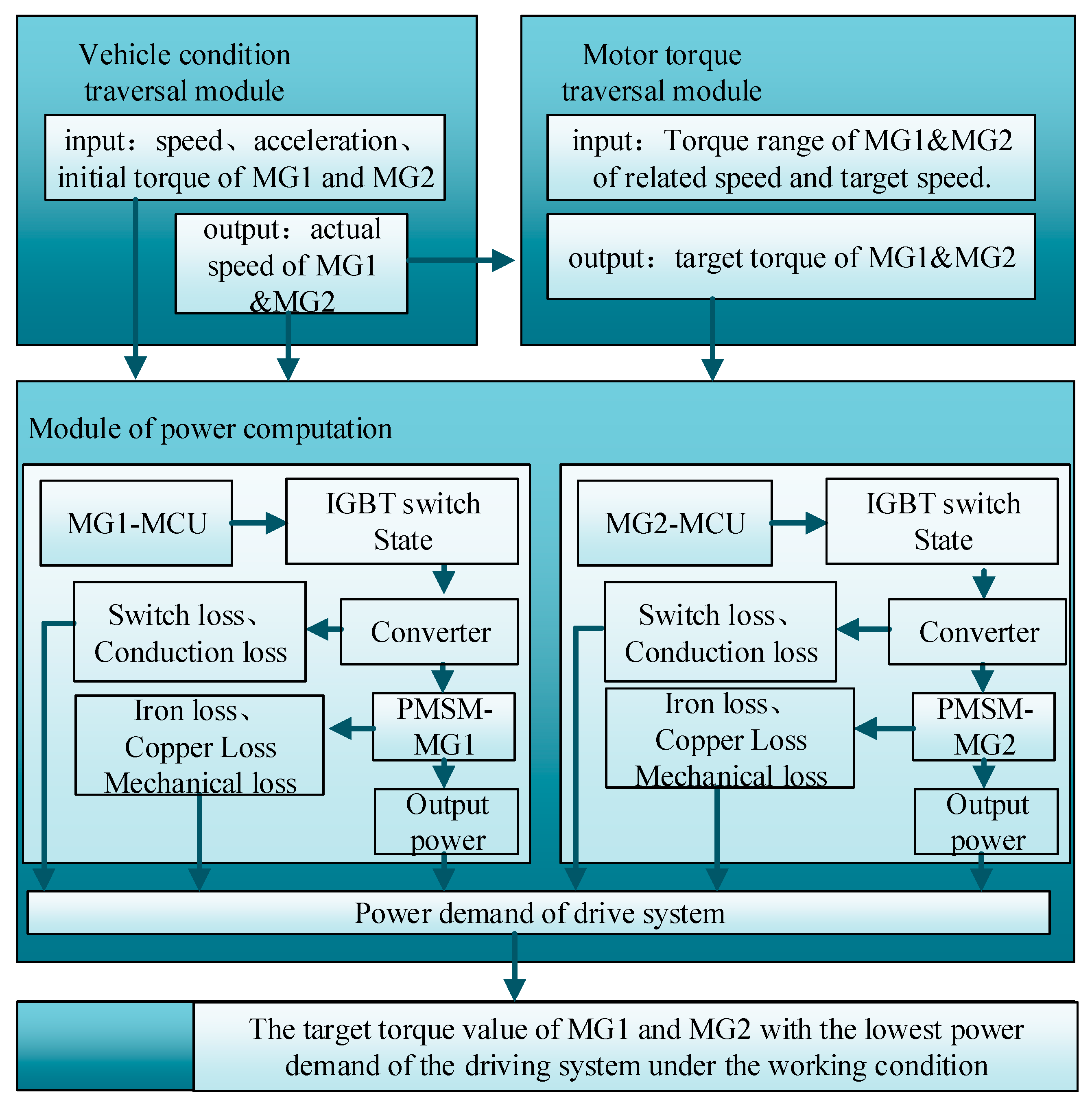
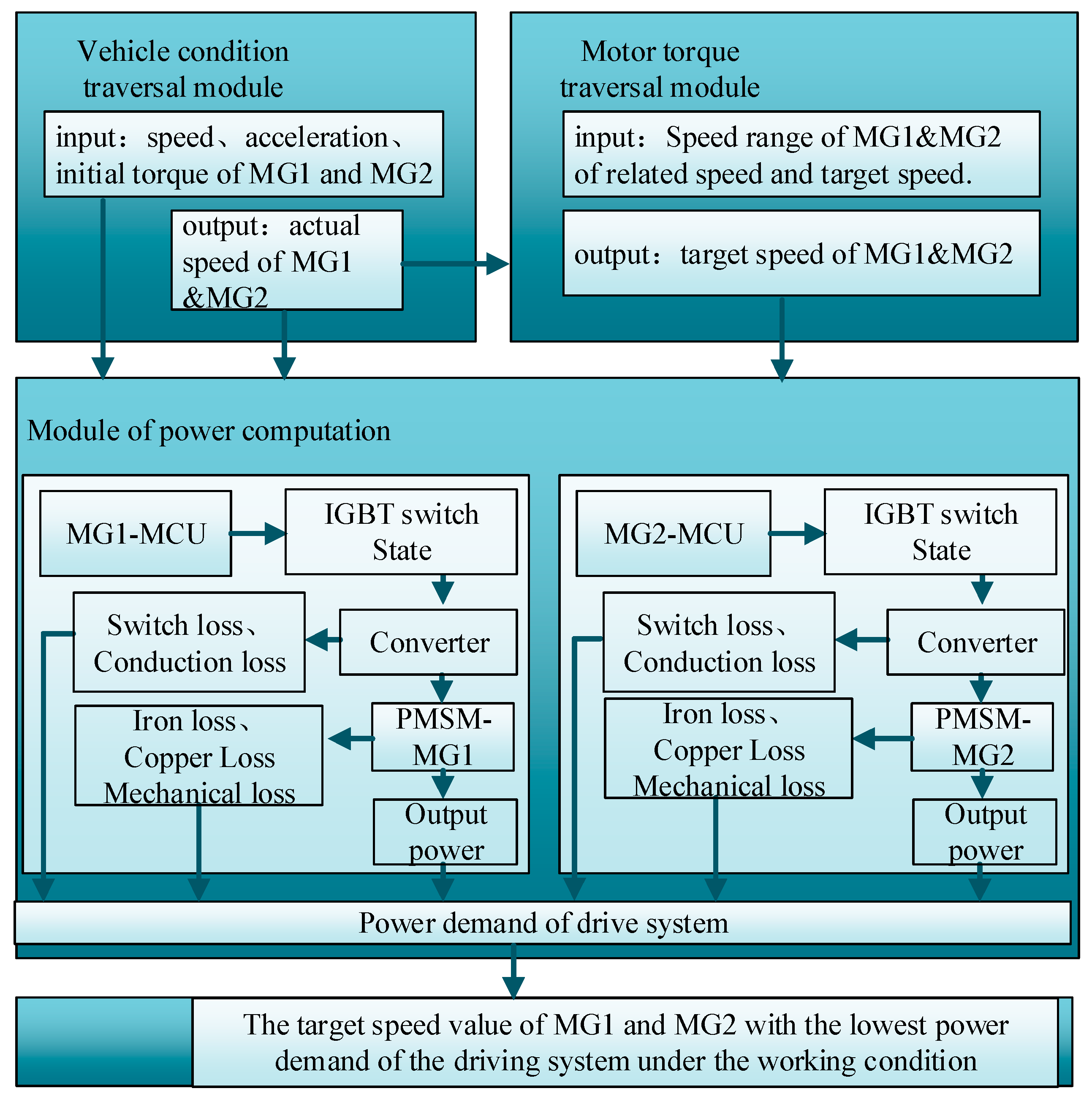
4.1. System Power Distribution Strategy
4.2. Simulation Analyses
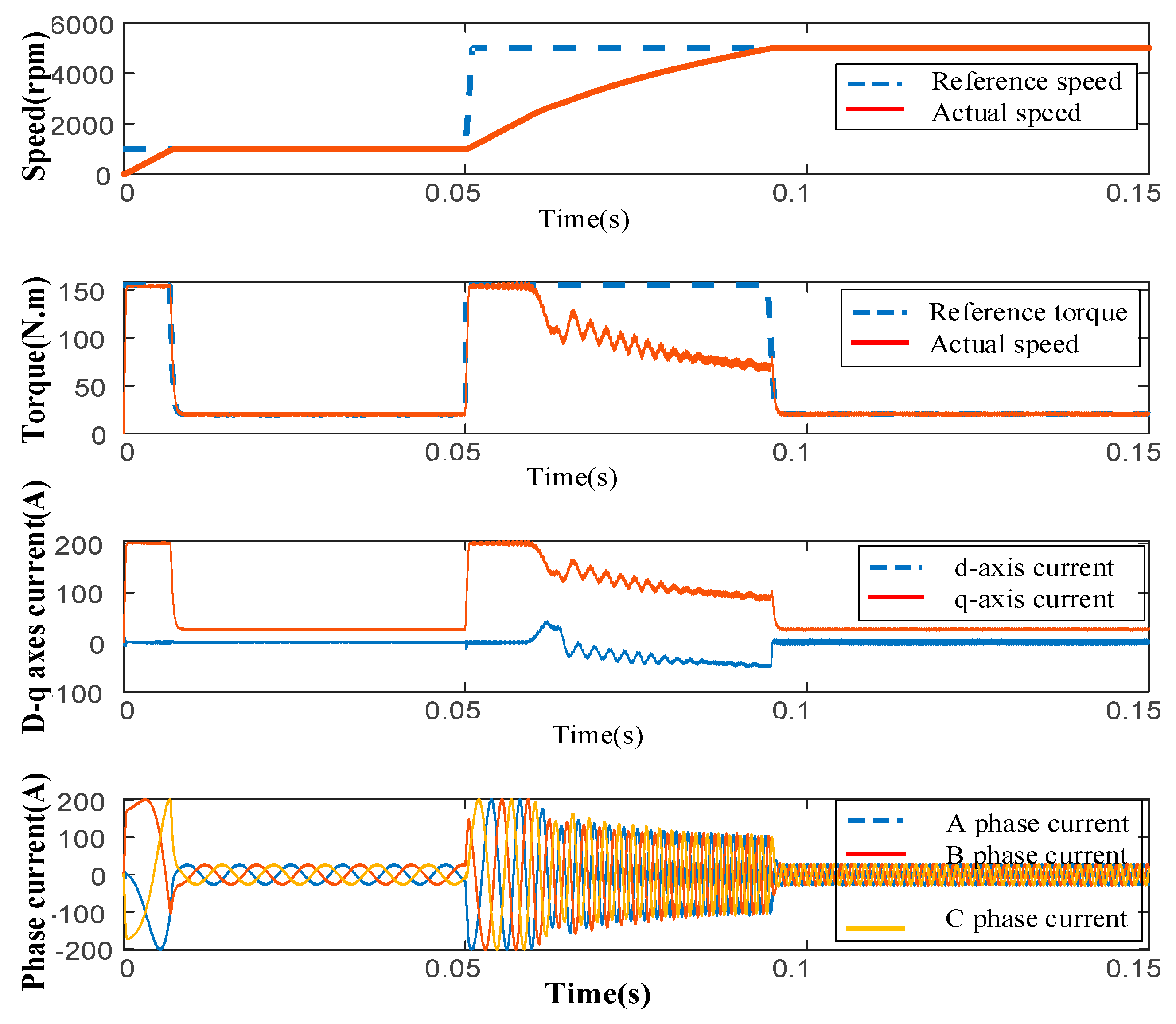
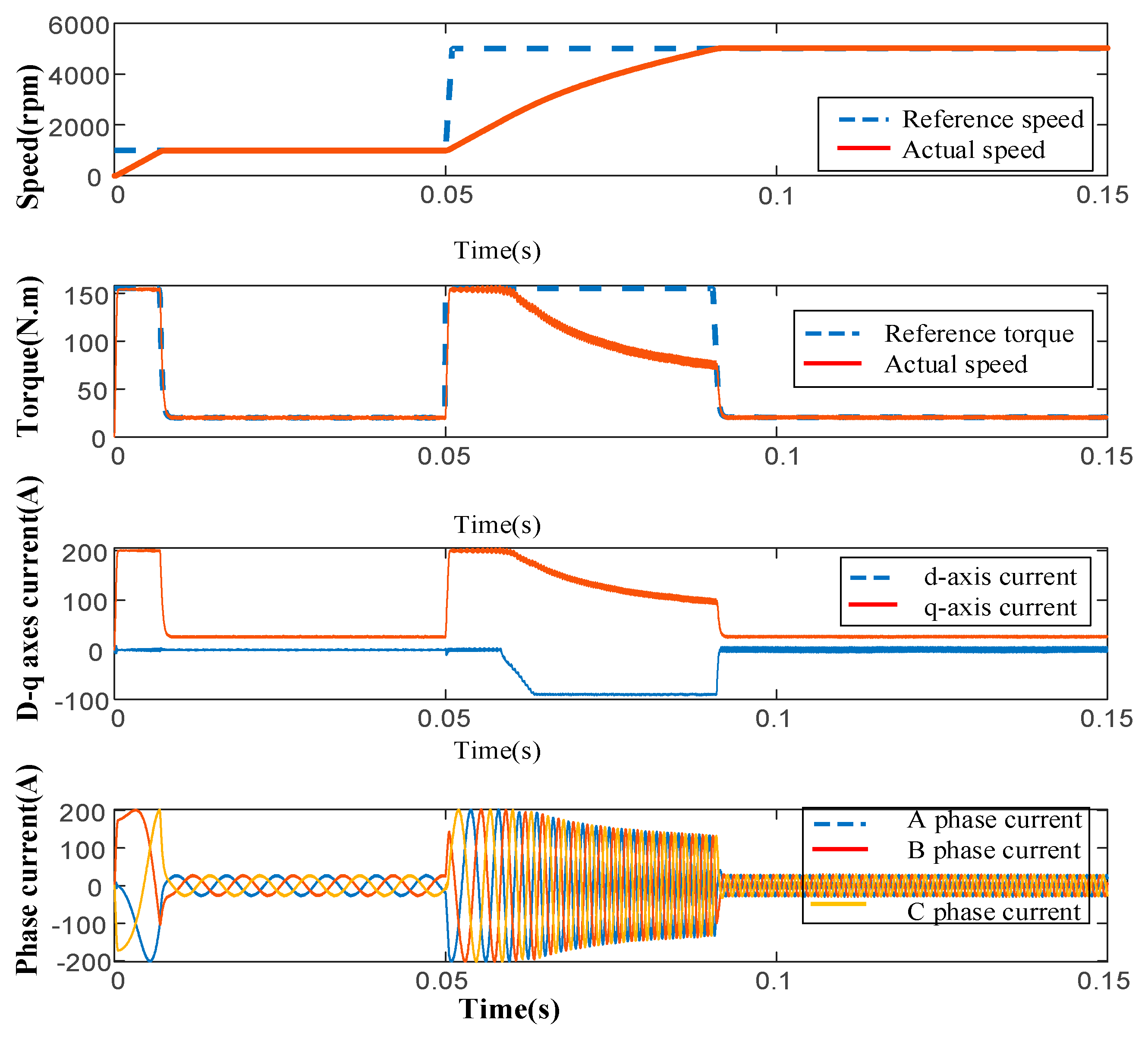
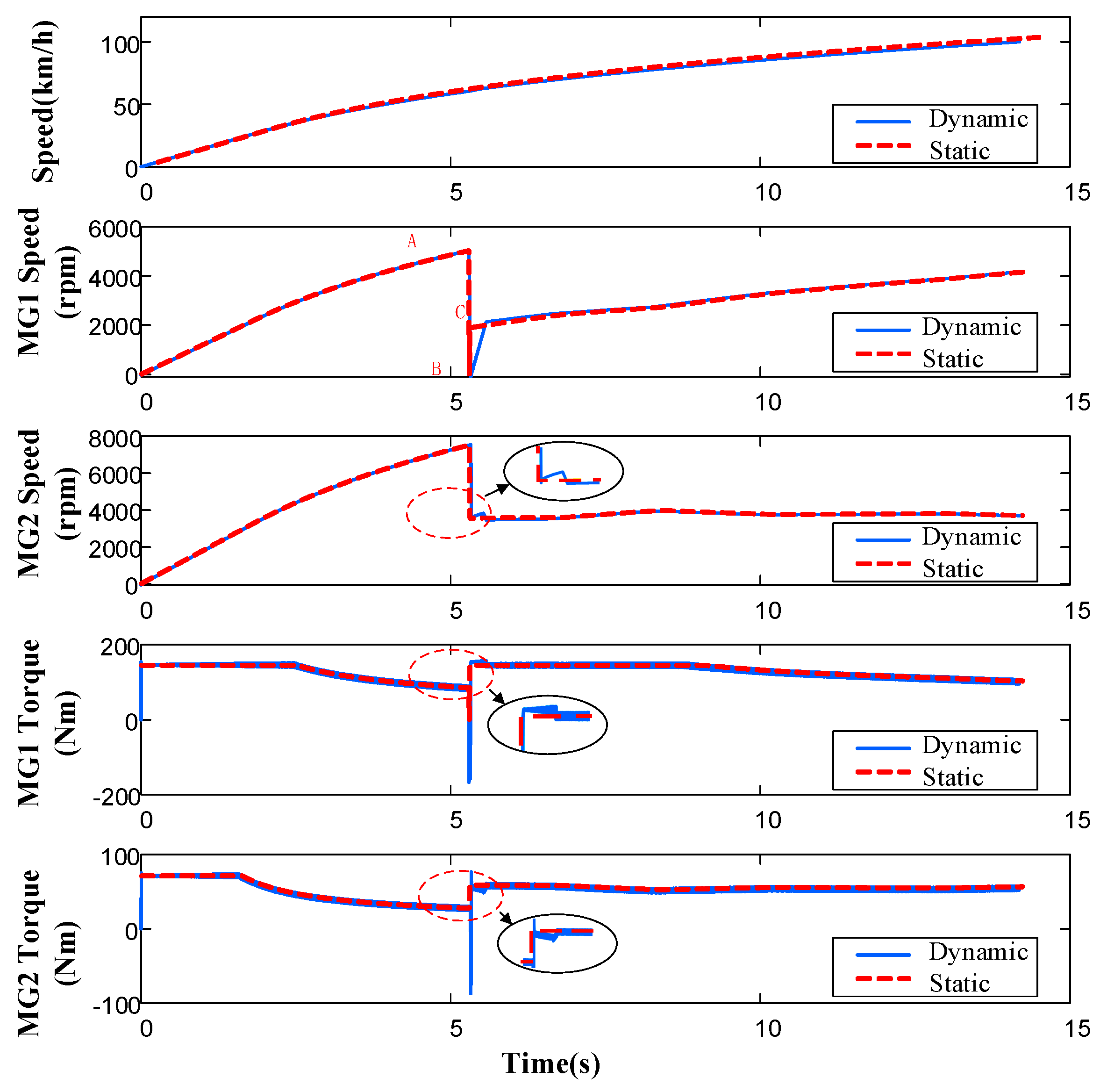
4.2.1. 0–100 km/h Acceleration Simulation
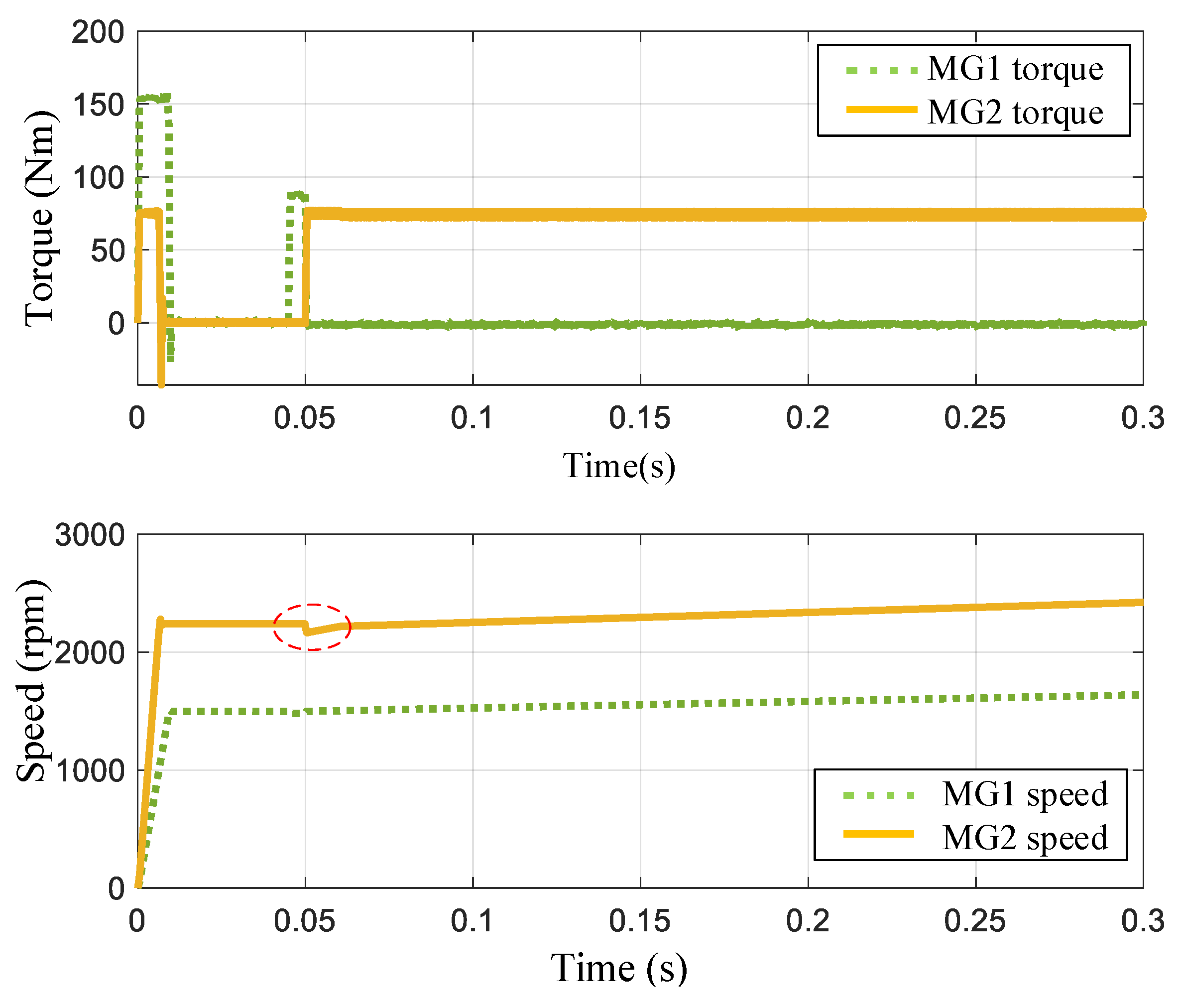
4.2.2. Torque Coupling Mode Performance Simulation
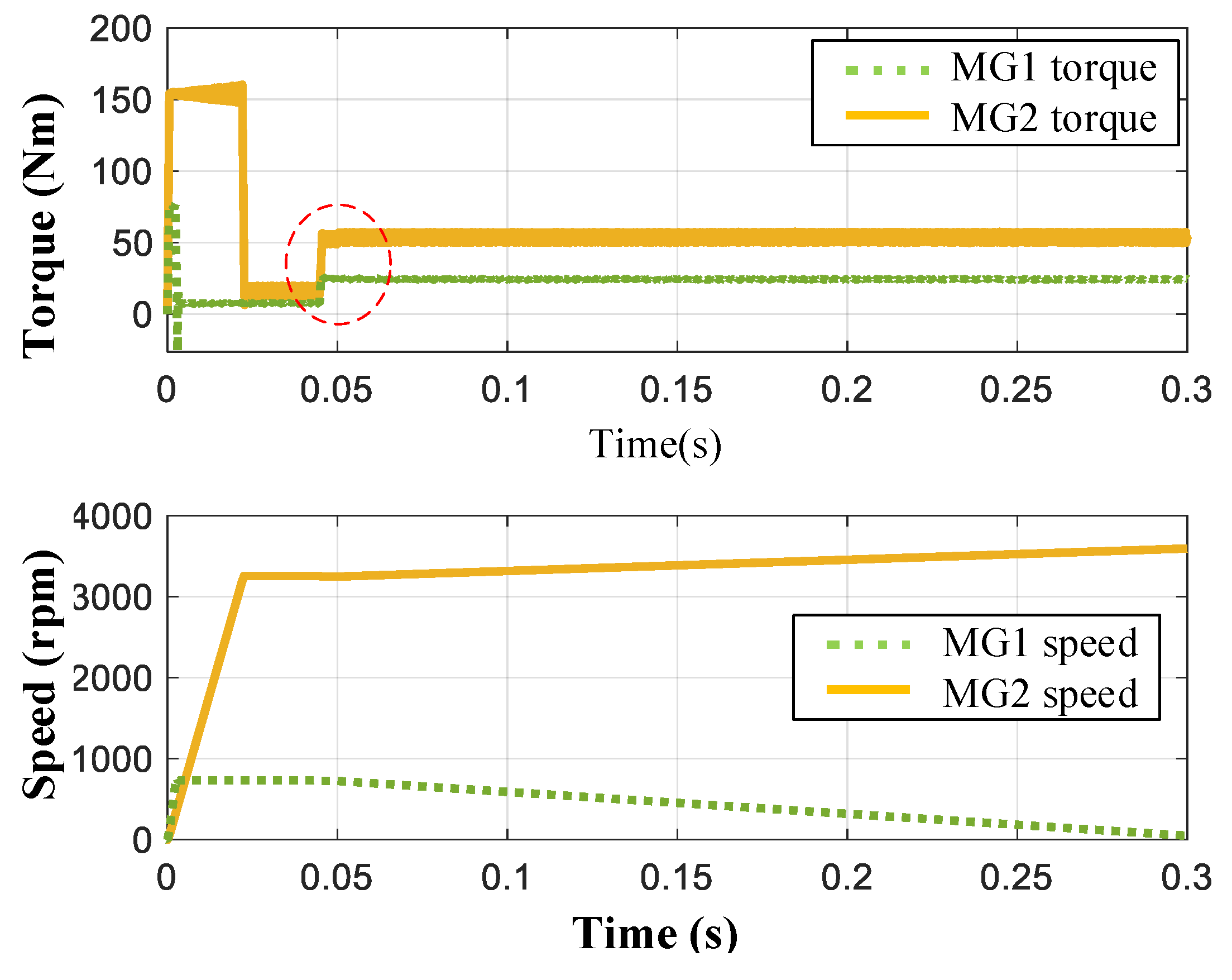
4.2.3. Speed Coupling Mode Performance Simulation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Armature current vector of the d-axis | |
| Armature current vector of the q-axis | |
| Voltage vector of the d-axis | |
| Voltage vector of the q-axis | |
| Iron loss current of the d-axis | |
| Iron loss current of the q-axis | |
| Current vector of the d-axis | |
| Current vector of the q-axis | |
| Inductance of the d-axis | |
| Inductance of the q-axis | |
| Copper loss resistance | |
| Iron loss resistance | |
| Flux | |
| Electrical angular velocity | |
| Salient pole ratio | |
| Eddy current loss coefficient | |
| Hysteresis loss coefficient | |
| Armature current | |
| Terminal voltage | |
| Electromagnetic torque | |
| Number of pole pairs | |
| Load torque | |
| J | Moment of inertia |
| Angular velocity | |
| Electrical angle | |
| n1* | Target speed |
| Inverter switching frequency |
References
- Zeng, J. Research on the Drive Control Strategy of the New Dual Motor Coupling Drive System. Master’s Thesis, Chongqing University, Chongqing, China, 2015. [Google Scholar]
- Ramadan, H.; Becherif, M.; Claude, F. Energy management improvement of hybrid electric vehicles via combined GPS/rule-based methodology. IEEE Trans. Autom. Sci. Eng. 2017, 14, 586–597. [Google Scholar] [CrossRef]
- Han, S.M.; Yin, X.F.; Wu, X.H. Mode-Switch Strategy for Dual-Motor Coupling System of Electric Vehicles Based on Optimal Dynamic Performance. In Proceedings of the 2015 International Conference on Electrical, Automation and Mechanical Engineering, Phuket, Thailand, 26–27 July 2015. [Google Scholar]
- Zhang, S.; Zhang, C.; Han, G.; Wang, Q. Optimal control strategy design based on dynamic programming for a dual-motor coupling-propulsion system. Sci. World J. 2014, 2014, 958239. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, W. Research on Parameter Matching, Coordinated Control and Performance Evaluation of Permanent Magnet Synchronous Motor for Vehicle. Ph.D. Thesis, Jilin University, Changchun, China, 2010. [Google Scholar]
- Li, F.; Wang, Y.; Wang, R. Simulation of speed-control system for PMSM based on sliding mode control. In Proceedings of the 2013 International Conference on Mechatronic Sciences, Electric Engineering and Computer (MEC), Shenyang, China, 20–22 December 2013. [Google Scholar]
- Zhou, F. Research on Power System Parameter Matching and Vehicle Control Strategy of Pure Electric Vehicle. Ph.D. Thesis, Jilin University, Changchun, China, 2013. [Google Scholar]
- Hu, S.; Liang, Z.; Zhang, W.; He, X. Research on the Integration of Hybrid Energy Storage System and Dual Three-Phase PMSM Drive in EV. IEEE Trans. Ind. Electron. 2017, 65, 6602–6611. [Google Scholar] [CrossRef]
- Zhao, S.; Huang, X.; Fang, Y.; Zhang, J. Compensation of DC-Link Voltage Fluctuation for Railway Traction PMSM in Multiple Low-Switching-Frequency Synchronous Space Vector Modulation Modes. IEEE Trans. Veh. Technol. 2018, 67, 235–250. [Google Scholar] [CrossRef]
- Athavale, A.; Sasaki, K.; Gagas, B.S.; Kato, T.; Lorenz, R.D. Variable Flux Permanent Magnet Synchronous Machine (VF-PMSM) Design Methodologies to Meet Electric Vehicle Traction Requirements with Reduced Losses. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016. [Google Scholar]
- Iyer, L.V.; Lai, C.; Dhulipati, H.; Mukundan, S.; Mukherjee, K.; Kar, N.C. A novel MTPA theory based bottom-up approach towards parametric and structural design of interior PMSM for electric vehicles. Int. Trans. Electr. Energy Syst. 2018, 28, e2489. [Google Scholar] [CrossRef]
- Omara, A.M.; Sleptsov, M.A. Performance assessment of battery-powered electric vehicle employing PMSM powertrain system. In Proceedings of the 2017 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St. Petersburg, Russia, 1–3 February 2017. [Google Scholar]
- Dang, L.; Bernard, N.; Bracikowski, N.; Berthiau, G. Design optimization with flux weakening of high-speed PMSM for electrical vehicle considering the driving cycle. IEEE Trans. Ind. Electron. 2017, 64, 9834–9843. [Google Scholar] [CrossRef]
- Sepulchre, L.; Fadel, M.; Pietrzak-David, M.; Porte, G. Flux-weakening strategy for high speed PMSM for vehicle application. In Proceedings of the 2016 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Toulouse, France, 2–4 November 2016. [Google Scholar]
- Fodorean, D.; Idoumghar, L.; Brevilliers, M.; Minciunescu, P.; Irimia, C. Hybrid Differential Evolution Algorithm employed for the Optimum Design of a High-Speed PMSM used for EV Propulsion. IEEE Trans. Ind. Electr. 2017, 64, 9824–9833. [Google Scholar] [CrossRef]
- Hu, J.; Zu, G.; Jia, M.; Niu, X. Parameter matching and optimal energy management for a novel dual-motor multi-modes powertrain system. Mech. Syst. Signal Process. 2019, 116, 113–128. [Google Scholar] [CrossRef]
- Pairo, H.; Shoulaie, A. Operating Region and Maximum Attainable Speed of Energy-Efficient Control Methods of Interior Permanent Magnet Synchronous Motors. IET Power Electron. 2017, 10, 555–567. [Google Scholar] [CrossRef]
- Fernandez-Bernal, F.; Garcia-Cerrada, A.; Faure, R. Determination of parameters in interior permanent magnet synchronous motors with iron losses without torque measurement. Ind. Appl. IEEE Trans. 2000, 37, 1265–1272. [Google Scholar] [CrossRef]
- Shinohara, A.; Inoue, Y.; Morimoto, S.; Sanada, M. Direct Calculation Method of Reference Flux Linkage for Maximum Torque per Ampere Control in DTC-Based IPMSM Drives. IEEE Trans. Power Electron. 2016, 32, 2114–2122. [Google Scholar] [CrossRef]
- Weizhe, Q.; Qi, C. Flux weakening control of IPMSM used for xEV traction. In Proceedings of the 2015 IEEE 11th International Conference on Power Electronics and Drive Systems, Sydney, NSW, Australia, 17 August 2015. [Google Scholar]
- Chen, Y.Z.; Fang, Y.T.; Huang, X.Y.; Zhang, J. Torque and Flux Weakening Control with MTPV for Interior Permanent Magnet Synchronous Motor. In Proceedings of the 2016 IEEE Vehicle Power and Propulsion Conference (VPPC), Hangzhou, China; 17–20 October 2016. [Google Scholar]
- Ekanayake, S.; Pouramin, A.; Dutta, R.; Rahman, M.F. Verification of a novel voltage control strategy for MTPV control of a fractional-slot concentrated-winding IPMSM. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017. [Google Scholar]
- Fadel, M.; Sepulchre, L.; David, M.; Porte, G. MTPV Flux Weakening Strategy for PMSM High Speed Drive. IEEE Trans. Ind. Appl. 2018, 54, 6081–6089. [Google Scholar]
- Lin, P.Y.; Lee, W.T.; Chen, S.W.; Hwang, J.C.; Lai, Y.S. Infinite speed drives control with MTPA and MTPV for interior permanent magnet synchronous motor. In Proceedings of the IECON 2014–40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 26 February 2015. [Google Scholar]
- Kim, B.; Kwak, M.; Chung, T.; Lee, Y.; Jung, J. A method for improving HEV motor system efficiency considering battery voltage variation. In Proceedings of the 8th International Conference on Power Electronics—ECCE, Asia, Jeju, Korea, 7 July 2011. [Google Scholar]

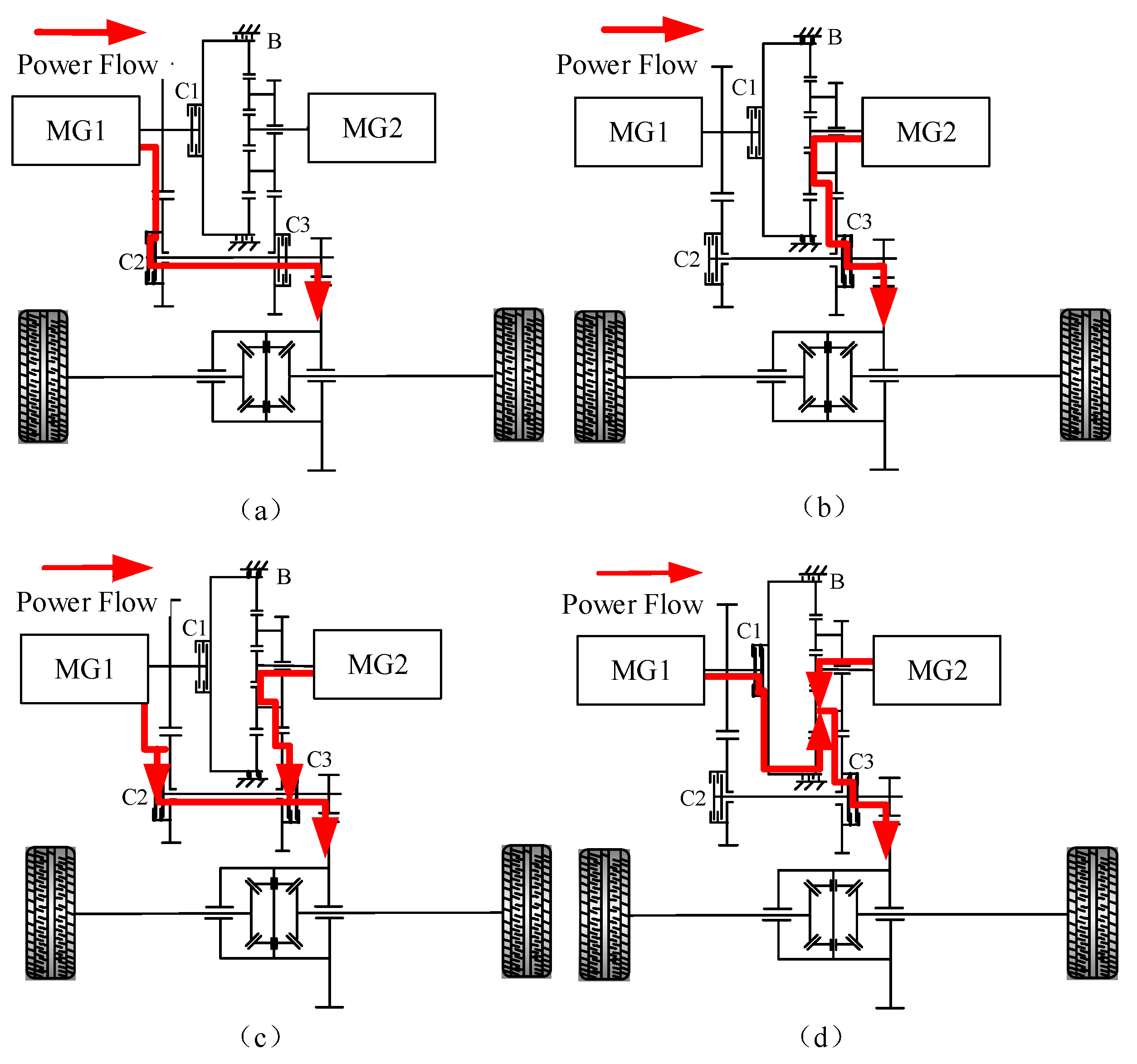

| Mode | MG1 | MG2 | C1 | C2 | C3 | B | Power Flow |
|---|---|---|---|---|---|---|---|
| M1 | M | C | OFF | OFF | ON | OFF | Figure 2a |
| M2 | C | M | OFF | ON | OFF | ON | Figure 2b |
| M3 | M | M | OFF | ON | ON | ON | Figure 2c |
| M4 | M | M | ON | ON | OFF | OFF | Figure 2d |
| Component | Quantity (Unit) | Value |
|---|---|---|
| MG1 | Rated/peak power (kW) | 22/46.5 |
| Rated/maximum speed (rpm) | 2880/5636 | |
| Rated/maximum torque (Nm) | 73/154 | |
| MG2 | Rated/peak power (kW) | 10/20.5 |
| Rated/maximum speed (rpm) | 3300/8338 | |
| Rated/maximum torque (Nm) | 29/59 | |
| Planetary gear | Ratio k | 2.6 |
| Gear 1 | Ratio i1 | 2.92 |
| Gear 2 | Ratio i2 | 1.2 |
| Final drive | Ratio i0 | 4.05 |
| Battery pack | Type | Li-ion |
| Rated voltage (V) | 333 | |
| Rated capacity (Ah) | 78 |
| Symbol | Value |
|---|---|
| 8 | |
| 0.0642 Vs | |
| (1e−2H) | 0.0707 |
| (1e−2H) | 0.0707 |
| 0.0354 Ω |
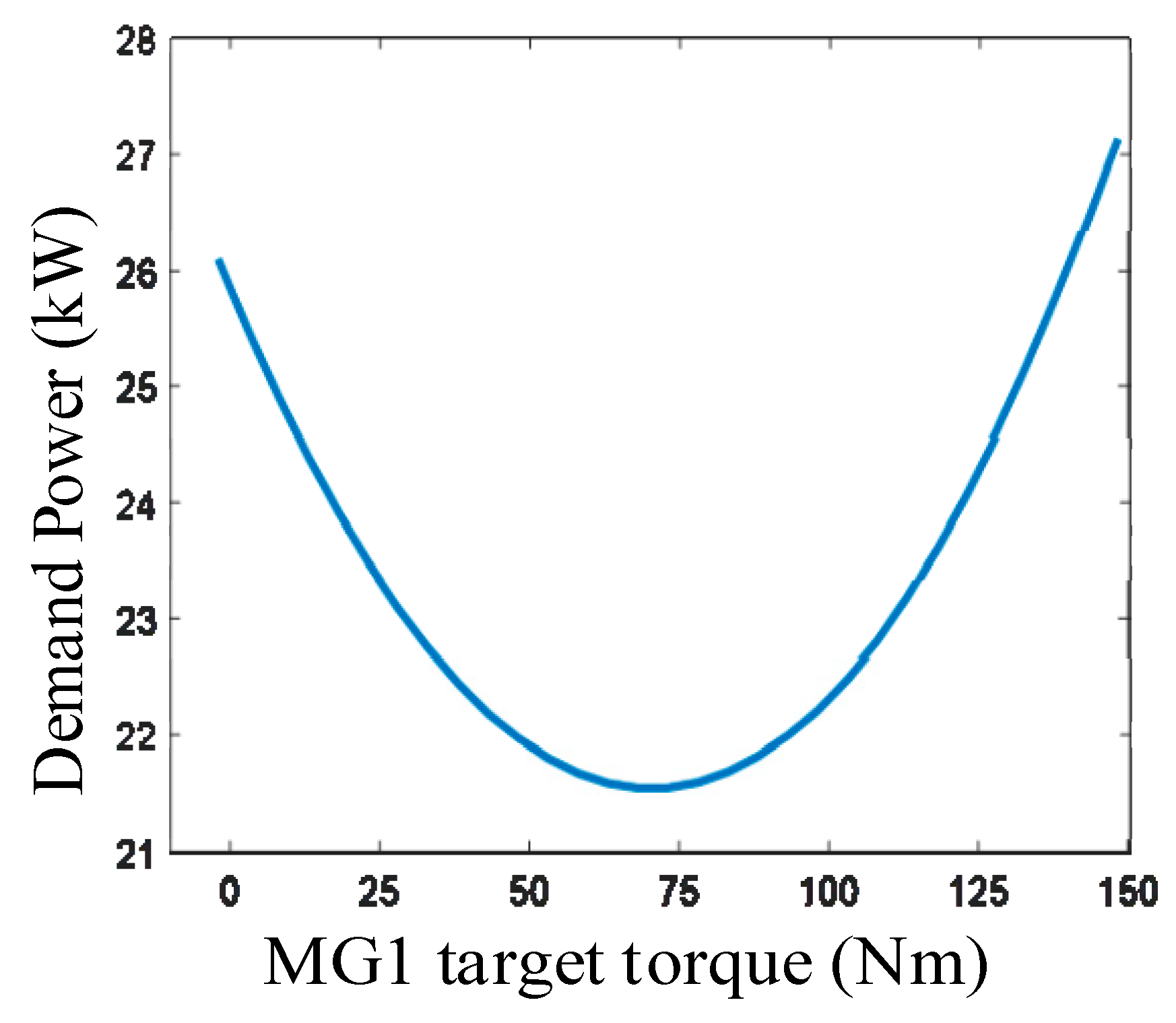
| MG1 Target Torque/Nm | MG1 Power/kW | MG2 Power/kW | Demand Power/kW |
|---|---|---|---|
| −2 | 0.248 | 25.856 | 26.104 |
| 68 | 13.476 | 8.073 | 21.549 |
| 88 | 17.814 | 4.007 | 21.822 |
| 148 | 32.297 | −5.157 | 27.140 |
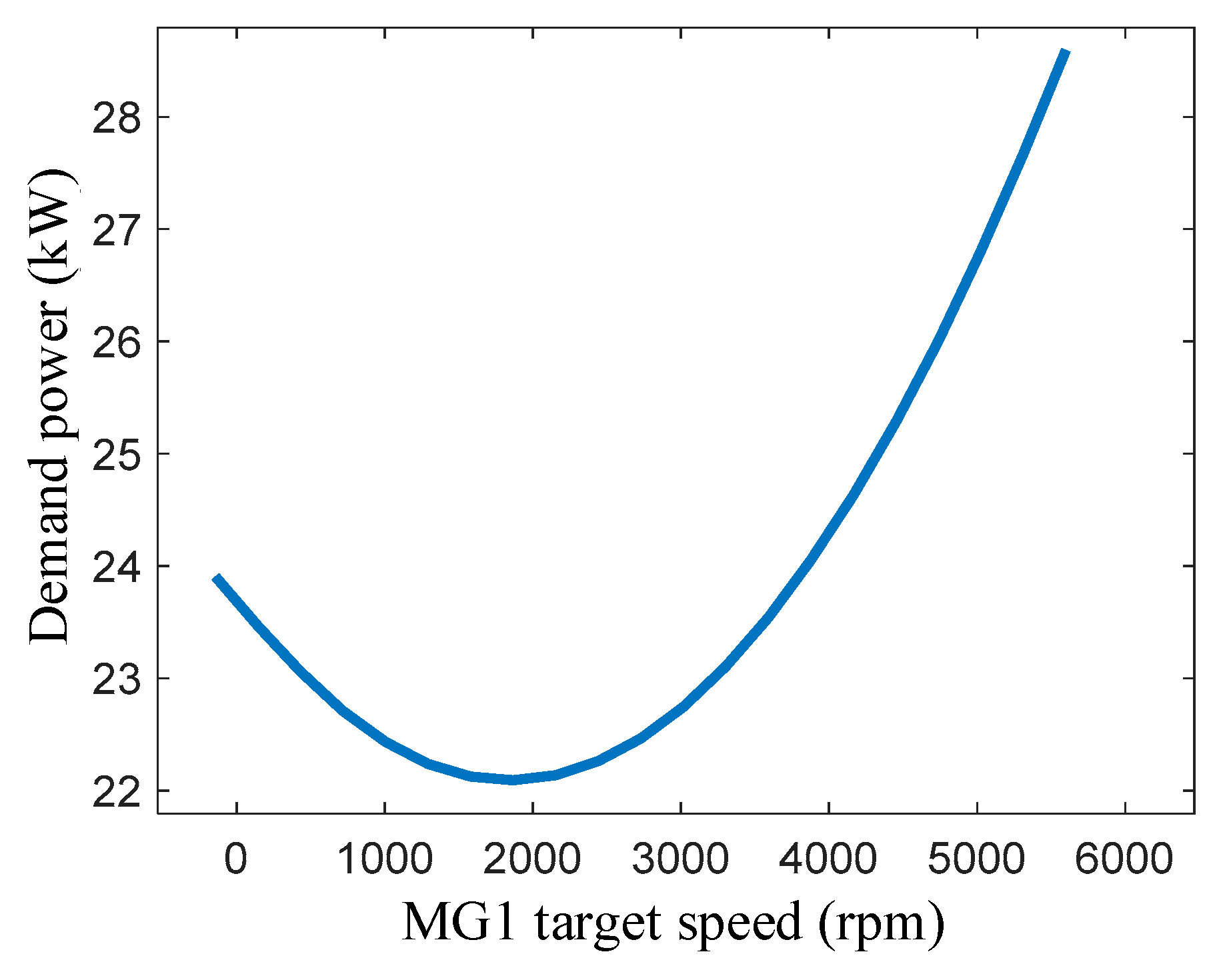
| MG1 Target Speed/rpm | MG1 Power/kW | MG2 Power/kW | Demand Power/kW |
|---|---|---|---|
| −295 | 7.615 | 16.291 | 23.906 |
| 1867 | 14.347 | 7.745 | 22.092 |
| 3590 | 21.53 | 2.013 | 23.543 |
| 5600 | 31.56 | −2.965 | 28.595 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Jia, M.; Xiao, F.; Fu, C.; Zheng, L. Motor Vector Control Based on Speed-Torque-Current Map. Appl. Sci. 2020, 10, 78. https://doi.org/10.3390/app10010078
Hu J, Jia M, Xiao F, Fu C, Zheng L. Motor Vector Control Based on Speed-Torque-Current Map. Applied Sciences. 2020; 10(1):78. https://doi.org/10.3390/app10010078
Chicago/Turabian StyleHu, Jianjun, Meixia Jia, Feng Xiao, Chunyun Fu, and Lingling Zheng. 2020. "Motor Vector Control Based on Speed-Torque-Current Map" Applied Sciences 10, no. 1: 78. https://doi.org/10.3390/app10010078
APA StyleHu, J., Jia, M., Xiao, F., Fu, C., & Zheng, L. (2020). Motor Vector Control Based on Speed-Torque-Current Map. Applied Sciences, 10(1), 78. https://doi.org/10.3390/app10010078







