Characteristic Length and Time Scales of the Highly Forward Scattering of Photons in Random Media
Abstract
:1. Introduction
2. Materials and Methods
2.1. Time-Domain Photon Transport Models
2.1.1. Radiative Transfer Equation (RTE)
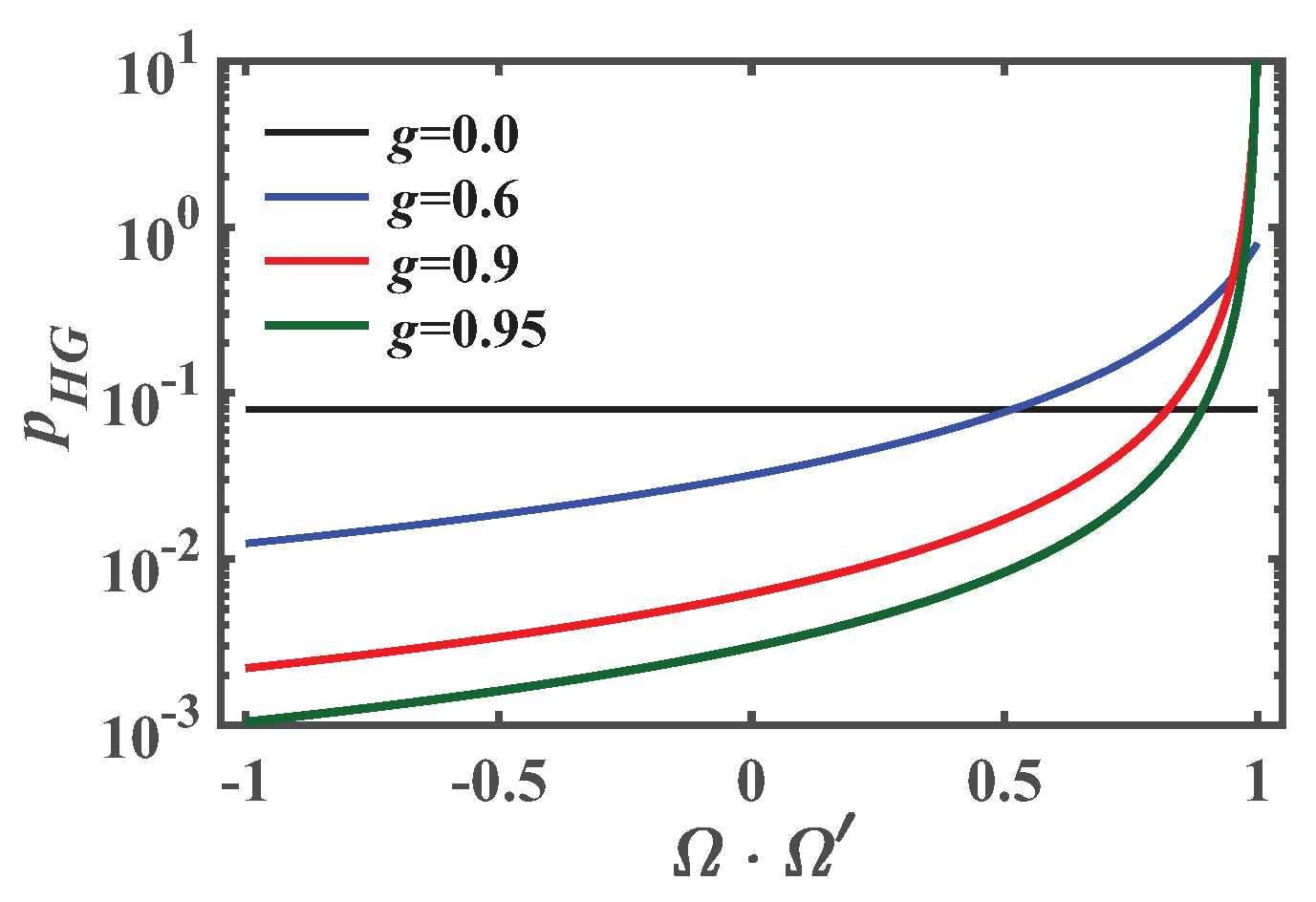
2.1.2. Henyey-Greenstein Phase Function and Anisotropy Factor
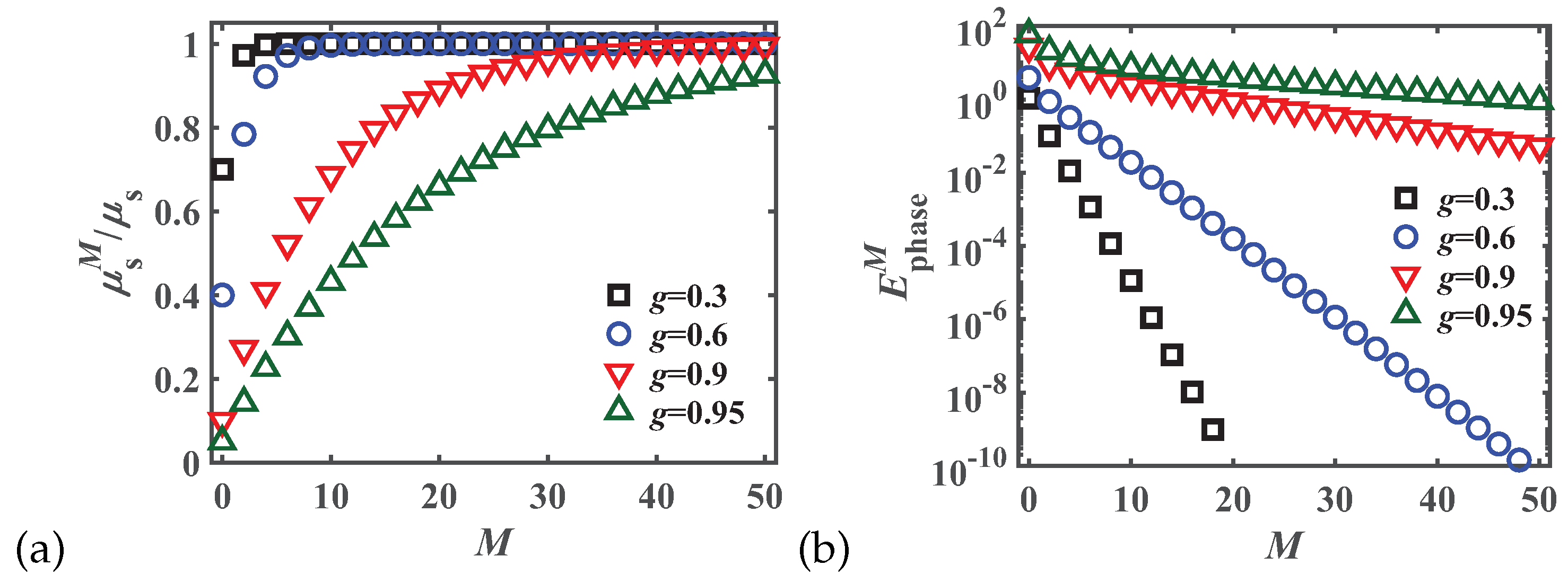
2.1.3. M-th Order Delta-Eddington Equation (dEM)
2.1.4. Photon Diffusion Equation (PDE)
2.2. Analytical Solutions (AS) of the Time-Domain Photon Transport Models
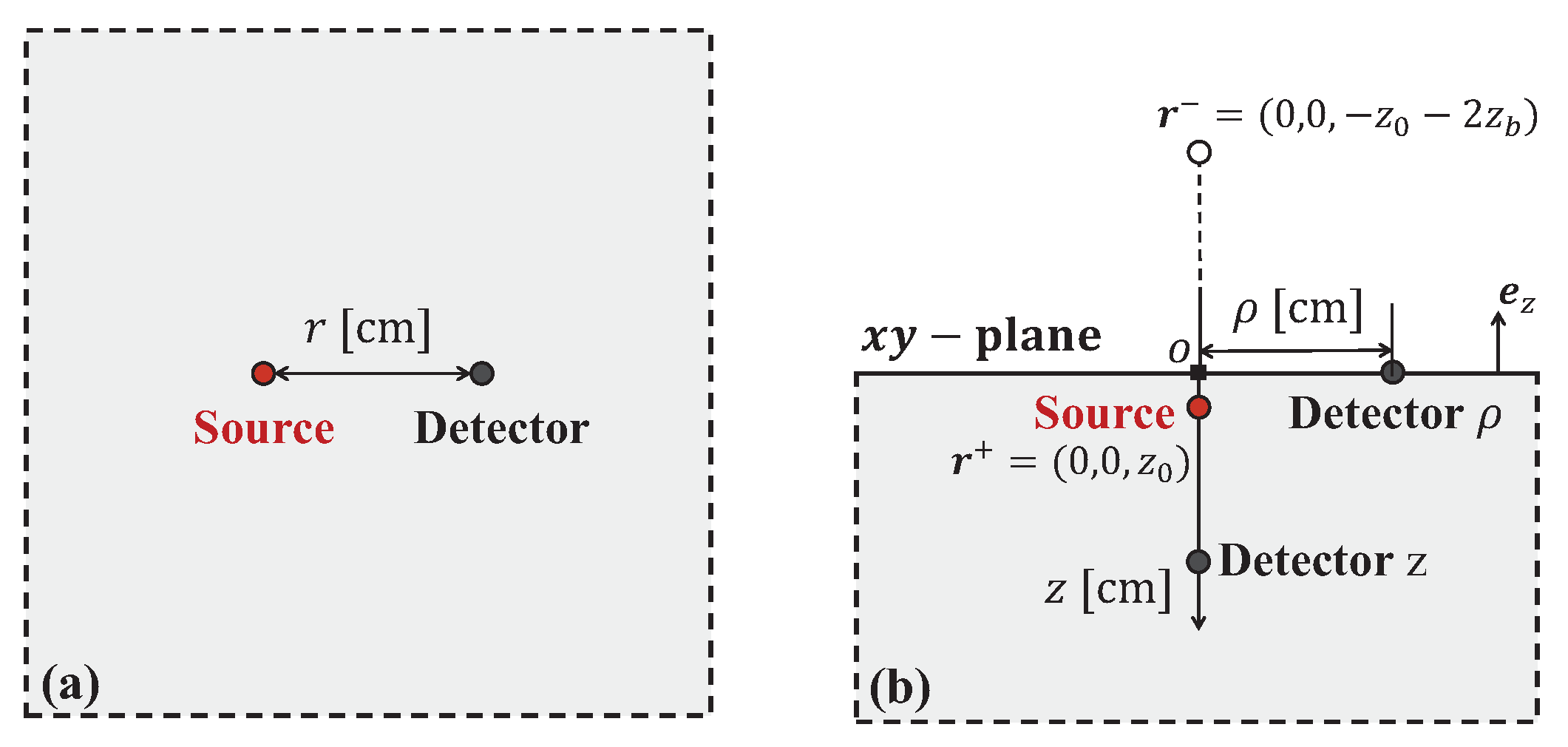
2.2.1. 3D Infinite Homogeneous Media
2.2.2. 3D Semi-Infinite Homogeneous Media
2.3. Optical Properties, Source-Detector (SD) Distances, and Computations of the Analytical Solutions
3. Results
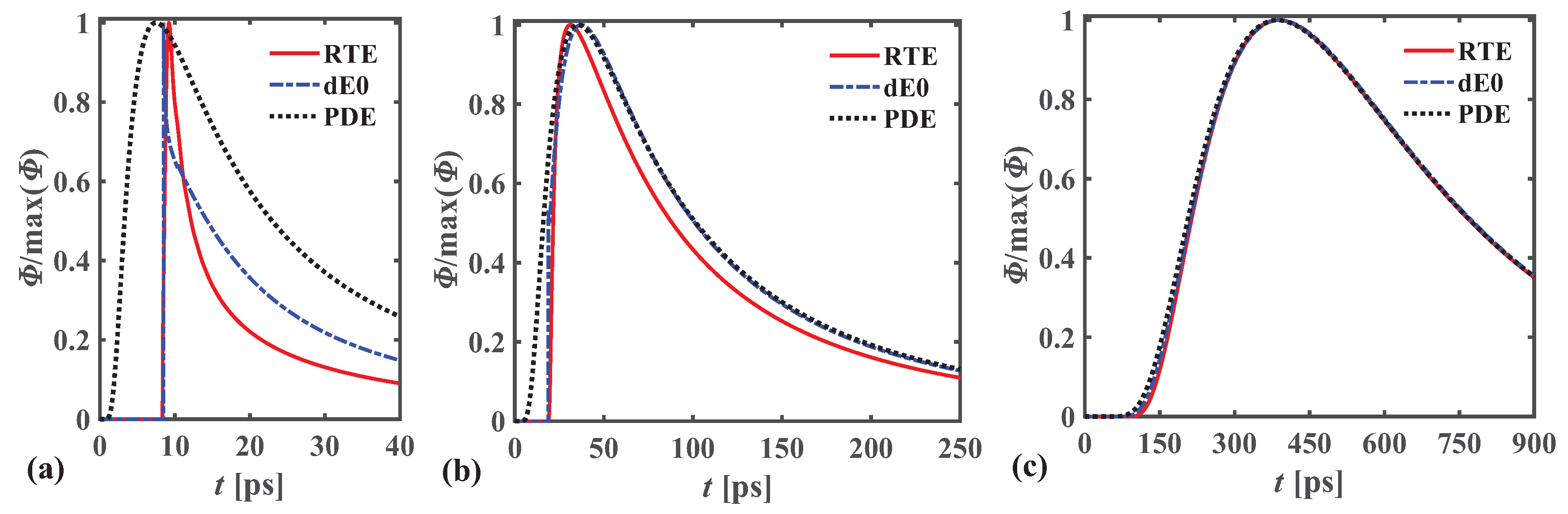
3.1. Classification of the Length and Time Scales of Photon Transport
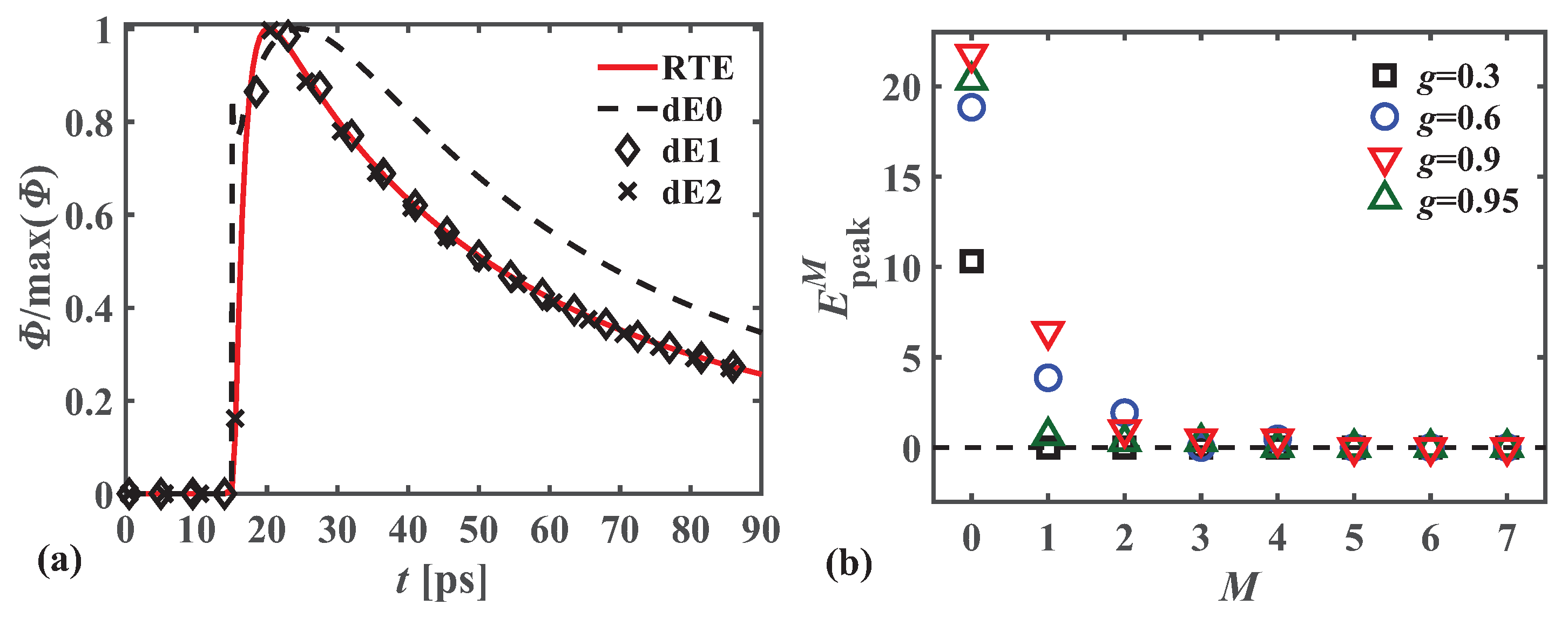
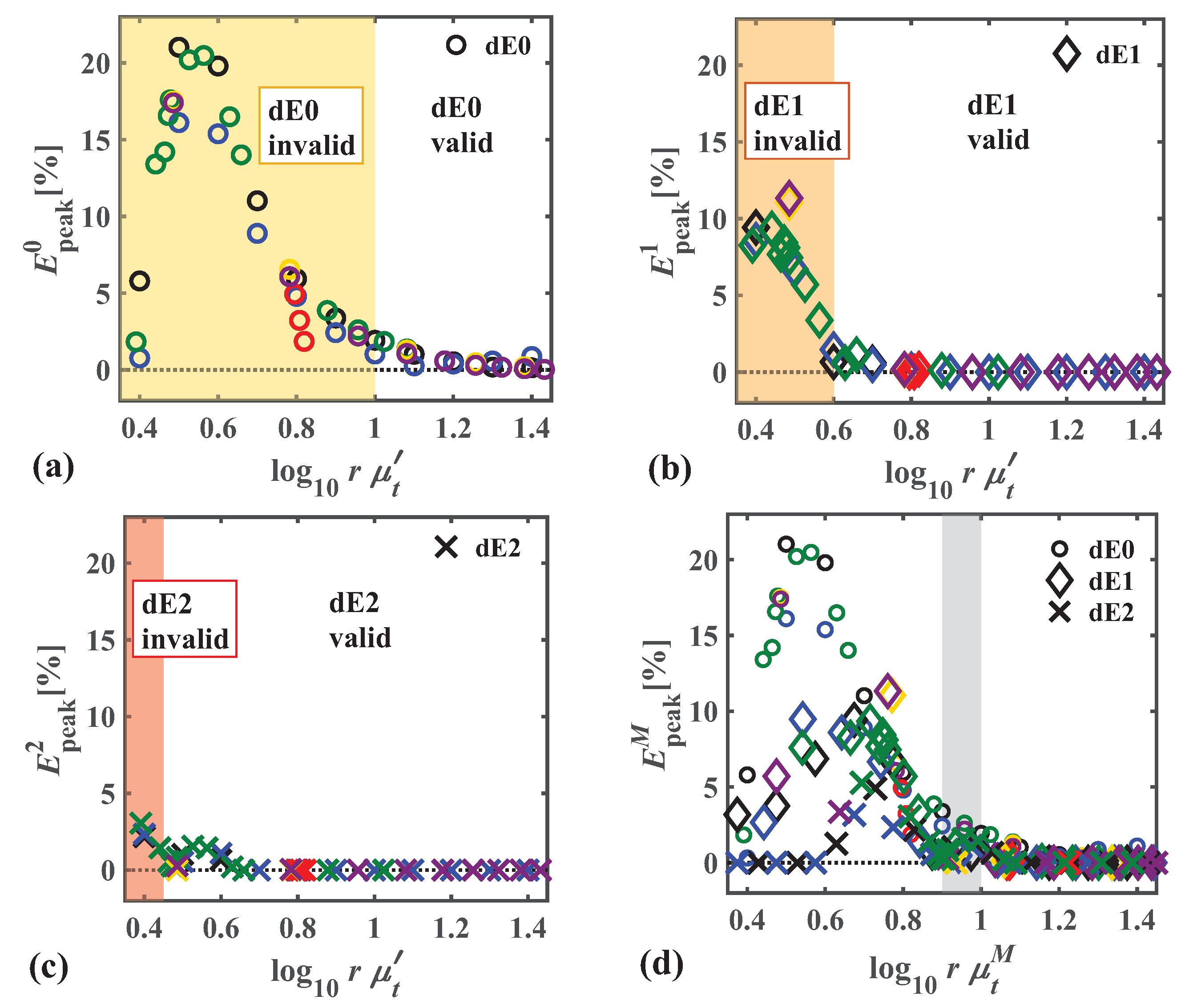
3.2. Length and Time Scales for the dEM to Be Valid in the Scattering Regime
3.3. Influence of the Boundary Conditions on the Crossover Lengths and Times
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
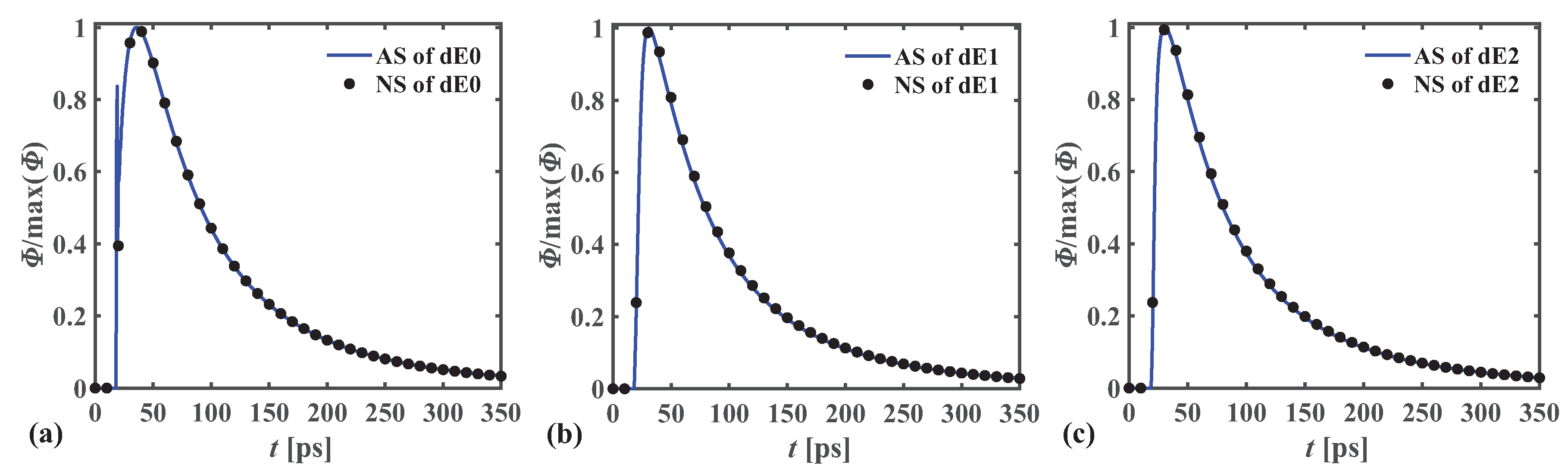
Appendix A. Verification of the Analytical Solutions of the dEM for 3D Infinite Homogeneous Media
References
- Gibson, A.P.; Hebden, J.C.; Arridge, S.R. Recent advances in diffuse optical imaging. Phys. Med. Biol. 2005, 50, R1–R43. [Google Scholar] [CrossRef] [PubMed]
- Okawa, S.; Hoshi, Y.; Yamada, Y. Improvement of image quality of time-domain diffuse optical tomography with lp sparsity regularization. Biomed. Opt. Express 2011, 2, 3334–3348. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yamada, Y.; Okawa, S. Diffuse Optical Tomography: Present Status and Its Future. Opt. Rev. 2014, 21, 185–205. [Google Scholar] [CrossRef]
- Yamada, Y.; Suzuki, H.; Yamashita, Y. Time-Domain Near-Infrared Spectroscopy and Imaging: A Review. Appl. Sci. 2019, 9, 1127. [Google Scholar] [CrossRef] [Green Version]
- Ntziachristos, V. Going deeper than microscopy: The optical imaging frontier in biology. Nat. Methods 2010, 7, 603–614. [Google Scholar] [CrossRef] [PubMed]
- Bizheva, K.K.; Siegel, A.M.; Boas, D.A. Path-length-resolved dynamic light scattering in highly scattering random media: The transition to diffusing wave spectroscopy. Phys. Rev. E 1998, 58, 7664–7667. [Google Scholar] [CrossRef] [Green Version]
- Guerin, W.; Chong, Y.D.; Baudouin, Q.; Liertzer, M.; Rotter, S.; Kaiser, R. Diffusive to quasi-ballistic random laser: Incoherent and coherent models. J. Opt. Soc. Am. B 2016, 33, 1888–1896. [Google Scholar] [CrossRef] [Green Version]
- Tarvainen, T.; Vauhkonen, M.; Kolehmainen, V.; Kaipio, J. A hybrid radiative transfer – diffusion model for optical tomography. Appl. Opt. 2005, 44, 876–886. [Google Scholar] [CrossRef]
- Fujii, H.; Okawa, S.; Yamada, Y.; Hoshi, Y. Hybrid model of light propagation in random media based on the time-dependent radiative transfer and diffusion equations. J. Quant. Spectrosc. Radiat. Transfer 2014, 147, 145–154. [Google Scholar] [CrossRef] [Green Version]
- Yoo, K.M.; Liu, F.; Alfano, R.R. When does the diffusion approximation fail to describe photon transport in random media? Phys. Rev. Lett. 1990, 64, 2647–2650. [Google Scholar] [CrossRef]
- Hielscher, A.H.; Alcouffe, R.E.; Barbour, R.L. Comparison of finite-difference transport and diffusion calculations for photon migration in homogeneous and heterogeneous tissues. Phys. Med. Biol. 1998, 43, 1285–1302. [Google Scholar] [CrossRef] [PubMed]
- Venugopalan, V.; You, J.S.; Tromberg, B.J. Radiative transport in the diffusion approximation: An extension for highly absorbing media and small source-detector separations. Phys. Rev. E 1998, 58, 2395–2407. [Google Scholar] [CrossRef] [Green Version]
- Machida, M.; Panasyuk, G.Y.; Schotland, J.C.; Markel, V.A. The Green’s function for the radiative transport equation in the slab geometry. J. Phys. A Math. Theor. 2010, 43, 065402. [Google Scholar] [CrossRef]
- Fujii, H.; Hoshi, Y.; Okawa, S.; Kosuge, T.; Kohno, S. Numerical modeling of photon propagation in biological tissue based on the radiative transfer equation. In Proceedings of the 4th International Symposium on Slow Dynamics in Complex Systems, Sendai, Japan, 2–7 December 2013; Volume 1518, pp. 579–585. [Google Scholar]
- Fujii, H.; Okawa, S.; Yamada, Y.; Hoshi, Y.; Watanabe, M. A coupling model of the radiative transport equation for calculating photon migration in biological tissue. In Proceedings of the SPIE for Biophotonics Japan, Tokyo, Japan, 27–28 October 2015; Volume 9792, pp. 1–5. [Google Scholar]
- Joseph, J.H.; Wiscombe, W.J.; Weinman, J.A. The delta-Eddington approximation for radioactive flux transfer. J. Atmos. Sci. 1976, 33, 2452–2459. [Google Scholar] [CrossRef]
- Welch, A.; van Gemert, M. Optical-Thermal Response of Laser-Irradiated Tissue; Plenum Press: London, UK, 1995. [Google Scholar]
- Klose, A.D.; Hielscher, A.H. Modeling Photon Propagation In Anisotropically Scattering Media with the Equation Of Radiative Transfer. Proc. SPIE 2003, 4955, 624–633. [Google Scholar]
- Cong, W.; Shen, H.; Cong, A.; Wang, Y.; Wang, G. Modeling photon propagation in biological tissues using a generalized Delta-Eddington phase function. Phys. Rev. E 2007, 76, 051913. [Google Scholar] [CrossRef] [Green Version]
- Boulet, P.; Collin, A.; Consalvi, J.L. On the finite volume method and the discrete ordinates method regarding radiative heat transfer in acute forward anisotropic scattering media. J. Quant. Spectrosc. Radiat. Transfer 2007, 104, 460–473. [Google Scholar] [CrossRef]
- Klose, A.D.; Hielscher, A.H. Optical tomography with the equation of radiative transfer. Int. J. Numer. Methods Heat Fluid Flow 2008, 18, 443–464. [Google Scholar] [CrossRef]
- Jia, J.; Kim, H.K.; Hielscher, A.H. Fast linear solver for radiative transport equation with multiple right hand sides in diffuse optical tomography. J. Quant. Spectrosc. Radiat. Transfer 2015, 167, 10–22. [Google Scholar] [CrossRef] [Green Version]
- Kamran, F.; Abildgaard, O.H.A.; Subash, A.A.; Andersen, P.E.; Andersson-engels, S.; Khoptyar, D. Computationally effective solution of the inverse problem in time-of-flight spectroscopy. Opt. Express 2015, 23, 6937–6945. [Google Scholar] [CrossRef] [Green Version]
- Qin, J.; Lu, R. Measurement of the optical properties of fruits and vegetables using spatially resolved hyperspectral diffuse reflectance imaging technique. Postharvest Biol. Technol. 2008, 49, 355–365. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Radiative Transfer; Dover: New York, NY, USA, 1960. [Google Scholar]
- Henyey, L.G.; Greenstein, L.J. Diffuse radiation in the galaxy. J. Astrophys. 1941, 93, 70–83. [Google Scholar] [CrossRef]
- Cheong, W.F.; Prahl, S.A.; Welch, A.J. A review of the optical properties of biological tissue. IEEE J. Quantum Electron 1990, 26, 2166–2185. [Google Scholar] [CrossRef] [Green Version]
- Germer, C.T.; Roggan, A.; Ritz, J.P.; Isbert, C.; Albrecht, D.; Müller, G.; Buhr, H.J. Optical properties of native and coagulated human liver tissue and liver metastases in the near infrared range. Lasers Surg. Med. 1998, 23, 194–203. [Google Scholar] [CrossRef]
- Dehaes, M.; Gagnon, L.; Vignaud, A.; Valabr, R.; Grebe, R.; Wallois, F.; Benali, H. Quantitative investigation of the effect of the extra-cerebral vasculature in diffuse optical imaging: A simulation study. Biomed. Opt. Express 2011, 2, 680–695. [Google Scholar] [CrossRef] [Green Version]
- Furutsu, K.; Yamada, Y. Diffusion approximation for a dissipative random medium and the applications. Phys. Rev. E 1994, 50, 3634–3640. [Google Scholar] [CrossRef]
- Liemert, A.; Kienle, A. Infinite space Green’s function of the time-dependent radiative transfer equation. Biomed. Opt. Express 2012, 3, 543. [Google Scholar] [CrossRef] [Green Version]
- Fujii, H.; Yamada, Y.; Chiba, G.; Hoshi, Y.; Kobayashi, K.; Watanabe, M. Accurate and efficient computation of the 3D radiative transfer equation in highly forward-peaked scattering media using a renormalization approach. J. Comput. Phys. 2018, 374, 591–604. [Google Scholar] [CrossRef]
- Paasschens, J.C.J. Solution of the time-dependent Boltzmann equation. Phys. Rev. E 1997, 56, 1135–1141. [Google Scholar] [CrossRef]
- Martelli, F.; Sassaroli, A.; Pifferi, A.; Torricelli, A.; Spinelli, L.; Zaccanti, G. Heuristic Green’s function of the time dependent radiative transfer equation for a semi-infinite medium. Opt. Express 2007, 15, 18168–18175. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Stochastic Problems in Physics and Astronomy. Rev. Mod. Phys. 1943, 15, 1–88. [Google Scholar] [CrossRef]
- Egan, W.G.; Hilgeman, T.W. Optical Properties of Inhomogeneous Materials; Academic: New York, NY, USA, 1979. [Google Scholar]
- Patterson, M.S.; Chance, B.; Wilson, B.C. Time resolved reflectance and transmittance for the non- invasive measurement of tissue optical properties. Appl. Opt. 1989, 28, 2331–2336. [Google Scholar] [CrossRef] [PubMed]
- Simon, E.; Foschum, F.; Kienle, A. Hybrid Green’s function of the time- dependent radiative transfer equation for anisotropically scattering semi-infinite media scattering semi-infinite media. J. Biomed. Opt. 2013, 18, 015001. [Google Scholar] [CrossRef] [PubMed]
- Klose, A.D.; Netz, U.; Beuthan, J.; Hielscher, A.H. Optical tomography using the time-independent equation of radiative transfer - Part 1: Forward model. J. Quant. Spectrosc. Radiat. Transfer 2002, 72, 691–713. [Google Scholar] [CrossRef]
- Fujii, H.; Chiba, G.; Yamada, Y.; Hoshi, Y.; Kobayashi, K. Numerical treatment of highly forward scattering on radiative transfer using the delta-M approximation and Galerkin quadrature method. In Proceedings of the 9th International Symposium on Radiative Transfer, RAD-19, Athens, Greece, 3–7 June 2019; pp. 261–268. [Google Scholar]
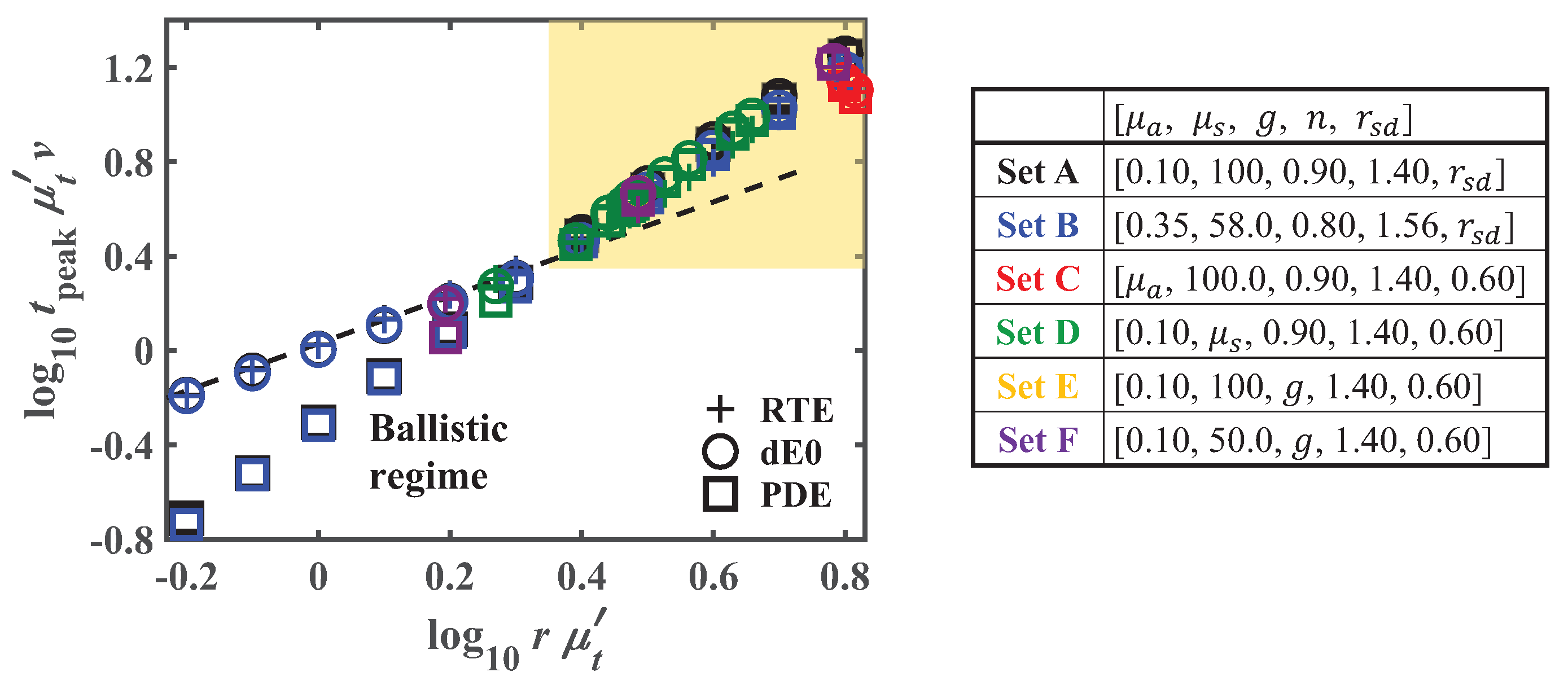


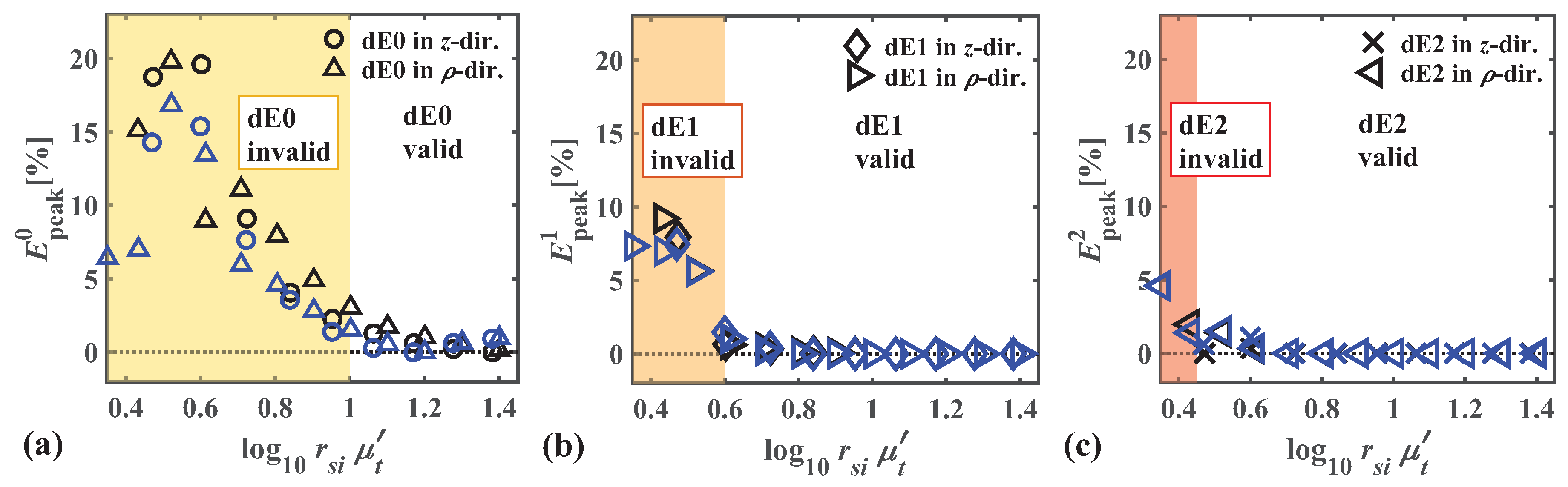
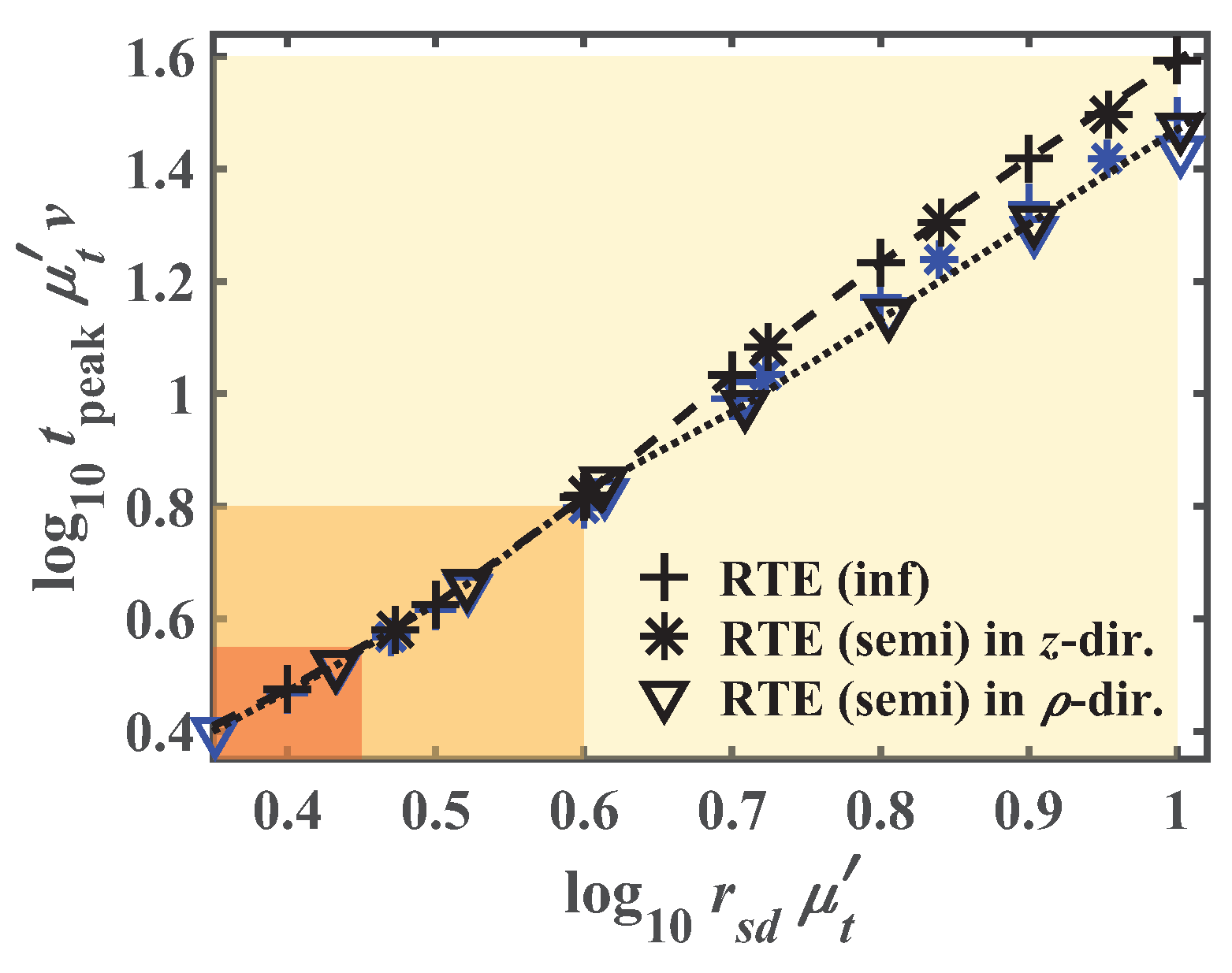
| Parameter Sets: | Range | Color |
|---|---|---|
| Set A: | : 0.15–10.0 | Black |
| Set B: | : 0.15–10.0 | Blue |
| Set C: | : 0.10–1.00 | Red |
| Set D: | : 30.0–200 | Green |
| Set E: | g: 0.10–0.95 | Yellow |
| Set F: | g: 0.10–0.95 | Purple |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fujii, H.; Ueno, M.; Kobayashi, K.; Watanabe, M. Characteristic Length and Time Scales of the Highly Forward Scattering of Photons in Random Media. Appl. Sci. 2020, 10, 93. https://doi.org/10.3390/app10010093
Fujii H, Ueno M, Kobayashi K, Watanabe M. Characteristic Length and Time Scales of the Highly Forward Scattering of Photons in Random Media. Applied Sciences. 2020; 10(1):93. https://doi.org/10.3390/app10010093
Chicago/Turabian StyleFujii, Hiroyuki, Moegi Ueno, Kazumichi Kobayashi, and Masao Watanabe. 2020. "Characteristic Length and Time Scales of the Highly Forward Scattering of Photons in Random Media" Applied Sciences 10, no. 1: 93. https://doi.org/10.3390/app10010093
APA StyleFujii, H., Ueno, M., Kobayashi, K., & Watanabe, M. (2020). Characteristic Length and Time Scales of the Highly Forward Scattering of Photons in Random Media. Applied Sciences, 10(1), 93. https://doi.org/10.3390/app10010093





