An Adaptive Target Tracking Algorithm Based on EKF for AUV with Unknown Non-Gaussian Process Noise
Abstract
1. Introduction
- We propose a target tracking method based on EKF (TT-EKF) to simultaneously estimate the states of an AUV and an MRS.
- We estimate the noise statistics of the heading and forward speed of an AUV and an MRS by using the variational Bayesian algorithm. The noisy forward speed is modeled by the Gaussian mixture distribution (GMD). The noisy heading angle is modeled by a von Mises (vM) distribution.
- We build a neural network compensator to make up for the prediction error caused by the process noise.
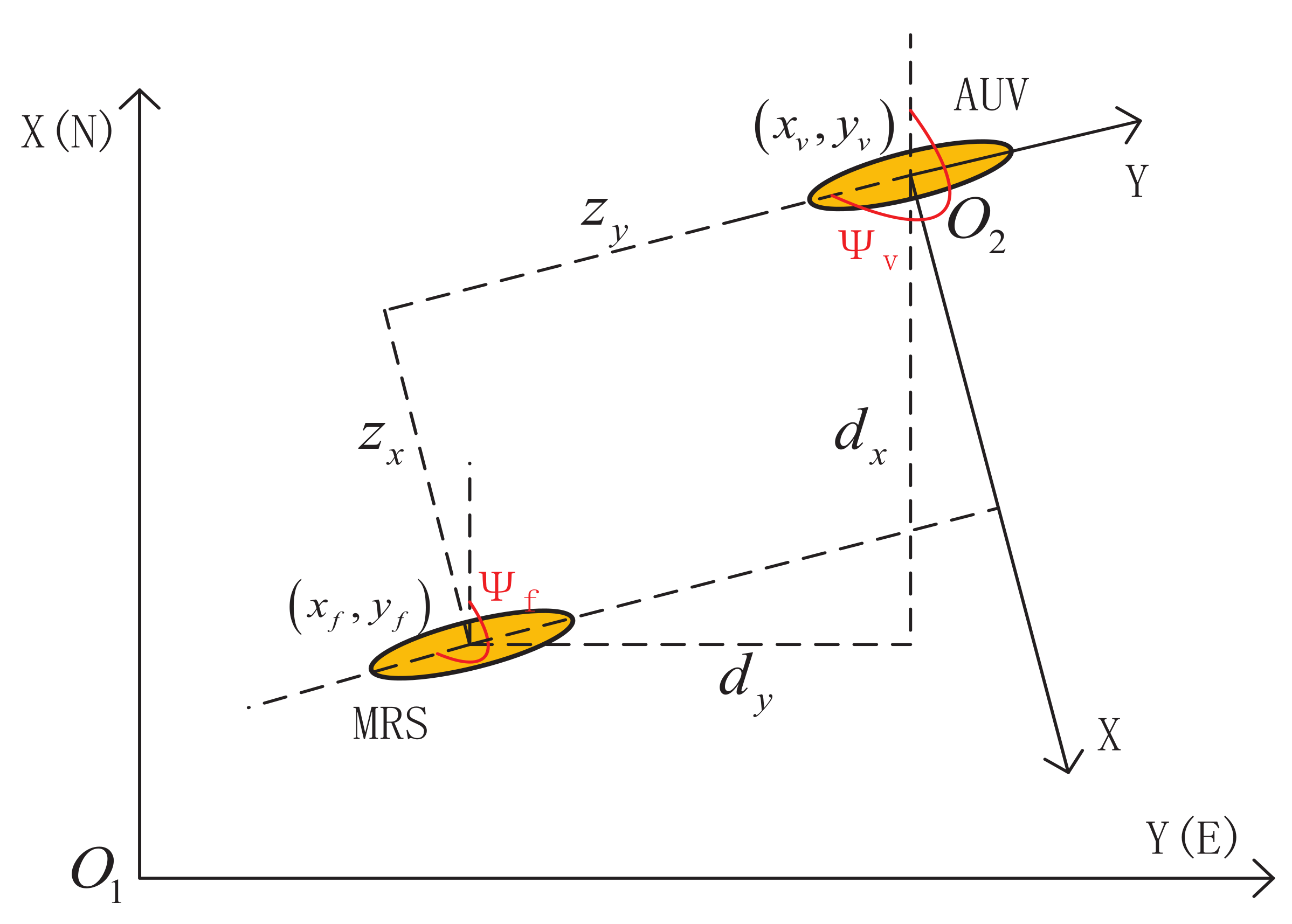
2. System Overview
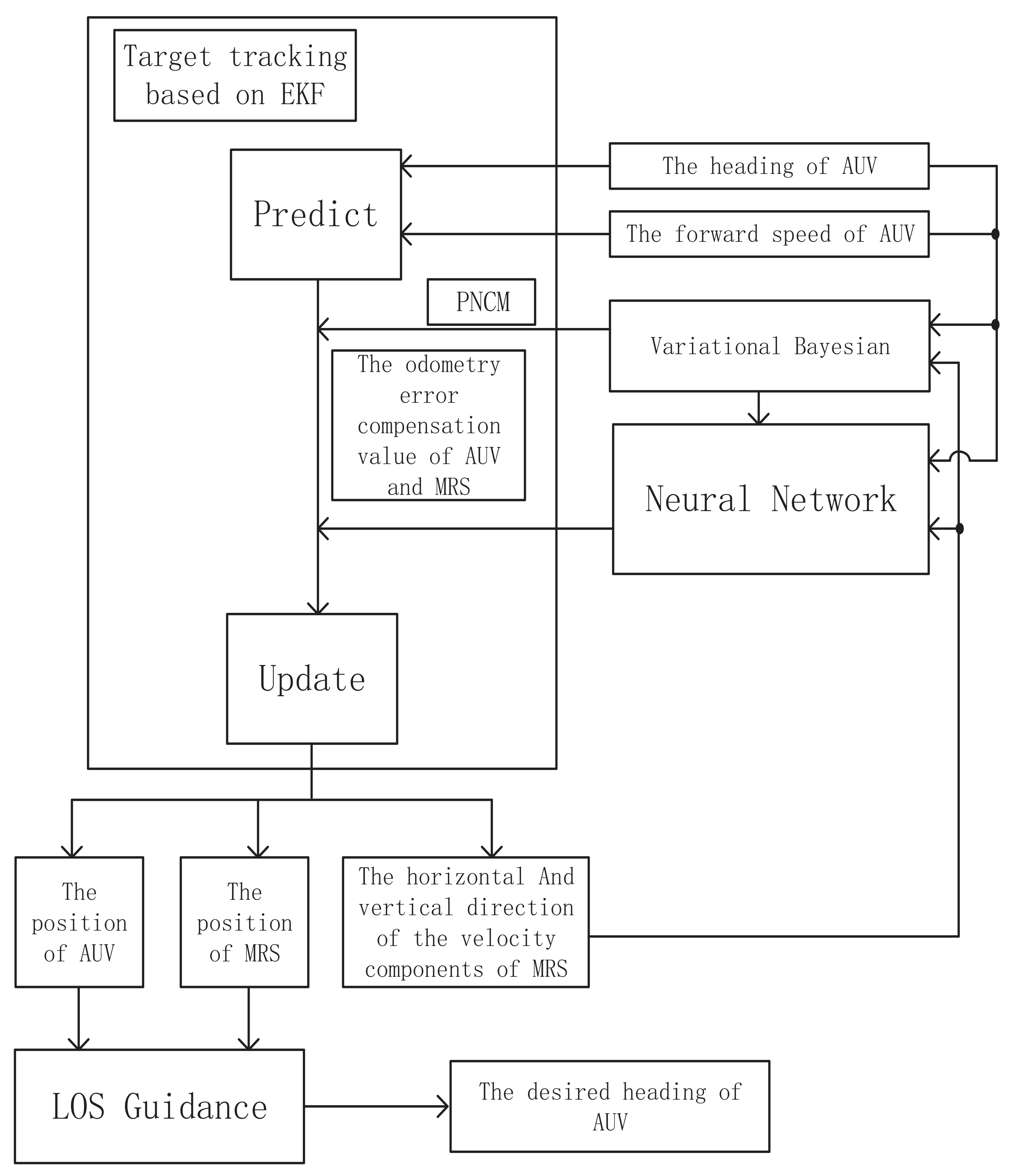
3. Target Tracking Method Based on EKF
4. Adaptive Target Tracking Algorithm Based on EKF
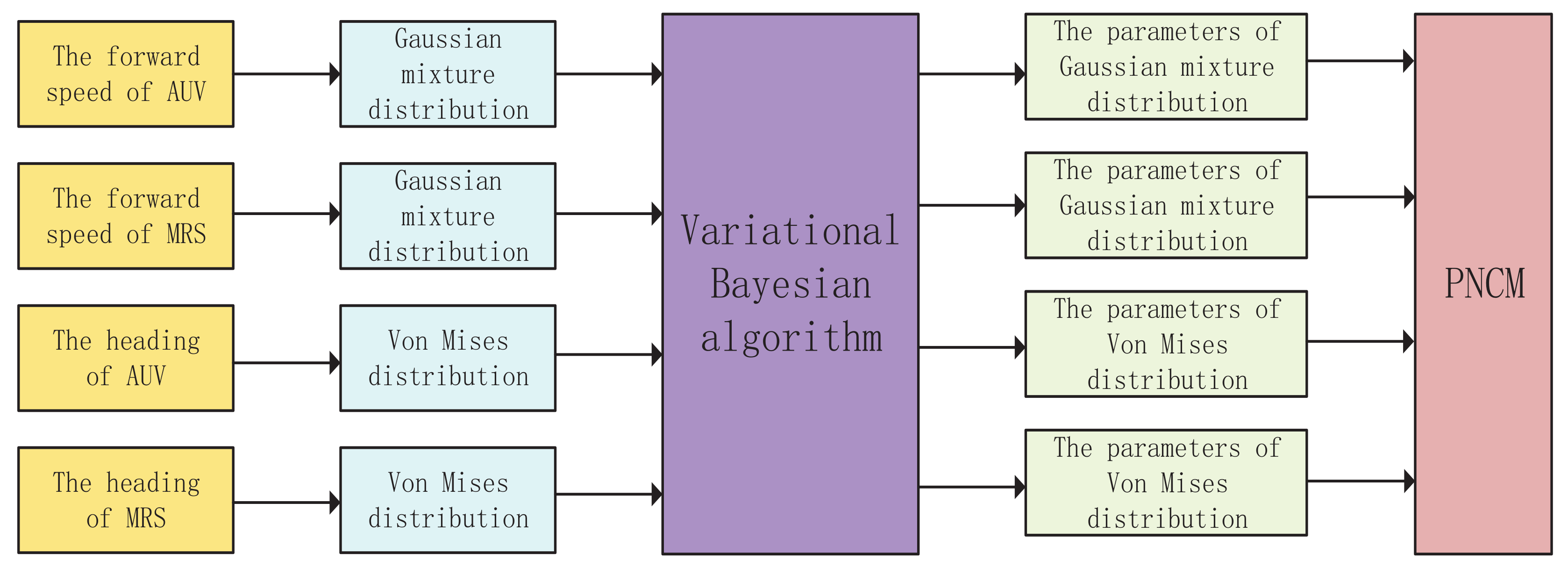
5. Variational Bayesian
5.1. Modeling of Forward Speed and Heading
5.2. Parameters Estimation Based on VB
5.2.1. Parameter Estimation of GMD
5.2.2. Parameter Estimation of vM Distribution
5.3. Estimation of PNCM
6. Neural Network
7. Algorithm Process
- Initialization
- -
- Initilize the PNCM Q, the measurement noise covariance matrix R, the initial state .
- -
- Initilize the parameters used in VB algorithm.
- -
- Initilize the neural network parameters state , which contains the linkweight and threshold value.
- -
- Initilize the prediction error , whose all compents are equals to 0.
- Perform the algorithmFor do for each time instant
- -
- Predict state and its covariance matrix via Equations (5) and (6).
- -
- If
- -
- Perform the state updating via Equations (7)–(11) based on Extended Kalman filter.
- -
end For
8. MATLAB Simulation and Experimental Data Analysis
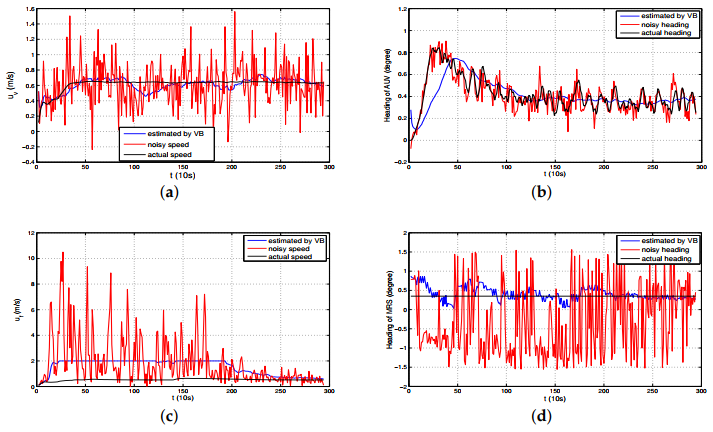
8.1. MATLAB Simulation
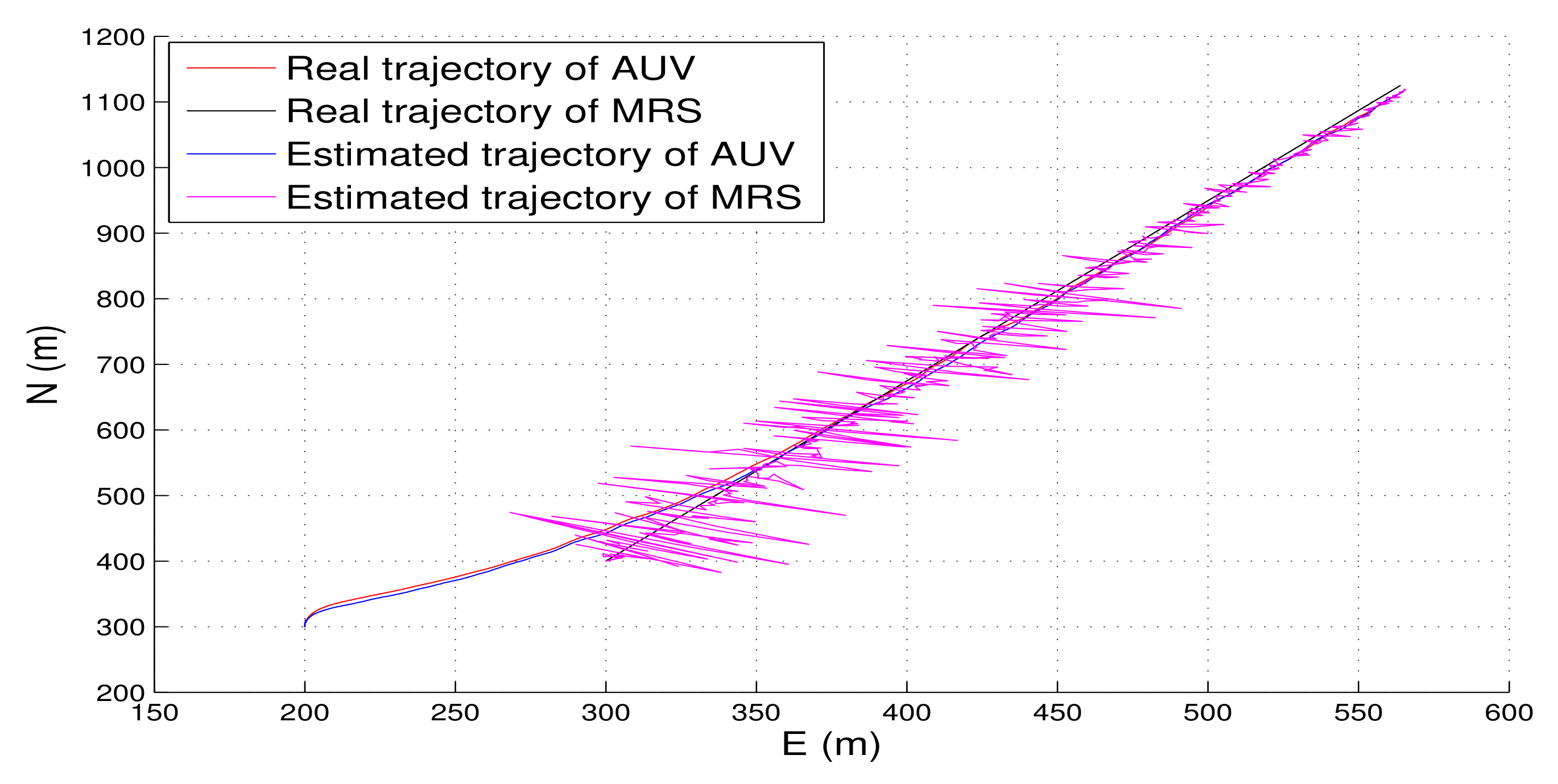
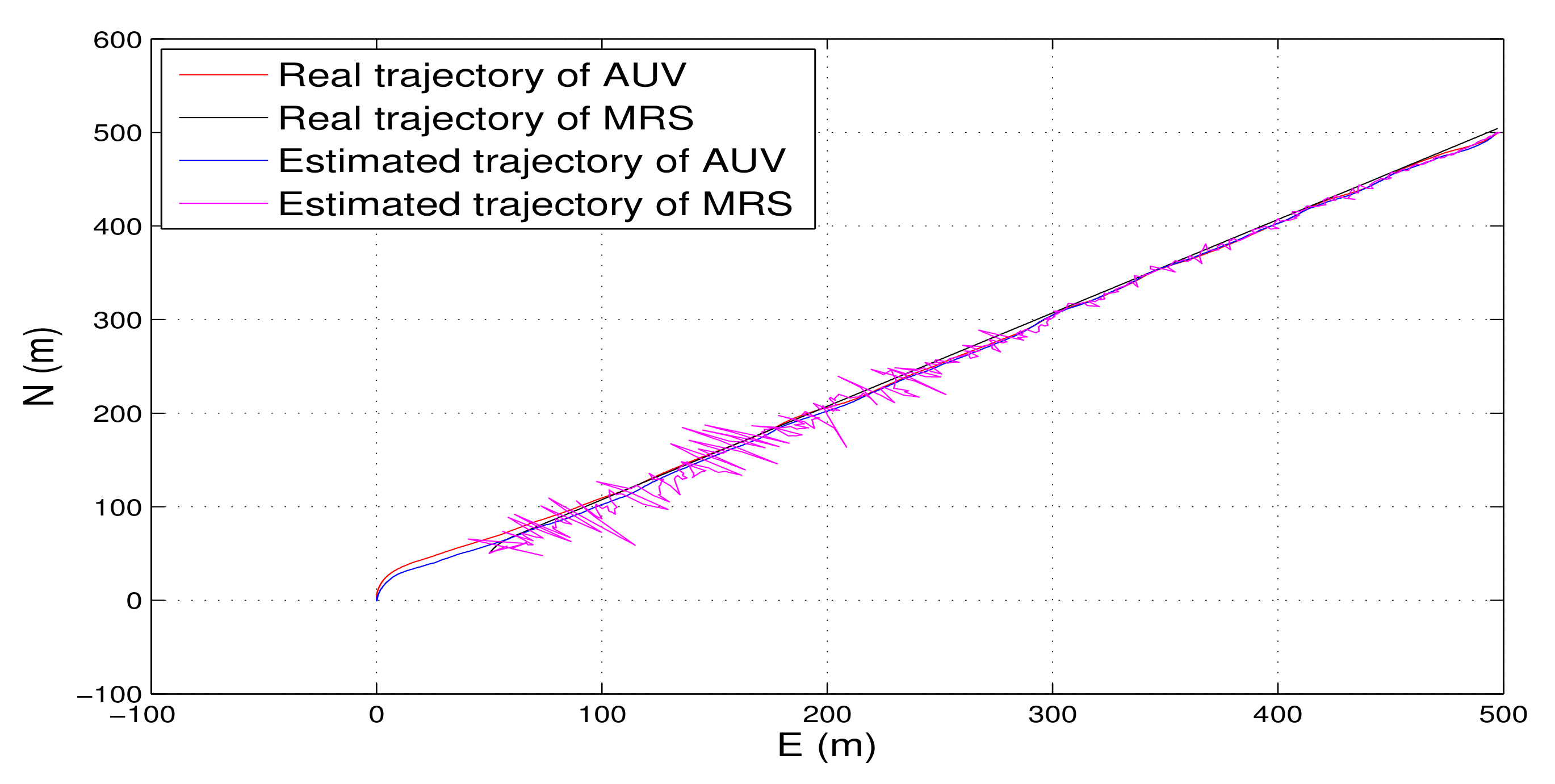
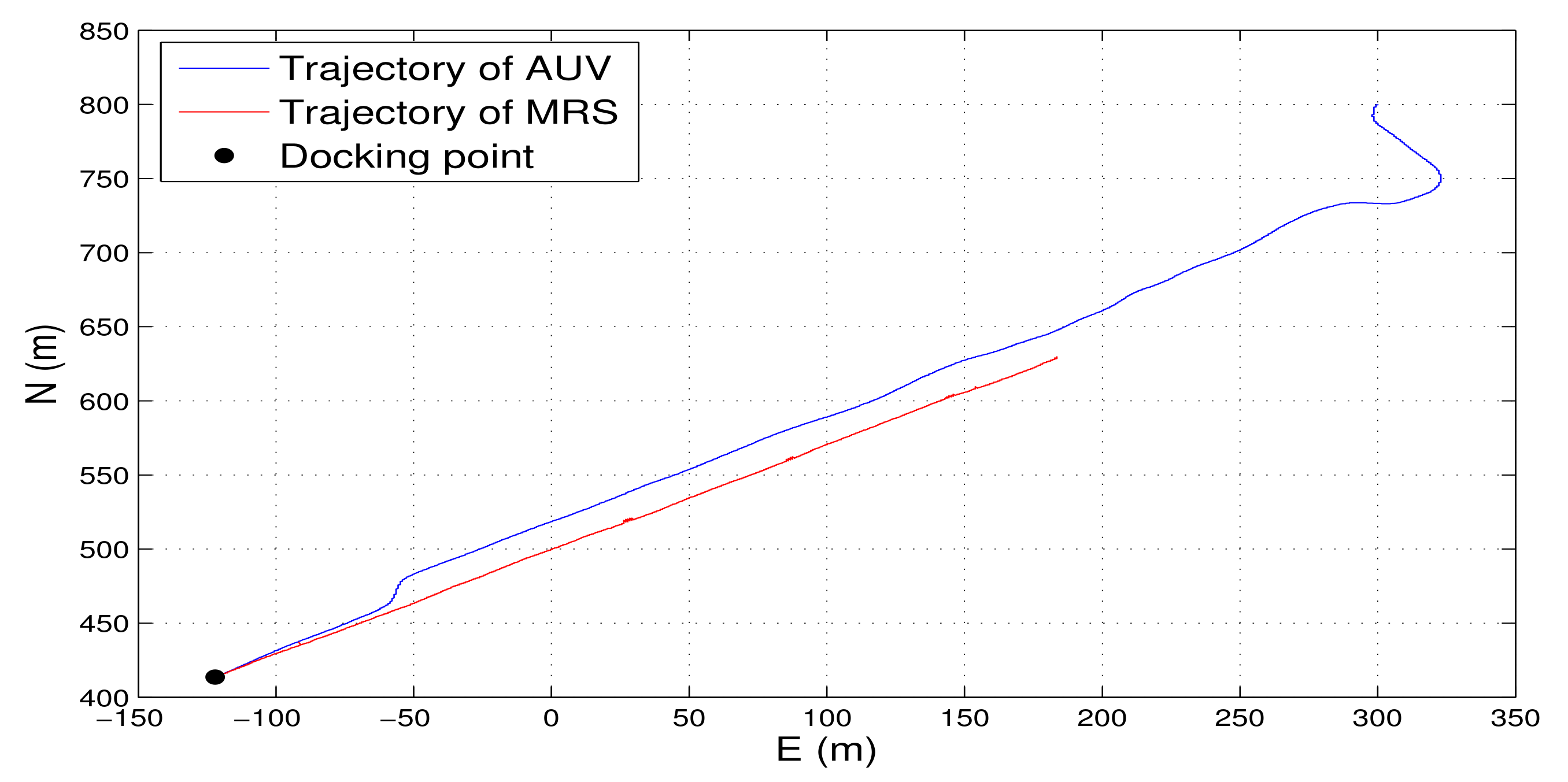
8.2. Experimental Data Analysis
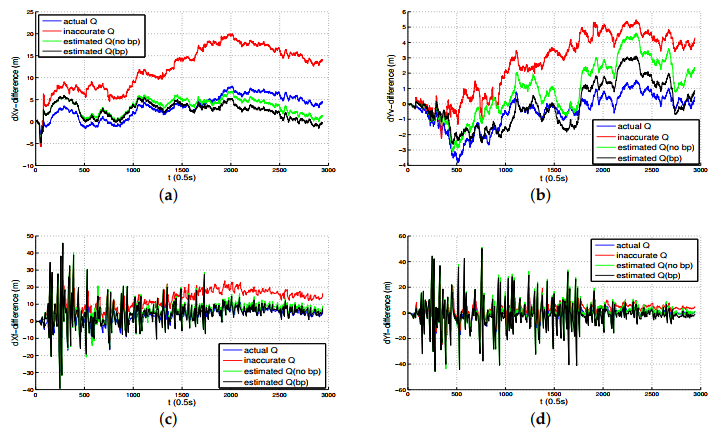
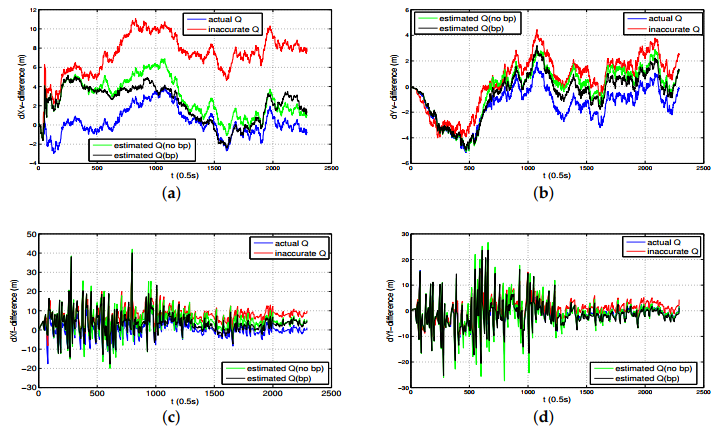
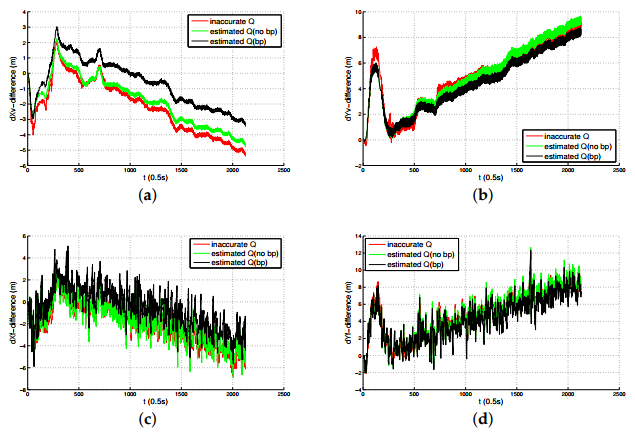
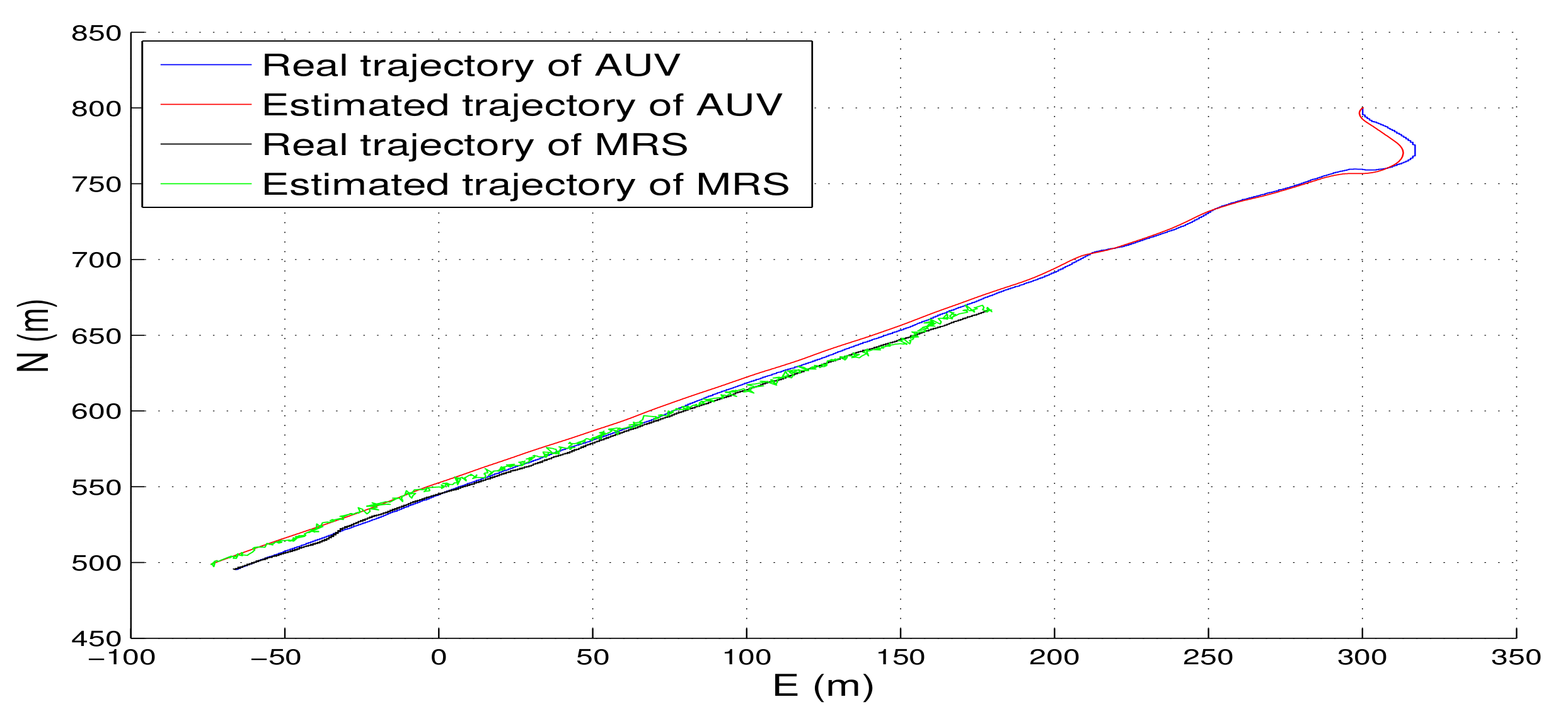
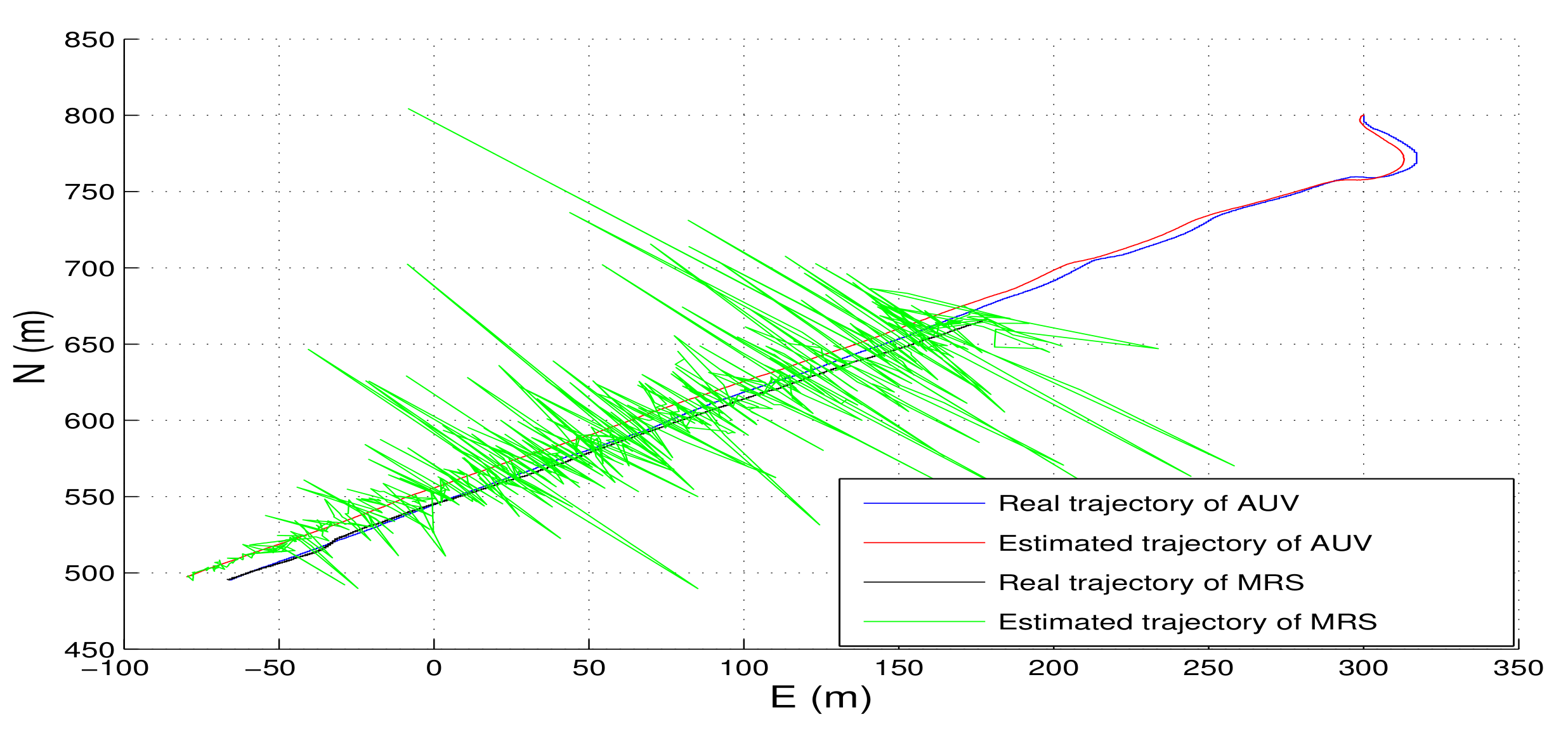
- As the PNCM is unknown, we assumed the PNCM is , which is inaccurate. The contrast between the red lines and the blue lines indicates that the inaccurate process noise statistics leads to the degradation of the state estimation performance of TT-EKF.
- The contrast between the red lines and the green lines indicates that the state estimation performance of TT-EKF has been improved with the PNCM is estimated by VB algorithm.
- The contrast between the green lines and the black lines indicates that the state estimation performance of TT-EKF has been further improved with the prediction error compensator based on neural network.
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Wang, Y.; Liu, K.; Feng, X. Optimal AUV trajectories for bearings-only tracking. Robot 2014, 36, 179–184. [Google Scholar] [CrossRef]
- Miller, A.B.; Miller, B. Underwater target tracking using bearing-only measurements. J. Commun. Technol. Electr. 2018, 63, 643–649. [Google Scholar] [CrossRef]
- Modalavalasa, N.; Rao, G.S.; Prasad, K.S.; Laveti, G.; Kumar, M.N.V.S.S. A new method of target tracking by EKF using bearing and elevation measurements for underwater environment. Robot. Auton. Syst. 2015, 74, 221–228. [Google Scholar] [CrossRef]
- Elhaki, O.; Shojaei, K. Neural network-based target tracking control of underactuated autonomous underwater vehicles with a prescribed performance. Ocean Eng. 2018, 167, 239–256. [Google Scholar] [CrossRef]
- Huang, Y.; Liang, W.; Yu, H.B.; Xiao, Y. Target tracking based on a distributed particle filter in underwater sensor networks. Wirel. Commun. Mob. Comput. 2008, 8, 1023–1033. [Google Scholar] [CrossRef]
- Ge, Q.; Shao, T.; Duan, Z.; Wen, C. Performance analysis of the kalman filter with mismatched noise covariance. IEEE Trans. Autom. Control 2016, 61, 4014–4019. [Google Scholar] [CrossRef]
- Durovic, Z.M.; Kovacevic, B.D. Robust estimation with unknown noise statistics. IEEE Trans. Autom. Control 1999, 44, 1292–1296. [Google Scholar] [CrossRef]
- Dong, Z.; You, Z. Finite-horizon robust kalman filtering for uncertain discrite time-varying systems with uncertain-covariance white noises. IEEE Signal Process. Lett. 2006, 13, 493–496. [Google Scholar] [CrossRef]
- Mohamed, A.H.; Schwarz, K.P. Adaptive kalman filtering for INS/GPS. J. Geol. 1999, 73, 193–203. [Google Scholar] [CrossRef]
- Odelson, B.J.; Rajamani, M.R.; Rawlings, J.B. A new autocovariance least-squares method for estimating noise covariance. Automatica 2006, 42, 303–308. [Google Scholar] [CrossRef]
- Mehra, R.K. On the identification of variances and adaptive kalman filtering. IEEE Trans. Autom. Control 1970, 15, 175–184. [Google Scholar] [CrossRef]
- Myers, K.A.; Tapley, B.D. Adaptive sequential estimation with unknown noise statistics. IEEE Trans. Autom. Control 1976, 21, 520–523. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Wu, Z.; Li, N.; Chambers, J. A novel adaptive kalman filter with inaccurate process and measurement noise covariance matrices. IEEE Trans. Autom. Control 2018, 63, 594–601. [Google Scholar] [CrossRef]
- Sarkka, S.; Nummenmaa, A. Recursive noise adaptive kalman filtering by variational Bayesian approximations. IEEE Trans. Autom. Control 2009, 54, 596–600. [Google Scholar] [CrossRef]
- Assa, A.; Plataniotions, K.N. Adaptive kalman filtering by covariance sampling. IEEE Signal Process. Lett. 2017, 24, 1288–1292. [Google Scholar] [CrossRef]
- Gao, X.; You, D.; Katayama, S. Seam tracking monitoring based on adaptive kalman filter embedded elman neural network during high-power filber laser welding. IEEE Trans. Ind. Electr. 2011, 59, 4315–4325. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Tzikas, D.G.; Likas, C.L.; Galatsanos, N.P. The variational approximation for bayesian inference. IEEE Signal Process. Mag. 2008, 25, 131–146. [Google Scholar] [CrossRef]
- Blei, D.M.; Kucukelbir, A.; Mcauliffe, J.D. Variational inference: a review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Agamennoni, G.; Nieto, J.I.; Nebot, E.M. Approximate inference in state-space models with heavy-tailed noise. IEEE Trans. Signal Process. 2012, 60, 5024–5037. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Shao, D.Z.X.; Chen, G. Kalman filtering through the feedback adaption of prior error covariance. Signal Process. 2018, 152, 47–53. [Google Scholar] [CrossRef]
- Wang, H.R.; Deng, Z.H.; Feng, B.; Ma, H.B.; Xia, Y.Q. An adaptive Kalman filter estimating process noise covariance. Neurocomputing 2017, 223, 12–17. [Google Scholar] [CrossRef]
- Hong, X.; Duan, K.Q.; Yuan, H.D.; Xie, W.C.; Wang, Y.L. Black box variational inference to adaptive kalman filter with unknown process noise covariance matrix. Signal Process. 2020, 169, 107413. [Google Scholar] [CrossRef]
- Zheng, R.; Lv, H.Q.; Yu, C.; Han, X.J.; Li, M.Z.; Wei, A.B. Technical Research, System Design and Implementation of Docking between AUV and Autonomous Mobile Dock Station. Robot 2019, 1–9. [Google Scholar] [CrossRef]
- Li, Q.L.; Song, Y.; Hou, Z.G. Neural network based FastSLAM for autonomous robots in unknown environments. Neurocomputing 2015, 165, 99–110. [Google Scholar] [CrossRef]
- Taghia, J.; Ma, Z.Y.; Leijon, A. Bayesian estimation of the von-Mises fisher mixture model with variational inference. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1701–1715. [Google Scholar] [CrossRef] [PubMed]




| Weight | Mean | Variance | |
|---|---|---|---|
| 1 | |||
| 2 |
| Actual Q | Inaccurate Q | Estimated Q (without bp) | Estimated Q (with bp) | |
|---|---|---|---|---|
| 5.6855 × 10 | 5.3567 × 10 | 5.7135 × 10 | 3.3989 × 10 | |
| 2.0301 × 10 | 7.2603 × 10 | 5.1868 × 10 | 4.8194 × 10 | |
| L | 2.5986 × 10 | 1.2617 × 10 | 5.7582 × 10 | 5.1593 × 10 |
| t | 100 s | 200 s | 300 s | 400 s |
|---|---|---|---|---|
| Actual position | (331.01,207.22) | (370.68,245.43) | (422.29,284.41) | (477.54,317.33) |
| actual Q | (329.11,207.87) | (369.25,246.80) | (423.31,285.92) | (479.70,317.90) |
| inaccurate Q | (323.96,207.45) | (363.40,245.09) | (414.81,283.07) | (473.37,315.39) |
| estimated Q(no bp) | (326.53,207.59) | (366.73,246.62) | (420.99,285.78) | (477.17,317.72) |
| estimated Q(bp) | (326.52,207.55) | (366.76,246.25) | (447.80,285.95) | (477.61,319.12) |
| t | 500 s | 600 s | 700 s | 800 s |
| Actual position | (535.55,344.73) | (594.86,369.41) | (654.22,393.33) | (713.85,415.49) |
| actual Q | (533.87,344.7846) | (592.64,368.40) | (651.53,393.00) | (712.38,416.18) |
| inaccurate Q | (526.65,342.11) | (584.92,365.57) | (642.26,389.63) | (700.71,412.20) |
| estimated Q(no bp) | (531.37,344.63) | (590.19,368.26) | (649.19,392.91) | (710.20,416.11) |
| estimated Q(bp) | (531.69,346.76) | (591.02,370.20) | (650.15,394.58) | (711.33,417.79) |
| t | 900 s | 1000 s | 1100 s | 1200 s |
| Actual position | (773.11,439.49) | (833.72,461.50) | (893.95,484.39) | (955.16,505.29) |
| actual Q | (771.08,437.31) | (829.35,458.91) | (890.63,480.38) | (953.20,502.14) |
| inaccurate Q | (757.83,432.76) | (817.41,454.64) | (879.46,476.35) | (942.66,498.38) |
| estimated Q(no bp) | (768.99,437.29) | (827.15,458.86) | (888.36,480.31) | (950.90,502.07) |
| estimated Q(bp) | (770.10,439.21) | (828.71,460.69) | (890.19,482.29) | (952.53,504.23) |
| t | 1300 s | 1400 s | 1470 s | |
| Actual position | (1015.0,527.84) | (1075.1,548.96) | (1116.2,564.99) | |
| actual Q | (1015.4,525.38) | (1075.8,547.80) | (1117.3,562.70) | |
| inaccurate Q | (1005.5,521.75) | (1066.0,544.10) | (1107.5,558.91) | |
| estimated Q(no bp) | (1013.0,525.27) | (1073.4,547.68) | (1114.9,562.59) | |
| estimated Q(bp) | (1014.7,527.47) | (1075.0,550.01) | (1116.6,564.98) |
| t | 100s | 200 s | 300 s | 400 s |
|---|---|---|---|---|
| Actual position | (425.62,309.33) | (468.55,324.95) | (518.72,343.21) | (569.95,361.86) |
| actual Q | (423.40,307.87) | (465.77,327.89) | (522.56,339.75) | (565.80,370.07) |
| inaccurate Q | (418.16,307.41) | (459.91,325.95) | (514.08,337.08) | (559.67,367.68) |
| estimated Q(no bp) | (420.67,307.57) | (465.98,324.37) | (519.27,342.07) | (564.27,369.43) |
| estimated Q(bp) | (420.66,307.53) | (466.01,324.01) | (519.80,342.23) | (564.70,370.83) |
| t | 500 s | 600 s | 700 s | 800 s |
| Actual position | (619.21,379.78) | (667.99,397.54) | (716.69,415.27) | (774.61,436.35) |
| actual Q | (617.92,379.42) | (664.96,395.76) | (712.44,416.51) | (772.05,436.80) |
| inaccurate Q | (611.10,376.80) | (657.22,392.95) | (702.91,413.09) | (760.39,432.78) |
| estimated Q(no bp) | (615.34,381.67) | (662.36,396.33) | (709.57,416.38) | (770.31,435.70) |
| estimated Q(bp) | (615.66,383.80) | (663.20,398.27) | (710.53,418.05) | (771.45,437.38) |
| t | 900 s | 1000 s | 1100 s | 1200 s |
| Actual position | (833.52,457.79) | (889.72,478.24) | (942.95,497.62) | (993.39,515.98) |
| actual Q | (829.13,457.78) | (880.61,481.03) | (936.05,494.27) | (986.33,516.49) |
| inaccurate Q | (815.99,453.40) | (868.64,476.87) | (924.83,490.16) | (975.98,512.76) |
| estimated Q(no bp) | (827.45,458.12) | (877.66,483.40) | (934.00,492.94) | (984.60,516.06) |
| estimated Q(bp) | (828.57,460.04) | (879.21,485.23) | (935.84,494.92) | (986.23,518.22) |
| t | 1300 s | 1400 s | 1470 s | |
| Actual position | (1042.4,533.81) | (1091.1,551.54) | (1125.2,563.94) | |
| actual Q | (1037.5,533.98) | (1087.7,552.10) | (1118.7,562.71) | |
| inaccurate Q | (1027.3,530.24) | (1077.9,548.28) | (1108.8,558.88) | |
| estimated Q(no bp) | (1034.5,533.93) | (1085.3,551.78) | (1116.0,562.42) | |
| estimated Q(bp) | (1036.1,536.12) | (1086.8,554.10) | (1117.7,564.81) |
| Weight | Mean | Variance | |
|---|---|---|---|
| 1 | |||
| 2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, L.; Xu, H.; Feng, X.; Han, X.; Yu, C. An Adaptive Target Tracking Algorithm Based on EKF for AUV with Unknown Non-Gaussian Process Noise. Appl. Sci. 2020, 10, 3413. https://doi.org/10.3390/app10103413
Dong L, Xu H, Feng X, Han X, Yu C. An Adaptive Target Tracking Algorithm Based on EKF for AUV with Unknown Non-Gaussian Process Noise. Applied Sciences. 2020; 10(10):3413. https://doi.org/10.3390/app10103413
Chicago/Turabian StyleDong, Lingyan, Hongli Xu, Xisheng Feng, Xiaojun Han, and Chuang Yu. 2020. "An Adaptive Target Tracking Algorithm Based on EKF for AUV with Unknown Non-Gaussian Process Noise" Applied Sciences 10, no. 10: 3413. https://doi.org/10.3390/app10103413
APA StyleDong, L., Xu, H., Feng, X., Han, X., & Yu, C. (2020). An Adaptive Target Tracking Algorithm Based on EKF for AUV with Unknown Non-Gaussian Process Noise. Applied Sciences, 10(10), 3413. https://doi.org/10.3390/app10103413





