Author Contributions
Investigation, J.S.; Methodology, N.J., J.S., B.K., H.S., D.P., S.J., C.S. and G.P.J.; Project administration, B.K., H.S., D.P., S.J., C.S. and G.P.J.; Resources, B.K., H.S., D.P., C.S. and G.P.J.; Software, N.J.; Validation, B.K., H.S., S.J., C.S. and G.P.J.; Visualization, N.J.; Writing—original draft, H.S., D.P., S.J., C.S. and G.P.J.; Writing—review and editing, B.K., H.S., D.P., S.J., C.S. and G.P.J. All authors have read and agreed to the published version of the manuscript.
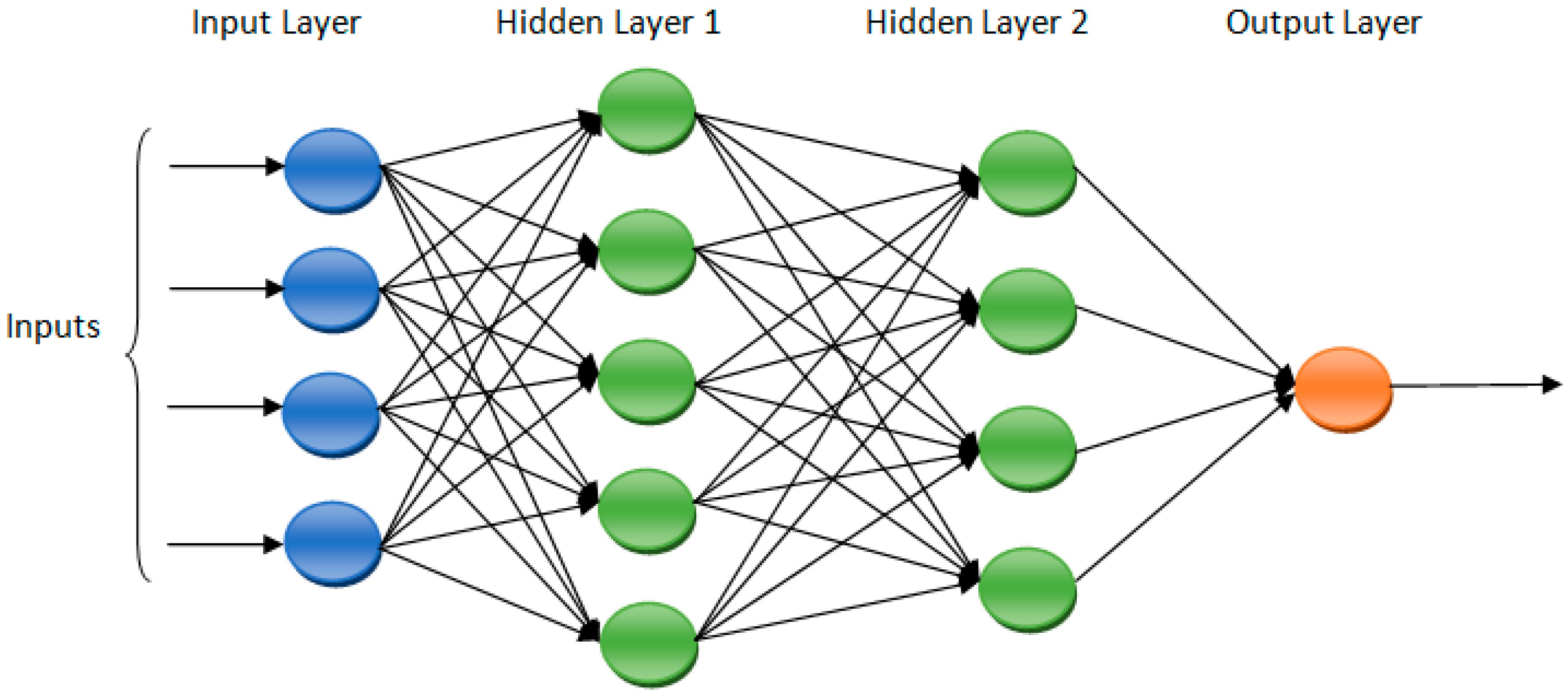
Figure 1.
Artificial neural network.
Figure 1.
Artificial neural network.
Figure 2.
Architecture of the Fuzzy inference system.
Figure 2.
Architecture of the Fuzzy inference system.
Figure 3.
Structure of five-layer ANFIS.
Figure 3.
Structure of five-layer ANFIS.
Figure 4.
Methodology of the proposed multi-layered inference system.
Figure 4.
Methodology of the proposed multi-layered inference system.
Figure 5.
Membership Functions of input variable “Smoking”.
Figure 5.
Membership Functions of input variable “Smoking”.
Figure 6.
Membership Functions of input variable “Haematuria”.
Figure 6.
Membership Functions of input variable “Haematuria”.
Figure 7.
Membership function of output variable “Layer 2”.
Figure 7.
Membership function of output variable “Layer 2”.
Figure 8.
Rules used at layer 2 of proposed systems.
Figure 8.
Rules used at layer 2 of proposed systems.
Figure 9.
Flow diagram of developed intelligent system.
Figure 9.
Flow diagram of developed intelligent system.
Figure 10.
Membership function for input variable 1 i.e., Haematuria.
Figure 10.
Membership function for input variable 1 i.e., Haematuria.
Figure 11.
Membership function for input variable 2 i.e., RBCC.
Figure 11.
Membership function for input variable 2 i.e., RBCC.
Figure 12.
Membership function for input variable 3 i.e., Flank Pain.
Figure 12.
Membership function for input variable 3 i.e., Flank Pain.
Figure 13.
Rules in ANFIS for renal cancer.
Figure 13.
Rules in ANFIS for renal cancer.
Figure 14.
Training error at 4 epochs.
Figure 14.
Training error at 4 epochs.
Figure 15.
Bar chart for comparison of FIS and ANFIS.
Figure 15.
Bar chart for comparison of FIS and ANFIS.
Table 1.
Input variables used in layer 1 of the proposed system.
Table 1.
Input variables used in layer 1 of the proposed system.
| SNo | Input Parameters | Ranges | Semantic Sign |
|---|
| 1 | Smoking | <4.3 | Acute |
| [0.2, 9] | Moderate |
| >5.8 | Chronic |
| 2 | Dialysis | <4.5 | No |
| >1.9 | Yes |
| 3 | OE | <4.5 | Little Bit |
| >1.9 | Excessive |
| 4 | GOH | <4.4 | Low |
| [0.5, 9.2] | Moderate |
| >5.8 | High |
Table 2.
Input variables used in layer 2 of the proposed system.
Table 2.
Input variables used in layer 2 of the proposed system.
| SNo | Input Parameters | Ranges | Semantic Sign |
|---|
| 1. | | <27 | 1+ |
| | | [10, 50] | 2+ |
| | | [15, 85] | 3+ |
| | | >55 | 4+ |
| 2. | RBCC | <0.45 | Low |
| | | [0.05, 0.95] | Normal |
| | | >0.58 | High |
| 3. | FP | <0.48 | Low |
| | | [0.05, 0.95] | Medium |
| | | >0.52 | High |
| 4. | TS | <7.2 | Smaller |
| | | >4.5 | Larger |
| 5. | VHLG | <0.51 | No |
| | | >0.17 | Yes |
| 6. | HBP | <96 | Normal |
| | | >76 | High |
| 7. | TCEE | <5.5 | Low |
| | | [1.6, 9.3] | Moderate |
| | | >6.2 | High |
Table 3.
Output variables.
Table 3.
Output variables.
| SNo | | Output Variables | Semantic Sign |
|---|
| 1. | Layer 1 | Renal Cancer | Cancer Present |
| | | | No Cancer |
| 2. | Layer 2 | Cancer Stage | Minor |
| | | | Moderate |
| | | | Serious |
| | | | Critical |
Table 4.
Parameter of layer 1.
Table 4.
Parameter of layer 1.
| SNo | Input Variables | Linguistic Variables | Mean | Standard Deviation (σ) | Frequency (f) |
|---|
| 1. | Smoking | Acute | 2.43 | 1.07 | 115 |
| | | Moderate | 4.88 | 0.60 | 67 |
| | | Chronic | 7.44 | 1.28 | 18 |
| 2. | Dialysis | No | 2.17 | 1.02 | 144 |
| | | Yes | 7.40 | 1.41 | 56 |
| 3. | Occupational Exposure | Little Bit | 2.58 | 1.22 | 147 |
| | | Excessive | 7.56 | 1.50 | 53 |
| 4. | Genetic or hereditary | Low | 2.45 | 1.36 | 102 |
| | | Moderate | 5.19 | 0.50 | 44 |
| | | High | 8.33 | 0.78 | 54 |
Table 5.
Parameters of Layer 2.
Table 5.
Parameters of Layer 2.
| SNo | Input Variables | Linguistic Variables | Mean | Standard Deviation (σ) | Frequency (f) |
|---|
| 1. | Haematuria | 1+ | 12 | 6.81 | 65 |
| | | 2+ | 41.70 | 6.15 | 72 |
| | | 3+ | 64.17 | 10.26 | 38 |
| | | 4+ | 137.53 | 59.17 | 25 |
| 2. | Red blood cell count | Low | 0.25 | 0.07 | 81 |
| | | Normal | 0.45 | 0.07 | 64 |
| | | High | 0.65 | 0.13 | 55 |
| 3. | Flank Pain | Low | 0.22 | 0.07 | 96 |
| | | Medium | 0.40 | 0.09 | 89 |
| | | High | 0.76 | 0.08 | 15 |
| 4. | Tumor Size | Smaller | 5.50 | 1.57 | 162 |
| | | Larger | 8.24 | 0.71 | 38 |
| 5. | Von Hippel-Lindau syndrome | No | 0.30 | 0.05 | 147 |
| | | Yes | 0.60 | 0.12 | 53 |
| 6. | High Blood Pressure | Normal | 73.34 | 4.78 | 75 |
| | | High | 92.88 | 15.09 | 125 |
| 7. | Trichloroethylene Exposure | Low | 2.554 | 0.39 | 10 |
| | | Moderate | 4.01 | 0.82 | 97 |
| | | High | 7.71 | 1.07 | 93 |
Table 6.
Parameters of outputs.
Table 6.
Parameters of outputs.
| SNo | Layer | Output Variables | Linguistic Variables | Mean | Standard Deviation (σ) | Frequency (f) |
|---|
| 1. | Layer 1 | Renal Cancer | Cancer Present | 5.86 | 0.32 | 74 |
| | | | No Cancer | 2.12 | 1.52 | 126 |
| 2. | Layer 2 | Cancer Stage | Minor | 2.07 | 0.21 | 68 |
| | | | Moderate | 5.10 | 0.79 | 85 |
| | | | Serious | 8.04 | 0.73 | 22 |
| | | | Critical | 8.67 | 0.11 | 25 |
Table 7.
Structure of ANFIS for renal cancer.
Table 7.
Structure of ANFIS for renal cancer.
| Structure | |
|---|
| The number of Layers of ANFIS | 5 |
| Inputs | 7 |
| Number of Rules | 864 |
| Output | 1 |
| Type of membership functions for input variables | Gaussian |
Table 8.
Confusion Matrix for fold 1.
Table 8.
Confusion Matrix for fold 1.
| Minor | Moderate | Serious | Critical | Class Name |
|---|
| 15 | 00 | 00 | 00 | Minor |
| 00 | 12 | 01 | 00 | Moderate |
| 00 | 00 | 10 | 00 | Serious |
| 01 | 00 | 00 | 11 | Critical |
Table 9.
Confusion Matrix for fold 2.
Table 9.
Confusion Matrix for fold 2.
| Minor | Moderate | Serious | Critical | Class Name |
|---|
| 15 | 00 | 00 | 00 | Minor |
| 01 | 12 | 00 | 00 | Moderate |
| 00 | 00 | 09 | 01 | Serious |
| 01 | 00 | 00 | 11 | Critical |
Table 10.
Confusion Matrix for fold 3.
Table 10.
Confusion Matrix for fold 3.
| Minor | Moderate | Serious | Critical | Class Name |
|---|
| 14 | 01 | 00 | 00 | Minor |
| 00 | 12 | 01 | 00 | Moderate |
| 00 | 00 | 10 | 00 | Serious |
| 00 | 00 | 00 | 12 | Critical |
Table 11.
Confusion Matrix for fold 4.
Table 11.
Confusion Matrix for fold 4.
| Minor | Moderate | Serious | Critical | Class Name |
|---|
| 15 | 00 | 00 | 00 | Minor |
| 00 | 12 | 01 | 00 | Moderate |
| 00 | 01 | 09 | 00 | Serious |
| 00 | 00 | 00 | 12 | Critical |
Table 12.
Matrix with reduced dimensions for fold 1.
Table 12.
Matrix with reduced dimensions for fold 1.
| No | Yes | Class Name |
|---|
| 27 | 01 | No |
| 01 | 21 | Yes |
Table 13.
Matrix with reduced dimensions for fold 2.
Table 13.
Matrix with reduced dimensions for fold 2.
| No | Yes | Class Name |
|---|
| 27 | 02 | No |
| 01 | 20 | Yes |
Table 14.
Matrix with reduced dimensions for fold 3.
Table 14.
Matrix with reduced dimensions for fold 3.
| No | Yes | Class Name |
|---|
| 26 | 00 | No |
| 01 | 22 | Yes |
Table 15.
Matrix with reduced dimensions for fold 4.
Table 15.
Matrix with reduced dimensions for fold 4.
| No | Yes | Class Name |
|---|
| 27 | 01 | No |
| 01 | 21 | Yes |
Table 16.
Calculated performance parameters for fuzzy inference system.
Table 16.
Calculated performance parameters for fuzzy inference system.
| Parameters | Fold 1 | Fold 2 | Fold 3 | Fold 4 | Overall |
|---|
| 95.45% | 95.23% | 95.65% | 95.45% | 95.44% |
| 96.42% | 93.10% | 100% | 96.42% | 96.48% |
| 95.45% | 90.90% | 100% | 95.45% | 95.45% |
| 96% | 94% | 98% | 96% | 96% |
Table 17.
Confusion Matrix for fold 1.
Table 17.
Confusion Matrix for fold 1.
| Minor | Moderate | Serious | Critical | Class Name |
|---|
| 15 | 00 | 00 | 00 | Minor |
| 00 | 13 | 01 | 00 | Moderate |
| 00 | 00 | 10 | 00 | Serious |
| 00 | 00 | 00 | 11 | Critical |
Table 18.
Confusion Matrix for fold 2.
Table 18.
Confusion Matrix for fold 2.
| Minor | Moderate | Serious | Critical | Class Name |
|---|
| 15 | 00 | 00 | 00 | Minor |
| 00 | 13 | 01 | 00 | Moderate |
| 00 | 00 | 10 | 00 | Serious |
| 01 | 00 | 00 | 10 | Critical |
Table 19.
Confusion Matrix for fold 3.
Table 19.
Confusion Matrix for fold 3.
| Minor | Moderate | Serious | Critical | Class Name |
|---|
| 15 | 00 | 00 | 00 | Minor |
| 00 | 14 | 00 | 00 | Moderate |
| 00 | 00 | 10 | 00 | Serious |
| 00 | 00 | 00 | 11 | Critical |
Table 20.
Confusion Matrix for fold 4.
Table 20.
Confusion Matrix for fold 4.
| Minor | Moderate | Serious | Critical | Class Name |
|---|
| 15 | 00 | 00 | 00 | Minor |
| 00 | 13 | 01 | 00 | Moderate |
| 00 | 01 | 09 | 00 | Serious |
| 00 | 00 | 00 | 11 | Critical |
Table 21.
Matrix with reduced dimensions for fold 1.
Table 21.
Matrix with reduced dimensions for fold 1.
| No | Yes | Class Name |
|---|
| 28 | 01 | No |
| 00 | 21 | Yes |
Table 22.
Matrix with reduced dimensions for fold 2.
Table 22.
Matrix with reduced dimensions for fold 2.
| No | Yes | Class Name |
|---|
| 28 | 01 | No |
| 01 | 20 | Yes |
Table 23.
Matrix with reduced dimensions for fold 3.
Table 23.
Matrix with reduced dimensions for fold 3.
| No | Yes | Class Name |
|---|
| 29 | 00 | No |
| 00 | 21 | Yes |
Table 24.
Matrix with reduced dimensions for fold 4.
Table 24.
Matrix with reduced dimensions for fold 4.
| No | Yes | Class Name |
|---|
| 29 | 00 | No |
| 01 | 20 | Yes |
Table 25.
Calculated performance parameters for ANFIS.
Table 25.
Calculated performance parameters for ANFIS.
| Parameters | Fold 1 | Fold 2 | Fold 3 | Fold 4 | Overall |
|---|
| 100% | 95.23% | 100% | 95.23% | 97.61% |
| 96.55% | 96.55% | 100% | 100% | 98.27% |
| 95.45% | 95.23% | 100% | 100% | 97.67% |
| 98% | 96% | 100% | 98% | 98% |
Table 26.
Calculated parameters from the developed systems.
Table 26.
Calculated parameters from the developed systems.
| Models/Parameters | Classification Accuracy | Sensitivity | Specificity | Precision |
|---|
| Fuzzy | 96% | 95.44% | 96.48% | 95.45% |
| ANFIS | 98% | 97.61% | 98.27% | 97.67% |