Analysis of Distributed Measurement Method for Array Antenna Position
Abstract
:1. Introduction
2. Scheme and Principle
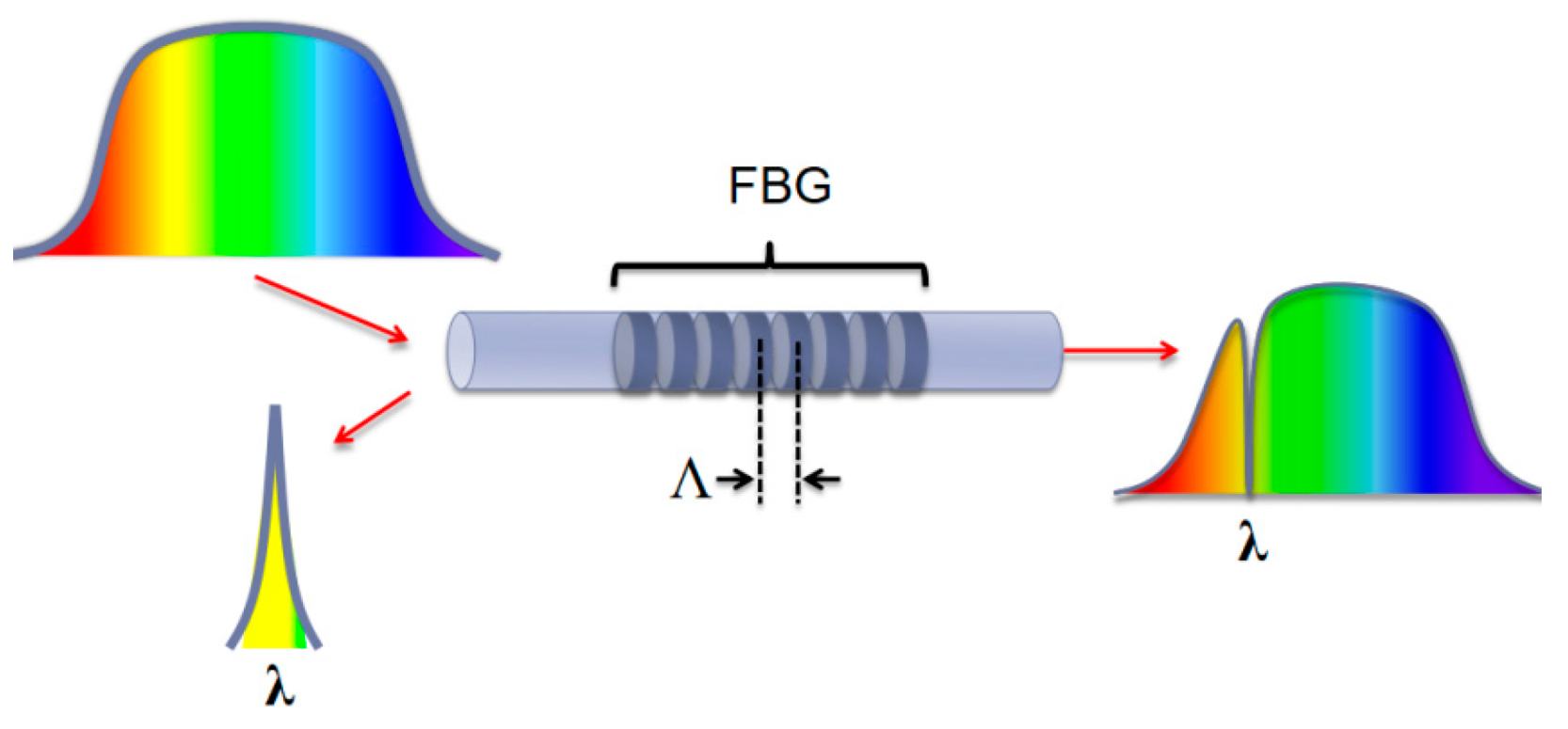
2.1. Fiber Bragg Grating (FBG) Sensing Technology
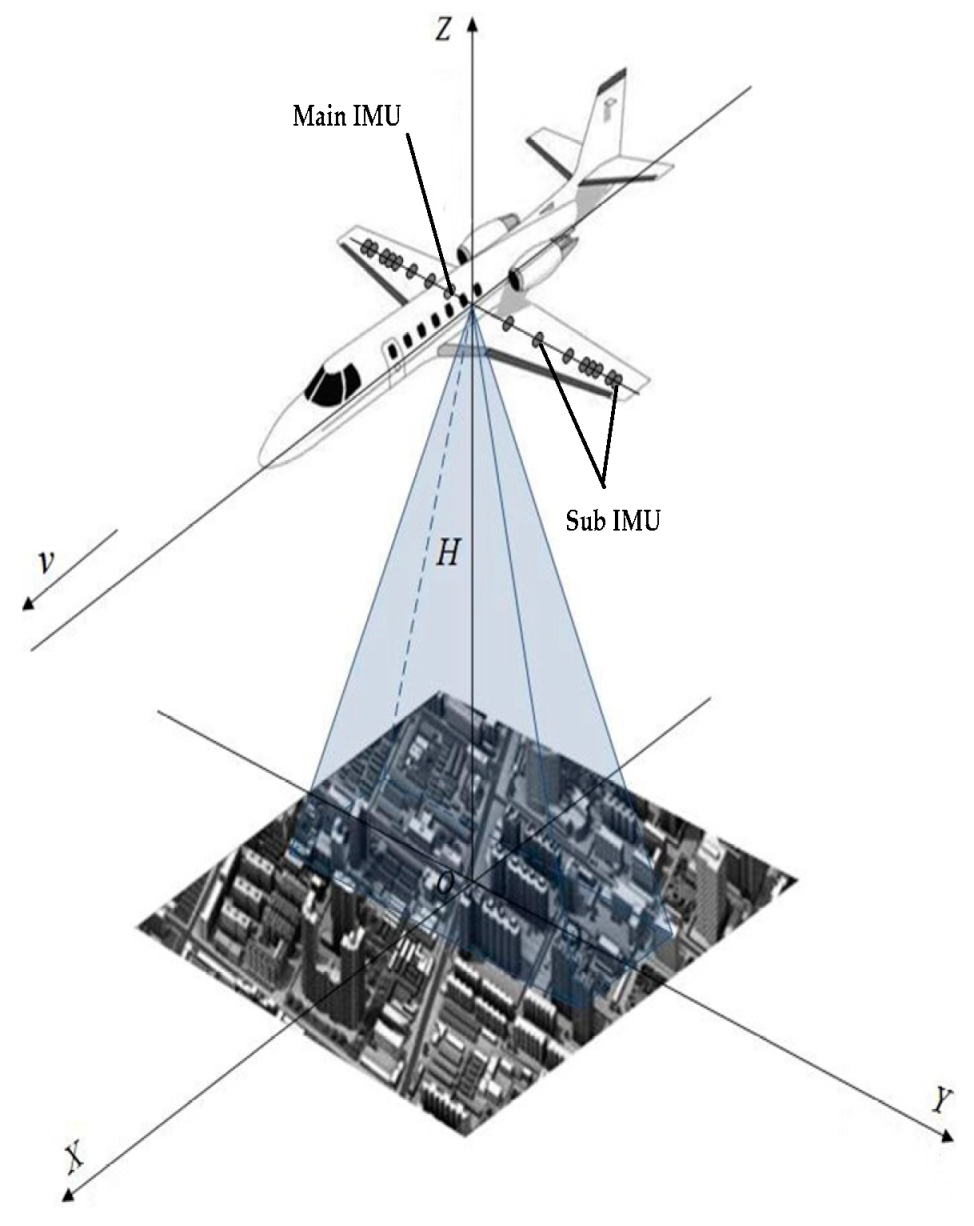
2.2. Distributed Position and Orientation System (POS) Technology
2.3. Error Analysis of Distributed POS Technology
2.3.1. Lever Arm Effect Error
2.3.2. Navigation Equation of Strapdown Inertial Navigation System
2.3.3. Attitude Error Equation
2.3.4. Error Model of Inertial Device
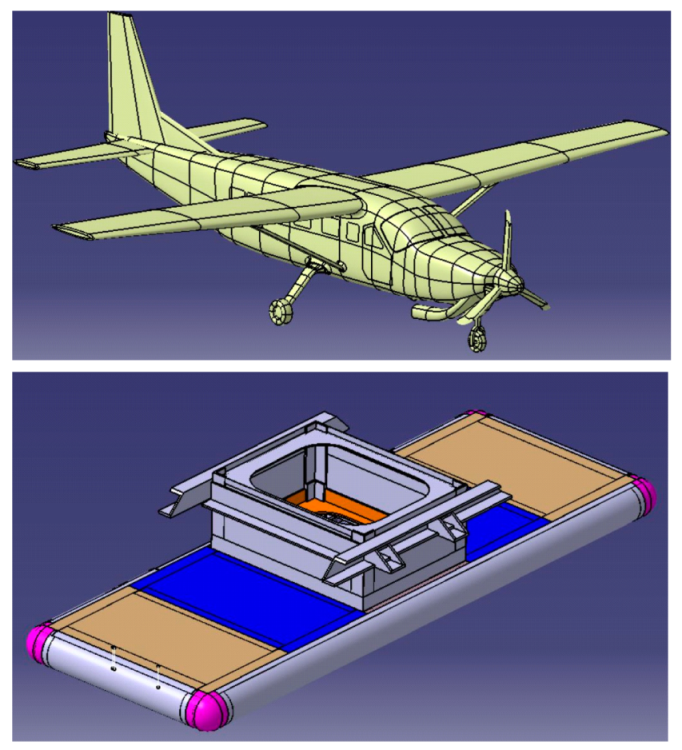
3. Structural Design and Method
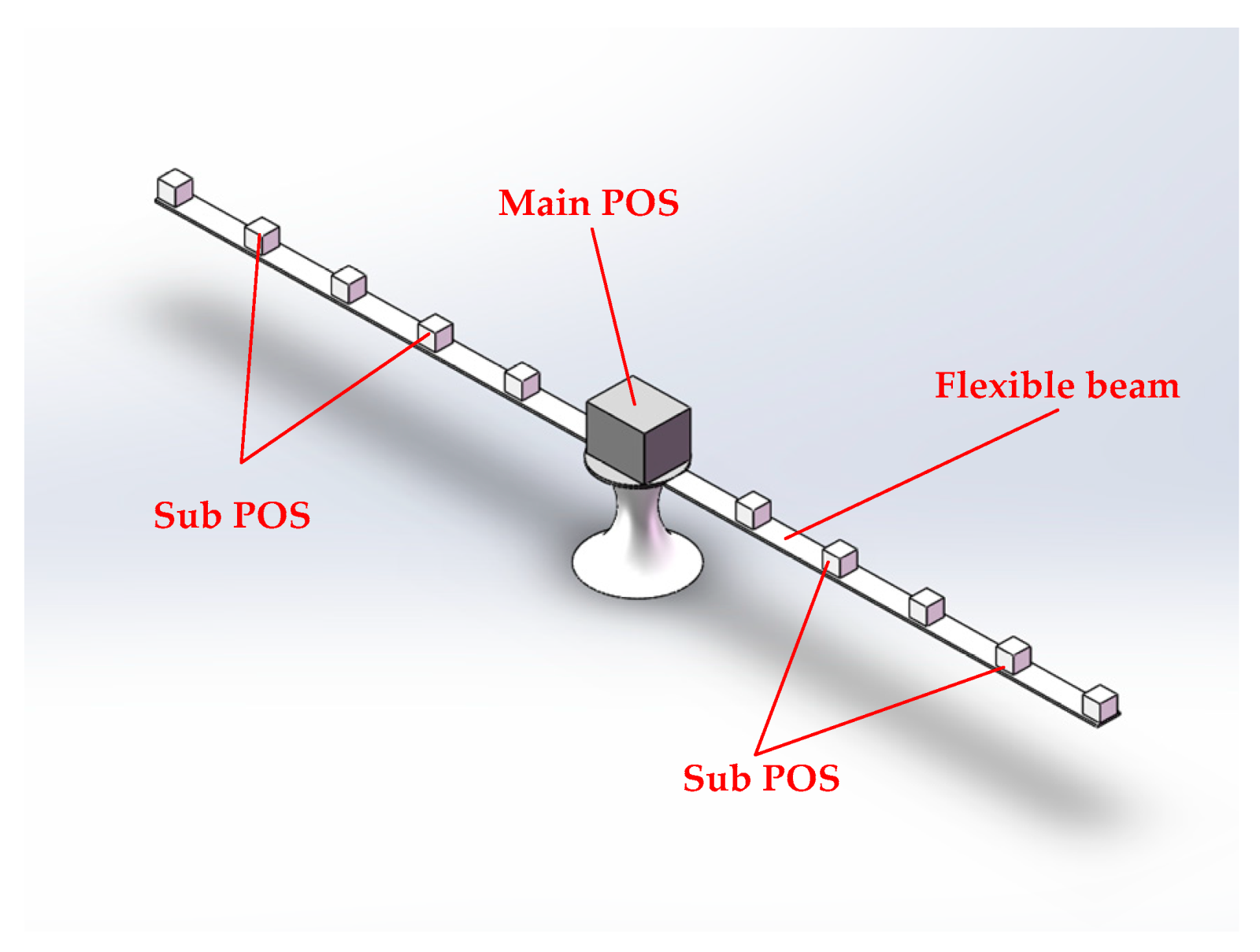
3.1. Structural Design
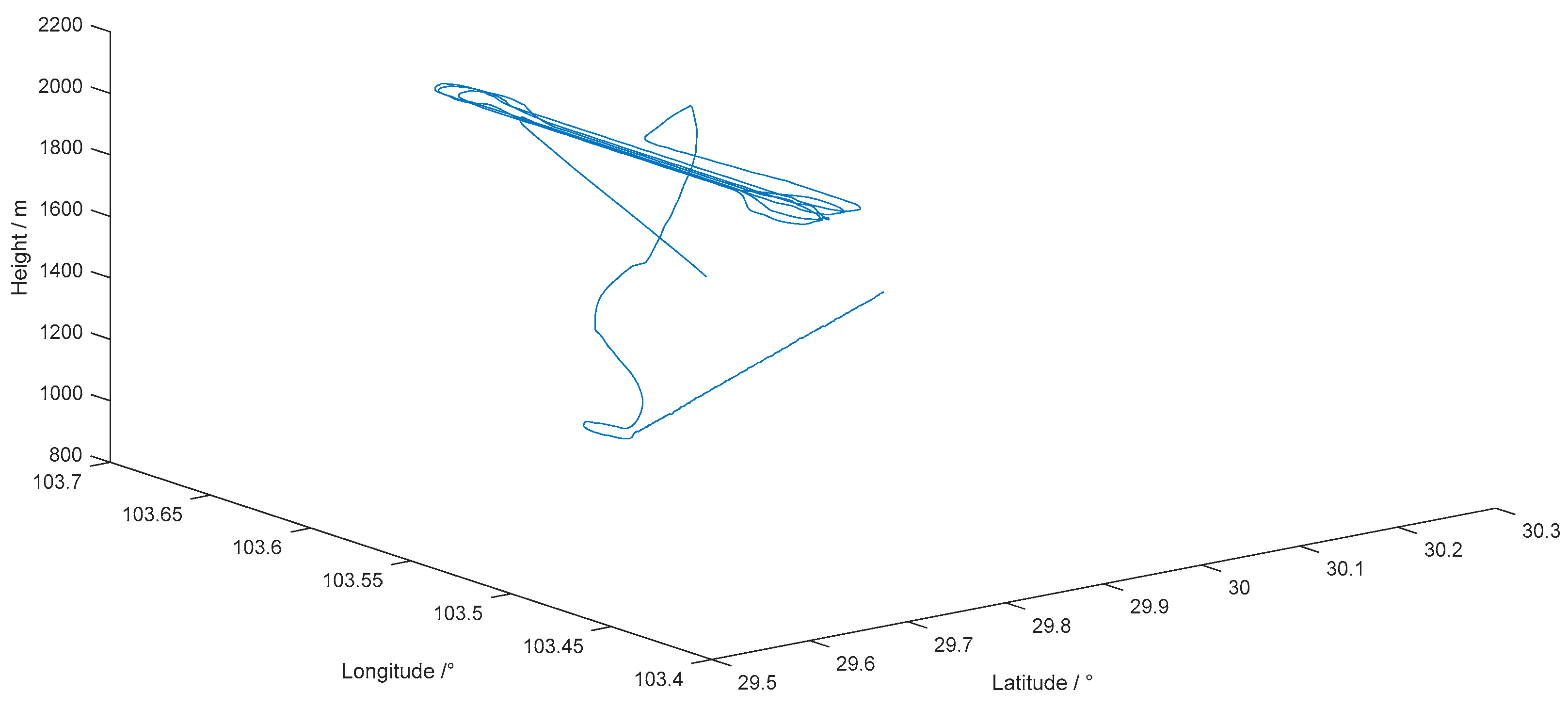
3.2. Measuring Method
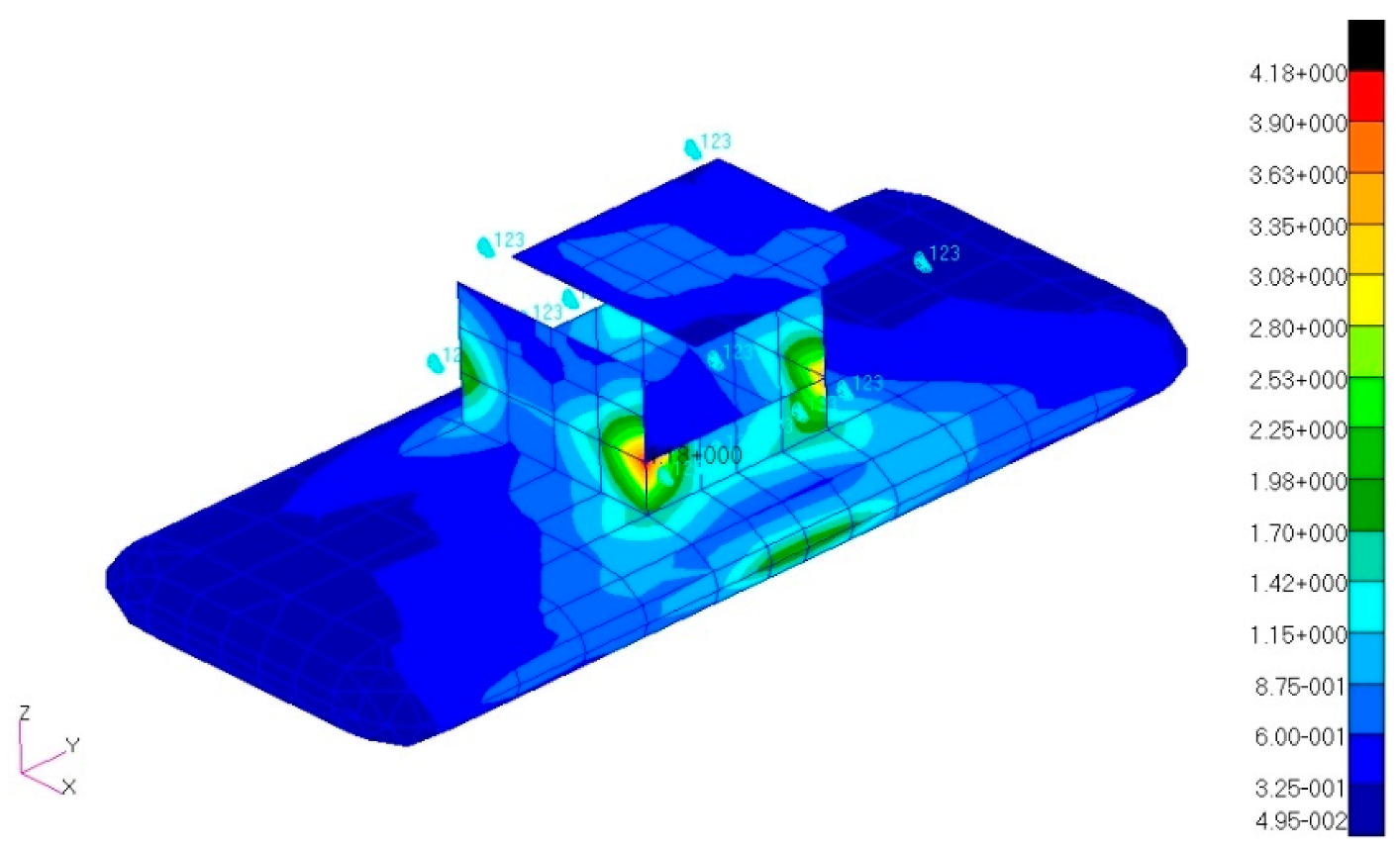
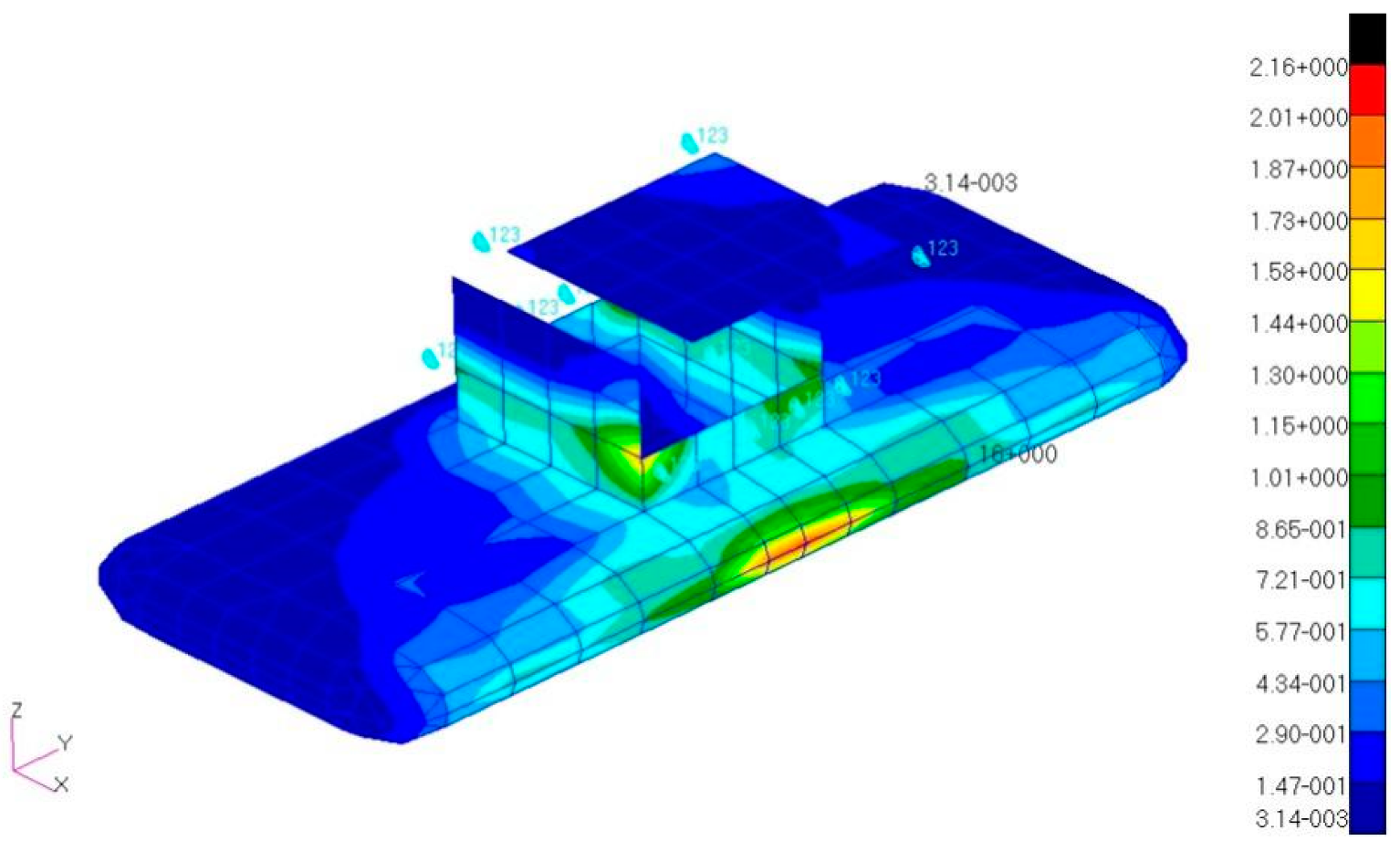
3.3. Strength Check
3.3.1. Overload Increment in Case of Vertical Gust
3.3.2. Overload Increment of Lateral Gust
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wiley, C.A. Pulsed Doppler Radar Methods and Apparatus. U.S. Patent No. 3,196,436, 20 July 1965. [Google Scholar]
- Tong, X.; Zhao, W.; Xing, J. Status and development of china high-resolution earth observation system and application. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3738–3741. [Google Scholar]
- Pedlar, D.N.; Coe, D.J. Target Geolocation Using SAR. IEEE Radar Sonar Navig. 2015, 152, 35–42. [Google Scholar] [CrossRef]
- Jiang, L.M.; Lin, H. Integrated analysis of SAR interferometric and geological data for investigating long-term reclamation settlement of ChekLapKokAirport, Hong Kong. Eng. Geol. 2010, V110, 77–92. [Google Scholar] [CrossRef]
- Arnold, E.J.; Yan, J.B.; Hale, R.D. Identifying and compensating for phase center errors in wing-mounted phased arrays for ice sheet sounding. IEEE Trans. Antennas Propag. 2014, 62, 3416–3421. [Google Scholar] [CrossRef]
- Fang, J.C.; Liu, Z.C. In-flight alignment of POS based on state-transition matrix. IEEE Sens. J. 2015, V15, 3258–3264. [Google Scholar] [CrossRef]
- Bakunowicz, J.; Meyer, R. In-flight wing deformation measurements on a glider. Aeronaut. J. 2014, 120, 1917–1931. [Google Scholar] [CrossRef] [Green Version]
- Pallek, D.; Butefisch, K.A.; Quest, J.; Strudthoff, W. Model deformation measurement in ETW using the Moire technique. In Proceedings of the International Congress on Instrumentation in Aerospace Simulation Facilities, Gottingen, Germany, 25–29 August 2003; pp. 110–114. [Google Scholar]
- Boden, F.; Jentink, H.; Petit, C. IPCT Wing Deformation Measurements on a Large Transport Aircraft. In Advanced In-Flight Measurement Techniques; Springer: Berlin/Heidelberg, Germany, 2013; pp. 93–115. [Google Scholar]
- Klinge, F. Cross correlation based optical measurement techniques for fluid dynamics and structure analysis BOS, IPCT. In Proceedings of the Lecture in Tampere University of Technology, Tampere, Finland, 11 October 2004. [Google Scholar]
- Kompenhans, J.; Schroder, A.; Engler, R.; Klinge, F.; Stasicki, B. Development and application of image based measurements techniques for aerodynamic investigation in wind tunnels. In Proceedings of the International Conference High Speed Flow: Fundamental Problems, Zhukovsky, Russia, 2–24 September 2004. [Google Scholar]
- AIM² Newsletter No. 3 Available NOW. Available online: http://aim2.dlr.de/project/index.html (accessed on 28 January 2020).
- Fang, J.C.; Zhang, Z.; Gong, X. Modeling and simulation of transfer alignment for distributed POS. J. Chin. Inert. Technol. 2012, 20, 379–385. [Google Scholar]
- Zhu, Z.; Guo, T. Effect of distributed POS transfer alignment on InSAR interferometic measurement. J. Chin. Inert. Technol. 2014, 22, 432–438. [Google Scholar]
- Amanzadeh, M.; Aminossadati, S.M.; Kizil, M. Recent developments in fibre optic shape sensing. Measurement 2018, 128, 119–137. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Chen, X.Y. Fiber Bragg gratings sensors for aircraft wing shape measurement: Recent applications and technical analysis. Sensors 2019, 19, 55. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Di, S.R. Fiber optic sensors for structural health monitoring of aircraft composite structures: Recent advances and applications. Sensors 2015, 15, 18666–18713. [Google Scholar]
- Vorathin, E.; Hafizi, Z.M.; Ghani, S.C.; Lim, K.S. Real-time monitoring system of composite aircraft wings utilizing Fibre Bragg Grating Sensor. Innov. Aerosp. Eng. Technol. 2016, 152, 12024. [Google Scholar] [CrossRef]
- Ma, Z.; Chen, X.Y. Strain Transfer Characteristics of Surface-attached FBGs in Aircraft Wing Distributed Deformation Measurement. Optik 2020, 207, 164468. [Google Scholar] [CrossRef]
- Alvarez, M.J.; Carvajal, C.A.; Sierra, P.J. In-flight and wireless damage detection in a UAV composite wing using fiber optic sensors and strain field pattern recognition. Mech. Syst. Signal Process. 2020, 136, 106526. [Google Scholar] [CrossRef]
- Chan, P.H.M. Fiber Optics Sensing System (FOSS) at NASA Armstrong Flight Research Center (AFRC): Summary and Recent Deployments. In Proceedings of the 3rd Edwards Technical Symposium, Edwards AFB, Edwards, CA, USA, 10 September 2018. [Google Scholar]
- Hill, K.; Meltz, G. Fiber Bragg grating technology fundamentals and overview. J. Lightw. Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef] [Green Version]
- Iwashima, T.; Inoue, A.; Shigematsu, M. Temperature compensation technique for fibre Bragg gratings using liquid crystalline polymer tubes. Electron. Lett. 1997, 33, 417–419. [Google Scholar] [CrossRef]
- Jones, D.; Roberts, C.; Tarrant, D.; Chun, Y.; Ching-Fang, L. Transfer Alignment Design and Evaluation Environment. In Proceedings of the First IEEE Regional Conference on Aerospace Control Systems, Westlake Village, CA, USA, 25–27 May 1993. [Google Scholar]
- Spalding, K.; Missouri, S.L. An efficient rapid transfer alignment filter. In AIAA Guidance, Navigation and Control Conference; AIAA: Hilton Head Island, SC, USA, 1992; pp. 1276–1286. [Google Scholar]
- Pehlivanoglu, A.G.; Ercan, Y. Investigation of flexure effect on transfer alignment performance. J. Navig. 2013, 66, 1–15. [Google Scholar] [CrossRef] [Green Version]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Z.; Chen, X. Analysis of Distributed Measurement Method for Array Antenna Position. Appl. Sci. 2020, 10, 3480. https://doi.org/10.3390/app10103480
Ma Z, Chen X. Analysis of Distributed Measurement Method for Array Antenna Position. Applied Sciences. 2020; 10(10):3480. https://doi.org/10.3390/app10103480
Chicago/Turabian StyleMa, Zhen, and Xiyuan Chen. 2020. "Analysis of Distributed Measurement Method for Array Antenna Position" Applied Sciences 10, no. 10: 3480. https://doi.org/10.3390/app10103480
APA StyleMa, Z., & Chen, X. (2020). Analysis of Distributed Measurement Method for Array Antenna Position. Applied Sciences, 10(10), 3480. https://doi.org/10.3390/app10103480