A Novel Indoor Ranging Algorithm Based on a Received Signal Strength Indicator and Channel State Information Using an Extended Kalman Filter
Abstract
:1. Introduction
- A cross-layer approach including MAC layer and physical layer that enable fine-grained indoor ranging in WLANs. Our proposed method includes two parts, RSSI-based ranging model and CSI-based ranging model.
- Indoor ranging research based on RSSI and CSI in the environment of high-load Access Point (AP). This paper demonstrates the feasibility of this method in a high-load AP environment.
- The method we propose is also the first one that uses extend Kalman filtering to combine RSSI-based signal attenuation model and CSI-based ranging model to perform distance estimation.
- The experimental evaluation in two representative indoor environments to confirm the feasibility of our design and its effect on the ranging results. The experimental results show that the proposed algorithm outperforms existing algorithms.
2. Related Work
2.1. Characteristics of RSSI and CSI
- (1)
- It has excellent resistance to interference in the 2.4 GHz band signal and has less fluctuation in a stable environment. It can also reflect the changes in the environment.
- (2)
- The use of OFDM technology to distinguish signals of different paths as finely as possible.
2.2. RSSI-Based Signal Attenuation Model for Indoor Ranging
2.3. CSI-Based Signal Attenuation Model for Indoor Ranging
2.4. The Extended Kalman Filtering Algorithm
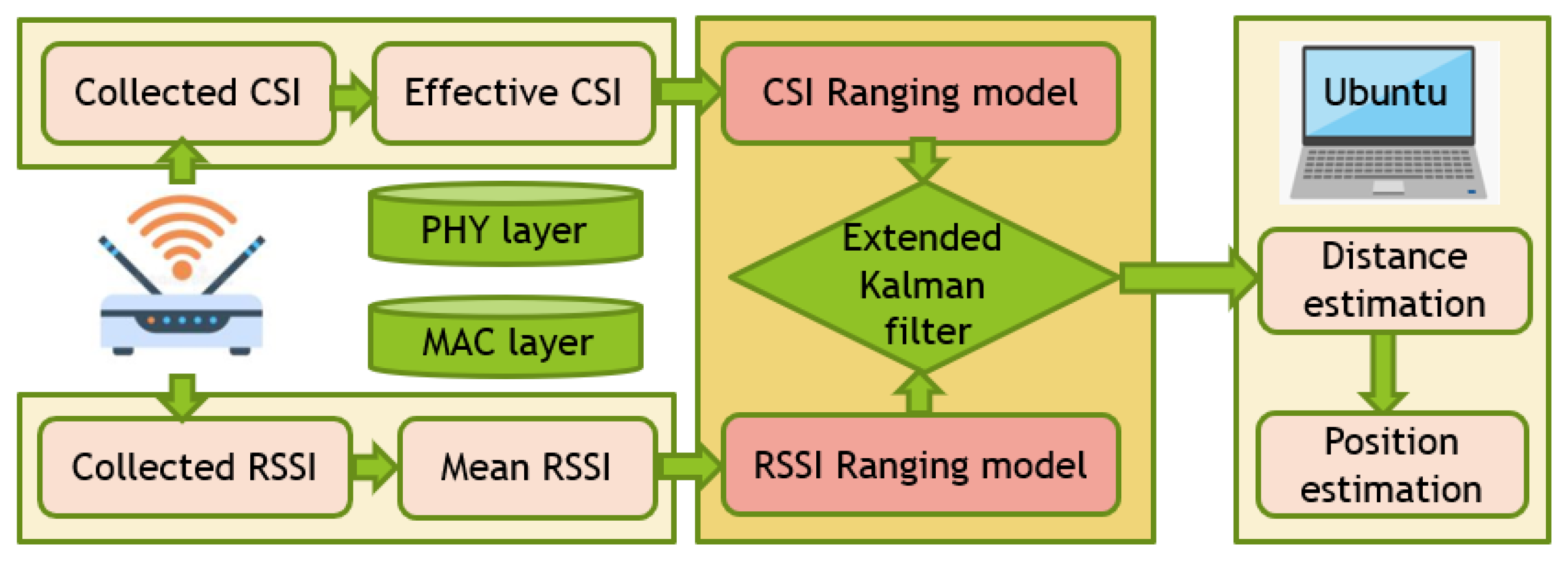
3. Indoor Localization Architecture and Methodology
3.1. Indoor Localization Architecture
3.2. The Extended Kalman Filtering Algorithm Model
4. Experimental Environment and Results
4.1. Experimental Environment
4.2. Experimental Results
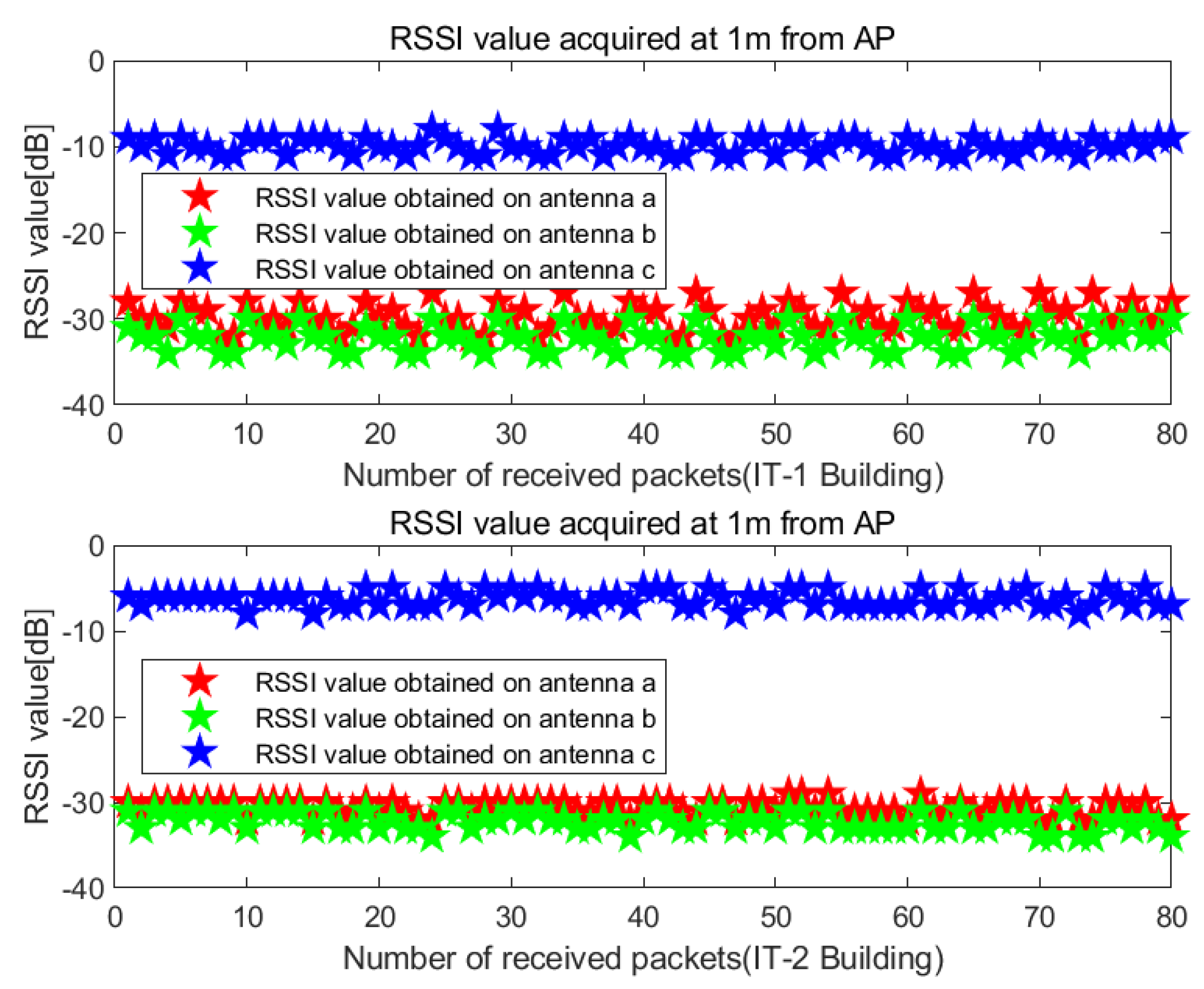
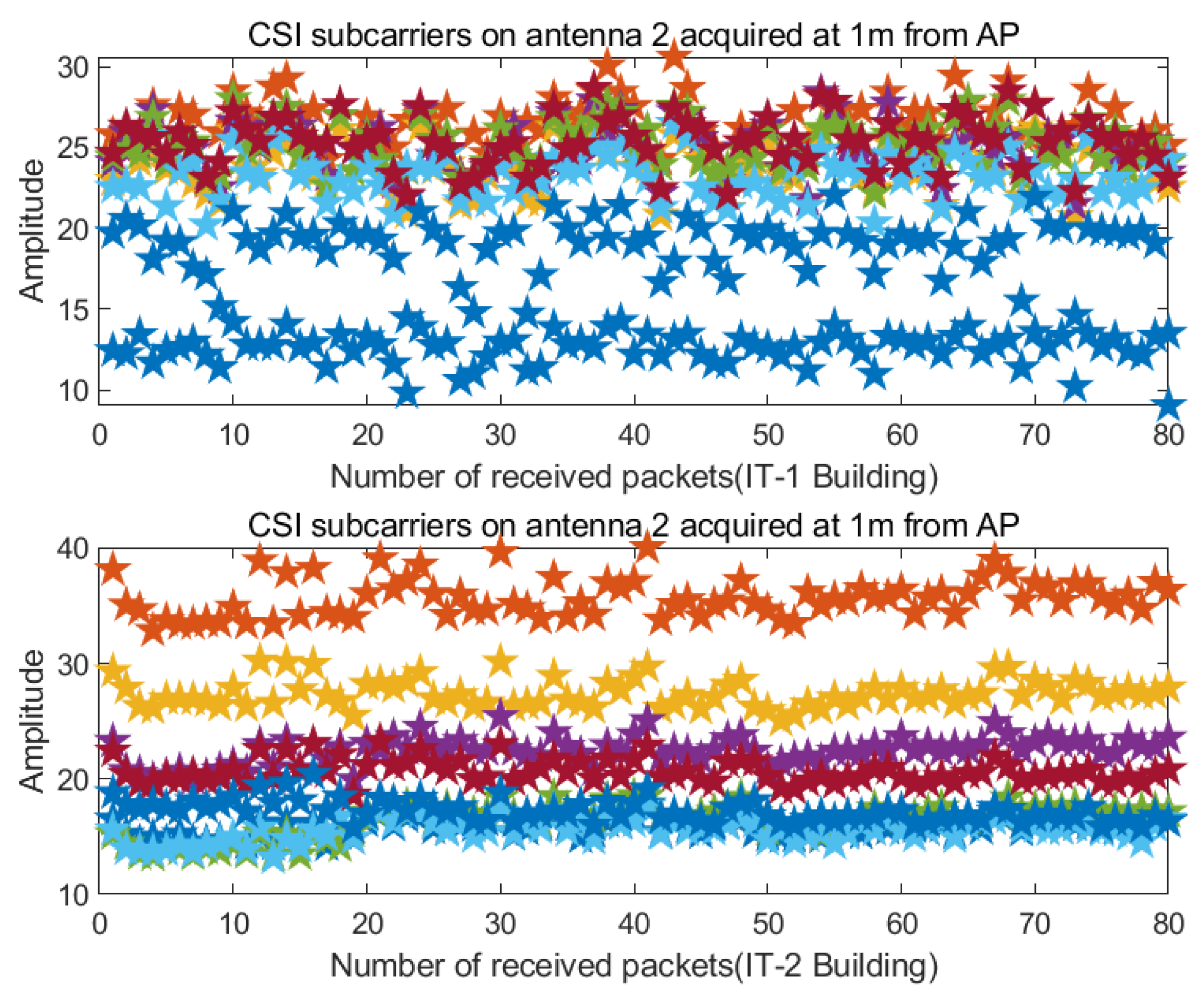
4.2.1. Data Collection and Processing of RSSI and CSI
4.2.2. Three-Dimensional Diagram of Nonlinear Ranging Model
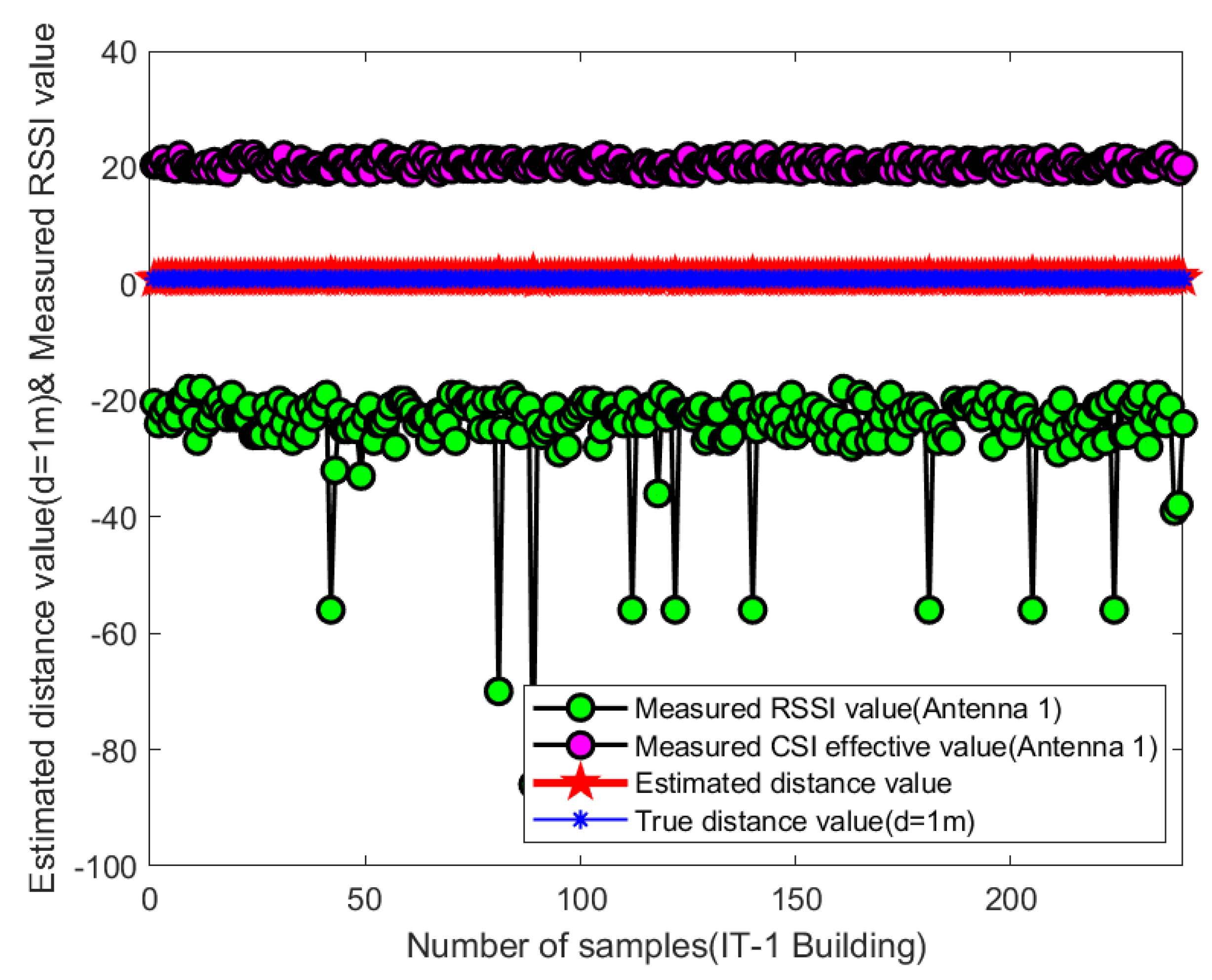
4.2.3. Distance Estimation Based on Extended Kalman Filtering
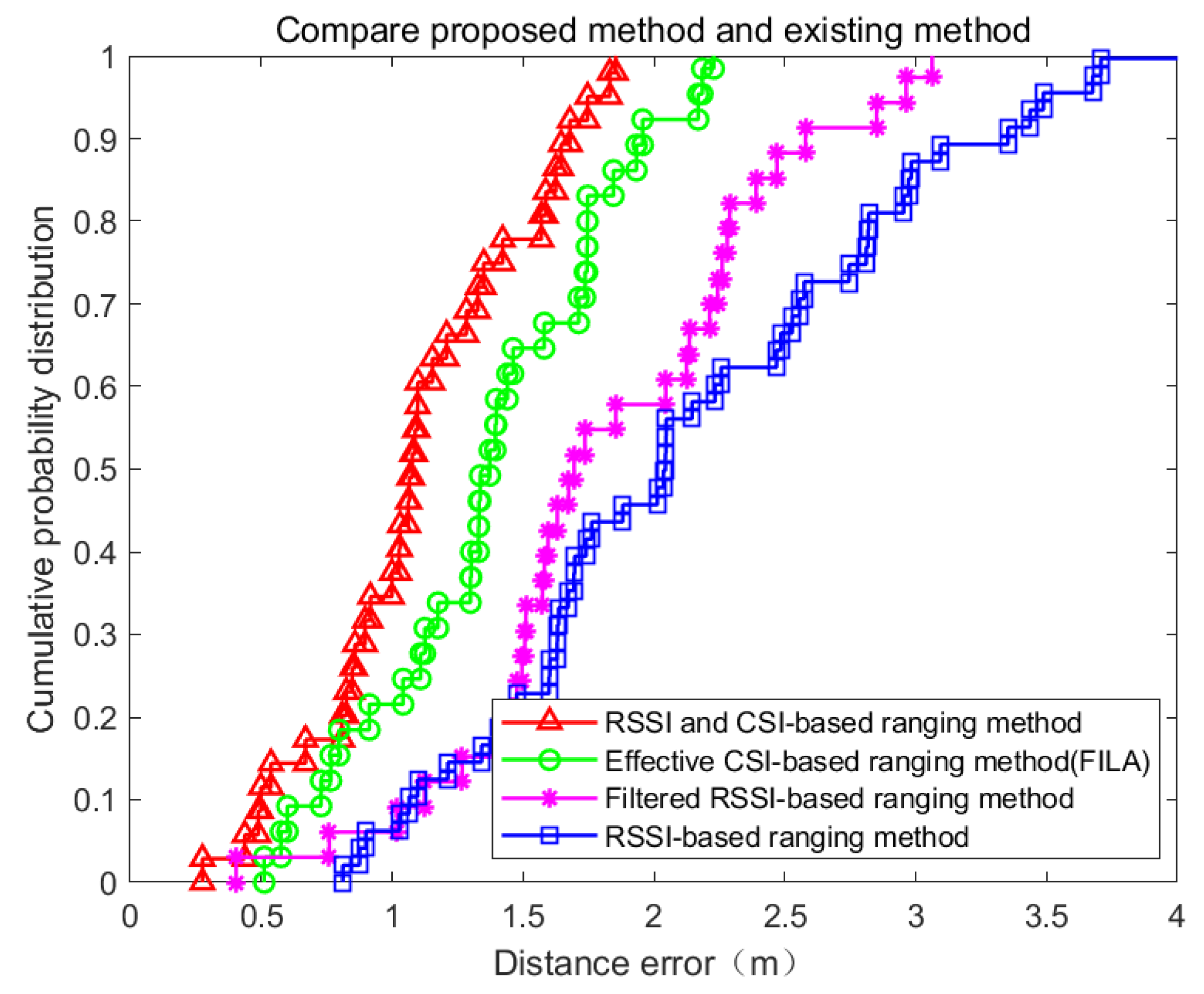
4.2.4. Performance Evaluation
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Rycroft, M.J. Understanding GPS. Principles and applications. Second Edition. J. Atmos. Sol.-Terr. Phys. 1997, 59, 598–599. [Google Scholar] [CrossRef]
- El-rabbany, A. Introduction to GPS: The Global Position System; Artech House: New York, NY, USA, 2006. [Google Scholar]
- Crow, B.P.; Widjaja, I.; Kim, J.G.; Sakai, P.T. IEEE 802.11 wireless local area networks. IEEE Commun. Mag. 1997, 35, 116–126. [Google Scholar] [CrossRef]
- Chen, H.X.; Hu, B.J.; Zheng, L.L.; Wei, Z.H. An Accurate AoA Estimation Approach for Indoor Localization Using Commodity Wi-Fi Devices. In Proceedings of the 2018 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC 2018), Qingdao, China, 14–17 September 2018. [Google Scholar]
- Güvenç, I.; Chong, C.C. A survey on TOA based wireless localization and NLOS mitigation techniques. IEEE Commun. Surv. Tutor. 2009, 11, 107–124. [Google Scholar] [CrossRef]
- Makki, A.; Siddig, A.; Saad, M.; Cavallaro, J.R.; Bleakley, C.J. Indoor Localization Using 802.11 Time Differences of Arrival. IEEE Trans. Instrum. Meas. 2016, 65, 614–623. [Google Scholar] [CrossRef]
- Xu, J.; Liu, W.; Lang, F.; Zhang, Y.; Wang, C. Distance Measurement Model Based on RSSI in WSN. Wirel. Sens. Netw. 2010, 2, 606. [Google Scholar]
- Wu, K.; Xiao, J.; Yi, Y.; Gao, M.; Ni, L.M. FILA: Fine-grained indoor localization. In Proceedings of the IEEE INFOCOM, Orlando, FL, USA, 25–30 March 2012. [Google Scholar]
- Wang, K.; Yu, X.; Xiong, Q.; Zhu, Q.; Lu, W.; Huang, Y.; Zhao, L. Learning to improve WLAN indoor positioning accuracy based on DBSCAN-KRF Algorithm from RSS Fingerprint Data. IEEE Access 2019, 7, 72308–72315. [Google Scholar] [CrossRef]
- Xie, C.; Guan, W.; Wu, Y.; Fang, L.; Cai, Y. The LED-ID Detection and Recognition Method Based on Visible Light Positioning Using Proximity Method. IEEE Photonics J. 2018, 10, 1–16. [Google Scholar] [CrossRef]
- Destiarti, A.R.; Kristalina, P.; Sudarsono, A. Mobile cooperative tracking with RSSI ranging in EKF algorithm for indoor wireless sensor network. In Proceedings of the 2016 International Conference on Knowledge Creation and Intelligent Computing (KCIC 2016), Manado, Indonesia, 15–17 November 2016. [Google Scholar]
- Xiao, J.; Wu, K.; Yi, Y.; Ni, L.M. FIFS: Fine-grained indoor fingerprinting system. In Proceedings of the 2012 21st International Conference on Computer Communications and Networks (ICCCN 2012), Munich, Germany, 30 July–2 August 2012. [Google Scholar]
- Wang, X.; Gao, L.; Mao, S.; Pandey, S. DeepFi: Deep learning for indoor fingerprinting using channel state information. In Proceedings of the 2015 IEEE Wireless Communications and Networking Conference (WCNC 2015), New Orleans, LA, USA, 9–12 March 2015. [Google Scholar]
- Chapre, Y.; Ignjatovic, A.; Seneviratne, A.; Jha, S. CSI-MIMO: Indoor Wi-Fi fingerprinting system. In Proceedings of the Conference on Local Computer Networks (LCN), Edmonton, AB, Canada, 8–11 September 2014. [Google Scholar]
- Hsieh, C.H.; Chen, J.Y.; Nien, B.H. Deep Learning-Based Indoor Localization Using Received Signal Strength and Channel State Information. IEEE Access 2019, 7, 33256–33267. [Google Scholar] [CrossRef]
- Simon, D. Kalman filtering with state constraints: A survey of linear and nonlinear algorithms. IET Control Theory Appl. 2010, 4, 1303–1318. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Du, H.; Ye, Q.; Liu, C. Utilizing CSI and RSSI to Achieve High-Precision Outdoor Positioning: A Deep Learning Approach. In Proceedings of the IEEE International Conference on Communications, Shanghai, China, 20–24 May 2019. [Google Scholar]
- Zhang, L.; Ding, E.; Hu, Y.; Liu, Y. A novel CSI-based fingerprinting for localization with a single AP. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 51. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, Z.; Liu, Y. From RSSI to CSI: Indoor localization via channel response. ACM Comput. Surv. 2013, 46, 1–32. [Google Scholar]
- Wang, X.; Gao, L.; Mao, S.; Pandey, S. CSI-Based Fingerprinting for Indoor Localization: A Deep Learning Approach. IEEE Trans. Veh. Technol. 2017, 66, 763–776. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Feng, Y. RSSI-based Algorithm for Indoor Localization. Commun. Netw. 2013, 5, 37. [Google Scholar] [CrossRef]
- Pathak, O.; Palaskar, P.; Palkar, R.; Tawari, M. Wi-Fi Indoor Positioning System Based on RSSI Measurements from Wi-Fi Access Points—A Tri-lateration Approach. Int. J. Sci. Eng. Res. 2014, 5, 1234–1238. [Google Scholar]
- Li, G.; Geng, E.; Ye, Z.; Xu, Y.; Lin, J.; Pang, Y. Indoor positioning algorithm based on the improved rssi distance model. Sensors 2018, 18, 2820. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zanca, G.; Zorzi, F.; Zanella, A.; Zorzi, M. Experimental comparison of RSSI-based localization algorithms for indoor wireless sensor networks. In Proceedings of the Workshop on Real-World Wireless Sensor Networks (REALWSN 2008); ACM: Glasgow, Scotland, 2008. [Google Scholar]
- Adachi, T. IEEE802.11n. Kyokai Joho Imeji Zasshi/J. Inst. Image Inf. Telev. Eng. 2011, 65, 950–953. [Google Scholar] [CrossRef]
- Letor, N.; Torfs, W.; Blondia, C. Multimedia multicast performance analysis for 802.11n network cards. In Proceedings of the IFIP Wireless Days, Dublin, Ireland, 21–23 November 2012. [Google Scholar]
- Lin, M.F.; Tzu, J.Y.; Lin, L.; Lee, H.M. The IEEE802.11n capability analysis model based on mobile networking architecture. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009. [Google Scholar]
- Wang, X.; Gao, L.; Mao, S. CSI Phase Fingerprinting for Indoor Localization with a Deep Learning Approach. IEEE Internet Things J. 2016, 3, 1113–1123. [Google Scholar]
- Lee, S.H.; Lim, I.K.; Lee, J.K. Method for Improving Indoor Positioning Accuracy Using Extended Kalman Filter. Mob. Inf. Syst. 2016, 2016. [Google Scholar] [CrossRef] [Green Version]
- Ben Kilani, M.; Raymond, A.J.; Gagnon, F.; Gagnon, G.; Lavoie, P. RSSI-based indoor tracking using the extended Kalman filter and circularly polarized antennas. In Proceedings of the 2014 11th Workshop on Positioning, Navigation and Communication (WPNC 2014), Dresden, Germany, 12–13 March 2014. [Google Scholar]
- Halperin, D.; Hu, W.; Sheth, A.; Wetherall, D. Tool release: Gathering 802.11n traces with channel state information. Comput. Commun. Rev. 2011, 41, 53. [Google Scholar] [CrossRef]
- Liu, X.L.; Hu, W.; Pu, Q.; Wu, F.; Zhang, Y. ParCast: Soft video delivery in MIMO-OFDM WLANs. In Proceedings of the Annual International Conference on Mobile Computing and Networking (MOBICOM), Istanbul, Turkey, 22–26 August 2012. [Google Scholar]














| Category | RSSI | CSI |
|---|---|---|
| Time resolution | Packet | Multipath signal cluster |
| Frequency resolution | None | Subcarrier |
| Stability | Low | High |
| Dimension | One dimension | High dimension |
| Universality | All Wi-Fi devices | Some Wi-Fi devices |
| Data Information | Properties |
|---|---|
| Bfee-count | Number of Bfee count beamforming sent to user space by drive record |
| Nrx | Number of Nrx receiving antennas (Intel5300 network card is usually 3) |
| Ntx | Number of Ntx transmit antennas |
| rssi-a, rssi-b, rssi-c | Received signal strength of each receiving antenna |
| rate | Rate the transmission rate of each packet |
| noise | noise |
| CSI | CSI data itself is a three-dimensional arrays of Nrx * Ntx * 30 |
| Indoor Ranging Algorithm | Mean Ranging Error | Standard Deviation |
|---|---|---|
| RSSI-based algorithm | 2.041 m | 1.214 m |
| Filtered RSSI-based algorithm | 1.696 m | 0.908 m |
| CSI-based algorithm (FILA) | 1.381 m | 0.577 m |
| RSSI and CSI-based algorithm (Proposed algorithm) | 1.049 m | 0.623 m |
| Indoor Ranging Algorithm | Mean Ranging Error | Standard Deviation |
|---|---|---|
| RSSI-based algorithm | 1.798 m | 1.279 m |
| Filtered RSSI-based algorithm | 1.669 m | 1.243 m |
| CSI-based algorithm (FILA) | 1.395 m | 0.972 m |
| RSSI and CSI-based algorithm (Proposed algorithm) | 1.103 m | 0.612 m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Park, J.G. A Novel Indoor Ranging Algorithm Based on a Received Signal Strength Indicator and Channel State Information Using an Extended Kalman Filter. Appl. Sci. 2020, 10, 3687. https://doi.org/10.3390/app10113687
Wang J, Park JG. A Novel Indoor Ranging Algorithm Based on a Received Signal Strength Indicator and Channel State Information Using an Extended Kalman Filter. Applied Sciences. 2020; 10(11):3687. https://doi.org/10.3390/app10113687
Chicago/Turabian StyleWang, Jingjing, and Joon Goo Park. 2020. "A Novel Indoor Ranging Algorithm Based on a Received Signal Strength Indicator and Channel State Information Using an Extended Kalman Filter" Applied Sciences 10, no. 11: 3687. https://doi.org/10.3390/app10113687







