CMOS Fixed Pattern Noise Removal Based on Low Rank Sparse Variational Method
Abstract
1. Introduced
2. Existing Methods
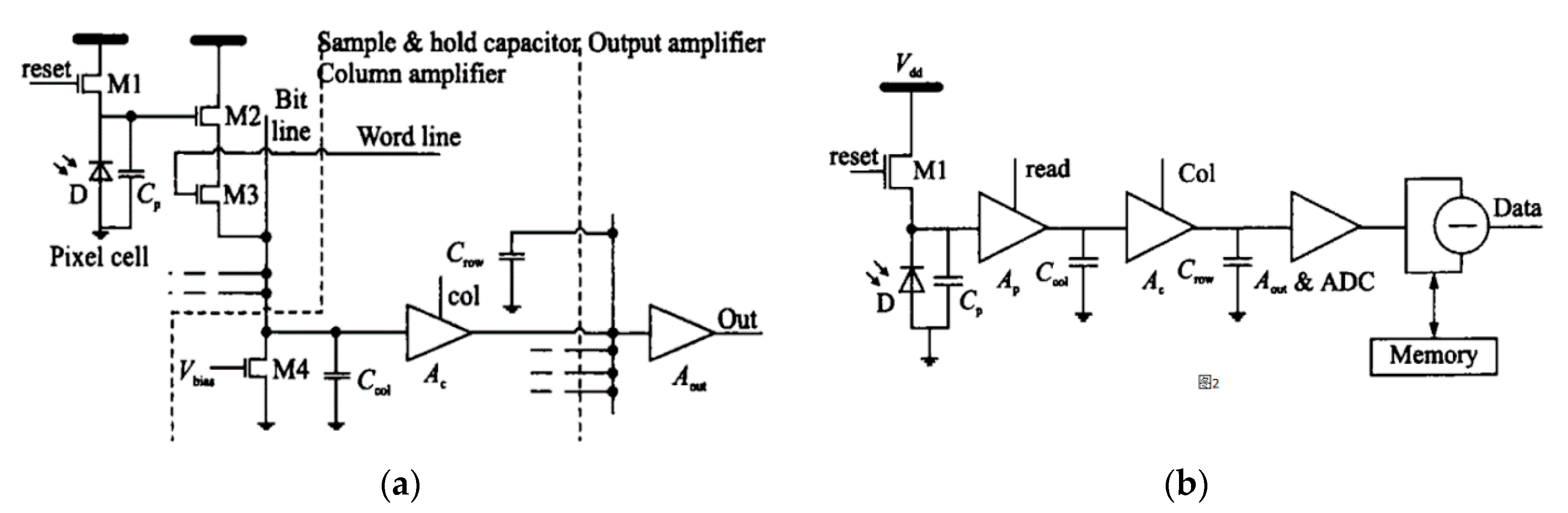
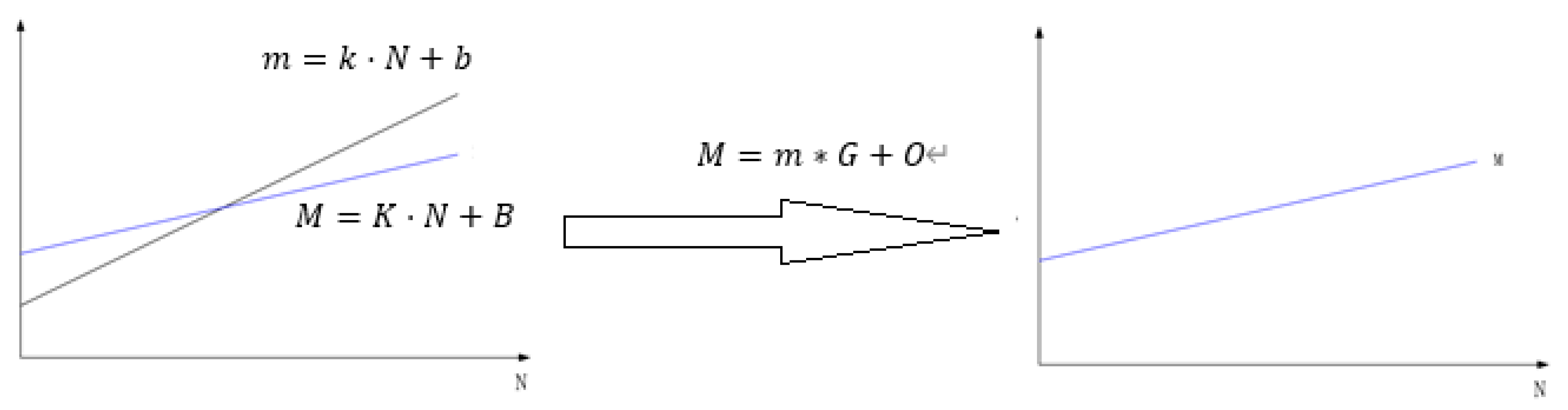
2.1. Calibration-Based Method
2.2. Scene-Based Method
3. Motivation for Presenting this Method
4. Proposed Model
| Algorithm 1 Low-Rank sparase variationnal destripe (LRSUTV) |
| 1. Get image Y with FPN 2. The initial matrix U = 0, S = 0, H = 0, J = 0, K = 0 3. Initial optimization factor , 4. For n = 1:N do 5. Calculating the optimal solution of U via Fourier Transformation by (9) 6. Calculating low rank S by singular value decomposition (SVD) by (12) (13) 7. calculating H J K through soft thresholds by (14), (16), (18) 8. , by method of dual gradient rise by (19), (20), (21) 9. End for 10. Separate clear image U and stripe S |
5. Experimental Results and Discussions
5.1. Experimental Environment
5.2. Simulation Experiment
- Aperiodic stripe noise
Subjective Qualitative Evaluation
5.3. Periodic Stripe Noise
Subjective Qualitative Evaluation
5.4. Quantitative Objective Evaluation
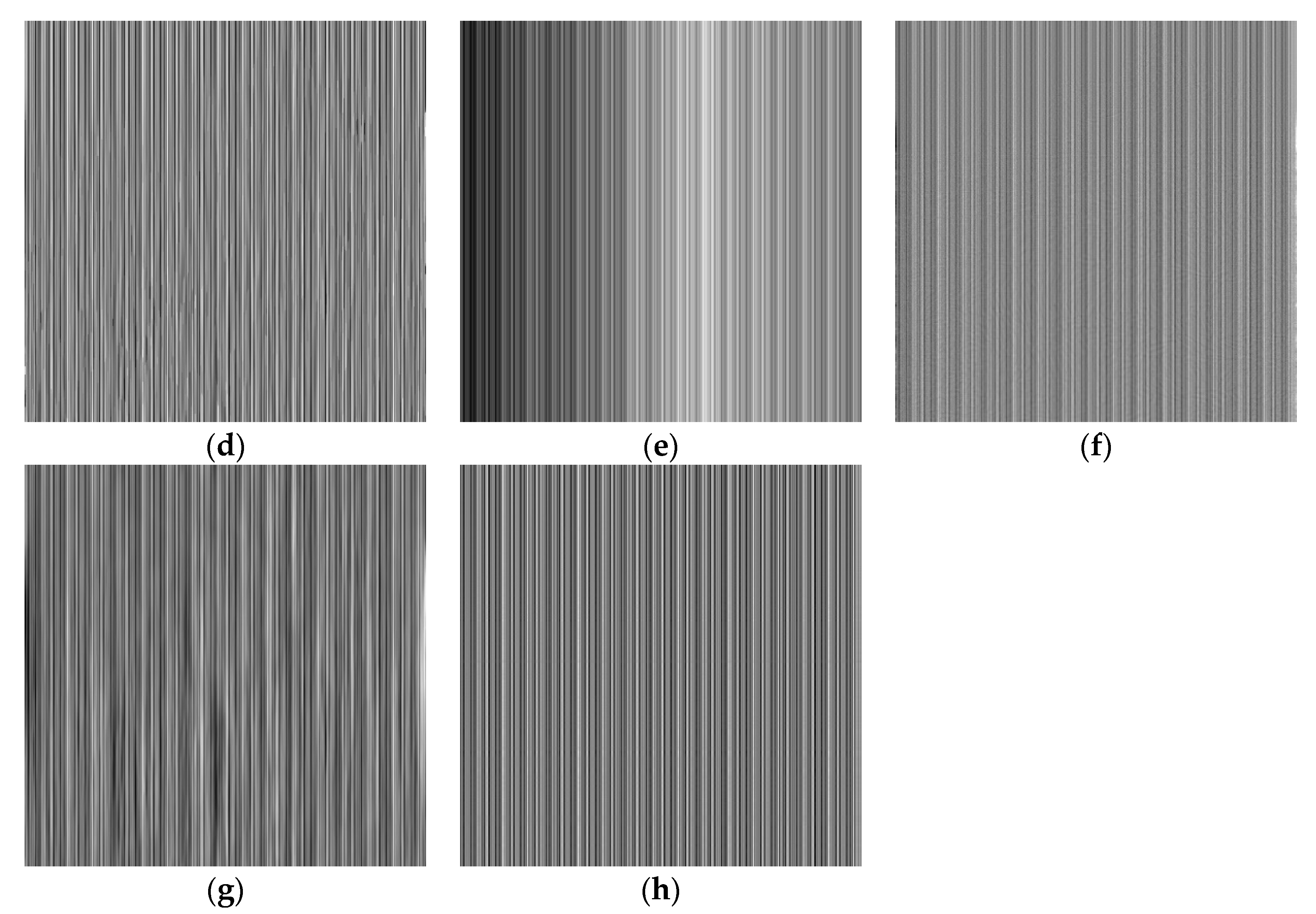
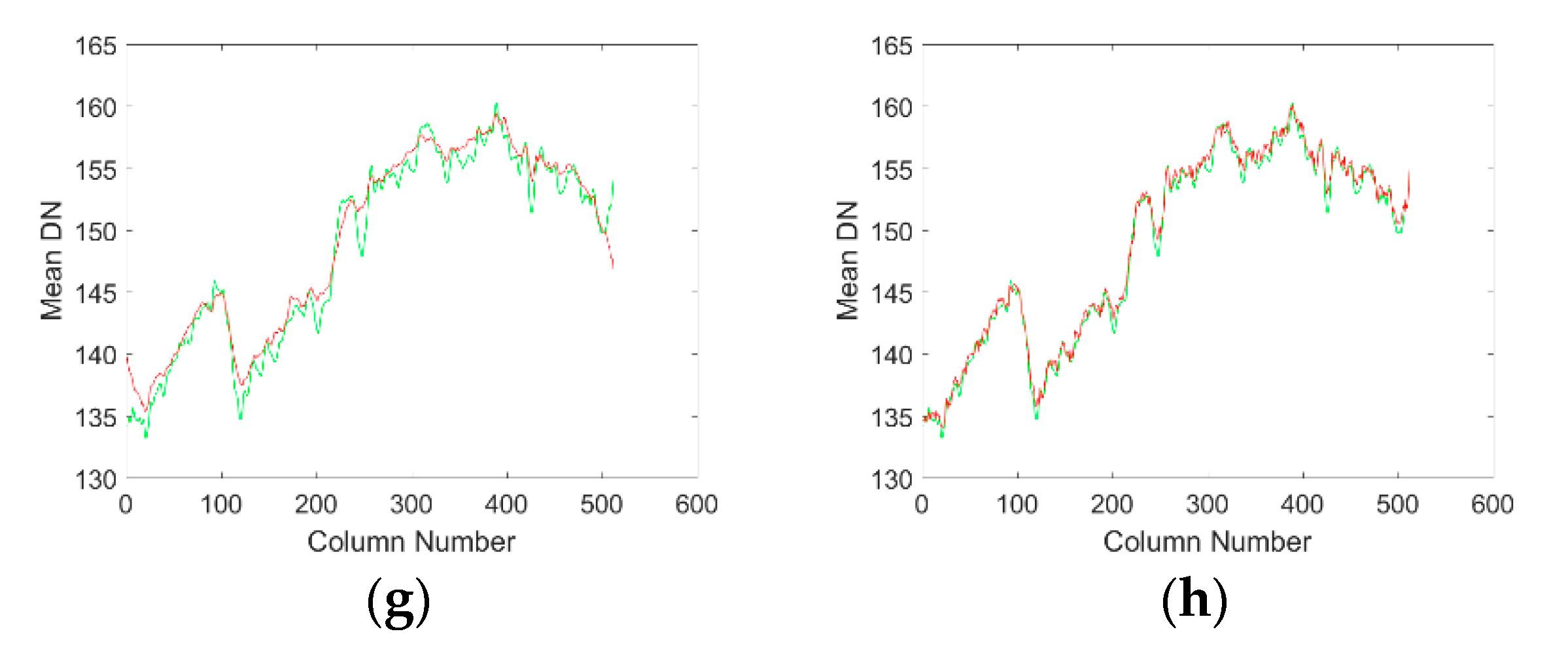
5.5. Actual Image Testing
5.6. Discussion
5.6.1. Parameter Selection
5.6.2. Program Run Time
6. Summary
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Babcock, H.P.; Huang, F.; Speer, C.M. Correcting Artifacts in Single Molecule Localization Microscopy Analysis Arising from Pixel Quantum Efficiency Differences in sCMOS Cameras. Sci. Rep. 2019, 9, 18058. [Google Scholar] [CrossRef]
- Mandracchia, B.; Hua, X.; Guo, C.; Son, J.; Urner, T.; Jia, S. Fast and accurate sCMOS noise correction for fluorescence microscopy. Nat. Commun. 2020, 11, 94. [Google Scholar] [CrossRef]
- Yu, L.; Guoyu, W. A New Fixed Mode Noise Suppression Technology for CMOS Image Sensor. Res. Prog. SSE 2006, 3, 345–348. [Google Scholar]
- Xiaozhi, L.; Shengcai, Z.; Shuying, Y. Design of low FPN column readout circuit in CMOS image sensor. J. Sens. Technol. 2006, 3, 697–701. [Google Scholar]
- Bao, J.Y.; Xing, F.; Sun, T.; You, Z. CMOS imager non-uniformity response correction-based high-accuracy spot target localization. Appl. Opt. 2019, 58, 4560–4568. [Google Scholar] [CrossRef]
- Brouk, I.; Nemirovsky, A.; Nemirovsky, Y. Analysis of noise in CMOS image sensor. In Proceedings of the 2008 IEEE International Conference on Microwaves, Communications, Antennas and Electronic Systems, Tel-Aviv, Israel, 13–14 May 2008. [Google Scholar]
- Xing, S.-X.; Zhang, J.; Sun, L.; Chang, B.-K.; Qian, Y.-S. Two-Point nonuniformity correction based on LMS. In Infrared Components and Their Applications; International Society for Optics and Photonics: Bellingham, WA, USA, 2005. [Google Scholar]
- Huawei, W.; Caiwen, M.; Jianzhong, C.; Haifeng, Z. An adaptive two-point non-uniformity correction algorithm based on shutter and its implementation. In Proceedings of the 2013 5th IEEE International Conference on Measuring Technology and Mechatronics Automation, Hong Kong, China, 16–17 January 2013. [Google Scholar]
- Lim, J.H.; Jeon, J.W.; Kwon, K.H. Optimal Non-Uniformity Correction for Linear Response and Defective Pixel Removal of Thermal Imaging System. In Proceedings of the International Conference on Ubiquitous Information Management and Communication, Phuket, Thailand, 4–6 January 2019; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Zhou, B.; Ma, Y.; Li, H.; Liang, K. A study of two-point multi-section non-uniformity correction auto division algorithm for infrared images. In Proceedings of the 5th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Optoelectronic Materials and Devices for Detector, Imager, Display, and Energy Conversion Technology, Dalian, China, 22–29 October 2010; International Society for Optics and Photonics: Bellingham, WA, USA, 2020; p. 76583X. [Google Scholar]
- Honghui, Z.; Haibo, L.; Xinrong, Y.; Qinghai, D. Adaptive non-uniformity correction algorithm based on multi-point correction. Infrared Laser Eng. 2014, 43, 3651–3654. [Google Scholar]
- Rui, L.; Yang, Y.; Wang, B.; Zhou, H.; Liu, S. S-Curve Model-Based Adaptive Algorithm for Nonuniformity Correction in Infrared Focal Plane Arrays. Acta Opt. Sin. 2009, 29, 927–931. [Google Scholar] [CrossRef]
- Yang, H.; Huang, Z.; Cai, H.; Zhang, Y. Novel real-time nonuniformity correction solution for infrared focal plane arrays based on S-curve model. Opt. Eng. 2012, 51, 077001. [Google Scholar] [CrossRef]
- Rozkovec, M.; Čech, J. Polynomial based NUC implemented on FPGA. In Proceedings of the 2016 IEEE Euromicro Conference on Digital System Design (DSD), Limassol, Cyprus, 31 August–2 September 2016. [Google Scholar]
- Gross, W.; Hierl, T.; Schulz, M.J. Correctability and long-term stability of infrared focal plane arrays. Opt. Eng. 1999, 38, 862–869. [Google Scholar]
- Chatard, J.P. Physical Limitations To Nonuniformity Correction In IR Focal Plane Arrays. In Focal Plane Arrays: Technology and Applications; International Society for Optics and Photonics: Bellingham, WA, USA, 1988. [Google Scholar]
- Pande-Chhetri, R.; Abd-Elrahman, A. De-striping hyperspectral imagery using wavelet transform and adaptive frequency domain filtering. ISPRS J. Photogramm. Remote Sens. 2011, 66, 620–636. [Google Scholar] [CrossRef]
- Jinsong, C.; Yun, S.; Huadong, G.; Weiming, W.; Boqin, Z. Destriping CMODIS data by power filtering. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2119–2124. [Google Scholar] [CrossRef]
- Munch, B.; Trtik, P.; Marone, F.; Stampanoni, M. Stripe and ring artifact removal with combined wavelet—Fourier filtering. Opt. Express 2009, 17, 8567–8591. [Google Scholar] [CrossRef] [PubMed]
- Gadallah, F.; Csillag, F.; Smith, E. Destriping multisensor imagery with moment matching. Int. J. Remote Sens. 2000, 21, 2505–2511. [Google Scholar] [CrossRef]
- Wegener, M. Destriping multiple sensor imagery by improved histogram matching. Int. J. Remote Sens. 1990, 11, 859–875. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Fang, H.; Liu, H. Simultaneous Destriping and Denoising for Remote Sensing Images With Unidirectional Total Variation and Sparse Representation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1051–1055. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Fang, H.; Luo, C. Anisotropic spectral-spatial total variation model for multispectral remote sensing image destriping. IEEE Trans. Image Process. 2015, 24, 1852–1866. [Google Scholar] [CrossRef]
- Fehrenbach, J.; Weiss, P.; Lorenzo, C. Variational Algorithms to Remove Stationary Noise: Applications to Microscopy Imaging. IEEE Trans. Image Process. 2012, 21, 4420–4430. [Google Scholar] [CrossRef]
- Lu, X.; Wang, Y.; Yuan, Y. Graph-Regularized Low-Rank Representation for Destriping of Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4009–4018. [Google Scholar] [CrossRef]
- Zhang, H.; He, W.; Zhang, L.; Shen, H.; Yuan, Q. Hyperspectral Image Restoration Using Low-Rank Matrix Recovery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4729–4743. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Total-Variation-Regularized Low-Rank Matrix Factorization for Hyperspectral Image Restoration. IEEE Trans. Geosci. Remote Sens. 2016, 54, 178–188. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Wu, T.; Zhong, S. Remote Sensing Image Stripe Noise Removal: From Image Decomposition Perspective. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7018–7031. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, L. A MAP-Based Algorithm for Destriping and Inpainting of Remotely Sensed Images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1492–1502. [Google Scholar] [CrossRef]
- Bouali, M.; Ladjal, S. Toward Optimal Destriping of MODIS Data Using a Unidirectional Variational Model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2924–2935. [Google Scholar] [CrossRef]
- Yanovsky, I.; Dragomiretskiy, K. Variational Destriping in Remote Sensing Imagery: Total Variation with L1 Fidelity. Remote Sens. 2018, 10, 300. [Google Scholar] [CrossRef]
- Sun, Y.-J.; Huang, T.-Z.; Ma, T.-H.; Chen, Y. Remote Sensing Image Stripe Detecting and Destriping Using the Joint Sparsity Constraint with Iterative Support Detection. Remote Sens. 2019, 11, 608. [Google Scholar] [CrossRef]
- Song, Q.; Wang, Y.; Yan, X.; Gu, H. Remote Sensing Images Stripe Noise Removal by Double Sparse Regulation and Region Separation. Remote Sens. 2018, 10, 998. [Google Scholar] [CrossRef]
- Dou, H.-X.; Huang, T.-Z.; Deng, L.-J.; Zhao, X.-L.; Huang, J. Directional ℓ0 Sparse Modeling for Image Stripe Noise Removal. Remote Sens. 2018, 10, 361. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, T.-Z.; Zhao, X.-L.; Deng, L.-J.; Huang, J. Stripe noise removal of remote sensing images by total variation regularization and group sparsity constraint. Remote Sens. 2017, 9, 559. [Google Scholar] [CrossRef]
- El Gamal, A.; Fowler, B.A.; Min, H.; Liu, X. Modeling and estimation of FPN components in CMOS image sensors. Int. Soc. Opt. Photonics 1998, 3301, 168–177. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Lin, Z.; Liu, R.; Su, Z. Linearized Alternating Direction Method with Adaptive Penalty for Low-Rank Representation. Adv. Neural Inf. Process. Syst. 2011, 612–620. [Google Scholar]
- Cao, Y.L.; He, Z.W.; Yang, J.X.; Ye, X.P.; Cao, Y.P. A multi-scale non-uniformity correction method based on wavelet decomposition and guided filtering for uncooled long wave infrared camera. Signal Process. Image 2018, 60, 13–21. [Google Scholar] [CrossRef]
- Xie, X.-F.; Zhang, W.; Zhao, M.; Zhi, X.-Y.; Wang, F.-G. Sequence arrangement of wavelet transform for nonuniformity correction in infrared focal-plane arrays. In Proceedings of the 2011 International Conference on Optical Instruments and Technology: Optoelectronic Imaging and Processing Technology, Beijing, China, 6–9 November 2011. [Google Scholar]
- Yang, J.H.; Zhao, X.L.; Ma, T.H.; Chen, Y.; Huang, T.Z.; Ding, M. Remote sensing images destriping using unidirectional hybrid total variation and nonconvex low-rank regularization. J. Comput. Appl. Math. 2020, 363, 124–144. [Google Scholar] [CrossRef]
- Song, Q.; Wang, Y.H.; Yang, S.N.; Dai, K.H.; Yuan, Y. Guided total variation approach based non-uniformity correction for infrared focal plane array. In Proceedings of the 10th International Conference on Graphics and Image Processing (ICGIP 2018), Chengdu, China, 6 May 2019. [Google Scholar]
- Huang, Z.H.; Zhang, Y.Z.; Li, Q.; Li, Z.T.; Zhang, T.X.; Sang, N.; Xiong, S.Q. Unidirectional variation and deep CNN denoiser priors for simultaneously destriping and denoising optical remote sensing images. Int. J. Remote Sens. 2019, 40, 5737–5748. [Google Scholar] [CrossRef]

















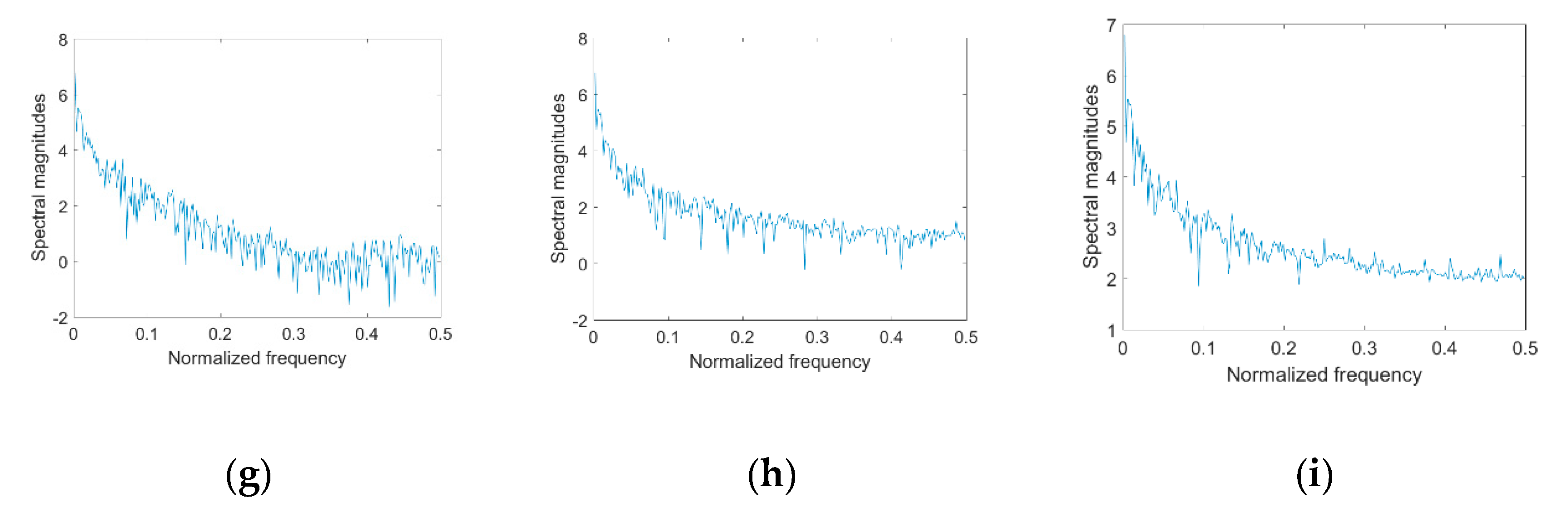

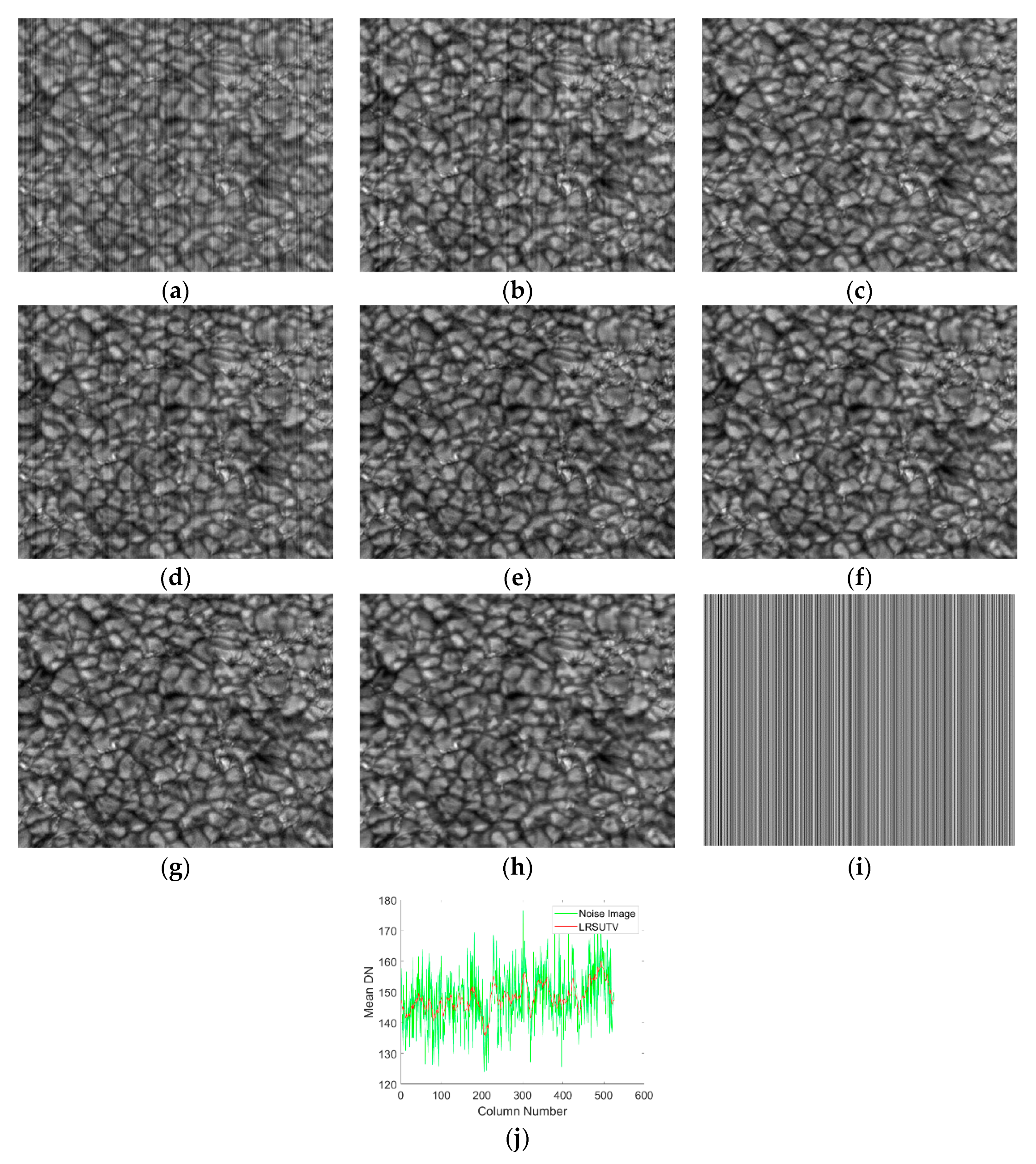


| Images | Method | σ = 4 | σ = 8 | σ = 12 | σ = 16 | σ = 20 |
|---|---|---|---|---|---|---|
| Solar Active Region | WAFT | 31.59958 | 31.34382 | 30.87000 | 30.50006 | 28.54466 |
| UTV | 31.31853 | 31.16326 | 30.87973 | 30.82699 | 29.55368 | |
| ASSTV | 31.61487 | 31.32085 | 30.76171 | 30.16115 | 27.63940 | |
| VSNR | 29.55233 | 29.45862 | 29.28992 | 29.38995 | 29.41818 | |
| SILR | 32.15904 | 32.06835 | 31.75536 | 31.81308 | 30.89457 | |
| L0 | 31.48390 | 31.21754 | 30.97054 | 31.10174 | 30.95841 | |
| LRSUTV | 32.39316 | 32.19943 | 31.86411 | 31.93278 | 31.05222 |
| Images | Method | σ = 4 | σ = 8 | σ = 12 | σ = 16 | σ = 20 |
|---|---|---|---|---|---|---|
| Solar photospheric layer | WAFT | 33.95483 | 33.70573 | 33.00279 | 31.98996 | 29.77545 |
| UTV | 33.83339 | 33.79097 | 33.56776 | 33.27398 | 31.70765 | |
| ASSTV | 34.03604 | 33.77074 | 33.04330 | 31.79459 | 29.08905 | |
| VSNR | 32.69314 | 32.72424 | 32.73020 | 32.76216 | 32.39804 | |
| SILR | 35.43197 | 35.46269 | 35.19106 | 34.89504 | 33.39456 | |
| L0 | 33.79005 | 33.69596 | 33.57622 | 33.38637 | 32.86435 | |
| LRSUTV | 36.80814 | 35.74191 | 35.52385 | 35.42470 | 33.80298 |
| Images | Method | σ = 4 | σ = 8 | σ = 12 | σ = 16 | σ = 20 |
|---|---|---|---|---|---|---|
| Solar active region | WAFT | 0.979698 | 0.976763 | 0.971173 | 0.959207 | 0.911204 |
| UTV | 0.973915 | 0.973032 | 0.971825 | 0.968449 | 0.946812 | |
| ASSTV | 0.97961 | 0.976334 | 0.969964 | 0.954213 | 0.889726 | |
| VSNR | 0.972853 | 0.972645 | 0.972404 | 0.972431 | 0.972587 | |
| SILR | 0.9813 | 0.980956 | 0.980165 | 0.97885 | 0.970024 | |
| L0 | 0.977923 | 0.977109 | 0.976615 | 0.976124 | 0.975494 | |
| LRSUTV | 0.98914 | 0.981068 | 0.980475 | 0.97893 | 0.976364 |
| Images | Method | σ = 4 | σ = 8 | σ = 12 | σ = 16 | σ = 20 |
|---|---|---|---|---|---|---|
| Solar photospheric layer | WAFT | 0.942124 | 0.927306 | 0.897961 | 0.852761 | 0.768504 |
| UTV | 0.941753 | 0.935944 | 0.927616 | 0.907744 | 0.853808 | |
| ASSTV | 0.942987 | 0.929386 | 0.902473 | 0.85379 | 0.74729 | |
| VSNR | 0.877748 | 0.878157 | 0.880637 | 0.87524 | 0.878135 | |
| SILR | 0.9517 | 0.945622 | 0.9384 | 0.922522 | 0.887166 | |
| L0 | 0.938884 | 0.927177 | 0.927061 | 0.915114 | 0.909504 | |
| LRSUTV | 0.957022 | 0.950072 | 0.940674 | 0.928795 | 0.895663 |
| Method | Key Parameter |
|---|---|
| WAFT | k = 2.8 |
| UTV | |
| ASSTV | |
| VSNR | |
| SILR | |
| L0 | |
| LRSUTV |
| Size | WAFT | UTV | ASSTV | VSNR | SILR | L0 | LRSUTV |
|---|---|---|---|---|---|---|---|
| 512 × 512 | 0.1196 | 4.9194 | 18.0126 | 9.6413 | 20.2170 | 27.9707 | 20.4003 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Li, X.; Li, J.; Xu, Z. CMOS Fixed Pattern Noise Removal Based on Low Rank Sparse Variational Method. Appl. Sci. 2020, 10, 3694. https://doi.org/10.3390/app10113694
Zhang T, Li X, Li J, Xu Z. CMOS Fixed Pattern Noise Removal Based on Low Rank Sparse Variational Method. Applied Sciences. 2020; 10(11):3694. https://doi.org/10.3390/app10113694
Chicago/Turabian StyleZhang, Tao, Xinyang Li, Jianfeng Li, and Zhi Xu. 2020. "CMOS Fixed Pattern Noise Removal Based on Low Rank Sparse Variational Method" Applied Sciences 10, no. 11: 3694. https://doi.org/10.3390/app10113694
APA StyleZhang, T., Li, X., Li, J., & Xu, Z. (2020). CMOS Fixed Pattern Noise Removal Based on Low Rank Sparse Variational Method. Applied Sciences, 10(11), 3694. https://doi.org/10.3390/app10113694





