Anti-Disturbance Control for Quadrotor UAV Manipulator Attitude System Based on Fuzzy Adaptive Saturation Super-Twisting Sliding Mode Observer
Abstract
:1. Introduction
- (1)
- In order to alleviate the estimation chattering problem of traditional SMESO, a new observer named fuzzy adaptive saturation super-twisting extended state observer (FASTESO) is proposed, in which a saturation function is invited to replace the discontinued sign function, meanwhile a super-twisting algorithm is introduced to prevent excessively high observer gain and TD [19] and is incorporated for avoiding directly using acceleration information, which is full of noise.
- (2)
- To stay robustness under disturbances with unknown bounds, fuzzy logic rules are introduced as an adaptive algorithm to adaptively adjust the observer switching gains. Furthermore, it also contributes to the chattering attenuation under high switching gain with low estimation value and observer performance improvement under low switching gain with high estimation value.
- (3)
- The proposed method is verified with effectiveness on a quadrotor UAV manipulator prototype in several simulations and experiments.
2. Preliminaries
2.1. Notation
2.2. Quaternion Operations
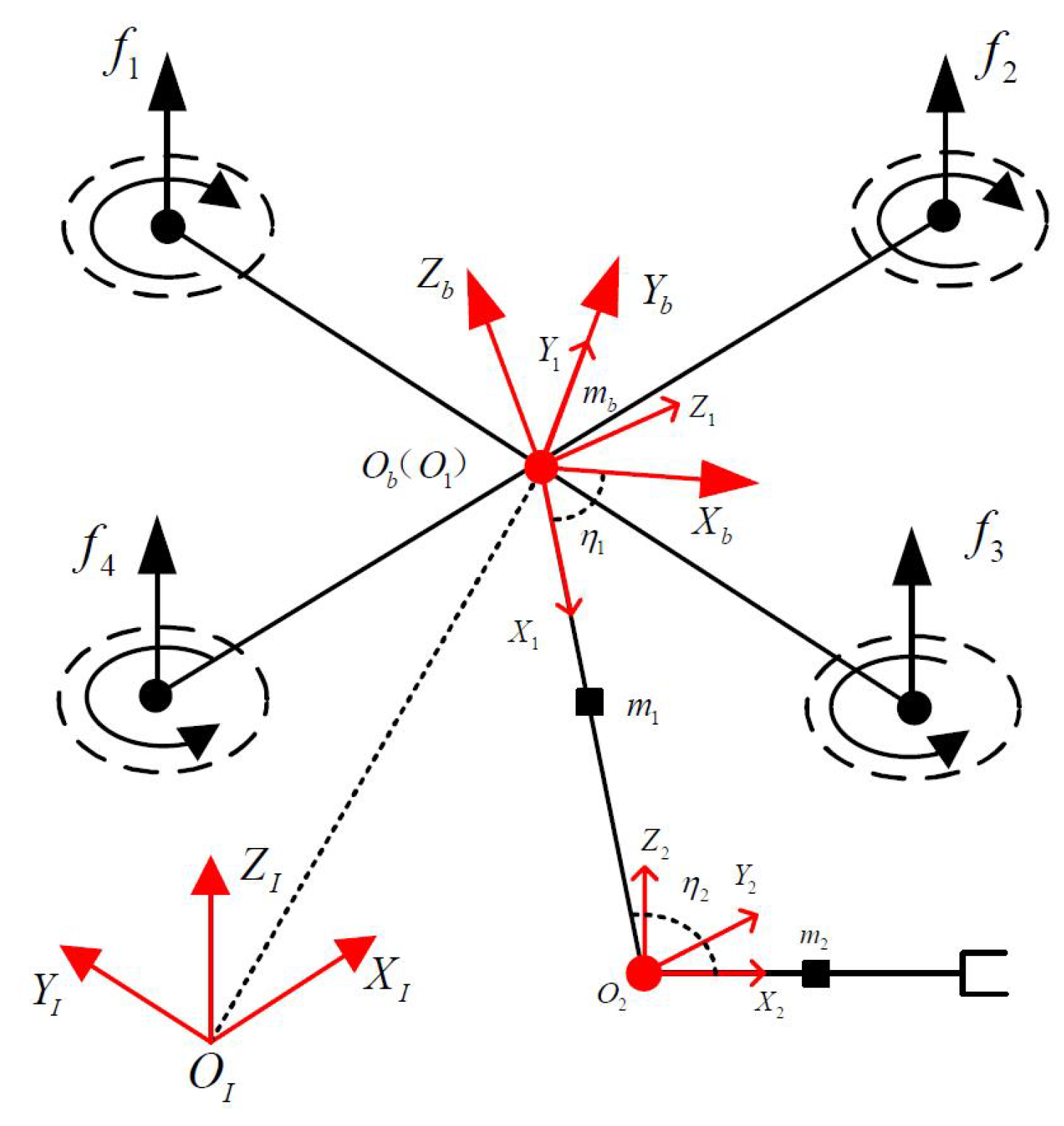
3. Models of UAV
3.1. Kinematic Model
3.2. Dynamic Model
4. Method
4.1. FASTESO
4.1.1. Construction of Traditional Super-Twisting Extended State Observer (STESO)
4.1.2. Saturation Function
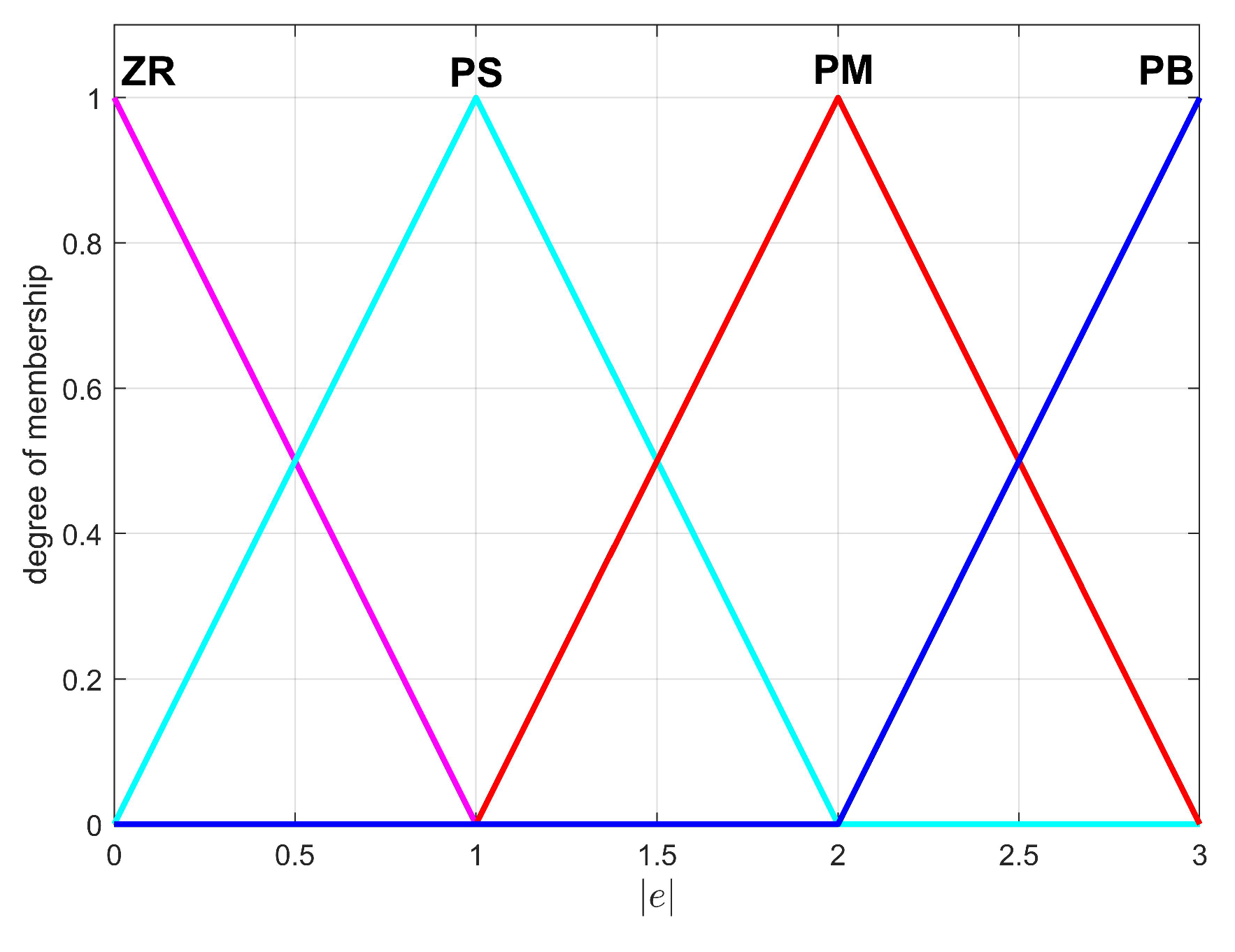
4.1.3. Adaptive Switching Gains with Fuzzy Logic Rules
4.2. Attitude Controller
5. Simulation
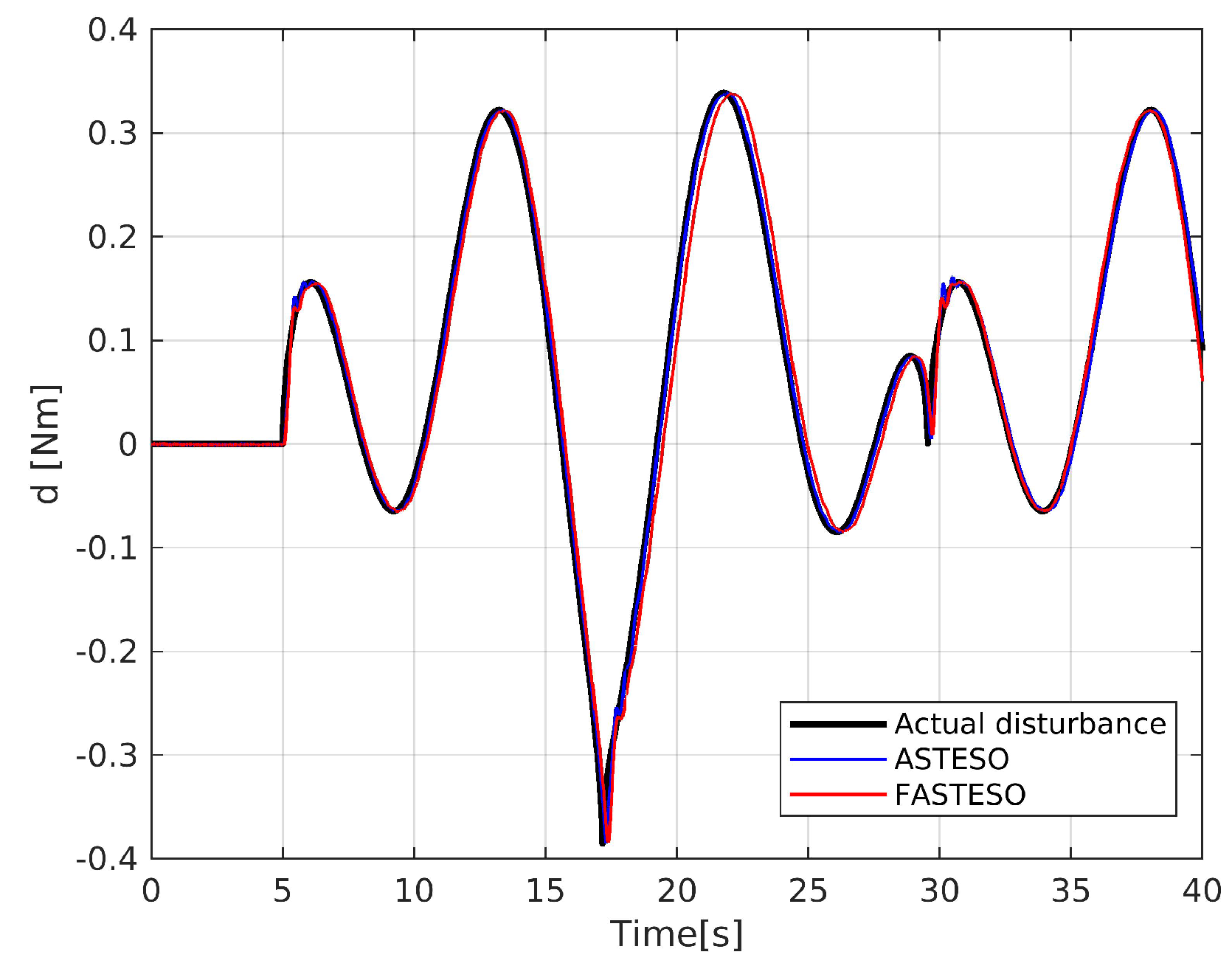
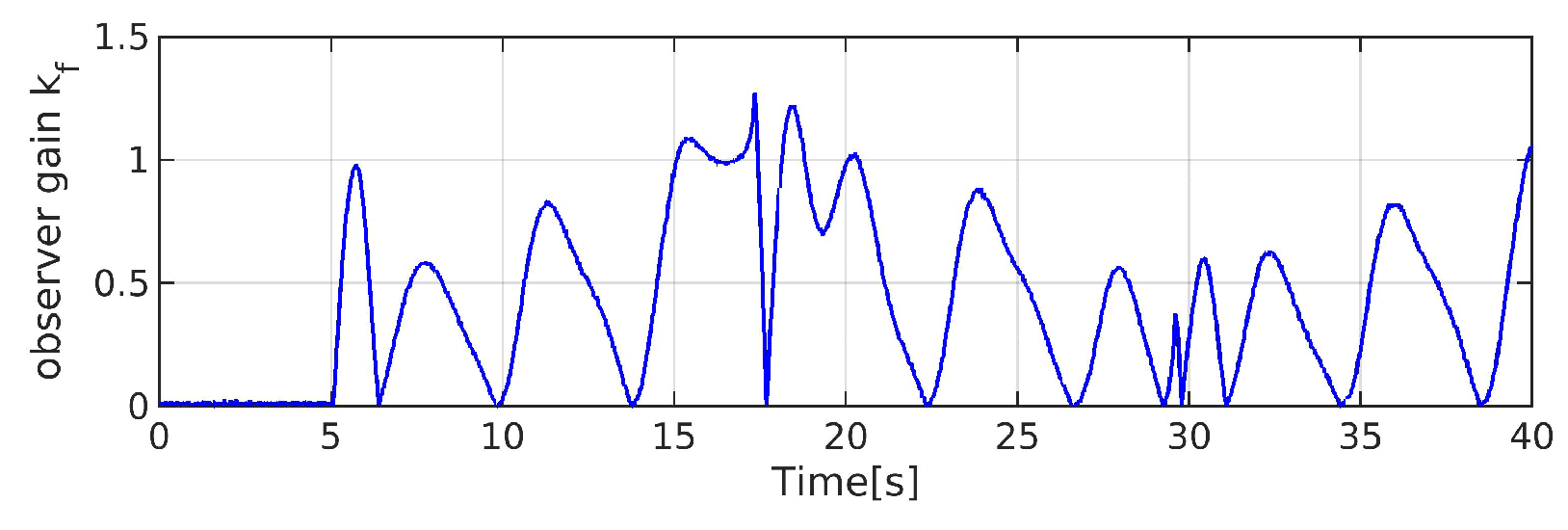
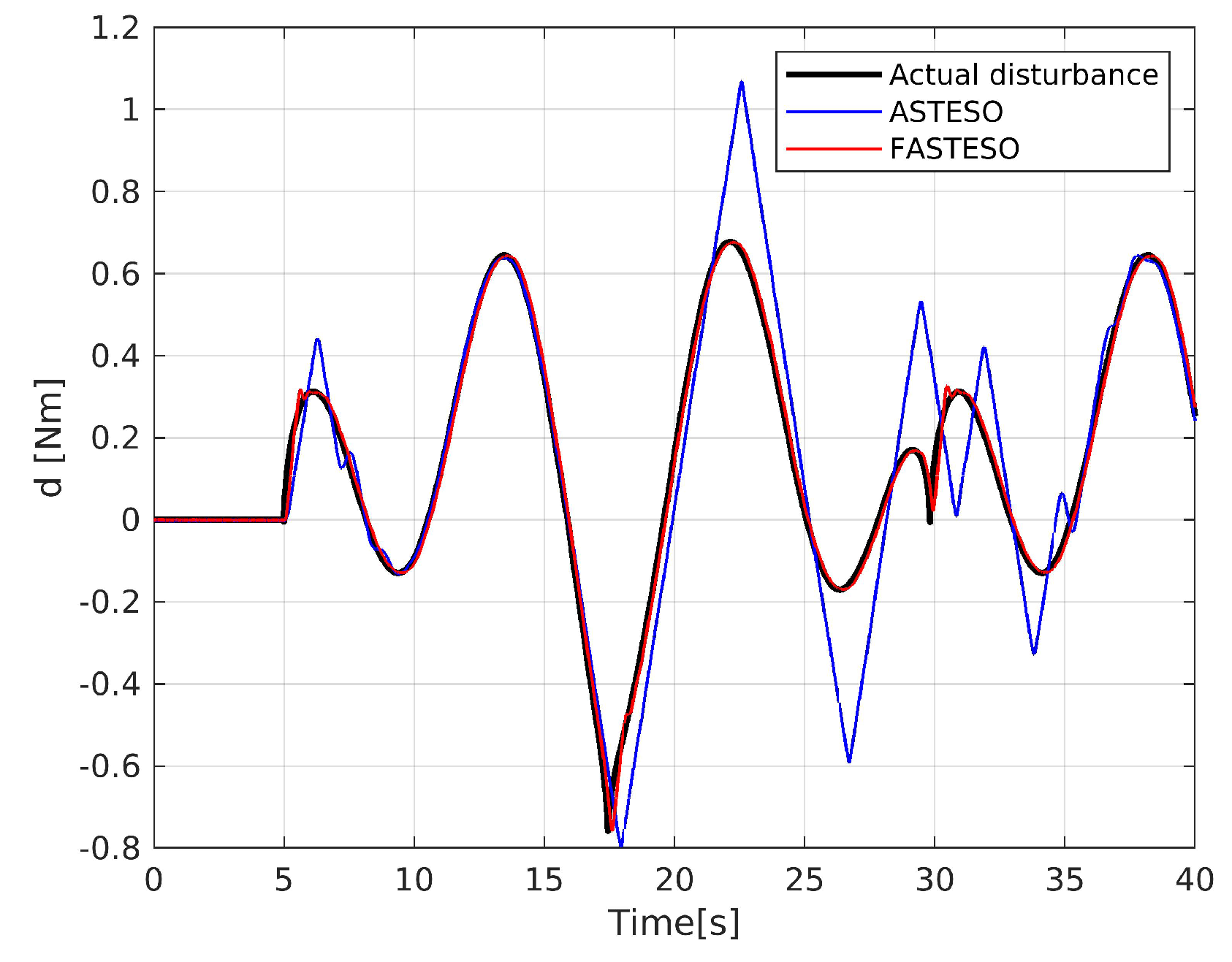
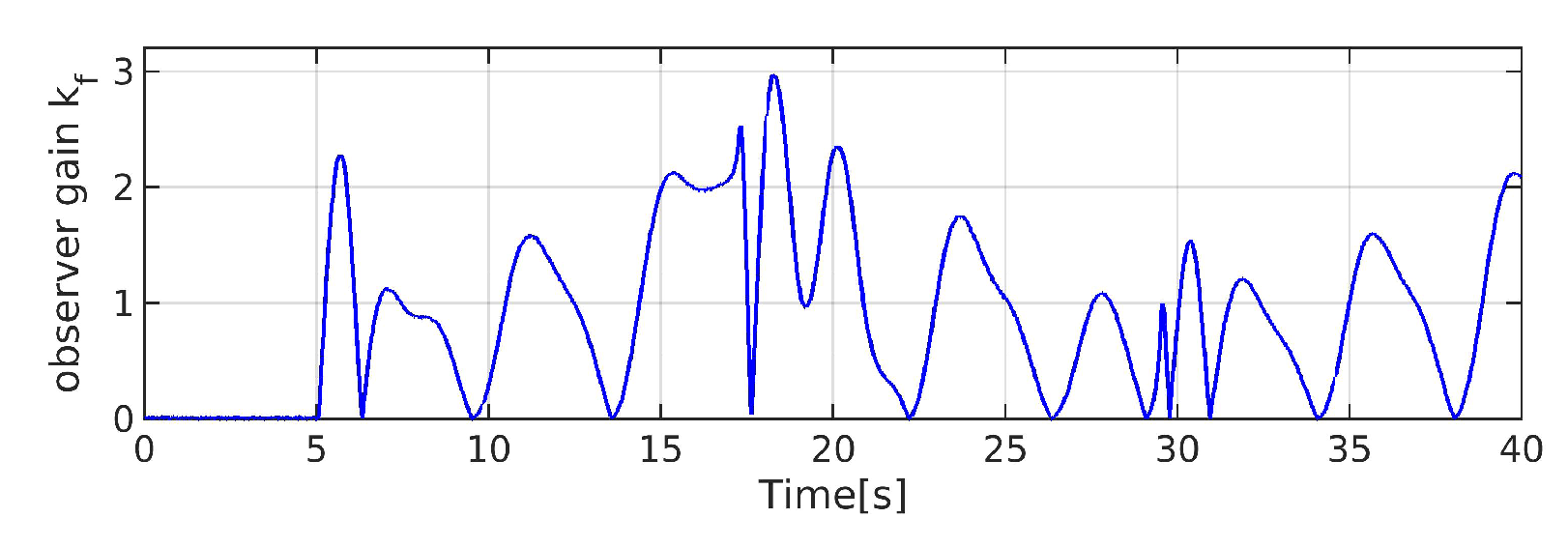
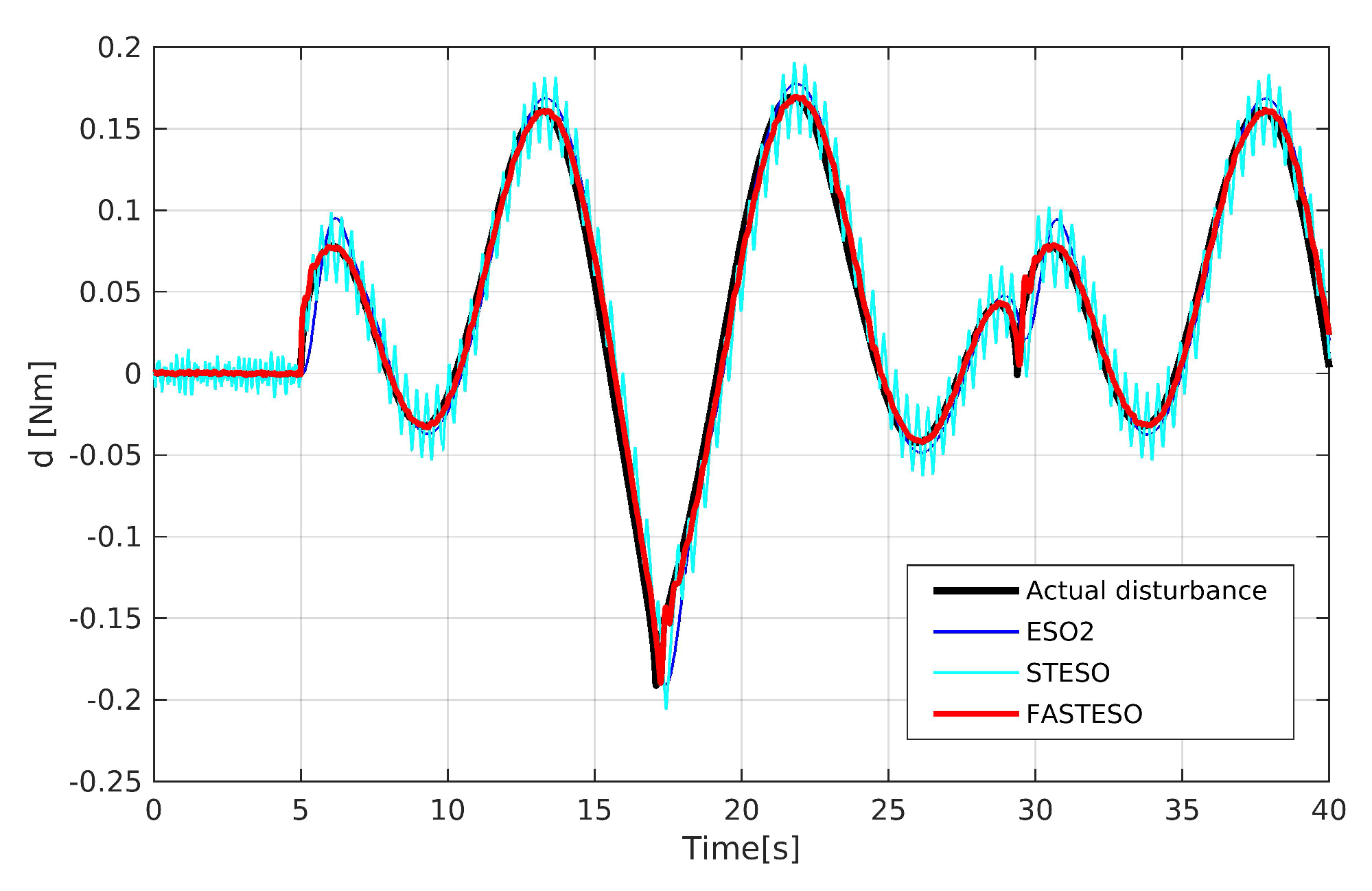
5.1. CASE 1 (Observers Performance Comparison)
5.1.1. Domestic Observers Comparison
5.1.2. Various Observers Comparison
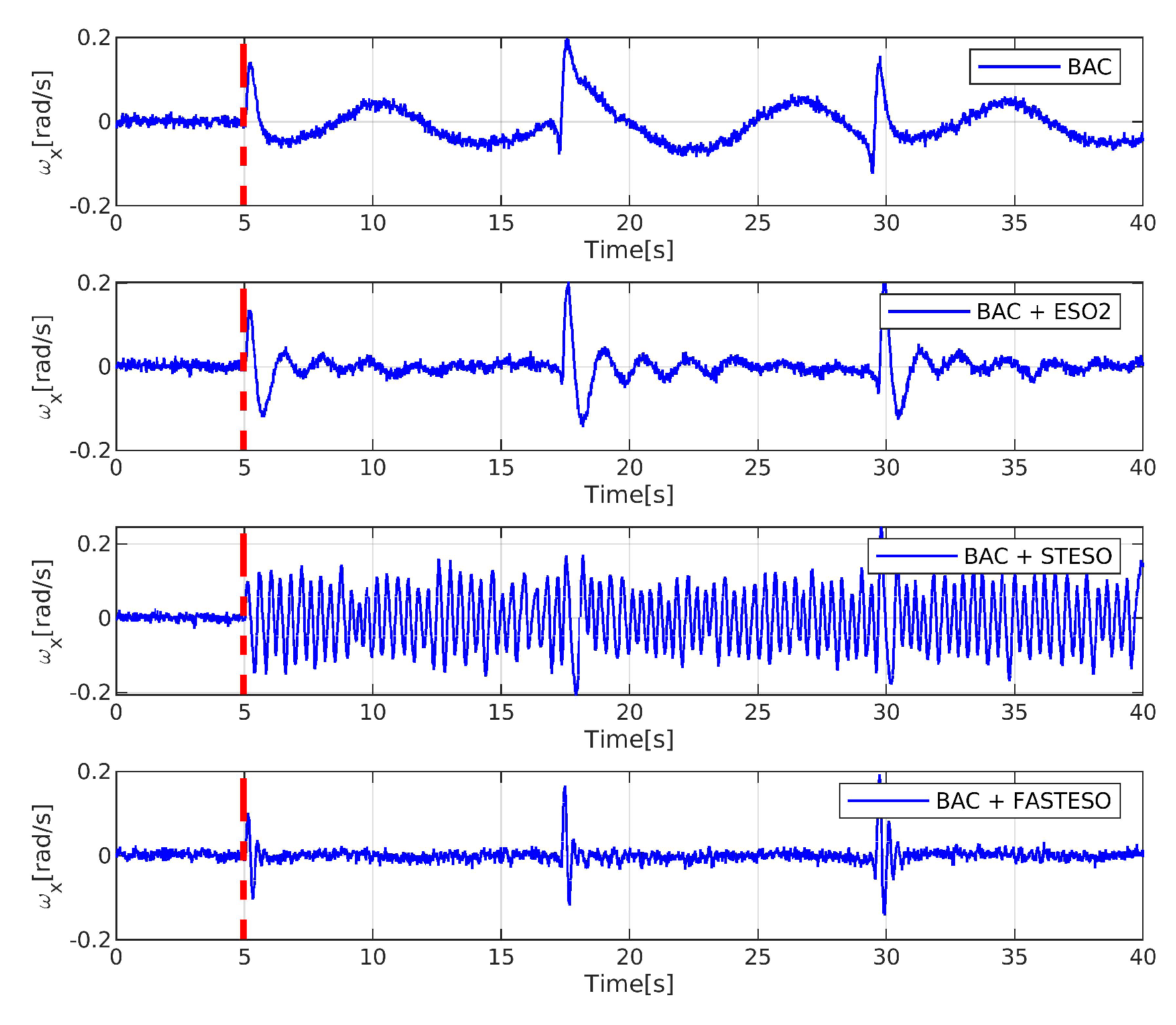
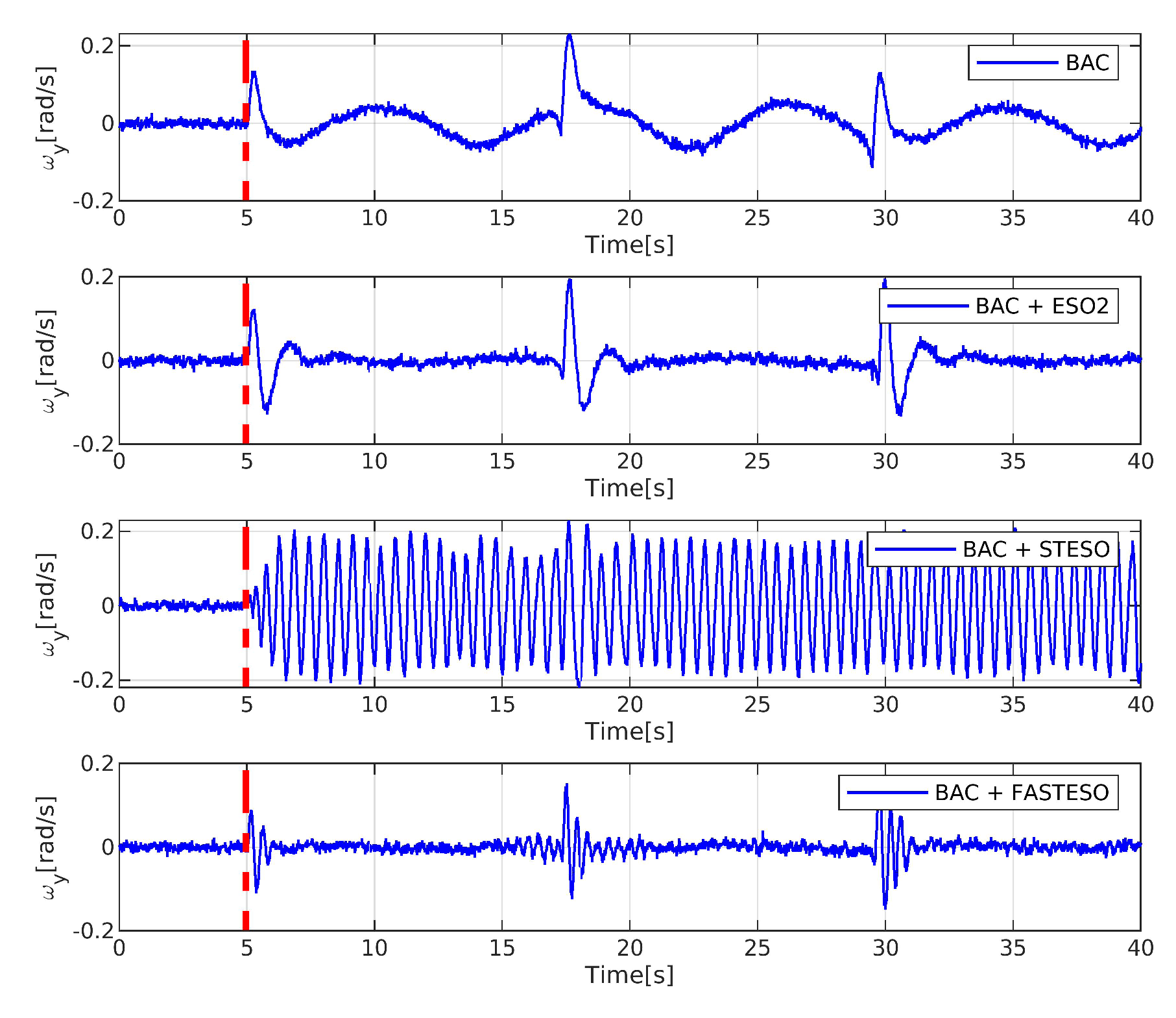
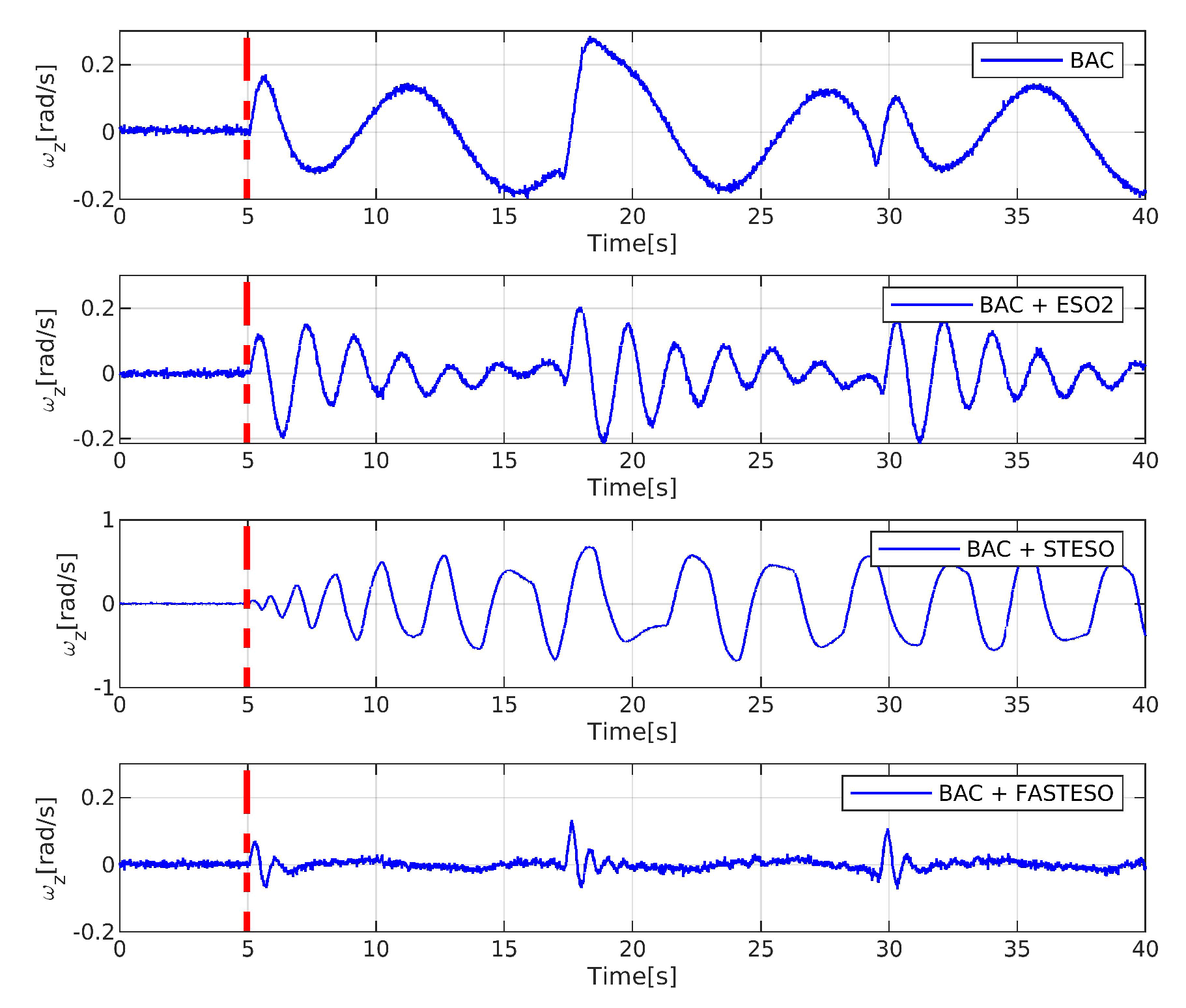
5.2. CASE 2 (Composite Comparison)
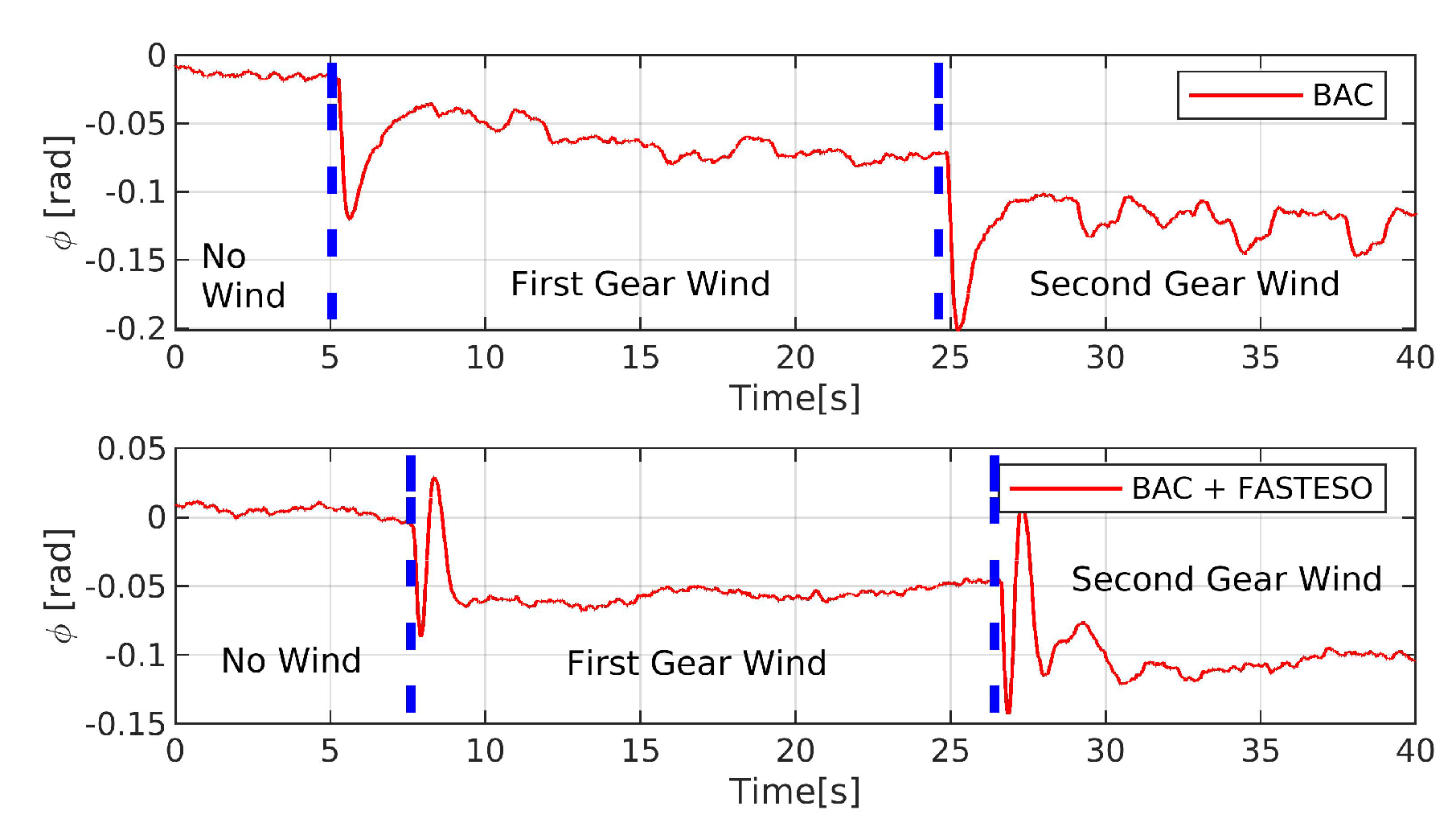
6. Experiment
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FASTESO | Fuzzy adaptive saturation super-twisting extended state observer |
References
- Premachandra, C.; Ueda, D.; Kato, K. Speed-Up Automatic Quadcopter Position Detection by Sensing Propeller Rotation. IEEE Sens. J. 2018, 19, 2758–2766. [Google Scholar] [CrossRef]
- Nakajima, K.; Premachandra, C.; Kato, K. 3D environment mapping and self-position estimation by a small flying robot mounted with a movable ultrasonic range sensor. J. Electr. Syst. Inf. Technol. 2017, 4, 289–298. [Google Scholar] [CrossRef]
- Premachandra, C.; Otsuka, M.; Gohara, R.; Ninomiya, T.; Kato, K. A study on development of a hybrid aerial/terrestrial robot system for avoiding ground obstacles by flight. IEEE/CAA J. Autom. Sin. 2018, 6, 327–336. [Google Scholar] [CrossRef]
- Ryll, M.; Muscio, G.; Pierri, F.; Cataldi, E.; Antonelli, G.; Caccavale, F.; Bicego, D.; Franchi, A. 6D interaction control with aerial robots: The flying end-effector paradigm. Int. J. Robot. Res. 2019, 38, 1045–1062. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Seo, H.; Shin, J.; Kim, H.J. Cooperative aerial manipulation using multirotors with multi-dof robotic arms. IEEE/ASME Trans. Mechatronics 2018, 23, 702–713. [Google Scholar] [CrossRef]
- Jiao, R.; Dong, M.; Chou, W.; Yu, H.; Yu, H. Autonomous Aerial Manipulation Using a Hexacopter Equipped with a Robotic Arm. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 1502–1507. [Google Scholar]
- Ruggiero, F.; Trujillo, M.A.; Cano, R.; Ascorbe, H.; Viguria, A.; Peréz, C.; Lippiello, V.; Ollero, A.; Siciliano, B. A multilayer control for multirotor UAVs equipped with a servo robot arm. In Proceedings of the 2015 IEEE international conference on robotics and automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4014–4020. [Google Scholar]
- Jiao, R.; Chou, W.; Ding, R.; Dong, M. Adaptive robust control of quadrotor with a 2-degree-of-freedom robotic arm. Adv. Mech. Eng. 2018, 10, 1687814018778639. [Google Scholar] [CrossRef]
- Alexis, K.; Papachristos, C.; Siegwart, R.; Tzes, A. Robust model predictive flight control of unmanned rotorcrafts. J. Intell. Robot. Syst. 2016, 81, 443–469. [Google Scholar] [CrossRef]
- Achtelik, M.; Bierling, T.; Wang, J.; Höcht, L.; Holzapfel, F. Adaptive control of a quadcopter in the presence of large/complete parameter uncertainties. In Proceedings of the Infotech@ Aerospace 2011, St. Louis, MO, USA, 29–31 March 2011; p. 1485. [Google Scholar]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods—An overview. IEEE Trans. Ind. Electron. 2015, 63, 1083–1095. [Google Scholar] [CrossRef] [Green Version]
- Cristofaro, A.; Johansen, T.A. Fault tolerant control allocation using unknown input observers. Automatica 2014, 50, 1891–1897. [Google Scholar] [CrossRef]
- Pu, Z.; Yuan, R.; Yi, J.; Tan, X. A class of adaptive extended state observers for nonlinear disturbed systems. IEEE Trans. Ind. Electron. 2015, 62, 5858–5869. [Google Scholar] [CrossRef]
- Kim, S.; Choi, S.; Kim, H.; Shin, J.; Shim, H.; Kim, H.J. Robust control of an equipment-added multirotor using disturbance observer. IEEE Trans. Control Syst. Technol. 2017, 26, 1524–1531. [Google Scholar] [CrossRef]
- Wang, C.; Song, B.; Huang, P.; Tang, C. Trajectory tracking control for quadrotor robot subject to payload variation and wind gust disturbance. J. Intell. Robot. Syst. 2016, 83, 315–333. [Google Scholar] [CrossRef]
- Chen, M.; Xiong, S.; Wu, Q. Tracking flight control of quadrotor based on disturbance observer. IEEE Trans. Syst. Man, Cybern. Syst. 2019. [Google Scholar] [CrossRef]
- Mokhtari, M.R.; Cherki, B.; Braham, A.C. Disturbance observer based hierarchical control of coaxial-rotor UAV. ISA Trans. 2017, 67, 466–475. [Google Scholar] [CrossRef]
- Wang, L.; Su, J. Robust disturbance rejection control for attitude tracking of an aircraft. IEEE Trans. Control Syst. Technol. 2015, 23, 2361–2368. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Liu, J.; Vazquez, S.; Wu, L.; Marquez, A.; Gao, H.; Franquelo, L.G. Extended state observer-based sliding-mode control for three-phase power converters. IEEE Trans. Ind. Electron. 2016, 64, 22–31. [Google Scholar] [CrossRef] [Green Version]
- Madoński, R.; Herman, P. Survey on methods of increasing the efficiency of extended state disturbance observers. ISA Trans. 2015, 56, 18–27. [Google Scholar] [CrossRef]
- Muñoz, F.; Bonilla, M.; Espinoza, E.S.; González, I.; Salazar, S.; Lozano, R. Robust trajectory tracking for unmanned aircraft systems using high order sliding mode controllers-observers. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 346–352. [Google Scholar]
- Cai, W.; She, J.; Wu, M.; Ohyama, Y. Disturbance suppression for quadrotor UAV using sliding-mode-observer-based equivalent-input-disturbance approach. ISA Trans. 2019, 92, 286–297. [Google Scholar] [CrossRef]
- Shi, D.; Wu, Z.; Chou, W. Super-twisting extended state observer and sliding mode controller for quadrotor UAV attitude system in presence of wind gust and actuator faults. Electronics 2018, 7, 128. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Son, J.; Lee, J. A high-speed sliding-mode observer for the sensorless speed control of a PMSM. IEEE Trans. Ind. Electron. 2010, 58, 4069–4077. [Google Scholar]
- Rong, Y.; Jiao, R.; Kang, S.; Chou, W. Sigmoid Super-Twisting Extended State Observer and Sliding Mode Controller for Quadrotor UAV Attitude System With Unknown Disturbance. In Proceedings of the 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; pp. 2647–2653. [Google Scholar]
- Lippiello, V.; Ruggiero, F. Cartesian impedance control of a UAV with a robotic arm. IFAC Proc. Vol. 2012, 45, 704–709. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Xu, H.; Xu, L.; Heilman, L.E. Sensorless direct field-oriented control of three-phase induction motors based on “Sliding Mode" for washing-machine drive applications. IEEE Trans. Ind. Appl. 2006, 42, 694–701. [Google Scholar] [CrossRef]
- Kang, K.L.; Kim, J.M.; Hwang, K.B.; Kim, K.H. Sensorless control of PMSM in high speed range with iterative sliding mode observer. In Proceedings of the Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition, 2004 (APEC’04), Anaheim, CA, USA, 22–26 February 2004; Volume 2, pp. 1111–1116. [Google Scholar]
- Jiao, R.; Wang, Z.; Chu, R.; Dong, M.; Rong, Y.; Chou, W. An Intuitional End-to-End Human-UAV Interaction System for Field Exploration. Front. Neurorobot. 2019, 13, 117. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.C. Fuzzy logic in control systems: Fuzzy logic controller. I. IEEE Trans. Syst. Man, Cybern. 1990, 20, 404–418. [Google Scholar] [CrossRef] [Green Version]
- Palm, R. Robust control by fuzzy sliding mode. Automatica 1994, 30, 1429–1437. [Google Scholar] [CrossRef]
- Meier, L.; Honegger, D.; Pollefeys, M. PX4: A node-based multithreaded open source robotics framework for deeply embedded platforms. In Proceedings of the 2015 IEEE international conference on robotics and automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 6235–6240. [Google Scholar]
- Quan, Q. Flight Performance Evaluation of UAVs. 2018. Available online: http://flyeval.com/ (accessed on 15 April 2020).
- Meier, L.; Tanskanen, P.; Heng, L.; Lee, G.H.; Fraundorfer, F.; Pollefeys, M. PIXHAWK: A micro aerial vehicle design for autonomous flight using onboard computer vision. Auton. Robot. 2012, 33, 21–39. [Google Scholar] [CrossRef]

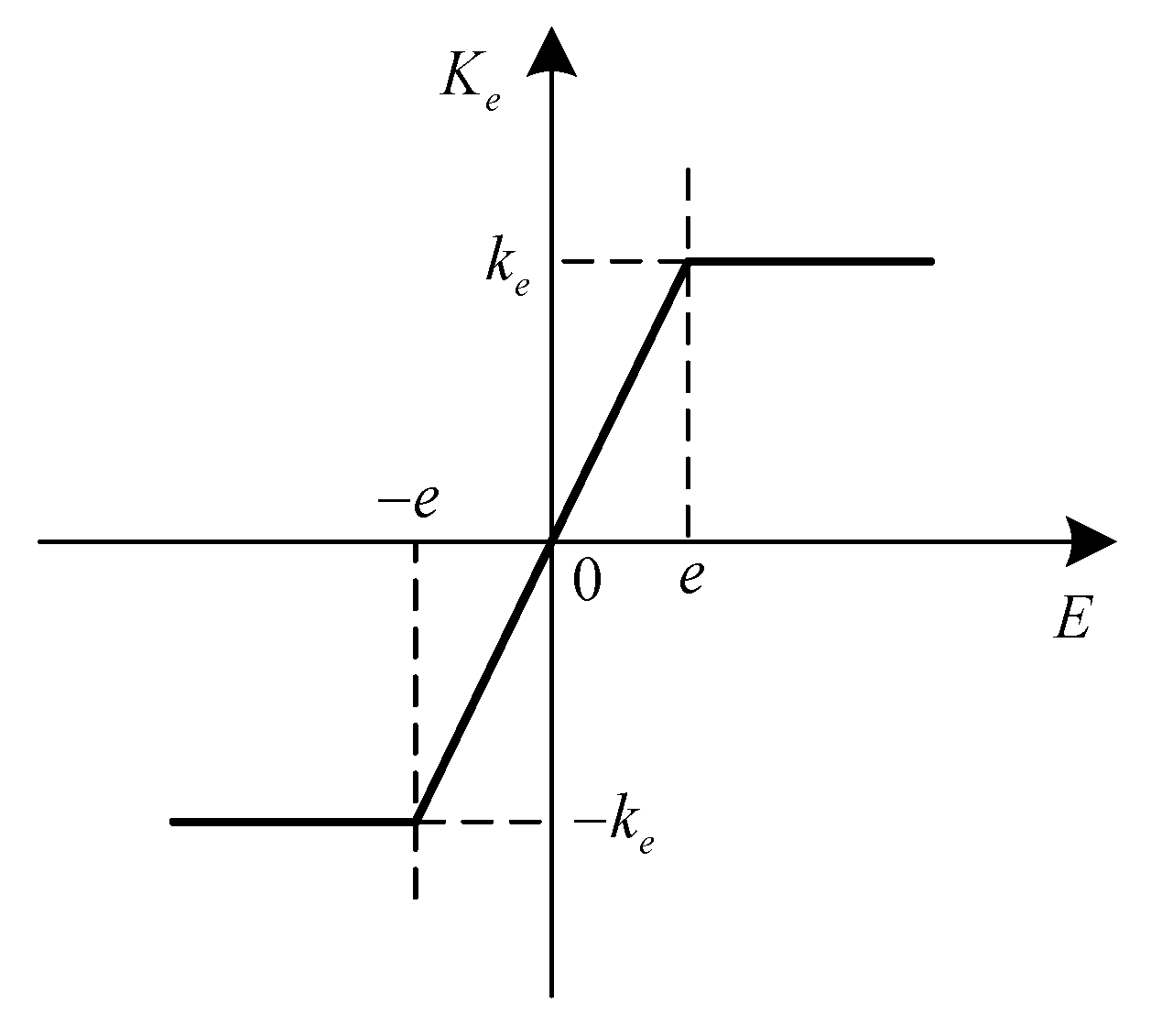





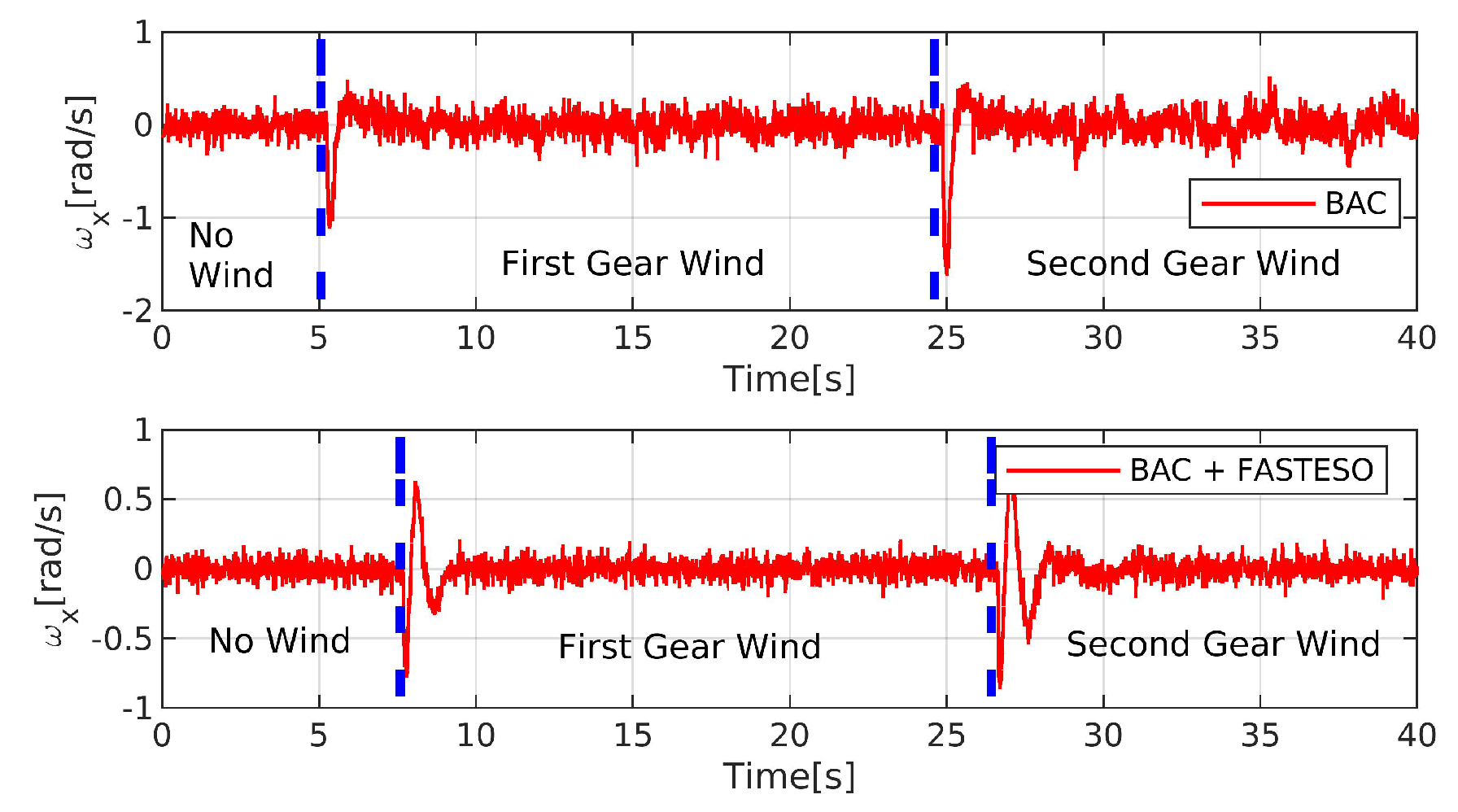

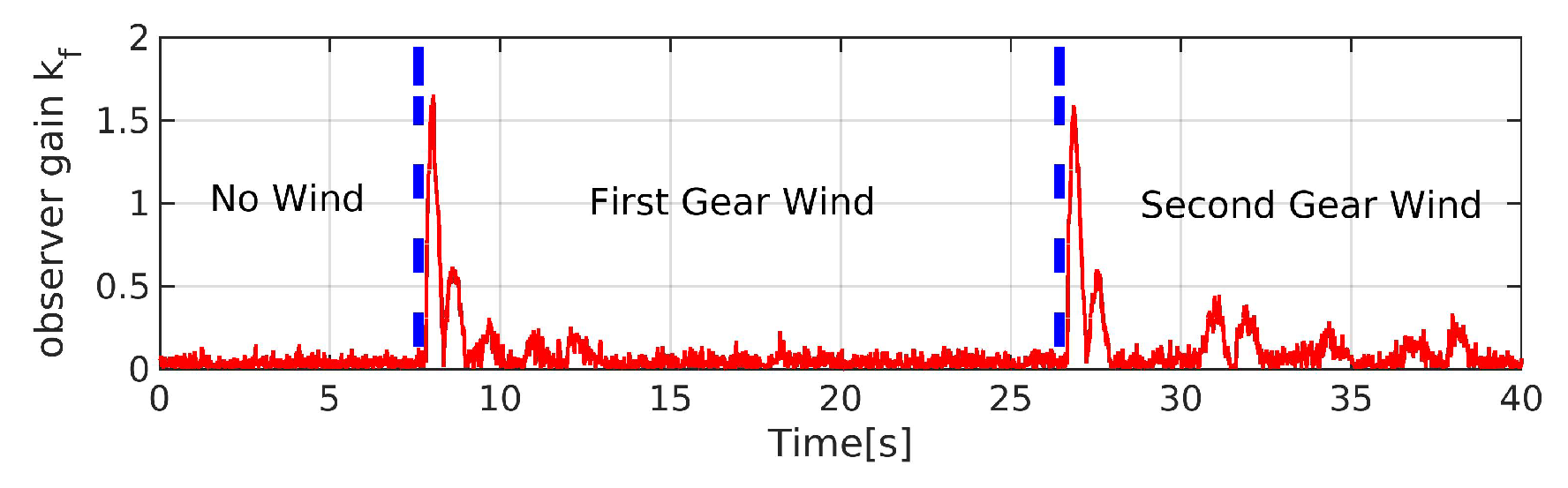
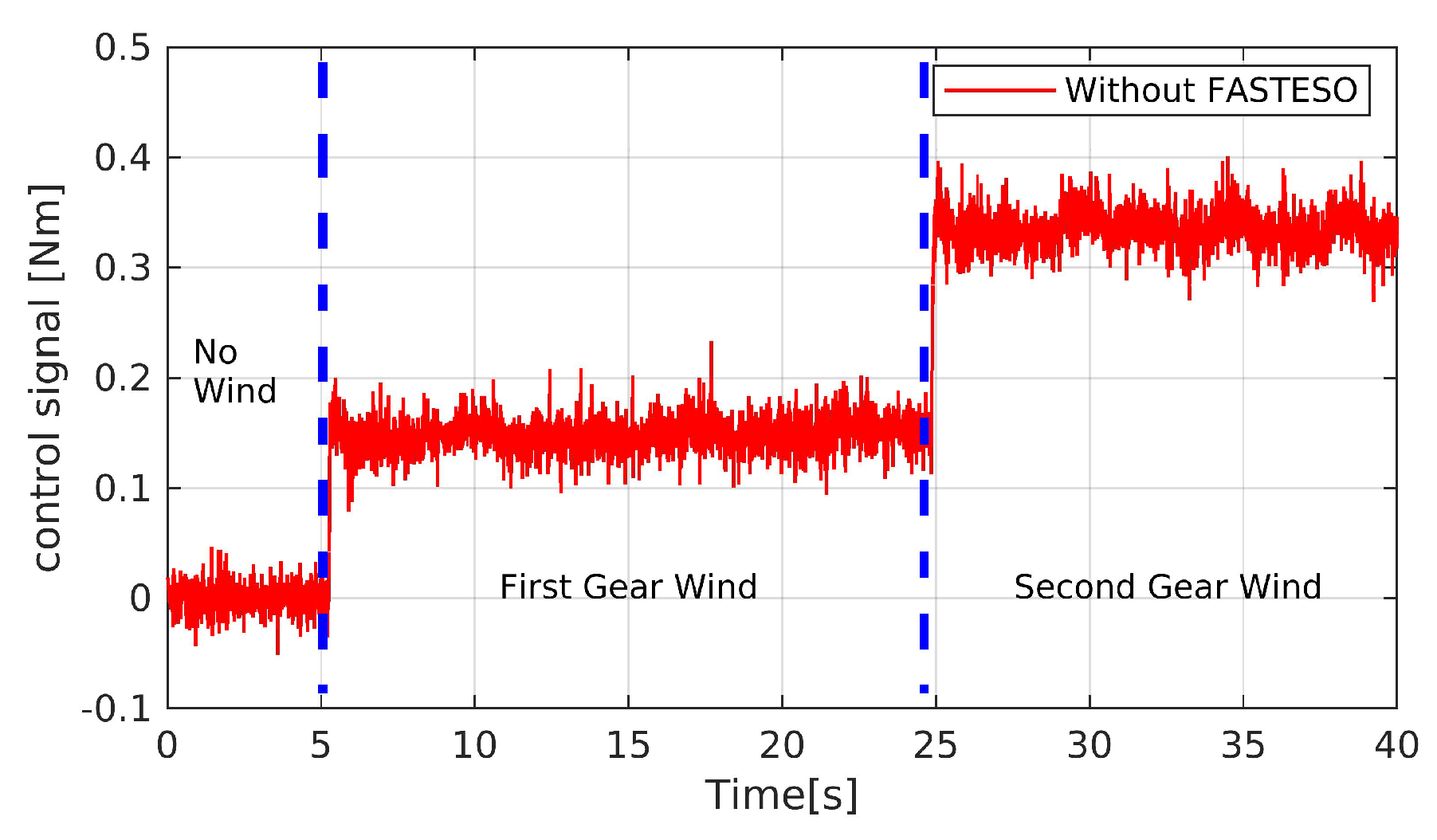

| Coefficients | Description | Value |
|---|---|---|
| Mass of the quadrotor base | 1.8 kg | |
| Pitch inertia | ||
| Roll inertia | ||
| Yaw inertia | ||
| l | Quadrotor base size | 0.205 m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, R.; Chou, W.; Rong, Y.; Dong, M. Anti-Disturbance Control for Quadrotor UAV Manipulator Attitude System Based on Fuzzy Adaptive Saturation Super-Twisting Sliding Mode Observer. Appl. Sci. 2020, 10, 3719. https://doi.org/10.3390/app10113719
Jiao R, Chou W, Rong Y, Dong M. Anti-Disturbance Control for Quadrotor UAV Manipulator Attitude System Based on Fuzzy Adaptive Saturation Super-Twisting Sliding Mode Observer. Applied Sciences. 2020; 10(11):3719. https://doi.org/10.3390/app10113719
Chicago/Turabian StyleJiao, Ran, Wusheng Chou, Yongfeng Rong, and Mingjie Dong. 2020. "Anti-Disturbance Control for Quadrotor UAV Manipulator Attitude System Based on Fuzzy Adaptive Saturation Super-Twisting Sliding Mode Observer" Applied Sciences 10, no. 11: 3719. https://doi.org/10.3390/app10113719
APA StyleJiao, R., Chou, W., Rong, Y., & Dong, M. (2020). Anti-Disturbance Control for Quadrotor UAV Manipulator Attitude System Based on Fuzzy Adaptive Saturation Super-Twisting Sliding Mode Observer. Applied Sciences, 10(11), 3719. https://doi.org/10.3390/app10113719






