Influence of Tunnel Boring Machine (TBM) Advance on Adjacent Tunnel during Ultra-Rapid Underground Pass (URUP) Tunneling: A Case Study and Numerical Investigation
Abstract
:1. Introduction
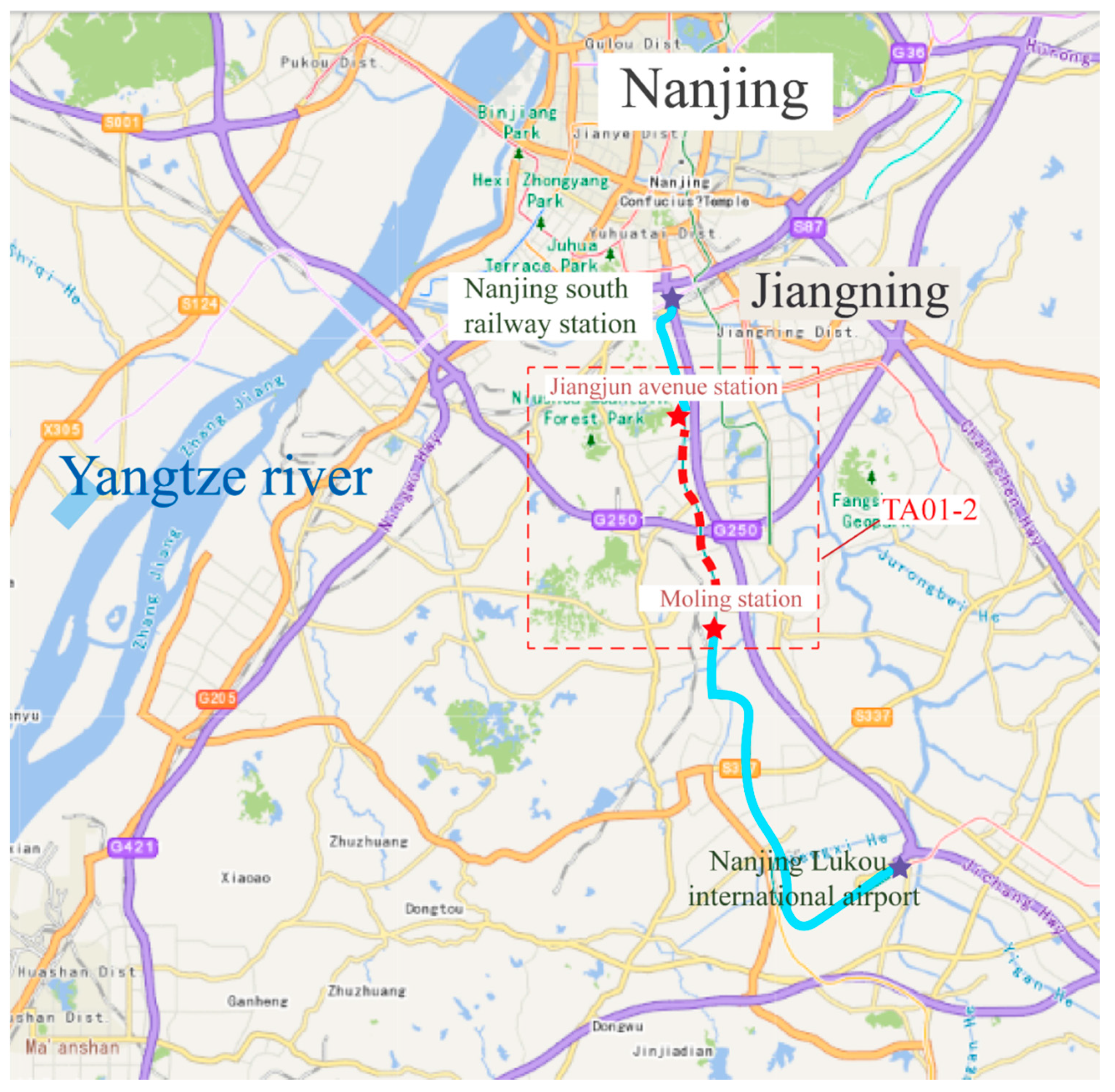
2. Revisit the URUP Demonstration Project at Nanjing
2.1. Project Overview
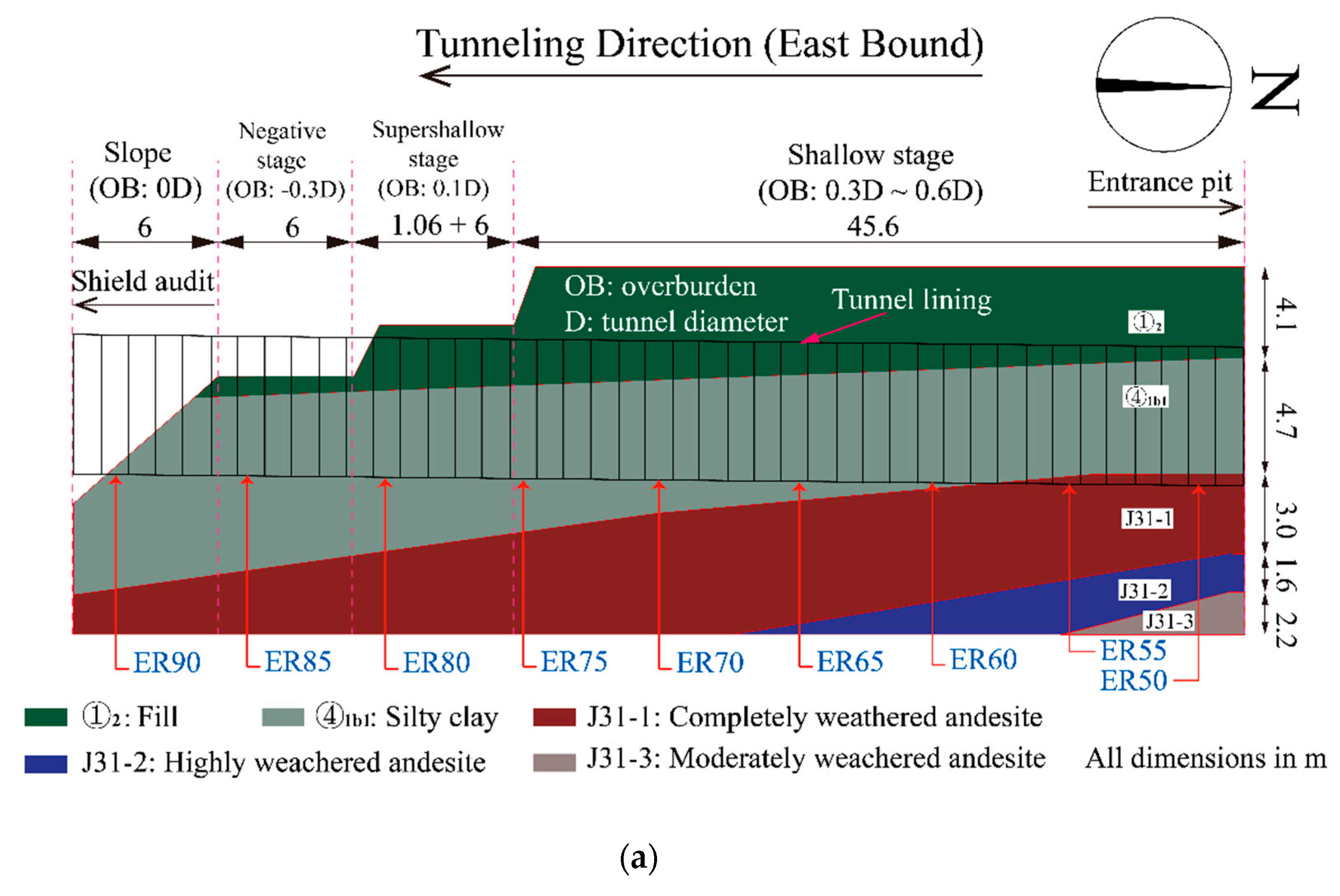
2.2. Tunneling Procedure
2.3. On-Site Monitoring of Segment Internal Force
3. FEA Model and Validation
3.1. Overview of Finite Element Model
3.2. Material Properties and Modelling Procedure
3.3. Modelling Procedure
- (1).
- Firstly, the initial geostatic stress of the soil was generated with the initial displacement of ground less than 10−6 m.
- (2).
- Secondly, the soil elements of the first seven slices (the width of each slice was 1.2 m) at EB were removed to simulate the space occupied by the TBM after it was launched. The non-uniformly distributed displacement boundary (as demonstrated by the yellow arrows in Figure 6a) was applied at the soil nodes around the excavated soils to simulated the volume loss caused by the TBM. This assumed tunnel convergence is characterized by a parameter , which is the tunnel contraction around the excavation region. For detailed description of this non-uniformly distributed displacement boundary, please refer to the previous research of the URUP project [34]. The contraction parameter can be expressed as:where is the contraction at the tunnel crown. and are the radius of the cutter head and shield body, respectively. is the angle of the polar coordinate system with the origin located at the central of the excavation region.
- (3).
- Thereafter, one slice soil element in the model was deactivated with the corresponding displacement boundary activated and deactivated, as illustrated in Figure 6b; the grouting pressure was applied at adjacent soils with two rings behind the TBM tail, and corresponding lining and grout layer were activated simultaneously (as illustrated in Figure 6c).
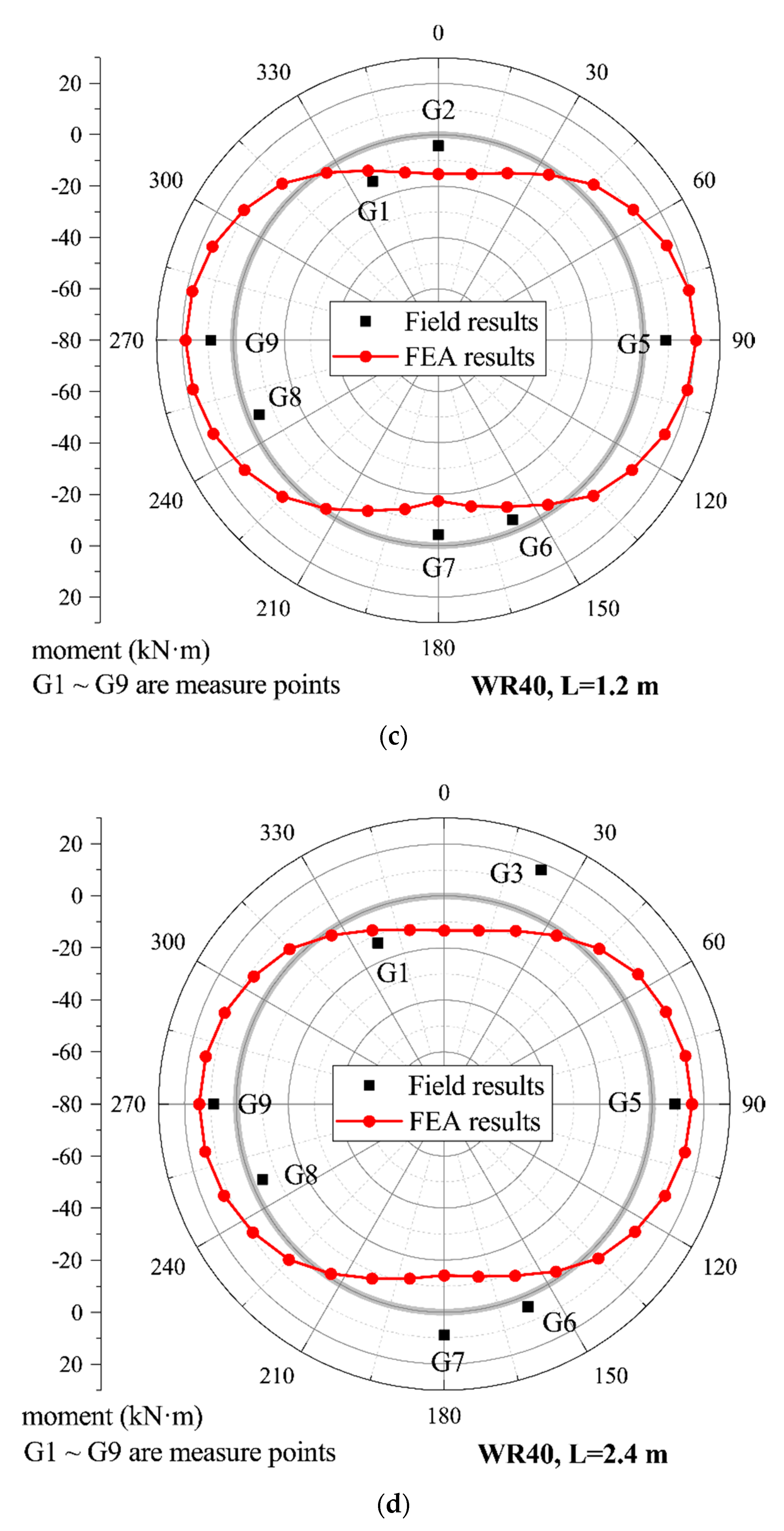
3.4. Model Validation
4. Influence of TBM-Driven Process on Adjacent URUP Tunnel
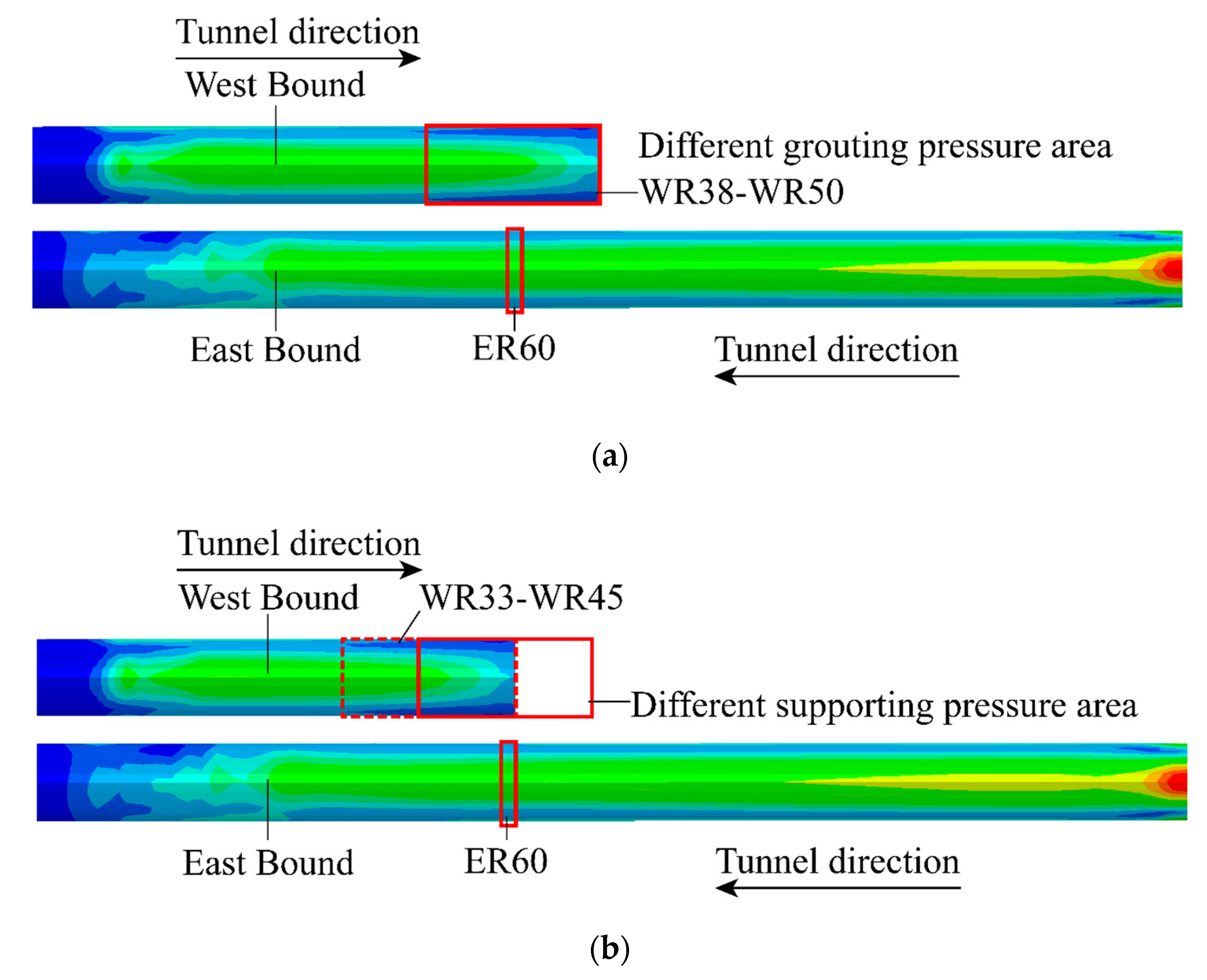
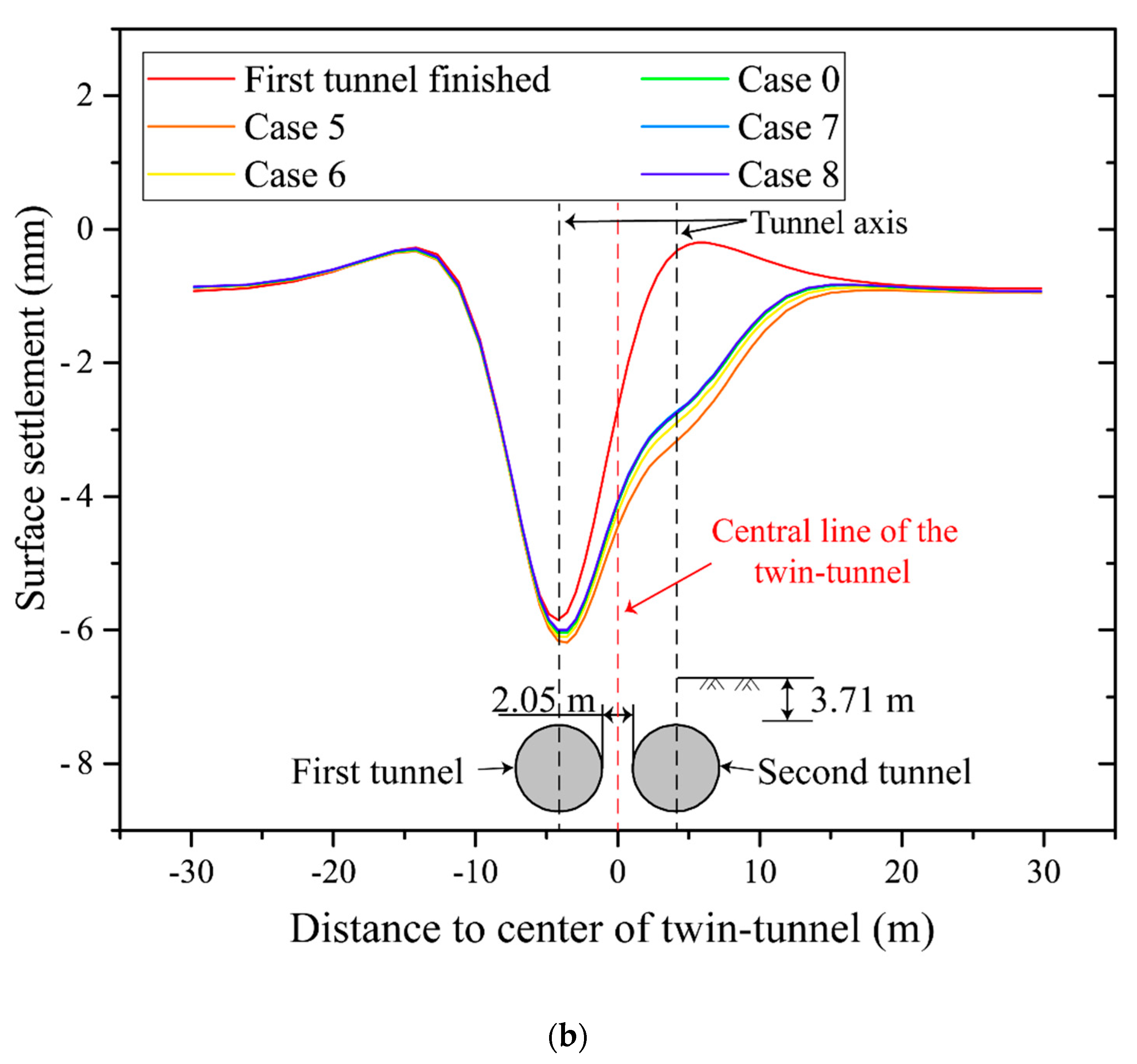
4.1. Ground Surface Settlement
4.2. Tunnel Displacement and Convergence
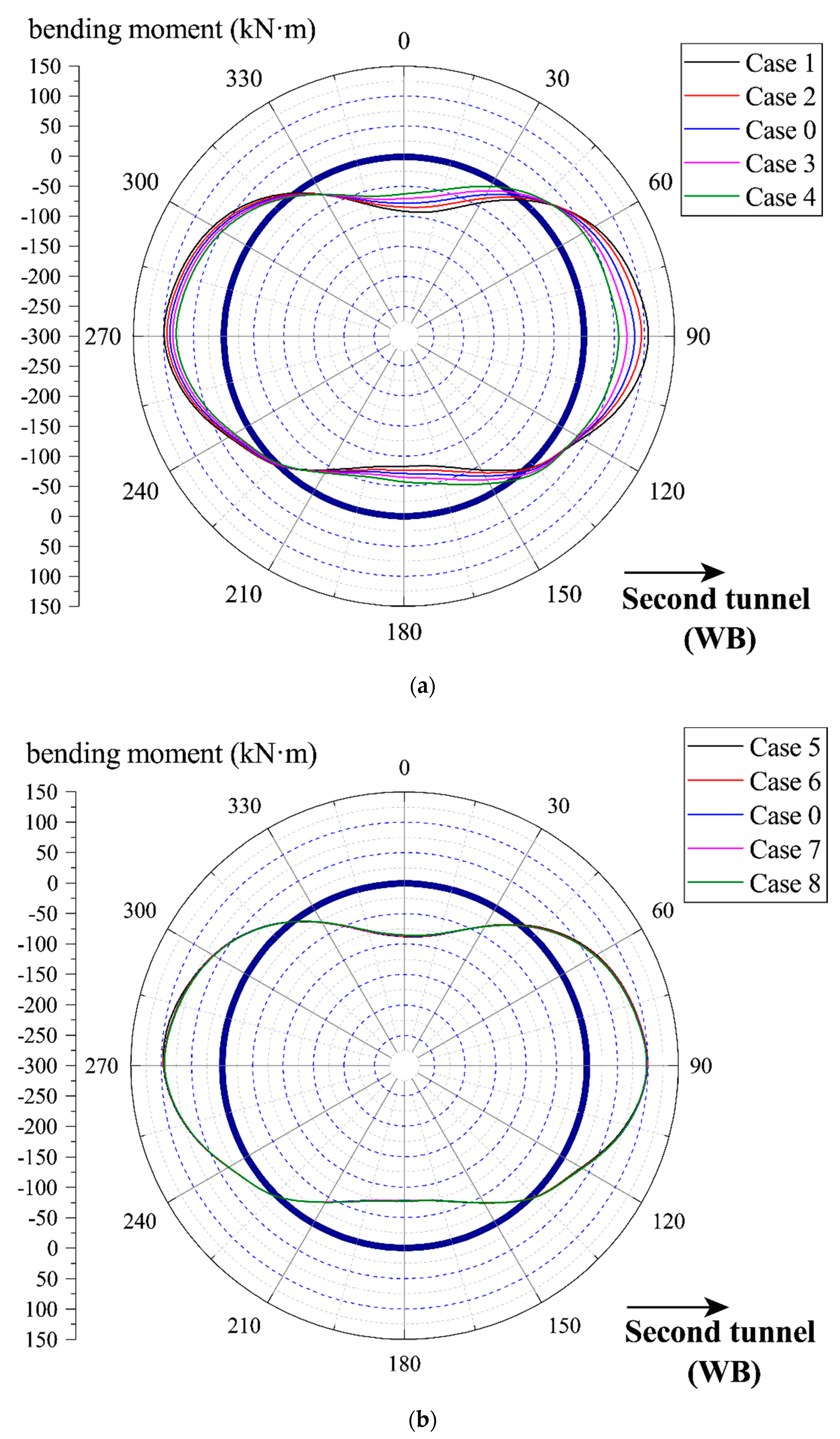
4.3. Bending Moment of Lining Segment
5. Conclusions
- (1)
- A typical horizontal ovalization of the first tunnel was monitored, with the maximum and minimum bending moment located at the sidewall and top of the tunnel, respectively.
- (2)
- To take the TBM geometry into consideration, a non-uniform contraction mode with the maximum contraction mm was employed in the FEA model. The model was validated by comparison with the monitored bending moment. The FEA results show that a double-bottom settlement type occurred during the tunneling process of the second tunnel. In addition, the surface settlement of the first tunnel induced by the second tunnel advance is more sensitive to the grouting pressure than face supporting pressure.
- (3)
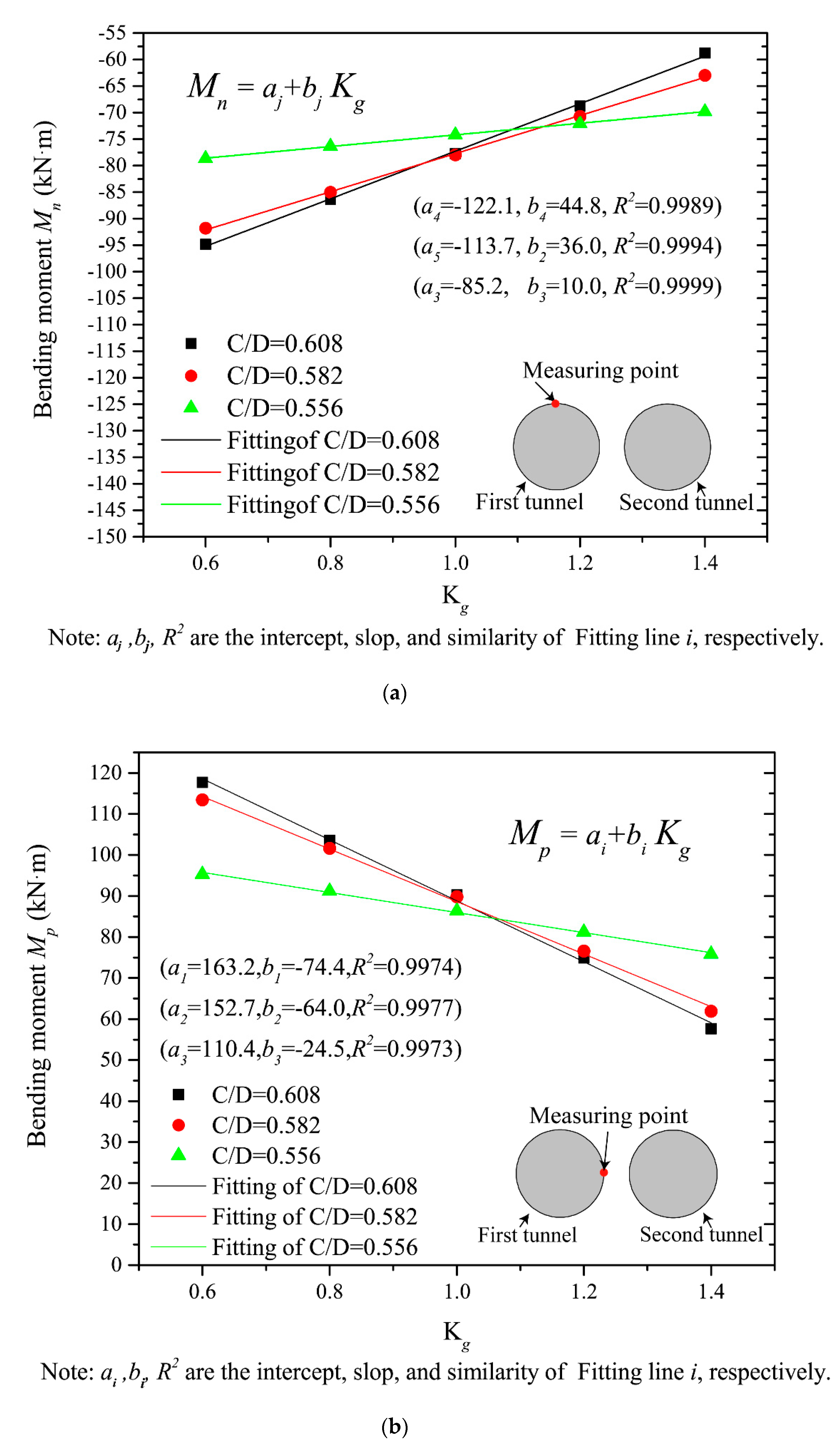
- The grouting pressure during the second tunnel construction has significant influence on the convergence of the adjacent first tunnel lining, ascribing to the squeezing effect caused by the grouting pressure. However, the face supporting pressure does not have notably influence on the first tunnel convergence.
- (4)
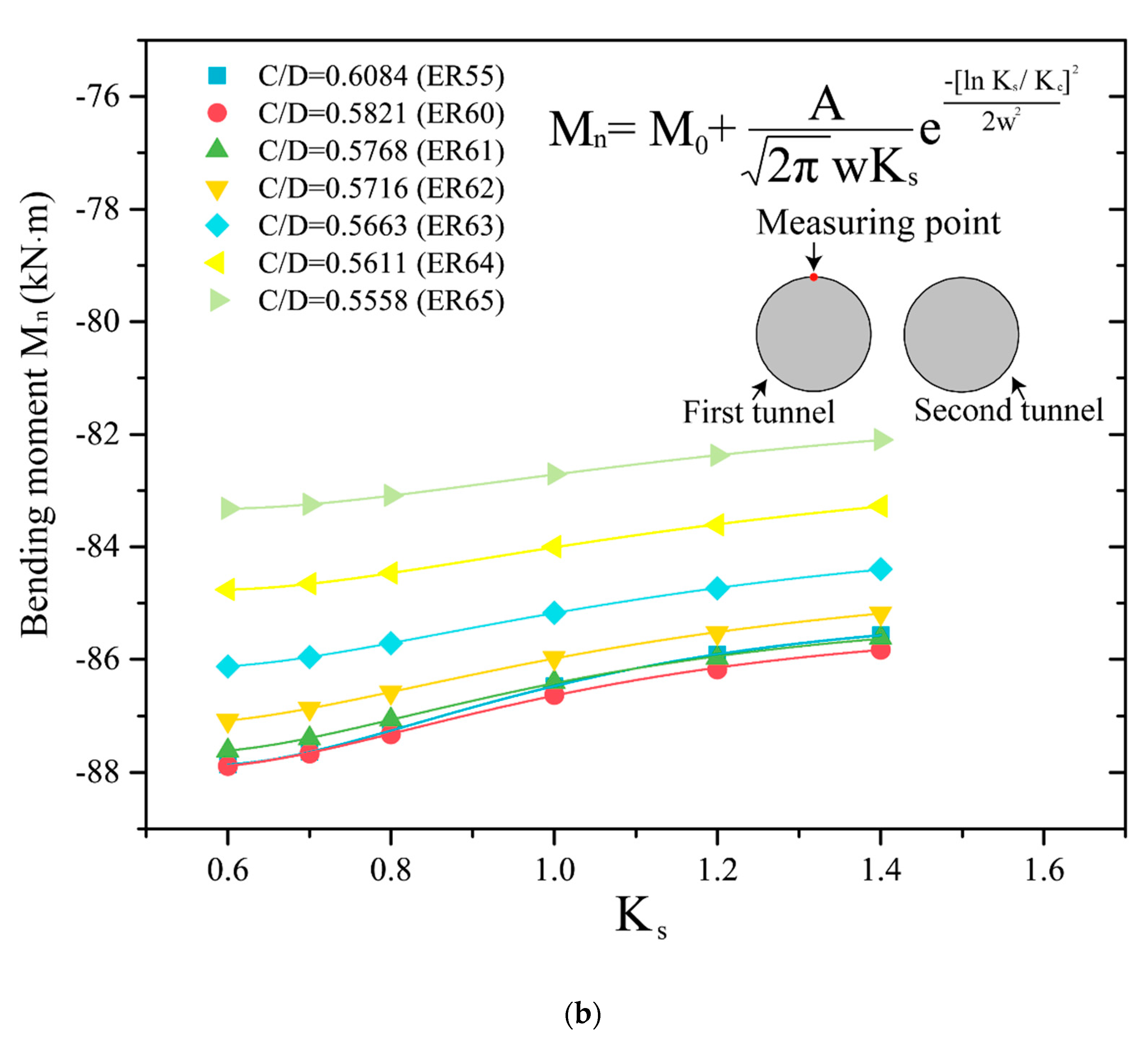
- The relationship between the bending moment and the grouting pressure coefficient can be fitted in a linear function. A is the most suitable choice since the variation of the bending moment in the first tunnel is stable with the TBM advance of the second tunnel. The relationship between the face supporting pressure and the bending moment under different tunnel depths can be fitted by a lognormal function. A critical C/D ratio, under which the horizontal and vertical soil arching effect disappear, can be deduced to be within the range of 0.55–0.60.
Author Contributions
Funding
Conflicts of Interest
References
- Liu, C.; Zhang, Z.X.; Regueiro, R.A. Pile and pile group response to tunnelling using a large diameter slurry shield—Case study in Shanghai. Comput. Geotech. 2014, 59, 21–43. [Google Scholar] [CrossRef]
- Berthoz, N.; Branque, D.; Wong, H.; Subrin, D. TBM soft ground interaction: Experimental study on a 1 g reduced-scale EPBS model. Tunn. Undergr. Space Technol. 2018, 72, 189–209. [Google Scholar] [CrossRef]
- Chen, R.-P.; Li, J.; Kong, L.-G.; Tang, L.-J. Experimental study on face instability of shield tunnel in sand. Tunn. Undergr. Space Technol. 2013, 33, 12–21. [Google Scholar] [CrossRef]
- Berthoz, N.; Branque, D.; Subrin, D.; Wong, H.; Humbert, E. Face failure in homogeneous and stratified soft ground: Theoretical and experimental approaches on 1 g EPBS reduced scale model. Tunn. Undergr. Space Technol. 2012, 30, 25–37. [Google Scholar] [CrossRef]
- Leung, C.; Meguid, M.A. An experimental study of the effect of local contact loss on the earth pressure distribution on existing tunnel linings. Tunn. Undergr. Space Technol. 2011, 26, 139–145. [Google Scholar] [CrossRef]
- Zhang, M.; Li, S.; Li, P. Numerical analysis of ground displacement and segmental stress and influence of yaw excavation loadings for a curved shield tunnel. Comput. Geotech. 2020, 118, 103325. [Google Scholar] [CrossRef]
- Zhang, C.; Cai, Y.; Zhu, W. Numerical Study and Field Monitoring of the Ground Deformation Induced by Large Slurry Shield Tunnelling in Sandy Cobble Ground. Adv. Civ. Eng. 2019, 2019, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Avgerinos, V.; Potts, D.M.; Standing, J.R. Numerical investigation of the effects of tunnelling on existing tunnels. Geotechnique 2017, 67, 808–822. [Google Scholar] [CrossRef]
- Lavasan, A.A.; Zhao, C.; Barciaga, T.; Schaufler, A.; Steeb, H.; Schanz, T. Numerical investigation of tunneling in saturated soil: The role of construction and operation periods. Acta Geotech. 2017, 13, 671–691. [Google Scholar] [CrossRef]
- Do, N.-A.; Dias, D.; Oreste, P. 3D numerical investigation of mechanized twin tunnels in soft ground—Influence of lagging distance between two tunnel faces. Eng. Struct. 2016, 109, 117–125. [Google Scholar] [CrossRef]
- Hong, Y.; Soomro, M.A.; Ng, C.W.W.; Wang, L.Z.; Yan, J.J.; Li, B. Tunnelling under pile groups and rafts: Numerical parametric study on tension effects. Comput. Geotech. 2015, 68, 54–65. [Google Scholar] [CrossRef]
- Do, N.-A.; Dias, D.; Oreste, P.; Djeran-Maigre, I. Three-dimensional numerical simulation of a mechanized twin tunnels in soft ground. Tunn. Undergr. Space Technol. 2014, 42, 40–51. [Google Scholar] [CrossRef]
- Liu, H.Y.; Small, J.C.; Carter, J.P. Full 3D modelling for effects of tunnelling on existing support systems in the Sydney region. Tunn. Undergr. Space Technol. 2008, 23, 399–420. [Google Scholar] [CrossRef]
- Chehade, F.H.; Shahrour, I. Numerical analysis of the interaction between twin-tunnels: Influence of the relative position and construction procedure. Tunn. Undergr. Space Technol. 2008, 23, 210–214. [Google Scholar] [CrossRef]
- Li, S.; Li, P.; Zhang, M.; Liu, Y. Influence of Approaching Excavation on Adjacent Segments for Twin Tunnels. Appl. Sci. 2019, 10, 98. [Google Scholar] [CrossRef] [Green Version]
- Qiao, X.; Liu, W. Study on the Horizontal Axis Deviation of a Small Radius TBM Tunnel Based on Winkler Foundation Model. Appl. Sci. 2020, 10, 784. [Google Scholar] [CrossRef] [Green Version]
- Marshall, A.M.; Haji, T. An analytical study of tunnel–pile interaction. Tunn. Undergr. Space Technol. 2015, 45, 43–51. [Google Scholar] [CrossRef] [Green Version]
- Camós, C.; Molins, C. 3D analytical prediction of building damage due to ground subsidence produced by tunneling. Tunn. Undergr. Space Technol. 2015, 50, 424–437. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Jiang, J.; Xie, K.-H.; Huang, W.-M. Analytical solutions for nonlinear consolidation of soft soil around a shield tunnel with idealized sealing linings. Comput. Geotech. 2014, 61, 144–152. [Google Scholar] [CrossRef]
- Pinto, F.; Whittle, A. Ground Movements due to Shallow Tunnels in Soft Ground. I: Analytical Solutions. J. Geotech. Geoenviron. 2014, 140, 04013040. [Google Scholar] [CrossRef] [Green Version]
- Fahimifar, A.; Zareifard, M.R. A theoretical solution for analysis of tunnels below groundwater considering the hydraulic-mechanical coupling. Tunn. Undergr. Space Technol. 2009, 24, 634–646. [Google Scholar] [CrossRef]
- Osman, A.S.; Bolton, M.D.; Mair, R.J. Predicting 2D ground movements around tunnels in undrained clay. Geotechnique 2006, 56, 597–604. [Google Scholar] [CrossRef] [Green Version]
- Pham, A.T.; Sugimoto, M. The Effects of Tangential Ground-Lining Interaction on Segmental Lining Behavior Using the Beam-Spring Model. Appl. Sci. 2020, 10, 1084. [Google Scholar] [CrossRef] [Green Version]
- Mooney, M.A.; Grasmick, J.; Kenneally, B.; Fang, Y. The role of slurry TBM parameters on ground deformation: Field results and computational modelling. Tunn. Undergr. Space Technol. 2016, 57, 257–264. [Google Scholar] [CrossRef]
- Fargnoli, V.; Boldini, D.; Amorosi, A. Twin tunnel excavation in coarse grained soils: Observations and numerical back-predictions under free field conditions and in presence of a surface structure. Tunn. Undergr. Space Technol. 2015, 49, 454–469. [Google Scholar] [CrossRef]
- Li, Q. Long-Term Settlement Mechanisms of Shield Tunnels in Shanghai Soft Clay. Ph.D. Thesis, Hong Kong University of Science and Technology, Hong Kong, China, 2013. [Google Scholar]
- Standing, J.R.; Selemetas, D. Greenfield ground response to EPBM tunnelling in London Clay. Geotechnique 2013, 63, 989–1007. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, Y.-S.; Shen, S.-L.; Sun, W.-J. Field performance of underground structures during shield tunnel construction. Tunn. Undergr. Space Technol. 2012, 28, 272–277. [Google Scholar] [CrossRef]
- Wongsaroj, J.; Soga, K.; Mair, R.J. Modelling of long-term ground response to tunnelling under St James’s Park, London. Geotechnique 2007, 57, 75–90. [Google Scholar] [CrossRef]
- Bezuijen, A.; Talmon, A.; Kaalberg, F.; Plugge, R. Field measurements of grout pressures during tunnelling of the Sophia rail tunnel. Soils Found. 2004, 44, 39–48. [Google Scholar] [CrossRef] [Green Version]
- Ge, X. Response of a Shield-Driven Tunnel to Deep Excavations in Soft Clay. Ph.D. Thesis, Hong Kong University of Science and Technology, Hong Kong, China, 2002. [Google Scholar]
- Peck, B. Deep Excavations and Tunneling in Soft Ground. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, Mexico, 1969; Volume 1, pp. 225–290. [Google Scholar]
- Liu, C.; Zhang, Z.X.; Kwok, C.Y.; Jiang, H.Q.; Teng, L. Ground responses to tunneling in soft soil using the URUP method. J. Geotech. Geoenviron. 2017, 143, 04017023. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Liu, C.; Huang, X.; Kwok, C.Y.; Teng, L. Three-dimensional finite-element analysis on ground responses during twin-tunnel construction using the URUP method. Tunn. Undergr. Space Technol. 2016, 58, 133–146. [Google Scholar] [CrossRef] [Green Version]
- Hamdy, H.A.; Enieb, M.; Abdelmoamen Khalil, A.; Ahmed, A.S.H. Twin tunnel configuration for Greater Cairo metro line No. 4. Comput. Geotech. 2015, 68, 66–77. [Google Scholar]
- Gan, X.; Yu, J.; Gong, X.; Zhu, M. Characteristics and Countermeasures of Tunnel Heave due to Large-Diameter Shield Tunneling Underneath. J. Perform. Constr. Facil. 2020, 34, 04019081. [Google Scholar] [CrossRef]
- Zick, P.; Sugihara, H.; Takatoku, Y.; Sada, S. URUP (Ultra Rapid Underpass)—TBM excavation in soft ground from the surface elevation (zero overburden) without shaft and/or large scaled open cut pit. In Proceedings of the Transportation Research Board 92nd Annual Meeting, Washington, DC, USA, 13–17 January 2013; pp. 13–1080. [Google Scholar]
- Fujiki, H.; Nakamura, T.; Izawa, M. URUP (Ultra rapid Under Pass) method—The first Shield Tunneling method for launching and arrival at the ground level. In Proceedings of the World Tunneling Congress, Budapest, Hungary, 23–28 May 2009; pp. 112–116. [Google Scholar]
- Hayashi, M.; Miki, K.; Yokomizo, F.; Yoshida, M.; Izawa, M. The demonstration work of URUP method. In Proceedings of the 61st Annual Conference of Japan Society of Civil Engineers, Shiga Prefecture, Japan, 20 September 2006; pp. 485–486. [Google Scholar]
- Chen, J.S.; Mo, H.H. Numerical study on crack problems in segments of shield tunnel using finite element method. Tunn. Undergr. Space Technol. 2009, 24, 91–102. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, B.; Xie, X.; Liu, C. Characteristics and causes of cracking and damage of shield tunnel segmented lining in construction stage—A case study in Shanghai soft soil. Eur. J. Environ. Civil. Eng. 2017, 1–15. [Google Scholar] [CrossRef]
- Chen, W.; Jeng, D.; Chen, W.; Chen, G.; Zhao, H. Seismic-induced dynamic responses in a poro-elastic seabed: Solutions of different formulations. Soil Dyn. Earthq. Eng. 2020, 131, 106021. [Google Scholar] [CrossRef]
- Abaqus/CAE User’s Guide; Abaqus Software: Providence, RI, USA, 2010.
- Liu, W.; Xu, M.; Chen, Z.F. Parameters calibration and verification of concrete damage plasticity model of ABAQUS. Ind. Constr. 2014, 44, 167–171, 213. (In Chinese) [Google Scholar]
- Birtel, V.; Mark, P. Parameterised Finite Element Modelling of RC Beam Shear Failure. In Proceedings of the 19th Annual International ABAQUS Users’ Conference, Boston, MA, USA, 23–25 May 2006; pp. 95–108. [Google Scholar]
- Kasper, T.; Meschke, G. A 3D finite element simulation model for TBM tunnelling in soft ground. Int. J. Numer. Anal. Met. 2004, 28, 1441–1460. [Google Scholar] [CrossRef]
- Lin, X.T.; Chen, R.P.; Wu, H.N.; Cheng, H.Z. Three-dimensional stress-transfer mechanism and soil arching evolution induced by shield tunneling in sandy ground. Tunn. Undergr. Space Technol. 2019, 93, 13. [Google Scholar] [CrossRef]














| β | |||||||
|---|---|---|---|---|---|---|---|
| 1.39 | 15 | 0.30 | 31.9 | 42.8 | 0.828 | 1.031 | |
| 1.37 | 25 | 0.27 | 23.9 | 55.2 | 0.871 | 0.99 | |
| 1.57 | 25 | 0.25 | 32.9 | 110.8 | 0.822 | 0.7 | |
| 2.23 | 60 | 0.20 | 0.5 | ||||
| 2.54 | 2.1 × 10−3 | 0.21 | 0.3 | ||||
| Lining | 2.5 | 3.61 × 10−4 | 0.20 | ||||
| Grout | 1.9 | 5 | 0.40 |
| Grouting Pressure at Tunnel Crown | Grouting Pressure Gradient (kN/m) | Ground Contraction | (mm) | |
|---|---|---|---|---|
| 0.4 | Earth pressure | 7 | Non-uniform | 6 |
| Case | ||
|---|---|---|
| 0 | 1 | 1 |
| 1 | 0.6 | 1 |
| 2 | 0.8 | 1 |
| 3 | 1.2 | 1 |
| 4 | 1.4 | 1 |
| 5 | 1 | 0.6 |
| 6 | 1 | 0.8 |
| 7 | 1 | 1.2 |
| 8 | 1 | 1.4 |
| Fitting Curves | M0 | Kc | w | A | R2 |
|---|---|---|---|---|---|
| 1 | 104.8 | 0.825 | 0.306 | 1.154 | 0.9961 |
| 2 | 104.3 | 0.830 | 0.337 | 1.203 | 0.9983 |
| 3 | 104.1 | 0.824 | 0.325 | 1.041 | 0.9942 |
| 4 | 103.5 | 0.855 | 0.346 | 1.091 | 0.9881 |
| 5 | 102.4 | 0.939 | 0.370 | 1.410 | 0.9985 |
| 6 | 101.7 | 0.911 | 0.314 | 0.964 | 0.9950 |
| 7 | 101.7 | 0.884 | 0.400 | 1.195 | 0.9999 |
| 8 | 99.9 | 0.826 | 1.093 | 3.112 | 0.9993 |
| 9 | −85.2 | 0.711 | 0.455 | −1.977 | 0.9999 |
| 10 | −85.4 | 0.712 | 0.497 | −1.983 | 0.9996 |
| 11 | −85.2 | 0.716 | 0.510 | −1.993 | 0.9995 |
| 12 | −84.5 | 0.748 | 0.577 | −2.379 | 0.9998 |
| 13 | −83.7 | 0.788 | 0.597 | −2.442 | 0.9994 |
| 14 | −82.5 | 0.835 | 0.603 | −2.379 | 0.9999 |
| 15 | −81.4 | 0.851 | 0.610 | −2.069 | 0.9999 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Peng, Z.; Pan, L.; Liu, H.; Yang, Y.; Chen, W.; Jiang, H. Influence of Tunnel Boring Machine (TBM) Advance on Adjacent Tunnel during Ultra-Rapid Underground Pass (URUP) Tunneling: A Case Study and Numerical Investigation. Appl. Sci. 2020, 10, 3746. https://doi.org/10.3390/app10113746
Liu C, Peng Z, Pan L, Liu H, Yang Y, Chen W, Jiang H. Influence of Tunnel Boring Machine (TBM) Advance on Adjacent Tunnel during Ultra-Rapid Underground Pass (URUP) Tunneling: A Case Study and Numerical Investigation. Applied Sciences. 2020; 10(11):3746. https://doi.org/10.3390/app10113746
Chicago/Turabian StyleLiu, Chao, Zhuohua Peng, Liufeng Pan, Hai Liu, Yubing Yang, Weiyun Chen, and Huaqin Jiang. 2020. "Influence of Tunnel Boring Machine (TBM) Advance on Adjacent Tunnel during Ultra-Rapid Underground Pass (URUP) Tunneling: A Case Study and Numerical Investigation" Applied Sciences 10, no. 11: 3746. https://doi.org/10.3390/app10113746
APA StyleLiu, C., Peng, Z., Pan, L., Liu, H., Yang, Y., Chen, W., & Jiang, H. (2020). Influence of Tunnel Boring Machine (TBM) Advance on Adjacent Tunnel during Ultra-Rapid Underground Pass (URUP) Tunneling: A Case Study and Numerical Investigation. Applied Sciences, 10(11), 3746. https://doi.org/10.3390/app10113746






