Data Augmentation Method by Applying Color Perturbation of Inverse PSNR and Geometric Transformations for Object Recognition Based on Deep Learning

Abstract

Deep learning is applied in various manufacturing domains. To train a deep learning network, we must collect a sufficient amount of training data. However, it is difficult to collect image datasets required to train the networks to perform object recognition, especially because target items that are to be classified are generally excluded from existing databases, and the manual collection of images poses certain limitations. Therefore, to overcome the data deficiency that is present in many domains including manufacturing, we propose a method of generating new training images via image pre-processing steps, background elimination, target extraction while maintaining the ratio of the object size in the original image, color perturbation considering the predefined similarity between the original and generated images, geometric transformations, and transfer learning. Specifically, to demonstrate color perturbation and geometric transformations, we compare and analyze the experiments of each color space and each geometric transformation. The experimental results show that the proposed method can effectively augment the original data, correctly classify similar items, and improve the image classification accuracy. In addition, it also demonstrates that the effective data augmentation method is crucial when the amount of training data is small.

1. Introduction

In smart manufacturing, enormous amounts of data are acquired from sensors. The complexity of data poses challenges when processing these data, such as a high computational time. Deep learning, which achieves remarkable performance for various applications, provides advanced analytical tools to overcome such issues in smart manufacturing [1]. This technique has been progressing because of many factors such as the developing graphics processing units and the increasing amounts of data that need to be processed. Therefore, studies investigating deep learning as data-driven artificial intelligence techniques are rapidly increasing. It is applied in various domains, such as optimization, control and troubleshooting, and manufacturing. Specifically, deep learning is used in applications such as visual inspection processes, fault diagnoses of induction motors and boiler tubes, crack detection, and monitoring of tool condition [2,3,4,5,6,7,8].

Deep learning stands out in the research domains that are related to visual systems. Since 2010, the ImageNet Large Scale Visual Recognition Challenge has been organized every year [9]. Several object recognition, object detection, and object classification algorithms are evaluated in this challenge. In 2012, a deep learning algorithm based on convolutional neural networks was developed for object recognition, which showed significant improvements in object recognition. AlexNet won the challenge in the same year, i.e., 2012, with a top five test error rate of 15.3% for 1000 different object categories [10]. VGGNet and GoogLeNet were proposed in 2014, whereas ResNet was proposed in 2015; as time progressed, these deep learning algorithms proved to be more efficient in performing object classification than humans [11,12,13].

In deep learning, features are extracted via self-learning. Training the network begins with preparing the training data. We must collect enormous amounts of data to train the deep learning network and apply it to object recognition, as the classification accuracy is related to the amount of training data. One method of collecting training data involves downloading images from the Internet using image-crawling tools or by manually saving each image individually. In addition, we can utilize the existing image databases such as ImageNet and Microsoft CoCo [14,15]. However, collecting numerous image data for image classification of the assembly of electrical components or picking and placing these components is challenging. As the images of such components for assembly or picking are generally uncommon, it is difficult to obtain numerous component images in existing databases or websites. Furthermore, it is significantly difficult to capture the parts manually to create a sufficient amount of training data. As another example, it is also challenging to collect the training images in visual inspection processes such as discriminating defective products and crack or defect detection. Because the defective rate is meager in manufacturing domains, sample images of defects are few. However, generally, to enhance the performance of deep learning, we must collect numerous training datasets. This is because the classification result is influenced by the number of training images.

To compensate for the data deficiency, a pre-trained model can be retrained using the available training data. This is because the pre-trained model already contains the information of the extracted features favorably in the weights of the feature extraction layers. However, this method is limited in terms of increasing the classification accuracy, as eventually, it needs to augment the training data to improve its classification performance.

Collecting extensive training datasets is another solution for overcoming the problem of data deficiency. Many researches demonstrated the relationship between the amount of the training dataset and classification accuracy. There are many data augmentation techniques to increase the number of training images. Geometric transformation is usually applied for image data augmentation. However, there are limitations to augmenting the training data via geometric transformation, such as the linearization and standardization of data.

The overall research objective is to recognize and classify ten components for picking, placing, and assembling work. However, this yields data deficiency when training the deep learning network to recognize and classify components because these components are uncommon, as previously mentioned. Therefore, we propose a method for effectively improving the object classification accuracy of the deep learning network in the case of a small dataset in various manufacturing domains. To accomplish the goal of object recognition, even if there are few images, we focus on a method generating the massive training data from image data augmentation methods. Our study makes three main contributions:

• the extraction of the target object from the background while maintaining the original image ratio;
• color perturbation based on the predefined similarity between the original and generated images because of the decision of the reasonable perturbation range;
• data augmentation by combining color perturbation and geometric transformation.

We eliminate the background, extract the target object, generate the image by tuning pixel values, and transform to implement this concept. Mainly, the background is eliminated by considering the characteristics of the CIE L*a*b* color space. Besides, an object in an image is extracted such that it is proportional to the ratio of the object in the original image. Next, we change the image by determining the reasonable range for color perturbation and tuning the pixel values based on color space, following which, we combine the tuned images with the geometric transformations. This is unlike the traditional method, which arbitrarily adds the pixel values to the RGB color space. Subsequently, we train the pre-trained network by using the generated images. This step is called transfer learning. To verify the proposed method, we compare and analyze the experiments with one another in terms of the color perturbation of three color spaces and two geometric transformations. We compare the classification result of the trained networks by using test images.

The rest of this paper is organized as follows. In Section 2, we introduce works related to data augmentation, color spaces, similarity calculation, and transfer learning. In Section 3, we discuss the performance of the proposed method that applies deep learning to perform object recognition on a small dataset. In Section 4, we present the experimental results of the proposed method. Finally, in Section 5, we provide the conclusions.

2. Related Works

To train a deep learning network for image classification effectively, we must collect an enormous amount of training data because the image classification accuracy is related to the amount of training data. Data deficiency may result in overfitting or inaccurate image classification results. Therefore, many studies were performed to generate images to counter data deficiency. In this section, we explain the traditional methods related to improving classification accuracy, such as data augmentation and transfer learning. Furthermore, to improve the efficiency of data augmentation, the characteristics of the color space and similarity calculation are also investigated.

2.1. Data Augmentation

Data augmentation, which is used to generate several images from original images by changing the original image, has been developed to improve the model performance via generalization, avoiding overfitting, and training the network to become a robust classifier [16,17].

Geometric transformation is one of the traditional data augmentation methods. It is simple and consumes lower computational time compared with other data generation methods such as generative adversarial networks. Some of the generally applied data augmentation methods are: arbitrary rotation, vertical transformation, horizontal transformation, cropping, scaling, perspective shifting, shearing, zooming, and color jittering [17].

In these data augmentation methods, several techniques are used to perform color jittering. By isolating a single color channel, a simple color-based augmentation can be performed. Another technique for color jittering is to add a random value to the color channel. In addition to this technique, the information of the color histogram or principal component analysis with respect to the color channel can be utilized for performing color jittering [18]. Because it is a simple data augmentation method, we expand this concept to compensate for the data deficiency.

Some data augmentation-based studies demonstrated that the classification results obtained by combining a method with other algorithms resulted in better performance compared with the case of applying only one algorithm. In [19], the classification result obtained upon combining two algorithms resulted in better performance compared with the combination of three algorithms. Therefore, we combined two geometric transformations with color jittering for augmenting the small training data.

2.2. Characteristics of Color Space

Color is an important factor in image processing techniques such as object recognition. The characteristics of color comprise brightness, hue, and saturation. The brightness of a color can be represented using the power as a function of wavelength. Different parts of a spectrum are referred to as long, medium, and short according to the wavelength of their peak response. Conversely, colors such as red, green, blue, yellow, and orange are closely related to the wavelength of light that ranges from 400 to 700 nm. The color is visible to the physical eye because of trichromatism, in which color information is derived from three types of cone cells present in the human eyes. Using each of the three cones, the luminance of an object $L\left(\lambda \right)$ elicits a particular response as follows:

$$\begin{array}{c}\hfill \rho ={\int }_{\lambda }L\left(\lambda \right)M_r\left(\lambda \right)d\lambda \\ \hfill \gamma ={\int }_{\lambda }L\left(\lambda \right)M_g\left(\lambda \right)d\lambda \\ \hfill \beta ={\int }_{\lambda }L\left(\lambda \right)M_b\left(\lambda \right)d\lambda \end{array}$$

(1)

In (1), $M_r\left(\lambda \right)$, $M_g\left(\lambda \right)$, and $M_b\left(\lambda \right)$ denote the respective spectral responses of the red, green, and blue cones. In addition, the results of the above-mentioned equations are $\rho$, $\gamma$, and $\beta$, known as tristimulus values. These tristimulus values describe the color that a human can see and represent [20].

2.2.1. RGB Color Space

The color space is divided as the space is being built. Among the color spaces, the RGB color space, which is comprised of red, green, and blue, is well known. Red, green, and blue are called primary colors. Primary colors are fundamental for vision. The RGB color space is a basic color space and depends on the intensity of the light [21,22].

From (1), if $\lambda$ and a monochromatic stimulus of wavelength ${\lambda }_s$ are equal, then $L\left(\lambda \right)$ is defined as $L_{\lambda }$. Using (1), the response of the cones to this stimulus is derived as follows:

$$\begin{array}{c}\hfill \rho =L_{\lambda }{M}_r\left({\lambda }_s\right)\\ \hfill \gamma =L_{\lambda }{M}_g\left({\lambda }_s\right)\\ \hfill \beta =L_{\lambda }{M}_b\left({\lambda }_s\right)\end{array}$$

(2)

In addition, three primary colors, namely, R, G, and B, are represented as follows:

$$\begin{array}{c}\hfill \rho =R{M}_r\left({\lambda }_r\right)+G{M}_r\left({\lambda }_g\right)+B{M}_r\left({\lambda }_b\right)\\ \hfill \gamma =R{M}_g\left({\lambda }_r\right)+G{M}_g\left({\lambda }_g\right)+B{M}_g\left({\lambda }_b\right)\\ \hfill \beta =R{M}_b\left({\lambda }_r\right)+G{M}_b\left({\lambda }_g\right)+B{M}_b\left({\lambda }_b\right)\end{array}$$

(3)

In (3), ${\lambda }_r$, ${\lambda }_g$, and ${\lambda }_b$ denote the wavelengths of R, G, and B, respectively. In addition, R, G, and B denote the intensities of R, G, and B, respectively. Using (2) and (3), the required tristimulus values are derived as follows:

$$\begin{array}{c}\hfill \left[\begin{array}{c}R\\ G\\ B\end{array}\right]=L_{\lambda }{\left[\begin{array}{ccc}{M}_r\left({\lambda }_r\right)& M_r\left({\lambda }_g\right)& M_r\left({\lambda }_b\right)\\ M_g\left({\lambda }_r\right)& M_g\left({\lambda }_g\right)& M_g\left({\lambda }_b\right)\\ M_b\left({\lambda }_r\right)& M_b\left({\lambda }_g\right)& M_b\left({\lambda }_b\right)\end{array}\right]}^{-1}\left[\begin{array}{c}{M}_r\left({\lambda }_s\right)\\ M_g\left({\lambda }_s\right)\\ M_b\left({\lambda }_s\right)\end{array}\right]\end{array}$$

(4)

This transformation matrix is constant and depends on the spectral response of the cones. The RGB color space can be transformed to another color space via a linear or non-linear transformation [20,23].

2.2.2. HSV Color Space

The HSV color space can instinctively represent color, whereas the RGB color space can represent color by combining red, green, and blue colors. The RGB color space can be transformed to the HSV color space as follows [23]:

$$\begin{array}{c}\hfill H=arccos\left(\frac{\frac{1}{2}\left(2R-G-B\right)}{\sqrt{{\left(R-G\right)}^2-\left(R-B\right)\left(G-B\right)}}\right)\end{array}$$

(5)

$$\begin{array}{c}\hfill S=\frac{max\left(R,G,B\right)-min\left(R,G,B\right)}{max\left(R,G,B\right)}\end{array}$$

(6)

$$\begin{array}{c}\hfill V=max(R,G,B)\end{array}$$

(7)

The HSV color space represents an image by using three constituents, namely hue, saturation, and value. Hue indicates the chromatic information, saturation the depth of purity of the color, and value the brightness of the color. The HSV color space easily distinguishes a color because it instinctively describes the color information, unlike the RGB color space. In addition, the HSV color space separates out the intensity from the color information. However, it has some limitations: if the saturation is low, it seems to represent gray color, even if the color is not gray; if the saturation is under a threshold, then the hue is unstable; if the intensity is significantly low or significantly high, the hue information is meaningless [24,25,26].

2.2.3. CIE L*a*b* Color Space

The CIE 1976 (L*, a*, b*) color space was introduced by Commission Internationale de I’Eclairage (CIE) in 1976. The CIE L*a*b* color space is based on the compressed CIE XYZ color space, which can predict spectral-power distributions that will be perceived as an identical color, coordinates nonlinearly. The CIE L*a*b* color space is perceptually uniform, whereas the CIE XYZ color space is not. The CIE L*a*b* color space is considered the most complete color space [22]. It is derived from CIE XYZ tristimulus values. In addition, the CIE XYZ color space can be derived from the RGB color space. The CIE XYZ color space was introduced in 1931 by CIE to match the perceived color of any given spectral energy distribution. The system of imaginary non-physical primaries is known as X, Y, and Z. Only Y contributes to the luminance, and X and Z have the value of chromaticity. All the colors can be matched on the basis of the positive amounts of X, Y, and Z, unlike the RGB color space [27].

The CIE L*a*b* color space is transformed from CIE XYZ tristimulus values as follows [28]:

$$\begin{array}{c}\hfill X=k\sum _{i=0}^{N-1}\overline{x}\left({\lambda }_i\right)l\left({\lambda }_i\right)r\left({\lambda }_i\right)\\ \hfill Y=k\sum _{i=0}^{N-1}\overline{y}\left({\lambda }_i\right)l\left({\lambda }_i\right)r\left({\lambda }_i\right)\\ \hfill Z=k\sum _{i=0}^{N-1}\overline{z}\left({\lambda }_i\right)l\left({\lambda }_i\right)r\left({\lambda }_i\right)\end{array}$$

(8)

$$\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]=\left[\begin{array}{ccc}0.412453& 0.357580& 0.180423\\ 0.212671& 0.715160& 0.072169\\ 0.019334& 0.119193& 0.950227\end{array}\right]\left[\begin{array}{c}R\\ G\\ B\end{array}\right]$$

(9)

$$L^{*}=116{\left(\frac{Y}{Y_n}\right)}^{\frac{1}{3}}-16$$

(10)

$$a^{*}=500\left({\left(\frac{X}{X_n}\right)}^{\frac{1}{3}}-{\left(\frac{Y}{Y_n}\right)}^{\frac{1}{3}}\right)$$

(11)

$$b^{*}=200\left({\left(\frac{Y}{Y_n}\right)}^{\frac{1}{3}}-{\left(\frac{Z}{Z_n}\right)}^{\frac{1}{3}}\right)$$

(12)

The CIE L*a*b* color space comprises L, a, and b components. The L component represents the luminosity layer, and the a and b components denote the chromaticity layers. As previously mentioned, the CIE L*a*b* color space is cognitively uniform because the L component is linearly related to the brightness recognized by the human eyes. Among the chromaticity layers, the values of a component are distributed from the red axis to the green axis. The green and red colors indicate negative and positive values of a component. The value of the b component is distributed following the blue to yellow axis. The blue color has negative values of the b component, and the yellow color has positive values of the b component. Conversely, the a component is related to red color, while the R component of the RGB color space is related to red color. In addition, the a component is related to green color, while the G component of the RGB color space is related to green color and not the R component of the RGB color space, unlike the case of red color [22].

2.3. Similarity Calculation

The peak signal-to-noise ratio (PSNR) represents the similarity between two images. If the PSNR is low, the two images have high numerical differences. In addition, PSNR is more sensitive than the structural similarity index measure [29]. Therefore, we computed the PSNR for calculating the similarity between two images.

The similarity between two images based on PSNR is calculated using (13) as follows [30]:

$$\begin{array}{cc}\hfill PSNR& =10{log}_{10}\left(\frac{MA{X}_I^2}{MSE}\right)\hfill \\ \hfill & =20{log}_{10}\left(\frac{MA{X}_I}{\sqrt{MSE}}\right)\hfill \\ \hfill & =20{log}_{10}\left(MA{X}_I\right)-10{log}_{10}\left(MSE\right)\hfill \end{array}$$

(13)

In (13), $MA{X}_I$ represents the maximum fluctuation determined by the type of input image. The pixel values of the input image can range from zero to 255. Therefore, in this study, the value of $MA{X}_I$ is 255. In addition, $MSE$ is calculated using (14) as follows:

$$MSE=\frac{1}{mn}\sum _{i=1}^m\sum _{j=1}^n{\left[I\left(i,j\right)-K\left(i,j\right)\right]}^2$$

(14)

Equation (14) demonstrates that PSNR is related to the difference calculated between the two images I and K.

2.4. Transfer Learning

Overfitting may be an issue in the training process. If overfitting occurs, the target function is perfectly mapped on each datum of the training dataset. However, it cannot predict the data that are not contained within the training dataset, as the algorithm attempts to train the characteristics of data by extending the training to learn the characteristics of the noise in the training data. Therefore, overfitting makes it difficult to generalize the trained model [31].

Data augmentation is applied to avoid overfitting. There is another common solution called transfer learning. The concept of transfer learning was introduced as memory-based learning [32]. Transfer learning is critical to overcoming data deficiency. The main reason is that transfer learning utilizes the information of the feature extraction layers of the pre-trained model. The pre-trained model is generally well trained using enormous amounts of training data. Conversely, it is competitive to utilize the weights of the feature extraction layers that have been previously trained. The concept of transfer learning is depicted in Figure 1 [33].

In this figure, the part of the feature extraction layers is retained, whereas the classification layers are cropped. Next, new classification layers that correspond to new training data are attached at the end of the network. Subsequently, the network is re-trained using new training data. This reduces the training computational time and improves the accuracy of the classification result.

In addition, the data augmentation in the procedure of transfer learning is implemented via linear transformation, non-linear transformation, auxiliary-variable addition, dynamic system-based simulation, and generative model-based generation, among others. In the image processing domain, data augmentation is implemented by adding noise, applying affine transforms such as translation, zoom, flipping, shear, and mirror, and via color perturbation [34].

3. Proposed Method

As previously mentioned, it is difficult to collect a sufficient amount of training data to apply deep learning because the target object of the manufacturing domain is not generally an uncommon item. This results in a trained classifier that is vulnerable. Therefore, in this study, we propose a method of augmenting the training data to counter data deficiency.

To compensate for the training data deficiency in the manufacturing domain, in this study, we propose a method of augmenting the data using a small dataset by changing the pixel value with respect to color spaces and transforming the image via rotation and flipping. The reason why we selected color perturbation is that the image is closely connected with luminance in the environment, and luminance has an influence on the color of the object in the image. The reason why we selected geometric transformation is that our experiments were conducted on a conveyor.

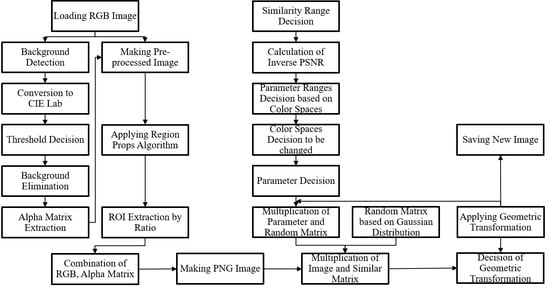
Unlike the traditional method, which randomly adds the values to apply the color perturbation, the proposed method applies the color perturbation based on the decision of a reasonable range, which is determined by the inverse PSNR equation. Furthermore, in case of the traditional method, the input size of the training image for training the deep learning network is just resized by the input size of the network applied for the transfer learning. Therefore, the ratio of the image is distorted, and it results in decreasing the image classification accuracy. Therefore, the proposed method crops and resizes the image by maintaining the ratio of the object size in the original image. To implement this, the center point of the object in the image is calculated. Furthermore, to analyze the effect of the number of training images, the combination of the color perturbation with respect to each color space and the combination of the geometric transformation are conducted. The overview of the proposed method is depicted in Figure 2. The proposed method is divided into three parts: image pre-processing (background elimination; ROI extraction while maintaining the ratio of the original image size), color perturbation via a random Gaussian distribution based on the inverse PSNR, and geometric transformations.

First, we capture the target objects that should be recognized by the deep learning network by using a vision sensor. In this study, the object images were comprised of 32 images for each category. Next, the background is eliminated to improve the classification accuracy by reducing the elements that have an influence on training the object. The objects for the image classification are laid on a color board. An object should be extracted from the image, without the color board as the background image. This step is shown in Figure 3.

To eliminate the background color, the characteristics of the CIE L*a*b* color space are used. If the background color is white, shadows hinder the background removal process. Therefore, a background with a different color is considered. As previously mentioned, the CIE L*a*b* color space is comprised of the red–green axis and blue–yellow axis, as depicted in Figure 4. Figure 5 depicts each component of each color space. Red, green, blue, and yellow are more distinct in each component in the CIE L*a*b* color space than the RGB color space [35,36]. Using this characteristic, we can easily extract the object from the background color. Because the colors of the object used for image classification are varied, such as red, green, blue, and black, the background colors of the board are determined as green and blue. The green and blue colors can be effectively extracted, as they have convenient values in the CIE L*a*b* color space that help distinguish the colors. The green color is located at the bottom of the a component, which is related to the red–green axis. In addition, the blue value is located at the bottom of the b component, which is related to the blue–yellow axis. Therefore, we selected green and blue colors as the background color. The process for eliminating the background is as follows:

$$\begin{array}{c}\hfill ALPHA=\left\{\begin{array}{cc}0,& Va{l}_{comp}<T{H}_{comp}\\ 1,& otherwise\end{array}\right.\end{array}$$

(15)

$ALPHA$ denotes the alpha matrix of the PNG image file. This matrix is related to the transparency of an image. The region that we consider as the background is removed and transparentized using the alpha matrix. The term $Va{l}_{comp}$ denotes a pixel value in each component layer. The component layer is determined as the a component if the background is green color or the b component if the background is blue color. The term $T{H}_{comp}$ denotes each threshold value with respect to the a or b component layer for extracting the green or blue color. In addition, $T{H}_{comp}$ is determined according to the characteristic depicted in Figure 4.

After background elimination, the image is cropped as the original image ratio is maintained as depicted in Figure 6. The image ratio is important because the distortion affects the classification accuracy during the training of the deep learning network. However, the training images are just resized according to the input size of the network that is used for transfer learning. In this case, the ratio of the image size of the training images is not maintained, and it may result in low classification accuracy. Therefore, we crop and resize the image while maintaining the ratio when extracting the target object from the image. For this procedure, a division algorithm is applied for extracting the object from the background by measuring the properties of the image regions [37,38]. The center of an object in an image is calculated by the region propsalgorithm. Then, the image is cropped and resized as the square shape. Its size is determined as the input size of the deep learning network used for training.

Next, the data augmentation is performed after image pre-processing. The main concept of the proposed method is to generate similar images to build an enormous amount of training data from a small amount of original image data. Because the number of training images affects the performance of the image classification that is based on a deep learning network, we must prepare a massive training dataset for training the deep learning network. Although the training data generated using the proposed method should be similar to the original data, they should be nonlinear to ensure the diversity required to train the network effectively. The reason behind considering similarity is that the similarity of training images in the same category should be guaranteed to a certain degree for the satisfactory performance of the classifier. Therefore, we proposed a data augmentation method by generating an image that is similar to the original one on the basis of a similarity calculation. In addition, we focused on color perturbation because color is affected by lighting and can be changed to another color. Therefore, to generate new images reasonably based on the color perturbation for training the network, we attempted to specify the range of transformation. To implement this concept, we considered the method of calculating the similarity between the original image and the generated image. Therefore, we applied the concept of PSNR for data augmentation.

$$\begin{array}{c}\hfill 10{log}_{10}\left(\frac{1}{mn}\sum _{i=1}^m\sum _{j=1}^n{\left[I\left(i,j\right)-K\left(i,j\right)\right]}^2\right)=20{log}_{10}\left(MA{X}_I^2\right)-PSNR\\ \hfill \sum _{i=1}^m\sum _{j=1}^n{\left[I\left(i,j\right)-K\left(i,j\right)\right]}^2=mn\ast {10}^{2{log}_{10}\left(MA{X}_I^2\right)-0.1PSNR}\end{array}$$

(16)

By using (16) derived from (13), the similarity between two images can be calculated. Therefore, we induce the method for generating similar images by inversely considering the PSNR equation. First, the range of the PSNR result value is set. Subsequently, by inversely calculating the PSNR equation, the perturbation range of pixel values is determined. Accordingly, a new image dataset that will contain the training data is generated. An image that is similar to the original image should be generated for augmenting the training data. In addition, the pixel values are generally changed because of the lighting in the environment. Therefore, the proposed method considers color perturbation. The inverse PSNR equation is used to realize a reasonable transformation.

The inverse PSNR can be used to determine the range of the transformation with respect to the color perturbation. To generate a new image while considering its similarity with the original image, the characteristics of the color space are concretely specified. Using the proposed method, the pixel values are tuned over one color space. For reference, the RGB and CIE L*a*b* color spaces have three and two chromaticity layers, respectively, while the HSV color space has only one layer, which is directly related to the chromaticity layer. In the case of HSV color space, it is difficult to distinguish the colors on the boundary as depicted in Figure 7 [39]. As depicted in the above figure, although the H value of the pixel is changed slightly, the red color can be shown as pink or otherwise. Furthermore, H values are similar in the case of yellow and green. Therefore, other color spaces for color perturbation should be considered. In the case of the CIE L*a*b* color space, the parts in which the pixels denote red color are distinct in the a-component layer unlike in the L- and b-component layers. The parts in which the pixels denote yellow color are distinct in the b-component layer. Owing to these characteristics of the CIE L*a*b* color space, we applied the RGB, CIE L*a*b*, and HSV color space to perform data augmentation for diverse transformation.

Color perturbation was performed on the basis of inverse PSNR and the characteristics of one, two, and three color spaces. After calculating the inverse PSNR, the matrix of the color perturbation was generated by adding values via the random Gaussian distribution. By determining the range of the perturbation, the interrelated images were generated to be similar to the original images. This affected the classification accuracy by reducing the generation of images as the outlier. Finally, we combined two geometric transformations for augmenting the training data. Because the experimental environment was related to a conveyor, rotation and flipping were applied after the procedure of color perturbation on the basis of the similarity of the generated images with the original images.

Transfer learning was applied to improve the training efficiency. Among the pre-trained networks, the VGGNet network was re-trained using new training images that were generated using the proposed method. We chose VGGNet because, in our previously conducted work, it showed better performance than those of other pre-trained networks.

4. Experimental Results and Discussion

In this study, we proposed a method to improve the image classification accuracy for small datasets. We applied transfer learning because a method that updates the weights of fully connected layers is more effective than one that updates the weights of all the layers of the network [34].

The aim of the experiment was to classify the objects of 10 categories. Identifying images from these categories is difficult because they are uncommon and not general items, whereas general items are contained in well-known and existing image datasets. Therefore, the training images should be collected first, although significantly few images were manually collected as the training data. The original images were acquired as the training data using the vision sensor. The number of original images was 32 in each category. In addition, the test data were collected in the same manner as before. The test data were not contained in the training dataset. All experimental results were verified with test data, which was not generated arbitrarily and just captured from the vision sensor. Classification accuracy in the tables indicates the results classifying the object of test data.

To verify the proposed method, first we compared the traditional method with the proposed one. Especially, to demonstrate the color perturbation with respect to the characteristic of color spaces and the geometric transformations, we compared and analyzed the experiments of each color space and each geometric transformation.

Table 1. Classification accuracies of traditional methods and methods that use the inverse PSNR.

Method	Number of Training Images	Classification Accuracy
Traditional Method #1	2880	47.0%
Traditional Method #2	2880	34.0%
RGB PSNR	2880	50.0%
Lab PSNR	3200	63.0%
HSV PSNR	3200	53.0%

presents the results of image classification by comparing the traditional methods with the methods that apply color perturbation based on the inverse PSNR with respect to three color spaces based on the proposed method.

The traditional methods work by adding random values in the color channels. Traditional Methods #1 and #2 arbitrarily transform the pixel values in terms of the RGB color space. Traditional Method #1 adds positive values, whereas Traditional Method #2 adds positive or negative values. As presented in this table, the case of adding only positive values had better performance compared with the case of adding positive or negative values. RGB PSNR indicates the generated training data by applying color perturbation based on the inverse PSNR with respect to the RGB color space. Lab PSNR represents the generated training data by applying color perturbation based on the inverse PSNR with respect to CIE L*a*b* color space. HSV PSNR denotes the generated training data by applying color perturbation based on the inverse PSNR with respect to HSV color space.

In addition, the methods that apply color perturbation based on the inverse PSNR had better classification accuracy than that of the traditional methods. To conduct the experiments in the same condition, we arbitrarily extracted an equal number of training images with respect to the methods listed in Table 1. The classification results are presented in

Table 2. Classification accuracy of traditional methods and the methods that use the inverse PSNR, with an equal number of training images.

Method	Number of Training Images	Classification Accuracy
Traditional Method #1	2800	44.0%
Traditional Method #2	2800	43.0%
RGB PSNR	2800	62.0%
Lab PSNR	2800	62.0%
HSV PSNR	2800	63.0%

.

In addition, Table 2 shows that the methods that applied color perturbation based on inverse PSNR could improve the classification accuracy better compared with the traditional methods. The combination of extracted images was reflected in the classification results. Next, another experiment was performed to compare the cases of joining the training data generated via the inverse PSNR together with respect to each color space. The results are presented in

Table 3. Comparison of the classification accuracy by joining the PSNR results.

Method	Number of Training Images	Classification Accuracy
RGB PSNR + Lab PSNR	6080	67.0%
Lab PSNR + HSV PSNR	6400	66.0%
RGB PSNR + HSV PSNR	6080	64.0%
RGB PSNR + Lab PSNR + HSV PSNR	9280	54.0%

.

From Table 3, it was evident that increasing the number of training images did not always guarantee an improvement to the classifier performance. This was because the classification result obtained upon joining the training data via inverse PSNR in terms of RGB, Lab, and HSV color spaces was 54.0%, while the classification results obtained upon joining two training datasets among the dataset generated via the inverse PSNR in terms of RGB, Lab, and HSV color space had higher performance than 54.0%.

In a previously conducted research, we generated the training dataset by applying Lab PSNR after applying RGB PSNR [40]. This was because the number of training images was critical for improving the classification accuracy. In addition, in this study, the classification result of combining RGB PSNR + Lab PSNR showed better performance when two training datasets were combined, as presented in Table 3. Therefore, we performed additional experiments regarding overlapping the inverse PSNR method on two color spaces: the first one (RGB-Lab PSNR) was applying Lab PSNR after applying RGB PSNR; the other one (Lab-RGB PSNR) was applying RGB PSNR after applying Lab PSNR. The reason behind considering the processing order was to ascertain whether the processing order was influential or not. The experimental results are presented in

Table 4. Comparison of the classification accuracy by overlapping the inverse PSNR method about two color spaces.

Method	Number of Training Images	Classification Accuracy
RGB-Lab PSNR	28,800	55.0%
Lab-RGB PSNR	28,800	57.0%

.

Comparing Table 1 and Table 4, the result obtained upon overlapping the inverse PSNR method on two color spaces was better than that obtained by adding up the three training datasets generated using the inverse PSNR method in terms of each color space. Therefore, we performed the experiment considering the following three categories: the case of the inverse PSNR method on only one color space, the case of adding up the training datasets, and the case of overlapping the inverse PSNR method on two color spaces. As previously mentioned, two geometric transformations, namely flipping and rotation, were applied to each training dataset performed using the inverse PSNR method, as the target experiment was related to the conveyor. First, we applied the flipping method after applying the color perturbation based on the inverse PSNR method. The results are presented in

Table 5. Classification accuracy obtained upon applying the inverse PSNR method and Geometric Transformation #1: flipping.

Number of Experiment	Color Perturbation	Geometric Transformation	Number of Training Data	Classification Accuracy
1	RGB PSNR	Flipping	11,520	77.0%
2	Lab PSNR	Flipping	12,800	74.0%
3	HSV PSNR	Flipping	12,800	65.0%
4	RGB PSNR + Lab PSNR	Flipping	24,320	82.0%
5	RGB PSNR + Lab PSNR + HSV PSNR	Flipping	37,120	65.0%
6	RGB-Lab PSNR	Flipping	112,500	70.0%
7	Lab-RGB PSNR	Flipping	112,500	79.0%

.

The experimental results showed that Experiment #4 yielded better performance than the other experiments. The training data were composed by adding the two training datasets generated using the inverse PSNR method with respect to the RGB color space and CIE L*a*b* color space, respectively, and then performing the flipping method (horizontal, vertical, and horizontal–vertical). Although Experiments #5, #6, #7 had more training data than that of Experiment #4, they showed lower performance regarding test data. This meant that the number of training datasets was not the only reason for the improvements in the classification results. With a sufficient amount of training data, the data should be effectively augmented to train the network. Next, we applied the rotation method as another geometric transformation to the training dataset. The results are presented in

Table 6. Classification accuracy obtained upon applying the inverse PSNR method and Geometric Transformation #2: rotation.

Number of Experiment	Color Perturbation	Geometric Transformation	Number of Training Data	Classification Accuracy
1	RGB PSNR	Rotation	103,680	84.0%
2	Lab PSNR	Rotation	115,200	91.0%
3	HSV PSNR	Rotation	115,200	89.0%
4	RGB PSNR + Lab PSNR	Rotation	218,880	92.0%
5	RGB PSNR + Lab PSNR + HSV PSNR	Rotation	334,080	91.0%
6	RGB-Lab PSNR	Rotation	1,036,800	93.0%
7	Lab-RGB PSNR	Rotation	1,036,800	91.0%

.

From Table 6, it is evident that applying the rotation method could significantly improve the classification accuracy. Because the objects were randomly laid down with respect to the rotation angle of the object in the conveyor environment, the rotation method was more influential than the flipping method. In this case, Experiment #6, which was related to overlapping the inverse PSNR method about two color spaces, had higher performance. In addition, we applied the flipping and rotation methods together, and the results are presented in

Table 7. Classification accuracy obtained upon applying the inverse PSNR method and two geometric transformations.

Number of Experiment	Color Perturbation	Geometric Transformation	Number of Training Data	Classification Accuracy
1	RGB PSNR	Rotation, Flipping	414,720	92.0%
2	Lab PSNR	Rotation, Flipping	460,800	92.0%
3	HSV PSNR	Rotation, Flipping	460,800	92.0%
4	RGB PSNR + Lab PSNR	Rotation, Flipping	875,520	95.0%
5	RGB-Lab PSNR	Rotation, Flipping	4,147,200	93.0%
6	Lab-RGB PSNR	Rotation, Flipping	4,147,200	94.0%

.

In the case of applying the flipping and rotation methods together, the performances of the trained networks slightly increased. In this case, the trained network of Experiment #4 by the training dataset adding up the two training data generated by the inverse PSNR method with respect to the RGB color space and CIE L*a*b* color space and performing the flipping method (horizontal, vertical, horizontal-vertical) had higher performance than those of others, as in Table 3 and Table 5.

Finally, we performed additional experiments by using an equal amount of training data. The smallest number of the generated training images was 1152 in the case of applying the color perturbation based on the inverse PSNR method with respect to the RGB color space and flipping transformation. Therefore, one-thousand training images were arbitrarily extracted in each category and used for training the network in the same manner as before. The experimental results are presented in

Table 8. Classification accuracy obtained upon applying the inverse PSNR method and two geometric transformations with an equal number of training images.

Color Perturbation	Geometric Transformation	Number of Training Data	Classification Accuracy (avg.)
RGB PSNR	Flipping	10,000	76.0%, 76.0%, 75.0% (75.7%)
Lab PSNR	Flipping	10,000	82.0%, 79.0%, 67.0% (76.0%)
HSV PSNR	Flipping	10,000	70.0%, 66.0%, 64.0% (66.7%)
RGB PSNR + Lab PSNR	Flipping	10,000	76.0%, 71.0%, 72.0% (73.0%)
RGB PSNR + Lab PSNR + HSV PSNR	Flipping	10,000	80.0%, 67.0%, 78.0% (75.0%)
RGB-Lab PSNR	Flipping	10,000	63.0%, 75.0%, 70.0% (69.3%)
Lab-RGB PSNR	Flipping	10,000	71.0%, 63.0%, 69.0% (67.7%)
RGB PSNR	Rotation	10,000	89.0%, 89.0%, 92.0% (90.0%)
Lab PSNR	Rotation	10,000	87.0%, 89.0%, 89.0% (88.3%)
HSV PSNR	Rotation	10,000	92.0%, 89.0%, 87.0% (89.3%)
RGB PSNR + Lab PSNR	Rotation	10,000	92.0%, 93.0%, 90.0% (91.7%)
RGB PSNR + Lab PSNR + HSV PSNR	Rotation	10,000	91.0%, 81.0%, 89.0% (87.0%)
RGB-Lab PSNR	Rotation	10,000	93.0%, 88.0%, 89.0% (90.0%)
Lab-RGB PSNR	Rotation	10,000	92.0%, 90.0%, 94.0% (92.0%)
RGB PSNR	Rotation, Flipping	10,000	88.0%, 90.0%, 87.0% (88.3%)
Lab PSNR	Rotation, Flipping	10,000	91.0%, 89.0%, 89.0% (89.7%)
HSV PSNR	Rotation, Flipping	10,000	86.0%, 91.0%, 91.0% (89.3%)
RGB PSNR + Lab PSNR	Rotation, Flipping	10,000	93.0%, 87.0%, 86.0% (88.7%)
RGB PSNR + Lab PSNR + HSV PSNR	Rotation, Flipping	10,000	91.0%, 88.0%, 88.0% (89.0%)
RGB-Lab PSNR	Rotation, Flipping	10,000	91.0%, 90.0%, 87.0% (89.3%)
Lab-RGB PSNR	Rotation, Flipping	10,000	84.0%, 89.0%, 90.0% (87.7%)

.

Because the amount of training data was reduced, the results of the classification accuracy tended to be slightly different than before. The experiment with the best performance with respect to average classification accuracy, as shown in Table 8, was the one in which the inverse PSNR method was applied in terms of overlapping CIE L*a*b* and RGB color space and rotation. The average classification accuracy was 92.0%, and the variance of the classification accuracy calculated using (17) was four. The experiment in which the inverse PSNR method was applied in terms of RGB and CIE L*a*b* color spaces and rotation achieved the second best performance. The average classification accuracy was 91.7%, and the variance of the classification accuracy calculated using (17) was 2.3.

$$VAR=ST{D}^2=\frac{1}{n-1}\sum _{i=1}^N{\left(x_i-\overline{x}\right)}^2$$

(17)

For the experimental results, we generally considered the best case wherein rotation and flipping were applied after the color perturbation with RGB and CIE L*a*b* color spaces by using the inverse PSNR. In addition, the results obtained using the proposed method applied to Table 7, which showed higher accuracy, tended to be similar to or lower than those of the proposed method applied to Table 6. In the case of applying the inverse PSNR method in terms of the RGB and CIE L*a*b* color spaces and two geometric transformations, the variance of the classification accuracy was 14.3. This meant that the classification accuracy was heavily influenced by the randomly extracted training data. In addition, the figure below shows that, as mentioned earlier, a sufficient amount of training dataset increased the classification accuracy.

In Figure 8, we compare the cases of using the traditional methods and the case of applying geometric transformation based on RGB PSNR + Lab PSNR training data, which was mostly the best case among the training data generated by the proposed method. The classification accuracy for Object #3 gradually increased in sequence. From Figure 8a,b, it was evident that the classification results were mostly misclassified to be of some output class. In the case of Figure 8c, Object #3 was mostly classified as Object #4. Their shapes were similar to a rectangle. By applying geometric transformations, the amount of the training data and the classification accuracy increased. Finally, Object #3 could be classified 100% using the re-trained classifier. In addition, Object #6 was mostly classified as Object #5, as depicted in Figure 8c. As depicted in Figure 9, Objects #4, #5, and #6 were significantly similar, especially when they were laid down in a standing position. However, using the proposed method, the classification accuracy for Object #6 could be improved. Because Object #8 was significantly similar to Object #7, as depicted in Figure 9, Object #8 was classified as Object #7, as depicted in Figure 8c. However, Object #8 could be classified 100.0% using the proposed method. Similarly, Object #9 was misclassified as Object #10, which was similar to Object #9. However, the proposed method could classify Object #9 with 100.0% accuracy.

5. Conclusions

In this study, we proposed a method to overcome data deficiency and improve classification accuracy. Accordingly, we eliminated the background color and extracted the object while maintaining the original image ratio. In addition, new training images were generated via color perturbation based on the inverse PSNR with respect to color spaces and geometric transformations.

Experiments were performed to demonstrate the reasonable combination by considering color spaces and geometric transformations and their combinations, respectively. First, we composed 11 training datasets to verify the validity of range determination for color perturbation: Traditional Method #1, Traditional Method #2, RGB PSNR, Lab PSNR, HSV PSNR, RGB PSNR + Lab PSNR, Lab PSNR + HSV PSNR, RGB PSNR + HSV PSNR, RGB PSNR + Lab PSNR + HSV PSNR, RGB-Lab PSNR, Lab-RGB PSNR. Traditional Methods #1 and #2 were related to adding the pixel values of the RGB color space arbitrarily. The other datasets were related to the proposed method. The experimental results showed that the classification accuracy could be improved by the proposed method as compared with the traditional methods, and the RGB PSNR + Lab PSNR training dataset showed better performance than the others.

Second, we composed 21 training datasets to verify the effectiveness of geometric transformations: flipping with RGB PSNR, flipping with Lab PSNR, flipping with HSV PSNR, flipping with RGB PSNR + Lab PSNR, flipping with RGB PSNR + Lab PSNR + HSV PSNR, flipping with RGB-Lab PSNR, flipping with Lab-RGB PSNR, rotation with RGB PSNR, rotation with Lab PSNR, rotation with HSV PSNR, rotation with RGB PSNR + Lab PSNR, rotation with RGB PSNR + Lab PSNR + HSV PSNR, rotation with RGB-Lab PSNR, rotation with Lab-RGB PSNR, flipping and rotation with RGB PSNR, flipping and rotation with Lab PSNR, flipping and rotation with HSV PSNR, flipping and rotation with RGB PSNR + Lab PSNR, flipping and rotation with RGB PSNR + Lab PSNR + HSV PSNR, flipping and rotation with RGB-Lab PSNR, flipping and rotation with Lab-RGB PSNR. The experimental results showed that the RGB PSNR + Lab PSNR with rotation and flipping method showed better performance in the training data generated by the proposed method.

The classification accuracy of the network trained using the generated dataset by color perturbation based on the similarity calculation, which was related to our contribution, showed better performance than the arbitrary color perturbation like the traditional methods. In general, the numerous image data showed a better performance of the classification accuracy. However, it was not absolute. Therefore, we plan to study effective data augmentation methods by evaluating the appropriate numerical value for improving the performance of the classification accuracy.

The experimental results showed that the proposed method could improve the classification accuracy by classifying similar objects, which were easy to misclassify. This indicated that color perturbation based on similarity was effective at improving the classification accuracy. In future work, we plan to develop other reasonable data augmentation methods to overcome data deficiency, including in the manufacturing domain.