Behavior of Longitudinal Plate-to-Rectangular Hollow Structural Section K-Connections Subjected to Cyclic Loading

Abstract

This study investigated the behavior of longitudinal plate-to-rectangular hollow section (RHS) K-connections to which concrete-filled composite branch members were jointed. At the connections, longitudinal plates with or without chord face stiffener were welded to the RHS chord member and the branch members were connected to the longitudinal plates by bolting (slip-critical connection). Cyclic tests were performed for three longitudinal plate-to-RHS K-connection specimens. The tests showed that the connection behavior was dominated by the plastification of the thin chord face and by the slip and hole-bearing resistance of the bolted joint. Chord face plastification was prevented or delayed by using the stiffened longitudinal plate. The strengths of the plate-to-RHS K-connections with or without the chord face stiffener, depending on the governing limit states, were estimated in accordance with current design codes, and the results were compared with the test results.

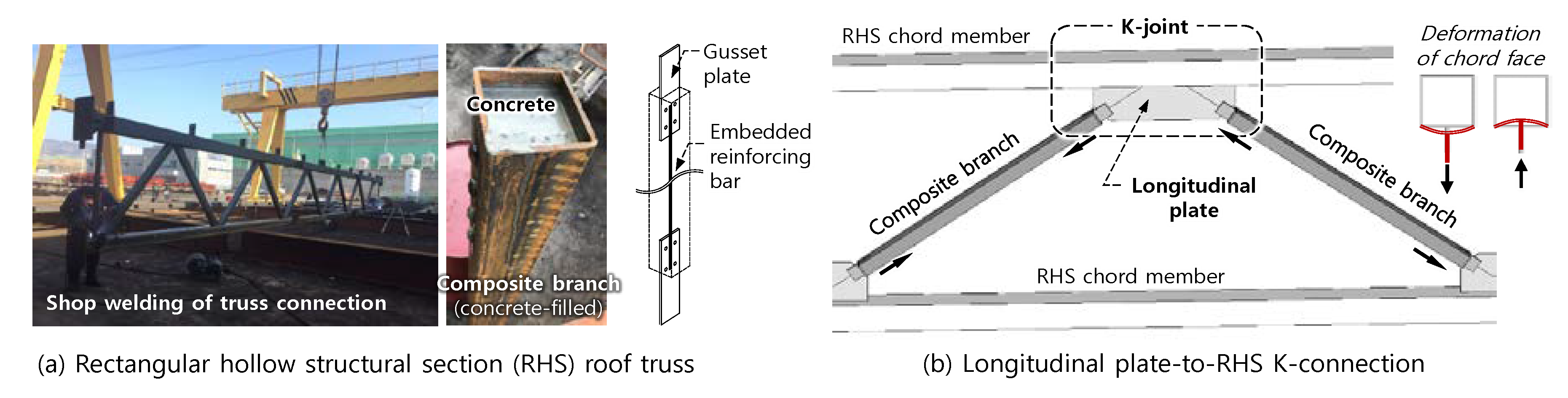
1. Introduction

The use of rectangular hollow structural section (RHS) trusses, as shown in Figure 1a, is increasing as an economical roof structure for long-span building structures such as factories and warehouses. In such RHS trusses, medium-size sections of 150 mm–300 mm in size are used as top and bottom chord members, and small-size sections of approximately 100 mm in size are used as diagonal and vertical branch members. Particularly for diagonal members that are subjected to large compression force, RHS members with greater buckling resistance may be advantageous. Furthermore, by filling concrete inside the hollow steel section, the resistance of RHS trusses can be enhanced (see Figure 1). For example, concrete-filled composite members have higher elastic buckling strength (P_e) and compressive resistance (P_no), as the filled concrete provides additional resistance. Thus, the compressive strength including length effects (i.e., P_n = P_no·${0.658}^{P_{no}/P_e}$) can be greatly increased [1,2].

Unlike diagonal and vertical branch members that are made of concrete-filled composite sections, top and bottom chord members are often made of hollow steel sections to make the roof truss lighter. At the connection where the filled composite branch members are joined with the hollow chord members, the thin RHS walls of the branch and chord members need to be directly welded to each other, or alternatively, longitudinal plate connection (i.e., plate-to-RHS connection, see Figure 1b) can be used [2,3,4]. The plate-to-RHS connection may be more convenient to assemble and erect the trusses and their members because the branch members are connected to the plate by bolting without field welding. However, the thin RHS wall of the chord member is weak to out-of-plane deformation, and consequently, the strength of the truss connection can decrease (see Figure 1b). This means, unless the connecting chord face is not appropriately stiffened, the excellent compression resistance of the composite branch member cannot be fully exploited.

In the past, many studies have been conducted to investigate the behavior and design method of plate-to-RHS connections [5,6,7,8,9,10]. Kosteski, Packer, and Puthli [5] investigated the strength of the plate-to-RHS connections with chord face stiffener by finite element analysis (see Figure 2b). The stiffened truss connections showed ductile behavior, and the strength increased as the deformation of the chord face increased. The connection strengths determined according to the “3% b_o rule” were in good agreement with the theoretical strengths by chord face plastification. The 3% b_o rule means that the connection strength is determined as the strength when the out-of-plane deformation of the connecting chord face reaches 3% of the width of the chord face (b_o). Cao, Packer, and Kosteski [6] developed a design guideline for unstiffened plate-to-RHS connections (see Figure 2a) based on experimental and analytical investigations. They considered chord face plastification and branch yielding as governing design limit states and suggested using the strength resistance factor of 1.0 based on the investigation result that, due to hardening behavior, the actual strength was sufficiently larger than the theoretical strength. Kosteski and Packer [7] studied the behavior of the “through plate”-to-RHS connections, in which the longitudinal plate was extended up to the opposite wall of the connecting chord face. The truss connections stiffened by the through plate showed deformation-controlled or ductile behavior, and the test strength was larger than the theoretical strength by chord face plastification (strength resistance factor = 1.0). Kosteski and Packer [8] investigated the behavior of longitudinal plate-to-RHS connections stiffened by chord face stiffener (see Figure 2b). The minimum thickness of the chord face stiffener was proposed to satisfy the limit states of strength and serviceability. In addition, the strength of the stiffened connections was estimated based on the yield lines on the chord face occurring along the perimeter of the stiffener. Cao, Packer, and Yang [9] investigated the effects of compressive and tensile loads applied to the chord member on the connection strength. The results showed that compressive loads significantly reduced the chord face plastification strength, while tensile loads had little effect.

At the plate-to-RHS connection with chord face stiffener (see Figure 2b), the stiffener can reduce deformation of the chord face and can increase strength and stiffness by distributing the force of the longitudinal plate directly to the side wall of the chord member. According to the previous studies by Packer, Cao, Kosteski, etc. [5,6,7,8,9], the strength of such stiffened connection increases as the thickness and width of the stiffener (i.e., t_s and b_s, respectively) become larger. In addition, the connection strength agrees well with the chord face plastification strength based on the yield line theory. However, the previous studies have focused mainly on T- or Y-connections, and thus, available test data on the behavior of the K-connections which are common in roof trusses with slope are rare.

This study investigated the behavior of RHS truss K-connections with chord face stiffener. Cyclic loading tests of three truss connections where one hollow chord member and two composite branch members were jointed were performed, and the stiffening effects and governing limit states depending on the chord face stiffener were investigated. The theoretical strengths of the K-connections with and without the chord face stiffener were compared with the test strengths, and the applicability of current design codes was discussed.

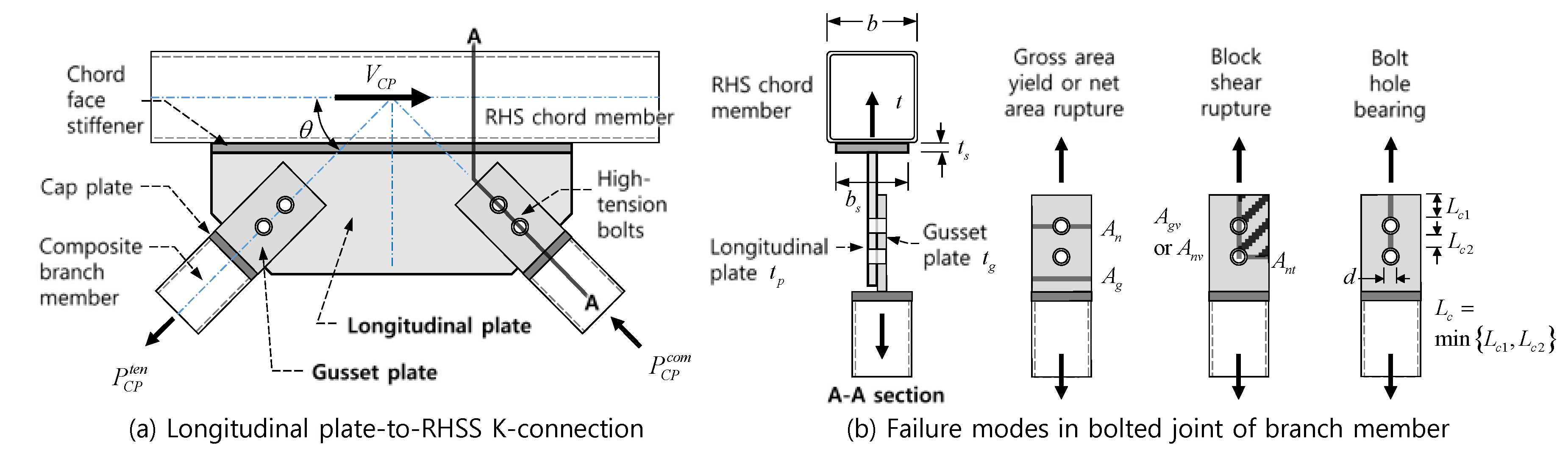
2. Theoretical Strength of Plate-to-RHS Connections

Figure 2 shows the plate-to-RHS connections with or without chord face stiffener. According to the CIDECT Design Guide 3 [4], the governing design limit state of the unstiffened and stiffened connections is chord face plastification; however, the distribution of yield lines on the chord face differs as follows [8]. For the connection without stiffener (see Figure 2a), yield lines occur at the center of the chord face nearby the longitudinal plate; on the other hand, for the connection with stiffener (see Figure 2b), yield lines on the chord face develop mainly along the perimeter of the chord face stiffener. Thus, the difference in the distribution of yield lines on the chord face needs to be accounted for in estimating the connection strength. Note that, according to AISC 360-10 [2] and CIDECT design guide 3, the plate-to-RHS truss connections should satisfy structural limits on material properties (e.g., F_y and F_u/F_y) and geometrical parameters (e.g., h/b, h/t, b/t, l_p/b, etc.). The limits of applicability are presented in

Table 1. Limits of applicability for plate-to-RHS truss connections.

Design code		AISC 360-10	CIDECT Design Guide 3
Chord member	Yield strength	Fy ≤ 360 MPa	Fy ≤ 460 MPa 3)
	Yield ratio	Fy/Fu ≤ 0.8	Fy/Fu ≤ 0.8 4)
	Width-to-thickness ratio	b/t ≤ 40 1)	b/t ≤ 40 and h/t ≤ 40 5)
	Height-to-width ratio	-	0.5 ≤ h/b ≤ 2.0
Longitudinal plate	Yield strength	Fyp ≤ Fu (t/tp) 2)	Fyp ≤ Fy
	Length	-	1 ≤ ηp (=lp/b) ≤ 4

¹⁾ This is given in Table K1.2A in AISC 360-10. ²⁾ This is given in Equation K1-3 in AISC 360-10 to prevent punching shear failure under plate shear load. ³⁾ For 355 MPa ≤ F_y ≤ 460 MPa, joint strength shall be reduced to 90%. ⁴⁾ For F_y /F_u > 0.8, F_y shall be taken as 0.8F_u. ⁵⁾ For compression, only class 1 and 2 sections are allowed.

.

Figure 3 shows the longitudinal plate-to-RHS K-connection investigated in this study. At the connection, concrete-filled composite branch members are joined with the longitudinal plate by bolting. Thus, when designing the truss connection, in addition to the wall plastification of the chord member, failure modes that may occur at the bolted joint of the branch members (i.e., bolt shear yield, hole bearing, connection slip, gross area yield, net area rupture, block shear rupture, etc.) need to be accounted for.

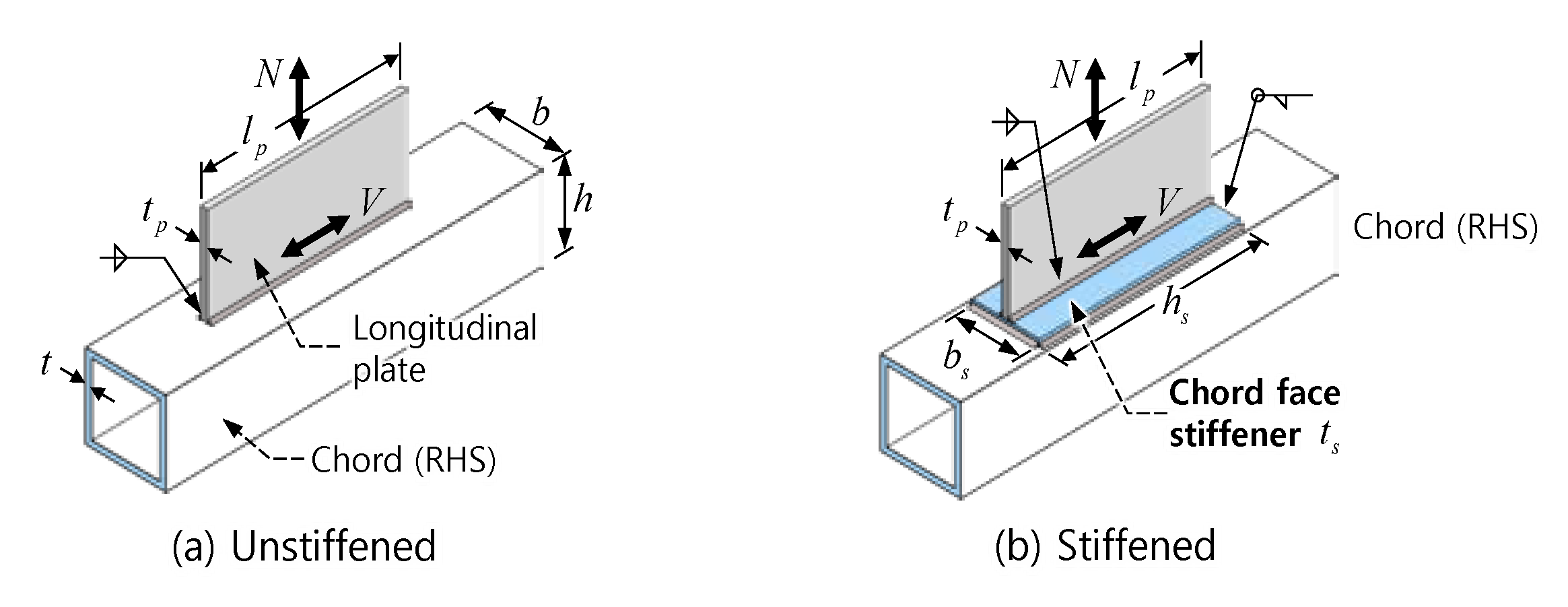
2.1. Connection Without Stiffener

The governing limit state of plate-to-RHS connections without stiffener is chord face plastification. According to AISC 360-10 and CIDECT Design Guide 3, the chord face plastification strength (N_CP) of plate-to-RHS T- or Y-connections can be computed as follows (see Figure 2a).

For AISC 360-10 (T- or Y-connections),

$$N_{CP}=\frac{F_y{t}^2}{1-t_p/b}\left[\frac{2l_p}{b}+4\sqrt{1-\frac{t_p}{b}}{Q}_f\right]$$

(1)

For CIDECT Design Guide 3 (T- or Y-connections),

$$N_{CP}=F_y{t}^2\left[\frac{2l_p}{b}+4\sqrt{1-\frac{t_p}{b}}\right]Q_f$$

(2)

where F_y = steel yield strength of the chord member; b and t = wall width and thickness of the chord member; l_p and t_p = length and thickness of the longitudinal plate; and Q_f = chord member stress function. The Q_f functions depending on the type of truss connections are presented in

Table 2. Chord member stress functions Q_f for RHS truss T-, Y-, and K-connections.

Joint Type		AISC 360-10	CIDECT Design Guide 3
Plate-to-RHS connection	T- and Y-connections	$Q_f=\sqrt{1-U^2}$1)	$Q_f={\left(1-\left|n\right|\right)}^{C_1}$ where C1 = 0.2 for n < 0 and 0.1 for n ≥ 0 2)
RHS-to-RHS connection	T-, Y-, and K-connections	$Q_f=1.3-0.4U\left(\frac{b}{b_s}\right)\le 1.0$1)	$Q_f={\left(1-\left|n\right|\right)}^{C_1}$ where C1 = 0.6-0.5(bs/b) (T- and Y- connections) or 0.5-0.5(bs/b) (K-connections) for n < 0 and 0.1 for n ≥ 0 2)

¹⁾U = N_u/[A_gF_y]+M_u/[SF_y], where N_u and M_u = axial load and moment, respectively, and A_g and S = gross section area and elastic section modulus of chord member, respectively. ²⁾ n = N_u/N_pl +M_u/M_pl, where N_pl and M_pl = axial yield strength and plastic moment strength of chord member, respectively.

. Note that the connection strength is expressed in terms of various symbols such as P, N, or V in Figure 2 and Figure 3, depending on the force direction to be considered; P is the connection strength represented as the tensile or compressive force of the branch member, while N and V are the components of P decomposed in the transverse and longitudinal directions of the chord member, respectively.

If the angle between the chord and branch members is θ (≤90°) in Y-connections, the connection strength P_CP in the branch axis can be computed by dividing N_CP by sin θ.

$$P_{CP}=\frac{N_{CP}}{\sin \theta }\mathrm{for}\mathrm{Y-connections}$$

(3)

Equation (3) applies to the Y-connections where only one branch member is joined with the chord member. For K-connections where both tensile and compressive branch members are joined with the chord member (see Figure 3), the transverse components of the tensile and compressive branch forces cancel out each other, and thus, the connection strength V_CP in the longitudinal direction of the chord member is determined as follows.

$$V_{CP}=\frac{2N_{CP}}{\tan \theta }\mathrm{for}\mathrm{K-connections}$$

(4)

According to the previous studies by Packer, Kosteski, etc. [5,6,7,8,9], the behavior of plate-to-RHS connections is governed by deformation-controlled action and the strength increases with increasing deformation. In this case, if the tensile and compressive branch members are not too close to be overlapped (or gap K-connection), it is possible to superpose the resistances of the tensile and compressive branch members that are independently determined.

2.2. Connection With Chord Face Stiffener

For longitudinal plate-to-RHS connections stiffened by the chord face stiffener of sufficient width and thickness, the mechanism of chord face plastification or the distribution of yield lines is similar to that of RHS-to-RHS truss connections. According to the CIDECT Design Guide 3, if the chord face stiffener satisfies the minimum thickness in Equation (5), the chord face plastification strength N_CP of stiffened plate-to-RHS connections can be estimated using the same method as that of RHS-to-RHS connections, as follows.

$$t_s\ge 0.5t\exp \left[3{\beta }^{*}\right]\mathrm{or}{t}_s\ge 0.5t\exp \left[3\left(\frac{b_s-t_p}{b-t}\right)\right]$$

(5)

For AISC 360-10,

$$N_{CP}=F_y{t}^2\left[\frac{2h_s}{b-b_s}+4\sqrt{\frac{b}{b-b_s}}\right]Q_f\mathrm{for}\mathrm{T}\text{- }\mathrm{and}\mathrm{Y-connections}$$

(6)

$$N_{CP}=9.8F_y{t}^2\left(\frac{b_s}{b}\right){\left(\frac{b}{2t}\right)}^{0.5}{Q}_f\mathrm{for}\mathrm{K-connection}$$

(7)

For CIDECT Design Guide 3,

$$N_{CP}=F_y{t}^2\left[\frac{2h_s}{\left(b-b_s\right)\sin \theta }+4\sqrt{\frac{b}{b-b_s}}\right]Q_f\mathrm{for}\mathrm{T}\text{- }\mathrm{and}\mathrm{Y-connections}$$

(8)

$$N_{CP}=14F_y{t}^2\left(\frac{b_s}{b}\right){\left(\frac{b}{2t}\right)}^{0.3}{Q}_f\mathrm{for}\mathrm{K-connection}$$

(9)

where h_s, b_s, and t_s = length, width, and thickness of the chord face stiffener, respectively (see Figure 2b). The chord member stress functions Q_f depending on the type of truss connections are presented in Table 2. Note that Equations (6) and (8) apply to the T- and Y-connections where one tensile or compression branch member is joined, whereas Equations (7) and (9) apply to the K-connections where both tensile and compression branch members are joined simultaneously.

The connection strength N_CP in Equations (7) and (9) is the force acting in the transverse direction to the chord axis. Thus, the connection strength V_CP in the longitudinal direction is determined by substituting N_CP into Equation (4).

2.3. Bolted Joint of Branch Member

The connection strength P_CP in the direction of the branch axis, computed by Equation (3), should not exceed the maximum force that the bolted joint of the branch member can carry. The design limit states those that need to be accounted for at the bolted joint include bolt shear yielding, connection slip, hole bearing, and the tensile yielding and block shear rupture of the gusset plate (see Figure 3b). Among various failure modes at the bolted joint, the slip and subsequent hole bearing are critical in the truss connection investigated in this study. According to AISC 360-16 [1], the slip strength and hole-bearing strength, P_slip and P_bearing, respectively, can be computed as follows.

$$P_{slip}=\mu h_f\left(N_b{T}_o\right)N_s$$

(10)

$$P_{bearing}=1.2L_c{t}_g{F}_{ug}\le 2.4d{t}_g{F}_{ug}$$

(11)

where μ = slip coefficient at the faying surface, taken as 0.33 for unpainted clean mill scale steel surfaces; h_f = filler coefficient, which is taken as 1.0 if a filler is not used; N_b = total number of bolts at the joint; T_o = pretension of a single bolt; N_s = number of frictional surfaces; L_c = clear distance in the direction of the force between the edge of the hole and the edge of the adjacent hole or edge of the gusset plate; d = bolt diameter; t_g = thickness of the gusset plate; and F_ug = ultimate strength of the gusset plate.

For the K-connection where both tensile and compressive branch members are jointed, the strengths of the bolted joints in the longitudinal direction of the chord member, V_slip and V_bearing, respectively, can be determined as follows.

$$V_{slip}=2P_{slip}\cos \theta \mathrm{for}\mathrm{K-connections}$$

(12)

$$V_{bearing}=2P_{bearing}\cos \theta \mathrm{for}\mathrm{K-connections}$$

(13)

If slip is not allowed at the bolted joint, the chord face plastification strength V_CP by Equation (4) should not exceed V_slip. However, even after slip occurs, the bolted joint may not fail until V_CP reaches V_slip plus V_bearing because hole bearing that is activated after the slip provides additional resistance.

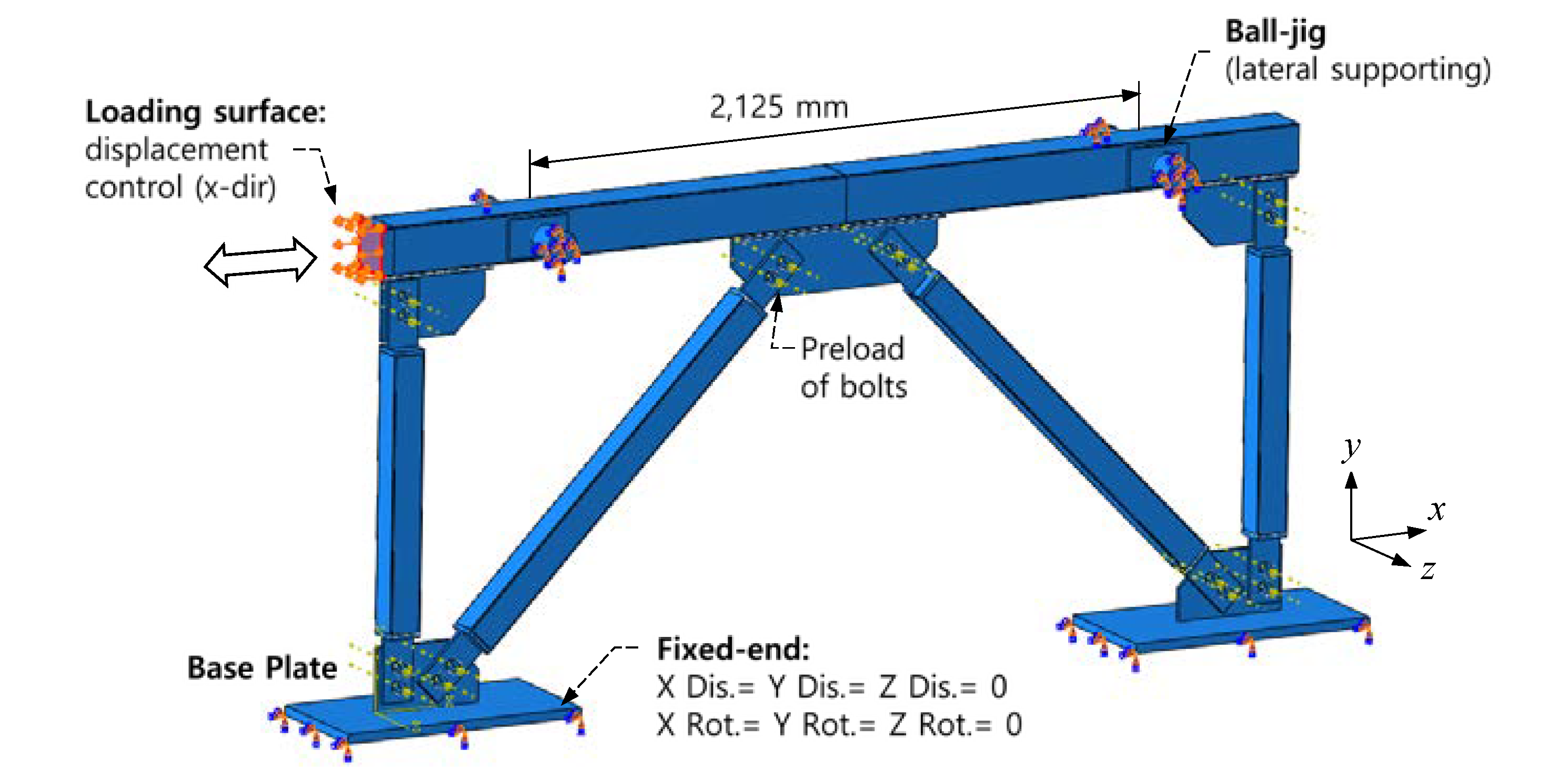
3. Test Program

3.1. Specimen Details

To investigate the behavior and failure mode of plate-to-RHS K-connections, cyclic loading tests of three truss specimens (N00-150, S15-150, and S25-200) were performed.

Table 3. Geometric parameters of plate-to-RHS truss connections.

Specimen	Type	Chord Member	Longitudinal Plate		Chord Face Stiffener
N00-150	Unstiffened	b = 150 mm; b/t = 33.3	lp = 700 mm tp = 15 mm	lp/b = 4.67	-
S15-150	Stiffened	b = 150 mm; b/t = 33.3		lp/b = 4.67	bs = 120 mm; ts = 15 mm; bs/b = 0.8
S25-200	Stiffened	b = 200 mm; b/t = 44.4		lp/b = 3.5	bs = 170 mm; ts = 25 mm; bs/b = 0.85

and Figure 4 show the test variables and connection details of the specimens. In the specimen names, the first letters N and S indicate the plate-to-RHS connections without and with chord face stiffener, respectively; the following numbers “15” and “25” indicate the thickness of the stiffeners (t_s =15 and 25 mm, respectively); and ‘150′ and ‘200′ indicate the width of the connecting chord face (b = 150 and 200 mm, respectively). As shown in Figure 4a, the plate-to-RHS K-connections were fabricated as follows. First, the longitudinal plate of thickness t_p = 15 mm and length l_p = 700 mm was welded to the connecting chord face. Then, two concrete-filled composite branch members were connected to the longitudinal plate by bolting (i.e., slip-critical joint). For the bolted joint, a T-stub including the gusset plate PL-100 × 310 of thickness 15 mm was used at the end of the branch members. To mitigate stress concentration at the weld joint, the gusset plate was extended by 90 mm inside and welded to the steel section (B-100 × 100 × 4.0) and embedded D10 bars; in addition, 4M8 bolts were installed to tie the gusset plate and steel section. The inclination angle between the chord and branch members was θ = 45°. The geometrical parameters of the chord and branch members, longitudinal plate, and chord face stiffener are summarized in Table 3.

A square hollow structural section of B-150 × 150 × 4.5 (h = b = 150 mm and t = 4.5 mm) was used for the chord member in N00-150 and S15-150, while a rectangular hollow structural section of B-150 × 200 × 4.5 (h = 150 mm, b = 200 mm, and t = 4.5 mm) was used in S25-200. For N00-150, the longitudinal plate (t_p = 15 mm and l_p = 700 mm) was welded to the connecting chord face (t = 4.5 mm) without stiffener; for S15–150 and S25-200, on the other hand, the same longitudinal plate was used along with the chord face stiffener of thickness 15 and 25 mm, respectively.

For N00-150, weld size was w = 1.41t = 6.5 mm at the joint between the longitudinal plate and chord face. For S15-150 and S25-200, w = 6.5 mm at the weld joint between the chord face and stiffener and w = 10 mm at the weld joint between the longitudinal plate and stiffener.

3.2. Material Strength and Test Setup

Table 4. Material strength.

Type		Member	Yield Strength (MPa)	Ultimate Strength (MPa)
RHS	4.5 mm	Chord	405	503
	4.0 mm	Branch	395	508
Plate	15 mm	Longitudinal plate and stiffener	429	574
	25 mm	Stiffener	328	519
Bolt	M24	Bolted joint of branch	1040	1102
Bar	D10	Branch	511	665

shows the material strengths of the hollow steel sections, plates, and bolts. For the steel sections used as the chord and branch members, yield strength was F_y = 405 MPa for B-150 × 150 × 4.5 and B-150 × 200 × 4.5, and F_y = 395 MPa for B-100 × 100 × 4.0. For the plates used as the longitudinal plate and chord face stiffener, yield strength was F_y = 429 MPa for thickness 15 mm and F_y = 328 MPa for thickness 25 mm. For the concrete of composite branch members, the average compression strength of three concrete cylinders (100 mm diameter and 200 mm height) was f_c’ = 57.4 MPa. The yield and ultimate strengths of high-tension M24 bolts used for the bolted joint of branch members were F_y = 1040 MPa and F_u = 1102 MPa, respectively.

Figure 5 shows the test setup for lateral loading. A hydraulic actuator of nominal loading capacity 1000 kN was attached to the left end of the chord member. The hydraulic actuator could exert its full loading capacity (i.e., 1000 kN) during positive loading (i.e., pushing to the right) whereas exerting only 65% of its loading capacity during negative loading (i.e., pulling to the left). As shown in Figure 5, four ball jigs were installed to the chord member as lateral support to minimize rotation of the planar truss. Lateral displacements were measured at both ends of the chord member, using the linear variable differential transducers (LVDTs) fixed to a vertical member standing independently.

3.3. Check for Limits of Applicability

For the plate-to-RHS K-connections of the specimens, the limits of applicability summarized in Table 1 were checked as follows.

• The steel yield strength of the chord member, F_y = 405 MPa, exceeded the upper limit of 360 MPa in AISC 360-10. According to the CIDECT Design Guide 3, the steel yield strength was smaller than the upper limit of 460 MPa. The yield ratio, F_y/F_u = 405/503 = 0.805, was slightly greater than the upper limit of 0.8.
• In all specimens, the yield strength of the longitudinal plate, F_yp = 429 MPa, did not satisfy the requirement of the CIDECT Design Guide 3, F_yp ≤ F_y (=405 MPa). For the longitudinal plate under shear force parallel to the chord axis, AISC 360-10 limits F_yp to be not greater than F_ut/t_p to prevent punching shear failure on the connecting chord face. However, for N00–150, F_yp was significantly larger than F_ut/t_p (=503·4.5/15 = 151 MPa).
• For S25-200, the wall width-to-thickness ratio of the chord member, b/t = 44.4, was slightly greater than the upper limit of 40 in AISC 360-10 and CIDECT Design Guide 3. On the other hand, the ratios of the chord width to the branch width, b_b/b = 0.667 and 0.5, were smaller than the upper limit of 0.85 in AISC 360-10, and the ratios of the stiffener width to the chord width, b_s/b = 0.8 and 0.85, did not exceed 0.85.
• For N00-150 and S15–150, the ratio of the plate length to the chord width, l_p/b = 4.67, exceeded the upper limit of 4 in the CIDECT Design Guide 3. On the other hand, for S25-200, l_p/b = 3.5 was within the limit.
• The minimum thickness of chord face stiffener computed by Equation (5) was 19.6 mm for S15-150 (provided thickness t_s = 15 mm) and 24.3 mm for S25-200 (provided thickness t_s = 25 mm). Thus, S15-150 did not satisfy the requirement.

4. Test Results

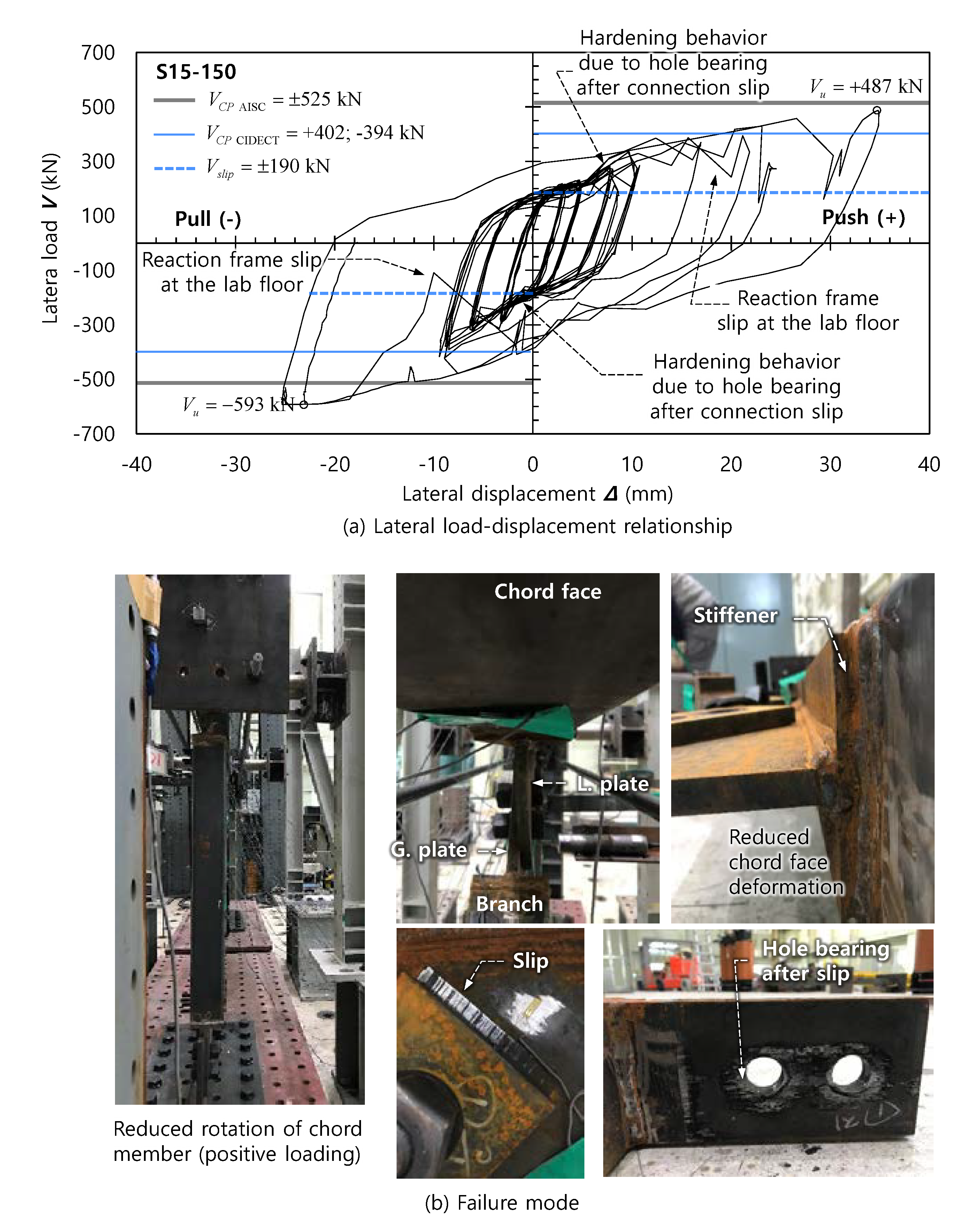
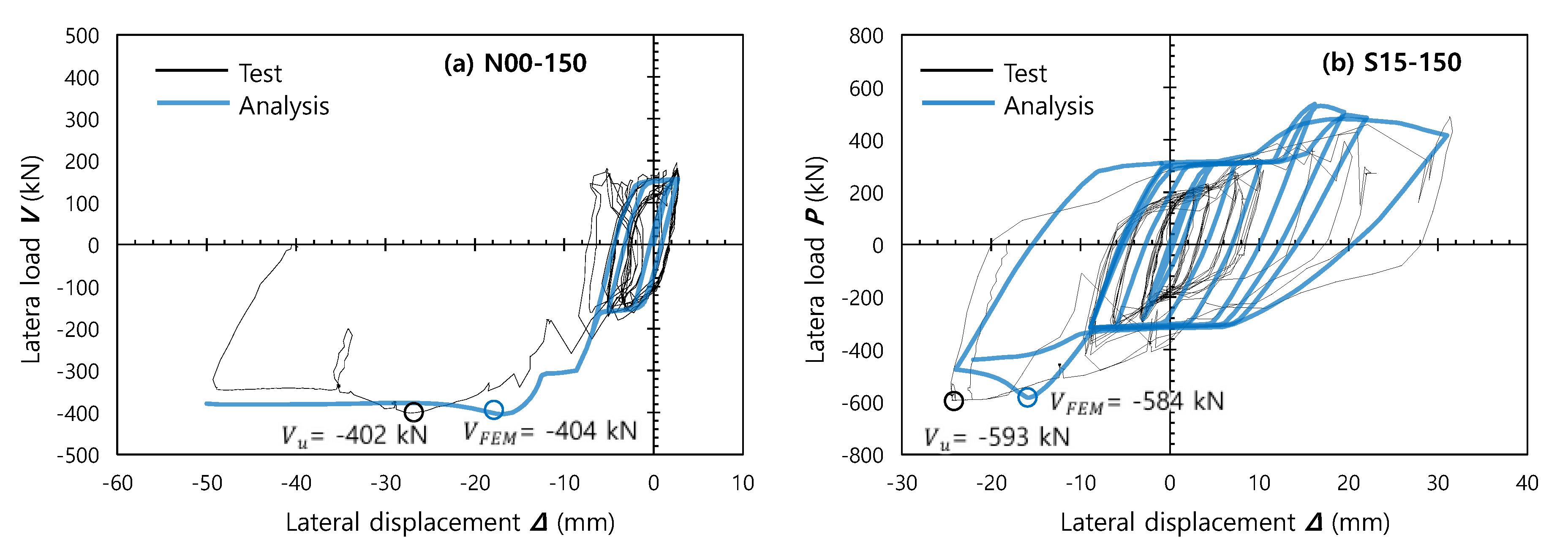
4.1. Load-Displacement Relationship and Failure Mode

Figure 6 shows the lateral load-displacement (V–Δ) relationship and failure mode of the unstiffened specimen N00-150. During the push in the positive direction where the chord member was under compression, the out-of-plane rotation or torsional deformation of the plane truss occurred largely. Such torsional effects were attributed to inappropriate lateral supporting: for N00-150 that was tested first, the location of ball jigs was different from Figure 5 and was concentrated at the center region (horizontal distance 1000 mm) of the chord member. Consequently, as lateral load exceeded 150 kN, the plane truss rotated and the strength was no longer increased. As shown in Figure 6b, out-of-plane deformation or distortion occurred significantly at the plate-to-RHS K-connection, and thus, loading in the positive direction was stopped. During the pull in the negative direction where the chord member was under tension, on the other hand, loading was continued until Δ = −50 mm. The maximum load V_u = −402 kN was reached at Δ = −27 mm (later drift ratio = −1.9%). At the load level of about V = −150 kN, the stiffness decreased as slip occurred at the bolted joint of branch members.

As shown in Figure 6b, the unstiffened K-connection of N00-150 underwent severe deformations of the connecting chord face (t = 4.5 mm and b/t = 33.3) and longitudinal plate (t_p = 15 mm). This shows that the governing limit state was chord face plastification. There was no weld rupture. At the bolted joint of the branch members, scratches on the faying surface were clearly shown and, due to subsequent hole bearing action, threaded marks or dents were left on the inner face of the hole.

Figure 7 shows the test results of the stiffened specimen S15-150. For S15-150, out-of-plane rotation and torsional effects were greatly reduced. As shown in Figure 7a, after robust initial elastic behavior, the stiffness decreased due to slip at the bolted joint of branch members at the load level of about V = ±200 kN; however, the strength and stiffness began to increase again, as the bolt was in contact with the hole edge and bearing action was activated. The maximum load in the positive direction, V_u = +487 kN, was less than that in the negative direction, V_u = −593 kN, due to torsional effects during the push in the positive direction. Note that, during the pull in the negative direction, S15-150 was not fully tested until its ultimate limit state due to the loading limit of the actuator (i.e., 650 kN). At the load level of V = ±400 kN, the load was sharply reduced as the reaction frame slipped on the floor; however, the load was recovered soon after.

As shown in Figure 7b, the deformations of the connecting chord face (t = 4.5 mm and b/t = 33.3) and longitudinal plate (t_p = 15 mm) were significantly reduced at the stiffened K-connection of S15–150 (compare with N00-150 in Figure 6b). There was no weld rupture, and the bolts had little or no deformation. At the bolted joint of branch members, scratches on the faying surface due to slip and, due to subsequent bearing action, threaded marks or dents on the inner face of the hole were clearly shown. This indicates that the governing limit states were the slip and subsequent hole bearing at the bolted joint in addition to chord face plastification.

Figure 8 shows the test results of the stiffened specimen S25-200. For S25-200, after robust linear elastic behavior until V = ±200 kN, the stiffness decreased as slip occurred at the bolted joint of branch members. The decrease in stiffness was more pronounced under positive loading due to torsional effects. After the slip, the load increased again as the bolts provided additional resistance through bearing action. The maximum loads in the positive and negative directions were V_u = +442 kN and −602 kN, respectively. Although the strength was temporarily decreased and then recovered as the reaction frame slipped on the floor, the cyclic behavior of S25-200 was stable overall. As shown in Figure 8a, S25-200 was not loaded further in the negative direction up to its ultimate limit state due to the limit on the loading capacity of the actuator.

As shown in Figure 8b, although the wall width-to-thickness of the connecting chord face (b/t = 44.4) exceeded the allowable limit of 40 specified in AISC 360-10 and CIDECT Design Guide 3, the deformations of the connecting chord face (t = 4.5 mm) and longitudinal plate (t_p = 15 mm) were greatly reduced and similar to those in S15-150. Slip occurred at the bolted joint of branch members. The slip occurred first at the K-connection to the top chord member and then followed at the bottom N-connection. Note that, despite the slip, the strength of the bolted joint of branch members was maintained stable.

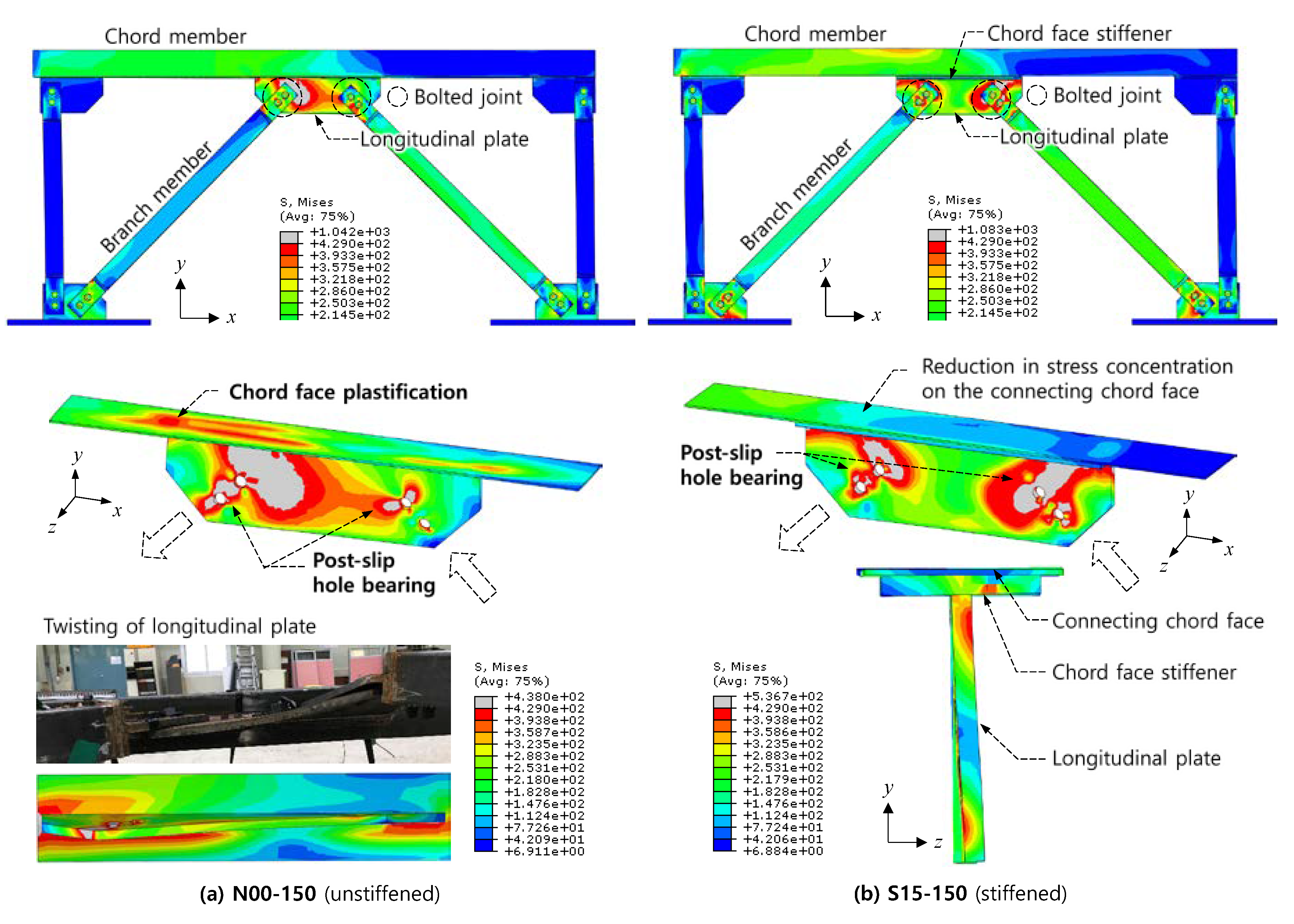
4.2. Effects of Chord Face Stiffener

For N00-150, the stiffness and strength began to degrade early as out-of-plane deformations of the connecting chord face and longitudinal plate occurred at the unstiffened connection. In particular, inappropriate lateral supporting increased such premature strength and stiffness degradation. On the other hand, for S15-150 and S25-200 with the plate-to-RHS K-connection stiffened by chord face stiffener, the deformations of the connective chord face and longitudinal plate were greatly reduced, and consequently, the lateral resistance of the trusses, such as strength and stiffness, was greatly improved. Note that such stiffening effects were achieved even in the state where the design parameters were beyond the limits of applicability specified in current design codes. For example, the steel yield strength of the chord member (F_y =405 MPa) exceeded the specified limit (=360 MPa) by 13%; for S15-150, the thickness of the chord face stiffener (t_s =15 mm) was only 77% of the minimum thickness specified in the CIDECT Design Guide 3; and for S25-200, the wall width-to-thickness ratio of the connecting chord face (b/t = 44.4) exceeded the specified limit (=40) by 11%.

For the stiffened specimens S15-150 and S25-200, chord face plastification was delayed, and instead, the slip and subsequent hole bearing at the bolted joint of branch members became the governing limit states. In general, slip may limit or delay strength development in the slip-critical bolted connection; however, the connection slip that occurs while maintaining the frictional resistance can have positive effects of increasing ductility and energy dissipation, particularly under seismic loading. In this study, as shown in Figure 6, Figure 7 and Figure 8, S15-150 and S25-200 with the stiffened truss K-connections displayed a hardening behavior dissipating considerable energy after the slip at the bolted joint of branch members. This indicates that, if the post-slip bearing resistance of the bolted joint of branch members is large enough to achieve stable cyclic behavior, the seismic performance of stiffened plate-to-RHS connections can be greatly improved by allowing slip at the slip-critical bolted joint.

5. Strength Evaluation

5.1. Theoretical Strengths

The chord face plastification strength V_CP of the unstiffened and stiffened plate-to-RHS K-connections was evaluated using the equations discussed in the previous Section 2. For the unstiffened connection N00-150, V_CP was computed by Equations (1) and (2) for the T- or Y-connections where one branch member is joined. Since both the tensile and compressive branch members were connected to one longitudinal plate, the plate length l_p in Equations (1) and (2) was replaced by an effective length 0.5l_p (=350 mm). For the stiffened connections S15-150 and S25-200, N_CP was computed by Equations (7) and (9), and V_CP was then determined from Equation (4). As shown in

Table 5. Theoretical strengths of plate-to-RHS truss connections.

Specimen	Chord Face Plastification Strength VCP (kN) 1)				Bolted Connection Strength (kN)
	AISC 360-10		CIDECT Design Guide 3		Slip	Post-slip ultimate
	Positive 2)	Negative 2)	Positive 2)	Negative 2)	Vslip	VSB (=Vslip + Vbearing)
N00-150	+154	−149	+135	−132	190	723 (=190 + 533)
S15-150	+525	−525	+402	−394	190	723 (=190 + 533)
S25-200 1)	+644	−644	+479	−463	190	723 (=190 + 533)

¹⁾ For N00-150, N_CP was computed by Equations (1) and (2), applying an effective length 0.5l_p instead of l_p. For S15-150 and S25-200, Equations (7) and (9) were used. V_CP was then computed by Equation (4). ²⁾ The chord member was in compression and tension under positive and negative loadings, respectively.

, the Q_f values (i.e., chord member stress function) were different depending on the direction of loading, and thus, the values of V_CP for the positive and negative loadings (i.e., under chord compression and tension, respectively) were separately computed. In the computation of Q_f, the axial loads of the chord member (=N_u) were approximated as the maximum loads V_u by the test and the moment was neglected (M_u ≒ 0). The theoretical strengths in Table 5 were computed based on the actual material strengths in Table 4.

Table 5 also presents the slip and hole-bearing resistances in the bolted joint of branch members, V_slip and V_bearing, respectively. V_slip (=190 kN) and V_bearing (=533 kN) were computed by Equations (10)–(13). In the computation of V_slip, the preload of the bolts was taken as T_o =204 kN measured by the torque wrench. Note that, for the stiffened truss connections, V_slip (=190 kN) was the smallest and thus the governing limit state was the slip at the bolted joint between the longitudinal plate and branch member. However, since bearing action was activated as the body of the bolts was in contact with the edge of the hole after slip, the ultimate resistance of the bolted joint was greater. Such post-slip ultimate strength was estimated by adding V_slip and V_bearing; V_SB = V_slip + V_bearing (=723 kN).

5.2. Comparison Between Theoretical and Test Strengths

Figure 6, Figure 7 and Figure 8 compare the test and theoretical strengths of the truss connections. The theoretical strengths V_CP (chord face plastification) and V_slip (connection slip) are represented as the horizontal solid and dotted lines. V_SB (post-slip ultimate strength, = 723 kN) is not included in the figures, as the strength value is over 700 kN. The behavior of the unstiffened and stiffened plate-to-RHS K-connections, such as governing limit states and related connection strengths, can be summarized as follows. Note that, since the truss connections did not develop their strength fully under positive loading due to torsional effects, the theoretical strengths were compared with the test strengths under negative loading only.

(1)

In all specimens, the maximum loads V_u were greater than V_slip (=190 kN), which was the slip resistance of the bolted joint of the branch members. Thus, in the load-displacement curves in Figure 6, Figure 7 and Figure 8, the stiffness degradation or slip behavior occurred roughly at the load levels of V = ±190 kN. However, the post-slip ultimate strength V_SB (= 723 kN) was greater than the maximum loads. This explains why hole bearing failure did not occur at the bolted joint while threaded marks or dents were left on the inner face of the hole (see Figure 7b and Figure 8b).

(2)

For N00-150, V_CP of AISC 360-10 and CIDECT Design Guide 3 (= −149 kN and −132 kN, respectively) was less than V_slip (=190 kN). This indicates that the behavior of the unstiffened plate-to-RHS K-connection was governed by chord face plastification. Basically, the chord face plastification was a ductile failure mode accompanying hardening behavior, as reported in the previous studies by Packer, Cao, and Kosteski [6,7]. Thus, during negative loading, the strength significantly increased with increasing displacement. Consequently, the maximum load in the negative direction, V_u = −402 kN, was much larger than V_CP.

(3)

For S15-150 and S25-200 with the stiffened plate-to-RHS K-connections, the overall behavior was governed by chord face plastification after connection slip at the bolted joint of the branch members. Overall, both AISC 360-10 and CIDECT Design Guide 3 gave reasonable estimates on the chord face plastification strengths V_CP of the stiffened connections. AISC 360-10 overestimated the connection strength; the test-to-theoretical strength ratio was V_u/V_CP = 1.13 for S15-150 (= −593 kN/−525 kN) and 0.93 for S25-200 (= −602 kN/−644 kN). On the other hand, the CIDECT Design Guide 3 underestimated the connection strength; V_u/V_CP = −593 kN/−394 kN = 1.51 for S15-150 and V_u/V_CP = −602 kN/−463 kN = 1.30 for S25-200.

As compared above, considering that the test strengths included over-strength effects due to post-yield hardening behavior, the CIDECT Design Guide 3 results in safe and conservative design for stiffened plate-to-RHS K-connections, whereas AISC 360-10 may result in less- or nonconservative design. When designing the plate-to-RHS connections stiffened by chord face stiffener, it is necessary to satisfy the limits of applicability presented in Table 1. Although some of the limits, such as yield strength (F_y ≤ 360 MPa), wall width-to-thickness ratio of the connecting chord face (b/t ≤ 40), and plate length-to-chord width ratio (b/l_p ≤ 4), etc. were violated, test data are not sufficient to investigate the effects of such variables on the connection behavior. Further study on the limits of applicability for RHS truss connections is required.

6. Finite Element Analysis

For the unstiffened and stiffened plate-to-RHS K-connections, N00-150 and S15-150, finite element modeling (FEM) was implemented using ABAQUS (Dassault Systèmes Simulia Corp., Providence, RI, USA). [11]. As shown in Figure 9a,b, the stress-strain relationships of steel materials used for the branch and chord members were idealized as the bilinear or trilinear relationships based on the actual stress–strain curves obtained from the material tensile tests. The yield and ultimate strengths (F_y and F_u) in Table 4 were used (E_s = 200,000 MPa and Poisson’s ratio = 0.3), and the Von Mises yield criterion was applied to address the behavior under multiaxial stresses. For the high-tension bolts, the trilinear σ‒ε relationships were idealized based on the yield and tensile strengths, F_y = 0.9F_u and F_u, respectively (see Figure 9c). To model the material nonlinearity of the steels and bolts under cyclic loading, isotropic and kinematic hardening rules (i.e., combined hardening rule) were used with the Von Mises yield criterion and associated flow rule. The kinematic hardening modulus and the rate at which hardening modulus decreases with plastic strain were assumed as C_k = 700 MPa and γ_k = 75, respectively. For the infilled concrete of the branch member (f_c’ = 57.4 MPa), the damaged plasticity model was applied. Under compression, a parabolic-linear model under compression was used as shown in Figure 9d. The tensile behavior of the concrete before cracking was assumed as a linear elastic relationship (f_ct’ = 0.21√fc’ = 1.59 MPa), and then, the following softening behavior was also simplified as linear. To simulate the inelastic behavior of the concrete under multiaxial stress, the Drucker–Prager plasticity model was applied.

Figure 10 shows the ABAQUS modeling image. All steel and concrete components of the plate-to-RHS K-connection specimens were meshed by the C3D8R element, a general-purpose linear brick element with reduced integration. The RHSs and filled concrete of the chord and branch member were divided by setting mesh size 20 mm. To account for stress flow with accuracy, the longitudinal plate and gusset plate at the joint were finely divided by setting mesh size as 7.5 mm. For the high-strength bolts and weld joints, the smallest mesh size 5 mm was applied. The interface of the weld joints was set to “tie”. On the other hand, “interaction” was applied to the steel-to-steel and steel-to-concrete contact surfaces to account for bearing under compression, friction under shear, and separation under tension. The friction coefficient was assumed as μ = 0.25 for the steel-to-steel contact surface and μ = 0.47 for the steel-to-concrete contact surface [12,13]. As shown in Figure 10, the ball jigs that were used for lateral supporting of the top chord member were also included in the analysis model. Note that, for N00-150 where the location of lateral supporting was different, the ball jigs in the analysis model were placed near the longitudinal plate at the center so that the distance between two ball jigs was 1000 mm.

As the boundary condition, the base plates at the bottom were considered as fixed in all directions or degrees of freedom. The analysis was performed in two phases. In the first phase, the preload of the high-tension bolts (T_o = 204 kN) was applied. Then, cyclic lateral loads were applied to the loading surface of the chord member. The analysis was performed by controlling the lateral displacement of the branch member. Geometric nonlinear was applied. Note that the preload of the bolts was kept constant during cyclic lateral loading, which was implemented by the “fixed at current length” option in ABAQUS.

Figure 11 compares the lateral load-displacement relationships of N00-150 and S15-150. The analysis and test results are denoted as the dashed and solid lines, respectively. Overall, the results of the FEM analysis, such as the elastic stiffness, slip at the bolted joint of the branch member, and post-slip ultimate strength, agreed well with the test results. For S15-150 with the chord face stiffener, the energy dissipation due to frictional slip at the bolted joint of the branch member was observed in the analysis, similar to in the test. However, the detailed behavior was different in the analysis and test, as follows. First, the slip strength at the bolted joint of the branch member was greater in the analysis than in the test. Second, the bolted joints underwent scratches on the faying surface due to slip and threaded marks or dents on the inner face of the hole (see Figure 6b, Figure 7b, and Figure 8b). Such effects were not taken into account for the analysis. Thus, for accurate analysis, fine modeling on the bolted joint is required.

Figure 12 shows the Mises stress distributions (S) and deformations at the peak points denoted in Figure 11. In the region where Mises stresses S are equal to or greater than the yield strength F_y (= 405 MPa for the RHS chord member and 429 MPa for the longitudinal plate and chord face stiffener), tensile or compressive yielding takes place and plastic strains occurs. For the unstiffened connection N00-150 (see Figure 12a), plastic regions where S ≥ F_y were both in the longitudinal plate and connecting chord face; particularly in the longitudinal plate, the plastic regions formed mainly around the bolt holes. This shows that, in the analysis, the behavior of N00-150 was governed by plastification of the connecting chord face and by slip and subsequent hole bearing at the bolted joint. For the stiffened connection S15-150 (see Figure 12b), on the other hand, the connecting chord face remained elastic as the chord face stiffener reduced stress concentration. Instead, plastic regions where S ≥ F_y were mainly in the longitudinal plate. This shows that the behavior of S15-150 was governed by slip and subsequent hole bearing at the bolted joint.

7. Summary and Conclusions

In this study, the behavior and design method of the plate-to-RHS K-connections stiffened by chord face stiffener were investigated. Cyclic loading tests were performed to investigate the stiffening effects of the chord face stiffener, and the applicability of current design codes such as AISC 360-10 and CIDECT Design Guide 3 was discussed. The conclusions are as follows.

(1)

The plate-to-RHS K-connections exhibited the deformation-controlled hardening behavior dissipating considerable energy after slip occurred at the bolted joint of branch members. Overall, the joint behavior was flexible due to out-of-plane deformations of the connecting chord face and longitudinal plate, and thus, there was not brittle failure such as weld rupture.

(2)

The behavior of the plate-to-RHS K-connections stiffened by chord face stiffeners was governed first by slip at the bolted joint of branch members and then by the plastification of the connecting chord face. For S15-150 and S25-200, as the chord face stiffener reduced the deformation of the connecting chord face, the initial stiffness and ultimate strength were greatly increased.

(3)

The provisions of current design codes, such as AISC 360-10 and CIDECT Design Guide 3, yielded a reasonable estimate of the chord face plastification strength of plate-to-RHS K-connections. The CIDECT Design Guide 3 resulted in the conservative estimate of the connection strengths, whereas AISC 360-10 slightly overestimated the strength of the stiffened connections.

If the post-slip-bearing resistance of the bolted joint of branch members is large enough to achieve stable cyclic behavior, the seismic performance of stiffened plate-to-RHS connections can be greatly improved by allowing slip at the slip-critical bolted joint. Thus, for the seismic design of RHS trusses, the following two-phase design may be applicable.

(1)

In the first phase, the plate-to-RHS connections are designed for unfactored service loads (i.e., serviceability limit state). The governing limit state of the truss connections is connection slip at the bolted joint of branch members.

(2)

In the second phase, the plate-to-RHS connections are designed for factored loads at the ultimate limit state. The governing limit state of the truss connections is the plastification of connecting chord face. The bolted joint of branch members should be checked for post-slip failure modes, such as hole-bearing failure and block shear rupture.