Extended Depth-of-Field of a Miniature Optical Endoscope Using Wavefront Coding
Abstract
:1. Introduction
2. Principle and Concept
3. Design and Simulation
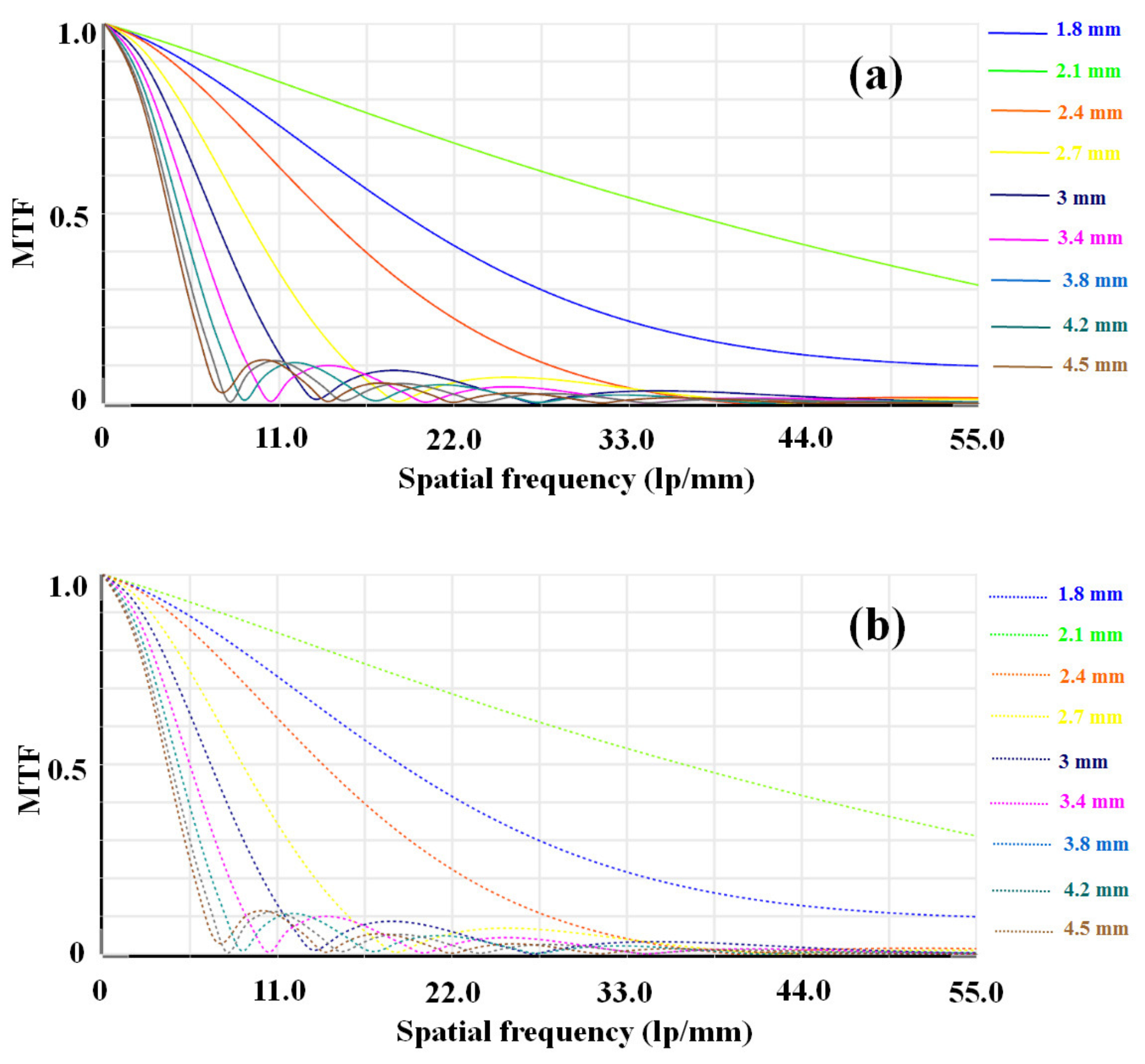
3.1. Initial Optical Endoscope
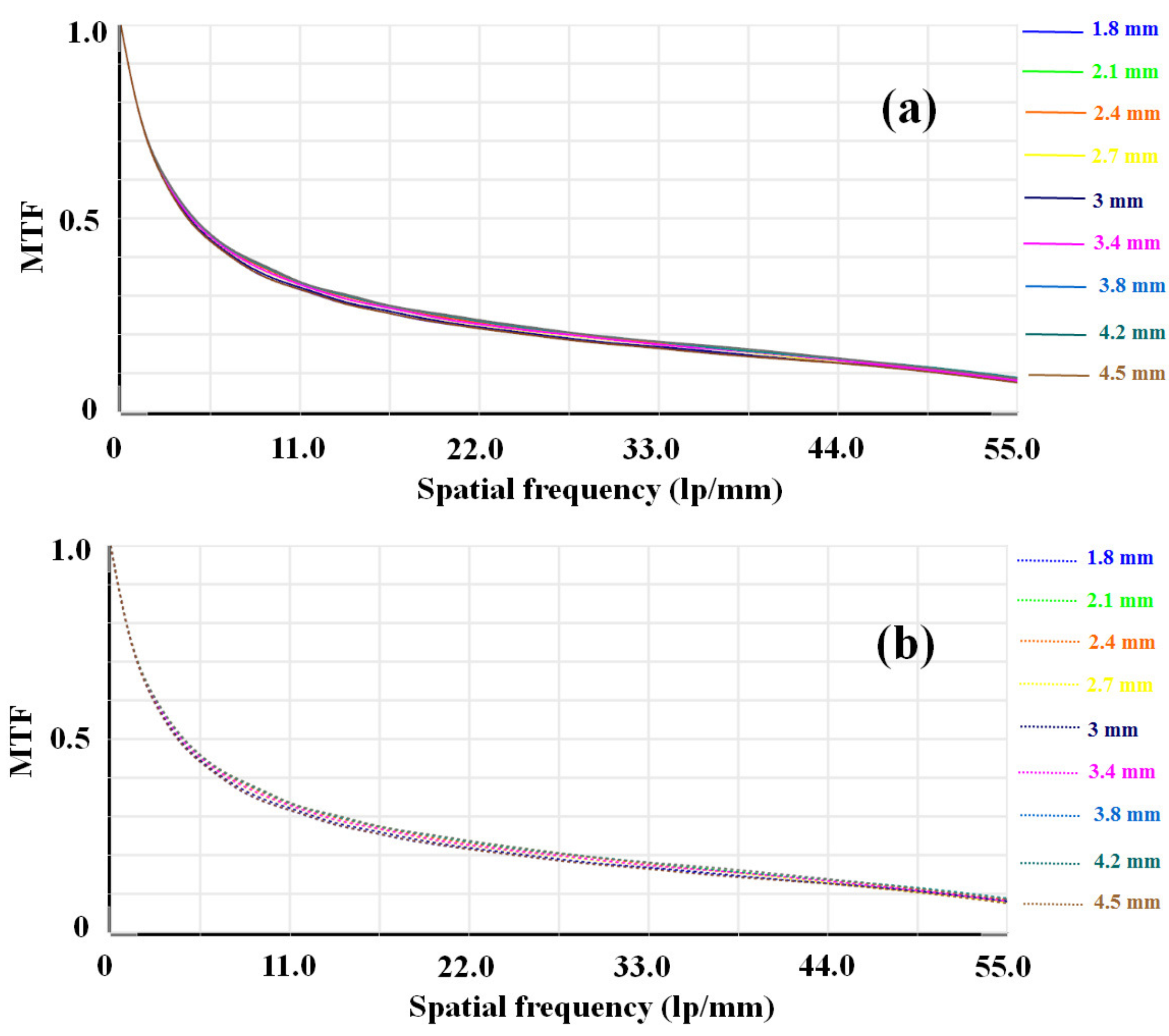
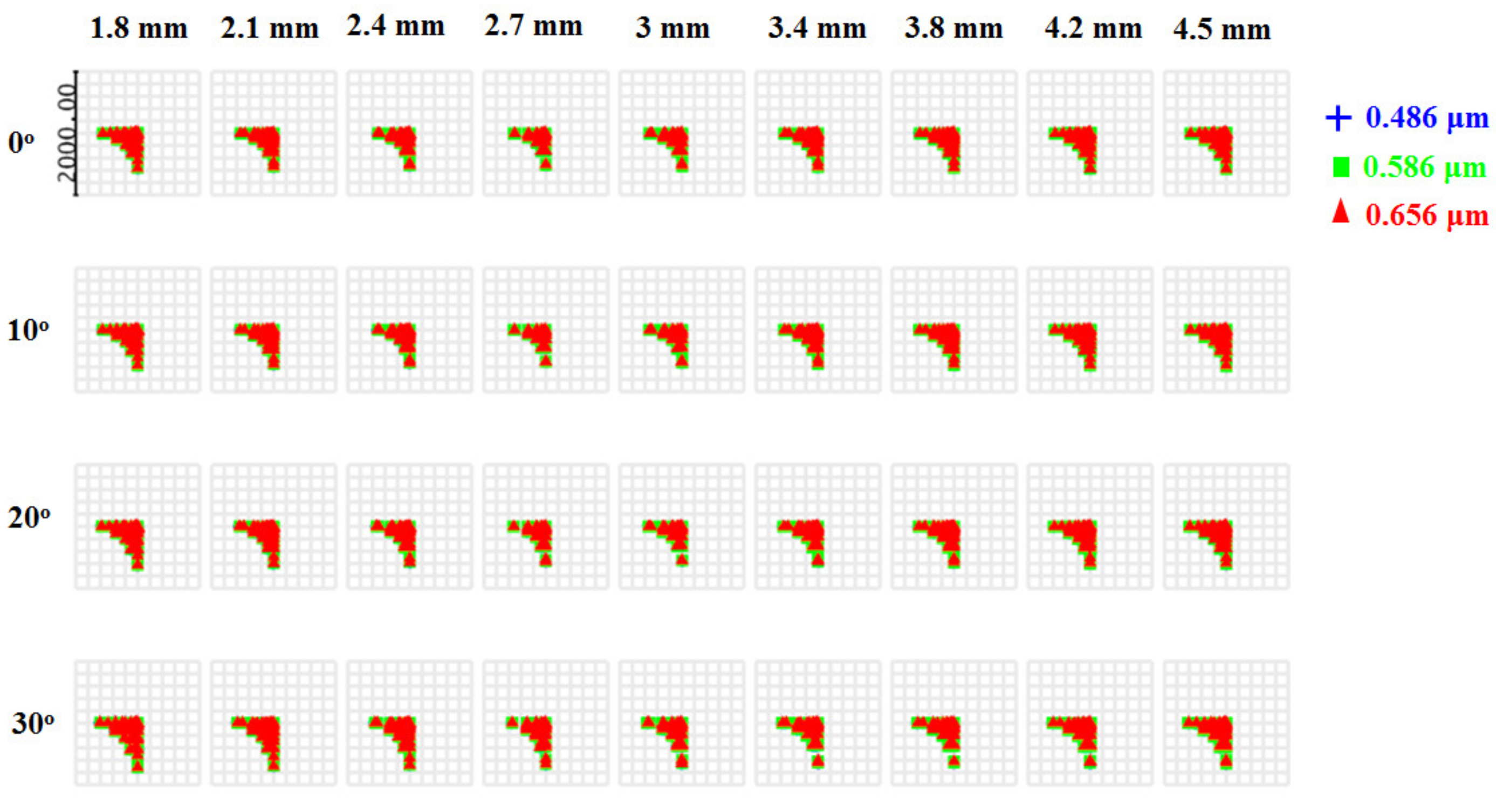
3.2. Optical Endoscope with Phase Mask
4. Restoration Algorithm with Tikhonov Regularization
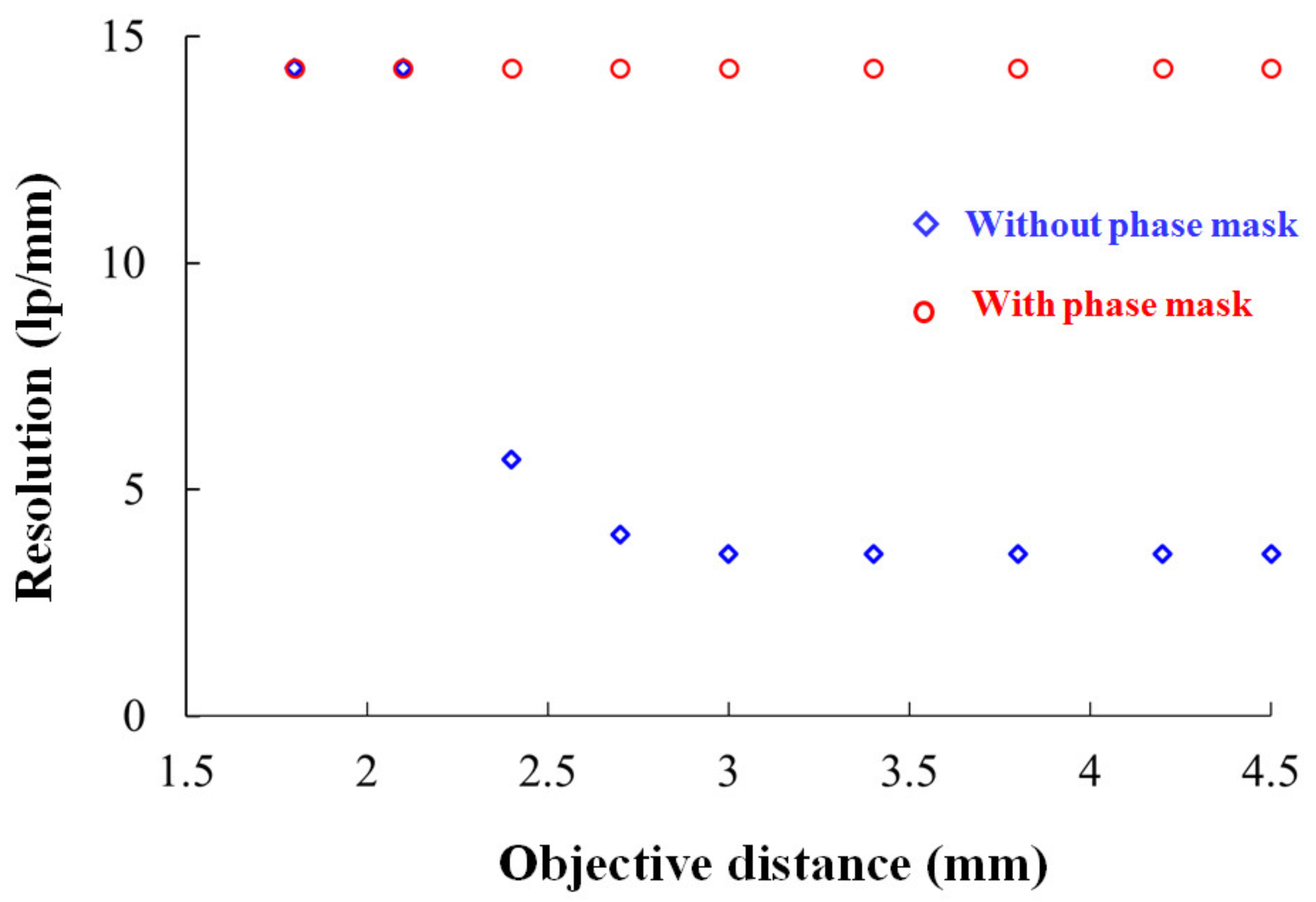
5. Results
6. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Stellingwerff, M.; Breen, J. Applications of optical and digital endoscopy. In Proceedings of the 2nd EAEA-Conference, Vienna, Austria, 30 August–1 September 1995; pp. 55–68. [Google Scholar]
- Garcia, M.; Gruev, V. Optical characterization of rigid endoscopes and polarization calibration methods. Opt. Express 2017, 25, 15713–15728. [Google Scholar] [CrossRef] [PubMed]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Ando, H. Phase shifting apodizers of three or more portions. Jpn. J. Appl. Phys. 1992, 31, 557. [Google Scholar] [CrossRef]
- Welford, W.T. Use of annular aperture to increase focal depth. J. Opt. Soc. Am. A 1960, 50, 749. [Google Scholar] [CrossRef]
- Shain, W.J.; Vickers, N.A.; Goldberg, B.B.; Bifano, T.; Mertz, J. Extended depth-of-field microscopy with a high-speed deformable mirror. Opt. Lett. 2017, 42, 995–998. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Hua, H. Extended depth-of-field microscopic imaging with a variable focus microscope objective. Opt. Express 2011, 19, 353–362. [Google Scholar] [CrossRef] [PubMed]
- Theriault, G.; Koninck, Y.D.; McCarthy, N. Extended depth of field microscopy for rapid volumetric two-photon imaging. Opt. Express 2013, 21, 10095–10104. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Shen, X.; Lin, Y.; Javidi, B. Extended depth-of-field 3D endoscopy with synthetic aperture integral imaging using an electrically tunable focal-length liquid-crystal lens. Opt. Lett. 2015, 40, 3564. [Google Scholar] [CrossRef] [PubMed]
- Shen, X.; Wang, Y.; Chen, H.; Xiao, X.; Lin, Y.; Javidi, B. Extended depth-of-focus 3D micro integral imaging display using a bifocal liquid crystal lens. Opt. Lett. 2015, 40, 538. [Google Scholar] [CrossRef] [PubMed]
- Dowski, E.R.; Cathey, W.T. Extended depth of field through wave-front coding. Appl. Opt. 1995, 34, 1859. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zammit, P.; Harvey, A.R.; Carles, G. Extended depth-of-field imaging and ranging in a snapshot. Optica 2014, 1, 209. [Google Scholar] [CrossRef]
- Castro, A.; Ojeda-Castaneda, J. Asymmetric phase masks for extended depth of field. Appl. Opt. 2004, 43, 3474. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.B.; He, L.R.; Yang, L.; Mao, C.S.; Zhao, M.; Li, J.L.; Yang, T. An extended depth-of-field imaging system with a non-rotationally symmetric phase mask. Rev. Sci. Instrum. 2018, 89, 103101. [Google Scholar] [CrossRef] [PubMed]
- Ben-Elizer, E.; Zalevsky, Z.; Marom, E.; Konforti, N. All-optical extended depth of field imaging sytem. J. Opt. A Pure Appl. Opt. 2003, 5, S164–S169. [Google Scholar] [CrossRef]
- Lipson, A.; Lipson, S.G.; Lipson, H. Optical Physics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Zhou, F.; Ye, R.; Li, G.; Zhang, H.; Wang, D. Optimized circularly symmetric phase mask to extend the depth of focus. J. Opt. Soc. Am. A 2009, 26, 1889. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Li, Y. Performance of an improved logarithmic phase mask with optimized parameters in a wavefront-coding system. Appl. Opt. 2010, 49, 229. [Google Scholar] [CrossRef] [PubMed]
- Gockenbach, M. Linear Inverse Problems and Tikhonov Regularization; The Mathematical Association of America: Washington, DC, USA, 2016. [Google Scholar]
- Calvetti, D.; Morigi, S.; Reichel, L.; Sgallari, F. Tikhonov regularization and the L-curve for large discrete ill-posed problems. J. Comput. Appl. Math. 2000, 123, 423. [Google Scholar] [CrossRef] [Green Version]
- Wach, H.B.; Dowski, E.R.; Cathey, W.T. Control of chromatic focal shift through wave-front coding. Appl. Opt. 1998, 37, 5359–5367. [Google Scholar] [CrossRef] [PubMed]








| Parameter | Data | Parameter | Data |
|---|---|---|---|
| Number of surfaces | 32 | Diameter of entrance pupil (mm) | 0.350 |
| Number of apertures | 8 | Position of entrance pupil (mm) | 3.181 |
| Effective focus distance (mm) | 3.212 | Diameter of exit pupil (mm) | 0.899 |
| Back focus distance (mm) | 1.474 | Position of exit pupil (mm) | 13.727 |
| F number of image space | 9.178 | Maximum of radial field of view () | 31.113 |
| F number of work | 15.435 | Paraxial imaging height (mm) | 3.194 |
| Diameter of aperture stop (mm) | 0.836 | Paraxial magnification | −1.664 |
| Main wavelength (m) | 0.586 | Angle magnification | −0.389 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Chen, M.; Wang, J.; Zhu, M.; Yang, T.; Zhu, S.; Xie, H. Extended Depth-of-Field of a Miniature Optical Endoscope Using Wavefront Coding. Appl. Sci. 2020, 10, 3838. https://doi.org/10.3390/app10113838
Yang L, Chen M, Wang J, Zhu M, Yang T, Zhu S, Xie H. Extended Depth-of-Field of a Miniature Optical Endoscope Using Wavefront Coding. Applied Sciences. 2020; 10(11):3838. https://doi.org/10.3390/app10113838
Chicago/Turabian StyleYang, Lei, Meng Chen, Jin Wang, Meng Zhu, Tong Yang, Shimin Zhu, and Hongbo Xie. 2020. "Extended Depth-of-Field of a Miniature Optical Endoscope Using Wavefront Coding" Applied Sciences 10, no. 11: 3838. https://doi.org/10.3390/app10113838
APA StyleYang, L., Chen, M., Wang, J., Zhu, M., Yang, T., Zhu, S., & Xie, H. (2020). Extended Depth-of-Field of a Miniature Optical Endoscope Using Wavefront Coding. Applied Sciences, 10(11), 3838. https://doi.org/10.3390/app10113838




