Deformation of Air Bubbles Near a Plunging Jet Using a Machine Learning Approach
Abstract
1. Introduction
2. Material and Methods
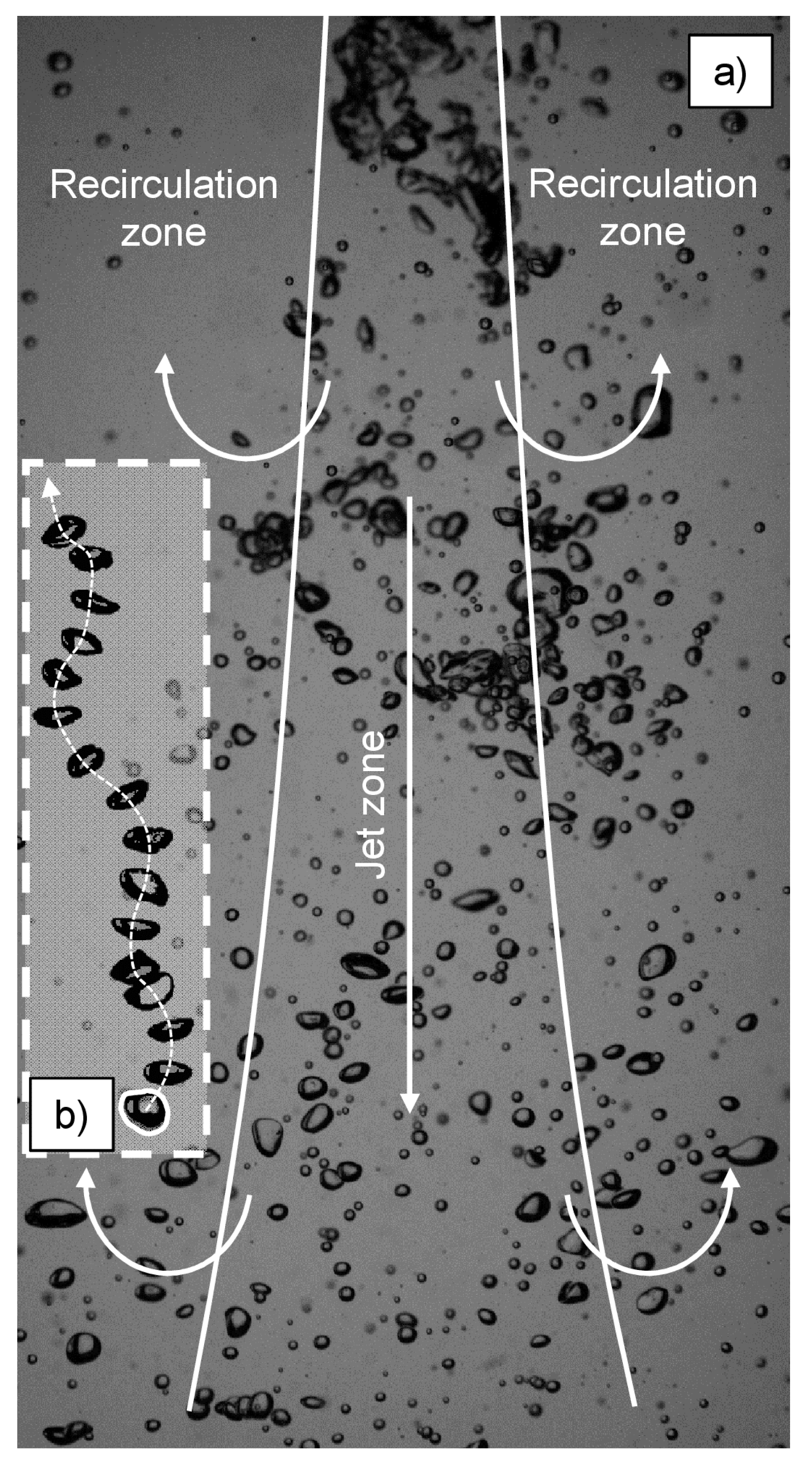
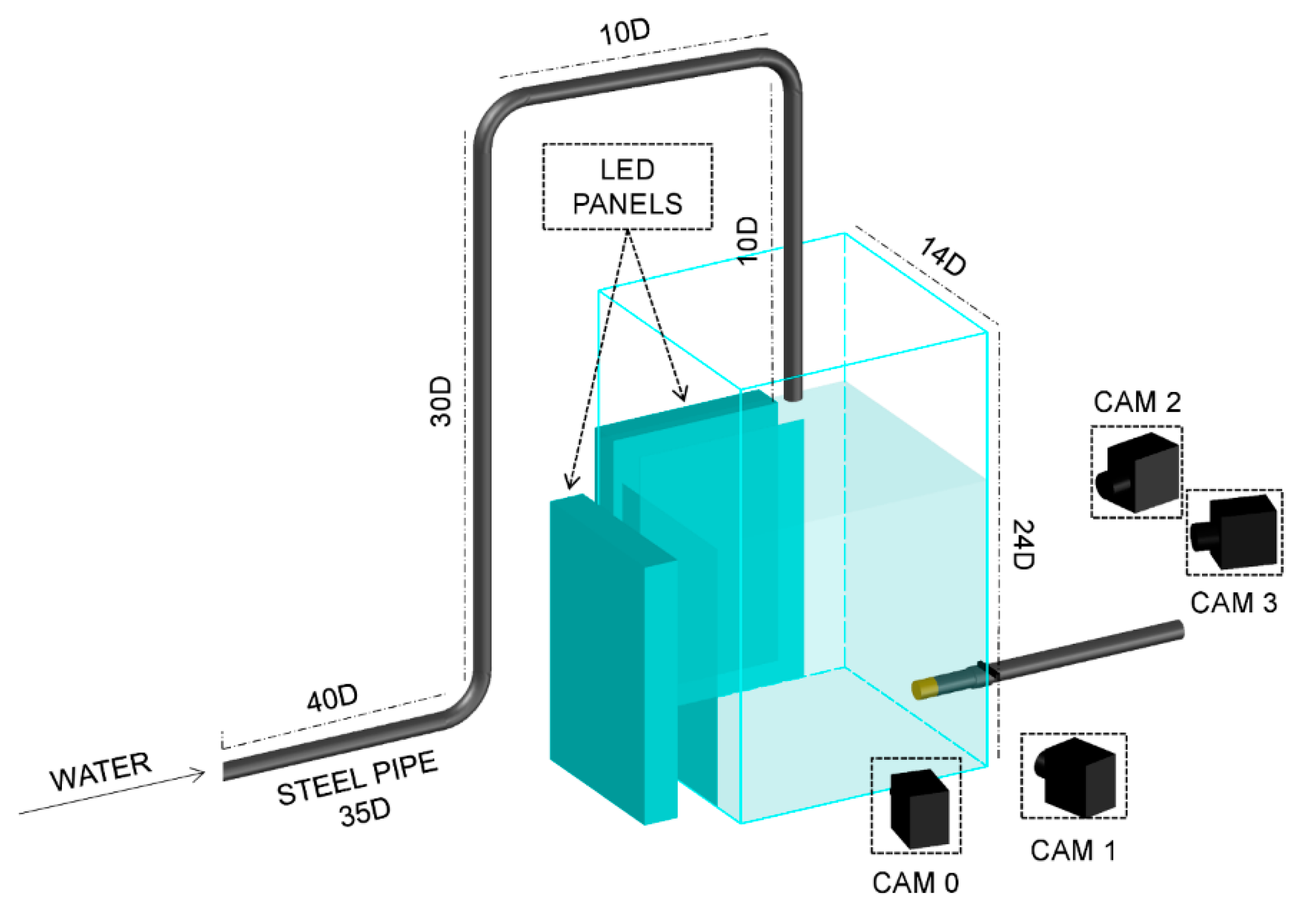
2.1. Experimental Setup
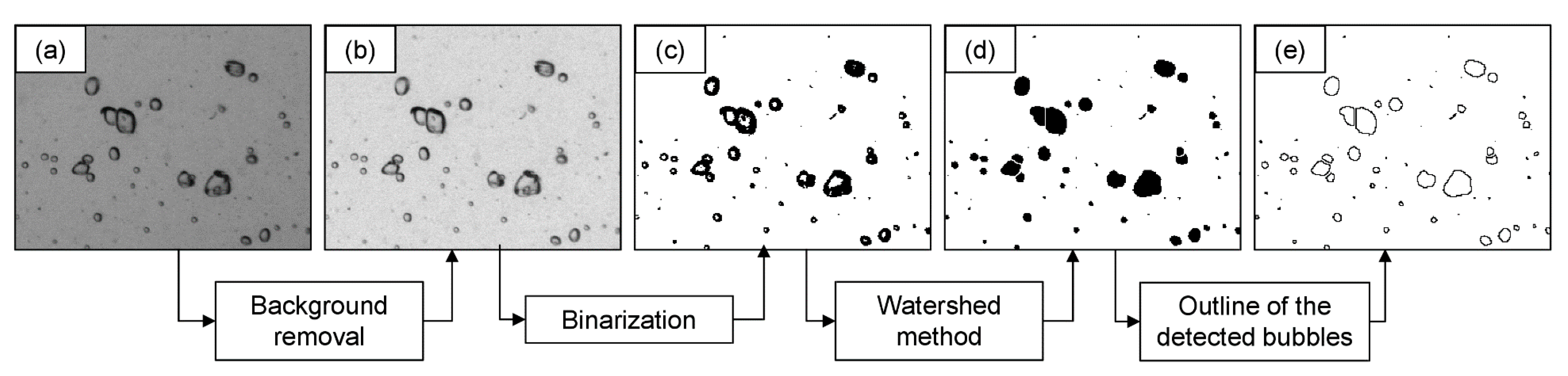
2.2. Volumetric Shadowgraph Technique
2.3. Algorithms
2.3.1. Additive Regression of Decision Stumps
2.3.2. K-Star
2.3.3. Bagging and Random Forest
2.3.4. Support Vector Regression
2.4. Evaluation Metrics and Cross-Validation
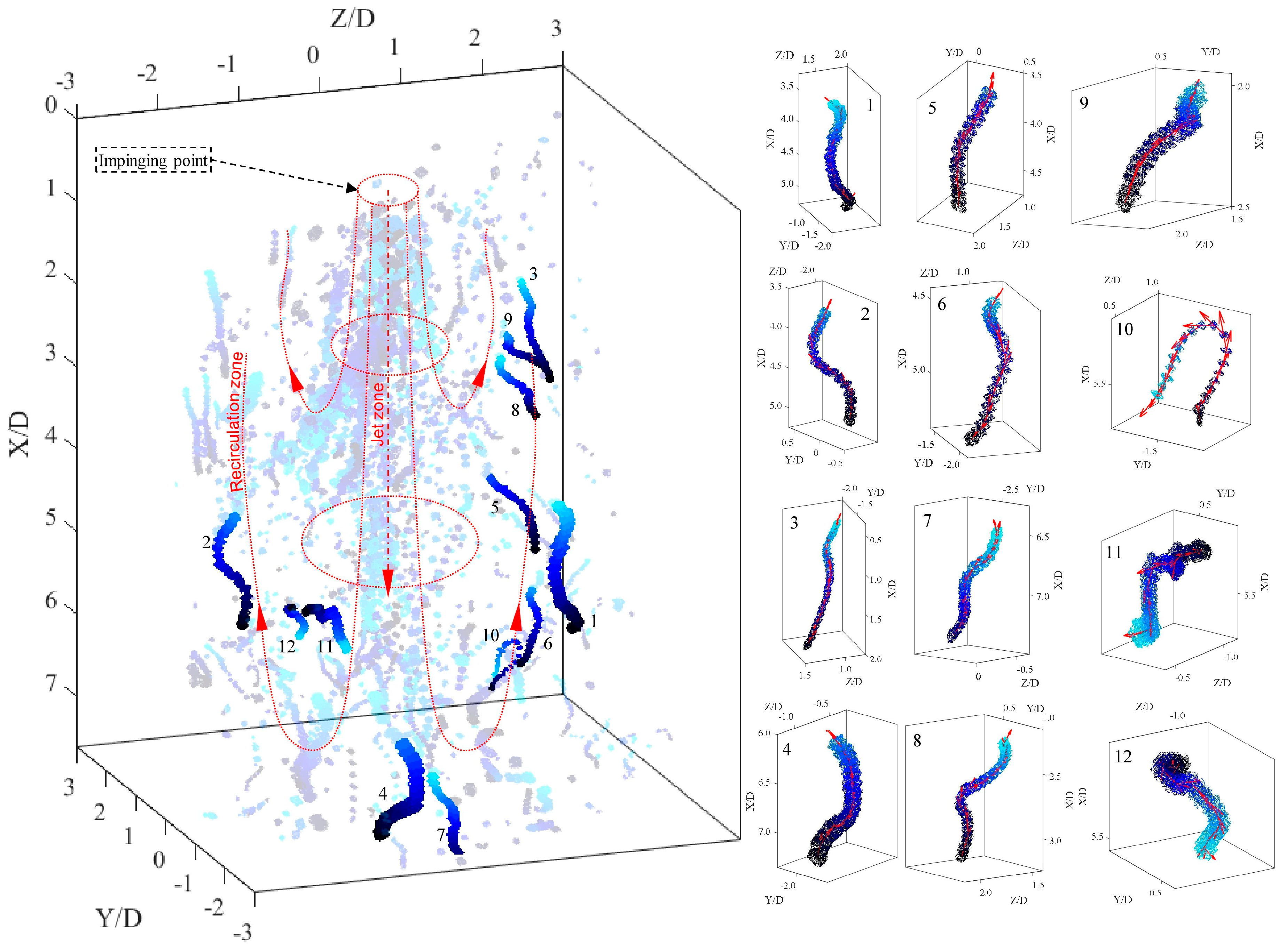
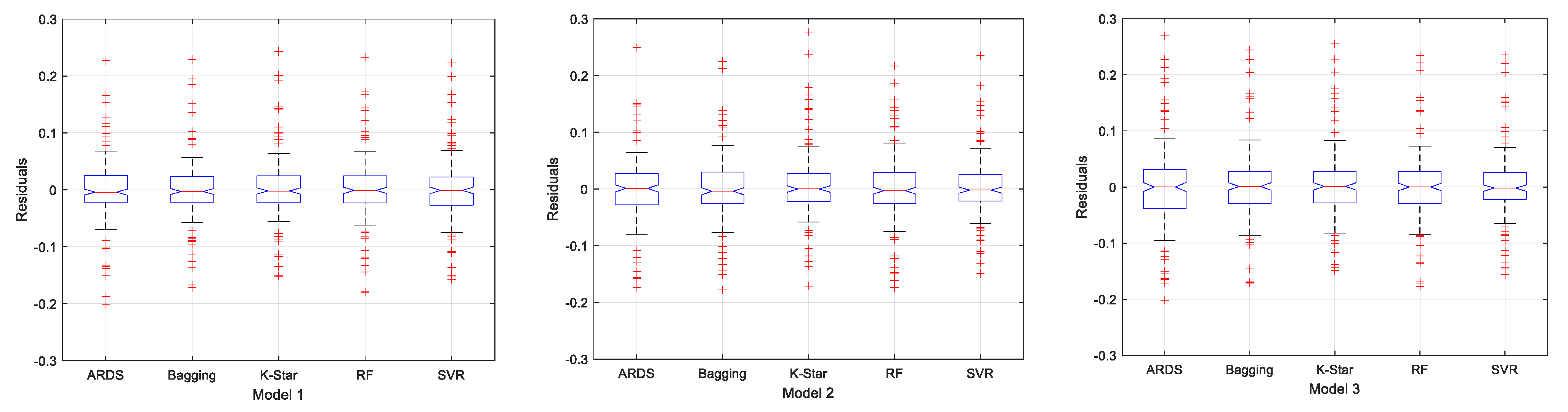
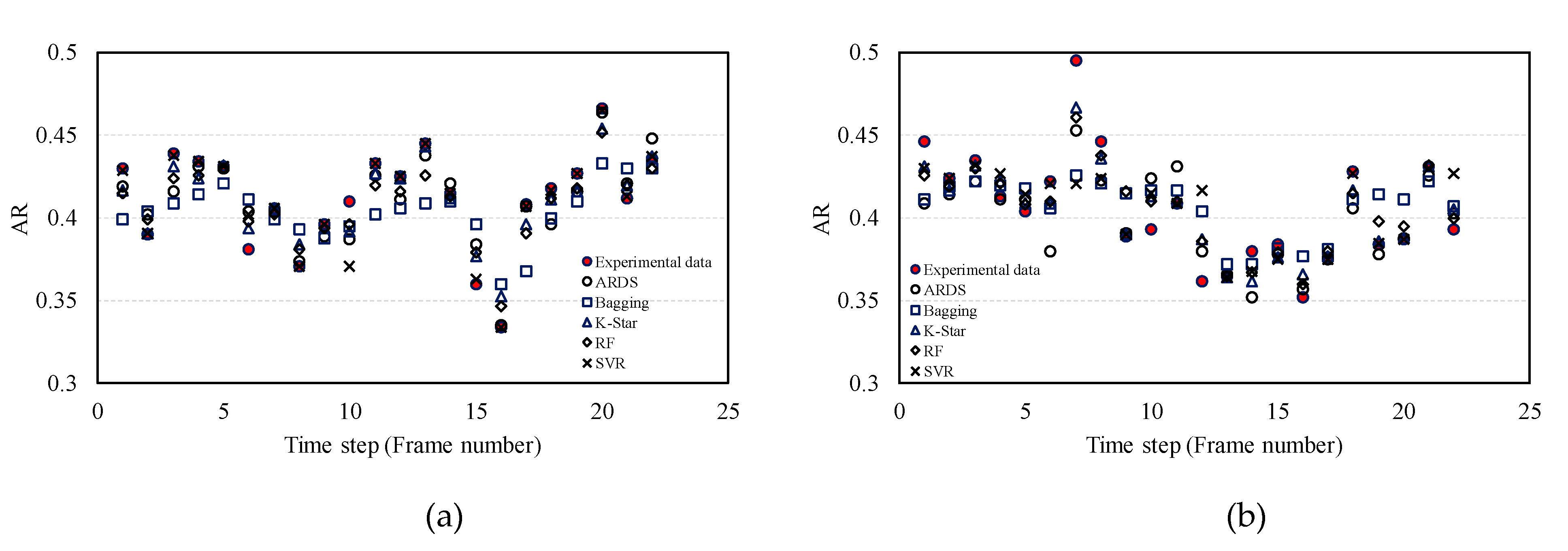
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rayleigh, L. On the pressure developed in a liquid during the collapse of a spherical cavity. Philos. Mag. 1919, 34, 94–98. [Google Scholar] [CrossRef]
- Plesset, M.S. The dynamics of cavitation bubbles. J. Appl. Mech. 1949, 16, 228–231. [Google Scholar] [CrossRef]
- Gilmore, F.R. The Growth or Collapse of a Spherical Bubble in a Viscous Compressible Liquid; California Institute of Technology: Pasadena, CA, USA, 1952; Unpublished. [Google Scholar]
- Fujikawa, S.; Akamatsu, T. Effects of the non-equilibrium condensation of vapour on the pressure wave produced by the collapse of a bubble in a liquid. J. Fluid Mech. 1980, 97, 3–512. [Google Scholar] [CrossRef]
- Keller, J.B.; Miksis, M. Bubble oscillations of large amplitude. J. Acoust. Soc. Am. 1980, 68, 2–633. [Google Scholar] [CrossRef]
- Prosperetti, A.; Crum, L.A.; Commander, K.W. Nonlinear bubble dynamics. J. Acoust. Soc. Am. 1988, 83, 2–514. [Google Scholar] [CrossRef]
- Fujiwara, A.; Danmoto, Y.; Hishida, K.; Maeda, M. Bubble deformation and flow structure measured by double shadow images and PIV/LIF. Exp. Fluids 2004, 36, 1–165. [Google Scholar] [CrossRef]
- Cao, Y.; Kawara, Z.; Yokomine, T.; Kunugi, T. Experimental and numerical study on nucleate bubble deformation in subcooled flow boiling. Int. J. Multiph. Flow 2016, 82, 93–105. [Google Scholar] [CrossRef]
- Feng, J.; Cao, J.; Jiang, J.; Sun, B.; Cai, Z.; Gao, Z. Single bubble breakup in the flow field induced by a horizontal jet—The experimental research. Asia Pac. J. Chem. Eng. 2019, 14, 1. [Google Scholar] [CrossRef]
- Korobeynikov, S.M.; Ridel, A.V.; Medvedev, D.A. Deformation of bubbles in transformer oil at the action of alternating electric field. Eur. J. Mech. B Fluids 2019, 75, 105–109. [Google Scholar] [CrossRef]
- Ekambara, K.; Dhotre, M.T.; Joshi, J.B. CFD simulations of bubble column reactors: 1D, 2D and 3D approach. Chem. Eng. Sci. 2005, 60, 23–6746. [Google Scholar] [CrossRef]
- Kerdouss, F.; Bannari, A.; Proulx, P. CFD modeling of gas dispersion and bubble size in a double turbine stirred tank. Chem. Eng. Sci. 2006, 61, 10–3322. [Google Scholar] [CrossRef]
- Rzehak, R.; Krepper, E. CFD modeling of bubble-induced turbulence. Int. J. Multiph. Flow 2013, 55, 138–155. [Google Scholar] [CrossRef]
- Fletcher, D.F.; McClure, D.D.; Kavanagh, J.M.; Barton, G.W. CFD simulation of industrial bubble columns: Numerical challenges and model validation successes. Appl. Math. Model. 2017, 44, 25–42. [Google Scholar] [CrossRef]
- Pfister, M.; Chanson, H. Two-phase air-water flows: Scale effects in physical modeling. J. Hydrodyn. Ser. B 2014, 26, 2–298. [Google Scholar] [CrossRef]
- Schmidt, E. Ähnlichkeitstheorie der Bewegung von Flüssigkeitsgasgemsichen (Similarity Theory of Motion in Fluid-Gas Mixtures). Forschungsheft 1934, 365, 1–3. (In German) [Google Scholar]
- Clift, R.; Grace, J.; Weber, M. Bubbles, Drops, and Particles; Academic Press: New York, NY, USA, 1978; p. 380. [Google Scholar]
- Tripathi, M.; Sahu, K.; Govindarajan, R. Dynamics of an initially spherical bubble rising in quiescent liquid. Nat. Commun. 2015, 6, 6268. [Google Scholar] [CrossRef]
- Cummings, P.D.; Chanson, H. Air Entrainment in the Developing Flow Region of Plunging Jets—Part 1: Theoretical Development. J. Fluids Eng. Trans. ASME 1997, 119, 3–602. [Google Scholar] [CrossRef]
- Ervine, D.A.; Falvey, H.T.; Withers, W.A. Pressure fluctuations on plunge pool floors. J. Hydraul. Res. 1997, 35, 257–279. [Google Scholar] [CrossRef]
- Liao, Y.; Rzehak, R.; Lucas, D.; Krepper, E. Baseline closure model for dispersed bubbly flow: Bubble coalescence and breakup. Chem. Eng. Sci. 2015, 122, 336–349. [Google Scholar] [CrossRef]
- Lunde, K.; Perkins, R.J. Shape Oscillations of Rising Bubbles. Flow Turbul. Combust. 1997, 58, 387–408. [Google Scholar]
- Avdeev, A.A. Bubble Systems; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Solomatine, D.P.; Xue, Y. M5 Model Trees and Neural Networks: Application to Flood Forecasting in the Upper Reach of the Huai River in China. J. Hydrol. Eng. 2004, 9, 6–501. [Google Scholar] [CrossRef]
- Ahmad, S.; Kalra, A.; Stephen, H. Estimating soil moisture using remote sensing data: A machine learning approach. Adv. Water Resour. 2010, 33, 1–80. [Google Scholar] [CrossRef]
- Nourani, V.; Kisi, Ö.; Komasi, M. Two hybrid artificial intelligence approaches for modeling rainfall–runoff process. J. Hydrol. 2011, 402, 41–59. [Google Scholar] [CrossRef]
- Kisi, O. Modeling discharge-suspended sediment relationship using least square support vector machine. J. Hydrol. 2012, 456, 110–120. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Etemad-Shahidi, A.; Lim, S.Y. Scour prediction in long contractions using ANFIS and SVM. Ocean Eng. 2016, 111, 128–135. [Google Scholar] [CrossRef]
- Granata, F.; Papirio, S.; Esposito, G.; Gargano, R.; De Marinis, G. Machine learning algorithms for the forecasting of wastewater quality indicators. Water 2017, 9, 2. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Ahmadi, K.; Daneshi, A. Application of support vector machine, random forest, and genetic algorithm optimized random forest models in groundwater potential mapping. Water Resour. Manag. 2017, 31, 9–2775. [Google Scholar] [CrossRef]
- Granata, F. Evapotranspiration evaluation models based on machine learning algorithms—A comparative study. Agric. Water Manag. 2019, 217, 303–315. [Google Scholar] [CrossRef]
- Arnon, T.A.; Ezra, S.; Fishbain, B. Water characterization and early contamination detection in highly varying stochastic background water, based on Machine Learning methodology for processing real- time UV-Spectrophotometry. Water Res. 2019, 155, 333–342. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F.; Gargano, R.; de Marinis, G. Equivalent Discharge Coefficient of Side Weirs in Circular Channel—A Lazy Machine Learning Approach. Water 2019, 11, 11. [Google Scholar] [CrossRef]
- Granata, F.; Gargano, R.; de Marinis, G. Artificial intelligence based approaches to evaluate actual evapotranspiration in wetlands. Sci. Total Environ. 2020, 703, 135653. [Google Scholar] [CrossRef] [PubMed]
- Shaban, H.; Tavoularis, S. Measurement of gas and liquid flow rates in two-phase pipe flows by the application of machine learning techniques to differential pressure signals. Int. J. Multiph. Flow 2014, 67, 106–117. [Google Scholar] [CrossRef]
- Granata, F.; de Marinis, G. Machine learning methods for wastewater hydraulics. Flow Meas. Instrum. 2017, 57, 1–9. [Google Scholar] [CrossRef]
- Mosavi, A.; Shamshirband, S.; Salwana, E.; Chau, K.W.; Tah, J.H. Prediction of multi-inputs bubble column reactor using a novel hybrid model of computational fluid dynamics and machine learning. Eng. Appl. Comput. Fluid Mech. 2019, 13, 1–492. [Google Scholar] [CrossRef]
- Li, Q.; Griffiths, J.G. Least squares ellipsoid specific fitting. In Proceedings of the Geometric Modeling and Processing, Beijing, China, 13–15 April 2004; pp. 335–340. [Google Scholar]
- Pereira, F.; Avellan, F.; Dupont, P. Prediction of cavitation erosion: An energy approach. J. Fluids Eng. 1998, 120, 4–727. [Google Scholar] [CrossRef]
- Di Nunno, F.; Alves Pereira, F.; Granata, F.; de Marinis, G.; Di Felice, F.; Gargano, R.; Miozzi, M. A shadowgraphy approach for the 3D Lagrangian description of bubbly flows. Meas. Sci. Technol. 2020, in press. [Google Scholar] [CrossRef]
- Tsai, R.Y. An Efficient and Accurate Camera Calibration Technique for 3D Machine Vision. In Proceedings of the Computer Vision and Pattern Recognition, Miami Beach, FL, USA, 22–26 June 1986; pp. 364–374. [Google Scholar]
- Trucco, E.; Verri, A. Introductory Techniques for 3-D Computer Vision; Prentice Hall: Englewood Cliffs, NJ, USA, 1998; p. 343. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, Y. 3D bubble reconstruction using multiple cameras and space carving method. Meas. Sci. Technol. 2018, 29, 7. [Google Scholar] [CrossRef]
- Ridler, T.; Calvard, S. Picture thresholding using an iterative selection method. IEEE Trans. Syst. Man Cybern. SMC-8 1978, 8, 630–632. [Google Scholar]
- Vincent, L.; Soille, P. Watersheds in digital spaces: An efficient algorithm based on immersion simulations. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 6–598. [Google Scholar] [CrossRef]
- Di Nunno, F.; Alves Pereira, F.; de Marinis, G.; Di Felice, F.; Gargano, R.; Granata, F.; Miozzi, M. Experimental study of air-water two-phase jet: Bubble size distribution and velocity measurements. J. Phys. Conf. Ser. 2018, 1110, 012011. [Google Scholar]
- Di Nunno, F.; Alves Pereira, F.; de Marinis, G.; Di Felice, F.; Gargano, R.; Granata, F.; Miozzi, M. Two-phase PIV-LIF measurements in a submerged bubbly water jet. J. Hydraul. Eng. 2019, 145, 9. [Google Scholar] [CrossRef]
- Lucas, B.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision. In Proceedings of the 7th International Joint Conference on Artificial Intelligence, Vancouver, BC, Canada, 24–28 August 1981; pp. 121–130. [Google Scholar]
- Miozzi, M.; Jacob, B.; Olivieri, A. Performances of feature tracking in turbulent boundary layer investigation. Exp. Fluids 2008, 45, 4–780. [Google Scholar] [CrossRef]
- Fdida, N.; Blaisot, J.B. Drop size distribution measured by imaging: Determination of the measurement volume by the calibration of the point spread function. Meas. Sci. Technol. 2009, 21, 2. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques, 2nd ed.; Morgan Kaufmann: Burlington, VT, USA, 2016; p. 560. [Google Scholar]
- Cleary, J.G.; Trigg, L.E. K*: An instance based learner using an entropic distance measure. In Proceedings of the 12th International Conference on Machine Learning, Tahoe City, CA, USA, 9–12 July 1995; pp. 108–114. [Google Scholar]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; Taylor & Francis: Abingdon, UK, 1984; p. 368. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]

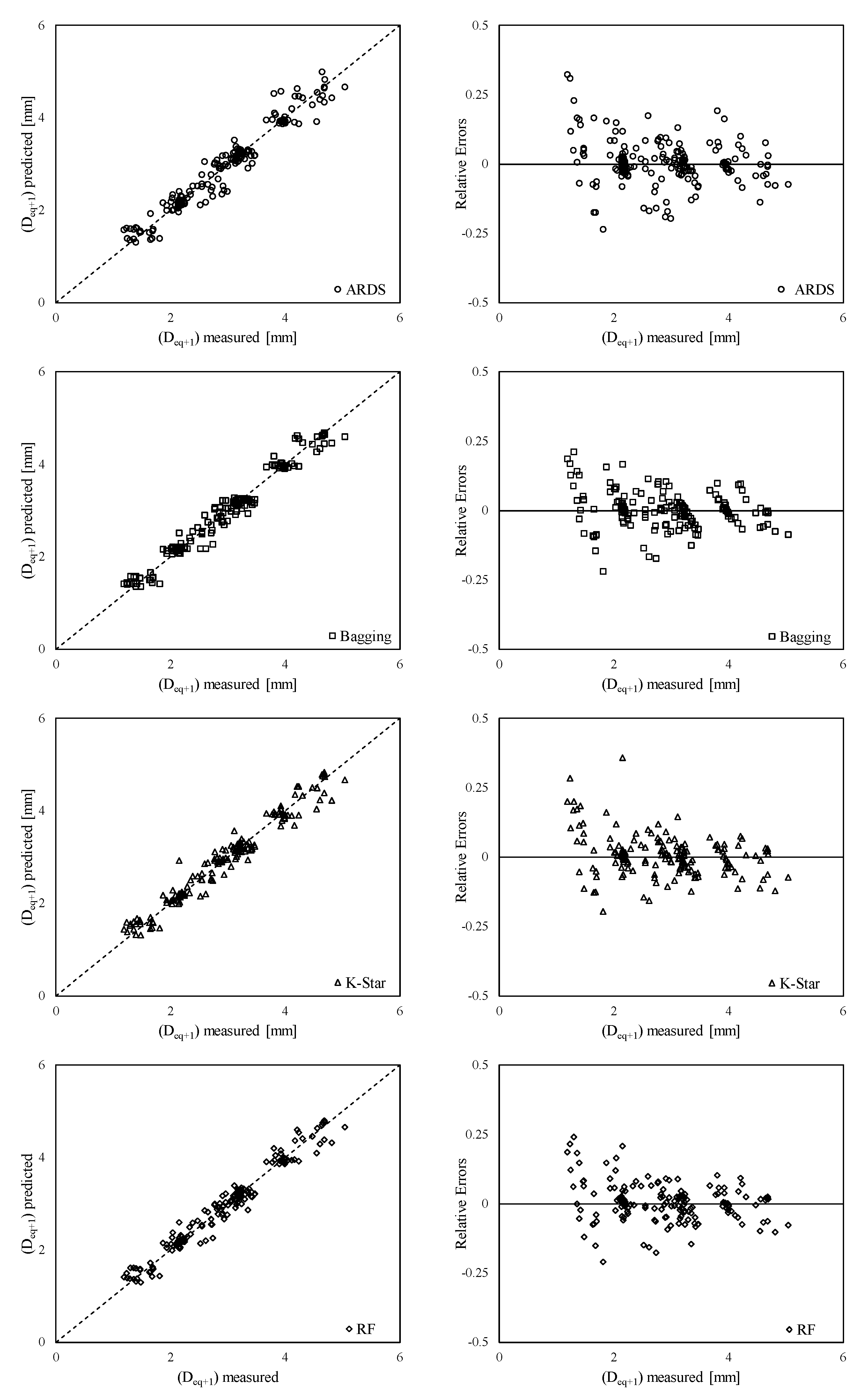


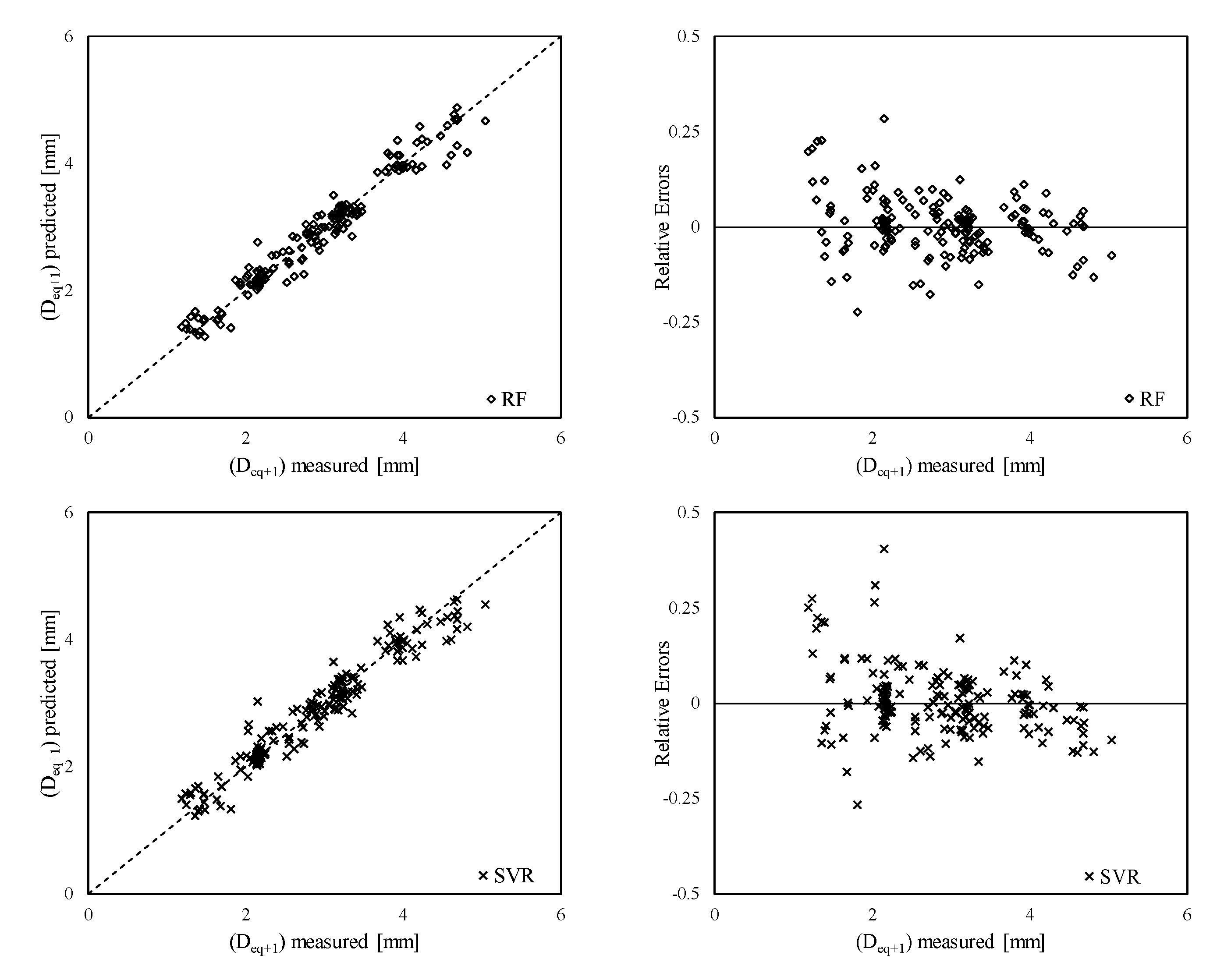

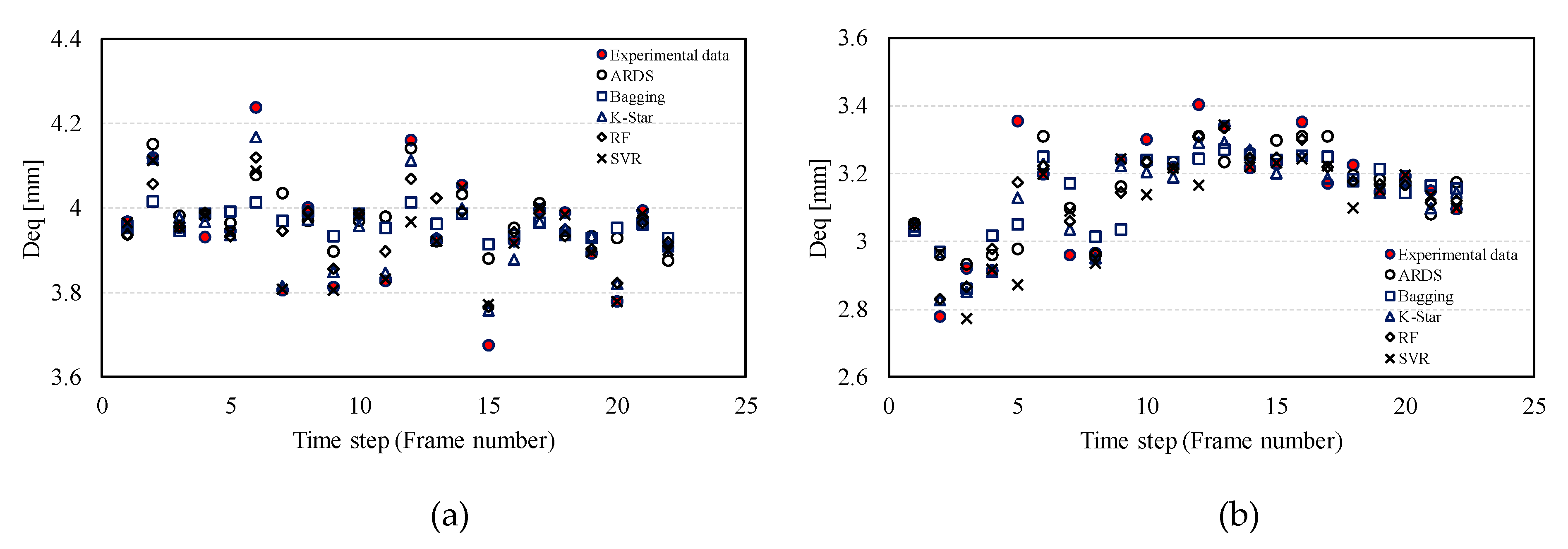
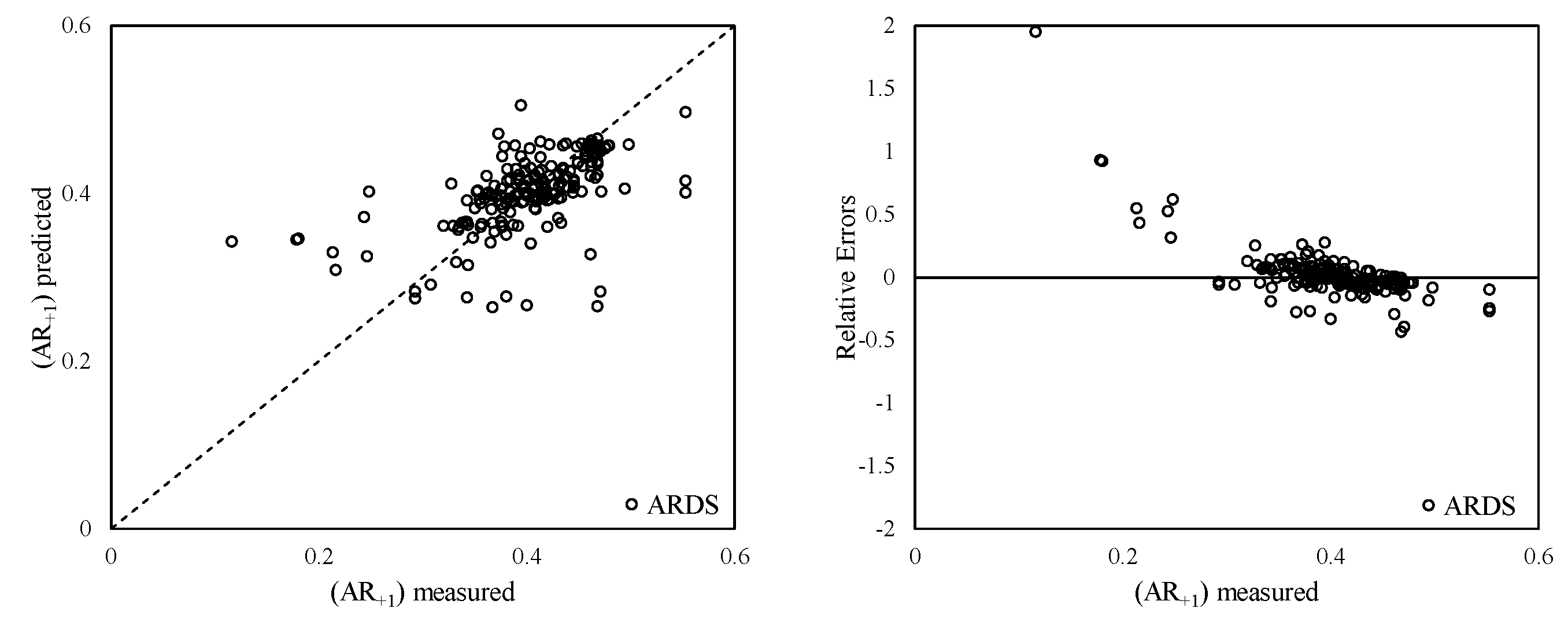

| Model Number | Input Variables | Algorithm | R2 | MAE [mm] | RMSE [mm] | RAE | |
|---|---|---|---|---|---|---|---|
| Deq+1 | 1 | hb, Vb, Web, Frb, Reb, Eo, Deq0 | ARDS | 0.9671 | 0.1132 | 0.1686 | 15.39% |
| Bagging | 0.9749 | 0.0974 | 0.1434 | 13.42% | |||
| K-Star | 0.9692 | 0.1111 | 0.1582 | 15.27% | |||
| RF | 0.9734 | 0.1047 | 0.1489 | 14.33% | |||
| SVR | 0.9472 | 0.1418 | 0.2020 | 20.18% | |||
| 2 | Web, Reb, Eo | ARDS | 0.9640 | 0.1209 | 0.1748 | 16.31% | |
| Bagging | 0.9742 | 0.0973 | 0.1448 | 13.61% | |||
| K-Star | 0.9629 | 0.1152 | 0.1717 | 16.29% | |||
| RF | 0.9676 | 0.1138 | 0.1645 | 15.42% | |||
| SVR | 0.9495 | 0.1466 | 0.2001 | 20.36% | |||
| 3 | Web, Frb, Reb | ARDS | 0.8425 | 0.2710 | 0.3552 | 36.80% | |
| Bagging | 0.9269 | 0.1706 | 0.2461 | 23.38% | |||
| K-Star | 0.9214 | 0.1749 | 0.2488 | 24.68% | |||
| RF | 0.9512 | 0.1354 | 0.2032 | 18.52% | |||
| SVR | 0.9546 | 0.1388 | 0.1931 | 19.10% | |||
| Deq+2 | 1 | hb, Vb, Web, Frb, Reb, Eo, Deq0 | ARDS | 0.9536 | 0.1495 | 0.1936 | 20.04% |
| Bagging | 0.9650 | 0.1284 | 0.1675 | 17.35% | |||
| K-Star | 0.9651 | 0.1278 | 0.1687 | 17.38% | |||
| RF | 0.9637 | 0.1346 | 0.1715 | 18.15% | |||
| SVR | 0.9413 | 0.1563 | 0.2123 | 22.12% | |||
| 2 | Web, Reb, Eo | ARDS | 0.9499 | 0.1555 | 0.2009 | 20.77% | |
| Bagging | 0.9590 | 0.1403 | 0.1820 | 18.88% | |||
| K-Star | 0.9481 | 0.1495 | 0.2003 | 20.86% | |||
| RF | 0.9553 | 0.1507 | 0.1898 | 20.32% | |||
| SVR | 0.9434 | 0.1655 | 0.2144 | 22.39% | |||
| 3 | Web, Frb, Reb | ARDS | 0.9261 | 0.1899 | 0.2470 | 25.75% | |
| Bagging | 0.9168 | 0.1894 | 0.2610 | 26.04% | |||
| K-Star | 0.9170 | 0.1843 | 0.2580 | 25.77% | |||
| RF | 0.9386 | 0.1682 | 0.2254 | 22.85% | |||
| SVR | 0.9410 | 0.1619 | 0.2147 | 22.58% | |||
| Deq+3 | 1 | hb, Vb, Web, Frb, Reb, Eo, Deq0 | ARDS | 0.9526 | 0.1437 | 0.1980 | 19.29% |
| Bagging | 0.9695 | 0.1181 | 0.1589 | 15.84% | |||
| K-Star | 0.9639 | 0.1272 | 0.1705 | 17.28% | |||
| RF | 0.9713 | 0.1137 | 0.1541 | 15.38% | |||
| SVR | 0.9399 | 0.1555 | 0.2153 | 21.92% | |||
| 2 | Web, Reb, Eo | ARDS | 0.9451 | 0.1570 | 0.2107 | 21.10% | |
| Bagging | 0.9670 | 0.1204 | 0.1670 | 16.17% | |||
| K-Star | 0.9422 | 0.1471 | 0.2094 | 20.86% | |||
| RF | 0.9632 | 0.1285 | 0.1734 | 17.39% | |||
| SVR | 0.9425 | 0.1645 | 0.2133 | 22.58% | |||
| 3 | Web, Frb, Reb | ARDS | 0.8932 | 0.2189 | 0.2950 | 29.47% | |
| Bagging | 0.8845 | 0.2228 | 0.3036 | 30.51% | |||
| K-Star | 0.9031 | 0.1971 | 0.2772 | 27.79% | |||
| RF | 0.9170 | 0.1974 | 0.2623 | 26.45% | |||
| SVR | 0.9416 | 0.1590 | 0.2162 | 21.74% |
| Model Number | Input Variables | Algorithm | R2 | MAE | RMSE | RAE | |
|---|---|---|---|---|---|---|---|
| AR+1 | 1 | hb, Vb, Web, Frb, Reb, Eo, Deq0 | ARDS | 0.5376 | 0.0244 | 0.0317 | 67.89% |
| Bagging | 0.4651 | 0.0254 | 0.0342 | 69.85% | |||
| K-Star | 0.3505 | 0.0277 | 0.0372 | 76.64% | |||
| RF | 0.4002 | 0.0276 | 0.0384 | 72.71% | |||
| SVR | 0.2976 | 0.0272 | 0.0373 | 76.96% | |||
| 2 | Web, Reb, Eo | ARDS | 0.4795 | 0.0283 | 0.0372 | 72.86% | |
| Bagging | 0.3884 | 0.0286 | 0.0376 | 77.28% | |||
| K-Star | 0.3573 | 0.0277 | 0.0369 | 77.11% | |||
| RF | 0.3302 | 0.0303 | 0.0407 | 79.89% | |||
| SVR | 0.3637 | 0.0279 | 0.0374 | 76.38% | |||
| 3 | Web, Frb, Reb | ARDS | 0.1463 | 0.0400 | 0.0540 | 107.30% | |
| Bagging | 0.1957 | 0.0321 | 0.0429 | 85.76% | |||
| K-Star | 0.2257 | 0.0311 | 0.0417 | 83.70% | |||
| RF | 0.2038 | 0.0303 | 0.0406 | 84.40% | |||
| SVR | 0.3023 | 0.0287 | 0.0387 | 79.55% | |||
| AR+2 | 1 | hb, Vb, Web, Frb, Reb, Eo, Deq0 | ARDS | 0.4628 | 0.0284 | 0.0385 | 72.66% |
| Bagging | 0.3401 | 0.0294 | 0.0386 | 80.03% | |||
| K-Star | 0.3783 | 0.0308 | 0.0420 | 77.99% | |||
| RF | 0.3772 | 0.0300 | 0.0409 | 78.33% | |||
| SVR | 0.4035 | 0.0280 | 0.0371 | 75.81% | |||
| 2 | Web, Reb, Eo | ARDS | 0.3354 | 0.0332 | 0.0439 | 83.01% | |
| Bagging | 0.3659 | 0.0312 | 0.0404 | 80.95% | |||
| K-Star | 0.4459 | 0.0315 | 0.0411 | 77.78% | |||
| RF | 0.4416 | 0.0311 | 0.0417 | 76.21% | |||
| SVR | 0.4242 | 0.0332 | 0.0432 | 80.22% | |||
| 3 | Web, Frb, Reb | ARDS | 0.0557 | 0.0434 | 0.0547 | 105.91% | |
| Bagging | 0.3282 | 0.0349 | 0.0434 | 86.55% | |||
| K-Star | 0.4226 | 0.0328 | 0.0411 | 80.80% | |||
| RF | 0.3466 | 0.0344 | 0.0448 | 84.39% | |||
| SVR | 0.4538 | 0.0334 | 0.0422 | 80.08% | |||
| AR+3 | 1 | hb, Vb, Web, Frb, Reb, Eo, Deq0 | ARDS | 0.1364 | 0.0358 | 0.0468 | 93.19% |
| Bagging | 0.3394 | 0.0301 | 0.0393 | 80.06% | |||
| K-Star | 0.1662 | 0.0345 | 0.0457 | 89.14% | |||
| RF | 0.3065 | 0.0315 | 0.0413 | 81.96% | |||
| SVR | 0.2293 | 0.0301 | 0.0403 | 83.25% | |||
| 2 | Web, Reb, Eo | ARDS | 0.4327 | 0.0295 | 0.0388 | 75.35% | |
| Bagging | 0.3878 | 0.0302 | 0.0389 | 78.77% | |||
| K-Star | 0.3258 | 0.0314 | 0.0399 | 84.21% | |||
| RF | 0.3190 | 0.0315 | 0.0411 | 82.30% | |||
| SVR | 0.3232 | 0.0294 | 0.0396 | 79.09% | |||
| 3 | Web, Frb, Reb | ARDS | 0.0371 | 0.0406 | 0.0511 | 104.77% | |
| Bagging | 0.1654 | 0.0355 | 0.0449 | 92.77% | |||
| K-Star | 0.2369 | 0.0337 | 0.0430 | 88.32% | |||
| RF | 0.2354 | 0.0336 | 0.0430 | 88.87% | |||
| SVR | 0.3501 | 0.0322 | 0.0411 | 83.04% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Nunno, F.; Alves Pereira, F.; de Marinis, G.; Di Felice, F.; Gargano, R.; Miozzi, M.; Granata, F. Deformation of Air Bubbles Near a Plunging Jet Using a Machine Learning Approach. Appl. Sci. 2020, 10, 3879. https://doi.org/10.3390/app10113879
Di Nunno F, Alves Pereira F, de Marinis G, Di Felice F, Gargano R, Miozzi M, Granata F. Deformation of Air Bubbles Near a Plunging Jet Using a Machine Learning Approach. Applied Sciences. 2020; 10(11):3879. https://doi.org/10.3390/app10113879
Chicago/Turabian StyleDi Nunno, Fabio, Francisco Alves Pereira, Giovanni de Marinis, Fabio Di Felice, Rudy Gargano, Massimo Miozzi, and Francesco Granata. 2020. "Deformation of Air Bubbles Near a Plunging Jet Using a Machine Learning Approach" Applied Sciences 10, no. 11: 3879. https://doi.org/10.3390/app10113879
APA StyleDi Nunno, F., Alves Pereira, F., de Marinis, G., Di Felice, F., Gargano, R., Miozzi, M., & Granata, F. (2020). Deformation of Air Bubbles Near a Plunging Jet Using a Machine Learning Approach. Applied Sciences, 10(11), 3879. https://doi.org/10.3390/app10113879










