A Fast Self-Learning Subspace Reconstruction Method for Non-Uniformly Sampled Nuclear Magnetic Resonance Spectroscopy
Abstract
:1. Introduction
2. Related Work
3. Methods
- (1)
- Fixing , is obtained by solving:The solution is:
- (2)
- Fixing , is obtained by solving:The solution is:
- (3)
- Fixing , is obtained by solving:The solution is:
- (4)
- Fixing , the solution of is:
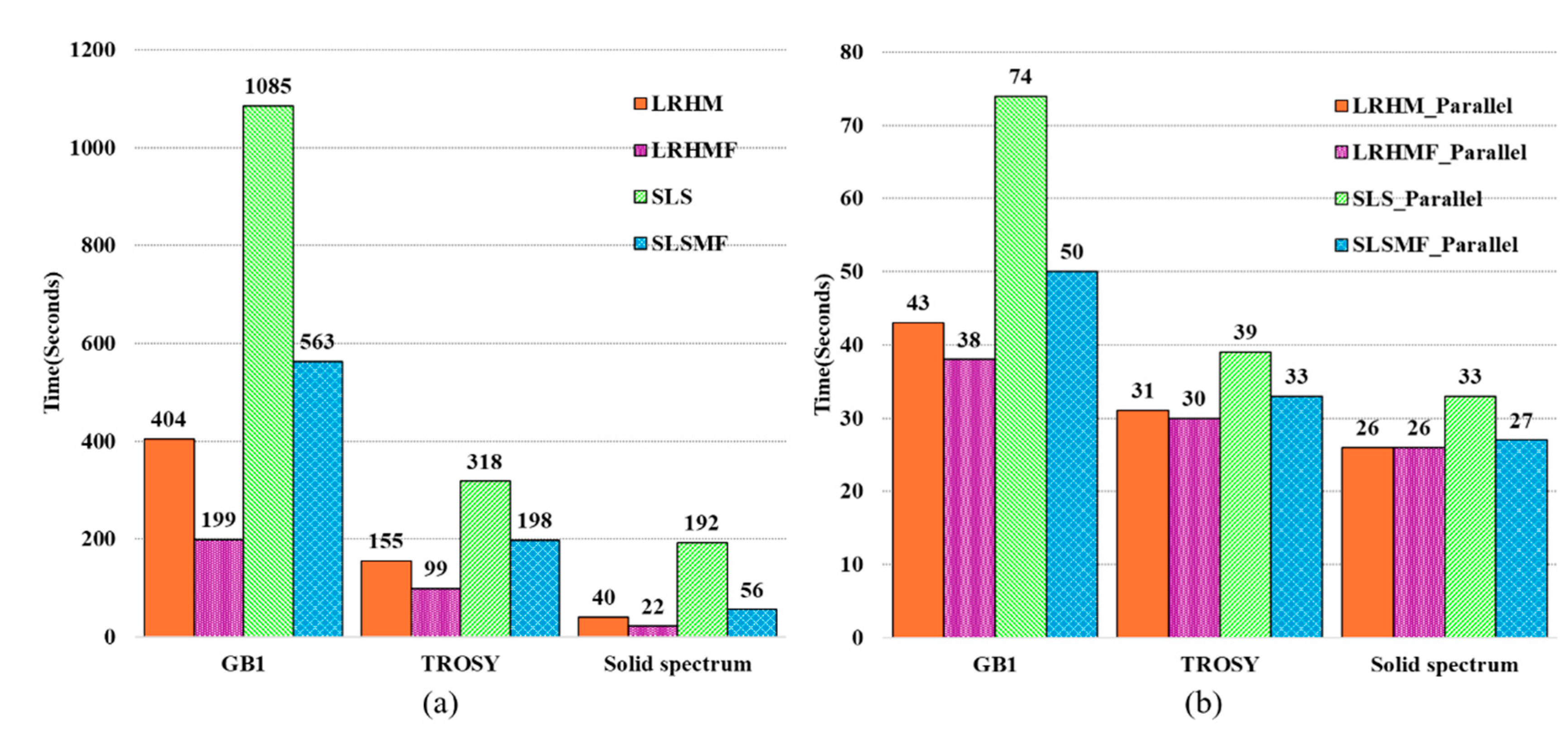
4. Experiments and Results
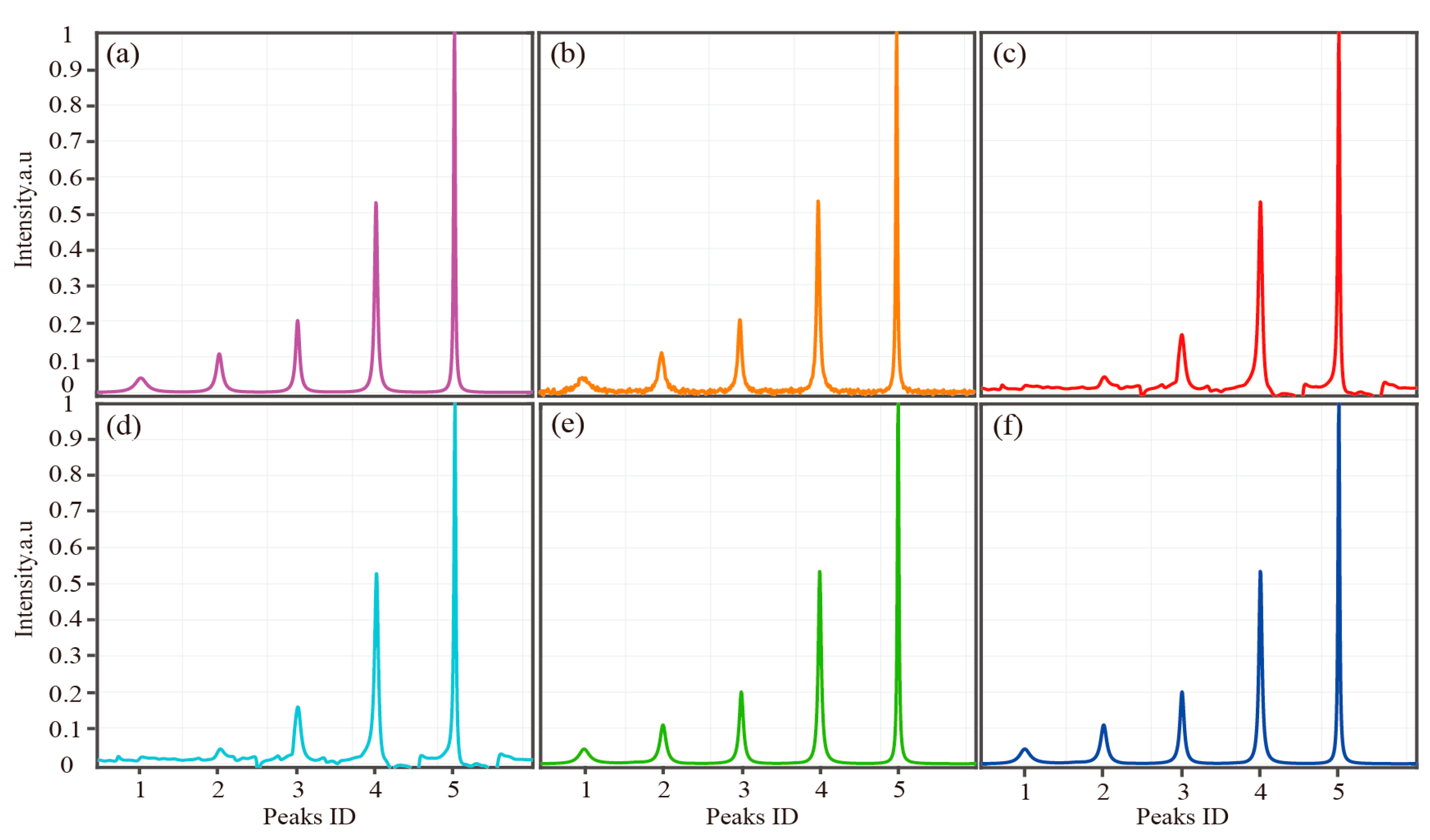
4.1. Reconstruction of Synthetic 1D NMR Spectra
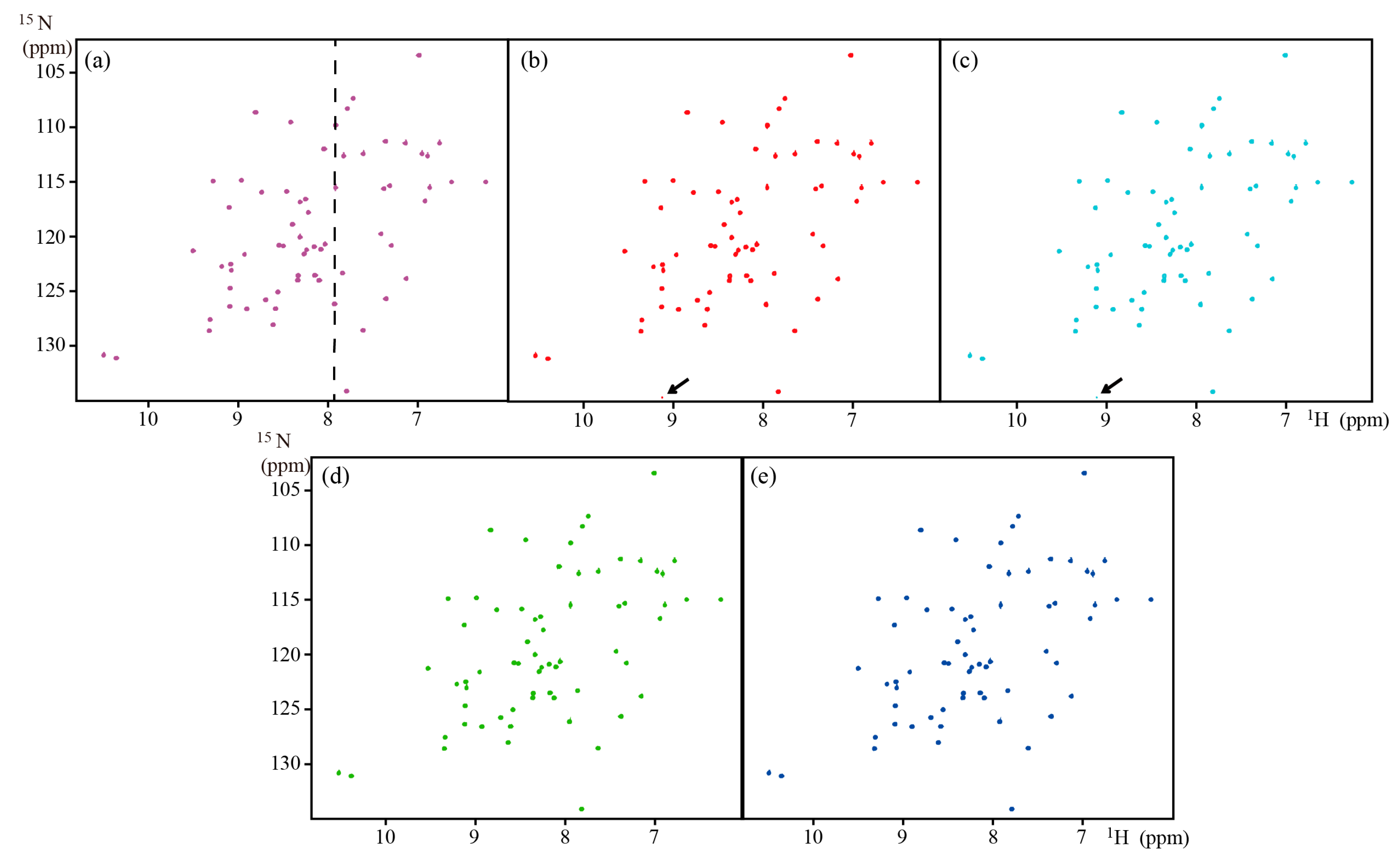
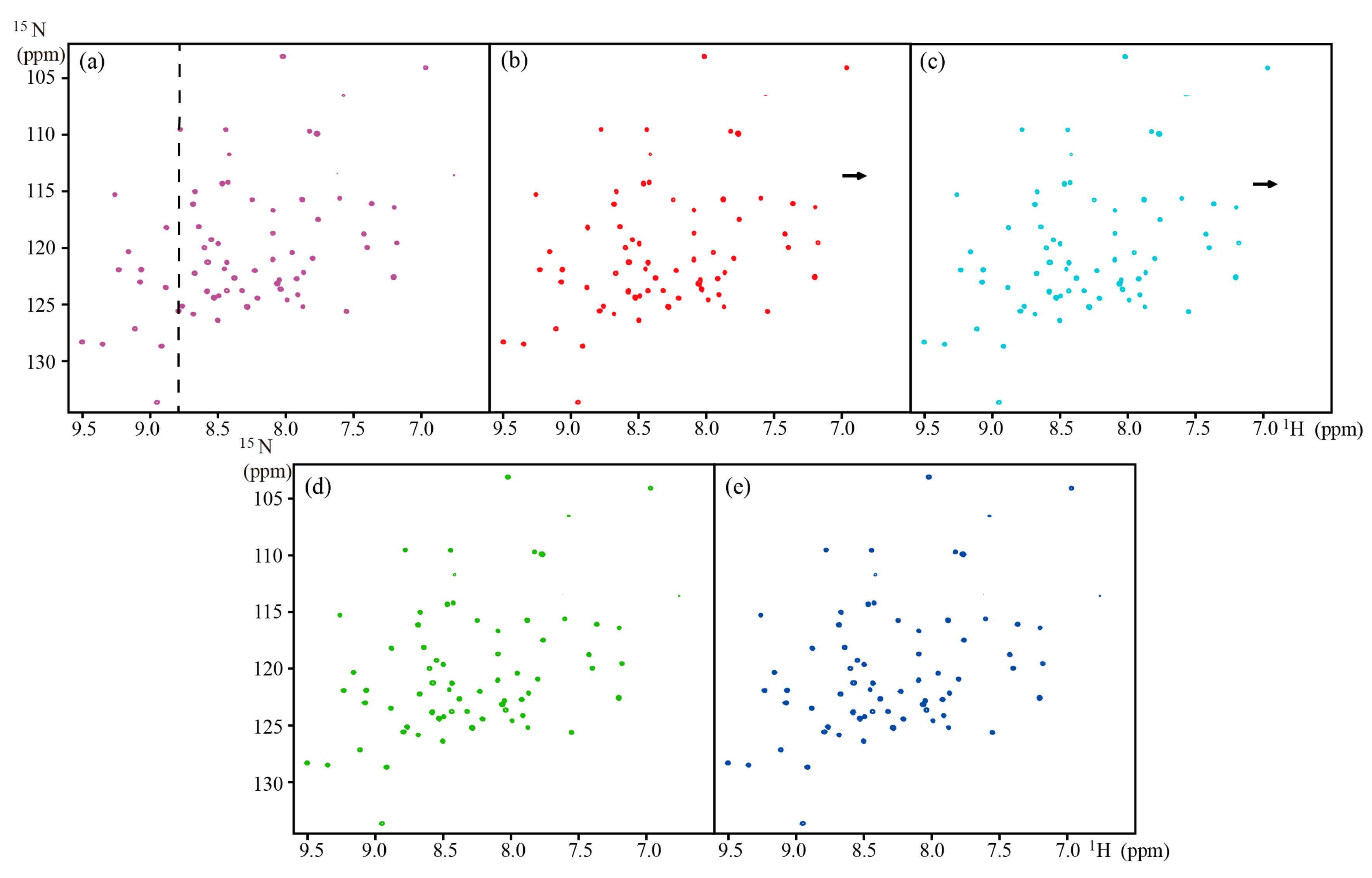
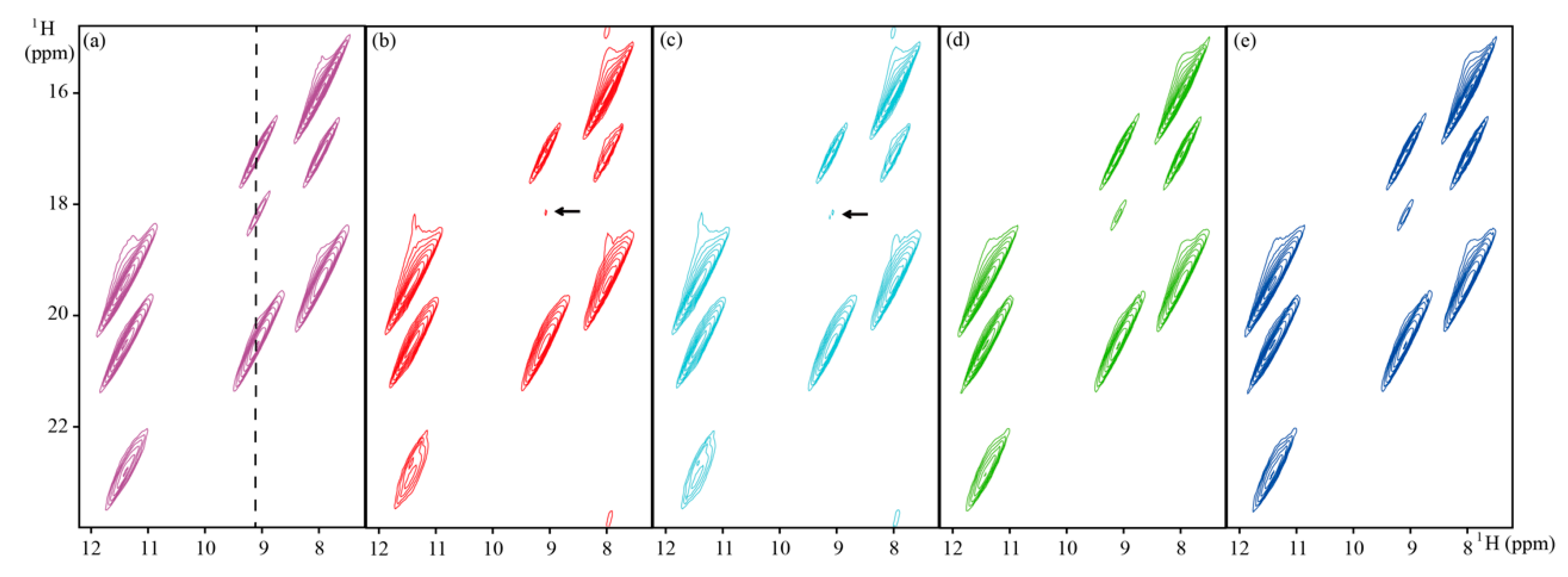
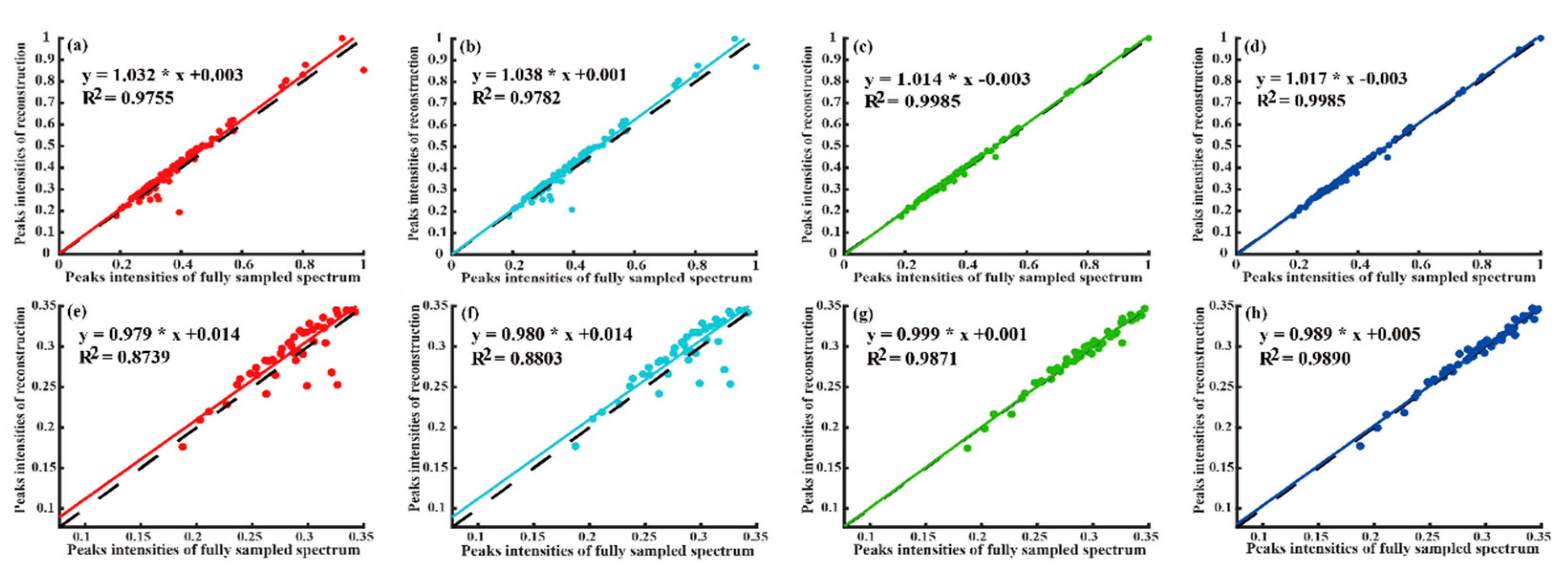
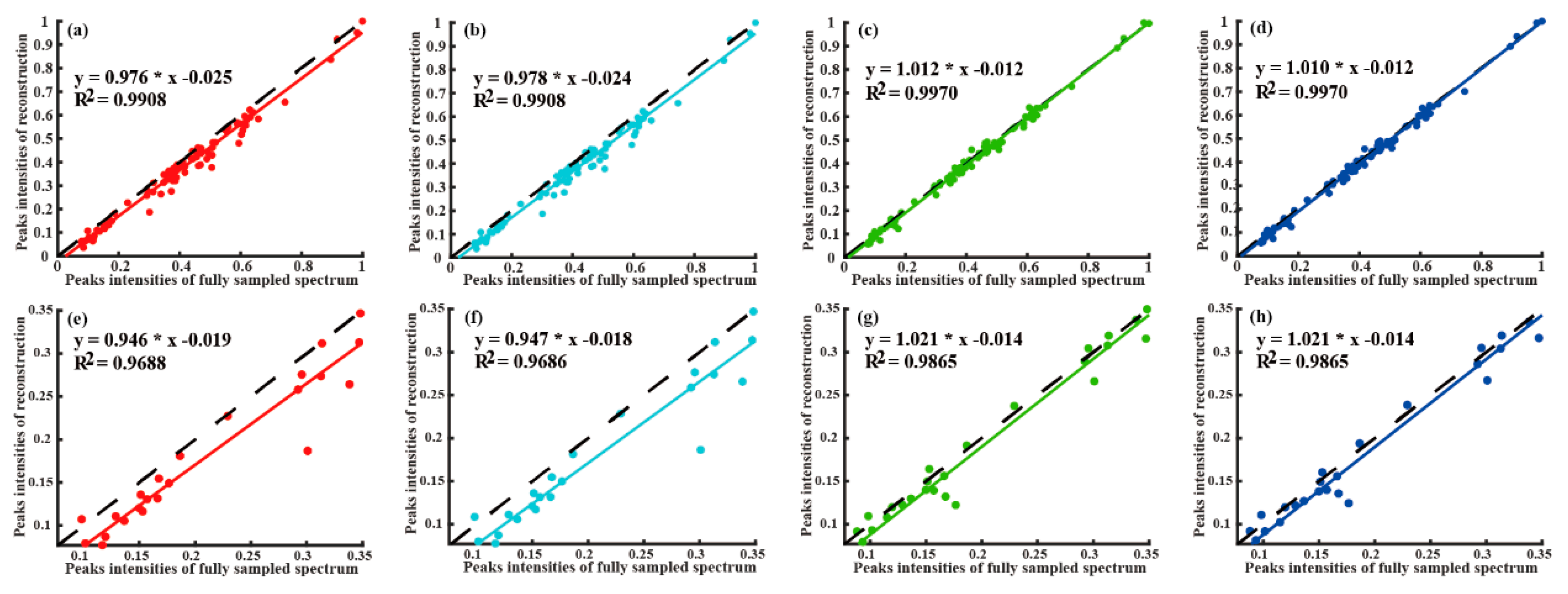
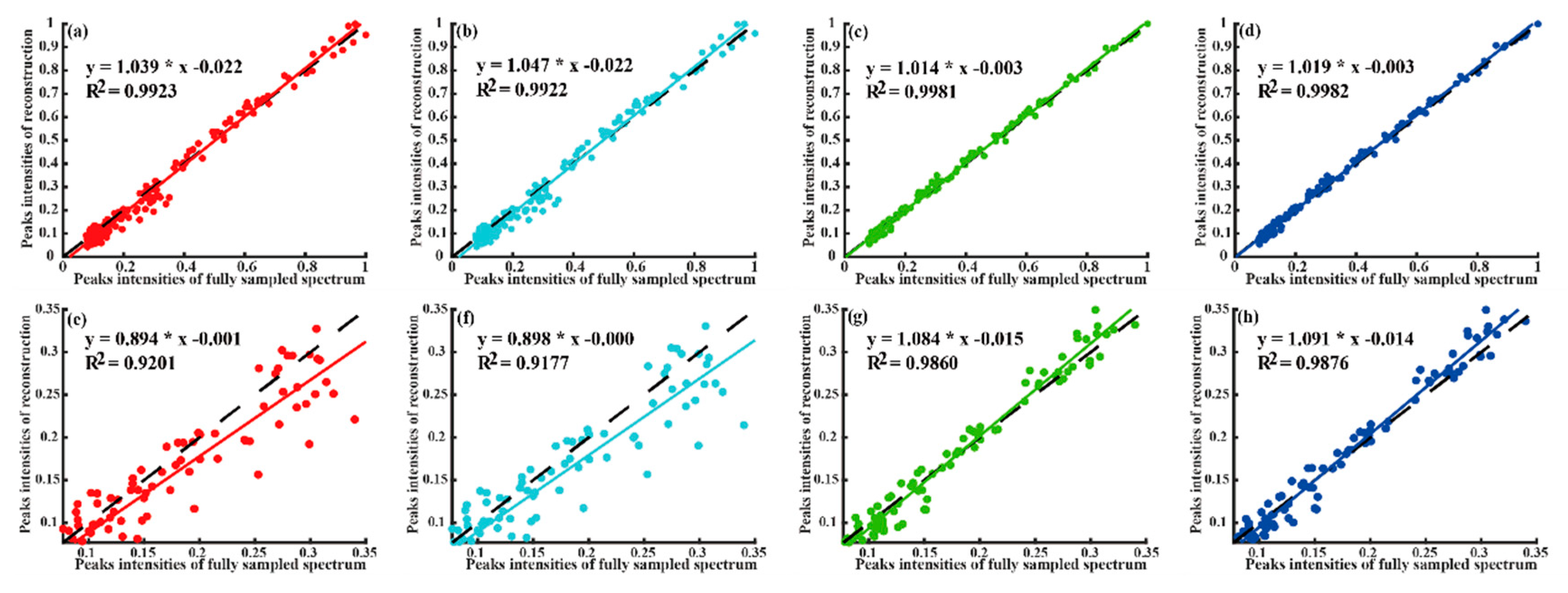
4.2. Reconstruction of 2D NMR Spectra
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cavalli, A.; Salvatella, X.; Dobson, C.M.; Vendruscolo, M. Protein structure determination from NMR chemical shifts. Proc. Natl. Acad. Sci. USA 2007, 104, 9615–9620. [Google Scholar] [CrossRef] [Green Version]
- Tkáč, I.; Öz, G.; Adriany, G.; Uğurbil, K.; Gruetter, R. In vivo 1H NMR spectroscopy of the human brain at high magnetic fields: Metabolite quantification at 4t vs. 7t. Magn. Reson. Med. 2009, 62, 868–879. [Google Scholar] [CrossRef] [Green Version]
- Besghini, D.; Mauri, M.; Simonutti, R. Time domain NMR in polymer science: From the laboratory to the industry. Appl. Sci. 2019, 9, 1801. [Google Scholar] [CrossRef] [Green Version]
- James, K. Understanding NMR Spectroscopy; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Orekhov, V.Y.; Jaravine, V.A. Analysis of non-uniformly sampled spectra with multi-dimensional decomposition. Prog. Nucl. Magn. Reson. Spectrosc. 2011, 59, 271–292. [Google Scholar] [CrossRef]
- Lam, F.; Li, Y.; Guo, R.; Clifford, B.; Liang, Z.-P. Ultrafast magnetic resonance spectroscopic imaging using spice with learned subspaces. Magn. Reson. Med. 2020, 83, 377–390. [Google Scholar] [CrossRef] [Green Version]
- Barna, J.C.J.; Laue, E.D.; Mayger, M.R.; Skilling, J.; Worrall, S.J.P. Exponential sampling, an alternative method for sampling in two-dimensional NMR experiments. J. Magn. Reson. 1987, 73, 69–77. [Google Scholar] [CrossRef]
- Mobli, M.; Hoch, J.C. Nonuniform sampling and non-fourier signal processing methods in multidimensional NMR. Prog. Nucl. Magn. Reson. Spectrosc. 2014, 83, 21–41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hyberts, S.G.; Takeuchi, K.; Wagner, G. Poisson-gap sampling and forward maximum entropy reconstruction for enhancing the resolution and sensitivity of protein NMR data. J. Am. Chem. Soc. 2010, 132, 2145–2147. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kazimierczuk, K.; Stanek, J.; Zawadzka-Kazimierczuk, A.; Koźmiński, W. Random sampling in multidimensional NMR spectroscopy. Prog. Nucl. Magn. Reson. Spectrosc. 2010, 57, 420–434. [Google Scholar] [CrossRef] [PubMed]
- Jiang, B.; Jiang, X.; Xiao, N.; Zhang, X.; Jiang, L.; Mao, X.; Liu, M. Gridding and fast fourier transformation on non-uniformly sparse sampled multidimensional NMR data. J. Magn. Reson. 2010, 204, 165–168. [Google Scholar] [CrossRef]
- Petrellis, N. Undersampling in orthogonal frequency division multiplexing telecommunication systems. Appl. Sci. 2014, 4, 79–98. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inform. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Qu, X.; Guo, D.; Cao, X.; Cai, S.; Chen, Z. Reconstruction of self-sparse 2D NMR spectra from undersampled data in the indirect dimension. Sensors 2011, 11, 8888–8909. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ying, J.; Lu, H.; Wei, Q.; Cai, J.-F.; Guo, D.; Wu, J.; Chen, Z.; Qu, X. Hankel matrix nuclear norm regularized tensor completion for $ n $-dimensional exponential signals. IEEE Trans. Signal. Process. 2017, 65, 3702–3717. [Google Scholar] [CrossRef] [Green Version]
- Lu, H.; Zhang, X.; Qiu, T.; Yang, J.; Ying, J.; Guo, D.; Chen, Z.; Qu, X. Low rank enhanced matrix recovery of hybrid time and frequency data in fast magnetic resonance spectroscopy. IEEE Trans. Bio-Med. Eng. 2018, 65, 809–820. [Google Scholar] [CrossRef]
- Lam, F.; Liang, Z.-P. A subspace approach to high-resolution spectroscopic imaging. Magn. Reson. Med. 2014, 71, 1349–1357. [Google Scholar] [CrossRef] [Green Version]
- Kazimierczuk, K.; Orekhov, V.Y. Accelerated NMR spectroscopy by using compressed sensing. Angew. Chem. Int. Ed. Engl. 2011, 50, 5556–5559. [Google Scholar] [CrossRef]
- Holland, D.J.; Bostock, M.J.; Gladden, L.F.; Nietlispach, D. Fast multidimensional NMR spectroscopy using compressed sensing. Angew. Chem. Int. Ed. 2011, 50, 6548–6551. [Google Scholar] [CrossRef]
- Goowicz, D.; Kasprzak, P.; Kazimierczuk, K. Enhancing compression level for more efficient compressed sensing and other lessons from NMR spectroscopy. Sensors 2020, 20, 1325. [Google Scholar] [CrossRef] [Green Version]
- Qu, X.; Mayzel, M.; Cai, J.-F.; Chen, Z.; Orekhov, V. Accelerated NMR spectroscopy with low-rank reconstruction. Angew. Chem. Int. Ed. 2014, 54, 852–854. [Google Scholar] [CrossRef]
- Guo, D.; Qu, X. Improved reconstruction of low intensity magnetic resonance spectroscopy with weighted low rank Hankel matrix completion. IEEE Access 2018, 6, 4933–4940. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, D.; Ye, J.; Li, X.; He, X. Fast and accurate matrix completion via truncated nuclear norm regularization. IEEE Trans. Pattern Anal. 2013, 35, 2117–2130. [Google Scholar] [CrossRef] [PubMed]
- Guo, D.; Tu, Z.; Lu, H.; Qiu, T.; Xiao, M.; Qu, X. Reconstruction of Highly Accelerated NMR Spectra with Self-learning Subspace. Submitt. Anal. Chem. 2020. [Google Scholar]
- Jennings, A.; Mckeown, J.J. Matrix Computation; John Wiley & Sons: Hoboken, NJ, USA, 1992. [Google Scholar]
- Guo, D.; Lu, H.; Qu, X. A fast low rank Hankel matrix factorization reconstruction method for non-uniformly sampled magnetic resonance spectroscopy. IEEE Access 2017, 5, 16033–16039. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, D.; Huang, Y.; Chen, Y.; Wang, L.; Huang, F.; Qu, X. Image reconstruction with low-rankness and self-consistency of k-space data in parallel MRI. Med. Image Anal. 2020, 63, 101687. [Google Scholar] [CrossRef] [Green Version]
- Hoch, J.C.; Stern, A.S. NMR Data Processing; Wiley-Liss: New York, NY, USA, 1996. [Google Scholar]
- Chen, D.; Wang, Z.; Guo, D.; Orekhov, V.; Qu, X. Review and prospect: Deep learning in nuclear magnetic resonance spectroscopy. Chem.-Eur. J. 2020. [Google Scholar] [CrossRef] [Green Version]
- Qu, X.; Huang, Y.; Lu, H.; Qiu, T.; Guo, D.; Agback, T.; Orekhov, V.; Chen, Z. Accelerated nuclear magnetic resonance spectroscopy with deep learning. Angew. Chem. Int. Ed. 2019. [Google Scholar] [CrossRef] [Green Version]
- Kazimierczuk, K.; Kasprzak, P. Modified omp algorithm for exponentially decaying signals. Sensors 2014, 15, 234–247. [Google Scholar] [CrossRef] [Green Version]
- Wan, S.; Mak, M.; Kung, S. Transductive learning for multi-label protein subchloroplast localization prediction. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017, 14, 212–224. [Google Scholar] [CrossRef]
- Srebro, N. Learning with Matrix Factorizations; Massachusetts Institute of Technology: Cambridge, MA, USA, 2004. [Google Scholar]
- Signoretto, M.; Cevher, V.; Suykens, J.A.K. An SVD-free approach to a class of structured low rank matrix optimization problems with application to system identification. Organometallics 2013, 12, 4283–4285. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Vanessa, V.; Pablo, R.; Jean-Francois, M.; Raoul, V. NMR-Mpar: A fault-tolerance approach for multi-core and many-core processors. Appl. Sci. 2018, 8, 465. [Google Scholar]
- Mayzel, M.; Kazimierczuk, K.; Orekhov, V.Y. The causality principle in the reconstruction of sparse NMR spectra. Chem. Commun. 2014, 50, 8947–8950. [Google Scholar] [CrossRef] [PubMed] [Green Version]
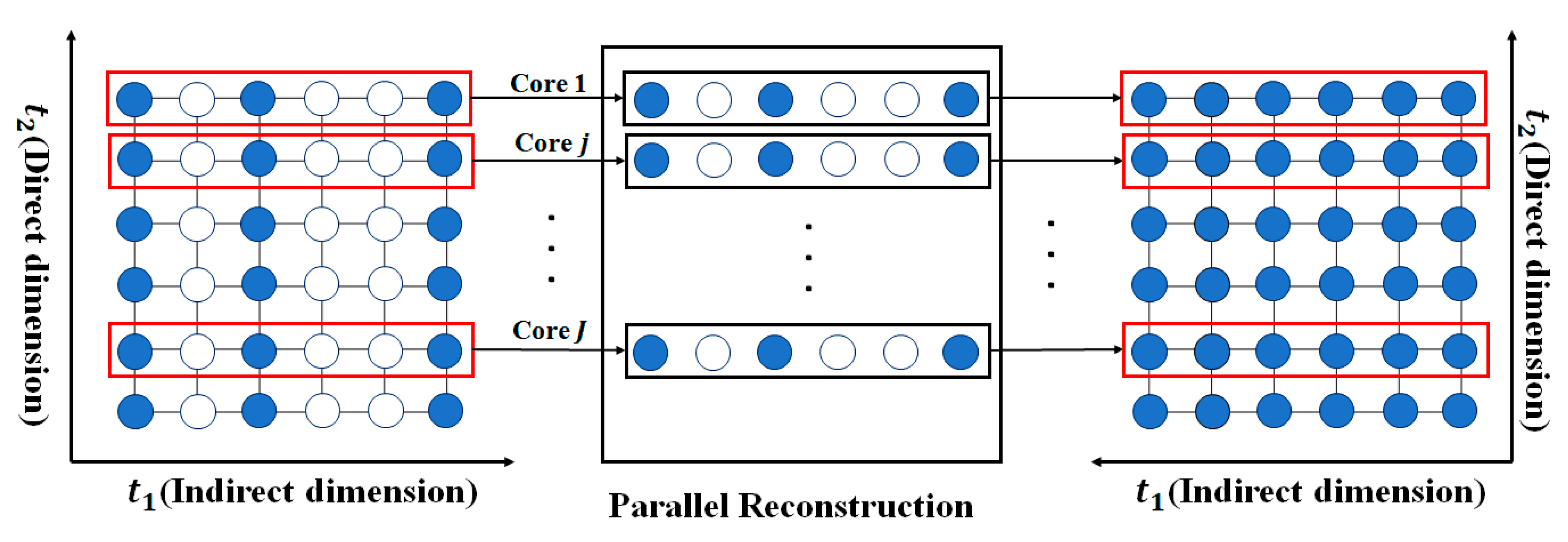



| Initialization: Input , , , set outer maximal iterations times , convergence condition , and maximal inner number of iterations . Initialize the solution , the dual variable , the number of iterations , and . Main: While () or (), do:
End for; Output: The reconstructed FID . |
| Type | Protein | Molecular Weight | Spectrometer Frequency | Sampling Type | Date Point | References |
|---|---|---|---|---|---|---|
| HSQC | GB1 | ~8.0 kDa | 600 MHz | Full | Figure 3 | |
| TROSY | Ubiquitin | ~8.6 kDa | 800 MHz | Full | Figure 4 | |
| Solid NMR | ~68 Da | 900 MHz | Full | Figure 5 |
| Peaks ID | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| Parameters | ||||||
| Amplitude () | 0.3 | 0.4 | 0.5 | 1 | 1 | |
| Damping factor | 0.01 | 0.02 | 0.03 | 0.04 | 0.08 | |
| Peak ID | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| Method | ||||||
| LRHM | 0.597 ± 0.384 | 0.859 ± 0.203 | 0.944 ± 0.090 | 0.991 ± 0.012 | 0.997 ± 0.004 | |
| LRHMF | 0.600 ± 0.384 | 0.857 ± 0.203 | 0.943 ± 0.090 | 0.991 ± 0.012 | 0.997 ± 0.004 | |
| SLS | 0.935 ± 0.183 | 0.974 ± 0.152 | 0.992 ± 0.039 | 0.999 ± 0.003 | 0.999 ± 0.001 | |
| SLSMF | 0.936 ± 0.181 | 0.974 ± 0.152 | 0.993 ± 0.035 | 0.999 ± 0.002 | 0.999 ± 0.001 | |
| Quality | Peak Intensity Correlation | High-Fidelity Reconstruction Peaks | Reconstruction Time (Seconds) | Fast Reconstruction | |||
|---|---|---|---|---|---|---|---|
| Method | Low Intensity Peaks | All Peaks | Computing Server | Personal Computer | |||
| LRHM | 0.9209 | 0.9826 | No | 116.5 | 138.2 | No | |
| LRHMF | 0.9222 | 0.9870 | No | 69.0 | 82.0 | Yes | |
| SLS | 0.9865 | 0.9979 | Yes | 290.2 | 381.8 | No | |
| SLSMF | 0.9877 | 0.9979 | Yes | 154.5 | 211.5 | Neutral | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, Z.; Liu, H.; Zhan, J.; Guo, D. A Fast Self-Learning Subspace Reconstruction Method for Non-Uniformly Sampled Nuclear Magnetic Resonance Spectroscopy. Appl. Sci. 2020, 10, 3939. https://doi.org/10.3390/app10113939
Tu Z, Liu H, Zhan J, Guo D. A Fast Self-Learning Subspace Reconstruction Method for Non-Uniformly Sampled Nuclear Magnetic Resonance Spectroscopy. Applied Sciences. 2020; 10(11):3939. https://doi.org/10.3390/app10113939
Chicago/Turabian StyleTu, Zhangren, Huiting Liu, Jiaying Zhan, and Di Guo. 2020. "A Fast Self-Learning Subspace Reconstruction Method for Non-Uniformly Sampled Nuclear Magnetic Resonance Spectroscopy" Applied Sciences 10, no. 11: 3939. https://doi.org/10.3390/app10113939
APA StyleTu, Z., Liu, H., Zhan, J., & Guo, D. (2020). A Fast Self-Learning Subspace Reconstruction Method for Non-Uniformly Sampled Nuclear Magnetic Resonance Spectroscopy. Applied Sciences, 10(11), 3939. https://doi.org/10.3390/app10113939





