Abstract
The quality of company asset management is significantly dependent on the quality of a system for asset wear margin identification. A pipeline–machine subsystem may be an essential part of assets in many production companies. It is necessary to build models of pipeline–machine subsystems and models of a system for the identification of subsystem wear margin. The method used consists of a decomposition of desired characteristics of an enterprise into desired characteristics of a pipeline–machine subsystem. Methods for the identification of real characteristics of a subsystem depend on the character of subsystem operation. In this study, hydrodynamic and thermodynamic models of the subsystem are built. Tests are conducted on industrial and laboratory objects. The boundaries of the subsystem are defined and changes in pressure, temperature and mass flow rate in the pipeline are presented. Causes of changes in the mentioned quantities are described. Desired characteristics of the subsystem resulting from decomposition are described. The presented methods of determining efficiency for steady working conditions and open flow use hydrodynamic and thermodynamic models. Energy efficiency of the subsystem is decomposed into efficiencies of main elements of the subsystem. A method is proposed for determining the subsystem’s energy efficiency in the case of the flow into a closed vessel. It is possible to determine the hydraulic efficiency of the subsystem components: the suction pipe, the discharge pipe and the machine. The efficiency of the machine determined by the hydrodynamic method is complementary to the efficiency obtained by the thermodynamic method. The machine set efficiency is composed of hydraulic efficiency of the machine; mechanical efficiency of the machine, the gearbox and motor; and electric efficiency of the motor. Hydraulic efficiency of the pipeline is related to substitute measure of wear margin—the coefficient of resistance. Pressure drop is a diagnostic symptom. Thermal efficiency of the heat exchanger is related to a substitute measure of wear margin—the coefficient of heat penetration. Temperatures and mass flow rate in the heat exchanger are diagnostic symptoms. It is possible to determine the capacity and efficiency of subsystems with one side closed—such as those filling hydrophore and gas vessels.
1. Introduction
The pipeline–machine subsystem, according to [1], can be regarded as a company asset. Condition monitoring is an essential element of asset management [2]. According to [3], “a condition-monitoring task is a scheduled task used to detect the potential onset of a failure so that action can be taken to prevent such failure. A potential failure is an identifiable condition that indicates that a functional failure is either about to occur or is in the process of occurring”. Preventive actions on items are performed within the framework of object maintenance. In the maintenance-related standard, [4] defined characteristics of items including availability, reliability and maintainability.
The literature (e.g., [5]) also contains sets of characteristics allowing us to describe item quality. One of these sets is divided into subsets: adequacy, dependability, safety, durability and effectiveness. The dependability subset includes such characteristics as reliability and availability. The effectiveness subset includes energy efficiency and capability.
Despite the rich literature, the term ‘condition of an item’ is insufficiently defined, and the relations ‘company management–item management’ and ‘item maintenance–item diagnosing’ are not clearly described, which hampers development and implementation of systems supporting effective and efficient company management. Another problem in this context is the diversity of production systems and the multiplicity of design solutions for subsystems and their components, which makes it difficult to find and develop solutions for each case of diagnostic methods and resources. These deficiencies in diagnostics may be solved by using the concept of ‘wear margin’ and creating subsystem models and/or models of functional units. The term ‘wear margin’ was introduced to some standards, e.g., in [6] and as ‘Abnutzungsvorrat’ in the standard DIN 31051 [7].
Following [8], it is assumed herein that:
- A production company gets benefits (including profits) by manufacturing products. The benefits obtained depend on product quality and the quality of company’s production system. Decision-making in company management is based on data on real values of the measures of characteristics describing company quality, product quality and quality of the production system. The company intending to change the value of a company quality property measure must cause a change in values of measures of specific characteristics of the production system. For such actions to be successful, a company must have an IT system that allows the measurement of real values of property measures and the comparison of real values with desired values.
- The quality of the technical part of the production system, specified at the design stage, rendered at the stage of system production, deteriorates during the system use. The technical production system can be decomposed deliberately into subsystems and/or functional units, while the desired quality of subsystems and functional units can be expressed by using the values of measures of selected characteristics belonging to a set of characteristics describing company quality. Subsystems/functional units in the technical production system execute specific partial objectives and have specific values of desired characteristic measures. The functional unit as a subsystem has strictly specified boundaries. During operation, a functional unit undergoes remedial actions if its wear margin is exhausted, i.e., if the real value of a measure of an essential characteristic will be smaller than the desired one.
- Some characteristics are present at the level of decomposition of systems into subsystems and/or functional units, whose measured values are rendered during manufacturing, degrade during use and can be restored during maintenance. The set of values of such characteristics is referred to as wear margin. Wear margin characteristics are those of free or built-in elements, working fluids, motion and load. The number of characteristics describing the wear margin of the functional unit is large, so it is justified to seek wear margin substitute measures and describe the relationship between the wear margin substitute measure and desired characteristic measure of a subsystem or functional unit. Substitute measures of wear margin generally are not measurable during the use of the production system. It is necessary to find measurable symptoms of wear margin and determine the relationship between wear margin measure and symptom measure.
These assumptions contribute to a new concept of the identification of maintained technical items. The concept implies that:
- The subsystem and/or a functional unit should have specific values of measurable characteristics;
- The relationship should be known between the measurable values of characteristics and substitute measures of wear margin or functional unit symptom measures;
- The relationship should be known between substitute measures of wear margin and functional unit symptom measures.
The relationship between wear margin measure and symptom measure must be reversible. Based on the value of symptom measures, we should be able to determine the value of wear margin substitute measures. This problem requires models of the symptom–wear margin relationships. Input quantities in such models are values of symptom measures, and output quantities are values of wear margin measures. There are two basic types of models: mathematical–physical and heuristic models using the tools of knowledge engineering. Knowledge engineering is a field of artificial intelligence, while tools of knowledge engineering include expert systems, neural networks and neuro-fuzzy systems. One advantage of heuristic models is that we do not need to know processes implemented in modeled items; the output and input quantities may be selected arbitrarily. The disadvantage is that they require training sets. Furthermore, their modeling results cannot be transferred onto other types of items of the same kind, and the newly acquired knowledge is implicit.
The use of heuristic models in diagnostics has been discussed in various publications, e.g., [9]. An example of the identification of a subsystem is given in [10], considering a combustion engine turbocharger subsystem. In [11], an industrial use of the on-line diagnostics of a steam–water line of a power boiler is described.
To solve the problems tackled in this article, heuristic models cannot be applied because no training sets exist and because input and output quantities must belong to a coherent system of explicit relations. There is, on the other hand, sufficient knowledge that allows us to search for substitute measures of wear margin and to create mathematical–physical models describing the relationships between symptom measures, substitute measures of wear margin of functional units and wear margin measures of subsystems.
A subsystem for transporting fluids from lower to higher energy areas is often part of technical production systems. This type of subsystem is referred to in this article as a pipeline–machine subsystem. This may be one main subsystem, or many of them may occur in various constructions executing various specific functions. The identification of the wear margin of such a subsystem should be performed right after manufacturing, periodically during system operation and each time after repairs. The literature does not contain a comprehensive description of the identification of such subsystem. There are publications addressing the identification of machines belonging to a subsystem. The available methods of identification presented in the literature refer to mainly identification in conditions of steady flow of a fluid in a subsystem [12,13,14]. This research aims to demonstrate the practical applicability of the new concept of identification and the development of identification methods for the pipeline–machine subsystem.
This article presents a pipeline–machine subsystem model, systematizes and develops methods for identifying a pipeline–machine subsystem under steady-state conditions of open flow and in conditions of flow into a closed vessel. It has been shown that main characteristics of a production system, adequacy and effectiveness can be related to the measurable efficiency and measurable capability (capacity in practice) of the subsystem. It has been confirmed that relationships exist between the measures of efficiency and substitute measures of pipeline wear margin. Besides, the author proposes methods of identification of the efficiency of subsystems filling closed vessels and verifies their practical usability.
2. Pipeline–Machine Subsystem: Boundaries, Characteristics, Curves and Losses
Pipeline–machine subsystems serve to transfer fluids (liquids, gases) from areas of lower mechanical energy to areas of higher mechanical energy and to transfer fluids from areas of higher thermal energy to areas of lower thermal energy. They also may be used to handle fluids in order to discharge contaminants, transfer heat or accomplish other goals.
Fluid behavior is described by hydromechanics (with the prefix “hydro-” indicating or denoting water, liquid or fluid) and thermodynamics. The type of fluid is considered to be specified if the fluid density ρ and specific heat are known.
There are two types of pipeline–machine subsystems:
- An open subsystem for continuous or intermittent operation, with constant or variable pressure and constant or variable temperature at the beginning of a suction pipe;
- A subsystem with a closed vessel at the end of the discharge pipe or suction pipe.
Figure 1 presents the boundaries of an open subsystem: the beginning (point 1) and end (point 2) of the transport process and the source and type of supplied energy . The pipeline in Figure 1 is shown as consisting of straight sections, and the change in height above reference plane was replaced by appropriate changes in pressure, i.e., height change indicated by was replaced with pressure change indicated by . Indicated subsystem elements include a suction pipe, an engine-driven machine and a discharge pipe. A machine and a driving engine make up a machine set. Pumps and compressors are generally driven by electric motors. In such cases, the subsystem is supplied with electric energy . Suction and discharge systems consist of pipeline sections and fixtures (valves, connectors, fittings) and devices built into pipeline sections. Physical quantities describing transported fluid are pressure , mass flow rate , volume flow rate and temperature . The values of these quantities change along a pipeline length (Figure 1). Changes are due to the operation of a machine and losses.
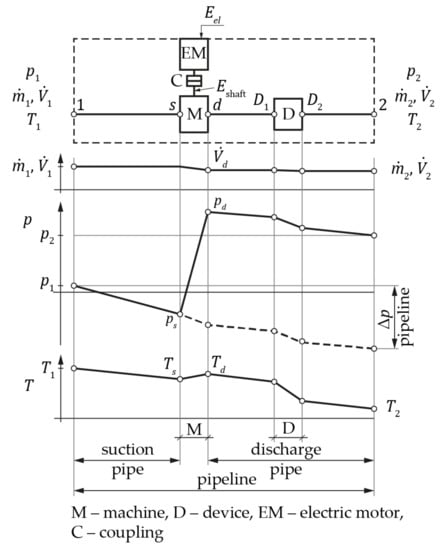
Figure 1.
Boundaries of an open pipeline–machine subsystem and qualitative changes of , and along the pipeline.
The value of pressure drop in a pipeline (Figure 1) depends on the volume flow rate . Following [15,16], we can assume that . The pressure–flow rate relationship is referred to as the pipeline curve . Such curves can be drawn for the discharge pipe and the suction pipe .
According to available literature, the values of , machine differential pressure and machine efficiency are also dependent on volume flow rate . Machine volume flow rate and machine efficiency curves are plotted after these relationships are found experimentally. The plotted curve shapes depend mainly on the type of machine: rotodynamic or positive displacement. For machines with a steep flow curve, the efficiency curve is made as . The method of plotting is presented in a standard appropriate for a given machine and its type (e.g., [17]).
Once the suction and discharge unit curves and machine curves are drawn, an operating point () is obtained (Figure 2).
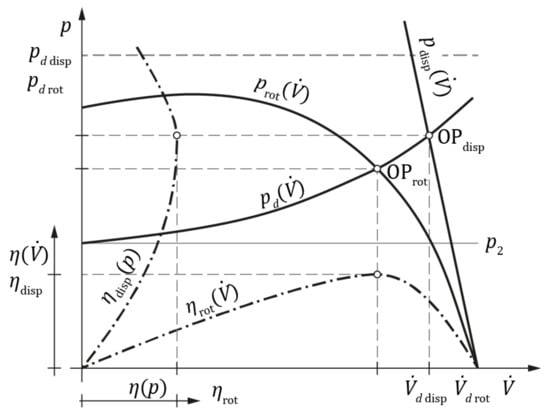
Figure 2.
The quality curve of the discharge pipe , rotodynamic machine , positive displacement machine , efficiency of the rotodynamic machine , efficiency of positive displacement machine , operating point of discharge pipe and rotodynamic machine and operating point of discharge pipe and positive displacement machine .
The values of pressure and flow rate at the operating point are (discharge pressure) and (volume flow rate), respectively (Figure 1).
Decomposing desired characteristics of a production system, we can assume that the pipeline–machine subsystem is generally expected to have proper capability, efficiency, reliability and availability. Therefore, it can be assumed that wear margin of an open subsystem is not exhausted if the subsystem delivers fluid to the destination under the following conditions:
- With capacity falling within the range , at pressure in the range of and temperature in the range of ;
- With efficiency values in the range ;
- With failure frequency rate not exceeding a limit value;
- With an acceptable value of availability.
Reliability and availability are characteristics whose measured values are determined after a specific period of subsystem use. We can only determine which characteristics of wear margin affect reliability and availability and define limit values of their measures.
In the pipeline–machine subsystem, we can distinguish the following measures a priori:
- Mass losses due to leakage of fluid outside the subsystem;
- Heat losses due to the exchange of heat between the fluid in a subsystem and the surroundings;
- Energy losses due to friction created by the flow of a liquid through the pipeline and the machine;
- Energy losses related to the conversion of energy supplied to the subsystem into the energy of the fluid.
It is purposeful to divide these losses into:
- Hydraulic losses, including fluid mass losses and losses due to friction of flowing fluid in subsystem elements;
- Thermal losses;
- Mechanical losses, namely in the machine, in the gearbox and in the engine;
- Electric losses, including losses during the conversion of electric energy into mechanical energy.
This division allows the classification of losses (neglecting thermal losses). Losses in the suction and discharge pipes are classified as hydraulic losses. Losses in the machine set are divided into hydraulic losses in the machine (pump, compressor); mechanical losses in the machine, the gear and the engine; and electric losses in the motor. Hydraulic losses in the machine add to hydraulic losses in the suction and discharge pipes.
During operation, the wear margin of the pipeline–machine subsystem gets exhausted due to unavoidable processes of wear in all components of the subsystem. The main causes of pipe wall destruction are corrosion, erosion, accumulation of failures, static and pulse loads, turbulent flow of a fluid, thermal shock, ice load, etc. [18]. The wear of machine elements is due to the impact of the flowing fluid on contacting elements and friction. The final effect is an increase in losses affecting the following characteristics determining the wear margin:
- Increase in roughness, surface flaws and wall punctures (capillary leaks) of subsystem elements;
- Increase in clearance width of the machine’s moving seals and reduced tightness of valves and static sealings [19,20,21].
Wall punctures, sealing failures and increased clearances of pump rotor sealings [19] (radial clearance in rotor sealings of nominal value 0.4 mm and a deviation of −0.1 may increase to more than 2 mm) increase mass losses of the fluid. Mass losses in the machine and discharge pipe manifest themselves as leakage of the transported fluid. In the suction pipe, another fluid may be sucked in from the surroundings. Mass losses can be measured by simultaneous measurement (two flowmeters) of mass flow rate at the beginning of the suction pipe and the end of the discharge pipe [22]. To detect leakages in a working subsystem, pipeline leak detectors are used, e.g., ultrasound detectors. These instruments generally do not allow measuring leakage value (mass loss). Special systems are created for leakage identification in pipelines [23]. The leakage value or the area of substitute section of the leak in a machine can be measured during tests of nonworking elements of a subsystem [24].
Wear leads to changes in the characteristic curves of the machine and the pipes. In systems with rotodynamic pumps, the subsystem efficiency may reach more than 90% [25]. The wear over several years may reduce the efficiency by 8–15%, occasionally up to 20% [19].
Figure 3 shows hypothetical curves of the discharge pipe and rotodynamic machine with nominal wear margins , and and exhausted wear margins , and .
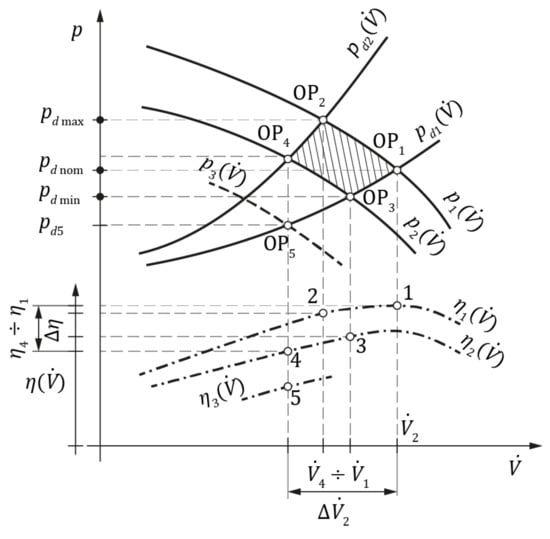
Figure 3.
Effects of wear. Index: 1—nominal wear margin; 2—exhausted wear margin.
Intersections of the discharge pipe and machine curves give four operating points, , , and , defining the field of subsystem’s wear margin (shaded area). In the absence of leakages in the discharge pipe, we can assume that the volume flow rate for is a nominal flow rate of the subsystem and that the interval of volume flow rate values determined by points and is equal to of the subsystem. In the same manner, and can be found. It follows from Figure 3 that the discharge pressure value, depending on the wear, may be higher or lower than the nominal pressure for point . An excessive value of discharge pressure may lead to secondary failures of the machine and pipeline. In the case of pumps, a drop in the wear margin of the suction pipe can cause the suction pressure to become lower than the cavitation pressure, which may result in cavitation wear of pump elements.
Simultaneous and uniform wear of the discharge pipe and the machine is not a regular occurrence. Fast wear of the pipe or the machine only is more likely. Figure 3 also presents a hypothetical curve for the machine with values of wear margin below an acceptable value. A situation is possible where the machine wear margin is exhausted and the subsystem has the volume flow rate within the desired range, in which case the efficiency value will be outside the desired range.
The subsystem efficiency is a characteristic whose value depends on the subsystem wear margin. The drop in efficiency under the same operating conditions of the subsystem is due to increased losses in the subsystem. The drop in efficiency below the limit value should initiate looking for the cause of the decease in efficiency. Methods of energy efficiency identification can be developed using the hydrodynamic and thermodynamic models of the pipeline–machine subsystem.
3. The Hydrodynamic Model of an Open Pipeline–Machine Subsystem
In open systems, for incompressible fluids and in absence of mass losses, the continuity equation and Bernoulli principle apply. Incompressible fluid is a fluid whose density in a specific range of temperature and pressure is negligibly small [26]. In fluid flows, incompressible fluids are real fluids with Mach number up to Ma = 0.3 (for air, 100 m/s = 360 km/h) [27]. Gases are considered as incompressible if they satisfy the Clapeyron equation. For diatomic gases, at pressures around 3 MPa, the error produced by the equation does not exceed 2% [28].
The measure of the quantity of fluid flowing through cross-section in a time unit is given as follows:
- The mass flow rate is calculated as
- The volume flow rate is calculated as
3.1. Subsystem Energy Efficiency
Energy efficiency is defined as
or
The energy efficiency of pipeline–machine subsystem is given by
where is fluid energy at the beginning of the subsystem, is fluid energy at the end of the subsystem, is energy delivered from outside to the engine of the set, is fluid power at the beginning of the subsystem, is fluid power at the end of the subsystem and is external power delivered to the motor of the set.
Energy measured in a selected cross-section of the subsystem is a sum of potential energy, kinetic energy and pressure [27]:
Without the change in height above reference plane and without change in flow velocity, the difference of energies results from the difference in pressures . If the energy supplied to the subsystem is electric energy , then the efficiency of the subsystem is given by
Electric energy delivered to the machine set is converted into hydraulic energy, proportional to the difference of discharge and suction pressures. Without including fluid mass losses, changes in conduit cross-section and height above reference plane, the energy efficiency of the machine set equals
The energy efficiency of the pipeline–machine subsystem is a product of hydraulic efficiency of subsystem components (the suction pipe, machine and discharge pipe); mechanical efficiency of the machine set; and electric efficiency of the motor.
where is the hydraulic efficiency of the suction pipe, is the hydraulic efficiency of the discharge pipe and is the hydraulic efficiency of the machine.
3.2. Energy Losses and Hydraulic Efficiency of the Suction and Discharge Pipes
A pipeline section can be composed of straight pipe sections and required built-in elements: elbows, branched pipes, cross-section changes and instruments. Built-in components in terms of hydrodynamics are contractions, flown-round bodies or a combination of both and, due to energy losses, are regarded as obstacles. Obstacles may also be undesired obstructions created due to manufacturing and installation errors (e.g., welding of pipelines) and as a result of wear. Characteristics of a straight section stem from characteristics of elements making up that section and characteristics obtained after inserting them, including inside diameter (m), length (m), absolute roughness of internal surface (peak height of asperities) (m) and relative roughness . Fluid characteristics include kinematic viscosity (m2/s) and density (kg/m3). Characteristics of fluid load and motion are fluid flow velocity , mean flow velocity (m2/s).and height above reference plane (m).
It follows from the energy equation that energy losses between two pipeline cross-sections can only result in a change of pressure energy [27] (Figure 4). Pressure drops (losses) along a straight section of a pipeline are described by the Darcy–Weisbach equation [27]:
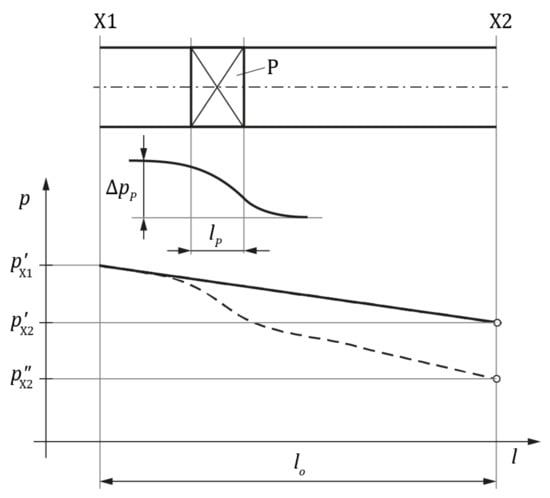
Figure 4.
Pressure loss between cross-sections 1 and 2 [29], where is an obstacle, is the length of the obstacle, is the loss at the obstacle (loss focused locally), () is the loss at the straight section (loss evenly distributed) and () is the total loss at the section .
The number is called the linear resistance coefficient or the friction factor. The coefficient depends on the value of Reynolds number Re (Re =) and relative roughness [26,27].
Pressure drops along an obstacle are accounted for by the coefficient , which reflects additional losses compared to losses on a straight section of a pipeline [27].
The values of coefficient are calculated experimentally.
The resistance coefficients and can be referred to as hydraulic resistance coefficients. Conduits in machines where a fluid flows also have a specific value of the hydraulic resistance coefficient . The resistance coefficients and should be regarded as wear margin measures [8] of a straight section and an obstacle. These coefficients are established at the manufacturing stage and get larger due to wear. Any device built in a pipeline can be regarded as an obstacle.
If there are no mass losses or changes in cross-section or height above reference plane between two cross-sections of a pipe, and , then the efficiency of a pipe section can be expressed in the following form:
Hence, the hydraulic efficiency of the suction pipe is
and hydraulic efficiency of the discharge pipe is
where represents the pressure losses in the discharge pipe and represents the pressure losses in the suction pipe.
3.3. Power Output and Machine Efficiency
The hydraulic power of fluid resulting from machine work is referred to as machine power output.
For conditions making gases incompressible, the power output of a compressor [30] can be calculated from the following formula:
with in cubic meters per second and in pascals.
The power output of a pump [31] is given by
The machine efficiency is determined as the ratio of power output to power input measured on the machine shaft .
Power measurement on the machine shaft requires a torque measuring device to be installed between the machine shaft and engine shaft. To determine power output, we need to measure the volume flow rate and differential pressure. It is best to measure pressure drops (differential pressure) by electronic manometers. A number of various flowmeter design solutions are offered for measurements of volume flow rate. Depending on the design, flowmeters measure volume flow rate directly or indirectly by determining flow rate from pressure difference or fluid velocity. Measurement accuracy varies depending on the principle of operation used in a flowmeter. Constriction flowmeters, which measure differential pressure at the constriction, are the most accurate. Measurements of fluid flow by Venturi flowmeters (measuring orifices) inserted in circular cross-section conduits running full are specified in standards [32,33].
In a pipeline–machine subsystem, significant periodical pressure pulsations and nonperiodical flow pulsations may occur, resulting in measuring instrument errors. Rotodynamic pumps and compressors generate pulses of low amplitude and frequency corresponding to the passing rotor blades. There are often no apparent symptoms of pulsation, as commonly used flowmeters and pressure or flow transducers generally have a large time constant [34]. Pulsations of volume flow rate may additionally cause mass losses in a machine and additional pressure losses in pipes [22].
To reduce the amplitude of pulsations in pipelines, additional devices are installed, namely equalization tanks or choking elements before the measurement point. It is also possible to eliminate measuring errors caused by pulsation [35] by using fast pressure and differential pressure transducers (constriction flowmeters) combined with a signal processor generating a signal proportional to the root of instantaneous values of pressure and the value of differential pressure.
Pressure pulsations can be used as diagnostically useful signals. The impacts of valve and piston-cylinder leaks on the value of pressure pulsation in a discharge pipe are presented in [36].
4. The Thermodynamic Model of an Open Pipeline–Machine Subsystem
If a difference in temperatures, , exists in a fluid flow in a pipeline, it means that heat is transported along with fluid itself.
Heat flow rate in a fluid flow rate is a product of fluid flow rate , specific heat capacity of the fluid and temperature difference .
Heat flow rate can change in a fluid flow rate, as heat flow can be perpendicular to the direction of fluid motion and it is possible to convert mechanical energy of the fluid (hydraulic energy) into heat energy.
4.1. Heat Flow Perpendicular to the Direction of Fluid Flow: Determination of the Heat Penetration Coefficient
In the case of heat flow perpendicular to the direction of pipeline fluid motion, the pipe wall is a barrier. Figure 5 presents a drop in temperature in a plane perpendicular to the pipeline axis (the ordinate of the coordinate system overlaps the pipeline section axis).
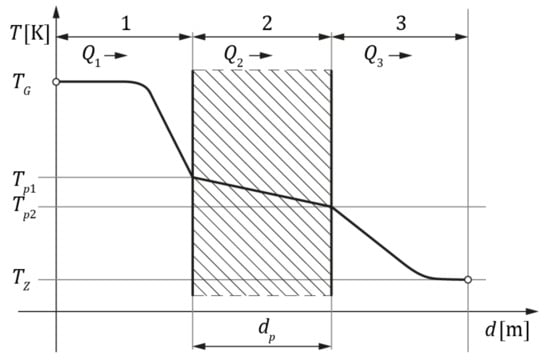
Figure 5.
Temperature drop from hot fluid, through the barrier, to cold fluid [37], where is the path of heat transport/distance from the pipeline axis, is the barrier thickness/pipe wall thickness, is the temperature of hot fluid (flowing in the pipeline) in the observation plane, is the temperature of cold fluid (flowing on pipeline outside surface) in the observation plane, and are temperatures at fluid–solid interface corresponding to the and temperatures at the internal and external surfaces of the barrier (pipeline wall), 1 and 3 indicate convection and 2 indicates heat conduction.
The process of heat transfer from the fluid flux of higher temperature through a barrier to the flux of lower temperature is called heat penetration. Heat flow through a pipe wall can be desired or undesired.
In the case of undesired heat flow, the energy of undesired flow is energy loss.
Desired heat flow perpendicular to the fluid flow is implemented in pipeline devices called heat exchangers. In heat exchangers, the process of heat exchange takes place at a certain pipeline section (along a specific length), which is related with temperature change along the heat exchanging section. Therefore, mean temperature must be determined. The logarithmic mean temperature difference is a universal measure of the mean temperature . The method of determining the mean logarithmic difference of temperatures based on an anticurrent heat exchanger is taken from [38] and shown in Figure 6.
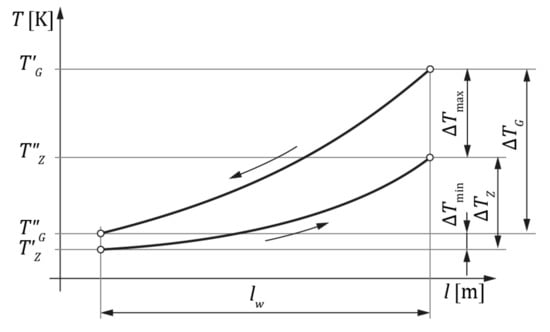
Figure 6.
Temperature as the function of fluid flux distance in an anticurrent heat exchanger under adiabatic conditions, where is the length of the heat exchanger; and are initial temperatures (inlet) of hot and cold fluid fluxes, respectively; and and are the final temperatures of the fluids (outlet).
The flow rate of heat penetrating barriers with surface area A is described in the following form [38,39]:
where is the heat penetration coefficient and .
Heat penetration coefficient [37,40] is a substitute measure of wear margin of the heat exchanger because it depends on properties of materials, shape of built-in elements, working fluids and quantities describing motion and load.
A possible experimental determination of the heat penetration coefficient is indicated in [41]. It follows from the heat exchanger’s heat/energy balance (Figure 5) that
because heat flow rate in a fluid flow rate
then
where and are hot and cold fluid flow rates, respectively, and and represent specific heat capacities at constant volume of hot and cold fluids, respectively.
Thermal efficiency of a heat exchanger is a concept known in the literature. Thermal efficiency (also denoted by ) is defined as a quotient of actually absorbed or transferred heat energy by the maximum energy that can be transferred at given inlet temperatures of both flow rates. If the inlet temperatures are denoted as and (Figure 6), then the maximum heat flow rate that can be transferred :
Because
then
Therefore, the value of the heat exchanger efficiency depends on the value of wear margin of the heat exchanger.
Equations for the effectiveness of simple geometry heat exchanger are given in [39].
4.2. Conversion of Mechanical Energy of Fluid into Heat Energy: Hydraulic Efficiency of a Machine
Energy losses in the pipeline–machine subsystem are converted mainly into heat energy. Heat energy raises the inner energy of fluid and the surrounding solids and can be transported with the fluid flow or can be transferred to the surroundings perpendicularly to the fluid flow.
In [25], losses in rotodynamic pumps are estimated as follows:
- Hydraulic losses in the rotor and pipes transporting fluid to and from the rotor are estimated to be approximately 4.5%;
- Mass losses/capacity losses dependent on return flow density through gaps, discharge holes, packings and slide bearings are estimated to be approximately 1.5%;
- Mechanical losses (approximately 4%) resulting from external friction of the rotor blade surfaces and other rotating elements (approximately 3%) and the shaft in packings and bearings are estimated to be approximately 1%.
Energy of hydraulic losses in the rotor and transporting inlet/outlet conduits is converted to heat energy of the flowing fluid. If it is possible to measure thermal energy of hydraulic losses and output energy, then we can determine hydraulic efficiency according to Equation (14):
Energy losses in a machine cause the difference of suction and discharge temperatures to increase. If the only heat source is hydraulic losses dependent on machine efficiency and there is no heat exchange with the surroundings, the energy losses derivative is equal to heat flux in the fluid flux.
For pumps [14],
or
The above thermodynamic method of efficiency determination allows us to determine the hydraulic efficiency of the pump with less than 1% error directly and continuously from the measurement of temperature difference between the suction and discharge connector pipes. Because the temperature difference in the pump does not exceed 0.05 K, temperatures must be measured with an accuracy of ±0.001 K [14,42].
In compressors, heat comes from the compression process itself, which makes the use of the thermodynamic method for the identification of hydraulic efficiency problematic.
5. Identification of a Pipeline–Machine Subsystem with a Closed Vessel at the End of the Discharge Pipe
In the case of a pipeline–machine subsystem with a closed vessel at the end of the discharge pipe, it is not possible to use the same methodology of identification as used for open pipeline–machine subsystems due to the changing pressure at the subsystem end. Specific methods of identification are required.
Closed vessels can be regarded as short-term storage of nonelectric energy. Theoretical maximum efficiency of compressed air energy storage has been defined in [43] as the “ratio of the maximum work that can be extracted from 1 kmol of air stored at temperature and pressure to the work required to compress 1 kmol of air from ambient temperature (300 K) and pressure (1 atmosphere)”. Vessels made for energy storage are called pressure vessels and are subject to mandatory technical inspection [44]. Filled pressure vessels can be used for the identification of the tightness of tested items [24].
A special case of a pipeline–machine subsystem is one where a closed vessel is found at one end. This vessel can be cyclically emptied, where negative pressure is created in the vessel; filled with gas, where positive pressure is created; and filled with liquid, where pressure of the enclosed air cushion acts on the liquid. Desired values of characteristic measures may be values within specific intervals of filling time, fluid pressure in the vessel and efficiency of the subsystem. Because the change of pressure during filling (Figure 2) changes the instantaneous capacity of the machine and the instantaneous efficiency, identification methods for open systems with steady-state flow cannot be applied. Based on basic knowledge of thermodynamics, the following identification methods for subsystems with vessels on the discharge side are proposed.
5.1. Identification of a Subsystem Delivering Gas to a Constant Volume Vessel
If a vessel has a constant volume , the pressure inside increases from to and temperature rises from to due to the gas filling process. The mass of the medium discharged into a vessel [28] is the difference between the mass in vessel after discharge and before discharge:
The values of gas temperatures in the vessel are difficult to determine. According to [28], the most accurate measurement of the input mass is obtained when pressure is measured after temperature becomes equal to ambient temperature , so
The mass defined by Equation (36) is expressed in moles. Mass in grams can be calculated by multiplying the number of moles by molar mass of a specific gas (g/mol), (g) = (mol) · (g/mol), and
However, the temperature after the discharge is completed can be estimated by measuring of gas in a conduit connecting the compressor with the vessel, assuming that the heat exchange with the surroundings is negligibly small during discharge. Heat delivered together with the gas discharged into the vessel heats the gas contained in the vessel before filling it up to a temperature . The quantity of heat delivered from the compressor to the air in the vessel is expressed as follows:
Heat required to heat gas contained in the vessel before the vessel is filled up is expressed as follows:
hence
The capacity of vessel filling can be defined as the quotient of discharged mass and the filling time of discharge .
Efficiency of filling the vessel can be referred to as the quotient of energy accumulated in the vessel and electric energy absorbed for its accumulation.
The efficiency of a subsystem filling a pressure vessel (machine set–vessel subsystem) can be calculated from Equations (7) and (52) for the efficiency of an open subsystem, substituting
5.2. Identification of a Hydrophore Filling Subsystem
A hydrophore is a tight pressure vessel of volume , which, before filling, contains in its lower part a liquid of volume and gas (mostly air) of pressure above the liquid. After filling, the volume occupied by the liquid increases to the value of and gas pressure increases to (Figure 7). Knowing the filling time, we can define the value of what we call herein vessel filling capacity, , of a hydrophore as
where represents the loss of compressed air volume or the increase in water volume and represents filling time.
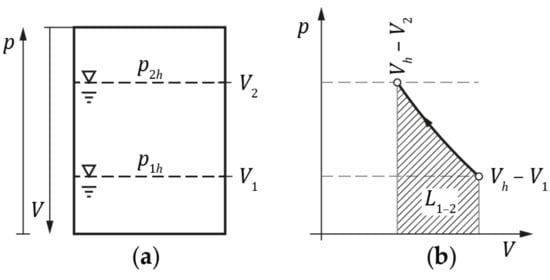
Figure 7.
(a) Liquid volumes and gas pressures in the hydrophore before and after filling the hydrophore. (b) Air pressure in the hydrophore, where is the initial volume of the liquid, is the final volume of the liquid, is the total volume of the hydrophore, is the initial gas pressure, is the final gas pressure and is the work performed during gas compression (hatched area).
For cost-effectiveness, the hydrophore should be as small as possible but have such functional volume that the actual work cycle of the device is not shorter than the limit value corresponding to the allowable frequency of pump switching [45].
The gas being filled into a hydrophore becomes compressed, so its volume decreases from to . Depending on the conditions, compression can be isothermal, polytropic or adiabatic. The volume of gas compressed to the same pressure depends on the type of compression. The work required for compression is called the external compression work .
The value of exponent of the compression polytropic curve for a specific system can be determined experimentally by using known thermodynamic relations [46] between the quantities of the polytropic process of perfect gases.
After finding the logarithms of last two terms on both sides,
When the calculated exponent of the polytropic curve assumes a value of external compression work can be determined from the following equation [46]:
When we can assume that the compression is isothermal. External compression work of isothermal process [46] is given as follows:
In the hydrophore, we can assume that the energy required to compress gas is equal to external work of the pump and that the liquid of volume obtains energy equal to external work
The external work of the pump, neglecting the height above reference plane, is equal to the pressure energy of the liquid with volume The pressure is a mean pressure acting on the liquid during the filling of the hydrophore vessel.
Efficiency of hydrophore filling can be determined as the quotient of the compression work and the electric energy required to perform the compression work:
Pressure in the hydrophore can be changed by supplying compressed air to the hydrophore. An increase in pressure at the same volume change will result in greater compression work and increased pressure energy. It is possible to determine discrete segments of pump curves and or .
Provided that the suction area pressure is constant, the efficiency of a subsystem filling a hydrophore (machine set–hydrophore subsystem) can be calculated from Equations (7) and (52) for the open subsystem efficiency, substituting
6. Results and Discussion
The lubrication subsystem of a ship’s main engine may be considered as an open pipeline–machine subsystem. It was stated in Section 2 that the wear margin of an open subsystem is not exhausted if the subsystem delivers fluid to the destination with capacity falling within the range , at pressure in the range of and temperature in the range of . This means that the fluid pressure and volume flow rate should be measured during operation. It follows from the author’s research that no such control may cause machine and sealing failures. The lubrication subsystem of a ship’s main engine was examined as it had been producing excessive levels of noise and vibrations. In normal operation, due to investment costs, the lubrication subsystem is expected to supply an engine with oil of temperature and pressure within required ranges of values. The real value of the pressure depends on oil flow resistance in an engine and on the volume flow rate of oil delivered to the engine, while an excessive value of oil volume flow rate is not harmful for the engine. The volume flow rate of oil produced by the pump is divided into that delivered to the engine and that returning to the pump suction pipe. It was found that during the oil flow rate division where the pressure at the engine inlet was close to the maximum required value, the pressure at pump discharge (Figure 1) exceeded maximum values for the sealing used in the pipes (oil leaks) and for the pump used. The examined subsystem was equipped with a screw displacement pump. Positive displacement machines are equipped with overload relief valves that open if a specific pressure is exceeded, which occurred in the examined case and resulted in opening and closing of relief valves, increased noise, damage to valve elements and drops in volume flow rate. It was also found during the tests that in similar ships, where the pressure on the engine inlet was maintained in the lower range of required pressure, no excessive vibrations of the pumps and no higher frequency of failures of lubricating subsystem elements were observed. Therefore, engine lubrication subsystems seem to need two things: the determination of the required oil flow rate and the measurement of this oil flow rate.
Due to the lack of recognized identification methodology applicable to a pipeline–machine subsystem with a closed vessel at the end of the discharge pipe, tests were performed to ascertain practical reality and plausibility of the methodology proposed in Section 5. Tests were conducted on industrial and laboratory subsystems with closed vessels at the end of the discharge pipe. The tested subsystems were equipped with sets consisting of a piston displacement machine (with piston-crank mechanism), belt transmission and electric motor. The time of vessel filling was measured as the working time of the machine (motor on/off time). The pressures were read out after the machine was switched off and the indications stabilized. Measurements were performed using the devices normally installed on the examined subsystems, while the electric power and energy was measured by the HT4022 tester. The tester enabled power and energy measurement on three phase-balanced systems. Electric energy could be measured with 1 Wh accuracy. The tests were conducted on two different subsystems, with one being a compressor with a pressure vessel and the other being a pump with a hydrophore.
In the former case, due to the inability to measure temperature, only the efficiency of filling the vessel was determined. The filling efficiency of a subsystem was determined for a 0.4 m3 air vessel and an air compressor of 80 m3/h capacity, driven by an 11 kW electric motor. Pressure in the vessel was measured by a manometer. To fill the vessel from pressure (1.0 bar) to pressure (6.5 bar), the subsystem absorbed energy was 0.231 kWh and the time of filling was 85 s. The subsystem efficiency, for such pressures calculated by Formula (50), was
In the second case, the filling capacity of a hydrophore (Equation (54)), the efficiency of filling the hydrophore (Equation (61)) and efficiency of subsystem filling (Equation (63)) were calculated by Equations (54), (61) and (63) for the filling of a subsystem consisting of an open vessel–pipeline–pump–pipeline–hydrophore vessel. That subsystem had a single-acting positive displacement plunger pump. According to the maker, the pump capacity is 1.40 (m3/h)/0.39 (L/s), the discharge head is 60 m H2O/6.0 bar (1 m H2O = 0.098 bar) and the motor power is 0.45 kW. The hydrophore vessel had a total volume of 70 L (0.070 m3). The measurements included air pressure and , filling time and electric energy of the electric power used by the motor during water volume change in the vessel by = 30 L ( = 0.015 m3, = 0.045 m3). Volumes were measured by a water level gauge integrated with the hydrophore. Time was measured with a stopwatch, and the pressure was measured with a manometer. No impact of pressure in the examined interval on filling time was found. The measured time of filling was 78 s. The calculated filling capacity of a hydrophore (vessel filling capacity) was 0.38 L/s. The other results of measurements and calculations are given in Table 1.

Table 1.
Summary of the test results for a displacement pump subsystem and a hydrophore vessel.
It follows from theoretical and experimental tests that, within the specific boundaries of a pipeline–machine subsystem with a machine driven by an electric motor, the methods and resources for identification tasks depend on the way the subsystem works.
In the case of an open subsystem, particularly in steady-state conditions, it is desired and possible to determine the initial, suction, discharge and final fluid pressures; the initial, suction, discharge and final fluid temperature; the volume flow rates at the beginning and at the end of a subsystem; and the electric energy or input power of the electric motor.
The measured values of these quantities allow us to calculate values of the efficiency of the whole subsystem, the hydrodynamic efficiency of the suction and discharge pipes, the hydrodynamic efficiency of the machine (pump) and the efficiency of the motor–machine set.
Desired value ranges can be defined for the hydrodynamic efficiency of the suction and discharge pipes and the efficiency of the whole set. If a real value of suction/discharge pipe hydrodynamic efficiency is found to be outside the desired range, we should start looking for the cause, using the relationships between efficiency, pressure drop and coefficients of hydraulic resistance. The characteristics of the wear margin affecting the value of a given hydraulic resistance coefficient make up a list of probable causes.
When it is found that the real value of the machine set efficiency lies outside the desired range, we should use other information to determine ranges of desired values of hydraulic efficiency of the machine, mechanical efficiency of the set and electric efficiency of the motor. If the real hydraulic efficiency of the machine is known (measured), we can confirm or exclude excessive wear of machine elements that contribute to hydraulic losses of the machine. If the real value of the hydraulic efficiency of the machine is within the desired range of values, we can assume that the real value of mechanical efficiency of the machines multiplied by the electric efficiency of the motor does not lie within desired value range. It is necessary to start diagnostic tests by methods suitable for pump/compressor–motor sets (which goes beyond the scope of these considerations).
If the real value of the final temperature of the fluid or real value of the thermal efficiency of the heat exchanger are outside the range of desired values, the cause may be an incorrect value of the heat penetration coefficient k for the pipeline elements. The real value of the coefficient can be determined. Characteristics of wear margin affecting the value of the heat penetration coefficient make up a list of probable causes of failures.
For a pipeline–machine subsystem with a closed vessel at the end of discharge pipe, it is possible to determine the capacity and filling efficiency and the subsystem efficiency from measured pressures and volumes of fluids in the vessel, temperature of the discharged fluid, electric energy input and vessel filling time. The filling efficiency is determined for not just one value, but rather for a certain range of pressures (pressures when the machine is switched on/off) with a specific mean pressure value. The value of the energy efficiency of the subsystem with a closed vessel at the end of discharge is much lower than the efficiency of open-vessel subsystems working in steady-state conditions. The efficiency increases as the on/off pressure range is narrowed and gets closer to the nominal pressure of the machine. A filled vessel can be part of a system for the identification of tightness of vessels/tanks and other objects; if it is possible to connect it with the working chamber of the machine, it can be used for the identification of mass losses in the machine.
7. Conclusions
The practical use of a new concept for the identification of maintained technical items has been demonstrated. Based on subsystems of fluid transport, it has been shown that the following objectives can be achieved:
- Determining desired characteristic measurement values of subsystems and decomposing these characteristics and their values into desired measurement values of subsystem functional unit characteristics;
- Determining substitute measures as well as symptom measures of functional unit wear margin;
- Identifying the relationships between the substitute measure and symptom measure of a functional unit wear margin, as well as identifying and the relationship between the subsystem wear margin measure and substitute/symptom measure of functional unit wear margin.
Two subsystems of fluid transport, independent of fluid type, have been distinguished: an open pipeline–machine subsystem and a pipeline–machine subsystem with a closed vessel at the end of the discharge pipe.
It has been demonstrated that wear margin of an open pipeline–machine subsystem is not exhausted if the subsystem delivers fluid to the destination under the following conditions: under the following conditions:
- With capacity falling within the range of [ ], at pressure in the range of [] and temperature in the range of [];
- With efficiency values in the range [ ];
- With failure frequency rate not exceeding a limit value;
- With an acceptable value of availability.
Using the hydrodynamic model and the thermodynamic model of an open pipeline–machine subsystem, methods of subsystem energy efficiency measurement and subsystem machine efficiency identification have been sorted out. These considerations involve symptom measures and substitute measures of subsystem functional unit wear margin, as well as relationships between the measures and methods for the identification of functional unit energy efficiency. It has been shown that, for pumps, the thermodynamic method allows us to measure the energy efficiency of the pump working chamber.
In the case of a pipeline–machine subsystem with a closed vessel at the end of the discharge pipe, it has been found that it is not possible to use the method of identification that is used for open pipeline–machine subsystems. Specific measures are proposed for the assessment of the subsystem wear margin: capacity of vessel filling, efficiency of filling the vessel and efficiency of a subsystem filling a pressure vessel. Methods of determining the capacity of vessel filling, efficiency of filling the vessel and efficiency of a subsystem filling a pressure vessel have been developed, based on thermodynamic relationships. Practical reality and plausibility of the proposed methodology have been confirmed experimentally. The wear margin of a pipeline–machine subsystem with a closed vessel at the end of the discharge pipe is not exhausted if the values of capacity of vessel filling, efficiency of a subsystem filling a pressure vessel or efficiency of filling the vessel do not exceed a limit value.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- ISO 55000:2014. Asset management—Overview, Principles and Terminology; International Organization for Standardization: Geneva, Switzerland, 2014.
- ISO 17359:2018. Condition Monitoring and Diagnostics of Machines—General Guidelines; International Organization for Standardization: Geneva, Switzerland, 2018; p. 1.
- ABS Guidance Notes on Equipment Condition Monitoring Techniques; American Bureau of Shipping: Houston, TX, USA, 2016.
- BS EN 13306:2010. English Version EN 13306:2010 Maintenance—Maintenance Terminology; British Standards Institution: London, UK, November 2010.
- Smalko, Z. The Functional quality signatures of man-machine system. Diagnostyka 2006, 4, 43–46. [Google Scholar]
- PN-82/N-04001. Exploitation of Technical Objects—Terminology; Polish Committee for Standardization: Warsaw, Poland, 1982.
- DIN 31051:2012-09. Fundamentals of Maintenance; German Institute for Standardization: Berlin, Germany, 2012.
- Bielawski, P. Measures and limits of machine wear margin of production systems. Probl. Eksploat. /Maint. Probl. 2016, 1, 129–159. [Google Scholar]
- Korbicz, J.; Kościelny, J.M.; Kowalczuk, Z.; Cholewa, W. (Eds.) Fault Diagnosis. Models, Artificial Intelligence, Application; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Nelles, O. Nonliner system identification with neuro-fuzzy methods. In Intelligent Hybrid Systems; Ruan, D., Ed.; Springer: Boston, MA, USA, 1997; pp. 283–310. ISBN 978-1-4613-7838-9. [Google Scholar]
- Kościelny, J.M.; Bartyś, M.; Syfert, M. Method of Multiple Fault Isolation in Large Scale Systems. IEEE Trans. Control Syst. Technol. 2012, 20, 1302–1310. [Google Scholar] [CrossRef]
- Stępniewski, M. Pumps, 2nd ed.; WNT: Warsaw, Poland, 1985; ISBN 83-204-0703-6. (in Polish) [Google Scholar]
- Thermal and Energy Measurements; Mieszkowski, M., Ed.; WNT: Warsaw, Poland, 1985; ISBN 83-204-0698-6. (in Polish) [Google Scholar]
- Clifford, T. Severn Trend Water Melbourne Real Time Pump and Turbine Network Optimisation; Pump Centre Conference: Telford, UK, 12 May 2016; Available online: https://riventa.com/wp-content/uploads/2016/05/Riventa-Pump-Centre-Conference-Keynote-2016.pdf (accessed on 1 April 2020).
- Jędral, W. Probable shape of pipeline characteristic curves. Pompy-Pompownie 2000, 5, 17–19, 35–37. (in Polish). [Google Scholar]
- Jędral, W. Rotodynamic Pumps; Wydawnictwo Naukowe PWN: Warsaw, Poland, 2001; ISBN 83-01-13552-2. (in Polish) [Google Scholar]
- ISO 9906:2012. Rotodynamic Pumps—Hydraulic Performance Acceptance tests—Grades 1, 2 and 3; International Organization for Standardization: Geneva, Switzerland, 2012.
- Timashev, S.; Bushinskaya, A. Diagnostics and Reliability of Pipeline Systems; Springer: Cham, Switzerland, 2016; ISBN 978-3-319-25305-3. [Google Scholar]
- Jędral, W. Efficiency of Pumps and Pumping Installations; Krajowa Agencja Poszanowania Energii S.A.: Warsaw, Poland, 2007; ISBN 978-83-921049-3-3. (in Polish) [Google Scholar]
- Białek, P.; Bielawski, P. Failure Analysis of Hydrogen Piston Compressors. In Advances in Technical Diagnostics; Timofiejczuk, A., Łazarz, B.E., Chaari, F., Burdzik, R., Eds.; Springer: Cham, Switzerland, 2018; pp. 69–80. ISBN 978-3-319-62041-1. [Google Scholar]
- Białek, P.; Bielawski, P.J. Failure analysis of refinery hydrogen reciprocating compressors. Diagnostyka 2018, 19, 83–92. [Google Scholar] [CrossRef]
- Garcia-Guarin, J.; Gómez, J.A.; Contrearas, D.A. Experimental study of pumps in a pipe bench. J. Phys. Conf. Ser. 2019, 1257, 012003. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, X.; Li, Y.; Tie, Y.; Zhang, Y.; Gao, J. Watwer Pipeline Leakage Detection Based on Machine Learning and Wireless Sensor Networks. Sensors 2019, 19, 5086. [Google Scholar] [CrossRef] [PubMed]
- Bielawski, P. Identification of the piston machine combustion chamber tightness. J. Qual. Maint. Eng. Submitted.
- Ostoja-Bębnowski, J.; Rusin, Z. Pump efficiency improvement. Pompy-Pompownie 2002, 2, 63–66. (in Polish). [Google Scholar]
- Jeżowiecka-Kabsch, K.; Szewczyk, H. Fluid Mechanics; Oficyna Wydawnicza Politechniki Wrocławskiej: Wrocław, Poland, 2001; ISBN 83-7085-597-0. (in Polish) [Google Scholar]
- Böswirth, L.; Bschorer, S. Technische Strömungslehre, 9th ed.; Vieweg; Teubner Verlag: Wiesbaden, Germany, 2012; ISBN 978-3-8348-1718-1. [Google Scholar]
- Gajl, J. Positive Displacement Compressor Testing. In Thermal and Energy Measurements; Mieszkowski, M., Ed.; WNT: Warsaw, Poland, 1985; pp. 501–558. ISBN 83-204-0698-6. (in Polish) [Google Scholar]
- Bielawski, P. Diagnosing of pipelines. Przegląd Spaw. 2016, 88, 72–76. (in Polish). [Google Scholar]
- Adamczewski, J. Testing of ventilators. In Thermal and Energy Measurements; Mieszkowski, M., Ed.; WNT: Warsaw, Poland, 1985; pp. 387–411. ISBN 83-204-0698-6. (in Polish) [Google Scholar]
- Filipiak, E. Testing of centrifugal pumps. In Thermal and Energy Measurements; Mieszkowski, M., Ed.; WNT: Warsaw, Poland, 1985; pp. 412–438. ISBN 83-204-0698-6. (in Polish) [Google Scholar]
- PN-EN ISO 5167-1:2005 Measurement of Fluid Flow by Means of Pressure Differential Devices Inserted in Circular Cross-Section Conduits Running Full—Part 1: General Principles and Requirements; Polish Committee for Standardization: Warsaw, Poland, 2005.
- PN-EN ISO 5167-2:2005 Measurement of Fluid Flow by Means of Pressure Differential Devices Inserted in Circular Cross-Section Conduits Running Full—Part 2: Orifice Plates; Polish Committee for Standardization: Warsaw, Poland, 2005.
- Turkowski, M. Measurements of fluid flow lux pulsations (1). Pomiary Automatyka Robotyka 2005, 10, 8–10. (in Polish). [Google Scholar]
- Turkowski, M. Measurements of fluid flux pulsations (2). Constriction flowmeters. Pomiary Automatyka Robotyka 2005, 11, 10–14. (in Polish). [Google Scholar]
- Manepatil, S.S.; Tiwari, A. Fault Diagnosis of Reciprocating Compressor Using Pressure Pulsations. In Proceedings of the International Compressor Engineering Conference at Purdue, Lafayette, IN, USA, 17–20 July 2006; Paper 1819. Available online: http://docs.lib.purdue.edu/icec/1819 (accessed on 1 April 2020).
- Bielawski, P. Diagnosing the wear margin of thermal nodes. Syst. Wspomagania w Inżynierii Produkcji 2017, 6, 7–16. (in Polish). [Google Scholar]
- Sperlich, V. Grundlagen der Technischen Thermodynamik; Universität Duisburg: Essen, Germany, 2007. [Google Scholar]
- Domański, R.; Jaworski, M.; Rebow, M.; Kołtyś, J. Some Problems of Thermodynamics: Computer-Based Approach; Wydawnictwo Naukowe PWN: Warsaw, Poland, 2000; ISBN 83-01-12978-6. (in Polish) [Google Scholar]
- Bielawski, P. Measures and symptoms of wear margin in functional unit nodes of production system items. J. Mach. Constr. Maint. Probl. Eksploat. 2017, 3, 117–126. [Google Scholar]
- Moeck, E.; Strickert, H. Technische Diagnostik an Schiffsmaschinenanlagen; Verlag Technik: Berlin, Germany, 1982. [Google Scholar]
- Papa, F.; Radulj, D. Thermodynamic method used for pump performance and efficiency testing program. Environ. Sci. Eng. Mag. 2013, 26, 44–48. [Google Scholar]
- Succar, S.; Williams, R.H. Compressed Air Energy Storage: Theory, Resources and Applications for Wind Power; Princeton Environmental Institute, Princeton University: Princeton, NJ, USA, 2008. Available online: https://www.nrc.gov/docs/ML1003/ML100361047.pdf, (accessed on 1 April 2020).
- EN 13445-5:2018. Unfired Pressure Vessels—Part 5: Inspection and Testing; European Committee for Standardization: Brussels, Belgium, 2018.
- Marczuk, M. Design and Operation of Hydrophore Devices, 2nd ed.; Arkady: Warsaw, Poland, 1973. (in Polish) [Google Scholar]
- Bańkowski, Z.; Bernhardt, M.; Chmielewski, H.; Dobrzański, T.; Gosztowtt, L.; Hausman, K.; Karaszkiewicz, A.; Kosieradzki, P.; Krotochwil, Z.; Kuczewski, S.; et al. Mechanic’s Little Manual, 15th ed.; WNT: Warsaw, Poland, 1984; ISBN 83-204-0434-7. (in Polish) [Google Scholar]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).