Method to Increase the Accuracy of Large Crankshaft Geometry Measurements Using Counterweights to Minimize Elastic Deformations
Abstract
1. Introduction
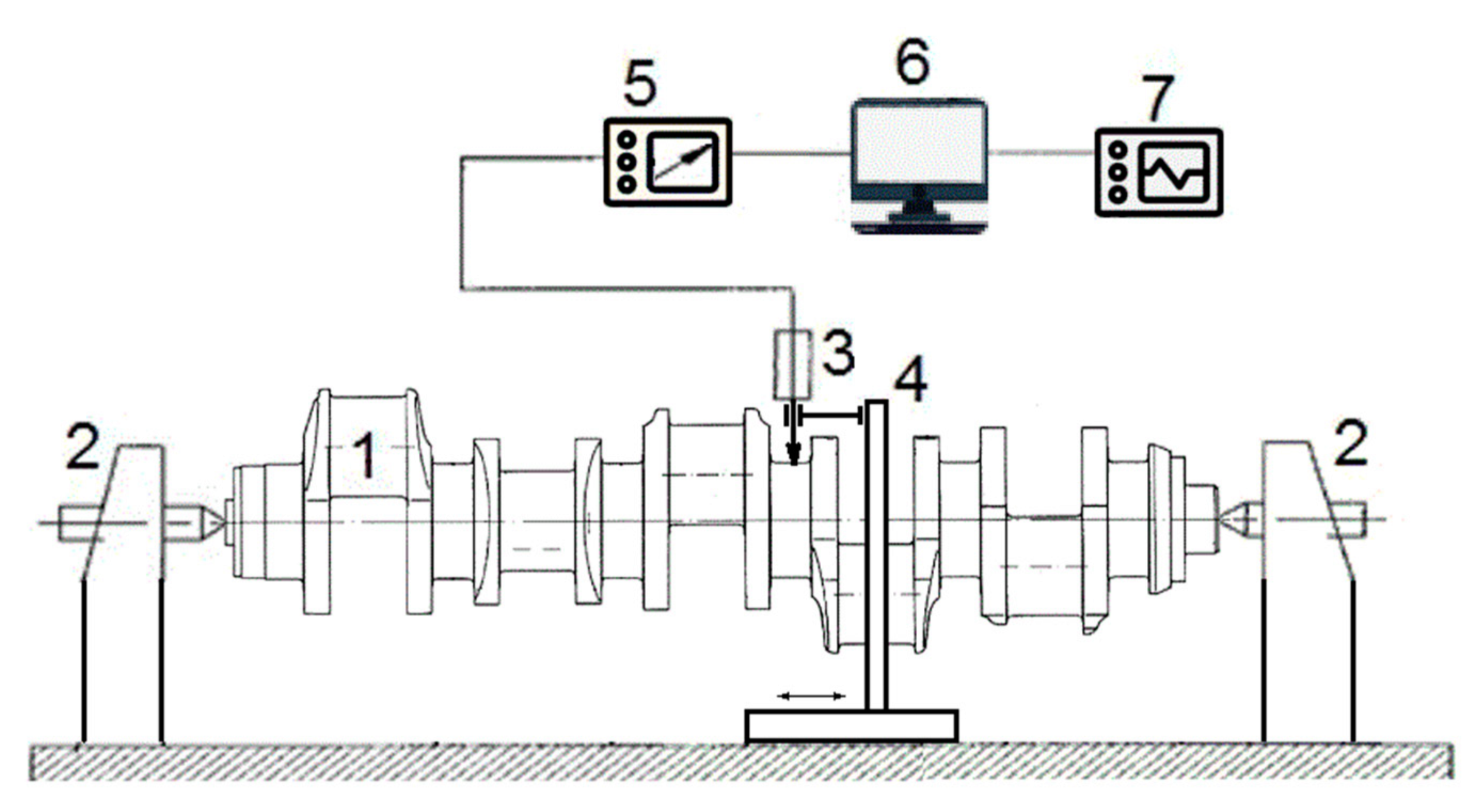
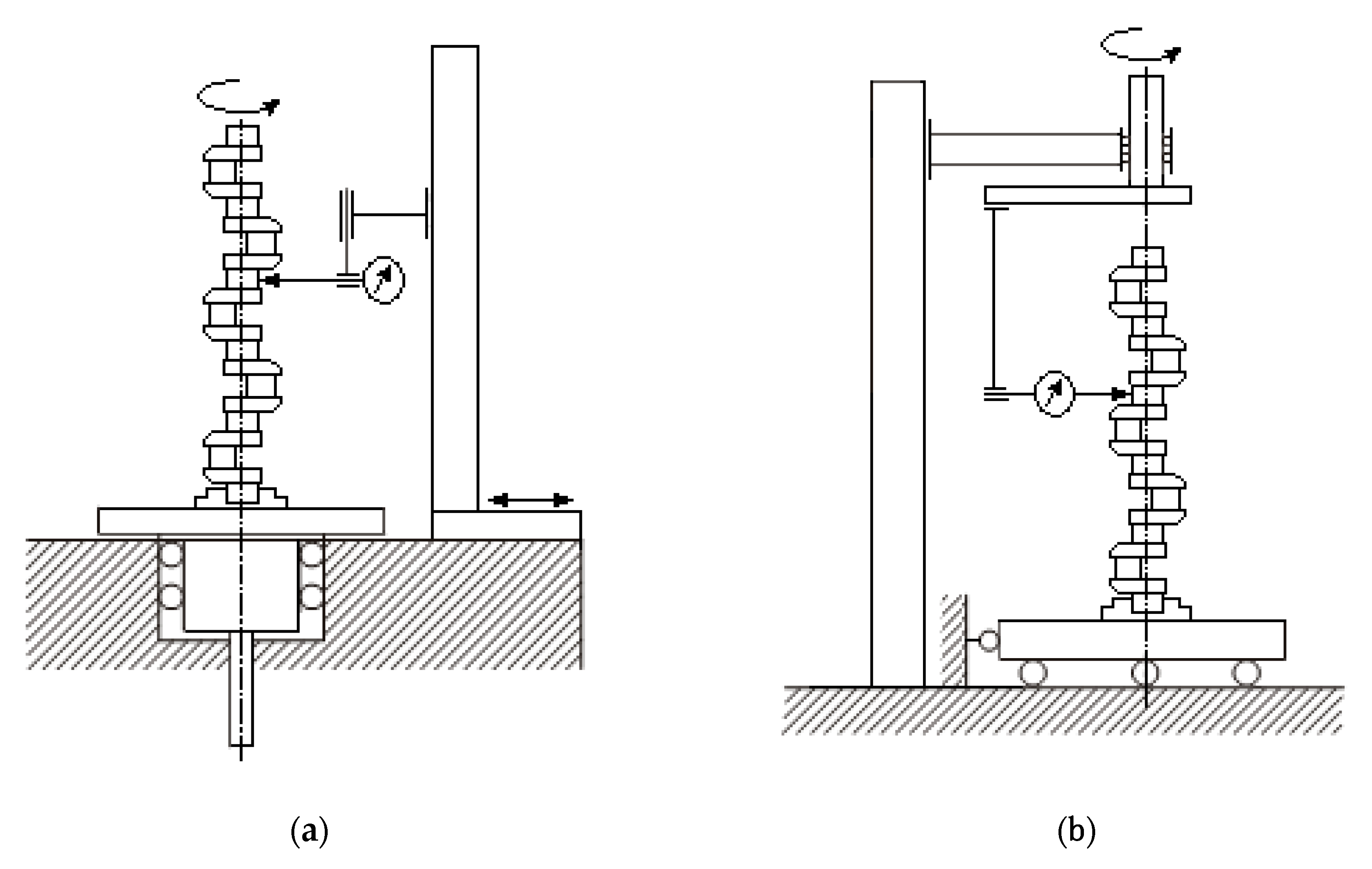
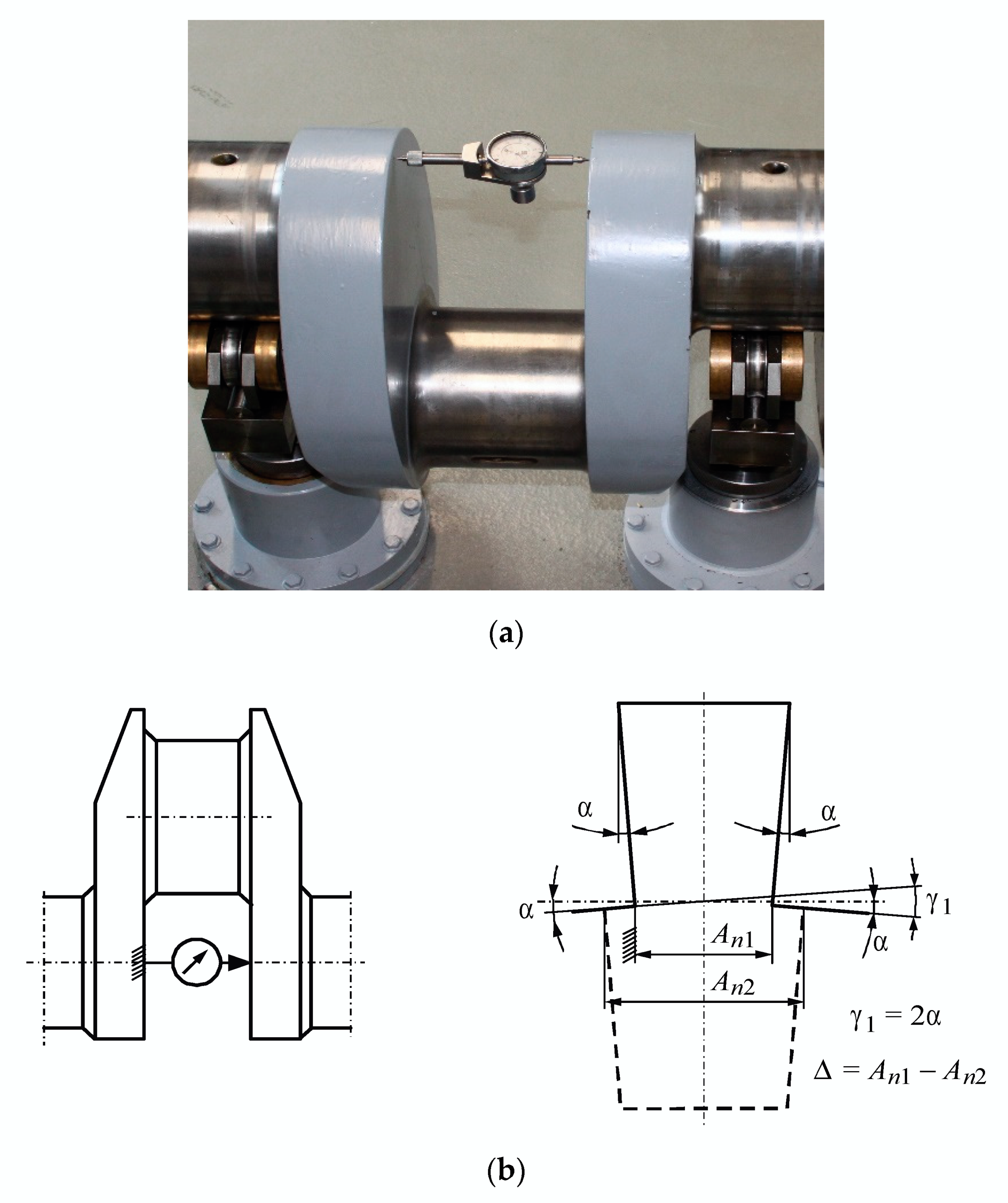
2. Crankshaft Geometry Measuring Methods
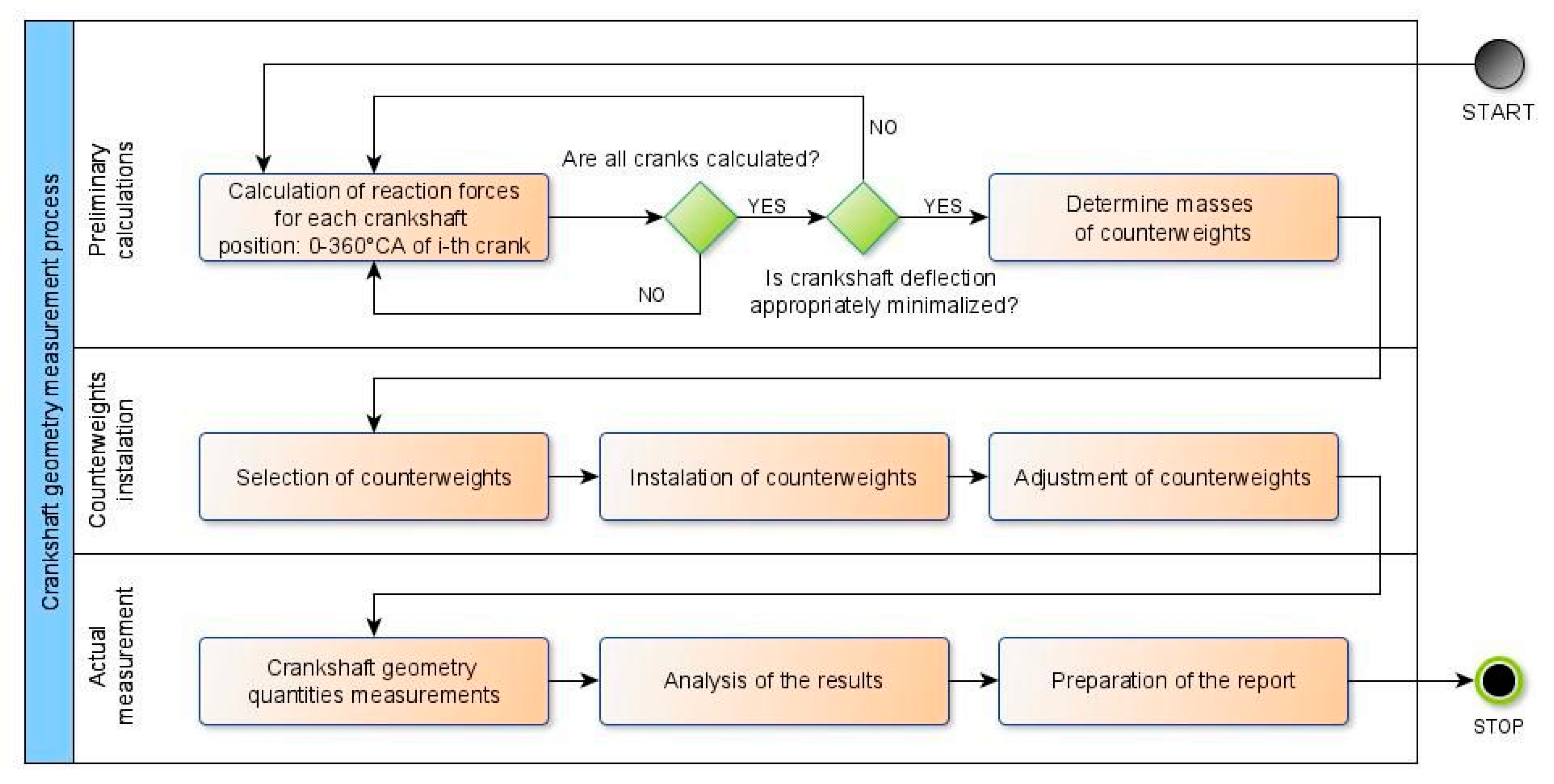
3. Materials and Methods
- Calculating the reaction forces at the supports of the analyzed shaft for specified increments of the rotation angle from 0–360°, e.g., every 15 degrees.
- Determining balancing masses, the locations of their centers of gravity, and the position of masses on the crank to obtain the minimum changes in reaction forces for a full shaft rotation (as shown in the example). In practice, a reaction force deviation equal to approx. 0.1–0.5% prevents a shaft’s elastic deformation from affecting the accuracy of profile measurements.
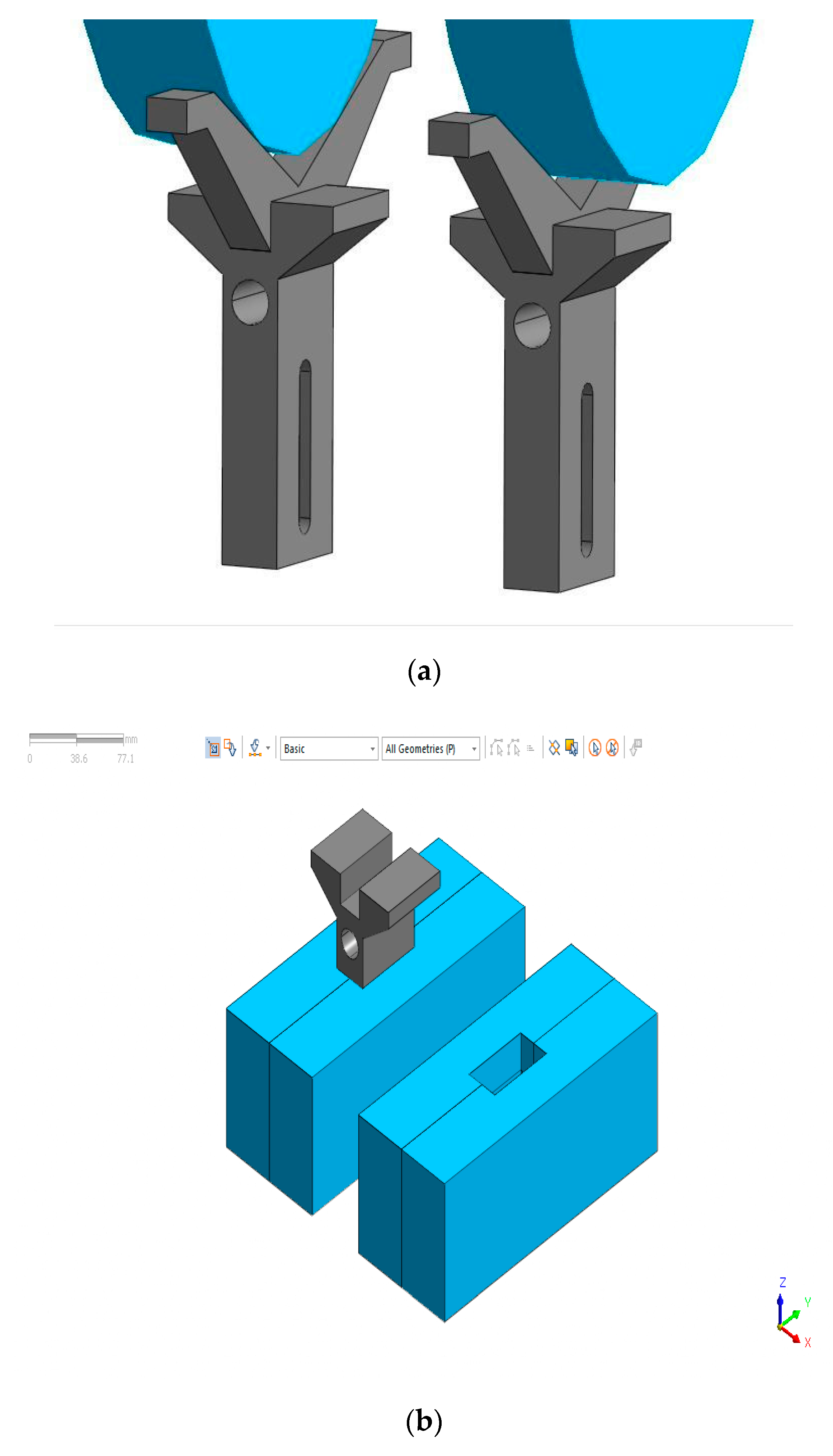
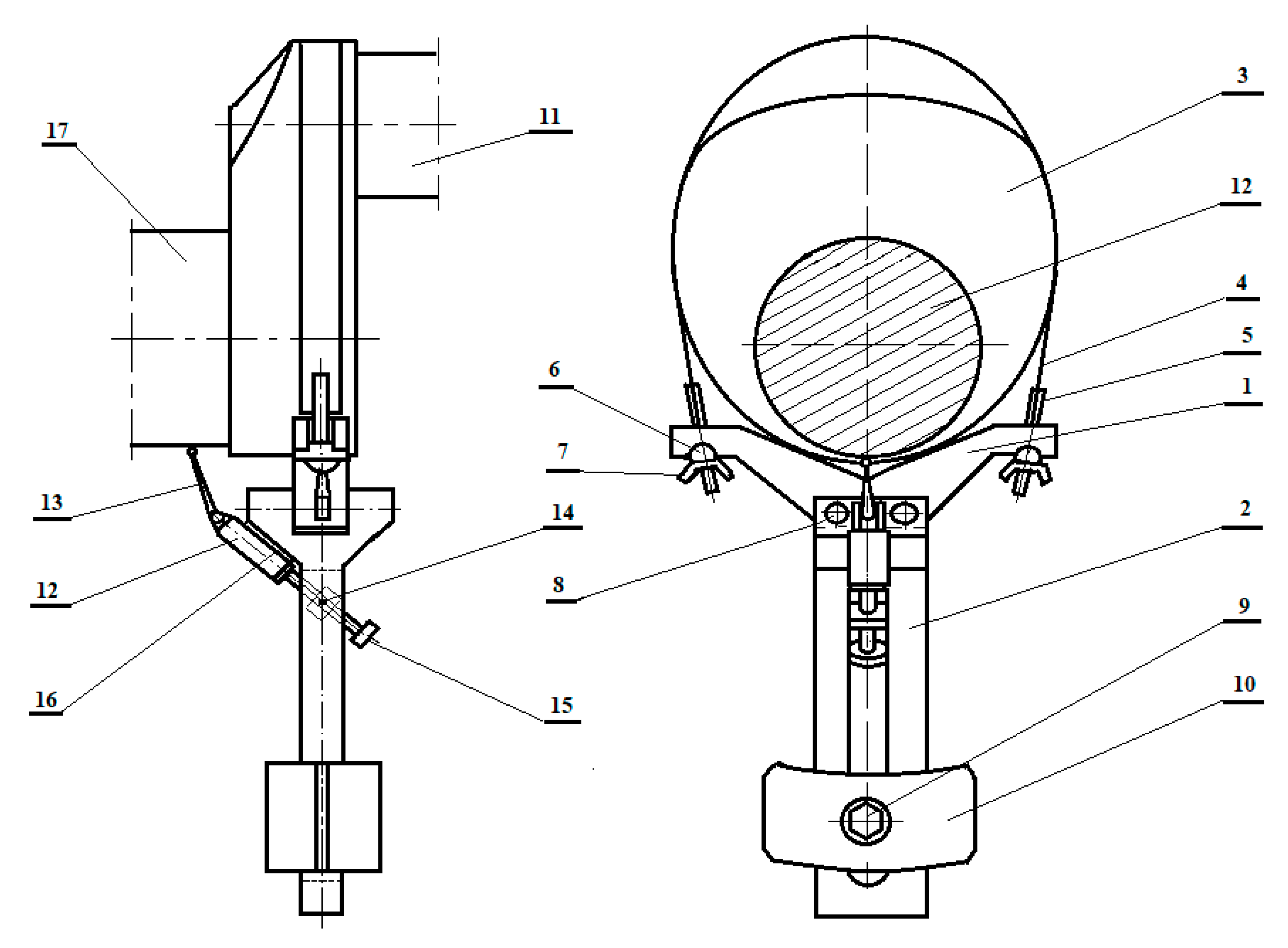
- Fitting the crank with a correction device with weights that correspond to the calculated reaction forces. The device should be installed in the crank’s plane of symmetry, perpendicular to the longitudinal axis of the crankshaft. The weight must be located symmetrically, opposite the crankpin, for which the indications of the correction device’s displacement sensor may be helpful.
- Adjusting weights so that the center of gravity of the device with the weights is as recommended in point 2. The center of gravity must also be located in the plane containing the axis of symmetry of the main journal and the crankpin, for the crank in which the device is installed.
- Implementing steps 3 and 4 for all crank webs.
- Properly measuring the geometry of the main journal by fully rotating the shaft, while gauging it with a dial displacement sensor or an electronic readout displacement sensor.
- Repeating step 6 for all main journals.
- Summarizing the results and drawing conclusions about the geometry of the shaft.
4. Results and Discussion
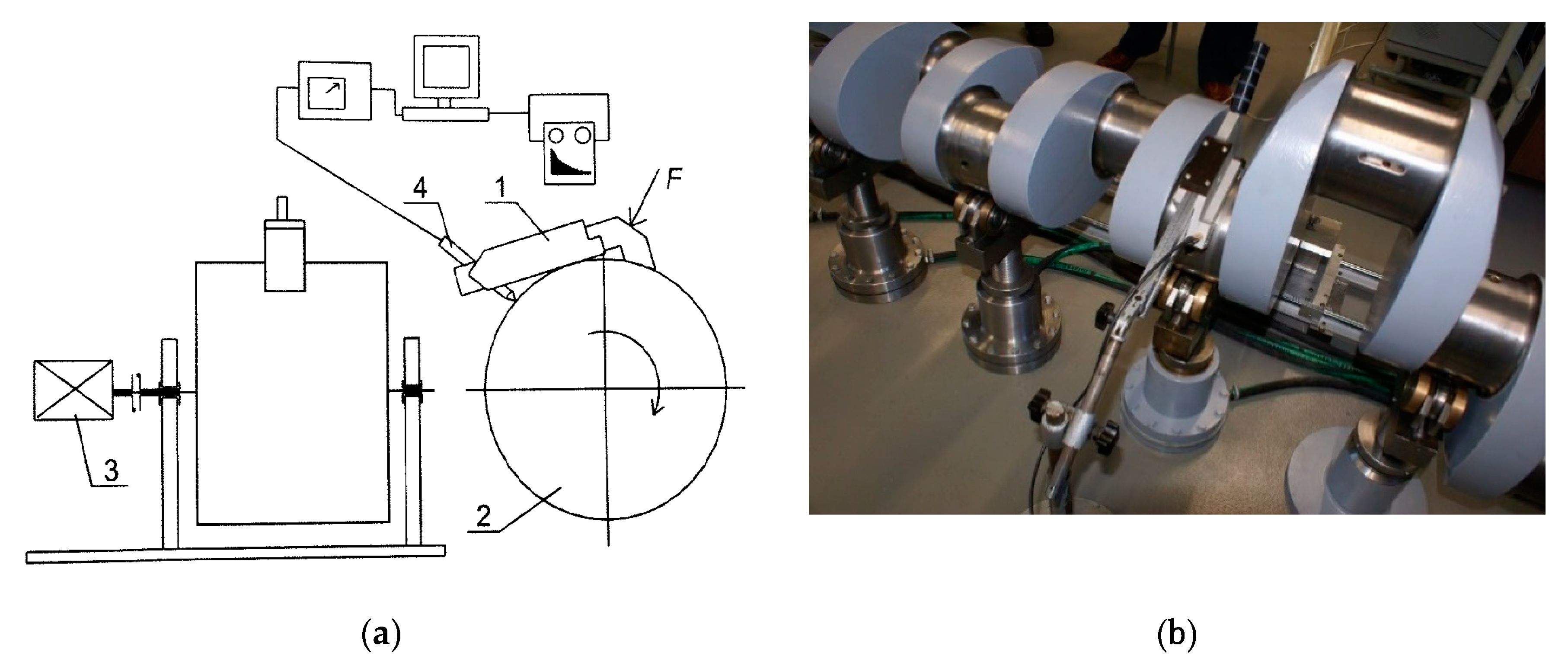
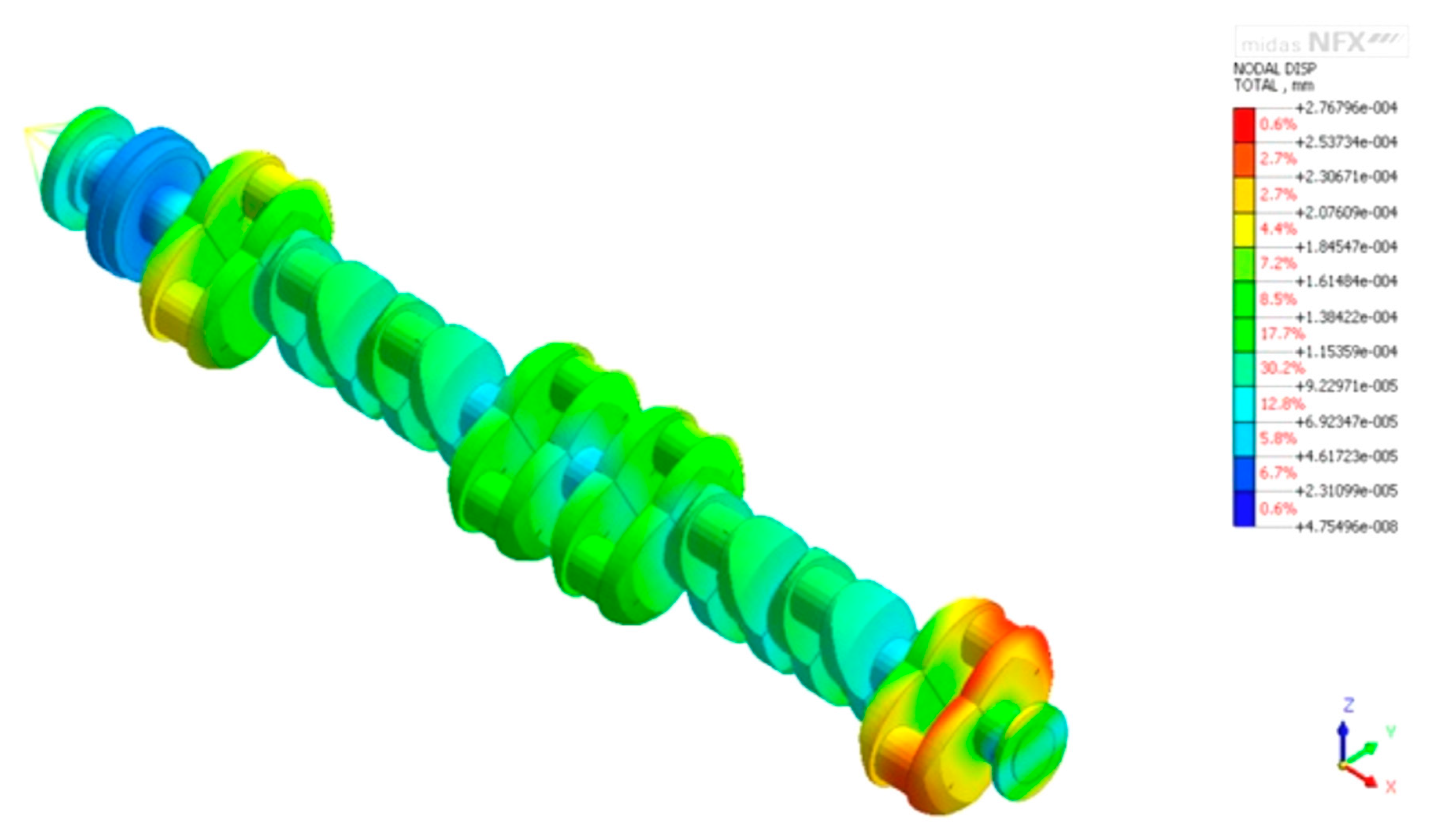
4.1. Calculations Confirming the Proposed Concept
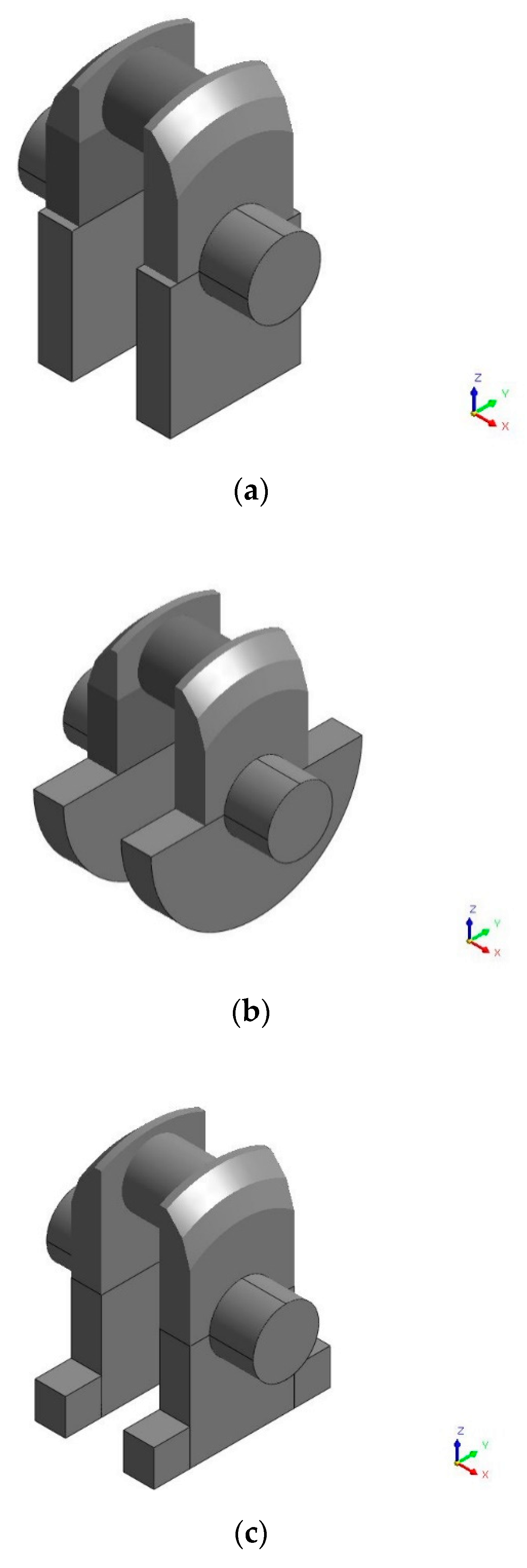
4.2. Example of an Embodiment of a Device to Stabilize Reaction Forces at Supports
5. Summary
- Increased accuracy of measurements of the geometry of large journals resting on fixed supports;
- The solution is versatile and can be used for different shafts and support methods;
- The solution does not require changing the construction and operation of the shaft support system at the measurement bench;
- There is no need to use flexible supports that exert variable reaction forces depending on the angle of rotation of the supported shaft, which significantly simplifies the measurement system;
- This solution may complement existing measurement systems by increasing their accuracy at little additional cost.
6. Patents
- Nozdrzykowski K., Chybowski L., Grządziel Z., Device for increasing accuracy of geometry measurements for large size crankshafts and a method for geometry measurements for large size crankshafts. Polish Patent Office, P.433522.
- Nozdrzykowski, K. Device for measuring positional deviation of axis of crankshaft pivot set. Polish 527 Patent Office, PL393829-A1; PL218653-B1.
Author Contributions
Funding
Conflicts of Interest
References
- Fonte, M.; Duarte, P.; Anes, V.; Freitas, M.; Reis, L. On the assessment of fatigue life of marine diesel engine crankshafts. Eng. Fail. Anal. 2015, 56, 51–57. [Google Scholar] [CrossRef]
- Sun, J.; Wang, J.; Gui, C. Whole crankshaft beam-element finite-element method for calculating crankshaft deformation and bearing load of an engine. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 299–303. [Google Scholar] [CrossRef]
- Zhao, Y.; Cao, S.Q. Modal Analysis of Large Marine Crankshaft. Front. Manuf. Des. Sci. III 2013, 271–272, 1022–1026. [Google Scholar] [CrossRef]
- Siemiątkowski, Z.; Rucki, M.; Morozow, D.; Martynowski, R.; Shelkovoy, A.; Gutsalenko, Y. Study of the geometry of grinding machines used for large scale crankshaft machining. Cut. Tools Technol. Syst. 2019, 91, 207–219. [Google Scholar] [CrossRef]
- Nozdrzykowski, K.; Chybowski, L. A Force-Sensor-Based Method to Eliminate Deformation of Large Crankshafts during Measurements of Their Geometric Condition. Sensors 2019, 19, 3507. [Google Scholar] [CrossRef]
- Niezgodziński, M.; Niezgodziński, T. Wytrzymałość Materiałów [Resistance of Materials]; PWN: Warsaw, Poland, 1979. [Google Scholar]
- Łukomski, Z. Technologia Spalinowa Silników Kolejowych i Okrętowych [Exhaust Gas Technology of Railway and Marine Engines]; WKiŁ: Warsaw, Poland, 1972. [Google Scholar]
- Dunaj, P.; Dolata, M.; Berczyński, S. Model Order Reduction Adapted to Steel Beams Filled with a Composite Material. In Information Systems Architecture and Technology: Proceedings of 39th International Conference on Information Systems Architecture and Technology–ISAT 2018; Springer: Cham, Switzerland, 2019; pp. 3–13. [Google Scholar]
- Kazienko, D.; Chybowski, L. Instantaneous Rotational Speed Algorithm for Locating Malfunctions in Marine Diesel EnginesLocating Malfunctions in Marine Diesel Engines. Energies 2020, 13, 1396. [Google Scholar] [CrossRef]
- Kazienko, D. The analysis of class survey methods and their impact on the reliability of marine power plants. Sci. J. Marit. Univ. Szczec. 2019, 55, 34–43. [Google Scholar] [CrossRef]
- Bejger, A.; Drzewieniecki, J.B. The Use of Acoustic Emission to Diagnosis of Fuel Injection Pumps of Marine Diesel Engines. Energies 2019, 12, 4661. [Google Scholar] [CrossRef]
- Siemiątkowski, Z.; Rucki, M.; Lavrynenko, S. Investigations on the modeled shrink-fitted joints of assembled crankshafts. J. Mach. Constr. Maint. 2018, 1, 33–44. [Google Scholar]
- Vijaya Ramnath, B.; Elanchezhian, C.; Jeykrishnan, J.; Ragavendar, R.; Rakesh, P.K.; Dhamodar, J.S.; Danasekar, A. Implementation of Reverse Engineering for Crankshaft Manufacturing Industry. Mater. Today Proc. 2018, 5, 994–999. [Google Scholar] [CrossRef]
- Yamagata, H. The crankshaft. In The Science and Technology of Materials in Automotive Engines; Elsevier: Amsterdam, The Netherlands, 2005; pp. 165–206. [Google Scholar]
- Dunaj, P.; Marchelek, K.; Chodźko, M. Application of the finite element method in the milling process stability diagnosis. J. Theor. Appl. Mech. 2019, 57, 353–367. [Google Scholar] [CrossRef]
- Przetakiewicz, W.; Bryll, K.; Kostecka, E.; Stochła, D.; Staude, M. Application of microscopy in the assesment of porosity in composite casts saturated with silumin. In Materials, Technologies, Constructions. “Special Purpose Materials”; Oficyna Wydawnicza Politechniki Rzeszowskiej: Rzeszów, Poland, 2019; pp. 21–28. [Google Scholar]
- Adamczak, S.; Janecki, D.; Stępień, K. Problems of Mathematical Modelling of Rotary Elements. In Proceedings of the International Symposium for Production Research 2018; Springer International Publishing: Cham, Switzerland, 2019; pp. 747–752. [Google Scholar]
- Janecki, D.; Stępień, K.; Adamczak, S. Investigating methods of mathematical modelling of measurementand analysis of spherical surfaces. In Proceedings of the X International Symposium on Measurement and Quality Control–ISMQC 2010, Osaka, Japan, 5–9 September 2010; pp. 1–4. [Google Scholar]
- PRS. Calculation of Crankshafts for Marine Diesel Engines; Polish Register of Shipping: Gdańsk, Poland, 2012; Volume 8/P. [Google Scholar]
- Trebuňa, P.; Mizerák, M.; Trojan, J.; Rosocha, L. 3D scanning as a modern technology for creating 3D models. Acta Tecnol. 2020, 6, 21–24. [Google Scholar] [CrossRef]
- Wei, G.; Tan, Q. Measurement of shaft diameters by machine vision. Appl. Opt. 2011, 50, 3246. [Google Scholar] [CrossRef] [PubMed]
- Miao, J.; Tan, Q.; Liu, S.; Bao, H.; Li, X. Vision measuring method for the involute profile of a gear shaft. Appl. Opt. 2020, 59, 4183. [Google Scholar] [CrossRef]
- Adamczak, S. Odniesieniowe Metody Pomiaru Zarysów Okrągłości Części Maszyn [Reference Methods for Measuring the Roundness Profiles of Machine Parts]; Kielce University of Technology: Kielce, Poland, 1998. [Google Scholar]
- Janecki, D.; Zwierzchowski, J.; Cedro, L. A problem of optimal cylindricity profile matching. Bull. Polish Acad. Sci. Tech. Sci. 2015, 63, 771–779. [Google Scholar] [CrossRef]
- Taylor Hobson. Talyrond® 2000 A High Precision Large Capacity Roundness System; Taylor Hobson: Berwyn, PA, USA, 2019. [Google Scholar]
- Mahr MarForm. Form Measuring Instruments; Mahr MarForm: Providence, RI, USA, 2020. [Google Scholar]
- Adamczak, S. Pomiary Geometryczne Powierzchni, Zarysy Kształtu, Falistości i Chropowatości; PWN: Warsaw, Poland, 2008. [Google Scholar]
- Carl Zeiss. UPMC CARAT S-ACC. Specifications and Performance Features; Carl Zeiss: Oberkochen, Germany, 2002. [Google Scholar]
- Wenzel Bridge Machines. Available online: https://www.wenzel-group.com/en/product/category/bridge-machines/ (accessed on 17 May 2020).
- ADCOLE 1200: Cylindrical Crankshaft/Camshaft Gage. Available online: https://www.adcole.com/portfolio/1200-cylindrical-crankshaft-camshaft-gage/ (accessed on 24 June 2020).
- Michalski, R.; Wieczorowski, M.; Glazowski, P.; Gapiński, B. Analysis of the Influence of Support During Measurement Using Coordinate Measuring Techniques. Adv. Sci. Technol. Res. J. 2019, 13, 22–29. [Google Scholar] [CrossRef]
- Urey, H.; DeWitt IV, F.A.; Luanava, S. Optical scanners for high-resolution RSD systems. In Proceedings of the SPIE-The International Society for Optical Engineering; Rash, C.E., Reese, C.E., Eds.; SPIE: Bellingham, WA, USA, 2002; Volume 4711, pp. 214–223. [Google Scholar]
- Bernal, C.; de Agustina, B.; Marín, M.M.; Camacho, A.M. Performance Evaluation of Optical Scanner Based on blue LED Structured Light. Procedia Eng. 2013, 63, 591–598. [Google Scholar] [CrossRef]
- Kuş, A. Implementation of 3D Optical Scanning Technology for Automotive Applications. Sensors 2009, 9, 1967–1979. [Google Scholar] [CrossRef]
- GOM ATOS Triple Scan-Industrial Optical 3D Digitizer. Available online: https://www.gom.com/metrology-systems/atos/atos-triple-scan.html (accessed on 17 May 2020).
- Moghtaderi, M. Diesel Engine Crankshaft Deflection Measurement. Available online: https://www.linkedin.com/pulse/diesel-engine-crankshaft-deflection-measurement-mahmoud-moghtaderi/ (accessed on 28 August 2019).
- MAN B&W Diesel A/S. MAN B&W 50-90 MC/MCE Instruction Manual; Works Written by an Organization or a Committee: Copenhagen, Denmark, 2013. [Google Scholar]
- Nozdrzykowski, K.; Chybowski, L.; Dorobczyński, L. Model-Based Estimation of the Reaction Forces in an Elastic System Supporting Large-Size Crankshafts During Measurements of their Geometric Quantities. Measurement 2020, 155, 107543. [Google Scholar] [CrossRef]
- Chybowski, L.; Nozdrzykowski, K.; Grządziel, Z.; Dorobczyński, L. Evaluation of Model-based Control of Reaction Forces at the Supports of Large-size Crankshafts. Sensors 2020, 20, 2654. [Google Scholar] [CrossRef]
- Leontopoulos, C.; Davies, P.; Park, K.R. Shaft alignment analysis: Solving the reverse problem. Proc. Inst. Mar. Eng. Sci. Technol. Part B J. Mar. Des. Oper. 2005, 8B, 3–12. [Google Scholar]
- Tiwari, R.; Lees, A.W.; Friswell, M.I. Identification of dynamic bearing parameters: A review. Shock Vib. Dig. 2004, 36, 99–124. [Google Scholar] [CrossRef]
- Lees, A.W. Vibration Problems in Machines Diagnosis and Resolution; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Friswell, M.I.; Mottershead, J.E. Finite Element Model Updating in Structural Dynamics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Hirdaris, S.E.; Lees, A.W. A conforming unified finite element formulation for the vibration of thick beams and frames. Int. J. Numer. Methods Eng. 2005, 62, 579–599. [Google Scholar] [CrossRef]
- Yu, B.Y.; Feng, Q.K.; Yu, X.L. Modal and vibration analysis of reciprocating compressor crankshaft system. In 7th International Conference on Compressors and their Systems 2011; Elsevier: Amsterdam, The Netherlands, 2011; pp. 295–303. [Google Scholar]
- Bejger, A.; Chybowski, L.; Gawdzińska, K. Utilising elastic waves of acoustic emission to assess the condition of spray nozzles in a marine diesel engine. J. Mar. Eng. Technol. 2018. [Google Scholar] [CrossRef]
- Mourelatos, Z.P. A crankshaft system model for structural dynamic analysis of internal combustion engines. Comput. Struct. 2001, 79, 2009–2027. [Google Scholar] [CrossRef]
- Tsitsilonis, K.; Mavrelos, C.; Stefanidis, F.; Gad, A.; Timmerman, M. Concept Design Considerations for the Next Generation of Mega-Ships. In Proceedings of the 13th International Marine Design Conference (IMDC 2018); Taylor & Francis: Boca Raton, FL, Poland, 2018; pp. 579–588. [Google Scholar]
- Tsitsilonis, K.-M.; Theotokatos, G.; Xiros, N.; Habens, M. Systematic Investigation of a Large Two-Stroke Engine Crankshaft Dynamics Model. Energies 2020, 13, 2486. [Google Scholar] [CrossRef]
- Arnulfi, G.L.; Blanchini, F.; Giannattasio, P.; Micheli, D.; Pinamonti, P. Extensive study on the control of centrifugal compressor surge. Proc. Inst. Mech. Eng. Part A J. Power Energy 2006, 220, 289–304. [Google Scholar] [CrossRef]
- Nozdrzykowski, K.; Grządziel, Z.; Harušinec, J. Determining and Analysing Support Conditions at Variable Construction of Crankshafts. New Trends Prod. Eng. 2018, 1, 553–560. [Google Scholar] [CrossRef][Green Version]






| Method | Measurement Technique | Fixing | Additional Support | Plane of the Shaft Axis | Measurement System Parameters | Support Conditions | Engine Type | |
|---|---|---|---|---|---|---|---|---|
| Non-reference | – in a device with centers | centers | none | horizontal | none | uncontrolled | high speed | |
| – in a device | with a rotary table | – centers – chuck – directly on a table | vertical | high speed, medium speed | ||||
| with a rotary spindle | ||||||||
| – using a measurement system with controlled reaction forces at the support | by external faces, in centers | Multi-point, on supports/vee blocks | horizontal | α, γ, φ, l1, L | monitored | medium speed low speed | ||
| Reference | - using vee blocks | in 2 vee blocks | none | horizontal | none | uncontrolled indirect control by measuring the deformation of crank webs (springing measurement) | high speed, medium speed | |
| in 4 vee blocks | selectively | medium speed | ||||||
| in n vee blocks | multi-point | low speed | ||||||
| – with a measurement system with controlled reaction forces at the support | by outermost external main journals in vee blocks | Multi-point, on flexible supports | horizontal | α, γ, φ, l1, L | monitored | medium speed low speed | ||
| Others | - coordinate measuring technique - using measurement arms | in 2 vee blocks | none | horizontal | none | uncontrolled | high speed | |
| in 4 vee blocks | selectively | medium speed | ||||||
| in n vee blocks | multi-point | low speed | ||||||
| – scanning, – photometry | in n vee blocks | multi-point | low speed | |||||
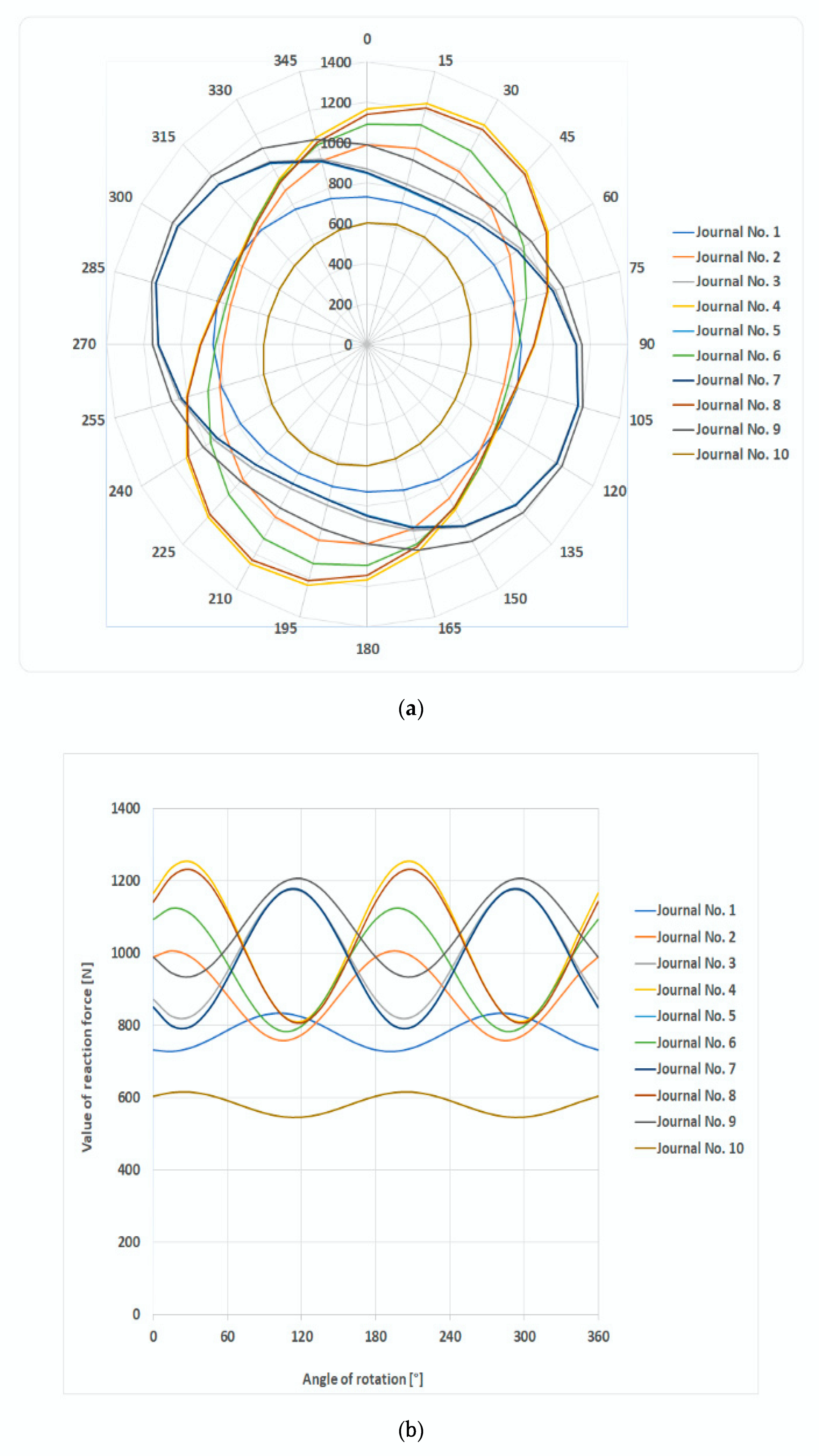
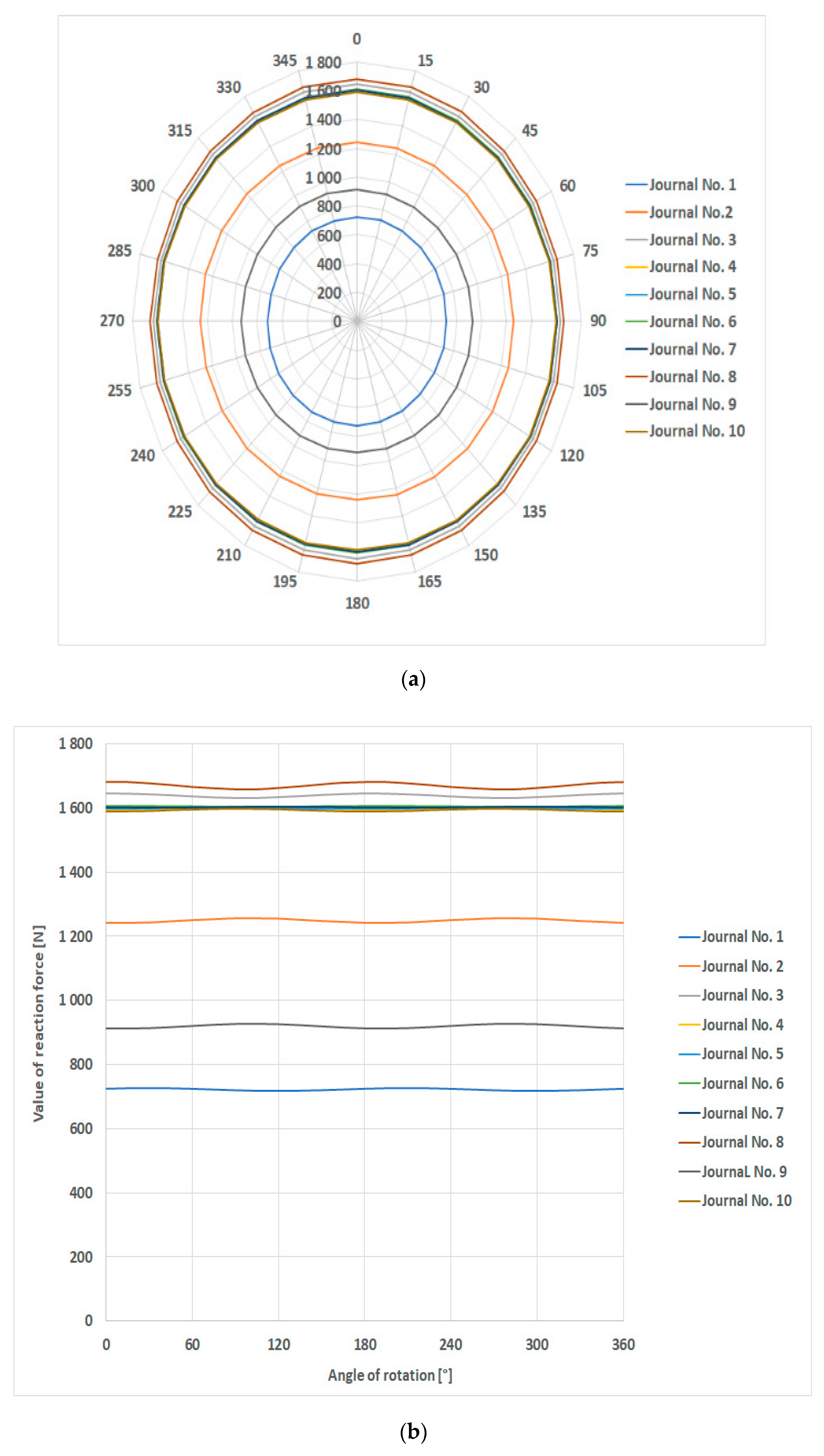
| Angular Position (°CA) | Main Journal Number (-) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Reaction Forces in Main Journals (N) | ||||||||||
| 0 | 731.62 | 988.50 | 871.12 | 1166.33 | 847.89 | 1093.01 | 852.04 | 1142.22 | 988.15 | 603.47 |
| 15 | 727.48 | 1005.43 | 823.76 | 1237.24 | 796.42 | 1123.70 | 799.74 | 1212.93 | 944.12 | 613.51 |
| 30 | 737.46 | 989.14 | 822.94 | 1253.23 | 795.30 | 1108.89 | 797.22 | 1231.62 | 933.95 | 614.59 |
| 45 | 758.88 | 943.98 | 868.88 | 1210.01 | 844.82 | 1052.54 | 845.15 | 1193.29 | 960.37 | 606.42 |
| 60 | 786.00 | 882.05 | 949.28 | 1119.16 | 931.72 | 969.75 | 930.69 | 1108.20 | 1016.30 | 591.19 |
| 75 | 811.57 | 819.94 | 1042.60 | 1005.03 | 1032.70 | 882.71 | 1030.91 | 999.16 | 1086.75 | 572.98 |
| 90 | 828.72 | 774.30 | 1123.82 | 898.19 | 1120.71 | 814.74 | 1118.97 | 895.38 | 1152.84 | 556.67 |
| 105 | 832.87 | 757.35 | 1171.18 | 827.29 | 1172.17 | 784.05 | 1171.26 | 824.67 | 1196.87 | 546.62 |
| 120 | 822.89 | 773.65 | 1172.00 | 811.30 | 1173.29 | 798.87 | 1173.78 | 805.98 | 1207.04 | 545.54 |
| 135 | 801.47 | 818.82 | 1126.05 | 854.53 | 1123.77 | 855.22 | 1125.85 | 844.31 | 1180.62 | 553.71 |
| 150 | 774.33 | 880.76 | 1045.65 | 945.37 | 1036.88 | 938.00 | 1040.31 | 929.40 | 1124.69 | 568.94 |
| 165 | 748.76 | 942.87 | 952.34 | 1059.50 | 935.90 | 1025.04 | 940.09 | 1038.44 | 1054.24 | 587.16 |
| 180 | 731.62 | 988.50 | 871.12 | 1166.33 | 847.89 | 1093.01 | 852.04 | 1142.22 | 988.15 | 603.47 |
| 195 | 727.48 | 1005.43 | 823.76 | 1237.24 | 796.42 | 1123.70 | 799.74 | 1212.93 | 944.12 | 613.51 |
| 210 | 737.46 | 989.14 | 822.94 | 1253.23 | 795.30 | 1108.89 | 797.22 | 1231.62 | 933.95 | 614.59 |
| 225 | 758.88 | 943.98 | 868.88 | 1210.01 | 844.82 | 1052.54 | 845.15 | 1193.29 | 960.37 | 606.42 |
| 240 | 786.00 | 882.05 | 949.28 | 1119.16 | 931.72 | 969.75 | 930.69 | 1108.20 | 1016.30 | 591.19 |
| 255 | 811.57 | 819.94 | 1042.60 | 1005.03 | 1032.70 | 882.71 | 1030.91 | 999.16 | 1086.75 | 572.98 |
| 270 | 828.72 | 774.30 | 1123.82 | 898.19 | 1120.71 | 814.74 | 1118.97 | 895.38 | 1152.84 | 556.67 |
| 285 | 832.87 | 757.35 | 1171.19 | 827.29 | 1172.17 | 784.05 | 1171.26 | 824.67 | 1196.87 | 546.62 |
| 300 | 822.89 | 773.65 | 1172.00 | 811.30 | 1173.29 | 798.87 | 1173.78 | 805.98 | 1207.04 | 545.54 |
| 315 | 801.47 | 818.82 | 1126.05 | 854.53 | 1123.77 | 855.22 | 1125.85 | 844.31 | 1180.62 | 553.71 |
| 330 | 774.33 | 880.76 | 1045.65 | 945.37 | 1036.88 | 938.00 | 1040.31 | 929.40 | 1124.69 | 568.94 |
| 345 | 748.76 | 942.86 | 952.34 | 1059.50 | 935.90 | 1025.04 | 940.09 | 1038.44 | 1054.24 | 587.16 |
| 360 | 731.62 | 988.50 | 871.12 | 1166.33 | 847.89 | 1093.01 | 852.04 | 1142.22 | 988.15 | 603.47 |
| Angular Position (°CA) | Main Journal Number (-) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Reaction Forces in Main Journals (N) | ||||||||||
| 0 | 724.00 | 1241.00 | 1645.00 | 1595.00 | 1601.00 | 1607.00 | 1603.00 | 1589.00 | 1680.00 | 913.00 |
| 15 | 725.60 | 1241.00 | 1644.00 | 1595.00 | 1601.00 | 1607.00 | 1603.00 | 1590.00 | 1680.00 | 912.40 |
| 30 | 726.10 | 1242.00 | 1642.00 | 1596.00 | 1601.00 | 1607.00 | 1602.00 | 1591.00 | 1676.00 | 913.70 |
| 45 | 725.40 | 1246.00 | 1639.00 | 1597.00 | 1602.00 | 1606.00 | 1602.00 | 1594.00 | 1671.00 | 916.60 |
| 60 | 723.80 | 1250.00 | 1635.00 | 1598.00 | 1602.00 | 1606.00 | 1603.00 | 1596.00 | 1665.00 | 920.30 |
| 75 | 721.60 | 1253.00 | 1632.00 | 1599.00 | 1602.00 | 1605.00 | 1603.00 | 1598.00 | 1661.00 | 923.90 |
| 90 | 719.50 | 1256.00 | 1630.00 | 1600.00 | 1602.00 | 1605.00 | 1604.00 | 1599.00 | 1658.00 | 926.30 |
| 105 | 717.90 | 1256.00 | 1630.00 | 1600.00 | 1602.00 | 1605.00 | 1605.00 | 1598.00 | 1658.00 | 926.90 |
| 120 | 717.40 | 1255.00 | 1633.00 | 1599.00 | 1602.00 | 1605.00 | 1605.00 | 1597.00 | 1662.00 | 925.60 |
| 135 | 718.10 | 1251.00 | 1636.00 | 1598.00 | 1601.00 | 1605.00 | 1605.00 | 1594.00 | 1667.00 | 922.70 |
| 150 | 719.70 | 1247.00 | 1640.00 | 1597.00 | 1601.00 | 1606.00 | 1605.00 | 1592.00 | 1673.00 | 919.00 |
| 165 | 721.90 | 1244.00 | 1643.00 | 1596.00 | 1601.00 | 1606.00 | 1604.00 | 1590.00 | 1678.00 | 915.40 |
| 180 | 724.00 | 1241.00 | 1645.00 | 1595.00 | 1601.00 | 1607.00 | 1603.00 | 1589.00 | 1680.00 | 913.00 |
| 195 | 725.60 | 1241.00 | 1644.00 | 1595.00 | 1601.00 | 1607.00 | 1603.00 | 1590.00 | 1680.00 | 912.40 |
| 210 | 726.10 | 1242.00 | 1642.00 | 1596.00 | 1601.00 | 1607.00 | 1602.00 | 1591.00 | 1676.00 | 913.70 |
| 225 | 725.40 | 1246.00 | 1639.00 | 1597.00 | 1602.00 | 1606.00 | 1602.00 | 1594.00 | 1671.00 | 916.60 |
| 240 | 723.80 | 1250.00 | 1635.00 | 1598.00 | 1602.00 | 1606.00 | 1603.00 | 1596.00 | 1665.00 | 920.30 |
| 255 | 721.60 | 1253.00 | 1632.00 | 1599.00 | 1602.00 | 1605.00 | 1603.00 | 1598.00 | 1661.00 | 923.90 |
| 270 | 719.50 | 1256.00 | 1630.00 | 1600.00 | 1602.00 | 1605.00 | 1604.00 | 1599.00 | 1658.00 | 926.30 |
| 285 | 717.90 | 1256.00 | 1630.00 | 1600.00 | 1602.00 | 1605.00 | 1605.00 | 1598.00 | 1658.00 | 926.90 |
| 300 | 717.40 | 1255.00 | 1633.00 | 1599.00 | 1602.00 | 1605.00 | 1605.00 | 1597.00 | 1662.00 | 925.60 |
| 315 | 718.10 | 1251.00 | 1636.00 | 1598.00 | 1601.00 | 1605.00 | 1605.00 | 1594.00 | 1667.00 | 922.70 |
| 330 | 719.70 | 1247.00 | 1640.00 | 1597.00 | 1601.00 | 1606.00 | 1605.00 | 1592.00 | 1673.00 | 919.00 |
| 345 | 721.90 | 1244.00 | 1643.00 | 1596.00 | 1601.00 | 1606.00 | 1604.00 | 1590.00 | 1678.00 | 915.40 |
| 360 | 724.00 | 1241.00 | 1645.00 | 1595.00 | 1601.00 | 1607.00 | 1603.00 | 1589.00 | 1680.00 | 913.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chybowski, L.; Nozdrzykowski, K.; Grządziel, Z.; Jakubowski, A.; Przetakiewicz, W. Method to Increase the Accuracy of Large Crankshaft Geometry Measurements Using Counterweights to Minimize Elastic Deformations. Appl. Sci. 2020, 10, 4722. https://doi.org/10.3390/app10144722
Chybowski L, Nozdrzykowski K, Grządziel Z, Jakubowski A, Przetakiewicz W. Method to Increase the Accuracy of Large Crankshaft Geometry Measurements Using Counterweights to Minimize Elastic Deformations. Applied Sciences. 2020; 10(14):4722. https://doi.org/10.3390/app10144722
Chicago/Turabian StyleChybowski, Leszek, Krzysztof Nozdrzykowski, Zenon Grządziel, Andrzej Jakubowski, and Wojciech Przetakiewicz. 2020. "Method to Increase the Accuracy of Large Crankshaft Geometry Measurements Using Counterweights to Minimize Elastic Deformations" Applied Sciences 10, no. 14: 4722. https://doi.org/10.3390/app10144722
APA StyleChybowski, L., Nozdrzykowski, K., Grządziel, Z., Jakubowski, A., & Przetakiewicz, W. (2020). Method to Increase the Accuracy of Large Crankshaft Geometry Measurements Using Counterweights to Minimize Elastic Deformations. Applied Sciences, 10(14), 4722. https://doi.org/10.3390/app10144722







